物性效应模型 第二讲
第二讲 面板数据线性回归模型
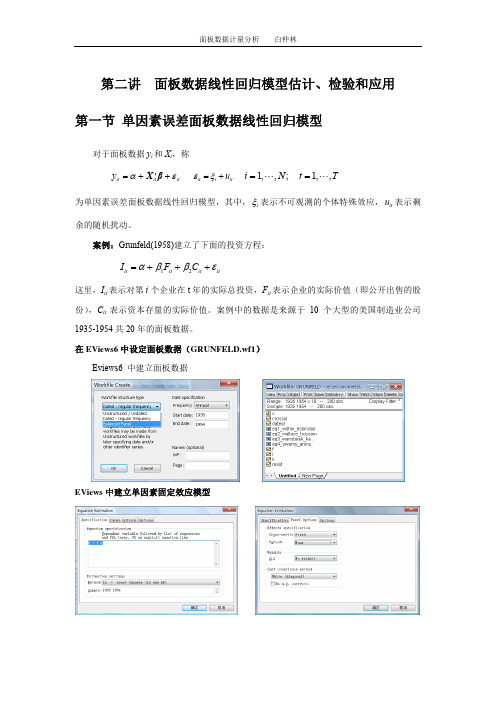
第二讲 面板数据线性回归模型估计、检验和应用 第一节 单因素误差面板数据线性回归模型对于面板数据y i 和X i ,称it it it y αε′=++X βit i it u εξ=+ 1,,;1,,i N t T ==""为单因素误差面板数据线性回归模型,其中,i ξ表示不可观测的个体特殊效应,it u 表示剩余的随机扰动。
案例:Grunfeld(1958)建立了下面的投资方程:12it it it it I F C αββε=+++这里,I it 表示对第i 个企业在t 年的实际总投资,F it 表示企业的实际价值(即公开出售的股份),C it 表示资本存量的实际价值。
案例中的数据是来源于10个大型的美国制造业公司1935-1954共20年的面板数据。
在EViews6中设定面板数据(GRUNFELD.wf1)Eviews6 中建立面板数据EViews 中建立单因素固定效应模型1.1 混合回归模型1 面板数据混合回归模型 假设1 ε ~ N (0, σ2I NT )对于面板数据y i 和X i ,无约束的线性回归模型是y i = Z i δi + εi i =1, 2, … , N(4.1)其中'i y = ( y i 1, … , y iT ),Z i = [ ιT , X i ]并且X i 是T×K 的,'i δ是1×(K +1)的,εi 是T×1的。
注意:各个体的回归系数δi 是不同的。
如果面板数据可混合,则得到有约束模型y = Z δ + ε(4.2)其中Z ′ = ('1Z ,'2Z , … ,'N Z ),u ′ = ('1ε,'2ε, … ,'N ε)。
2 混合回归模型的估计当满足可混合回归假设时,()1''ˆZ Z Z Y −=δ在假设1下,对于Grunfeld 数据,基于EViews6建立的混合回归模型3 面板数据的可混合性检验假设检验原理:基于OLS/ML 估计,对约束条件的检验。
第四讲物性效应模型

约定一次效应;
注:若描述大于二次效应,需增加节点层数。
麦克斯韦关系式在模型中的呈现规律:
12x11-6)
六种能量间物性效应模型
仅取 E T, 则为Heckmamn模型; 仅取 E,T k 则为Thurston模型; 仅取 ET,H则为4种能量间物性模型;
1)晶体六种能量关系式 晶体热力学中,吉布斯自由能
G * U S * T iS j E k D l H m B n K 0 p P q V r
任一参量是其余五个参数的函数
物性效应模型
简化:突出主效应,确定物理条件和边界条件。如:绝
热(等温等熵)时,机电效应模型变成TSDE梯型。
四个参数中任一参数是其他三个量的函数。
物性效应模型
若设定边界条件,本构方程中一个因变量只有两 个自变量相对应。
机 械 自 由 S = s E T + d ' E
交叉效应: D T E S, D S E *, S S T*
平行效应: D S T E , S D * E , S S * T
两种能量之间的耦合:(15种)
交叉效应系数相等,平行效应的系数互为倒数 且符号相反。
六种能量之间:每一物性量(广义力和广义位移) 与其它量之间的本构关系,一级近似可写为:
四种能量间的物性效应新模型
晶体力学能量矢量方程:
GUS*TiSjEkD l HmBn
(i,j1,2, 6;k,l1,2,3;m,n1,2,3)
G:可做功的吉布斯自由能; U:物质内能; S * 热能; TS:机械能;ED:电能;HB:磁能
光子自旋霍尔效应及其在物性参数测量中的应用

第42卷第2期2022年4月物理学进展PROGRESS IN PHYSICSVol.42No.2Apr.2022光子自旋霍尔效应及其在物性参数测量中的应用刘硕卿,陈世祯,罗海陆∗湖南大学物理与微电子科学学院自旋光子学实验室,湖南大学,长沙410082摘要:光子自旋霍尔效应是指光束在非均匀介质中传输时,自旋角动量相反的光子在垂直于入射面的方向发生的横向自旋相关分裂。
光子自旋霍尔效应可以和电子自旋霍尔效应作类比:自旋光子扮演自旋电子的角色,折射率梯度扮演外场的角色。
光子自旋霍尔效应源于光的自旋-轨道相互作用,和两类几何相位有关:一类是动量空间的自旋重定向Rytov-Vlasimirskii-Berry相位;另一类是斯托克斯参数空间的Pancharatnam-Berry相位。
光子自旋霍尔效应对物性参数非常敏感,结合量子弱测量技术,在物性参数测量、光学传感等领域具有重要的应用前景。
本文将简单分析光子自旋霍尔效应的物理根源,回顾近几年不同物理系统中光子自旋霍尔效应的研究进展,介绍光子自旋霍尔效应在物性参数测量中的应用。
最后,展望其在光学模拟运算、显微成像、量子成像等领域的可能发展方向。
关键词:光子自旋霍尔效应;光的自旋-轨道相互作用;几何相位;量子弱测量中图分类号:O436.3文献标识码:A DOI:10.13725/ki.pip.2022.02.001目录I.引言35II.光子自旋霍尔效应36A.自旋-轨道相互作用与几何相位361.光的自旋-轨道相互作用362.RVB相位与PB相位37B.RVB相位导致的光子自旋霍尔效应39C.PB相位导致的光子自旋霍尔效应40III.光子自旋霍尔效应的弱测量41A.量子弱测量41B.光子自旋霍尔效应的弱测量421.RVB相致光子自旋霍尔效应的弱测量422.PB相致光子自旋霍尔效应的弱测量43IV.基于光子自旋霍尔效应的物性参数测量44A.纳米金属薄膜结构与拓扑材料参数的精密测量44B.二维原子晶体结构参数的精密测量45C.化学溶液和生物分子的超灵敏传感应用46 V.总结与展望48致谢49参考文献49收稿日期:2021-01-15∗E-mail:I.引言早在1879年,美国科学家霍尔(Edwin Hall)就通过实验发现,当电流沿垂直外磁场的方向通过导体时,运动的载流子由于受到洛伦兹力的作用,会在导体两侧形成电势差,这一经典现象被称为霍尔效应(Hall effect)[1]。
物性讲义(磁性2)

取决于材料的磁导率。
磁导率是软磁材料的重要磁参量 最常用的是起始磁导率和最大磁导率
13
起始磁导率
(1) 考虑掺杂物的影响
相当于磁化曲线起始点的斜率 与可逆壁移阶段畴壁位移的难 易程度有关
2 μ 0MS 1 2 4π 2/3 μi R ( ) 3β 3a A1K1 d
a:掺杂物间距
R:掺杂物半径 A1:与交换积分常数A相关的常数 K1:磁晶各向异性常数 d:180°畴宽 :掺杂物体积百分数
1 n M r M S Vi cosθ i V 1
磁化各阶段的磁矩角分布的二维矢量模型
V:样品总体积 Vi:第i个晶粒的体积 i:第i个晶粒的MS方向与外磁场的夹角
剩磁是组织敏感参量 对晶体取向和畴结构十分敏感。Mr主要取决于MS 和i角,为获得高剩磁,首先应选高MS的材料, i角主要决定于晶粒的 取向与畴结构,通常用获得晶体织构或畴织构的办法来提高剩磁。
24
多晶体的矫顽力是各个晶粒的矫 顽力的平均效应值 其反磁化曲线应是各个晶粒的反 磁化曲线的综合反映
畴壁能密度梯度的最大值(
dγ ω ) max dx
与铁磁体的内应力、掺杂物和缺 陷的大小、数量与分布有密切的 关系
25
矫顽力的应力理论
铁磁体内部的应力阻碍畴壁运动
材料内部周期性分布的内应力对180°畴壁位移的公式:
若交换作用弱,在不高的温度下,原子热运动就破坏了原子 磁矩的规则排列,所以居里温度很低。
稀土金属即如此。
居里温度是内禀特性,主要取决于合金的成分。
合金居里点随成分的变化:
TC( 合金 ) TC(溶剂) (
dTC( 合金 ) dC
)C
12
C:溶质原子百分数
纳米效应.ppt

纳米微粒的表面原子数增多,比表面积大, 原子配位不足,表面原子的配位不饱和导 致大量的悬空键和不饱和键,表面能高, 使这些表面原子具有高的活性,极不稳定, 很容易与其他原子结合
特殊的光学性
黄金被细分到小于光波波长的尺寸时,即 失去了原有的富贵光泽而呈黑色。事实上,所 有的金属在超微颗粒状态都呈现为黑色。尺寸 越小,颜色愈黑,银白色的铂(白金)变成铂 黑,金属铬变成铬黑。金属超微颗粒对光的反 射率很低,通常可低于l%,大约几微米的厚度 就能完全消光
利用这个特性可以作为高效率的光热、光 电等转换材料,可以高效率地将太阳能转变为 热能、电能
美国学者报道氟化钙纳米材料在室温下可以大幅度弯 曲而不断裂。研究表明,人的牙齿之所以具有很高的 强度,是因为它是由磷酸钙等纳米材料构成的。呈纳 米晶粒的金属要比传统的粗晶粒金属硬3~5倍
三、量子尺寸效应
能带理论表明,金属费米能级附近电子能级一 般是连续的,这一点只有在高温或宏观尺寸情 况下才成立
小尺寸效应
表面效应
量子尺寸效应
宏观量子隧道效应
一、表面效应
表面效应是指纳米粒子的表面原子数与总原子 数之比随粒径的变小而急剧增大后所引起的性 质上的变化
纳米微粒尺寸小,表面能高,位于表面的原子 占相当大的比例。随着粒径减小,表面原子百 分数迅速增加
图3-1 表面原子数与粒径的关系
小尺寸的超微颗粒磁性与大块材料显著的不同,大块的纯 铁矫顽力约为 80安/米,而当颗粒尺寸减小到 2×10-2微 米以下时,其矫顽力可增加1千倍,若进一步减小其尺寸, 大约小于 6 × 10-3微米时,其矫顽力反而降低到零,呈现 出超顺磁性
岩石热物性参数分析及多场热效应耦合模型研究

岩石热物性参数分析及多场热效应耦合模型研究近年来,随着全球能源危机和环境问题的日益加剧,对可再生能源的开发利用迫在眉睫。
地热能具有绿色、连续、稳定、利用效率高等诸多优点,利用前景十分广阔,预计将会成为未来能源格局中重要组成部分。
除了被直接利用,发电和供热也是地热能的两种主要利用方法。
由于地热能有许多优点,它在缓解能源危机和提高生态环境方面扮演着越来越重要的作用。
干热岩(Hot Dry Rock,HDR)是一种新型的地热资源,由于其广泛的分布和巨大的储量引起了人们的关注,它是指地下高温但由于低孔隙度和渗透性而缺少流体的岩体,主要是各种变质岩或结晶岩类岩体,储存于干热岩中的热量需要通过人工压裂等技术形成增强型地热系统(Enhanced Geothermal System,EGS)才能得以开采。
EGS工程的概念就是通过注入井将冷水注入到目标储层,然后通过生产井提取热水用以发电,从而达到开发干热岩热量的目的。
EGS是一个复杂的系统工程,在这个过程中存在很多科学问题和工程问题,如资源靶区定位技术,人工压裂,微地震、示踪剂等监控监测技术,资源评价方法,地热地质模型,地下高温岩体的多场耦合过程,地热介质的换热特性机制,能源转换效率评价,发电系统高效利用,示范场地建设。
随着中国经济的快速发展以及节约能源、减少污染物排放的需要,目前存在的能源结构不再符合国内形势的要求,发展与利用可再生能源已经成为全社会的共识。
而地热资源在缓解能源供应压力和提升经济环境方面可以发挥重要的作用,中国作为能源消耗大国,需要大力开发地热资源和发展地热能技术,特别是干热岩。
由于干热岩属于新型地热资源,目前世界上还没有形成一套成熟理论对其进行开发利用,距离大范围推广还有很长的一段时间。
而中国在干热岩的开发研究方面正处于起步阶段,需要大量的理论研究、室内实验和现场试验,如热物性、物理力学参数的确定,储层改造及评价,水热交换及能量转换效率,地下高温岩体的多场耦合过程等。
聚合物系的物性(共103张PPT)
❖剪切速率小时,大分子不取向或取向甚微,呈牛顿性.
❖剪切速率渐增,大分子随剪切速率逐步取向,显示假 塑性.
❖剪切速率很高时,大分子来不及取向,或已充分取向,
流体黏度不再随剪切速率变化,流体又表现出牛顿性.
工业聚合反应装置
第29页,共103页。
江苏大学材料学院
0 0, Const,
牙膏、泥浆、 血浆等
n 1
顿 假塑性
橡胶、油漆、
流 流体 体 胀塑性
0 0, 0,
n1
尼龙等 生面团、浓
流体
淀粉糊
0 0, 0,
工业聚合反应装置
第23页,共103页。
n 1 江苏大学材料学院
非牛顿流体实例
牛顿流体( Newtonian fluid) 气体、水、酒、醋、低浓度牛乳、油等
江苏26大学材料学院
聚合物的粘性流动
h0
第一牛顿区
幂律区(假塑区)
工业聚合反应装置
第27页,共103页。
h
第二牛顿区
江苏27大学材料学院
实际聚合物熔体分三个区域 (缠结理论)
1、第一牛顿区 低切变速率,曲线的斜率n=1,符合牛顿流动定律。该区的粘度通 常称为零切粘度h,即切变速率的粘度。低剪切速率时,缠结与 解缠结速率处于一个动态平衡,表观粘度保持恒定,类似牛顿流体。
剪切应力与剪切速率之间的关系服从牛顿黏 性定律的流体,称为牛顿流体。
剪
切
应
力
•
τ
剪切速率
•
工业聚合反应装置
第15页,共103页。
江苏大学材料学院
牛顿流体 流动曲线实例 (Newtonian Fluids)
, 0.1 Pa
100
物料的光学特性第二章
式中各粘弹系数的计算结果列于表
2)在改善产品品质方面的应用
鱼糕是将鱼肉磨成糊后摊在木板上蒸熟而 成的一种日本食品。为研究鱼糕的流变特性, 把鱼糕切成长条作拉伸试验或切成方块形作压 缩试验。
试验结果表明,鱼糕的拉伸或压缩应变与时
间的关系曲线可用伯格斯模型加以解释,并根据 这些曲线计算弹性模量和粘性系数。用这种方法 对公认的“优质鱼糕”和“劣质鱼糕”进行实验 确立了“优质鱼糕模型”和“劣质鱼糕模型”。
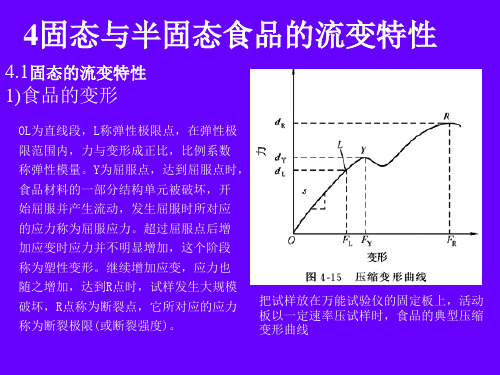
3种类型:①受正应力作用产生的轴向应变;⑦受表面压 力作用的体积应变;③受剪切应力作用发生的剪切应变。
(1)弹性模量(杨氏模量)
物体受正应力作用,产生轴向的变 形称拉伸(或压缩)变形,表示拉伸 变形的弹性模量也称作杨氏模量 σn=F/A εn=d/L σn=E·εn
比例系数E称弹性模量(杨氏模量),单位是N/m2
(3)滑块模型
滑块模型虽不能独立地用来表 示某种流变性质,但常与其他
流变元件组合,表示有屈服应 力存在的塑性流体性质。滑块 模型亦称为“摩擦片”、“文思 特滑片”。
2)麦克斯韦模型
由一个弹簧和一个阻尼器串 联组成,这是最早提出的粘弹模 型。这一模型可以用来形象地反 映应力松弛过程。 当模型一端受力而被拉伸一定 长度时,由于弹簧可在刹那间变 形,而阻尼器由于粘性作用来不 及移动,弹簧首先被拉开,然后 在弹簧恢复力作用下,阻尼器粘 性起作用,随时间的增加而逐渐 被拉开,弹簧受到的拉力也逐渐 减小,直到零。这就类似于应力 松弛过程。
蠕变:蠕变和应力松弛相反。蠕变是指把一定大小的力(应力)
施加于粘弹性体时,物体的变形(应变)随时间的变化而逐渐 增加的现象。要注意,蠕变是以一定大小的应力为条件的。
(2)曳丝性
当筷子插入其中,再提起时,会观察到一部分液体 被拉起形成丝状,把这种现象称为曳丝性,具有曳丝 性的液体,分子之间存在着一定的结合,形成了弱的 网络结构。曳丝性是黏性与弹性双重性质的表现。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
L = T −V
等效电路法
哈密尔顿原理:
形式紧凑,适用广泛 磁、热系统中仅定义一个哈密尔顿变量, 线性等效动量无用。 无法用直观现象描述热、磁动量,且储 能耗能表达充分 压力动量Г :流量横截面积比(流速)
等效电路法
广义位移和广义动量: 广义位移:对时间微分后成为流变量, 位移、角位移、电荷、磁通流、体积、 熵 广义动量:对时间微分后成为势变量, 动量、角动量、磁通匝连数、压力动量
等效电路法
统一模型:等效量概念(不同的能量域) 功率变量:相乘即得该能量域功率的变量 (易测量:力,速度) 哈密尔顿变量:能量变量,一致变量 (对时间微分即得功率变量)
等效电路法
标准的功率变量: 刚体运动:力F,速度V 刚体转动:力矩 ,角速度 Ω 电路:电势e,电流i 磁场:磁势M,磁流变化率 dφ dt * 不太象 流体:压力P,流速Q 热运动:温度T,熵变化率 ds dt * 不能直接 测量,但是与功率相关,更重要
1端口元件及建模
确定主要物理现象的代表元件 建立元件连接模型
(结果有不确定性) 无严格规定,一般分四步 ①把物理系统分成若干物理现象 ②确定主要现象对应物理元件,忽略次要部分 ③对未定义成理想元件的现象,用数学规律对现 象进行描述 ④根据数学表达式定义成组成系统的理想元件
1端口元件及建模
理想1端口元件
被动1端口元件:※ 存储能量,多数能 量域中可分为2种形式,机械系统:动能 和势能。 ※耗散能量 三种被动1端口元件: ①广义惯性元件,存储广义上的动能 ②广义容性元件,存储广义势能 ③广义阻尼,转换成不能用于工作的能量
理想1端口元件
对广义惯量元件: f = g ( p ) 机械:质量;电:电感; ε 存储能量: = ∫ dtef = ∫ fdp
理想1端口元件
热端口变量:(不用温度或熵流率),温度与热流率 但是:端口变量不再是功率变量,因热流率本身有功率单 位。与系统建模发展相背,但可用1端口元件描述。 采用2端口元件模型,但描述还是类似的: 热能的存储→能通过接触而实现升温,如沸水加热鸡蛋, 水中存储能量,为势,类似为机、电中的容性元件 没有其他方法存储热能,热系统中没有与质量或电感的等 效量,热动量变量没有定义 热系统中的阻尼仍然具有不可逆转性,在机电系统中阻尼 实际是向环境散热,热系统中考虑热行为,分为:执行能 量和不可逆的非执行能量,如容性储能或阻尼(例如热绝 缘子)
等效电路法
哈密尔顿函数: ∫ Ldt = 0 δ
t1 t2
: 拉格朗日函数 T:动能;V势能 哈密尔顿原理:拉格朗日函数从时刻t1到t2的时 间积分的变分等于零。即:受理想约束的保守 力学系统从t1时刻的某一位形转移到t2时刻的 另一位形的一切可能的运动中,实际发生的运 动使系统的拉格朗日函数在该时间区间上的定 积分取驻值,大多取极小值。
理想1端口元件
主动1端口元件:源(source)或穴(sink), 与环境实现能量交换 理想流源(穴):端口的流变量与其势无关 (类似恒流源) 理想势源(穴):端口的势变量与其流无关 (类似恒压源) *实际的源和理想1端口元件不可能一样,实际上 的源总工作在有限能量下,流源提高势,势源 增大流→必影响其输出。
τ
等效电路法
历史上的三种较经典的等效方法: 1. Firestone 又称迁移率模拟(mobility analogy) 1933 V、Ω、Q 和e 模拟等效 F、τ、p 和i 等效 (当时未包含热、磁 ) 电阻抗(电压电流之比)等效机械或流体 中的易变性为而不是机械阻抗
等效电路法
2. 通过型和跨接型模拟( Through and Across Analogy)Trent,1955 V、Ω、 p 和e 模拟等效(跨接型等效量) F、τ、 Q 和i 等效(通过型等效量)
等效电路模型
用势分析:忽略弹簧质量,k、b受力相等 速度不同
V, V-V1,V1
阻尼速度 V = (V − V1 ) + V1 弹簧速度 V − V1 节点流之和为零
流体 等效电路模型
体积流:串联,T型网络
阀:纯阻 单端口元件 管:惯性 水箱:电容,存贮势能
等效电路模型---射钉枪
理想1端口元件
流体阻尼:类似机械中的阻尼,导致压力损失 与机械中类似,一般不用线性方程表达。 热系统:用两个独立变量描述而非一个,1端口元件模 型不适用,采用2端口元件模型(多端口能量模型) 如:压力和温度作为独立变量,能量的存储或损失用这 两个量来描述 (前述机械、电、流体中均仅用一个变量描述) 需用两个端口描述:①温度和熵流率作为功率变量 ②压力和体积流率作为功率变量 也有过用1端口描述的尝试:如Karnopp(1990)
等效电路模型
等效电路:清晰明了,便于确定等效电量进行 测量、仿真。 电路中:kirchhoff定律:闭环电压为零,节 点进出电流相等,串联等电流,并联等电压 非电系统中:广义kirchhoff定律:势、流
闭环势之和为零 节点流之和为零
等效电路模型
质量m、弹簧k、阻尼b :同样速度v(流) 串联: v(流)相等,力源:各势之和
等效电路法
本课程:扩展的Maxwell等效 (扩展阻抗模拟) 包括:热、磁 磁势、温度→势变量 磁流变化率,熵变化率→流变量 ds V、 Q 、Ω 、 I、dφ dt 、 dt :流变量 F、τ、 p 、 e、 M 、 T :势变量
等效电路法
Maxwell等效分析法的优势: 机械、流体和电气中的阻抗全等效 刚体受力与流体受力等效 刚体质量与电路等效时与速度的相对基 准无关。Trent 和Firestone 模拟中的 非接地电容没有机械等效量。Maxwell等 效中,不考虑相对或绝对问题 Maxwell等效分析法的不足:机械和电气 拓扑结构上多不同
dp = edt
p 线性元件 f = I
p2 ε= 2I
理想1端口元件
e 对广义容性元件: = g ( q ) q :广义位移,相对测量量 机械:弹簧;电:电容 存储能量 ε = ∫ dtef = ∫ fdq
dq = fdt q 线性元件 e = c
q ε= 2c
2
理想1端口元件
对广义阻尼: e = g ( f )
dV F = ( P2 − P ) A = m 1 dt
理想1端口元件
流体容性:势能,流体压缩或重力场中随深度增 大而压力增大,类似弹簧及悬摆 压缩(气体压缩方程 ): PU γ =constant 压力、体积变化: γ γ −1 U ∆P + γ PU ∆U =0 势变量 ∆P γP 广义位移变量 ∆U ∆P = − ∆U U 非线性 负号:提供力与运动方向相反,类似弹簧 q γP c= e= 平衡值附近,近似为线性 U c
第二讲 机电系统建模方法
机电系统的建模问题---等效电路法 控制系统:方框图,传递函数,控制/运算 /转换环节
机电系统的建模问题
弹簧-质量-阻尼系统
机电系统的建模问题
弹簧-质量-阻尼系统-框图
F
1 M
&& xB来自1 D& x
1 D
x
1 积分环节: D
1 比例环节: M
K
机电系统的建模问题
建模:动态过程分析、仿真依据 (普遍方法) 常见机电系统:刚体移动,刚体转动, 流体运动,电气运动,电磁运动,热运 动(微分方程类似) 电路分析方法:成熟。 电阻,电容,电感,电压,电流
等效电路法
Maxwell等效分析法的不足:机械和电气拓 扑结构上多不同 电气系统中电阻串联 机械系统中机械阻尼并接 电气中:流相等,串联 机械中:流(速度)相等,并接阻尼、弹 簧
等效电路法
等效电路法
哈密尔顿变量:能量变量(通常出现在Hamilton系 统中) 定义:系统描述量,对时间的微分得到功率变量 刚体运动:位移x,动量p 刚体转动:角位移θ,角动量h 电气系统:电荷q,磁通匝连数λ 磁系统:磁通量φ(仅一个) 流体:体积U ,压力动量Г(大写), 热系统:熵s(仅一个)
并接测量 (测量特点) 串接测量
电、流体的阻抗和机械中的易变性等效
等效电路法
3. Maxwell等效分析(又称阻抗等效 impedance analogy )Maxwell 1865 (追溯)(1952,重印) V、 Q 、Ω 和 i:流变量(flow)反映对 象运动 F、τ、 p 和 e: 势变量(effort) 电阻抗、流体阻抗和机械阻抗是等效量
例:射钉枪
重要物理现象: 马达:理想转动源(角速度), 转架:考虑惯性,忽略变形→理想惯性器件 尼龙轮:摩擦→阻尼 转子:惯性
1端口元件及建模
活塞:有质量,忽略变形→刚体运动 弹簧:理想容性元件,质量远小于活塞,忽略 挡垫:假设不发生塑性变形,承受冲击,有阻尼,即挡 垫可用电容和电阻模型建模。 停止器:制动时使挡垫变形,本身不动不变性,系统模 型中忽略。 本系统中无需要重新建模的现象,均属于已有理想元件。 一个理想源:马达 五个理想惯性件:活塞、3个轮子、转架(轮子可忽略) 两个理想容性件:弹簧、挡垫 两个理想阻尼:尼龙轮、滚子挡垫 (忽略了电机到 转架之间的转动,无能量损失或存储)
理想源流:马达转速 惯性:旋转、活塞 容性:弹簧、挡垫 阻性:胶轮、挡垫 非电磁变换:旋转——移动
等效电路模型---射钉枪
简单起见:
挡垫非线性弹簧 非线性阻尼
轮子:非全接触,非线性阻尼-线性 弹簧、活塞:速度相等,串联 挡垫:固定在活塞上,包括阻、容性,另一端 固定不动,速度为零。差值即为速度,相等, 串联(简化了挡垫和变换过程)
等效电路法
刚体 转动 势变量 流变量 广义位移 广义动量 电 磁 流体 热
F V x p
τ Ω θ h
e i q λ
M
& Φ
P Q U Г
