第三章题解
第三章 信道与信道容量 习题解答

,
,求
,
,
和
;
(2) 求该信道的信道容量及其达到信道容量时的输入概率分布。
解:
(1)先写出
:
根据公式
计算联合概率:
信宿端符号分布概率:
根据公式
计算:
3
求各熵: 信源熵:
比特/消息
信宿熵:
比特/消息
可疑度:
平均互信息量: 噪声熵: (2)二元对称离散信道的信道容量:
比特/消息 比特/消息
比特/秒
信源等概分布时(
解:设下标 1为原状况,下标 2为改变后状况。由
可得:
,
倍
如果功率节省一半则
倍 ,为 了 使 功 率 节 省 一 半 又 不 损 失 信 息 量 I,根 据
,可以: (1) 加大信道带宽 W,用带宽换取信噪比
,
,
7
缺点是对设备要求高。 (2) 加大传输时间 T,用传输时间换取信噪比,同理可得:
缺点是传输速度降低了。
噪声熵:
(5)平均互信息量:
2.有一个生产 A、B、C、D四种消息的信源其出现的概率相等,通过某一通信系统传输时,B和 C无误,A 以 1/4概率传为 A,以 1/4概率误传为 B、C、D,而 D以 1/2概率正确传输,以 1/2概率误传为 C,
(1)试求其可疑度?(2)收到的信号中哪一个最可靠?(3)散布度为多少? 解:(1)
,
将各数据代入: 解得:
如果
则
将各数据代入: 解得:
14.在理想系统中,若信道带宽与消息带宽的比为 10,当接收机输入端功率信噪比分别为 0.1和 10时,试
比较输出端功率信噪比的改善程度,并说明
与
之间是否存在阀值效应。
第三章存储系统(习题解答)

第三章存储系统(习题解答)————————————————————————————————作者:————————————————————————————————日期:第三章存储系统(习题参考答案)1.有一个具有20位地址和32位字长的存储器,问:(1)该存储器能存储多少个字节的信息?(2)如果存储器由512K×8位SRAM芯片组成,需要多少芯片?(3)需要多少位地址作芯片选择?解:(1)∵ 220= 1M,∴ 该存储器能存储的信息为:1M×32/8=4MB (2)(1024K/512K)×(32/8)= 8(片)(3)需要1位地址作为芯片选择。
(选择两个512K×32位的存储体)2. 已知某64位机主存采用半导体存储器,其地址码为26位,若使用256K×16位的DRAM芯片组成该机所允许的最大主存空间,并选用模块板结构形式,问:(1)每个模块板为1024K×64位,共需几个模块板?(2)每个模块板内共有多少DRAM芯片?(3)主存共需多少DRAM芯片? CPU如何选择各模块板?解:(1)最大主存空间为:226×64位,每个模块板容量为:1024K×64位=220×64位设:共需模块板数为m:则:m=(226×64位)/(220×64位)= 64 (块)(2). 设每个模块板内有DRAM芯片数为n:n=(/) ×(64/16)=16 (片)(3) 主存共需DRAM芯片为:m×n = 64×16=1024 (片)每个模块板有16片DRAM芯片,容量为1024K×64位,需20根地址线(A19~A0)完成模块板内存储单元寻址。
一共有64块模块板,采用6根高位地址线(A25~A20),通过6:64译码器译码,产生片选信号对各模块板进行选择。
3.用16K×8位的DRAM芯片组成64K×32位存储器,要求:(1) 画出该存储器的组成逻辑框图。
第三章空间力系习题解答

3-10如图3-35所示的空间支架。已知:∠CBA=∠BCA=60°,∠EAD=30°,物体的重量为W=3kN,平面ABC是水平的,A、B、C各点均为铰接,杆件自重不计。试求撑杆AB和AC所受的压力FAB和FAC及绳子AD的拉力FT。
图3-35
3-11空间构架由三根直杆铰接而成,如图3-36所示。已知D端所挂重物的重量W=10kN,各杆自重不计。试求杆AD、BD、CD所受的力。
图3-41
3-17曲轴如图3-42所示,在曲柄E处作用一力F=30kN,在曲轴B端作用一力偶M而平衡。力F在垂直于AB轴线的平面内且与铅垂线成夹角a=10°。已知:CDGH平面与水平面间的夹角f=60°,AC=CH=HB=400mm,CD=200mm,DE=EG。不计曲轴自重,试求平衡时力偶矩M之值和轴承的约束反力。
习 题
3-1在边长为a的正六面体上作用有三个力,如图3-26所示,已知:F1=6kN,F2=2kN,F3=4kN。试求各力在三个坐标轴上的投影。
图3-26
3-2如图3-27所示,已知六面体尺寸为400 mm×300 mm×300mm,正面有力F1=100N,中间有力F2=200N,顶面有力偶M=20N·m作用。试求各力及力偶对z轴之矩的和。
图3-36
3-12空间桁架如图3-37所示。力F作用在ABDC平面内,且与铅垂线成45°角,ΔEAK≌ΔFBM,等腰三角形ΔEAK、ΔFBM和ΔNDB在顶点A、B和D处均为直角,又EC=CK=FD=DM。若F=10kN,试求各杆的受力。
图3-37
结点A
结点B
3-13三轮车连同上面的货物共重W=3kN,重力作用点通过C点,尺寸如图3-38所示。试求车子静止时各轮对水平地面的压力。
图3-42
新版化工原理习题答案第三章-非均相混合物分离及固体流态化-题解

第三章非均相混合物分离及固体流态化1.颗粒在流体中做自由沉降,试计算(1)密度为2 650 kg/m\直径为0.04 mm的球形石英顆粒在20 °C空气中自由沉降,沉降速度是多少?(2)密度为2 650 kg/m;,,球形度 0 = 0.6的非球形颗粒在20 £清水中的沉降速度为0. 1 m/ s,颗粒的等体积当量直径是多少?(3)密度为7 900 kg/m\克径为6.35 mm的钢球在密度为1 600 kg/n?的液体中沉降150 mm所需的时间为7.32 s,液体的黏度是多少?解:(1)假设为滞流沉降,则:18“查附录 20 °C 空气 p = 1.2O5kg/m\ //= 1.81 x IO'5Pa • s ,所以,“,=¥的吧:鵲眷吟9%沖276m方核算流型:=1.205X0.1276X004X10-=034<11.81X10'5所以,原假设正确,沉降速度为0. 1276 m/so(2)采用摩擦数群法4xl.81xl0-5 (2650-1.205)x9.81 $3x1.20 宁 xOf依0 = 0.6, ^Re"1 =431.9,查出:Re x =^A = o.3,所以:」O.3xl.81xlO-5in5 *d、= ------------- = 4.506 x 10 m = 45屮nc 1.205x0」(3)假设为滞流沉降,得:1/ = --------⑻,其中u{ = h/0 =0.15/7.32 m/s = 0.02(M9 m/s将已知数据代入上式得:J).00635'(7900J 600)5lp a s = 6.757Pa.s 18x0.02049核算流型n odu. 0.00635 x 0.02049 x 1600 n AOAO t -Re =匕_- = ----------------------- = 0.03081 < 1// 6.7572.用降尘室除去气体中的固体杂质,降尘室长5 m,宽5 m,高4.2 m,固体杂质为球形颗粒,密度为3000 kg/m\气体的处理量为3000 (标准)m7h o试求理论上能完全除去的最小颗粒直径。
教材第三章习题解答

第三章分子结构习题解答1.用列表的方式分别写出下列离子的电子分布式。
指出它们的外层电子分别属于哪种构型(8、9~17、18或18+2)?未成对电子数是多少?Al3+、V2+、V3+、Mn2+、Fe2+、Sn4+、Pb2+、I-【解答】离子离子的电子分布式外层电子构型未成对电子数Al3+1s22s22p68 0V2+1s22s22p63s23p63d39~17 3V3+1s22s22p63s23p63d29~17 2 Mn2+1s22s22p63s23p63d59~17 5 Fe2+1s22s22p63s23p63d69~17 4 Sn4+1s22s22p63s23p63d104s24p64d105s218+2 0 Pb2+1s22s22p63s23p63d104s24p64d104f145s25p65d106s218+2 0I-1s22s22p63s23p63d104s24p64d105s25p68 02.下列离子的能级最高的电子亚层中,属于电子半充满结构的是_________。
A.Ca2+;B.Fe3+;C.Mn2+;D.Fe2+;E.S2-【解答】B,C。
离子离子的电子分布式属于电子半充满的结构Ca2+1s22s22p63s23p6 ×Fe3+1s22s22p63s23p63d5∨Mn2+1s22s22p63s23p63d5∨Fe2+1s22s22p63s23p63d4×S2-1s22s22p63s23p2 ×3.指出氢在下列几种物质中的成键类型:HCl中_______;NaOH中_______;NaH中_______;H2中__________。
【解答】极性共价键;极性共价键;离子键;非极性共价键。
4.对共价键方向性的最佳解释是_________。
A.键角是一定的; B.电子要配对;C.原子轨道的最大重叠; D.泡利原理。
【解答】C。
分析:原子间相互成键时,必须符合原子轨道最大重叠原则和对称性匹配原则,因而原子间形成共价键时,总是按确定的方向成键,这决定了共价键的方向性。
物理化学第三章 习题解答

第三章 习题解答1. 在298 K 和标准压力下,含甲醇(B)的摩尔分数x B 为0.458的水溶液的密度为0.89463kg dm -⋅,甲醇的偏摩尔体积313(CH OH)39.80 cm mol V -=⋅,试求该水溶液中水的偏摩尔体积2(H O)V 。
解:3322(CH OH)(CH OH)(H O)(H O)V n V n V =+3330.45832(10.458)18()dm 0.02729 dm 0.894610mV ρ⨯+-⨯===⨯ 3313120.027290.45839.8010(H O)() cm mol 16.72 cm mol 10.458V ----⨯⨯=⋅=⋅-2. 298 K 和标准压力下,有一甲醇物质的量分数为0.4的甲醇-水混合物。
如果往大量的此混合物中加入1 mol 水,混合物的体积增加17.35 cm 3;如果往大量的此混合物中加1 mol 甲醇,混合物的体积增加39.01 cm 3。
试计算将0.4 mol 的甲醇和0.6 mol 的水混合时,此混合物的体积为若干?此混合过程中体积的变化为若干?已知298 K 和标准压力下甲醇的密度为0.79113g cm -⋅,水的密度为0.99713g cm -⋅。
解:312(H O)17.35cm mol V -=⋅313(CH OH)39.01 cm mol V -=⋅33322(CH OH)(CH OH)(H O)(H O)26.01 cm V n V n V =+=混合前的体积为:33[(18/0.9971)0.6(32/0.7911)0.4] cm 27.01 cm ⨯+⨯=31.00 cm V ∆=3. 298 K 时,K 2SO 4在水溶液中的偏摩尔体积V B 与其质量摩尔浓度的关系式为:1/2B 32.28018.220.222V m m =++,巳知纯水的摩尔体积V A , m = 17.96 cm 3·mol -1,试求在该溶液中水的偏摩体积与K 2SO 4浓度m 的关系式。
第三章部分习题解答
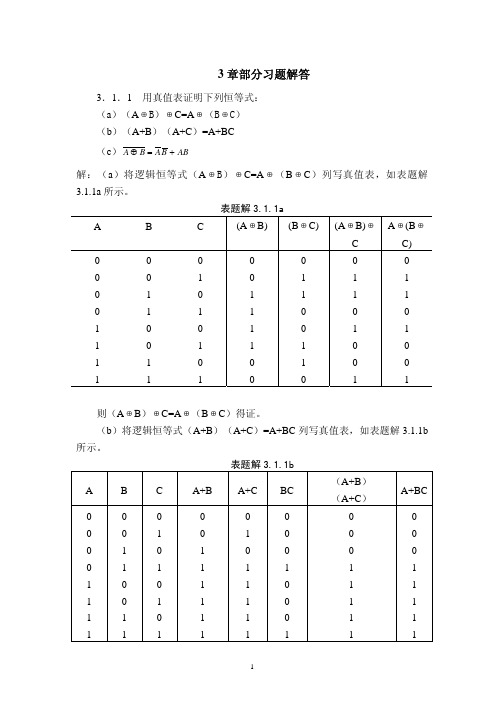
(b) ( A + B)(AB ) = AAB + BAB = AB
(c) ABC(B + C ) = ( A + B + C )(B + C ) = C + B( A + B ) = C + AB
(d) A + ABC + ABC + CB + CB = A(1 + BC + BC) + C(B + B ) = A + C
L3 = A3 ⊕ C
可分别用异或门、三态门设计逻辑电路,如图题解 3.4.4a、b 所示。
图题解 3.4.4
7
3.4.7 某雷达站有 3 部雷达 A、B、C,其中 A 和 B 功率消耗相等,C 的 功率是 A 的两倍。这些雷达由两台发电机 X 和 Y 供电,发电机 X 的最大输出功 率等于雷达 A 的功率消耗,发电机 Y 的最大输出功率是 X 的 3 倍。要求设计一 个逻辑电路,能够根据各雷达的启动和关闭信号,以最节约电能的方式启、停 发电机。
X = ABC + ABC + ABC + ABC = AB ⊕ C + B A ⊕ C
Y =AB+C 由逻辑表达式可设计出最节约电能的发电机启、停方式的逻辑电路,如图 题解 3.4.7b 所示。
表题解 3.4.7
A
B
C
X
Y
0
0
0
0
0
0
0
1
0
1
0
1
0
1
0
0
1
1
0
1
1
0
0
1
0
大学物理第三章 习题解答

第三章 习题解答(仅供参考)3.2 一根直杆在S 系中观察,其静止长度为l ,与x 轴的夹角为θ,S`系沿S 系的x 轴正向以速度v 运动,问S`系中观察到杆子与x `轴的夹角若何?[解答]直杆在S 系中的长度是本征长度,两个方向上的长度分别为l x = l cos θ和l y = l sin θ.在S`系中观察直杆在y 方向上的长度不变,即l`y = l y ;在x 方向上的长度是运动长度,根据尺缩效应得`x l l =因此``tan `yx l l θ==,可得夹角为 21/2`a r c t a n {[1(/)]t a n }v c θθ-=-3.3 在惯性系S 中同一地点发生的两事件A 和B ,B 晚于A 4s ;在另一惯性系S`中观察,B 晚于A 5s 发生,求S`系中A 和B 两事件的空间距离?[解答]在S 系中的两事件A 和B 在同一地点发生,时间差Δt = 4s 是本征时,而S`系中观察A 和B 两事件肯定不在同一地点,Δt ` = 5s 是运动时,根据时间膨胀公式`t ∆=, 即5=, 可以求两系统的相对速度为 v = 3c /5.在S`系中A 和B 两事件的空间距离为 Δl = v Δt ` = 3c = 9×108(m).3.5 S 系中观察到两事件同时发生在x 轴上,其间距为1m ,S`系中观察到这两个事件间距离是2m ,求在S`系中这两个事件的时间间隔.[解答]根据洛仑兹变换,得两个事件的空间和时间间隔公式`x ∆=2`t ∆= (1) 由题意得:Δt = 0,Δx = 1m ,Δx` = 2m .因此`x ∆=,2`t ∆=.(2)由(2)之上式得它们的相对速度为v = (3)将(2)之下式除以(2)之上式得 2``t v x c∆=-∆, 所以`t ∆==10-8(s).[注意]在S `系中观察到两事件不是同时发生的,所以间隔Δx` = 2m 可以大于间隔Δx = 1m .如果在S `系中观察到两事件也是同时发生的,那么Δx`就表示运动长度,就不可能大于本征长度Δx ,这时可以用长度收缩公式`x ∆=∆3.6 一短跑运动员,在地球上以10s 的时间跑完了100m 的距离,在对地飞行速度为0.8c 的飞船上观察,结果如何?[解答]以地球为S 系,则Δt = 10s ,Δx = 100m .根据洛仑兹坐标和时间变换公式`x =2`t =,飞船上观察运动员的运动距离为`x ∆=10=-4×109(m). 运动员运动的时间为 2`t ∆=100.8100/0.6c -⨯=≈16.67(s). 在飞船上看,地球以0.8c 的速度后退,后退时间约为16.67s ;运动员的速度远小于地球后退的速度,所以运动员跑步的距离约为地球后退的距离,即4×109m .3.8 已知S`系以0.8c 的速度沿S 系x 轴正向运动,在S 系中测得两事件的时空坐标为x 1 = 20m ,x 2 = 40m ,t 1 = 4s ,t 2 = 8s .求S`系中测得的这两件事的时间和空间间隔.[解答]根据洛仑兹变换可得S`系的时间间隔为2``21t t -=840.8(4020)/0.6c ---=≈6.67(s). 空间间隔为``21x x -=40200.8(84)0.6c --⨯-=≈-1.6×109(m).3.11 一粒子动能等于其非相对论动能二倍时,其速度为多少?其动量是按非相对论算得的二倍时,其速度是多少?[解答](1)粒子的非相对论动能为 E k = m 0v 2/2,相对论动能为 E`k = mc 2 – m 0c 2, 其中m 为运动质量m =.根据题意得22200m c m v =, 设x = (v/c )2,方程可简化为1x =+, 或1(1x =+ 平方得 1 = (1 – x 2)(1 - x ),化简得 x (x 2 – x -1) = 0.由于x 不等于0,所以 x 2 – x -1 = 0.解得x =, 取正根得速率为v == 0.786c . (2)粒子的非相对论动量为 p = m 0v , 相对论动量为`p mv ==根据题意得方程02m v =.很容易解得速率为2v c == 0.866c .3.12.某快速运动的粒子,其动能为4.8×10-16J ,该粒子静止时的总能量为1.6×10-17J ,若该粒子的固有寿命为2.6×10-6s ,求其能通过的距离.[解答]在相对论能量关系中E = E 0 + E k ,静止能量E 0已知,且E 0 = m 0c 2,总能量为22E mc ===,所以00k E E E +=, 由此得粒子的运动时为0`k E E t t E +∆==∆. 还可得00kE E E =+, 解得速率为v =∆=∆=∆粒子能够通过的距离为l v t c t8=⨯⨯⨯.310 2.610-3.14静止质子和中子的质量分别为m p = 1.67285×10-27kg,m n = 1.67495×10-27kg,质子和中子结合变成氘核,其静止质量为m0 = 3.34365×10-27kg,求结合过程中所释放出的能量.[解答]在结合过程中,质量亏损为Δm = m p + m n - m0 = 3.94988×10-30(kg),取c = 3×108(m·s-1),可得释放出的能量为ΔE = Δmc2 =3.554893×10-13(J).如果取c = 2.997925×108(m·s-1),可得释放出的能量为ΔE = 3.549977×10-13(J).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章题解
电子的能量分别为10eV ,100 eV ,1000 eV 时,试计算相应的德布罗意波长。
解:依计算电子能量和电子波长对应的公式
电子的能量
由德布罗意波长公式
3-2 设光子和电子的波长均为,试问:(1)光子的动量与电子的动量之比是多少 (2)光子的动能与电子的动能之比是多少
解:(1p 光子:p 电子=1:1
(2)由
光子动能与波长的对应的关系
电子动能与波长的关系
则知
3-3 若一个电子的动能等于它的静止能量,试求:(1)该电子的速度为多大(2)其相应的德布罗意波长是多少 解: (1)依题意,相对论给出的运动物体的动能表达式是:
2
mc
E =
2
0c m E E k +=
2
022c m mc =
2m m =
2
2021m c
v m m =-=
411
2
2=-c v
22
141c
v -=
22
43c v =
所以
0.866c
c 43v ≈=
(2) 根据电子波长的计算公式:
0.001715nm
eV
105111.226nm )
(1.226nm
3=⨯=
=
eV E k λ
3-4 把热中子窄束射到晶体上,由布喇格衍射图样可以求得热中子的能量.若晶体的两相邻布喇格面间距为,一级布喇格掠射角(入射束与布喇格面之间的夹角)为30°,试求这些热中子的能量. 解:根据布喇格衍射公式 nλ=dsinθ λ=dsinθ=×sin30°nm= nm
λ=
2
21.226nm ()13.622eV 185.56eV
k E λ
===
3-5 电子显微镜中所用加速电压一般都很高,电子被加速后的速度很大,因而必须考虑相对论修正.试证明:电子的德布罗意波长与加速电压的关系应为:
式中Vr=V(1+×10-6V),称为相对论修正电压,其中电子加速电压V 的单位是伏特.
分析:考虑德布罗意波长,考虑相对论情况质量能量修正,联系德布罗意关系式和相对论能量关系式,求出相对论下P 即
可解. 证明:
根据相对论质量公式
将其平方整理乘c2,得其能量动量关系式
2222220m c p c m c -=
题意得证.
3-6 (1)试证明:一个粒子的康普顿波长与其德布罗意波长之比等于
-⎪
⎭⎫E 式中Eo 和E 分别是粒子的静止能量和运动粒子的总能量.(康普顿波长λc=h/m0c ,m0为粒子静止质量,其意义在第六章中讨论)
(2)当电子的动能为何值时,它的德布罗意波长等于它的康普顿波长
证明:根据相对论能量公式将其平方整理乘c2
2222220m c p c m c -=
22224
0E p c m c =+
2
0k E E mc =+
k E E E =-
(1)相对论下粒子的德布罗意波长为:
粒子的康普顿波长为
(2)若粒子的德布罗意波长等于它的康顿波长
0722.55511211.55(KeV)
k E E E =-=-=
则电子的动能为. 则电子的动能为
注意变换:1. ΔP 转化为Δλ表示; 2. ΔE 转化为Δν表示;
3-7 一原子的激发态发射波长为600nm
解: 依 h t E ≥∆∆ 求Δt
2 ≥∆∆E t
3-8 一个电子被禁闭在线度为10fm 的区域中,这正是原子核线度的数量级,试计算它的最小动能.
解:
粒子被束缚在线度为r 的范围内,即Δx = r
那么粒子的动量必定有一个不确定度,它至少为:
x 2∆≥
∆
x p ∵
∴∴ 电子的最小平均动能为3-9 已知粒子波函数
⎭⎬⎫⎩
⎨⎧---
=c z b y a x N 2||2||2||
exp ψ,试求:(1)归一化常数N ;(2)粒子的x 坐标在0到a 之间的
几率;(3)粒子的y 坐标和z 坐标分别在-b →+b 和-c →+c.之间的几率. 解: (1)因粒子在整个空间出现的几率必定是一,所以归一化条件是:
⎰
+∞
∞
-ψ
dv = 1
即:
dz
e
dy e
dx e
N dv c
z b
y a
x ⎰⎰⎰⎰⎰⎰∞+∞--∞+∞
--∞+∞
--∞
+∞
-=22
22
22
22
ψ
=
1
822220
02==⎰⎰⎰∞-
∞
-
∞
-abc N d e
c d e
b d e
a N c
z c
z b
y b
y a
x a
x
所以 N
abc
81=
(2) 粒子的x 坐标在a →0区域内几率为:
dz
e
dy e
dx e
N c
z b
y a a
x ⎰⎰⎰∞+∞
--∞+∞
---22
22
22
2
()[])11(21141
2
e
e
abc N
-=--=-
(3) 粒子的
),(),,(c c z b b y -∈-∈区域内的几率为:
dz
e dy e dx e N c
c c z
b
b b y
a x
⎰⎰⎰+--+--∞
+∞--22
22
22
2
2
2
)11(8-=e abc N 2)11(-=e。
