统计学计算题辅导
统计学计算题复习(学生版)

统计学计算题复习(学生版)统计学复习提纲一、期末考卷题型1. 单项选择题;2. 多项选择题;3. 简答题4. 计算题二、知识点复习1. 统计学分类、指标、变量、参数、统计量等概念,以及各种统计图形;2.统计数据的相关内容,以及测量数据分布的测度的描述;平均数、中位数和众数的计算公式。
3. 调查的各种方式; 4. 组距数列的相关概念。
5. 置信区间的相关概念,以及单个总体均值、比例、方差的区间估计;6. 估计单个总体均值、比例时的样本容量的计算公式;7. 单个总体均值、比例、方差的假设检验;8. 相关系数和回归系数的相关知识;9. 一元、二元回归模型的EXCEL操作结果的解释以及模型的建立和检验;10. 时间序列的各种分类;平均速度等指标、移动平均法的概念等;平均发展水平的计算和季节指数的计算; 11.统计指数的相关概念,制作综合指数要点和原则,综合指数、平均指数的计算。
1统计学计算题复习一.平均数、中位数和众数的计算和三者之间的关系1.算术平均数。
也叫均值,是全部数据的算术平均,是集中趋势的最主要测度值。
主要适用于定距数据和定比数据,但不适用于定类数据和定序数据。
2.众数。
众数是一组数据中出现次数最多的变量值,用Mo表示。
主要用于测度定类数据的集中趋势。
组距式数列确定众数,是先根据出现次数确定众数所在组,然后利用下列公式计算众数的近似值:M?L?0f?f?1?i (f?f?1)?(f?f?1) 3.中位数。
中位数是一组数据按从小到大排序后,处于中间位置上的变量值,用Me表示。
主要用于测度定序数据的集中趋势。
分组数据计算中位数时,先根据公式N确定中位数所在的组,然后用下列公式计算2N?Sm?1中位数的近似值: M?L?2?i efm4.众数、中位数和算术平均数的关系 x?Me?Mo,数据是对称分布; x<Me<Mo,数据是左偏分布; x>Me>Mo,数据是右偏分布。
例题1:某地区有下列资料:人均月收入400以下400~500 500~600 600~700 700~800 800~900 900以上合计要求计算算术平均数、众数、中位数。
统计学原理简答题和计算题综合练习题参考答案

统计学原理简答题和计算题综合练习及参考答案一、简答题:1、举例说明统计标志与标志表现有何不同?答:标志是总体中各单位所共同具有的某特征或属性,即标志是说明总体单位属性和特征的名称。
标志表现是标志特征在各单位的具体表现,是标志的实际体现者。
标志是所要调查的项目,标志表现是调查所得到的结果。
例如:学生的“成绩”是标志,而成绩为“90”分则是标志表现。
2、简述品质标志与数量标志的区别并举例说明。
答:品质标志表明总体单位属性方面的特征,其标志表现只能用文字来表现;数量标志表明总体单位数量方面的特征,其标志表现可以用数值表示,即标志值。
例如某人的“职业”是品质标志;而“工资水平”就是数量标志。
3、变量分组的种类及应用条件。
答:变量分组是指按数量标志分组,分组的种类有单项式分组和组距式分组。
由于变量有离散型和连续型之分,所以变量分组要根据变量的类型。
如果离散型变量的变量值变动幅度比较小,则采用单项式分组,如果离散型变量的变量值变动幅度很大,项数又很多,就要采用组距式分组。
而连续变量由于不能一一列举变量值,所以不能作单项式分组,只能进行组距式分组。
4、简述结构相对指标和比例相对指标有什么不同并举例说明。
答:结构相对指标是以总体总量为比较标准,计算各组总量占总体总量的比重,来反映总体内部组成情况的综合指标。
比例相对指标是总体不同部分数量对比的相对数,用以分析总体范围内各个局部之间比例关系和协调平衡状况。
如:各工种的工人占全部工人的比重是结构相对指标。
而某地区工业企业中轻重工业比例就是比例相对指标。
5、简述调查对象、调查单位与填报单位的关系、区别并举例说明。
答:调查对象是应搜集其资料的许多单位的总体;调查对象由调查目的所决定。
调查单位是构成调查对象的每一个单位,它是进行登记的标志的承担者,是调查单位的组成要素;报告单位也叫填报单位,也是调查单位的组成要素,它是提交调查资料的单位,一般是基层企事业组织。
调查单位与填报单位有时一致,有时不一致。
统计学计算题目解析
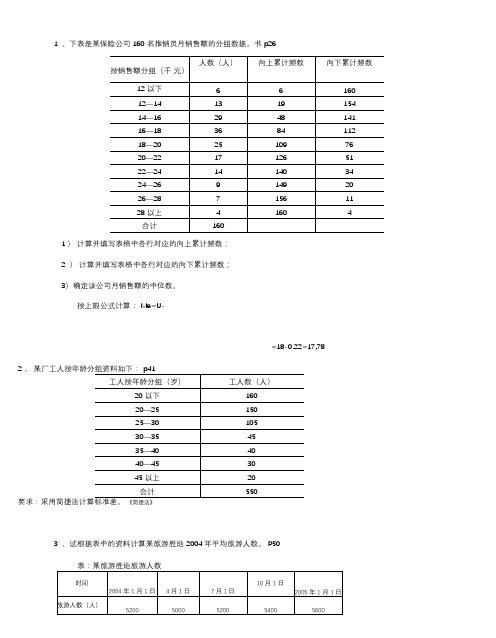
1、下表是某保险公司 160 名推销员月销售额的分组数据。
书 p261 )计算并填写表格中各行对应的向上累计频数;2)计算并填写表格中各行对应的向下累计频数;3)确定该公司月销售额的中位数。
按上限公式计算: Me=U-=18-0.22=17,78 2 、某厂工人按年龄分组资料如下: p41要求:采用简捷法计算标准差。
《简捷法》3、试根据表中的资料计算某旅游胜地 2004 年平均旅游人数。
P50表:某旅游胜地旅游人数4 、某大学 2004 年在册学生人数资料如表 3-6 所示,试计算该大学 2004 年平均在册学生人数时间1月1日3月1日 7月1日 9月1日 12 月 31 日 在册学生人数(人)340835283250359035755 、已知某企业 2004 年非生产人员以及全部职工人数资料如下表所示,求该企业第四季度非生产人员占全部职工 人数的平均比重。
表: 某企业非生产人员占全部职工人数比重时间9 月末 10 月末 11 月末 12 月末 非生产人数(人) 200 206 206 218 全部职工人数(人) 1000105010701108非生产人员占全部职 工人数比重( % )20.0 19.62 19.25 19.686、根据表中资料填写相应的指标值。
表:某地区 1999~2004 年国内生产总值发展速度计算表7 、根据表中资料计算移动平均数,并填入相应的位置。
P618 、根据表中资料计算移动平均数,并填入相应的位置。
P621977 10001978 11601979 13871980 15861981 14871982 14151983 16179、某百货商场某年上半年的零售额、商品库存额如下:(单位:百万元)日期1月2月3月4月5月6月零售额42.30 43.64 40.71 40.93 42.11 44.54月初库存额20.82 21.35 23.98 22.47 23.16 23.76试计算该商城该年上半年商品平均流转次数(注:商品流通次数 = 商品销售额 / 库存额; 6 月末商品库存额为24.73 百万元)。
统计学原理相关计算辅导

象总体按某一标志划分为若干性质不同但又有联系的几个部分称
统计分组。
总体的变异性是统计分组的客观依据。统计分组是总体内进
行的一种定性分类,它把总体划分为一个个性质不同的范围更小
的总体。
二、 统计分组的种类 ①统计分组按其任务和作用不同,分为类型分组、结构分组和分
析分组。类型分组的目的是划分经济类型,结构分类的目的是研究 同质总体的构成,分析分组的目的是研究现象总体内部诸标志间的 依从和制约关系。
统计学原理相关计算辅导
本课件PPT仅供大家学习使用 学习完请自行删除,谢谢! 本课件PPT仅供大家学习使用 学习完请自行删除,谢谢! 本课件PPT仅供大家学习使用 学习完请自行删除,谢谢! 本课件PPT仅供大家学习使用 学习完请自行删除,谢谢!
一、 统计分组的概念
根据统计研究任务的要求和研究现象总体的内在特点,把现
例1、古冶区华云制衣厂2003年6月份按工人劳动生产率高低分组人数资 料情况如下:
按工人劳动生产率 分组(件/人)
50-60 60-70 70-80 80-90 90以上
试计算该企业工人平均劳动生产率。
人数 (人)
150 100 70 30 16
已知
解:根据题意列计算表如下:
X=(下限+上限)/2
由第一列求的
按工人劳动生产率 分组(件/人)
50-60 60-70 70-80 80-90 90以上
合计
组中值
(件/x 人)
55 65 75 85 95
-----
比重 f
——— ∑f
40.98% 27.32% 19.13%
8.20% 4.37% 100.00%
=55× 40.98%+65×27.32%+75×19.13%+85×8.20%+95×4.37%=66
统计学原理计算题(公式)复习资料

《统计学原理》复习资料(计算部分)一、 编制分配数列(次数分布表) 统计整理公式a) 组距=上限-下限 b) 组中值=(上限+下限)÷2c) 缺下限开口组组中值=上限-1/2邻组组距 d) 缺上限开口组组中值=下限+1/2邻组组距1.某班40名学生统计学考试成绩分别为:57 89 49 84 86 87 75 73 72 68 75 82 97 81 67 81 54 79 87 95 76 71 60 90 65 76 72 70 86 85 89 89 64 57 83 81 78 87 72 61要求:⑴ 根据上述资料按成绩分成以下几组:60分以下,60~70分,70~80分,80~90分,90~100分,整理编制成分配数列。
⑵ 根据整理后的分配数列,计算学生的平均成绩。
解:分配数列成绩(分) 学生人数(人) 频率(%) 60以下 4 10 60—70 6 15 70—80 12 30 80—90 15 37.5 90—100 3 7.5 合计 40 100平均成绩 55465675128515953307076.754040xf x f⨯+⨯+⨯+⨯+⨯====∑∑(分)或 5510%6515%7530%8537.5%957.5%76.75fx x f=⋅=⨯+⨯+⨯+⨯+⨯=∑∑(分)2.某生产车间40名工人日加工零件数(件)如下:30 26 42 41 36 44 40 37 43 35 37 25 45 29 43 31 36 49 34 47 33 43 38 42 32 25 30 46 29 34 38 46 43 39 35 40 48 33 27 28要求:⑴ 根据以上资料分成如下几组:25~30,30~35,35~40,40~45,45~50,整理编制次数分布表。
⑵ 根据整理后的次数分布表,计算工人的平均日产量。
(作业10P 1) 解:次数分布表日加工零件数(件) 工人数(人)频率(%)25—307 17.5 30—35 8 20 35—40 9 22.5 40—45 10 25 45—50 6 15 合计 40100平均日产量 27.5732.5837.5942.51047.56150037.54040xf x f⨯+⨯+⨯+⨯+⨯====∑∑ 件或 27.517.5%32.520%37.522.5%42.525%47.515%37.5fx x f=⋅=⨯+⨯+⨯+⨯+⨯=∑∑ 件二、 算术平均数和调和平均数的计算 加权算术平均数公式 xfx f=∑∑(常用) fx x f=⋅∑∑(x 代表各组标志值,f 代表各组单位数,ff∑代表各组的比重)加权调和平均数公式 m x m x=∑∑ (x 代表各组标志值,m 代表各组标志总量)分析: m x mx=总产量工人平均劳动生产率(结合题目)总工人人数从公式可以看出,“生产班组”这列资料不参与计算,是多余条件,将其删去。
统计学计算题讲解

第二章六、计算题.1.下面是某公司工人月收入水平分组情况和各组工人数情况:月收入(元)工人数(人)400-500 20500-600 30600-700 50700-800 10800-900 10指出这是什么组距数列,并计算各组的组中值和频率分布状况。
答:闭口等距组距数列,属于连续变量数列,组限重叠。
各组组中值及频率分布如下:2.抽样调查某省20户城镇居民平均每人全年可支配收入(单位:百元)如下:88 77 66 85 74 92 67 84 77 94 58 60 74 64 75 66 78 55 70 66⑴根据上述资料进行分组整理并编制频数分布数列⑵编制向上和向下累计频数、频率数列答:⑴⑵某省20户城镇居民平均每人全年可支配收入分布表第三章六、计算题.⒈某企业生产情况如下:要求:⑴填满表内空格.⑵对比全厂两年总产值计划完成程度的好坏。
解:⑴某企业生产情况如下:单位:(万元)⑵该企业2005年的计划完成程度相对数为110.90%,而2006年只有102.22%,所以2005年完成任务程度比2006好。
⒉某工厂2006年计划工业总产值为1080万吨,实际完成计划的110%,2006年计划总产值比2005年增长8%,试计算2006年实际总产值为2005年的百分比?解:118.8%3.某种工业产品单位成本,本期计划比上期下降5%,实际下降了9%,问该种产品成本计划执行结果?解:95.79%4.我国“十五”计划中规定,到“十五”计划的最后一年,钢产量规定为7200万吨,假设“八五”期最后两年钢产量情况如下:(万吨)根据上表资料计算:⑴钢产量“十五”计划完成程度;⑵钢产量“十五”计划提前完成的时间是多少?解:⑴102.08%;⑵提前三个月5.某城市2005年末和2006年末人口数和商业网点的有关资料如下:计算:⑴平均每个商业网点服务人数;⑵平均每个商业职工服务人数;⑶指出是什么相对指标。
解: 某城市商业情况⑶上述两个指标是强度相对指标。
统计学计算题答案(课后)

9.(1)工人日产量平均数:45 60 55 140 65 260 75 150 85 50660=64.85(件 / 人)(2)通过观察得知,日产量的工人数最多为 260人,对应的分组为 60~70,则众数在60~70这一组中,则众数的取值范围在 60~70 之间。
利用下限公式计算众数:nx fi i i 1nf ii 1众数M °(f mfm 1 )=65.22 (件)(3)首先进行向上累计,计算出各组的累计频数:10.(1)全距 只=最大的标志值一最小的标志值 =95—55=40x f⑵平均日装配部件数x ―」55 4 65 12 75 24 85 6 95 450=73.8 (个)n_X i x f ii 1 n260 140 (260 140 (260 15C)(70 60)660 12330.5比较各组的累计频数和 330.5,确定中位数在60~70这一组 利用下限公式计算中位数:~~2-Sm 1M e L 壬60 660 2002(70 60) 65(件)260⑷分析:由于x M e M o ,所以该数列的分布状态为左偏。
平均差 A.Df ii 1|55 73.8 4 |65 73.8| 12 |75 73.8| 24 |85 73.8 6 |95 73.8 44 12 24 6 4=7.232 (件)⑷标准差系数V-100% x9.93 73.813.46%X i f i30 4 50 25 70 84 90 126 110 28267=81.16 (件)乙企业的平均日产量X 乙xf j 30 2 50 8 70 30 90 42 110 182(X i X) f ii 1nf ii 12 2 2 2 2(55 73.8) 4 (65 73.8)12 (75 73.8) 24 (85 73.8)6 (95 73.8) 4⑶方差4 12 24 6 4=98.56 (个)标准差n(x x)2 f ii 1n、、98.56 9.93(件)13.甲企业的平均日产量x 甲=83.2 (件)(30 81.16)2 4 (50 81.16)2 25 (70 81.16)2 84 (90 81.16)2 126 (110 81.16)228267n(X i x)2f ii 1 niii 1(30 83.22 2 (50 83.22 8 (70 832)30 (90 832)2 42 (110 832)218X100345.76 =18.59 (件)甲企业的标准差系数: V 甲甲100% 17.13 100% 21.11%X 甲81.16乙企业的标准差系数: V 乙乙100% 18.59 100%22.33%X 乙83.2由计算结果表明:甲企业的标准差系数小于乙企业, 因此甲企业 工人的日产量资料更有代表性。
统计学B常见计算题复习资料(教师版)

某厂劳动生产率计划比上年提高8%,实际仅提高4%,则其计划完成百分数为( )。
解答:计划完成百分数=实际/计划=(1+4%)/(1+8%)=96.30% 2.某企业某型号电视机,本年生产成本计划降低4%,实际降低了5%,则该产品成本计划完成百分数为( )。
解答:计划完成百分数=实际/计划=(1-5%)/(1-4%)=98.96%3.某工厂有五条相同的流水线,生产同一产品且生产速度相同,各流水线的合格率分别为 95%、92%、90%、85%、80%,那么该工厂产品的平均合格率是多少?如果某流水生产线有前后衔接的五道工序,各工序产品的合格率分别为95%、92%、90%、85%、80%,那么产品的平均合格率又是多少? 解答:295%92%90%85%80%88.40%51n x x x x n +++++++===595%88.24%n G x =⋅⋅==4.已知甲企业的费用额为100万元,费用率为5%,;乙企业的商品费用额为75万元,费用率为6%,则这两个企业的平均费用率为(5.38)%,若已知的变量改为商品销售额且金额不变,则平均费用率为(5.43)%。
解答:第一空:平均费用率=平均费用÷平均销售额=(总费用额/2)/(总销售额/2)=总费用额/总销售额=10075100755%6%++ =5.38%第二空:平均费用率=平均费用÷平均销售额=1005%756%10075⨯+⨯+=5.43%5.某企业40名销售人员四月份销售某产品的数据如下表(单位:台)。
(2)表1 月销售量情况表1248%50(1)8%(18%)7.36%3.79%2 3.79%7.58%8%7.58%8%7.58%0.42%15.58%p p P p p pn p n S p p z p P p P P σσ====-=⨯-====∆==⨯=-∆<<+∆→-<<+→<<9.某厂生产的某种零件的设计尺寸为15cm ,根据以往的资料,该种零件的标准差为0.85cm ,合格率为95%,若置信概率为95.45%,总体均值的允许误差不22(1212x x p z n z p n n σ=∆=∆∴=要求:(1)相关系数:0.9978 (2)可决系数:0.9957 (3)回归系数:0.6208 (4)估计标准误差:497.1784(5)估计回归方程:ˆ1449.39830.6208(1449.39830.6208) cy x y x =+=+或写成(6)回归系数意义:城镇居民家庭人均可支配收入每增加1元,人均消费性支出平均增加0.6208元(7)回归方程显著性检验:F统计量为4151.745,相应P值为9.67359E-23远小于规定显著性水平0.05,故回归方程作用显著(8)回归系数显著性检验:t统计量为64.4340,相应P值为9.67E-23远小于规定显著性水平0.05,故回归系数作用显著11.已知n = 5,Σx=40,Σx2=370,Σy=310,Σy2=20,700,Σxy=2,740。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
总体比例的假设检验
解:依题意,可建立如下假设: 样本比例 0.975 检验统计量: 给定α=0.1,查正态分布表得 1 . 645 由于 U ,应接受原假设,即认为厂方的 宣称是可信的
Z p P0 n p (1 p )
0 . 975 0 . 99 0 . 975 0 . 025 200 1 . 359
某车间工人日产量资料如下 :
日产量(件)
10-12 13-15 16-18 19-21
工人数(人)
10 20 30 40
计算该车间平均每个工人的日产量及标准差
平均数、标准差的计算
平均日产量
x
xf f
1700 100
17
标准差
(x x) f
2
3
f
平均数、标准差的计算
乙班学生的平均成绩
x
xf f
3870 50
77 . 4
乙班学生的标准差
(x x) f
2
f
9 . 29
平均数、标准差的计算
甲班学生的变异系数
v甲
x
9 .0 70
0 . 129
乙班学生的变异系数
v乙
x
9 . 29 77 . 4
0 . 120
6 26 30 24 8 3 100
150 910 1350 1320 520 225 4520
平均数、标准差的计算
x
Leabharlann fx f4520 100
45 . 2 ( kg )
即这100头长白母猪仔猪一月龄平均窝重为45.2kg
时间序列计算
环比发展速度 :
Ri
ai a i 1
( i 1, , n )
p
P (1 P ) n
95 % ( 95 % ) 1 400
1.09 %
在概率95 .45 %的保证下,全及一级品 率:
P p p 95 % 2 1.19 % 92 .82 % 97 .18 %
总体均值的假设检验
总体方差已知时对正态总体均值的假设检验 : 利用服从正态分布的统计量Z进行的假设检验 称为Z检验法。根据已知的总体方差、样本容 量n和样本平均数,计算出检验统计量Z的值。 对于给定的检验水平,查正态分布表可得临 界值,将所计算的Z值与临界值比较,便可做 出检验结论 。
甲、乙两班同时对《统计学原理》课程进行测试, 甲班平均成绩为70分,标准差为9.0分;乙班的 成绩分组资料如下 :
按成绩分组 学生人数(人) 60以下 60-70 70-80 80-90 90-100 2 6 25 12 5
计算乙班学生的平均成绩,并比较甲、乙两班哪个班的平 均成绩更有代表性?
平均数、标准差的计算
时间序列计算
1998年销售额比1997年增长的百分数
1 86 % 1 64 % 1 13 . 41 %
1992 1998年平均增长速度
x 1
n
R 1
6
1 . 86 1 10 . 90 %
统计指数计算
拉氏价格指数
Kp p1 q 0 p0q0
派氏价格指数
统计指数计算
拉氏价格指数
p1 q 0 p0q0 4520 3650 1 . 2384 123 . 84 %
Kp
派氏价格指数
p1 q 1 p 0 q1 5600 4510 1 . 2417 124 . 17 %
K
p
区间估计计算
当总体方差已知时,求μ的置信区间 。
总体均值的假设检验
例: 根据过去大量资料,某厂生产的产品的 使用寿命服从正态分布N(1020,1002)。 现从最近生产的一批产品中随机抽取16件, 测得样本平均寿命为1080小时。试在0.05的 显著性水平下判断这批产品的使用寿命是否 有显著提高?
总体均值的假设检验
解:根据题意,提出假设:H0: μ=1020;H1: μ>1020, x 1080 -1020 Z= = = 2 .4 检验统计量 / n 100 / 16 检验统计量由α=0.05,查表得临界值Z0.05= 1.645 由于Z=2.4>Zα=1.645,所以应拒绝H0而接受H1, 即这批产品的使用寿命确有显著提高
0
总体均值的假设检验
总体方差未知时对正态总体均值的假设检验 : 利用服从t分布的统计量去检验总体均值的方 法称为T检验法。其具体做法是:根据题意提 出假设;构造检验统计量T并根据样本信息计 算其具体值;对于给定的检验水平α,由t分 布表查得临界值;将所计算的t值与临界值比 较,做出检验结论。
定基发展速度 :
Ri ai a0 ( i 1, , n )
时间序列计算
环比增减速度 :
Gi a i a i 1 a i 1 ai a i 1 1 ( i 1, , n )
定基增减速度 :
Gi ai a0 a0 ai a0 1 ( i 1, , n )
总体均值的假设检验
例: 从长期的资料可知,某厂生产的某种电 子原件服从均值为200小时,标准差未知的正 态分布。通过改变部分生产工艺后,抽得10 件做样本,均值为204.8(小时), 标准差 S=5.789 ,试问电子原件的平均值数据是否 有所提高 。
总体均值的假设检验
解:根据题意建立如下假设: 检验统计量
H 0 : P 0 . 99 ;
H 1: P 0 . 99
/2
0 . 05
/2
因为0.129 〉0.120,所以乙班学生的平均成绩更 具有代表性
平均数、标准差的计算
将100头长白母猪的仔猪一月窝重(单位:kg)资料整 理成次数分布表如下,求其加权数平均数 组别 10— 组中值(x) 次数(f) 15 3 fx 45
20— 30— 40— 50— 60— 70— 合计
25 35 45 55 65 75
例题:已知某零件的直径服从正态分布,从该批产 品中随机抽取10件,测得平均直径为202.5mm,已 知总体标准差σ=2.5mm,试建立该种零件平均直径 的置信区间,给定置信度为0.95 。
区间估计计算
n 10 , x 202 . 5 , 2 . 5 , z 1 . 96
x z x z
T
2 . 622 t ( n 1) 1 . 8331
总体比例的假设检验
对总体比例的检验通常是在大样本条件下进 行的,根据正态分布来近似确定临界值,即 采用Z检验法。其检验步骤与均值检验时的步 骤相同,只是检验统计量不同 。
总体比例的假设检验
例: 调查人员在调查某企业的主要生产线时, 被告知性能良好生产稳定,产品合格率可达 99%。随机抽查了200件产品,其中195件产 品合格,判断厂方的宣称是否可信?(α= 10%)
H 0 : 200 ;
H 1: 200
x 0 S / n
204 . 8 200 5 . 789 / 10 2 . 622
由α=0.05,查表得临界值 。 由于, 所以拒绝H0接受H1,即 可以接受“在新工艺下,这种电子元件的平均值有 所提高的假设”
t ( n 1) t 0 .05 (10 1) 1 . 8331
区间估计计算
当总体比例的置信区间估计 。
例题:某机械厂日产某种产品8000件,现采 用纯随机不重复抽样方式,从中抽取400件进 行观察,其中有380件为一级品,试以概率 95.45%的可靠程度推断全部产品的一级品率 及一级品数量的范围。
区间估计计算
p 380 400 100 % 95 %
时间序列计算
几何平均法计算平均发展速度 :
R
n
a1 a0
a2 a1
an a n 1
n
an a0
时间序列计算
已知某商店1997年销售额比1992年增长64%, 1998年销售额比1992年增长86%,问1998年 销售额比1997年增长多少?1992 1998年间, 平均增长速度是多少?
n
1 . 96
2 .5 10
1 . 55
x x X x x
202 . 5 1 . 55 X 202 . 5 1 . 55
该种零件平均直径的置信区间为::[200.95,204.05]
区间估计计算
当总体方差未知时,求μ的置信区间 。
例题:某企业生产一种新的电子元件,用简单随机重 复抽样方法抽取25只作耐用时间试验,测试结果,平 均寿命6000小时,标准差300小时,试在95.45%(t=2) 概率保证下,估计这种新电子元件平均寿命区间 。
p1 q 1 p 0 q1
K
p
统计指数计算
同步练习题同类习题解答: 某农贸市场三种商品的价格和销售量资料如下:
商品 A B C 基期 零售价 3 5 8 零售量 250 420 100 报告期 零售价 4 6 10 零售量 350 500 120
试根据上表资料计算:拉氏形式的价格指数; 派氏形式的价格指数
平均数、标准差的计算
分组数据平均数的计算公式:
x1 f 1 x 2 f 2 x n f n f1 f 2 f n xf f
