1-1随机事件的关系与运算
合集下载
随机事件的关系与运算
（2）化简左式至右式
A B C AB C A BC A B C AB C A BC A B C
A B C.
目 录
前一页
后一页
退 出
后一页
退 出
5) 差事件
A B A AB AB
A B
A
S B S
A B
A A B
A B
发生当且仅当 A 发生 B 不发生.
目 录
前一页
后一页
退 出
第一章 概率论的基本概念
§1 随机事件的概率
6) 互不相容（互斥）
7) 对立事件 （逆事件）
A B
A B A B S
A
A
B
S
S
BA
请注意互不相容与对立事件的区别！
目 录 前一页 后一页 退 出
第一章 概率论的基本概念
§1 随机事件的概率
例如，在S4 中
事件 A={t|t1000} 表示 “产品是次品” 事件 B={t|t 1000} 表示 “产品是合格品” 事件 C={t|t1500} 表示“产品是一级品” 则 A与B是互为对立事件；
A B A B,
可推广 Ak Ak ,
k k
AB A B
A A .
k k k k
目 录 前一页 后一页 退 出
第一章 概率论的基本概念
§1 随机事件的概率
例1：设 A, B, C 为三个随机事件，用A, B, C 的运 算关系表示下列各事件. （1）A 发生.
A A A
A B B A, A B B A
A B C A B A C De Morgan（德摩根）定律:
A B C AB C A BC A B C AB C A BC A B C
A B C.
目 录
前一页
后一页
退 出
后一页
退 出
5) 差事件
A B A AB AB
A B
A
S B S
A B
A A B
A B
发生当且仅当 A 发生 B 不发生.
目 录
前一页
后一页
退 出
第一章 概率论的基本概念
§1 随机事件的概率
6) 互不相容（互斥）
7) 对立事件 （逆事件）
A B
A B A B S
A
A
B
S
S
BA
请注意互不相容与对立事件的区别！
目 录 前一页 后一页 退 出
第一章 概率论的基本概念
§1 随机事件的概率
例如，在S4 中
事件 A={t|t1000} 表示 “产品是次品” 事件 B={t|t 1000} 表示 “产品是合格品” 事件 C={t|t1500} 表示“产品是一级品” 则 A与B是互为对立事件；
A B A B,
可推广 Ak Ak ,
k k
AB A B
A A .
k k k k
目 录 前一页 后一页 退 出
第一章 概率论的基本概念
§1 随机事件的概率
例1：设 A, B, C 为三个随机事件，用A, B, C 的运 算关系表示下列各事件. （1）A 发生.
A A A
A B B A, A B B A
A B C A B A C De Morgan（德摩根）定律:
第02讲 随机事件的关系与运算
概率论与数理统计主讲：四川大学四川大学第2讲随机事件的关系与运算1第2讲随机事件的关系与运算四川大学四川大学第2讲随机事件的关系与运算3在上一讲第1 讲随机试验样本空间随机事件我们介绍了样本空间、样本点和事件的概念这一讲我们来讲事件的运算四川大学第2讲随机事件的关系与运算4§1.2样本空间随机事件四川大学第2讲随机事件的关系与运算5（三）随机事件的关系与运算四川大学第2讲随机事件的关系与运算6回忆事件的概念随机试验E 的样本空间S的子集A 称为E 的随机事件，简称事件。
当A 中某一个样本点出现时，就说事件A 发生了。
由一个样本点e 组成的单点集{e} 称为基本事件。
一般的事件是由基本事件复合而成的，而基本事件是不能再分解的事件。
四川大学第2讲随机事件的关系与运算7一个事件A 是样本空间S的一个子集，因此事件之间的关系以及事件的运算可以用集合之间的关系和集合运算来处理。
设试验E的样本空间为S，而A, B,（k=1, 2,…）是S的子集。
Ak四川大学第2讲随机事件的关系与运算8事件间的关系四川大学第2讲随机事件的关系与运算10第2讲随机事件的关系与运算12四川大学2. 事件的相等如果事件A 包含事件B ( )，事件B 也包含事件A ( ) ，即A 与B 有相同的样本点，则称事件A 与事件B 相等，记作A B=即A B =⇔and A B B A⊂⊂A B ⊃A B ⊂第2讲随机事件的关系与运算13四川大学例如，记A =“考试及格”，B =“考试成绩为90分”记C =“至少有50人排队”，D =“至少有30人排队”抛两颗骰子，两颗骰子出现的点数分别记为x 和y .记E =“x +y 为奇数”，F =“两次的骰子点数奇偶性不同”{|60100}A x x =≤≤C D ⇒⊂E F⇒=A B ⇒⊃{90}B ={50,51,...}C ={30,31,...}D =事件的运算四川大学第2讲随机事件的关系与运算14第2讲随机事件的关系与运算16四川大学1kk A ∞=∑1k k A ∞= 12...n A A A n 个事件A 1, A 2, …, A n 中至少有一个发生的事件称为这些事件的和事件，1nkk A == 12...n A A A +++1nkk A ==∑或可列个事件A 1, A 2, …A n , …中至少有一个发生的事件称为这些事件的和事件，或事件的并(和)可以推广到有限或可列个事件。
概率论与数据统计1-1 随机试验
事件 A={掷出奇数点}
事件B = {掷出点数为1,3,5｝
显然 A=B
B A
A B
S
3、两事件A与B的和
“事件A、B中至少有一个发生”是一事件
把这一事件称为A与B的和，
记作 A B, 或A B
A或 B
S
A B A+B
即 A U B A、B中至少有一个发生
问如何用 Bi 表示A和 A ？ A= B1B2
A B1B2 B1B2 B1B2 B1 B2
( B1B2 B1B2 ) ( B1B2 B1B2 )
例2 设A、B、C为三个事件，用A、B、 C的运算关系表示下列各事件.
1. A发生, B与C不发生
AB C
或
A B C
些随机事件。 1、包含关系
若果事件A的发生必然导致事件B发生，
则称事件A包含于B，或称B包含A
记作A B, 或B A
对任一事件A有：
B
A A B
S
φ A S
2、两事件A与B相等
若A B且B A 同时成立， 则称A 与B相等 记作A B,
试验E：掷一颗骰子，观察出现的点数
事件A、B对立(互逆）
AB 且A+B S
事件A、B互不相容（互斥）
c
两事件A、B互逆或互为对立事件: 除要求A、B互斥即AB= 外，还要求 A+B=S
6. “A、B都发生”与“A、B不都发生”是 对立事件. 正确 7. “A、B都发生”与“A、B都不发生”是 对立事件. 错误
因为A、B都发生是 A、B都不发生是
AB的对立事件是
AB
AB
概率论与数理统计笔记(重要公式)
r = A 中样本点数 / Ω 中样本点总数 n
= A 所包含的基本事件数 / 基本事件总数 条件概率:
对偶律： A B = A B , P ( AB ) 设 A, B 是两个事件， 且 P(B)>0， 称 P(A|B)= 为 贝叶斯公式: P( B) 在事件 B 发生条件下事件 A 发生的条件概率。显然， 当 P(A)>0 时，P(B|A)=
二项分布 X ~ B(n, p)： 指数分布 X ~ E(λ) 若随机变量 X 只取两个可能值 0, 1, …, n, 而 X 的分布律为 e x x 0 若随机变量 X 的概率密度为 f ( x) k k nk pk =P {X= xk }= Cn p q , k=0, 1, 2, …, n, x0 0
设 X 为离散型随机变量， 可能取值为 x1, x2, …, xk, … 且 P 概率密度的性质： (1) f(x)≥0 {X= xk }= pk, k=1, 2, …, 则称{pk}为 X 的分布律 表格形式: f ( x)dx =1 (2) X x1, x2, …, xk, … b P p1, p2, …, pk, … (3) P{a<X≤b}= F(b)-F(a)= f ( x)dx , a≤b a {pk}性质： (4) 设 x 为 f(x)的连续点，则 F’(x)存在，且 （1） pk≥0, k=1, 2, … F’(x)= f(x) （2） pk =1 均匀分布 X ~ U (a, b) k 1 若随机变量 X 的概率密度为 在求离散型随机变量的分布律时，首先要找出其所有可能 1 , a≤x≤b 的取值，然后再求出每个值相应的概率 ba f(x) = 在实际应用中，有时还要求“X 满足某一条件”这样事件的 概率， 求法就是把满足条件的 xk 所对应的概率 pk 相加可得 0, 其他 则称 X 服从区间[a,b]上的均匀分布，其分布函数为 其分布函数 F(x) = pk xk x 0, x≤a 0-1 分布： xa F(x) = , a<x<b 若随机变量 X 只取两个可能值 0, 1，且 ba P {X=1}=p, P{X=0}=q 1, x≥b 其中 0<p<1, q=1-p, 则称 X 服从 0-1 分布. X 的分布律为 设 X ~ U (a, b), a≤c<d≤b，即[a,b] [c,d]，则 X 0 1 d c P{c≤X≤d}= P q p ba
1随机事件与事件间的关系与运算介绍
1随机事件与事件间的关系与运算介绍事件是指在一个试验或观察中，可能发生的一系列结果的集合。
随机事件是指在试验过程中，其结果是由一定的概率决定的事件。
事件间的关系与运算是指通过不同的操作来描述和处理事件之间的关系。
事件间的关系包括并、交、差、互斥、包含和互余等。
1.并：指两个事件A和B同时发生的情况，用符号A∪B表示。
A∪B 的结果是包含了A和B两个事件的所有可能结果。
比如，A表示一枚硬币正面朝上，B表示一颗骰子掷出的结果是偶数，那么A∪B表示硬币正面朝上或者骰子掷出的结果是偶数。
2.交：指两个事件A和B同时发生的情况，用符号A∩B表示。
A∩B 的结果是A和B共同的可能结果。
比如，A表示一枚硬币正面朝上，B表示一颗骰子掷出的结果是偶数，那么A∩B表示硬币正面朝上并且骰子掷出的结果是偶数。
3.差：指事件A发生而事件B不发生的情况，用符号A-B表示。
A-B 的结果是事件A中除了事件B包含的结果之外剩余的可能结果。
比如，A 表示一枚硬币正面朝上，B表示一颗骰子掷出的结果是偶数，那么A-B表示硬币正面朝上但骰子掷出的结果不是偶数。
4.互斥：指两个事件A和B不可能同时发生的情况，用符号A∩B=∅表示。
如果A和B互斥，则它们的交集为空集。
比如，A表示一枚硬币正面朝上，B表示一枚硬币反面朝上，两个事件是互斥的，即硬币不可能同时正面和反面朝上。
事件间的运算包括概率加法和概率乘法。
1.概率加法：对于两个互斥事件A和B，其并的概率等于各自概率的和，即P(A∪B)=P(A)+P(B)。
这个运算用于计算两个互斥事件中至少发生一个的概率。
2.概率乘法：对于两个独立事件A和B，其交的概率等于各自概率的乘积，即P(A∩B)=P(A)×P(B)。
这个运算用于计算两个独立事件同时发生的概率。
需要注意的是，概率加法和概率乘法只适用于互斥事件和独立事件。
此外，事件间的包含和互余关系也常用于描述事件的关系。
1.包含：若事件A包含事件B，表示事件B发生必然导致事件A发生，用符号A包含B表示。
概率论-1-2随机事件间的关系及运算
若事件 A 的出现必然导致事件 B 不出现, B 出现也必然导致 A不出现,则称事件 A与B互不相
容, 即
A B AB .
实例 抛掷一枚硬币, “出现正面” 与 “出现反面” 是互不相容的两个事件.
实例 抛掷一枚骰子, 观察出现的点数 . “骰子出现1点”互斥 “骰子出现2点”
图示 A 与 B 互斥.
四、小结
1. 随机试验、样本空间与随机事件的关系
随机试验
样本空间 子集 随机事件
基本事件，复合事件，必然事件， 不可能事件都是随机事件
学习了事件的运算及运算律，运算的 目的是什么？
用简单事件表示复合事件（复合事件分解 成简单事件）
(*)2. 概率论与集合
S 样本空间，必然事件
互为对立事件
二、随机事件间的关系及运算
事件是集合，就可以用集合间的关系和运 算来处理,我们结合 p4 图来学习：
设试验 E 的样本空间为S, 而 A, B, Ak (k 1,2,)是 S 的子集.
二、随机事件间的关系及运算（续）
1. 包含关系 子事件 A B.
实例 “长度不合格” 必然导致 “产品不合格” 所以B=“产品不合格”包含A=“长度不合格”. 图示 B 包含 A.
(2) 三个事件都出现;
(3)三个事件至少有一个出现;
(4) 不多于一个事件出现; (5) A, B 至少有一个出现, C 不出现; (6) A, B, C 中恰好有两个出现.
解(1) ABC; (2) ABC; (3) A B C;
(4) ABC ABC ABC ABC;
(5) ( A B) C; (6) ABC ABC ABC.
复合事件—由若干个基本事件组合而成的事件.
.1-1随机试验与随机事件
将不确定性数量化，来尝试回答这 些问题，是直到20世纪初叶才开始的. 还不能说这个努力已经十分成功了，但 就是那些已得到的成果，已经给人类活 动的一切领域带来了一场革命. 这场革命为研究新的设想，发展自 然科学知识，繁荣人类生活，开拓了道 路. 而且也改变了我们的思维方法，使 我们能大胆探索自然的奥秘.
i 1
Ai Ai Ai Ai
i 1
n
n
n
n
i 1
i 1
例1 袋中有10个球，分别编号为1～10，从中任取 一球，设 A＝{取出的球号码为偶数}
B＝{取出的球号码为奇数} C＝{取出的球号码小于5} 则事件 （ 1） A B （ 2） A B
s
为必然事件 为不可能事件
5. A B 称事件A 与事件B 的差事件
A B 发生 事件 A 发生， 但事件 B 不发生
A1 , A2 ,, An ,的积事件记 A1 A2 An Ai
i 1
i 1
A
B
S
A B
6. AB 称事件A与事件B
互斥(互不相容)
s
A
A、B不可能同时发生
或，事件A 是事件B的子事件。 B A 事件A发生时事件B必发生 2. A B 称A事件与B相等 A B 且 B A S 称事件 A 与事件 B 3. A B A 的和（并）事件 A B B A B 发生 事件A与事件B 至少有一个发生 n A1 , A2 ,, An 的和事件记 A1 A2 An Ai
(H,T)： (T,H): (T,T)：
H H T T H T H T
义上提供了一个理想试 验的模型：
在每次试验中必有 一个样本点出现且仅有 一个样本点出现 .
1随机事件与事件间的关系与运算介绍
四
事件间的运算法则
1）幂等律: A A A,
AA A
2）交换律: A B B A, A B B A 3）结合律: 4）分配律:
A B C A B C A B C A B C
( A B) C A C B C; C ( A B) C A C B
2
A3
( 2 ) A1 A
2
A3 A 1 A2 A3 A 1 A2 A3
(3 ) A 1 A 2 A3
(4) A1 A2 A3
(5) (3) (2)
例2：已知A表示事件“全班学生英语成绩都及格”，则
A 表示什么含义？
§1
随机事件的概率
练习：设 A, B, C 为三个随机事件，用A, B, C 的运 算关系表示下列各事件. (1) A 发生，B 与 C 都不发生.
AB C .
(2) A ,B , C 都发生.
ABC .
(3) A ，B , C 至少有一个发生.
A B C.
目 录
前一页
后一页
退 出
(5) A ，B , C 都不发生.
ABC .
(6) A ，B , C 不多于一个发生.
ABC
AB C A BC A B C.
(7) A ，B , C 不多于两个发生.
A B A B , 且 B A.
例：若A=“不大于7的整数”，B=“小于或者等于7 的整数”，则A=B。
目 录 前一页 后一页 退 出
3) 和（并）事件 ：“事件A与B至少有一个发生”，称 为A与B的和事件，记为 例：某产品分为一，二，三，四 等品，其中一、二等品为合格品， 三、四等品为不合格品。若 Ai=“i 等品” (i=1，2，3 ,4）; B=“合格品”，C=“不合格品”， B A 则: B= A1+ A2 ， C= A3+ A4
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
E6: 将一枚硬币连抛三次，考虑正反面出现的情况； 将一枚硬币连抛三次，考虑正反面出现的情况；
S6 : {HHH, HHT, HTH, THH，HTT，THT，TTH, TTT } ， ， ，
E7: 将一枚硬币连抛三次，考虑正面出现的次数 将一枚硬币连抛三次，考虑正面出现的次数;
S7 : { 0, 1, 2, 3 }
B= A
请注意互不相容与对立事件的区别！ 请注意互不相容与对立事件的区别！
目 录 前一页 后一页 退 出
第一章 概率论的基本概念
§1 随机事件Biblioteka 概率例如， 例如，在S4 中 产品是次品” 事件 A={t|t<1000} 表示 “产品是次品” < 产品是合格品” 事件 B={t|t ≥ 1000} 表示 “产品是合格品” 事件 C={t|t≥1500} 表示“产品是一级品” ≥ 表示“产品是一级品” 则 A与 B 是互为对立事件； 与 是互为对立事件； A与 C 是互不相容事件； 与 是互不相容事件；
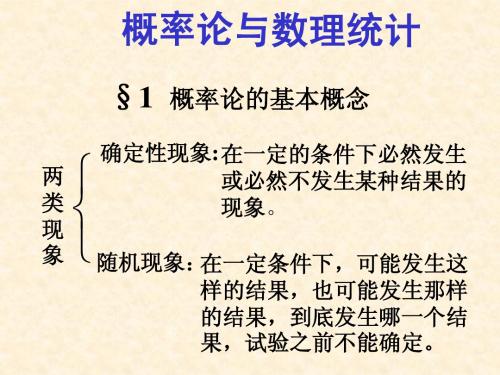
经济、科技、教育、 概率论与数理统计 在经济、科技、教育、管理和 军事等方面已得到广泛应用。 军事等方面已得到广泛应用。 在生活当中，经常会接触到一 现象： 在生活当中，经常会接触到一些现象： 确定性现象：在一定条件下必然发生的现象。 确定性现象：在一定条件下必然发生的现象。 随机现象：在个别实验中其结果呈现出不确定性 随机现象：在个别实验中其结果呈现出不确定性； 不确定性； 在大量重复实验中其结果又具有统计规律性的现象。 在大量重复实验中其结果又具有统计规律性的现象。 统计规律性的现象 概率论与数理统计是研究和揭示随机现象统计规律 概率论与数理统计是研究和揭示随机现象统计规律 性的一门学科，是重要的一个数学分支。 性的一门学科，是重要的一个数学分支。
8. 生物学中研究 群体的增长问题时， 群体的增长问题时， 提出了生灭型《随机模型》 提出了生灭型《随机模型》，传染病流行问 题要用到多变量非线性《生灭过程》 题要用到多变量非线性《生灭过程》； 9. 许多服务系统，如电话通信、船舶 许多服务系统，如电话通信、 装卸、机器维修、病人候诊、存货控制、 装卸、机器维修、病人候诊、存货控制、 水库调度、购物排队、红绿灯转换等， 水库调度、购物排队、红绿灯转换等，都
数理统计Ⅱ 数理统计Ⅱ
教材： 概率论与数理统计》 教材：《概率论与数理统计》 第三版 浙江大学 盛骤等 编 高等教育出版社 教 师： 杨晓霞 办公室: 办公室: 理学院 203 电 话: 62338357
e-mail: yxx77@
概率(或然率或几率 概率 或然率或几率) —— 随机事件出现 或然率或几率 其起源与博弈问题有关. 的可能性的量度—— 其起源与博弈问题有关 的可能性的量度 概率论是一门研究客观世界随机现象数量 概率论是一门研究客观世界随机现象数量 数学分支学科. 规律的 数学分支学科 16世纪意大利学者开始研究掷骰子等赌博 世纪意大利学者开始研究掷骰子等赌博 中的一些问题； 世纪中叶 法国数学家B. 世纪中叶， 中的一些问题；17世纪中叶，法国数学家 帕 斯卡、荷兰数学家C. 斯卡、荷兰数学家 惠更斯 基于排列组合的方 的赌博问题， 解决了“ 法，研究了较复杂 的赌博问题， 解决了“ 合理 分配赌注问题” 分配赌注问题” ( 即得分问题 ).
目 录
前一页
后一页
退 出
E1：抛一枚硬币，观察正面 （Heads）、反面 抛一枚硬币，观察正面H（ ）、反面 ）、反面T （Tails）出现的情况。 ）出现的情况。 S1 : { H , T } E2：抛一颗骰子，观察出现的点数。 抛一颗骰子，观察出现的点数。 E4：观察某一电子元件的寿命。 观察某一电子元件的寿命。
本学科的应用
概率统计理论与方法的应用几乎遍及 所有科学技术领域、 所有科学技术领域、工农业生产和国民经 济的各个部门中. 济的各个部门中 例如 1. 气象、水文、地震预报、人口控制 气象、水文、地震预报、 及预测都与《概率论》紧密相关； 及预测都与《概率论》紧密相关； 2. 产品的抽样验收，新研制的药品能 产品的抽样验收， 否在临床中应用，均要用到《假设检验》 否在临床中应用，均要用到《假设检验》；
第一章 概率论的基本概念
§1 随机事件的概率
这些试验具有以下特点： 这些试验具有以下特点： 1. 可以在相同的条件下重复进行； 可以在相同的条件下重复进行； 2. 进行一次试验之前不能确定哪一个结果会出现； 进行一次试验之前不能确定哪一个结果会出现； 3. 每次试验的可能结果不止一个，并且能事先明确 每次试验的可能结果不止一个， 试验的所有可能结果。 试验的所有可能结果。 称具备上面三个特点的试验为随机试验。 称具备上面三个特点的试验为随机试验。
3. 寻求最佳生产方案要进行《实验设计》 寻求最佳生产方案要进行《实验设计》 数据处理》 和《数据处理》； 4. 电子系统的设计 火箭卫星的研制及其 电子系统的设计, 发射都离不开《可靠性估计》; 发射都离不开《可靠性估计》 5. 处理通信问题, 需要研究《信息论》； 处理通信问题 需要研究《信息论》 6. 探讨太阳黑子的变化规律时 《时间 探讨太阳黑子的变化规律时,《 序列分析》方法非常有用; 序列分析》方法非常有用 7. 研究化学反应的时变率，要以《马尔 研究化学反应的时变率，要以《 可夫过程》 来描述; 可夫过程》 来描述
第一章 概率论的基本概念
§1 随机事件的概率
3) 随 机 事 件
随机事件 : 称试验 E 的样本空间 S 的子集为 E 的 随机事件， 等等； 随机事件，记作 A, B, C 等等； 由一个样本点组成的单点集； 基本事件 : 由一个样本点组成的单点集； 本身； 必然事件 : 样本空间 S 本身； 空集 不可能事件 : 空集。 我们称一个随机事件发生当且仅当它所包 我们称一个随机事件发生当且仅当它所包 随机事件发生当且仅当 含的一个样本点在试验中出现。 在试验中出现 含的一个样本点在试验中出现。
目 录 前一页 后一页 退 出
第一章
概率论的基本概念
§1 随机事件的概率 §2 等可能概型 §3 条件概率 §4 独立性
目 录
前一页
后一页
退 出
第一章 概率论的基本概念
§1 随 机 事 件 的 概率
一 随机试验
二 事件间的关系与运算
三 频率与概率
目 录
前一页
后一页
退 出
第一章 概率论的基本概念
事件 A U B
α
发生当且仅当 A, B 至少发生一个 .
U Aα 表示 Aα 中至少发生一个 α
目 录
.
前一页 后一页 退 出
第一章 概率论的基本概念
§1 随机事件的概率
4) 积（交）事件 A I B = AB
事件 A I B 发生当且仅当 A , B 同时发生 同时发生.
A
B S
I Aα 表示所有 Aα 同时发生 . α
S2 : { 1, 2, 3, 4, 5, 6 } S E3：观察某一时间段通过某一路口的车辆数。 3 : {0,1,2,3……} 观察某一时间段通过某一路口的车辆数。 S4 : { t | t ≥ 0 }
E5：观察某地区一昼夜的最低温度和最高温度。 观察某地区一昼夜的最低温度和最高温度。
S5 : { ( x , y ) | T 0≤ x ≤ y ≤ T1 }
α
目 录 前一页 后一页
退 出
第一章 概率论的基本概念
§1 随机事件的概率
考察下列事件间的包含关系： 考察下列事件间的包含关系：
AB
AB AB
A
B
AU B
B B
A A U B A U
目 录
前一页
后一页
退 出
第一章 概率论的基本概念
§1 随机事件的概率
5) 差事件
A B = A AB = AB
E1：抛一枚硬币，观察正面 （Heads）、反面 抛一枚硬币，观察正面H（ ）、反面 ）、反面T （Tails）出现的情况。 ）出现的情况。 E2：抛一颗骰子，观察出现的点数。 抛一颗骰子，观察出现的点数。 E3：观察某一时间段通过某一路口的车辆数。 观察某一时间段通过某一路口的车辆数。 E4：观察某一电子元件的寿命。 观察某一电子元件的寿命。 E5：观察某地区一昼夜的最低温度和最高温度。 观察某地区一昼夜的最低温度和最高温度。 E6: 将一枚硬币连抛三次，考虑正反面出现的情况； 将一枚硬币连抛三次，考虑正反面出现的情况； E7: 将一枚硬币连抛三次，考虑正面出现的次数 将一枚硬币连抛三次，考虑正面出现的次数;
二 、 事件间的关系与运算
1) 包含关系
A B
A B S
如果A发生必导致 发生，则 如果 发生必导致B发生 发生必导致 发生，
A B
2）相等关系 ）
A = B A B , 且 B A.
目 录 前一页 后一页 退 出
第一章 概率论的基本概念
§1 随机事件的概率
3) 和（并）事件
AU B
A
B S
§1 随机事件的概率
一、 随 机 试验 1) 随机试验 随机试验（Experiment ）
这里试验的含义十分广泛， 这里试验的含义十分广泛，它包括各种各样 的科学实验，也包括对事物的某一特征的观察。 的科学实验，也包括对事物的某一特征的观察。 其典型的例子有： 其典型的例子有：
目 录
前一页
后一页
退 出
对客观世界中随机现象的分析产生了概率 论；使 概率论 成为 数学的一个分支的真正奠 基人是瑞士数学家J.伯努利 伯努利； 基人是瑞士数学家 伯努利；而概率论的飞速 发展则在17世纪微积分学说建立以后 世纪微积分学说建立以后. 发展则在 世纪微积分学说建立以后 第二次世界大战军事上的需要以及大工业 与管理的复杂化产生了运筹学、系统论、 与管理的复杂化产生了运筹学、系统论、信息 控制论与数理统计学等学科. 论、控制论与数理统计学等学科 数理统计学是一门研究怎样去有效地收集 研究怎样去有效地收集、 数理统计学是一门研究怎样去有效地收集、 整理和分析带有随机性的数据， 整理和分析带有随机性的数据，以对所考察的 问题作出推断或预测， 问题作出推断或预测，直至为采取一定的决策 数学分支学科. 和行动提供依据和建议的 数学分支学科