六年级下册奥数专题练习-余数问题-全国通用
六年级下册数学专题练习：数论(五) 余数问题-全国通用 无答案
【知识点概述】一、带余除法的定义及性质：1.带余除法的定义：一般地，如果a是整数，b是整数（b≠0）,若有a÷b=q……r，也就是a＝b×q＋r, 0≤r＜b；(1)当0r=时：我们称a可以被b整除，q称为a除以b的商或完全商(2)当0r≠时：我们称a不可以被b整除，q称为a除以b的商或不完全商2.和余数相关的一些重要性质：(以下a,b,c均为自然数)性质1：余数小于除数性质2：=⨯+被除数除数商余数除数（被除数-余数）商=÷=÷商（被除数-余数）除数性质3：a与b的和除以c的余数，等于a,b分别除以c的余数之和，或这个和除以c的余数。
例如：23，16除以5的余数分别是3和1，所以23+16=39除以5的余数等于4，即前两个余数的和3+1.当余数的和比除数大时，所求的余数等于余数之和再除以c的余数。
例如：23，19除以5的余数分别是3和4，所以23+19=42除以5的余数等于3+4=7除以5的余数，即2.性质4：a与b的乘积除以c的余数，等于a,b分别除以c的余数的积，或者这个积除以c所得的余数。
例如：23，16除以5的余数分别是3和1，所以(2316)⨯除以5的余数等于⨯=。
313当余数的和比除数大时，所求的余数等于余数之积再除以c的余数。
例如：23，19除以5的余数分别是3和4，所以(2319)⨯除以5的余数等于⨯=除以5的余数，即2.3412【注】对于上述性质3，4，我们都可以推广到多个自然数的情形，尤其是性质4，对于我们求一个数的n次方除以一个数的余数时非常的有用。
二、数的同余1.同余定义若两个整数a、b被自然数m除有相同的余数，那么称a、b对于模m同余，用式子表示为：a≡b ( mod m )同余式读作：a同余于b，模m由同余的性质，我们可以得到一个非常重要的推论：若两个数a，b除以同一个数m得到的余数相同，则a，b的差一定能被m整除用式子表示为：如果有a≡b ( mod m )，那么一定有a－b＝mk,k是整数，即m|(a－b)这个性质非常重要，是将同余问题与前面学过的整除问题相联系的纽带，一定要熟练掌握。
六年级下册数学试题-奥数专题训练：第二讲 余数问题(无答案)全国通用
第二讲余数问题【知识要点】三大余数定理：1.余数的加法定理a与b的和除以c的余数，等于a,b分别除以c的余数之和，或这个和除以c的余数。
当余数的和比除数大时，所求的余数等于余数之和再除以c的余数。
2.余数的乘法定理a与b的乘积除以c的余数，等于a,b分别除以c的余数的积，或者这个积除以c 所得的余数。
当余数的和比除数大时，所求的余数等于余数之积再除以c的余数。
3.同余定理若两个整数a、b被自然数m除有相同的余数，那么称a、b对于模m同余，用式子表示为：a≡b ( mod m )，左边的式子叫做同余式。
同余式读作：a同余于b，模m。
由同余的性质，我们可以得到一个非常重要的推论：若两个数a，b除以同一个数m得到的余数相同，则a，b的差一定能被m整除用式子表示为：如果有a≡b ( mod m )，那么一定有a－b＝mk,k是整数，即m|(a－b) 【经典例题】【例1】用某自然数a去除1992，得到商是46，余数是r ，求a和r ．【基础巩固】甲、乙两数的和是1088，甲数除以乙数商11余32，求甲、乙两数．【例2】有一个大于1的整数，除45，59，101所得的余数相同，求这个数.【基础巩固】有一个整数，除39，51，147所得的余数都是3，求这个数.a ，求ab×ba．【例3】两位自然数ab与ba除以7都余1，并且b【基础巩固】学校新买来118个乒乓球，67个乒乓球拍和33个乒乓球网，如果将这三种物品平分给每个班级，那么这三种物品剩下的数量相同．请问学校共有多少个班？【例4】有一个整数，用它去除70，110，160所得到的3个余数之和是50，那么这个整数是______．【基础巩固】用自然数n去除63，91，129得到的三个余数之和为25，那么n=________【自我检测】1.有两个自然数相除，商是17，余数是13，已知被除数、除数、商与余数之和为2113，则被除数是多少？2. 22003与20032 的和除以7的余数是________．3.号码分别为101，126，173，193的4个运动员进行乒乓球比赛,规定每两人比赛的盘数是他们号码的和被3除所得的余数.那么打球盘数最多的运动员打了多少盘?4.六名小学生分别带着14元、17元、18元、21元、26元、37元钱，一起到新华书店购买《成语大词典》．一看定价才发现有5个人带的钱不够，但是其中甲、乙、丙3人的钱凑在一起恰好可买2本，丁、戊2人的钱凑在一起恰好可买1本．这种《成语大词典》的定价是多少元？5.某年的10月有五个星期六，4个星期日，这年的10月1日是星期几？【兴趣拓展】一个大于1的数去除290，235，200时，得余数分别为a，2a，++a，5则这个自然数是多少？。
小学数学六年级奥数专项训练题《求余数》
小学数学六年级奥数专项训练题《求余数》
1、《求余数》难度：★★★★
22019+20192除以7的余数是多少？
答：余数是。
解析：【】
2、《实际工期》难度：★★★
一项工程，甲、乙两人合做8天可完成。
甲单独做需12天完成。
现两人合做几天后，余下的工程由乙独自完成，使乙前后两段所用时间比为1:3？
：两人合做天后，余下的工程由乙独自完成，使乙前后两段所用时间比为1:3。
解析：【】
3、《正方形》难度：★★★
洋洋家有一块正方形的地，它的周长和它的面积相等，这块正方形地的面积是多少平方米？边长是多少米？
答：面积是16平方米，边长是4米。
解析：【】
4、《赔还是赚》难度：★★★
王婶的水果商店进了两批水果，售出价都是96元，第一批水果热销，比成本价高20%卖出，第二批水果滞销，在成本价基础上降价1/5卖出，总的来说这两批水果（填赚或赔）了多少元？
：这两批水果了元钱。
解析：【】
5、《让利销售》难度：★★★★
孙某的小杂货店新进一批皮球，进价每只1.5元，卖出价每只2元。
卖到只剩20只皮球时，开始让利，以9折售出。
皮球全部卖完后，共得利润86元。
这批皮球的总数是多少只？
答：这批皮球的总数是只。
解析：【】。
六年级奥数专题练习：余数问题
六年级奥数专题练习：余数问题
一、同余的定义：
①若两个整数a、b除以m的余数相同，则称a、b对于模m同余。
②已知三个整数a、b、m，如果m|a-b，就称a、b对于模m同余，记作a≡b(modm)，读作a同余于b模m。
二、同余的*质：
①自身*：a≡a(modm)；
②对称*：若a≡b(modm)，则b≡a(modm)；
③传递*：若a≡b(modm)，b≡c(modm)，则a≡c(modm)；
④和差*：若a≡b(modm)，c≡d(modm)，则a+c≡b+d(modm)，a-c≡b-d(modm)；
⑤相乘*：若a≡b(modm)，c≡d(modm)，则a×c≡b×d(modm)；
⑥乘方*：若a≡b(modm)，则an≡bn(modm)；
⑦同倍*:若a≡b(modm)，整数c，则a×c≡b×c(modm×c)；
三、关于乘方的预备知识：
①若A=a×b，则MA=Ma×b=（Ma）b
②若B=c+d则MB=Mc+d=Mc×Md
四、被3、9、11除后的余数特征：
①一个自然数M，n表示M的各个数位上数字的和，则M≡n(mod9)或（mod3）；
②一个自然数M，X表示M的各个奇数位上数字的和，Y表示M 的各个偶数数位上数字的和，则M≡Y-X或M≡11-（X-Y）(mod11)；
五、费尔马小定理：如果p是质数（素数），a是自然数，且a不能被p整除，则ap-1≡1(modp)。
投诉。
小学奥数题库《数论》余数问题带余除法5星题(含解析)全国通用版
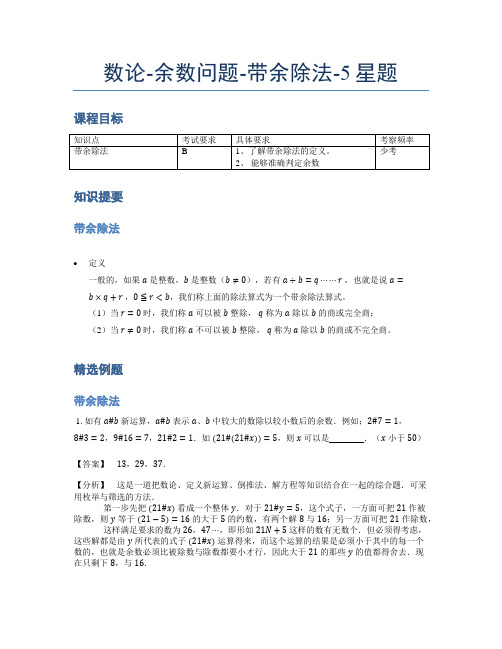
数论-余数问题-带余除法-5星题课程目标知识提要带余除法•定义一般的，如果a是整数，b是整数（b≠0），若有a÷b=q⋯⋯r，也就是说a=b×q+r，0≦r<b，我们称上面的除法算式为一个带余除法算式。
（1）当r=0时，我们称a可以被b整除，q称为a除以b的商或完全商；（2）当r≠0时，我们称a不可以被b整除，q称为a除以b的商或不完全商。
精选例题带余除法1. 如有a#b新运算，a#b表示a、b中较大的数除以较小数后的余数．例如；2#7=1，8#3=2，9#16=7，21#2=1．如(21#(21#x))=5，则x可以是．（x小于50）【答案】13，29，37．【分析】这是一道把数论、定义新运算、倒推法、解方程等知识结合在一起的综合题．可采用枚举与筛选的方法．第一步先把(21#x)看成一个整体y．对于21#y=5，这个式子，一方面可把21作被除数，则y等于(21−5)=16的大于5的约数，有两个解8与16；另一方面可把21作除数，这样满足要求的数为26，47⋯，即形如21N+5这样的数有无数个．但必须得考虑，这些解都是由y所代表的式子(21#x)运算得来，而这个运算的结果是必须小于其中的每一个数的，也就是余数必须比被除数与除数都要小才行，因此大于21的那些y的值都得舍去．现在只剩下8，与16．第二步求：(21#x)=8与(21#x)=16．对于(21#x)=8可分别解得，把21作被除数时：x=13，把21作除数时为：x=29，50，⋯形如21N+8的整数（N是正整数）．对于(21#x)=16，把21作被除数无解，21作除数时同理可得：x=37，58⋯所有形如21N+16这样的整数．（N是正整数）．所以符合条件的答案是13，29，37．2. 字母a,b,c,d,e,f,g分别代表1至7中的一个数字，若a+b+c=c+d+e=c+f+g，则c可取的值有个．【答案】3【分析】a+b+c=c+d+e=c+f+g,a+b+c+c+d+e+c+f+g=(a+b+c+d+e+f+g)+2c=(1+2+3+4+5+6+7)+2c=28+2c28+2c是3的倍数，28÷3⋯1,所以2c÷3⋯2,c=1或4或7都可满足；构造：当c=1时，(28+2)÷3=10,所以a+b=d+e=f+g=9,a=2,b=7,d=3,e=6,f=4,g=5;当c=4，(28+2×4)÷3=12,所以a+b=d+e=f+g=8,a=1,b=7,d=2,e=6,f=3,g=5;当c=7，(28+2×7)÷3=14,所以a+b=d+e=f+g=7,a=1,b=6,d=2,e=5,f=3,g=4.综上，共有3种情况．3. 1×3×5×⋯×1991的末三位数是多少？【答案】625【分析】首先，仅考虑后三位数字，所求的数目相当于1×3×5×⋯×991的平方再乘以993×995×997×999的末三位．而993×995×997×999=993×999×995×997=(993000−993)×(995000−995×3)=(993000−993)×(995000−2985),其末三位为7×15=105;然后来看前者．它是一个奇数的平方，设其为(5k)2（k为奇数），由于(5k)2=25k2=25+25(k2−1),而奇数的平方除以8余1，所以k2−1是8的倍数，则25(k2−1)是200的倍数，设25(k2−1)=200m，则(5k)2=25+25(k2−1)=25+200m,所以它与105的乘积(5k)2×105=(25+200m)×105=21000m+2625,所以不论m的值是多少，所求的末三位都是625．4. 如果某整数同时具备如下三条性质：（1）这个数与1的差是质数；（2）这个数除以2所得的商也是质数；（3）这个数除以9所得的余数是5．那么我们称这个整数为幸运数，求出所有的两位幸运数．【答案】14【分析】条件（1）也就是这个数与1的差是2或奇数，这个数只能是3或者是偶数，再根据条件（3），除以9余5，在两位的偶数中只有14，32，50，68，86，这五个数满足条件；其中86与50不符合（1），32与68不符合（2）．三个条件都符合的只有14，所以这个数是14．5. 求证：可以找到一个各位数字都是4的自然数，它是1996的倍数．【答案】见解析．【分析】1996÷4=499，下面证明可以找到1个各位数字都是1的自然数，它是499的倍数．取500个数：1，11，111，⋯⋯，111⋯⋯1（500个1）．用499去除这500个数，得到500个余数a1，a2，a3，⋯，a500．由于余数只能取0，1，2，⋯，498这499个值，所以根据抽屉原则，必有 2 个余数是相同的，这 2 个数的差就是 499 的倍数，差的前若干位是 1，后若干位是 0：11⋯100⋯0．又 499 和 10 是互质的，所以它的前若干位由 1 组成的自然数是 499 的倍数，将它乘以 4，就得到一个各位数字都是 4 的自然数，这是 1996 的倍数．6. 用 1、2、3、4、5 各一个可以组成 120 个五位数，你能否从这 120 个数里面找出 11 个数来，使得它们除以 11 的余数各不相同？如果五个数字是 1、3、4、6、8 呢？【答案】 不能；不能．【分析】 （1）不能．五位数有 3 个奇位数字和 2 个偶位数字，将 1、2、3、4、5 分到奇偶位有 C 52=10 种方法，那么形成的五位数最多只能产生 10 种除以 11 的余数，无法出现 11 种除以 11 的余数．（2）不能．与（1）同理．当然，想不到这个的同学一一枚举即可，（1）中很明显余数为 0 的是构造不出来的，此外，余数为 2、4、6 也无法构造出来．（2）中余数为 6、7、10 的是构造不出来的．7. 任意给定一个正整数 n ，一定可以将它乘以适当的整数，使得乘积是完全由 0 和 7 组成的数．【答案】 见解析．【分析】 考虑如下 n +1 个数：7，77，777，⋯⋯，77⋯7⏟n 位，77⋯7⏟n+1位，这 n +1 个数除以 n 的余数只能为 0，1，2，⋯⋯，n −1 中之一，共 n 种情况，根据抽屉原理，其中必有两个数除以 n 的余数相同，不妨设为 77⋯7⏟p 位和 77⋯7⏟q 位（p >q ），那么 77⋯7⏟p 位−77⋯7⏟q 位=77⋯7⏟(p−q)位00⋯0⏟q 位 是 n 的倍数，所以 n 乘以适当的整数，可以得到形式为 77⋯7⏟(p−q)位00⋯0⏟q 位的数，即由 0 和 7 组成的数．8. 两个不等的自然数 a 和 b ，较大的数除以较小的数，余数记为 a ⊙b ，比如 5⊙2=1，7⊙25=4，6⊙8=2．（1）求 1991⊙2000，(5⊙19)⊙19，(19⊙5)⊙5；（2）已知 11⊙x =2，而 x 小于 20，求 x ；（3）已知 (19⊙x)⊙19=5，而 x 小于 50，求 x ．【答案】 （1）9；3；1；（2）x =3,9,13；（3）x =12,26,33,45．【分析】 （1）1991⊙2000=9；由5⊙19=4，得(5⊙19)⊙19=4⊙19=3；由19⊙5=4，得(19⊙5)⊙5=4⊙5=1．（2）我们不知道11和x哪个大（注意，x≠11），即哪个作除数，哪个作被除数，这样就要分两种情况讨论．①x<11，这时x除11余2，x整除11−2=9．又x⩾3（因为x应大于余数2），所以x=3或9．②x>11，这时11除x余2，这说明x是11的倍数加2，但x<20，所以x=11+2=13．因此（2）的解为x=3,9,13．（3）这个方程比（2）又要复杂一些，但我们可以用同样的方法来解．用y表示19⊙x，不管19作除数还是被除数，19⊙x都比19小，所以y应小于19．方程y⊙19=5，说明y除19余5，所以y整除19−5=14，由于y⩾6，所以y=7,14．当y=7时，分两种情况解19⊙x=7．①x<19，此时x除19余7，x整除19−7=12．由于x⩾8，所以x=12．②x>19，此时19除x余7，x是19的倍数加7，由于x<50，所以x=19+7= 26，x=19×2+7=45．当y=14时，分两种情况解19⊙x=14．①x<19，这时x除19余14，x整除19−14=5，但x大于14，这是不可能的．②x>19，此时19除x余14，这就表明x是19的倍数加14，因为x<50，所以x=19+14=33．总之，方程(19⊙x)⊙19=5有四个解，x=12,26,33,45．9. 箱子里面有两种珠子，一种每个19克，另一种每个17克，所有珠子的重量为2017克，求两种珠子的数量和所有可能的值．【答案】107，109，111，113，115，117【分析】设19克的珠子有a个，17克的珠子有b个，根据题意列方程得19a+17b=2017利用余数分析法解不定方程．由于2017÷19余3所以有17b÷19余3，解得b=8从而得出a=99，即19×99+17×8=2017,即找到一组解为{a=99b=8此时a+b=99+8=107，由于19和17互质，那么只需要将a顺次减少17，b顺次增大19即可得出其他解{a=82b=27{a=65b=46{a=48b=65{a=31b=84{a=14b=103对于a+b的和而言，共可算得6个答案，分别为：107，109，111，113，115，117．10. 一个自然数除以8得到的商加上这个数除以9的余数，其和是13．求所有满足条件的自然数．【答案】108，100，92，84，76，68，60，52，44．【分析】本题考査学生掌握带余除法及枚举筛选的综合能力．设所求的自然数为n，且设n除以8商x余r，n除以9商a余y，于是有n=8x+r=9a+y(其中x+y=13)．又已知0⩽y⩽8，0⩽r⩽7，下面分类讨论：若y=0，则x=13，得8×13+r=9a，解出r=4，故n=8×13+4=108；若y=1，则x=12，得8×12+r=9a+1，解出r=4，故n=8×12+4=100；类似地，若y=2、3、4、5、6、7、8，则分别有x=11、10、9、8、7、6、5，解得r=4，故n=8×11+4=92；n=8×10+4=84；n=8×9+4=76；n=8×8+4=68；n=8×7+4=60；n=8×6+4=52；n=8×5+4=44．答：满足条件的然数共有9个：108、100、92、84、76、68、60、52、44．说明：本题也可以先确定r=4．由y=13−x代人可得8x+r=9a+(13−x)，即9x−9a=13−r，于是13−r的差应是9的倍数，又0⩽r⩽7，故r=4．。
小学六年级奥数题及答案-余数问题
小学六年级奥数题及答案:余数问题
教案是教师为顺利而有效地开展教学活动，根据课程标准，教学大纲和教科书要求及学生的实际情况，以课时或课题为单位，对教学内容、教学步骤、教学方法等进行的具体设计和安排的一种实用性教学文书，包括教材简析和学生分析、教学目的、重难点、教学准备、教学过程及练习设计等，下面是由小编为大家整理的范文模板,仅供参考,欢迎大家阅读.
以下是小编为大家整理的【小学六年级奥数题及答案:余数问题】，供大家参考！
把1至_这_个自然数依次写下来得到一个多位数_3456789....._,这个多位数除以9余数是多少?
答案与解析：
首先研究能被9整除的数的特点：如果各个数位上的数字之和能被9整除，那么这个数也能被9整除;如果各个位数字之和不能被9整除，那么得的余数就是这个数除以9得的余数。
解题：首先，任意连续9个自然数之和能被9整除，也就是说，一直写到_能被9整除。
所以答案为1
小学六年级奥数题及答案:余数问题.到电脑，方便收藏和打印：。
小学奥数题库《数论》余数问题中国剩余定理2星题(含解析)全国通用版
数论-余数问题-中国剩余定理-2星题课程目标知识提要中国剩余定理•概述中国剩余定理即我们常说的“物不知数”，是利用同余式组来求解的一类问题。
A、一个数分别除以两个数余数相同的时候，将原数减去这个余数之后可以整除那两个数B、上述情况下的余数虽有不同，但与各自对应的除数的差相同，将原数加上这个差之后便可以整除C、其他情况下，凑出相同余数之后，运用第一种情况的方法．精选例题中国剩余定理1. 5年级3班同学上体育课，排成3行少1人，排成4行多3人，排成5行少1人，排成6排多5人，问上体育课的同学最少人．【答案】59．【分析】分析题意知，这个班的人数除以3余2，除以4余3，除以5余4，除以6余5，凑缺相同，这个班人数为[3、4、5、6]−1=59（人）．2. 一个数，除以11余7，除以13余9，除以19余15，问满足条件的最小自然数是．【答案】2713．【分析】我们发现两个算式除数与余数的差都相等，所以把他们都处理成都缺4能被整除，这样得[11、13、19]−4=2713．3. 一个大于10的数，除以5余3，除以7余1，问满足条件的最小自然数为．【答案】43．【分析】根据总结，我们发现两个数的除数与余数的和都是5+3=7+1=8，这样我们可以把余数都处理成都余8，所以[5、7]=35，所以这个数就是35+8=43．4. 一个大于10的数，除以5余3，除以7余1，除以9余8，问满足条件的最小自然数为．【答案】323．【分析】根据总结，我们发现三个数中两个数的除数与余数的和都是5+3=7+1=8，这样我们可以把余数都处理成都余8，所以[5、7、9]=315，所以这个数就是315+8=323．5. 一个大于100的数，除以9余3，除以11余1，问满足条件的最小自然数为．【答案】111．【分析】据题意，我们发现两个数的除数与余数的和都是9+3=11+1=12，这样我们可以把余数都处理成都余12，所以[9、11]=99，所以这个数就是99+12=111．6. 一个大于2000数，除以11余5，除以13余3，除以17余16，问满足条件的最小自然数为．【答案】2447．【分析】根据题意，我们发现三个算式中两个数的除数与余数的和都是11+5=13+3= 16，这样我们可以把余数都处理成都余16，所以[11、13、17]=2431，所以这个数就是2431+16=2447．7. 有一堆水果糖，如果按8块一份来分，最后剩下2块；如果按9块一份来分，最后剩3块；如果按10块一份来分，最后剩下4块．这堆糖至少有块．【答案】354【分析】这堆水果糖的总数被8除余2，被9除余3，被10除余4，如果增加6块就刚好是8、9、10的公倍数，又8、、9、10的最小公倍数是360．所以这堆水果糖至少有360−6=354(块)．8. 某个自然数除以2余1，除以3余2，除以4余1，除以5也余1，则这个数最小是．【答案】41【分析】这个自然数除以2、4、5都余1，[2,4,5]=20，所以这个数应满足1+20n，同时除以3余2，所以最小是41．9. 有一筐苹果，甲班分，每人3个还剩11个；乙班分，每人4个还剩10个；丙班分，每人5个还剩12个．那么这筐苹果至少个．【答案】62【分析】设有x个苹果．因为11除以3余2，所以x除以3余2；因为10除以4余2，所以x除以4余2；因为12除以5余2，所以x除以5余2．又因为x大于12，x=[3,4,5]+2=60+2=62（个）．10. 一个自然数能被11整除，除以13余12；除以15余13；这个数最小为．【答案】1078．【分析】n除以15余13：最小为13，通式为13+15k1；n除以13余12：k1最小为6，则有13+15×6=103，通式为103+[15,13]k2=103+ 195k2．n除以11余0：k2最小为5，则有103+195×5=1078．11. 一个大于3的数，除以7余4，除以9余6，除以11余8，问满足条件的最小自然数是．【答案】690．【分析】我们发现两个算式除数与余数的差都相等，所以把他们都处理成都缺3能被整除，这样得[7、9、11]−3=690．12. 一个大于2的数，除以3余1，除以5余3，除以7余5，问满足条件的最小自然数是．【答案】103．【分析】我们发现两个算式除数与余数的差都相等，所以把他们都处理成都缺2能被整除，这样得[3、5、7]−2=103．13. 小明心里想了一个正整数．并且求出了它分别被14和21除后所得的余数，已知这两个余数的和是33，则该整数被42除的余数是．【答案】41【分析】该整数除以14的余数不大于13，除以21余数不大于20，所以这两个余数的和不大于33，而由题有这两个余数的和恰好是33，所以该整数除以14余数是13，除以21余数是20．这个数加上1就是14和21的倍数，而[14,21]=42，所以这个数可以表示成42k−1的形式，被42除的余数是41．14. 智慧老人到小明的年级访问，小明说他们年级共一百多名同学，老人请同学们按三人一行排队，结果多出一人，按五人一行排队，结果多出二人，按七人一行排队，结果多出一人，老人说我知道你们年级人数应该是人．【答案】127【分析】根据条件，该数除以3余1，除以5余2，除以7余1，逐级满足法，令该数为a，则a÷3⋯⋯1 ①a÷5⋯⋯2 ②a÷7⋯⋯1 ③符合条件①的有1，4，7，10，13，16，⋯．同时满足①、②的最小值为7，以后a=7+15m均满足①、②；现在来看(7+15m)除以7余1，则15m除以7余1，则m最小取1，符合，最小的符合的数为a=22．以后每隔[3,5,7]=105即符合．由于该年级有100多名学生，为22+105= 127．15. 某个两位数是2的倍数，加1是3的倍数，加2是4的倍数，加3是5的倍数，那么这个两位数是．【答案】62【分析】由题可知，此数是一个2的倍数，并且除以3、4、5都余2的数，这样的数最小是2，因为这个数是两位数，2+[3、4、5]=62.16. 某数除以11余8，除以13余10，除以17余12，那么这个数的最小可能值是．【答案】998【分析】观察到11−8＝13−10＝3，因此除以11余8，除以13余10的最小自然数为11×13−3＝140,设某数为a，则a＝143m−3m为非零自然数，只需143m−3除以17余12，而143÷17＝8⋯7,只需(7m−3)÷17＝n⋯12,即7m−15是17的倍数所以，m＝7，所以a＝143×7−3＝998.17. —个自然数被3除余2，被5除余4，并且这个数大于100且小于125，那么这个数是．【答案】104或119【分析】被3除余2，被5除余4，求出3和5的最小公倍数15，估算15的哪一个倍数大于100小于125，经计算可知，105和120介于100到125之间，再用105和120分别减1即可，这个自然数是104或119．18. 我国南宋数学家杨辉在其《续古摘奇算法》上记载了这样一个问题：“二数余一，五数余二，七数余三，九数余四，问本数．”用现代语言表述就是：“有一个数用2除余1，用5除余2，用7除余3，用9除余4，问这个数是多少？”请将满足条件的最小的自然数写在这里．【答案】157【分析】（解法一）先考虑除以5余2，除以7余3，除以9余4；用剩余定理得5×7×5+5×9×1+7×9×4=472[5,7,9]=315，故472±315k都符合除以5余2，除以7余3，除以9余4最小是472−315=157，且也符合除以2余1．（解法二）除以2余1的数有：1，3，5，7，9，11，13，15，17，⋯；除以5余2的数有：2，7，12，17⋯；除以7余3的数有：3，10，17⋯；所以满足“用2除余1，用5除余2，用7除余3”的数的形式为[2,5,7]n+17=70n+17（n为自然数）此时只需要找一个最小的n，满足除以9余4即可．当n=2时，满足除以9余4，所以满足条件的最小的自然数为70⋯2+17=15719. 一个大于10的自然数，除以5余3，除以7余1，除以9余8，那么满足条件的自然数最小为．【答案】323【分析】根据总结，我们发现三个数中前两个数的除数与余数的和都是5+3=7+1=8这样我们可以把余数都处理成8，即一个数除以5余3相当于除以5余8，除以7余1相当于除以7余8，所以可以看成这个数除以5、7、9的余数都是8，那么它减去8之后是5、7、9的公倍数．而[5,7,9]=315所以这个数最小为315+8=323.20. 红星小学组织学生划船．若乘坐大船，除1条船坐6人外，其余每船均坐17人；若乘小船，则除1条船坐2人外，其余每船均坐10人．如果学生的人数超过100、不到200，那么学生共有人．【答案】142【分析】除1条船坐6人外，其余每船均坐17人，说明总人数可以表示成17m+6的形式；除1条船坐2人外，其余每船均坐10人，说明总人数可以表示成10n+2的形式；那么有17m+6=10n+2，化简得17m+4=10n，经分析m的个位只能是8．又学生的人数超过100、不到200，所以m=8，学生的人数是17×8+6=142．21. 一个大于10的自然数，除以5余3，除以7余1，除以9余4，那么满足条件的自然数最小为．【答案】148【分析】观察发现三个数中前两个数的除数与余数的和都是5＋3＝7＋1＝8,这样我们可以把余数都处理成8，即一个数除以5余3相当于除以5余8，除以7余1相当于除以7余8，所以满足前两个条件的自然数为a＝35m＋8,下一步只需要a除以9余4，35÷9＝3⋯8,只需8＋8m除以9余4，只需8m除以9余5，最小的m＝4，因此满足所有条件的最小自然数为8＋35×4＝148.22. 有一个自然数用7除余3，用9除余4，请按照从小到大的顺序，将满足条件的前两个自然数写在这里．【答案】31，94【分析】除以7余3的数有：3，10，17，24，31⋯；除以9余4的数有：4，13，22，31⋯；所以满足“除以7余3，除以9余4”的数的形式为[7,9]n+31=63n+31（n为自然数）按照从小到大的顺序，将满足条件的前两个自然数为31，94．23. 在1到100这100个数中，被2，3，5除都有非零的余数，且余数彼此不等的数有个．【答案】6【分析】根据余数不能比除数大．一个数除以2，余数只能是1．而要求余数彼此不等，所以，这些数除以3，余数只能是2．满足以上两个条件的数为6的倍数少1．有：5、11、17、23、29、35、41、47、53、59、65、71、77、83、89、95．再满足被5除有余数，且余数不为1和2，（个位不能为5、1、7）．符合条件的数只有：23、29、53、59、83、89，共6个数．24. 一个数除以2、3、5、7、11的余数分别是1、2、3、4、5，求符合条件的最小的奇数．【答案】1523．【分析】本题实际上就是求被3、5、7、11除的余数分别是2、3、4、5的最小奇数，符合条件的最小偶数是368，只要将368加上3×5×7×11就能求得符合条件的最小奇数，这个数是368+3×5×7×11=1523．25. 有一个自然数，除以2余1，除以3余2，除以4余3，除以5余4，除以6余5，除以7余6，则这个数最小是．【答案】419．【分析】分析题意知，这个数加1就能被2,3,4,5,6,7整除，所以这个数为[2、3、4、5、6、7]−1=420−1=419．26. 一个数除以3余2，除以5余3，除以7余2，求适合此条件的最小数．【答案】23．【分析】由中国剩余定理得这个数为23．27. （1）一个自然数除以4余3，除以5也余3，这个自然数最小是多少？（2）一个自然数除以5余1，除以7余3，这个自然数最小是多少？【答案】（1）3；（2）31【分析】（1）这个自然数减去3以后是4和5的公倍数，所以最小是3．（2）这个自然数加上4以后是5和7的公倍数，所以最小是31．28. 今有物不知其数，三三数之剩二，五五数之剩四，七七数之剩三，问物几何？【答案】59【分析】70×2+21×4+15×3=269；269−105−105=59；29. 小朋友们做游戏，若7人分成一组，则最后余下5人；若9人分成一组，则最后余下5人；若11人分成一组，则最后余下5人．那么一起做游戏的小朋友至少有人．【答案】698【分析】分析题意知，小朋友的人数是7，9，11的公倍数减5，所以做游戏的小朋友的人至少有[7、9、11]+5=698（人）30. 有一批图书总数在1000本以内，若按24本书包成一捆，则最后一捆差2本；若按28本书包成一捆，最后一捆还是差2本书；若按32本包一捆，则最后一捆是30本．那么这批图书共有本．【答案】670．【分析】由题意知，这批数的总数除以24余22，除以28余26，除以32余30，[24、28、32]=672，所以这批书的数量为672k−2，又因为这批图书总数在1000本以内，所以k=1，这本书为670．31. 已知自然数A除以11余5，除以9余7，除以13余3，这个数最小是多少？【答案】1303【分析】本题属于“物不知数”问题，可以运用中国剩余定理，但需要先要找出11与9的公倍数中除以13余1的数、11与13的公倍数中除以9余1的数以及9与13的公倍数中除以11余1的数．比较麻烦．实际上，观察可知11+5=9+7=13+3=16,也就是说这个数减去16后是11、9、13的公倍数，那么这个数最小就是11、9、13的最小公倍数加上16，为11×9×13+16=1303.32. 有一个自然数，用它分别去除61、90、130都有余数，3个余数的和是26，这3个余数中最大的一个是多少？【答案】11【分析】．简答：61、90和130的和减去26得到255，255的约数中验证得满足条件的只有17，所以这个自然数是17，所以余数中最大的是130除以17的余数1133. —个盒子中装有棒棒糖100多个，如果每次取5个最后剩4个，如果每次取4个最后剩3个，如果每次取3个最后剩2个．那么如果每次取12个，最后剩多少个？【答案】11【分析】简答：除以5余4，除以4余3，除以3余2的数最小是59，满足上述条件的100以上的数是59加上若干个60，如119、179等，这些数除以12余11．34. （1）一个数除以7余2，除以11余1．这个数最小是多少？（2）有一队解放军战士，人数在150人到200人之间，从第一个开始依次按1，2，3，⋯，9的顺序报数，最后一名战士报的数是3；如果按1，2，⋯，7的顺序报数，最后一名战士报的数是4．请问：一共有多少名战士？【答案】（1）23；（2）165【分析】（1）采用逐步满足条件法．满足条件第二个条件的数位1、12、23、⋯发现23同时满足第一个条件，因此这个数最小是23．（2）战士的人数除以9余3，除以7余4，满足这两个条件最小的数是39，不断加63，直到满足限制条件，最后得到165．35. 一个自然数在1000和1200之间，且被3除余1，被5除余2，被7除余3，求符合条件的数．（使用中国剩余定理求解）【答案】1102【分析】70+21×2+15×3=70+42+45=157，157+105n在1000到1200之间．可以先写成52+105n，105×10+1050，1050+52=1102．36. 已知两个连续的两位数除以5的余数之和是5，除以6的余数之和是5，除以7的余数之和是1．求这两个两位数．【答案】77和78【分析】两个连续的两位数除以5的余数之和是5，则可以判断出第一个数除以5余2．除以6的余数之和是5，则可以判断出第一个数除以6余2或余5．除以7的余数之和是1，则可以判断出第一个数除以7余0．满足第一、三两个条件的数有7、42、77，再考虑第二个条件，只有77满足．因此这两个数为77和78．37. 一个三位数除以4余3，除以6也余3．这个三位数最大是多少？【答案】999【分析】这是一道余同的问题．满足条件的数可以表示为[4,6]×n+3，其中n为自然数．要求满足条件的最大三位数，应令n为83，即[4,6]×83+3=999．38. 一个小于200的数，它除以11余8，除以13余10，这个数是几？【答案】140．【分析】分析题意，我们发现这两个算式除数与余数的差都等于11−8=13−10=3，观察发现这个数加上3后就能同时被11和13整除，所以[11、13]=143，所以这个数是143−3=140．39. 被2，3，5除余1且不等于1的最小整数是几？【答案】31【分析】除1以外，被2除余1的所有整数是：3,5,7,9,11,⋯,27,29,31,33,⋯被3除余1的所有整数是：4,7,10,13,16,19,22,25,28,31,⋯被5除余1的所有整数是：6,11,16,21,26,31,36,⋯上面三列数中，第一个同时出现的数是31，所以31是同时满足被2，3，5除均余1且不等于1的最小数．40. 有5000多根牙签，可按6种规格分成小包．如果10根一包，那么最后还剩9根．如果9根一包，那么最后还剩8根．第三、四、五、六种的规格是，分别以8，7，6，5根为一包，那么最后也分别剩7，6，5，4根．原来一共有牙签多少根？【答案】5039【分析】设这包牙签有n根，那么加上1根后为n+1根此时有n+1根牙签即可以分成10根一包，又可以分成9根一包，还可以分成8、7、6、5根一包．所以，n+1是10、9、8、7、6、5的倍数，即它们的公倍数．[10,9,8,7,6,51=23×32×5×7=2520，即n+1是2520的倍数，在满足题下只能是2520×2=5040，所以n=5039．即原来一共有牙签5039根．41. 炒饭老师非常喜欢吃炒饭．有一天，炒饭老师给自己炒了一桶的炒饭．他算了一下，如果他每天吃3碗，最后剩下2碗；如果每天吃4碗，最后剩下2碗；如果每天吃5碗，最后剩下2碗．问炒饭老师炒了至少多少碗炒饭？【答案】62【分析】炒饭老师炒的饭的碗数减去2是3，4，5的公倍数，所以老师炒的饭的最小值为[3,4,5]+2=60+2=62（碗）．42. 被3，5除余2的最小两位数是几？【答案】2【分析】被5除余2的所有整数是：2,7,12,17,22,27,32,37⋯被3除余2的所有整数是：2,5,8,11,14,17⋯所以，被3，5除余2的最小两位数是2．43. 韩信点兵：有兵四五百，五五数之余三，七七数之余四，九九数之余五．那么这队兵有多少人？【答案】473【分析】先列出除以9余5的数，从中找除以7余4的数，再从剩下的数中找除以5余3的数．44. 刘叔叔养了400多只兔子，如果每3只兔子关在一个笼子里，那么最后一个笼子里有2只；如果每5只兔子关在一个笼子里，那么最后一个笼子里也有2只；如果每7只兔子关在一个笼子里，那么最后一个笼子里有5只．请问：刘叔叔一共养了多少只兔子？【答案】467【分析】兔子数除以3余2，除以5余2，除以7余5．所有满足前两个条件的数为2+ [3,5]×n，其中n为自然数，即2、17、32、47、⋯其中47同时满足第三个条件．所有满足条件的数为47+[3,5,7]×m，其中m为自然数．m取4时满足条件，为467．45. 一个两位数分别除以7、8、9，所得的余数的和为20．问：这个两位数是多少？【答案】62【分析】余数的和为20，则这个两位数除以7、8、9的余数分别为6、7、7或6、6、8或5、7、8．其中只有6、6、8的情况存在满足条件的两位数为62．46. 有一个自然数，用它去除25，38，43所得到的3个余数之和是18，那么这个自然数是多少？【答案】11【分析】设这个数为x，由题意可得：① $\left\{\begin{gathered}25 \div x = a \cdots {r_1} \hfill \\38 \div x = b \cdots {r_2} \hfill \\43 \div x = c \cdots {r_3} \hfill \\\end{gathered} \right. \Rightarrow 25 + 38 + 43 - 18 = 88$ 为x的倍数；②88=2×2×2×11③枚举验证⇒x=11．47. 一个数除以3余2，除以5余3，除以7余4，问满足条件的最小自然数．【答案】53．【分析】分析题目，我们发现前面两种都不符合，所以我们只能用最普遍的“中国剩余定理”：3、5的公倍数 3、7的公倍数 5、7的公倍数15 21 3530 42 7045 63 10560 84 140… … …找出除以7余4的 除以5余3 除以3余2．可以找出分别是：60 63 35可见60+63+35=158满足我们的条件，但不是最小的自然数，处理方法就是减去最小公倍数的若干倍，使结果在最小公倍数之内．所以答案为：158−105=53．48. （1）一个三位数除以6余2，除以8余2，那么这个三位数最小是多少？（2）—个数除以3余2，除以5余4，除以7余6，那么这个数最小是多少？（3）—个数除以6余2，除以11余1，那么这个数最小是多少？【答案】（1）122；（2）104；（3）5649. 有一个整数，用它去除63，90，130所得到的3个余数之和是25，那么这3个余数中最大的一个是多少？【答案】20【分析】设这个数为x，由题意可得：① $\left\{\begin{gathered}63 \div x = a \cdots {r_1} \hfill \\90 \div x = b \cdots {r_2} \hfill \\130 \div x = c \cdots {r_3} \hfill \\\end{gathered} \right. \Rightarrow 63 + 90 + 130 - 25 =258$ 为x的倍数；②258=2×3×43③枚举验证⇒x=43．所以 $\left\{ \begin{gathered}63 \div 43 \cdots 20 \hfill \\90 \div 43 \cdots 4 \hfill \\130 \div 43 \cdots 1 \hfill \\\end{gathered} \right.$，显然这3个余数中最大的一个是20．50. 一个自然数除以7余3，除以27余5，这个自然数最小是多少？【答案】59【分析】除以27余5的数有5、32、59、⋯，其中除以7余3的最小的数是59．51. 一个数除以3余2，除以5余3，除以7余4，问这个数是多少？【答案】53【分析】如果用剩余定理相信大家会做了，接下来看逐步满足法．第一个条件，除以3余2，最小是2；先记下2．第二个条件，除以5余3，原来已经有了2，要保持满足第一个条件不变，那么在2的基础上增加3的倍数，这样除以3余2不会变．2+3n的形式．这个数要满足第二个条件，除以5余3．在2+3n中，2已经余2了，3n需要余1，所以n=2即可．这样满足前两个条件的最小的数是8．第三个条件，除以7余4.8+3×5n的形式．3×5n=15n除以7要余4−1=3，15除以7余1，所以n最小是3，这个数是8+45=53满足题意．52. 有一个数，除以3余2，除以4余1，问这个数除以12余几？【答案】5【分析】方法一：除以3余2的数有：2，5，8，11，14，17，20，23，⋯；它们除以12的余数是：2，5，8，11，2，5，8，11，⋯；除以4余1的数有：1，5，9，13，17，21，25，29，⋯；它们除以12的余数是：1，5，9，1，5，9，⋯；一个数除以12的余数是唯一的．上面两行余数中，只有5是共同的，因此这个数除以12的余数是5．方法二：一个数，除以3余2，除以4余1，可以理解为除以3余3+2，除以4余4+1，所以这个数减去5后，既能被3整除，又能被4整除，设这个数为a，则a=12m+5，（m为自然数）所以这个数除以12余5．53. （1）一个数除以21余17，除以20也余17．这个数最小是多少？第二小是多少？（2）—个数除以11余7，除以10余6．这个数最小是多少？第二小是多少？【答案】（1）17；437（2）106；216【分析】（1）这是一道余同的问题．这个数最小是17，第二小是[21,10]+17=437．（2）这是一道缺同的问题．这个自然数加上4即可被11和10整除，[11,10]=110，因此这个数最小为110−4=106．第二小的是110×2−4=216．54. 一个自然数在1000和1200之间，且被3除余1，被5除余2，被7除余3，求符合条件的数．（使用逐步满足法）【答案】1102【分析】方法1（比较法）：我们先找出被3除余1的数：1，4，7，10，13，16，19，22，25，28，31，34，37，40，43，46，49，52，⋯；被5除余2的数：2，7，12，17，22，27，32，37，42，47，52，57，⋯；被7除余3的数：3，10，17，24，31，38，45，52，⋯；三个条件都符合的最小的数是52，其后的是一次加上3、5、7的最小公倍数，直到加到1000和1200之间．结果是105×10+52=1102.方法2（逐步满足的比较法）：先列出除以3余1的数：1，4，7，10，13，16，⋯；再列出除以5余2的数：2，7，12，17，22，27，⋯；这两列数中，首先出现的公共数是7．3与5的最小公倍数是15．两个条件合并成一个就是7+15×整数，列出这一串数是7，22，37，52，⋯；再列出除以7余3的数：3，10，17，24，31，38，45，52，⋯；就得出符合题目条件的最小数是52．事实上，我们已把题目中三个条件合并成一个：被105除余52．那么这个数在1000和1200之间，应该是105×10+52=1102.方法3（逐步满足法）：设这个自然数为a，被3除余1，被5除余2，可以理解为被3除余3×2+1，被5除与5+2，所以满足前面两个条件的a=15m+7（m为自然数），只需15m+7除以7余3，即15m除以7余3，而15÷7=2⋯⋯1，只需m除以7余3，m最小为3，所以满足三个条件的最小自然数为3×15+7=52，那么这个数在1000和1200之间，应该是105×10+52=1102.55. 今有物不知其数，三三数之剩一，四四数之剩三，五五数之剩二，问物几何？【答案】7【分析】40×1+45×3+36×2=247，3×4×5=60，247÷60=4⋯⋯7，最少是7．56. 今有一堆石子，三个三个数余2个，五个五个数余2个，七个七个数余4个，这堆石子最少有多少个？【答案】32【分析】70×2+21×2+15×4=242；244−105−105=32；57. 有一个正整数除以7、8、9的余数分别为1、5、4，求这个数至少是多少？【答案】85【分析】除以7余1的数至少是1，为满足这一特点每次要加7，加了4个7后首次满足除以8余5；然后每次加56，加了一个后满足除以9余4，此时这个数是85．58. 一个大于10的数，除以3余1，除以5余2，除以11余7，问满足条件的最小自然数是多少？【答案】172【分析】法一：仔细分析可以发现3×2+1=5+2=7，所以这个数可以看成被3、5、11除余7，由于[3,5,11]=165，所以这个数最小是165+7=172．法二：事实上，如果没有“大于10”这个条件，7即可符合条件，所以只需要在7的基础上加上3、5、11的最小公倍数，得到172即为所求的数．59. 一个自然数除以8、9、11后分别余2、7、3，而所得的三个商的和是622，这个数是多少？【答案】1906．【分析】设这个数为x．x除以8余2：最小为2，通式为2+8k1；x除以9余7：k1最小为4，则有2+8×4=34，通式为34+[8,9]k2=34+72k2．x除以11余3：k2最小为4，则有34+72×4=322．则x=322+[8,9,11]n=322+792n．322+792n−28+322+792n−79+322+792n−311=622 40+99n+35+88n+29+72n=622259n=518n=2x=322+792×2=1906．60. 有一个整数，用它去除53，89，127所得到的3个余数之和是23，那么这个整数是多少？【答案】41【分析】设这个数为x，由题意可得：① $\left\{\begin{gathered}53 \div x = a \cdots {r_1} \hfill \\89 \div x = b \cdots {r_2} \hfill \\127 \div x = c \cdots {r_3} \hfill \\\end{gathered} \right. \Rightarrow 53 + 89 + 127 - 23 =246$ 为x的倍数；②246=2×3×41③枚举验证⇒x=41．61. 一个数除以5余3，除以6余4，除以7余1，求满足条件的最小的自然数？【答案】148．【分析】设这个数为n．n除以5余3：最小为3，通式为3+5k1；n除以6余4：k1最小为5，则有3+5×5=28，通式为28+[5,6]k2=28+30k2．n除以7余1：k2最小为4，则有n=28+30×4=148．62. 有三个连续自然数，其中最小的能被15整除，中间的能被17整除，最大的能被19整除，请写出一组这样的三个连续自然数．【答案】2430，2431，2432．【分析】设三个连续自然数中最小的一个为n，则其余两个自然数分别为n+1，n+2．依题意可知：15∣n，17∣(n+1)，19∣(n+2)，根据整除的性质对这三个算式进行变换：15∣n 17∣(n +1)19∣(n +2)→→→15∣2n 17∣(2n +2)19∣(2n +4)→→→15∣(2n −15)17∣(2n −15)19∣(2n −15)}⇒[15,17,19]∣(2n −15)从上面可以发现 2n −15 应为 15、17、19 的公倍数．由于 [15,17,19]=4845，所以 2n −15=4845(2k −1)（因为 2n −15 是奇数），可得 n =4845k −2415．当 k =1 时 n =2430，n +1=2431，n +2=2432，所以其中的一组自然数为 2430、2431、2432．63. 有一个数，除以 3 余数是 2，除以 4 余数是 1．问这个数除以 12 余数是几？【答案】 5【分析】 满足条件的最小值是 5，那么所有满足条件的数肯定具有 [3,4]k +5=12k +5 的形 式，除以 12 —定是余 5 的．64. （1）一个三位数除以 8 余 3，除以 12 也余 3．这个三位数最小是多少？（2）—个三位数除以 6 余 1，除以 10 余 5．这个三位数最小是多少？【答案】 （1）123；（2）115【分析】 （1）这是一道余同的问题．满足条件的数可表示为 [8,12]×n +3，其中 n 为自然数．要求满足条件的最小三位数，应令 n 为 5，即 [8,12]×5+3=123．（2）这是一道缺同的问题．满足条件的数可表示为 [6,10]×n −5，其中 n 为自然数．要求满足条件的最小三位数，应令 n 为 4，即 [6,10]×4−5=115．65. 一个布袋中装有 5000 多个小球，如果 10 个一包，最后还剩 9 个，如果 9 个一包，最后还剩 8 个 ⋯⋯ 如果 5 个一包，最后还剩 4 个，那么如果 13 个一包，最后还剩多少个？【答案】 8 个【分析】 简答：布袋中的小球数除以 10 余 9，除以 9 余 8，除以 8 余 7⋅⋯，除以 5 余 4，[5,6,7,8,9,10]=[5,7,8,9]=5×7×8×9=2520，所以，布袋中球数是 2520−1+2520=5039，5039÷13 余 8．66. （1）—个三位数除以 4 余 2，除以 6 余 2，那么这个三位数最小是多少？（2）—个三位数除以 3 余 1，除以 4 余 2，除以 6 余 4，那么这个三位数最小是多少？（3）—个数除以 9 余 2，除以 12 余 5，那么这个数最小是多少？【答案】 （1）110；（2）106；（3）29【分析】 简答：（1）[4,6]=12，14+12×8=110；（2）按“差同”计算；（3）按“差同”计算．67. 一个数被5除余3，被7除余4，被9除余5，这个数最小是几？【答案】158【分析】7和9的公倍数9和5的公倍数5和7的公倍数6345351269070135105180140225175210245280⋯⋯⋯在7和9的公倍数中，除以5余1的最小数是126；在5和9的公倍数中，除以7余1的最小数是225；在5和7的公倍数中，除以9余1的最小数是280；那么126×3+225×4+280×5=2678．[5,7,9]=315．所以，最小的数为2678−315×8=158．68. 一个自然数在1000和1200之间，且被3除余1，被5除余2，被7除余3，求符合条件的数．【答案】1102【分析】方法1：先列出除以3余1的数：1，4，7，10，13，16，⋯；再列出除以5余2的数：2，7，12，17，22，27，⋯；这两列数中，首先出现的公共数是7．3与5的最小公倍数是15．两个条件合并成一个就是7+15×整数，列出这一串数是7，22，37，52，⋯；再列出除以7余3的数：3，10，17，24，31，38，45，52，⋯；就得出符合题目条件的最小数是52．事实上，我们已把题目中三个条件合并成一个：被105除余52．那么这个数在1000和1200之间，应该是105×10+52=1102．方法2：我们先找出被3除余1的数：1，4，7，10，13，16，19，22，25，28，31，34，37，40，43，46，49，52，⋯；被5除余2的数：2，7，12，17，22，27，32，37，42，47，52，57，⋯；被7除余3的数：3，10，17，24，31，38，45，52，⋯；三个条件都符合的最小的数是52，其后的是一次加上3、5、7的最小公倍数，直到加到1000和1200之间．结果是105×10+52=1102．方法3：设这个自然数为a，被3除余1，被5除余2，可以理解为被3除余3×2+1，被5除与5+2，所以满足前面两个条件的a=15m+7（m为自然数），只需15m+7除以7余3，即15m除以7余3，而15÷7=2⋯1，只需m除以7余3，m最小为3，所以满足三个条件的最小自然数为3×15+7=52，那么这个数在1000和1200之间，应该是105×10+52=1102．69. 一个数除以3、5、7、11的余数分别是2、3、4、5，求符合条件的最小的数：【答案】368．【分析】将3、5、7、11这4个数3个3个分别计算公倍数，如表：5、7、11公倍数3、7、11公倍数3、5、11公倍数3、5、7公倍数3852311651057704623302101155693495315……………………除3余2的最小数是770除5余3的最小值是693除7余4的最小值是165 3、5、7公倍数中被11除余5的数不太好找，但注意到210除以11余1，所以210×5=1050被11除余5，由此可知770+693+165+1050=2678是符合条件的一个值，又3、5、7、11的最小公倍数是1155，所以2678−1155×2=368是符合条件的最小值．70. 有一个自然数，用它分别去除63，90，130都有余数，3个余数的和是25．这3个余数中最大的一个是多少？【答案】20【分析】设这个除数为M，设它除63，90，130所得的余数依次为a，b，c，商依次为A，B，C．63÷M=A⋯⋯aa+b+c=25，则(63+90+130)−(a+b+c)=(A+B+C)×M,即283−25=258=(A+B+C)×M.所以M是258的约数．258=2×3×43显然当除数M为2、3、6时，3个余数的和最大为3×(2−1)=3,3×(3−1)=6,3×(6−1)=15所以均不满足．而当除数M为43×2，43×3，43×2×3时，它除63的余数均是63，所以也不满足．那么除数M只能是43，它除63，90，130的余数依次为20，4，1，余数的和为25，满足．显然这3个余数中最大的为20．71. 有一个整数，用它分别去除157、234和324，得到的三个余数之和是100，这个整数是多少？。
六年级下册数学试题-小升初能力训练：数论综合——余数问题(解析版)全国通用
第05讲 数论综合——余数问题【一】了解“除法算式——a b qr b r ÷=> ()” 及应用1：一个两位数除以一位数，所得的商若是最小的两位数，那么被除数最大是 .1010989108=910898÷=⇒∴÷=∴⨯+=最小的两位数是两位数一位数余数 求最大值一位数最大是，余数最大是 两位数 两位数2：用某自然数a 去除1707，得到商是37，余数是r ，求a 和r.17073717073717073746546461707463755375424545451707453742424645542a r a r a ra a r a a r a a r r =+⎧÷=⇒⎨>⎩÷==⎧∴=⇒÷=⇒⎨=⎩+=<=⎧∴=⇒÷=⇒⎨=⎩==⎧⎧⎨⎨==⎩⎩综上：或3：523除以一个数得到的商是10，并且除数与余数的差是5，求除数与余数.带 余 除 法52310523105555523(5)105231152310(5)x x x x x x ÷=÷=+∴÷+=∴÷=∴=++法一： 法二：除数余数 除数余数余数与除数的差是 余数与除数的差是 若设余数为，则除数为 若给余数加上 除数 =52311=48=43434348x ∴÷=∴ 除数，余数 余数是，除数是4：两数相除，商4余8，被除数、除数、商、余数四数之和等于415，则被除数是 .484848484841532448794848415794798324A B A B A B A B A B A B x A x B x x x A =+⎧÷=⇒=+÷=⇒⎨+++=⎩=⎧+∴⎨=⎩++++===⨯+=法一： 法二： 若设为，则为 则5：某个除法算式的被除数、除数、商与余数之和为115，如果被除数和除数都扩大为原来的2倍，得到的除法算式中被除数、除数、商与余数之和为223，那么原来的算式中商是 .11522222222311522237A B CD A B C D A B C D A B C D C ÷=⇒+++=÷=⇒+++=∴=⨯-=22222(22)22222a b q r a bq r a bq ra b bq r b q r a b q r a b q r÷=⇒=+⇒=+÷=+÷=∴÷=⇒÷=证明：6：某个整数除36，商和余数相等，那么这个整数可能是 .3636(1)136=8111735b c c bc c c b b b cb ÷=⇒=+=++>是的因数，但是枚举：、、、7：在大于2015的自然数中，被57除后，商与余数相等的数共有多少个？5758575756201558=3443355635122a c c c a c c c c c =+=⎧÷=⇒⎨<⎩÷⇒∴=-+= 的最大值是 的最小值是 个数（个）【二】余数性质（余数特征+余数可加可减可乘性+余数周期性）251425281253393999100001000100109999(91)99999a b c d e abcde a b c d ea b c d abcde a ⎧⎪⎨⎪⎩⎧⎨⎩=⨯+⨯+⨯+⨯+++++=⨯+⨯+⨯+⨯+=⨯被和整除：末位尾系被和整除：末位被和整除：末位被、整除：各位数字和是、的倍数和系被整除：两位一段，求和 证明： [弃9法 整特征]除0000100999999711131110001001()10000100010010()bc dea bc abcde ab cde ab cde ab abc a bc de a bd c de e +⨯+=⨯+⨯+⎧⎨⎩=⨯+=⨯+-=⨯+⨯+++⨯+⨯+ 被、和整除：三位一段，奇数段偶段和差系被整除：奇位和偶位和 证明： [()(999)910019911999910019911(]a a b b c c d e c a d e a b c d a c m e a mc e b c nf b nc f a b mc e nc f m n d b ++-+⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪=⨯++⨯-+⨯++⨯-+⎪=⨯+⨯+⨯+⨯+⎩÷==+⎧⎧⇒⎨⎨÷==+⎩⎩+=+++=+ 对于（1） 余数可加可减可乘2)()()()()()()()()()()()1192329c e f a b ce f a b mc e nc f m n c e f a b ce f a b mc e nc f mnc mcf nec ef a b ce f ++⇒+÷+⇒-=+-+=-+-⇒-÷-⇒⨯=+⨯+=+++⇒⨯÷⨯⇒÷÷ （2） （3） 余数可加 举性余数可减性余数可乘性例259753295⎧⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪÷⎧⎧⎪⎨⎨⎪÷⎩⎩⎩或者（一）余数特征+余数可加可减可乘性的“基础练习”1：将假分数5051525354557⨯⨯⨯⨯⨯化成带分数后，真分数部分是多少？5051525354557505152535455123456(24)(35)681561166(mod 7)⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯≡⨯⨯⨯⨯⨯≡⨯⨯⨯⨯=⨯⨯≡⨯⨯≡只要计算除以的余数即可（二）余数特征+余数可加可减可乘性的“拓展练习”71310010100101010110101100101001010110101101010110ABCDABCDABCD BCD DAB B C D D A B A B C D ABC DAB CDA BCD CDA ABC C D A A B C A B C D A B ⎧=+=+++++⎪=+++⎪⎨=+=+++++⎪⎪=+++⎩-=++证明：判断能被和整除奇段和 偶段和 奇偶10110110101109191919191()91713713C D A B C D B A D C B A D C ABCDABCDABCD +----=-+-=-+-=⨯∴ 能被和整除1：（1）求20172017201720172017个除以9的余数. （2）求20146666个除以7的余数.201712017201720172017201711120171(mod 9)≡≡≡个个 20146666666666100120146335466666666666660302(mod 7)=⨯÷=∴≡≡-≡≡≡个2：求1020162017201620162016个除以7的余数.9201620163603603602016201620167020162016201670201720162016201620172016000(mod 7)1428577110000001000000711000712017201600020172016(mod 7)20÷∴÷⇒≡⨯+=∴÷∴÷⇒≡个10个个个个172016201710000201620177110000742016701404=⨯+÷÷÷∴=⨯+=余数可乘，余数3：求15!除以17的余数.15!4!(56)(71113)(89)(10121415)243010017225210015!7131541415916021069654636181(mod 7)15!(29)(36)(413)(57)(815)(1012)(1114)171=⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯=⨯⨯⨯⨯⨯⇒≡⨯⨯⨯⨯⨯≡⨯⨯≡⨯⨯≡⨯≡⨯≡≡=⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯法一：法二：每个括号内两数之积都是除以 余 15!171∴÷ 的(2)!1(mod )p p p ⇔-≡延伸说明：上一题的（2）是威尔逊原理内容： 是质数（三）余数周期性的“基础练习”1：兔子数列：1、1、2、3、5、8、13、……，第2017项除以5的余数.5112303314044320224101123033020201720100172÷=兔子数列每一项除以的余数如下：周期是， ，即余2：分别求出23456789103333333333、 、 、 、 、 、 、 、 、 除以7的余数.发现规律，并求出1003除以7的余数. 并试求231001+3+3+3++3除以7的余数.234567891010043333333333326451326461006164334(mod 7)⇒÷=⇒≡≡、 、 、 、 、 、 、 、 、 、 、 、 、 、 、 、 、 、 周期是若为01231002+2+2+2++2除以7呢？61016165(132645)1613262116162(mod 7)⇒÷=⇒≡+++++⨯++++≡⨯+≡周期是 原式3：今天是周四，100010天之后将是周几？234567891010004101010101010101010103264513264610006166410104(mod 7)⇒÷=⇒≡≡⇒、 、 、 、 、 、 、 、 、 、 、 、 、 、 、 、 、 、 周期是周一（四）余数周期性的“拓展练习” 1：求3332除以31的余数.33133333231535334812228(mod 31)n ∴÷=⇒≡≡≡研究除以的余数容易发现周期是只要考虑除以的余数，容易发现周期是42：求332的末位数字.33133481333(mod10)÷=⇒≡≡寻找末位就是相当于除以10的余数周期现象：1、3、9、7、1、3、9、7、……，周期是4(1)(2)(3)x Nx N x N x x 以下是固定值，是变量对于，其个位数字是4个一循环 对于，其个位数字是10个一循环 对于，其个位数字是20个一循环3：求123420132014123420132014+++++除以10所得的余数是多少？12341920201234192014765636901636567490944,201420100141001004(14765636901636)=463463++++++++++++++++++++++++=÷=⨯++++++++++++++除以10的余数就是相当于寻找其个位数字，底数指数都是变化的，即周期为先计算的个位数字：为“”其个位数字是即个整周期还多出14个个位数字即为“”的个3位数字是 ，即答案就是34：求2007200720072007200712342006++++计算结果的个位数字是多少？200732007320073200720072007200720073333311(mod10)22(mod10)20072007(mod10)1234200612342006(mod10)≡≡≡+++++≡+++++首先，按规律，底数不变指数变化，其个位数字的周期是每4个一循环 即 、 、 得到： 然后，按规律，底数变化指数不变，其个位数字的周期是每10个一循环 33333333333333331234105(mod10)1234200652001234561(mod10)+++++≡+++++≡⨯++++++≡ 又因为， 所以，【一】化余数为整除（余数相同） （一）余数已知1：某个整数除41，余数是5，那么这个整数可能是几？ 415(415)03603636181296b bbb b ÷⇒-÷⇒÷⇒=是的因数，、、、、2：某个整数除31，余数是7，那么这个整数可能是几？ 317(317)024********b bbb b ÷⇒-÷⇒÷⇒=是的因数，、、同 余 问 题3：某个整数除67、151得到的余数都是11，那么这个整数可能是几？(6711)05606711(15111)01400561408415111(15167)0840(56,140,84)28112814b b b b b b b b b b b b -÷÷⎧⎧÷⎧⎪⎪⇒-÷⇒÷⇒⇒⎨⎨⎨÷⎩⎪⎪-÷÷⎩⎩=>∴=是、、的公因数是最大公因数的因数，且、4：某个额整数除229、337得到的余数都是13，这个整数最大是几？最小是几？ (22913)021*******(33713)0324033713(337229)01080216324108(216,324,108)1081310818b b b b b b b b b b b b -÷÷⎧⎧÷⎧⎪⎪⇒-÷⇒÷⎨⎨⎨÷⎩⎪⎪-÷÷⎩⎩⇒⇒=>∴是、、的公因数是最大公因数的因数，且最大为，最小为（二）余数未知1：某个大于1的整数除41、11得到的余数相等，那么这个整数可能是几？ 41(4111)030030302153105611b rb bb b br÷⎧⇒-÷⇒÷⇒=⎨÷⎩是的因数，、、、、、2：某个大于1的整数除89、71得到的余数相同，那么这个整数可能是几？89(8971)01801818293671b rb bb b br÷⎧⇒-÷⇒÷⇒=⎨÷⎩是的因数，、、、、3：某个大于1的整数除17、53、113得到的余数相同，那么这个整数可能是几？ 17(5317)036053(11317)0960369660113(11353)0600(36,96,60)12122634b r b bb r b b b b b r b b b ÷-÷÷⎧⎧⎧⎪⎪⎪÷⇒-÷⇒÷⇒⇒⎨⎨⎨⎪⎪⎪÷-÷÷⎩⎩⎩=∴=是、、的公因数是最大公因数的因数、、、、【二】化余数为整除（余数不同） （一）余数已知1：某个整数除47余5，除65余2，那么这个整数可能是几？ 475(475)04204263652(652)0630(42,63)215217b bbb b b bbb b ÷-÷÷⎧⎧⎧⇒⇒⇒⇒⎨⎨⎨÷-÷÷⎩⎩⎩=>∴=是、的公因数是最大公因数的因数，且、2：（拓展）用一个数除200余5，除300余1，除400余10，这个数是多少？ 13（二）余数未知1：某个整数除29、56的余数分别是a 、3a +，这个数可能是几？ 2929(5329)0240245635333324128462924529125298524,12,8()56248561285680294129654(),6()56405662b aba bbb ba baa b b b b b b b ÷÷⎧⎧⇒⇒-÷⇒÷⇒⎨⎨÷+÷⎩⎩+≥⇒>∴=÷÷÷⎧⎧⎧===⎨⎨⎨÷÷÷⎩⎩⎩÷÷⎧⎧==⎨⎨÷÷⎩⎩是的因数、、、、验证：舍去舍去舍去综上2412b =，、2：某个整数除47、121、232的余数分别是a 、2a +、5a +，这个数可能是几？4747(11947)07201212119(22747)018002325227(227119)0108072180108(72,180,108)36536181296473636b a b a b b b a b a b b b a b a b b b b b b b ÷÷-÷÷⎧⎧⎧⎧⎪⎪⎪⎪÷+⇒÷⇒-÷⇒÷⎨⎨⎨⎨⎪⎪⎪⎪÷+÷-÷÷⎩⎩⎩⎩⇒⇒=>∴=÷=是、、的公因数是最大公因数的因数，且、、、、验证：114718114712111213613,181211813,12121121(),2323616232181623212447924765912194(),612161()23297232643618b b b b b ÷÷⎧⎧⎧⎪⎪⎪÷=÷=÷⎨⎨⎨⎪⎪⎪÷÷÷⎩⎩⎩÷÷⎧⎧⎪⎪=÷=÷⎨⎨⎪⎪÷÷⎩⎩=舍去舍去舍去综上，、3：一个自然数除429、791、500所得的余数分别是5a +、2a 、a ，求这个自然数的和a 的值.429+54248482(848791)0570791279127912(1000791)0209050050010002(1000848)0152057209152(57,209,15b a ba b a b b b a ba b a b b b a b a b a b b b b ÷÷÷-÷÷⎧⎧⎧⎧⎧⎪⎪⎪⎪⎪÷⇒÷⇒÷⇒-÷⇒÷⎨⎨⎨⎨⎨⎪⎪⎪⎪⎪÷÷÷-÷÷⎩⎩⎩⎩⎩⇒⇒是、、的公因数是最大公因数的因数2)19519571911192091912152196196b b b b a =>∴=÷⎧⎪=÷⎨⎪÷⎩==，且验证：综上，，4：已知60、154、200被某数除所得的余数分别是1a -、2a 、31a -，求这个自然数的值. 22222333361(3721154)03567060161154154154(61154)2001201(9394201)09193020135679193(3567,9193)b a b b b a b a b a b a b a b ab a b a b b b a b b ⎧⎛÷⇒-÷⇒÷÷-÷⎪ ⎧⎧ ÷⎪⎪⎪⎝÷⇒÷⇒⎨⎨⎨⎛⨯÷⎪⎪⎪÷-÷⇒-÷⇒÷ ⎩⎩⎪ ÷⎝⎩⇒⇒=是、的公因数是最大公因数的因数29296029229154299200292629b b b ∴=÷⎧⎪=÷⎨⎪÷⎩=验证：综上，5：（拓展）糖果254粒，饼干210块，水果186个. 某幼儿园人数超过40人，平均分给学生，余下糖果、饼干、水果比是1:3:2，求共有多少人？没人每种各分多少个？5082(508186)032202541862210321031862(440210)02300(254186)3322230(322,230)4640223254202210201862b ab b b a b a b a b a b a b b b a b b b b b ⎧÷⎧⇒-÷⇒÷÷⎧⎨⎪÷⎪⎪⎩÷⇒⎨⎨÷⎧⎪⎪÷⇒-÷⇒÷⎨⎩⎪+÷⎩⎩⇒⇒=<∴=÷=÷÷是、的公因数是最大公因数的因数，且、验证：254231()23210233018623223b b ÷⎧⎧⎪⎪=÷⎨⎨⎪⎪÷⎩⎩=舍去，综上，6：有一个整数，用它除70、110、160所得到的3个余数之和是50，那么这个整数是多少？121233111221233370110(70110160)()340502900290160707070121101333531718316011b r b r b r r r bb b b rbr b b r b r b r b r b r r r b b b b r b r b ÷⎧⎪÷⇒++÷++⇒÷⇒÷⇒⎨⎪÷⎩÷≤÷≥+⎧⎧⎪⎪÷⇒≥+⇒≥+++⇒≥⇒≥⇒≥⎨⎨⎪⎪÷≥+⎩⎩∴=是的因数现在讨论的就是范围对来说，其中,290,2,145,5,58,10,29581105815229b b =÷==对于， ，不成立综上，【三】同余方程 1：（铺垫）（1）解同余方程：45(mod11)x ≡45(mod11)41151(45)110451144(mod11)5115245(mod11)4511(mod11)416(mod11)(4,7)14(mod 7)x x x x x x x x x x ≡÷⎧⇒-÷⇒-=⇒=⇒≡⎨÷⎩≡≡+≡=∴≡ 转化： 试除：(mod )(,)1(mod )(mod )()()0()()()()(,)1(mod )ac bc m c m a b m ac m x pac bc m ac bc m x y c a b m x y bc m y p c a b m x y c m m a b a b m a m b m a b a b m m m ≡=≡÷=⎧≡⇒-÷=-⇒-=-⎨÷=⎩-=-=-≡÷÷--=证明：若，当 时，有开始：对“”，有对“”，若，为的因数若想让“”，即让“的余数等于的余数”，即“化为分数相减为整数”同时，确实为整数，得证.（2）解同余方程：729(mod13)x x ≡+729(mod13)7131(729)130(29)135913()(59)130592677(mod13)2729(mod13)59(mod13)59132(mod13)5x x x r x x x rx x x x xx x x x x ≡+÷⎧⇒--÷⎨+÷⎩-=⨯⎧⇒-÷⇒⎨-=⇒=⇒≡⎩-≡≡≡+⨯ 转化： 试除： 35(mod13)(5,13)17(mod13)x ≡=∴≡2：用枚举法检验的方法，找出有那些整数x 满足：35(mod 7)x ≡，用一个同余式来表示结果.135(mod 7)411184(mod 7)235(mod 7)357(mod 7)312(mod 7)(4,7)14(mod 7)x x x x x x x ≡=≡≡≡+≡=∴≡ ，枚举得到、、、，表示为3：求解同余方程：3843(1)(mod13)x x +≡+. 8343(1)(mod13)83433(mod13)83334(mod13)5334313(mod13)58(mod13)58x x x x x x x x x +≡++≡+-≡-≡-+⨯≡≡+第一步：化简 第二步：（试除法） 134(mod13)XX 5383(mod13)560(mod13)1524(mod13)(5,13)112(mod13)211(mod13)(XX ) 5x x x x x x ⨯⨯≡⨯≡≡=∴≡≡⨯ （法） 法888(mod13)21113(mod13)4064(mod13)224(mod13)12(mod13)12(mod13)x x x x x ≡⨯≡+≡≡≡≡5：（拓展）老师选了一个两位数，然后讲这个数乘23，并且加上79，发现正好是111的倍数，你能猜出老师选的是什么数吗？23790(mod111)2311179(mod111)2332(mod111)235325(mod111)115160(mod111)x x x x x x +≡≡-≡⨯≡⨯≡设这个两位数为，得到 4160(mod111)40(mod111)40.x x ≡≡ 即这个两位数是一：余同加余，差同减差，和同加和 1：小强家有很多巧克力:。
小学奥数题库《数论》余数问题带余除法1星题(含解析)全国通用版
数论-余数问题-带余除法-1星题课程目标知识提要带余除法•定义一般的，如果a是整数，b是整数（b≠0），若有a÷b=q⋯⋯r，也就是说a=b×q+r，0≦r<b，我们称上面的除法算式为一个带余除法算式。
（1）当r=0时，我们称a可以被b整除，q称为a除以b的商或完全商；（2）当r≠0时，我们称a不可以被b整除，q称为a除以b的商或不完全商。
精选例题带余除法1. 有一个除法算式，被除数和除数的和是136，商是7，则除数是．【答案】17【分析】（1）被除数÷除数=7，因此我们能得到被除数是除数得7倍．（2）如果设除数是1份，那么被除数就是7份，它们的和是136．所以每份量为：136÷8=17．即除数是17．2. 在一个除法算式中，被除数是12，除数小于12，则可能出现的不同的余数之和是．【答案】15【分析】除数小于12且有不同余数，除数可能是11、10、9、8、7．余数分别是1、2、3、4、5．余数之和是1＋2＋3＋4＋5=15.3. 已知2008被一些自然数去除，得到的余数都是10．那么这些自然数共有个．【答案】11个【分析】2008−10=1998一定能被这些数整除，且这些数一定大于10，1998=2×3×3×3×37．1998的因数一共有：(1+1)×(3+1)×(1+1)=16个．其中小于10的有：1，2，3，6，9那么大于10的因数有16−5=11个．即这些自然数共有11个．4. 买一支水彩笔需要1元7角，用15元钱最多可以买这样的水彩笔支．【答案】8【分析】1元7角相当17角，15元相当于150角．可列出如下算式：150÷17=8⋯14.故最多可以买这样的水彩笔8支．5. 两数相除，商4余8，被除数、除数两数之和等于73，则被除数是．【答案】60【分析】被除数=4×除数+8，被除数减去8后是除数的4倍，所以根据和倍问题可知，除数为(73−8)÷(4+1)=13，所以，被除数为13×4+8=60．6. 有两个自然数相除，商是17，余数是13，已知被除数、除数、商与余数之和为2113，则被除数是．【答案】1968【分析】设除数为a，被除数为17a+13，即可得到(17a+13)+a+17+13=2113,那么除数=115，被除数=115×17+13=1968．7. 在一个除法算式中，如果商是16，余数是8，那么被除数最小是．【答案】152【分析】根据余数小于除数，得到除数最小为9，那么被除数的最小值为16×9+8=152．8. 在一个除法算式中，如果商是16，余数是8，那么被除数与除数的和最小是．【答案】161【分析】由上题152+9=161．9. （1）34÷4=8⋯⋯2，则[34÷4]=，{34÷4}=；（2）已知a÷125=b⋯⋯10，[a÷125]=6，求{a÷125} = ；（3）已知a÷20=3⋯⋯b，{a÷20}=0.45，求[a÷20] = ，a = ．【答案】（1）8,0.5；（2）0.08；（3）3,69【分析】（1）34÷4的整数部分就是商，因此为8，{34÷4}相当于余数除以4，因此为0.5．（2）如果a÷b=q⋯⋯r，[a÷b]=q,{a÷b}=r÷b方法1：b=6，a=6×125+10=760，{760÷125}=0.08；方法2：b=6，{a÷125}=10÷125=0.08．（3）如果a÷b=q⋯⋯r，[a÷b]=q，{a÷b}=r÷b，所以[a÷20]=3，b=0.45×20=9，a=3×20+9=69．10. 用一个自然数去除另一个自然数，商为5．被除数、除数的和是36，求这两个自然数各是多少？【答案】被除数为30，除数为6．【分析】被除数÷除数=5，所以根据和倍问题可知，除数为36÷(5+1)=6，所以被除数为5×6=30．11. 若a÷b=7⋯⋯9，则a的最小值是多少？【答案】79【分析】根据余数小于除数，得到除数最小为10，那么a的最小值为7×10+9=79．12. （1）25÷6=4⋯⋯1；34÷6=5⋯⋯4，那么(25+34)÷6=( )⋯⋯( )．（2）45÷7=6⋯⋯3；26÷7=3⋯⋯5，那么(45+26)÷7=( )⋯⋯( )．（3）a÷8⋯⋯5；b÷8⋯⋯6，那么(a+b)÷8⋯⋯( )．（4）a÷8⋯⋯5；b÷8⋯⋯6；c÷8⋯⋯7，那么(a+b+c)÷8⋯⋯( )．【答案】（1）(25+34)÷6=(9)⋯⋯(5)；（2）(45+26)÷7=(10)⋯⋯(1)．（3）(a+b)÷8⋯⋯(3)．（4）(a+b+c)÷8⋯⋯(2)．【分析】（1）(25+34)÷6=9⋯⋯5；（2）(45+26)÷7=10⋯⋯1．（3）所以余数的和为5+6=11，11÷8=1⋯⋯3，余数为3．（4）余数的和为5+6+7=18，18÷8=2⋯⋯2，余数为2．13. 请在下列括号中填上适当的数．（1）a÷8⋯⋯6；b÷8⋯⋯7，那么(a+b)÷8⋯⋯( )．（2）a÷10⋯⋯5；b÷10⋯⋯6；c÷10⋯⋯7，那么(2a+b+c)÷10⋯⋯( )．【答案】（1）5；（2）3【分析】（1）余数的和为6+7=13，13÷8=1⋯⋯5，余数为5．（2）2a+b+c=a+a+b+c，所以余数的和为5+5+6+7=23，23÷10=2⋯⋯3，余数为3．14. 1013除以一个两位数，余数是12．求出符合条件的所有的两位数．【答案】13,77,91【分析】1013−12=1001，1001=7×11×13，那么符合条件的所有的两位数有11,13,77,91，因为“余数小于除数”，所以舍去11，答案只有13,77,91．15. 1013除以一个两位数，余数是12．求出所有符合条件的两位数．【答案】13,77,91【分析】1013−12=1001，1001=7×11×13，那么符合条件的所有的两位数有11,13,77,91，因为“余数小于除数”，所以舍去11，答案只有13,77,91．16. 甲、乙两数的和是16，甲数除以乙数商是2余1，求甲数和乙数各是多少？【答案】乙=5，甲=11【分析】设乙数为a，即甲为2a+1，可得到(2a+1)+a=16，那么乙=5，甲=11．17. 2025除以一个两位数，余数是75，这个两位数是多少？【答案】78【分析】这个两位数是2025−75=1950的约数，其中比75大的只有78．18. 一个数除以另一个数，商是3，余数是3．如果除数和被除数都扩大10倍，那么被除数、除数、商、余数的和是263，求这2个自然数各是多少？【答案】5、18【分析】设除数为a，被除数为3a+3，即可得到10(3a+3)+10a+3+30=263,那么除数=5，被除数=5×3+3=18．19. 甲、乙两数的差是113，甲数除以乙数商7余5，则甲数和乙数各是多少？【答案】乙=18，甲=131【分析】设乙数为a，即甲为7a+5，可得到(7a+5)−a=113，那么乙=18，甲= 131．20. 两数相除，商4余8，被除数、除数、商数、余数四数之和等于415，则被除数是_______．【答案】324【分析】设被除数和除数分别为x，y，可以得到\[ \begin{cases} x = 4y + 8\hfill \\ x + y + 4 + 8= 415 \hfill \\ \end{cases} \]解方程组得\[ \left\{ \begin{gathered} x = 324 \hfill\\ y = 79 \hfill\\ \end{gathered} \right. \]即被除数为324．21. 78除以一个数得到的商是8，并且除数与余数的差是3，求除数和余数．【答案】除数为9，余数为6．【分析】78÷除数=8⋯⋯(余数−3)，81÷除数=9⋯⋯0被除数加上除数与余数的差3的和刚好是除数的9倍，则除数为(78+3)÷9=9，余数为6．22. 用某自然数a去除1992，得到商是46，余数是r，求a和r．【答案】a=43，r=14【分析】由1992是a的46倍还多r，得到1992÷46=43......14，得1992=46×43+ 14，所以a=43，r=14．23. 甲、乙两个数，甲数除以乙数商2余17，乙数的10倍除以甲数商3余45．求甲、乙二数．【答案】乙=24，甲=65【分析】设乙数为a，即甲为2a+17，可得到10a÷(2a+17)=3⋯⋯45，整理为10a= 3(2a+17)+45，那么乙=24，甲=65．24. 一个三位数除以43，商是a余数是b，求a+b的最大值．【答案】64【分析】试除法：999÷43=23⋯⋯10；999−10−1=988；988÷43=22⋯⋯42．余数最大为42，所以a+b的最大值为42+22=64．25. （1）82÷6=13⋯⋯4；50÷6=8⋯⋯2，那么(82−50)÷6=( )⋯⋯( )．（2）74÷6=12⋯⋯2；22÷6=3⋯⋯4，那么(74−22)÷6=( )⋯⋯( )．（3）a÷6余5；b÷6余1，那么(a−b)÷6余几呢？（4）a÷6余3；b÷6余5，那么(a−b)÷6余几呢？【答案】（1）(82−50)÷6=(5)⋯⋯(2)．（2）(74−22)÷6=(8)⋯⋯(4)．（3）余4．（4）余4．【分析】（1）(82−50)÷6=5⋯⋯2．（2）(74−22)÷6=8⋯⋯4．（3）余数的差是4，所以余数是4．（4）余数不够减时借1当6用来减，3+6=9，9−5=4，所以余数是4．26. 用一个自然数去除另一个自然数，商为8，余数是3．被除数、除数的和是48，求这两个自然数各是多少？【答案】被除数为43，除数为5．【分析】因为被除数减去3后使除数的8倍，所以根据和倍问题可知，除数为(48−3)÷(8+1)=5，所以被除数为5×8+3=43．27. 50除以一个一位数，余数是2．求出符合条件的一位数．【答案】3，4，6，8【分析】50÷除数=商⋯⋯2，50−2=48，48=除数×商，48=1×48=2×24=3×16=4×12=6×8，因为“余数小于除数且除数是一位数“那么符合条件的所有的数有3，4，6，8．28. 一个两位数除310，余数是37，求这样的两位数．【答案】39；91【分析】本题为余数问题基础题型，需要学生明白一个重要知识点，就是把余数问题---即“不整除问题”转化为整除问题．方法为用被除数减去余数，即得到一个除数的倍数；或者是用被除数加上一个“除数与余数的差”，也可以得到一个除数的倍数．本题中310−37=273，说明273是所求余数的倍数，而273=3×7×13，所求的两位数约数还要满足比37大，符合条件的两位数有39，91．29. 一个两位数除以13的商是6，除以11所得的余数是6，求这个两位数．【答案】83【分析】因为一个两位数除以13的商是6，所以这个两位数一定大于78，并且小于13×(6+1)=91；又因为这个两位数除以11余6，而78除以11余1，这个两位数为78+5=83．30. 43除以一个数得到的商是8，并且除数与余数的差是2，求除数和余数．【答案】除数为5，余数为3．【分析】43=8×除数+余数，被除数加上除数与余数的差2的和刚好是除数的9倍，则除数为(43+2)÷(8+1)=5，余数为3．31. 用一个自然数去除另一个自然数，商为7．被除数、除数的和是48，求这两个自然数各是多少？【答案】除数为6，被除数为42．【分析】被除数÷除数=7，所以根据和倍问题可知，除数为48÷(7+1)=6，所以被除数为6×7=42．32. 计算：（1）已知a÷25=b⋯⋯5，[a÷20]=4，求a=；（2）已知a÷10=7⋯⋯b，{a÷10}=0.5，求[a÷10]=，a=．【答案】（1）105；（2）7,75【分析】（1）b =4，a=4×25+5=105（2）a÷b=q⋯⋯r，[a÷b]=q，{a÷b}=r÷b，所以[a÷10]=7，b=0.5×10=5，a=7×10+5=75．33. 46除以一个一位数，余数是1．求出符合条件的一位数．【答案】3，5，9【分析】46÷除数=商⋯⋯1，46−1=45，45÷除数=商⋯⋯0，45=除数×商，45=3×15=5×9，因为“余数小于除数且除数是一位数”那么符合条件的所有的一位数有3，5，9．34. 博士要给小朋友们分糖，一共128块，如果每人分5块，最多可以分给几个小朋友？【答案】25【分析】128÷5=25⋯⋯3，最多分给25个小朋友，还剩3块．35. 128除以一个数得到的商是9，并且除数与余数的差是2，求除数和余数．【答案】除数为13，余数为11．【分析】128÷除数=9⋯⋯(余数−2)，130÷除数=10⋯⋯0被除数加上除数与余数的差2的和刚好是除数的10倍，则除数为(128+2)÷10=13，余数为11．36. 有一个整数，39，51，147被它除所得的余数都是3，求这个数．【答案】4；6；12【分析】方法一：39−3=36，147−3=144，(36,144)=12，12的约数是1,2,3,4,6,12，因为余数为3要小于除数，这个数是4，6，12．方法二：由于所得的余数相同，得到这个数一定能整除这三个数中的任意两数的差，也就是说它是任意两数差的公约数．51−39=12，147−39=108，(12,108)=12，所以这个数是4，6，12．37. 一个除法算式中，被除数、除数、商与余数都是自然数，并且商与余数相等．若被除数是47，则除数是多少？【答案】46【分析】设除数为b，商和余数都是c，这个算式就可以表示为：47÷b=c⋯⋯c，即b×c+c=47；c×(b+1)=47，所以c一定是47的因数，47的因数只有1和47；c为47肯定不符合条件，所以c=1，即除数是46，余数是1．38. 已知2012被一些正整数去除，得到的余数为10，则这样的正整数共有多少个？【答案】13个【分析】2012−10=2002一定能被这些数整除，2002=2×7×11×13．因为2002中一共有(1+1)×(1+1)×(1+1)×(1+1)=16个，排除小于10的因数1、2、7，满足条件的正整数共有16−3=13个．39. 188＋288＋388＋…＋2088除以9、11的余数各是多少？【答案】8；11．【分析】根据等差数列求和列式：188＋288＋388＋…＋2088=22760，所以22760÷9⋯⋯8；22760÷11⋯1．40. 著名的斐波那契数列是这样的：1，1，2，3，5，8，13，21，⋯，这串数列当中第2008个数除以3所得的余数为多少？【答案】0【分析】斐波那契数列的构成规则是从第三个数起每一个数都等于它前面两个数的和，由此可以根据余数定理将斐波那契数列转换为被3除所得余数的数列：1，1，2，0，2，2，1，0，1，1，2，0，⋯，第九项和第十项连续两个是1，与第一项和第二项的值相同且位置连续，所以斐波那契数列被3除的余数每8个一个周期循环出现，由于2008除以8的余数为0，所以第2008项被3除所得的余数为第8项被3除所得的余数为0．。
小学奥数数论问题余数问题练习题【五篇】
小学奥数数论问题余数问题练习题【五篇】分析：这个题没有告诉我们,这三个数除以这个数的余数分别是多少,但是因为所得的余数相同,根据性质2,我们能够得到：这个数一定能整除这三个数中的任意两数的差,也就是说它是任意两数差的公约数.101-45=56,101-59=42,59-45=14,(56,42,14)=14,14的约数有1,2,7,14,所以这个数可能为2,7,14.2.已知三个数127,99和一个小于30的两位数a除以一个一位数b的余数都是3,求a和b的值.分析：127-3=124,99-3=96,则b是124和96的公约数.而(124,96)=4,所以b=4.那么a的可能取值是11,15,19,23,27.3.除以99,余数是______.分析：所求余数与19×100,即与1900除以99所得的余数相同,所以所求余数是19.4.求下列各式的余数：(1)2461×135×6047÷11(2)19992000÷7分析：(1)5;(2)1999÷7的余数是4,19992000 与42000除以7 的余数相同.然后再找规律,发现4 的各次方除以7的余数的排列规律是4,2,1,4,2,1......这么3个一循环,所以由2000÷3 余2 能够得到42000除以7 的余数是2,故19992000÷7的余数是2 .【第二篇】(小学数学奥林匹克初赛)有苹果,桔子各一筐,苹果有240个,桔子有313个,把这两筐水果分给一些小朋友,已知苹果等分到最后余2个不够分,桔子分到最后还余7个桔子不够再分,求最多有多少个小朋友参加分水果分析：此题是一道求除数的问题.原题就是说,已知一个数除240余2,除313余7,求这个数为多少,我们能够根据带余除法的性质把它转化成整除的情况,从而使问题简化,因为240被这个数除余2,意味着240-2=238恰被这个数整除,而313被这个数除余7,意味着这313—7=306恰为这个数的倍数,我们只需求238和306的公约数便可求出小朋友最多有多少个了.240—2=238(个) ,313—7=306(个) ,(238,306)=34(人) .【第三篇】有一个大于1的整数,除45,59,101所得的余数相同,求这个数.分析：这个题没有告诉我们,这三个数除以这个数的余数分别是多少,但是因为所得的余数相同,根据性质2,我们能够得到：这个数一定能整除这三个数中的任意两数的差,也就是说它是任意两数差的公约数.101-45=56,101-59=42,59-45=14,(56,42,14)=14,14的约数有1,2,7,14,所以这个数可能为2,7,14.【第四篇】1.已知三个数127,99和一个小于30的两位数a除以一个一位数b的余数都是3,求a和b的值.分析：127-3=124,99-3=96,则b是124和96的公约数.而(124,96)=4,所以b=4.那么a的可能取值是11,15,19,23,27.2.除以99的余数是______.分析：所求余数与19×100,即与1900除以99所得的余数相同,所以所求余数是19.【第五篇】。
(完整版)小学奥数数论问题余数问题练习题.doc
小学奥数数论问题余数问题练习题【五篇】分析：这个题没有告诉我们 ,这三个数除以这个数的余数分别是多少 ,但是因为所得的余数相同 ,根据性质 2,我们能够得到：这个数一定能整除这三个数中的任意两数的差 ,也就是说它是任意两数差的公约数 .101-45=56,101-59=42,59-45=14,(56,42,14)=14,14的约数有 1,2,7,14,所以这个数可能为 2,7,14.2.已知三个数 127,99 和一个小于 30 的两位数 a 除以一个一位数 b 的余数都是 3,求 a 和 b 的值 .分析： 127-3=124,99-3=96,则 b 是 124 和 96 的公约数 .而(124,96)=4,所以 b=4. 那么 a 的可能取值是 11,15,19,23,27.3.除以 99,余数是 ______.分析：所求余数与 19×100,即与 1900 除以 99 所得的余数相同 ,所以所求余数是 19.4.求下列各式的余数：(1)2461 × 135× 6047 ÷ 11(2)19992000 ÷ 7分析： (1)5;(2)1999÷7的余数是4,19992000与42000除以7的余数相同.然后再找规律 ,发现 4 的各次方除以 7 的余数的排列规律是4,2,1,4,2,1......这么 3 个一循环 ,所以由 2000÷3 余 2 能够得到 42000 除以 7 的余数是 2,故 19992000÷7的余数是 2.【第二篇】(小学数学奥林匹克初赛 )有苹果 ,桔子各一筐 ,苹果有 240 个,桔子有 313 个,把这两筐水果分给一些小朋友 ,已知苹果等分到最后余 2 个不够分 ,桔子分到最后还余 7 个桔子不够再分 ,求最多有多少个小朋友参加分水果分析：此题是一道求除数的问题.原题就是说 ,已知一个数除 240 余 2,除 313 余7,求这个数为多少,我们能够根据带余除法的性质把它转化成整除的情况,从而使问题简化 ,因为 240 被这个数除余 2,意味着 240-2=238恰被这个数整除 ,而 313被这个数除余 7,意味着这 313—7=306 恰为这个数的倍数 ,我们只需求 238 和 306 的公约数便可求出小朋友最多有多少个了 .240—2=238(个) ,313—7=306(个) ,(238,306)=34(人) .【第三篇】有一个大于 1 的整数 ,除 45,59,101 所得的余数相同 ,求这个数 .分析：这个题没有告诉我们 ,这三个数除以这个数的余数分别是多少 ,但是因为所得的余数相同 , 根据性质 2,我们能够得到：这个数一定能整除这三个数中的任意两数的差 ,也就是说它是任意两数差的公约数 .101-45=56,101-59=42,59-45=14,(56,42,14)=14,14的约数有1,2,7,14,所以这个数可能为 2,7,14.【第四篇】1.已知三个数 127,99 和一个小于 30 的两位数 a 除以一个一位数 b 的余数都是 3,求 a 和 b 的值 .分析： 127-3=124,99-3=96,则 b 是 124 和 96 的公约数 .而(124,96)=4,所以 b=4. 那么 a 的可能取值是 11,15,19,23,27.2.除以 99 的余数是 ______.分析：所求余数与 19×100,即与 1900 除以 99 所得的余数相同 ,所以所求余数是 19.【第五篇】199419941994(1994个 1994)除以 15 的余数是 ______.分析：法 1：从简单情况入手找规律,发现 1994÷15余14,19941994 ÷ 15余 4,199419941994 ÷余15 9,1994199419941994 ÷ 15余 14,......,发现余数 3 个一循环,1994 ÷3=664...2,19941994 1994(1994个1994)除以 15 的余数是 4;法 2：我们利用最后一个例题的结论能够发现199419941994能被 3 整除 ,那么19941994199400 0能被 15 整除 ,1994 ÷3=664...2,19941994 1994(1994个1994)除以 15 的余数是4.。
六年级下册数学试题-同余问题(含部分答案)全国通用
1．余数的定义一般地，如果a是整数，b是整数(b≠0)，若有a÷b＝q…r，或者a＝b×q＋r，0≤r＜b；当r＝0时，我们称a能被b整除；当r≠0时，我们称a不能被b整除，r为a除以b的余数，q为a除以b的商。
2．余数的性质①被除数＝除数×商＋余数；除数＝(被除数－余数)÷商；商＝(被除数－余数)÷除数；②余数小于除数。
③如果a，b除以c的余数相同，就称a，b对于除数c来说是同余的，且有a与b的差能被c整除。
(a，b，c均为自然数)例如：17与11除以3的余数都是2，所以17－11能被3整除。
④a与b的和除以c的余数，等于a，b分别除以c的余数之和(或这个和除以c的余数)。
例如：23，16除以5的余数分别是3和1，所以(23＋16)除以5的余数等于3＋1＝4。
注意：当余数之和大于除数时，所求余数等于余数之和再除以c的余数。
例如：23，19除以5的余数分别是3和4，所以(23＋19)除以5的余数等于(3＋4)除以5的余数。
⑤a与b的乘积除以c的余数，等于a，b分别除以c的余数之积(或这个积除以c的余数)。
例如：23，16除以5的余数分别是3和1，所以(23×16)除以5的余数等于3×1＝3。
注意：当余数之积大于除数时，所求余数等于余数之积再除以c的余数。
例如：23，19除以5的余数分别是3和4，所以(23×19)除以5的余数等于(3×4)除以5的余数。
3．余数的四大判断法：⑴末位判断法——被4，25，8，125，16，625除的余数特征以4为例：一个数除以4的余数，等于它的末两位除以4的余数。
⑵数位和判断法——能被3，9整除的数特征以3为例：一个数除以3的余数，等于它的数位和除以3的余数。
⑶数位差判断法——能被11整除的数的特征一个数除以11的余数，等于它的奇位和减去偶位和之差(如不够减，奇位和加11后再减)除以11的余数(注意不要减反)。
小学奥数题库《数论》余数问题余数的性质4星题(含解析)全国通用版
数论-余数问题-余数的性质-4星题课程目标知识提要余数的性质•余数的基本性质被除数=除数×商+余数除数=（被除数−余数）÷商商=（被除数−余数）÷除数余数小于除数。
•余数的三大性质（1）余数的加法性质：和的余数等于余数的和，或这个和除以除数的余数。
（2）余数的减法性质：差的余数等于余数的差，不够减加除数再减。
（3）余数的乘法性质：积的余数等于余数的积，或者余数的积除以除数的余数。
精选例题余数的性质1. 有三所学校，高中A校比B校多10人，B校比C校多10人．三校共有高中生2196人．有一所学校初中人数是高中人数的2倍；有一所学校初中人数是高中人数的1.5倍；还有一所学校高中、初中人数相等．三所学校总人数是5480人，那么A校总人数是人．【答案】1484【分析】三所学校的高中生分别是：A校742人，B校732人，C校722人．如果A校或C校初中人数是高中人数的1.5倍，该校总人数是奇数，而按照给出条件得出其他两校总人数都是偶数，与三校总人数5480是偶数矛盾，因此只能是B校的初中人数是高中人数的1.5倍．三校初中的总人数是5480−2196=3284，被3除余2；732被3整除，722被3除余2，742被3除余1．从余数来看2×2+1=5，1×2+2=4，就断定初中人数是高中人数的2倍，只能是C校．所以，A校总人数是742+742=1484(人)．2. 在自然数1∼2011中，最多可以取出个数，使得这些数中任意四个数的和都不能被11整除．【答案】550【分析】2011÷11=182⋯9,可以全选余数是3、4、5的，因为3×4=12,5×4=20,在20和22之间还可以有一个21，所以还可以选一个余数是6的．所以是183×3+1=550,这种选法能选到550，选余数是6、7、8和一个余数是5的，还是可以选出550个．3. 如果两个自然数的积被13除余1，那么我们称这两个自然数互为“模13的倒数”，比如，2×7=14，被13除余1，则2和7互为“模13的倒数”；1×1=1，则1的“模的倒数”是它自身，显然，一个自然数如果存在“模13的倒数”，则它的倒数并不是唯一的，比如，14就是1的另一个“模13的倒数”，判断1，2，3，4，5，6，7，8，9，10，11，12是否有“模13的倒数”，并利用所得结论计算1×2×3×4×5×6×7×8×9×10×11×12（记为12!，读作12的阶乘）被13除所得的余数．【答案】12【分析】模13的倒数：(1,1)，(2,7)，(3,9)，(4,10)，(5,8)，(6,11)1×2×3×4×5×6×7×8×9×10×11×12=(2×7)×(3×9)×(4×10)×(5×8)×(6×11)×12,所以被13除所得的余数为12．4. （1）(123456789+23456879)÷3的余数是；（2）(12345687×24568×365878)÷9的余数是．【答案】（1）2；（2）0．【分析】根据余数定理可得．5. M、N为非零自然数，且2007M+2008N被7整除．M+N的最小值为．【答案】5【分析】2007除以7的余数是5，2008除以7的余数是6，所以5M+6N能被7整除试算，M+N最小值为3+2=5．6. 在1995，1998，2000，2001，2003中，若其中几个数的和被9除余7，则将这几个数归为一组．这样的数组共有组．【答案】4．【分析】1995，1998，2000，2001，2003除以9的余数依次是6，0，2，3，5．因为2+5=2+5+0=7，2+5+3+6=0+2+5+3+6=7+9，所以这样的数组共有下面4个：(2000,2003)，(1998,2000,2003)，(2000,2003,2001,1995)，(1998,2000,2003,2001,1995)．7. 三位数abc除以它的各位数字和的余数是1，三位数cba除以它的各位数字和的余数也是1．如果不同的字母代表不同的数字，且a>c，那么abc = ．【答案】452【分析】abc−cba=99(a−c)，故(a+b+c)∣[99(a−c)]，但(a+b+c)必定不是3的倍数，否则abc是3的倍数，abc÷(a+b+c)的余数必为3的倍数．故(a+b+c)∣[11(a−c)]，11是质数，且a+b+c>a−c，故(a+b+c)必为11的倍数．若a+b+c=11,则a+c−b=1，b=5，又a、b、c互不相同，a>c，故a=4,c=2,abc=452；若a+b+c=22，则a+c−b=12，b=5，又a、b、c互不相同，a>c，故a=9,c=8，但此解并未满足(a+b+c)∣[11(a−c)]的要求，故知此种情况无解．综上，本题有唯一答案452．8. 如果自然数 a 、b 、c 除以 14 都余 5，则 a +b +c 除以 14，得到的余数是 ．【答案】 1【分析】 已知 a ÷14⋯5，b ÷14⋯5，c ÷14⋯5，由余数的可加性得知：(a +b +c)÷14⋯19. 商店里有六箱货物，分别重 15，16，18，19，20，31 千克，两个顾客买走了其中的五箱．已知一个顾客买的货物重量是另一个顾客的 2 倍，那么商店剩下的一箱货物重量是 千克．【答案】 20【分析】 两个顾客买的货物重量是 3 的倍数．(15+16+18+19+20+31)÷(1+2)=119÷3=39⋯⋯2,剩下的一箱货物重量除以 3 应当余 2，只能是 20 千克．10. 由 1、4、7、10、13 组成甲组数，由 2、5、8、11、14 组成乙组数，由 3、6、9、12、15 组成丙组数．现在从三组数中各取一个数相加，共可以得到 个不同的和．【答案】 13【分析】 所得的和数一定是 3 的倍数，最小是 6，最大是 42，中间的 3 的倍数也都能得到，所以一共有 (42−6)÷3+1=13(个) 不同的和．11. 有一个整数，用它去除 70，110，160 所得到的 3 个余数之和是 50，那么这个整数是 ．【答案】 29【分析】 (70+110+160)−50=290，50÷3=16......2，除数应当是 290 的大于 17 小于 70 的约数，只可能是 29 和 58，110÷58=1......52，52>50，所以除数不是 58．70÷29=2......12，110÷29=3......23，160÷29=5......15，12+23+15=50，所以除数是 29．12. 四个最简真分数 12、a 3、b 5、c 67，满足：12−a 3+b 5+c 67=20092010．则 a +b +c = ．【答案】 32【分析】由题可得1005−670a+402b+30c=2009,整理得402b+30c−670a=1004,考虑除以5的余数，且b<5，推断出b=2，把b=2代入上式，可得3c−67a=20,所以c=29，a=1，a+b+c=32．13. 定义：1!=1，2!=1×2，3!=1×2×3，n!=1×2×3×⋯×n，则2011!+10除以2012的余数为．【答案】10【分析】2011!中包含2与1006，所以2011!是2012的倍数．那么余数为10．14. 将1至8填入方格中，使得数列□□,9,□□,□□,□□从第三个项开始，每一项都等于前面两项的和，那么这个数列的所有项之和是．【答案】198【分析】第三个数比第一个数多9，第四个数比第三个数多9；若第一个数除以9余a，则第三个数和第四个数也余a，第五个数则余2a，五个数总和除以9余4a；而由于1+2+3++9=45是9的倍数，易知a=0，即这五个数都是9的倍数；若设第一个数为18，则这五个数分别为18，9，27，36，63；6出现两次不符合要求；若设第一个数为27，则这五个数分别为27，9，36，45，81；符合要求．所有项之和为27+9+36+45+81=19815. 将1∼2015这2015个自然数依次写出，得到一个多位数123456789⋯20142015，这个多位数除以9，余数是．【答案】0【分析】乱切法，求多位数123456789⋯20142015除以9的余数，即要求1+2+3+4+5+⋯+2015=(1+2015)×20152=1008×2015除以9的余数，1008×2015≡0×8 (mod 9),则余数为0．16. 有8只盒子，每只盒内放有同一种笔．8只盒子所装笔的支数分别为17支、23支、33支、36支、38支、42支、49支、51支．在这些笔中，圆珠笔的支数是钢笔支数的2倍，铅笔支数是钢笔支数的3倍，只有一只盒里放的是水彩笔．这盒水彩笔共有支．【答案】49【分析】铅笔数是钢笔数的3倍，圆珠笔数是钢笔数的2倍，因此这三种笔支数的和是钢笔数的3+2+1=6(倍)．17+23+33+36+38+42+49+51=289，除以6余1，所以水彩笔的支数除以6余1，在上述8盒的支数中，只有49除以6余1，因此水彩笔共有49支．17. 22003与20032的和除以7的余数是．【答案】5．【分析】找规律．用7除2，22，23，24，25，26，…的余数分别是2，4，1，2，4，1，2，4，1，…，2的个数是3的倍数时，用7除的余数为1；2的个数是3的倍数多1时，用7除的余数为2；2的个数是3的倍数多2时，用7除的余数为4．因为22003=23×667+2，所以22003除以7余4．又两个数的积除以7的余数，与两个数分别除以7所得余数的积相同．而2003除以7余1，所以20032除以7余1．故22003与20032的和除以7的余数是4+1=5．18. 从1到999这999个自然数中有个数的各位数字之和能被4整除．【答案】248【分析】由于在一个数的前面写上几个0不影响这个数的各位数字之和，所以可以将1到999中的一位数和两位数的前面补上两个或一个0，使之成为一个三位数．现在相当于要求001到999中各位数字之和能被4整除的数的个数．一个数除以4的余数可能为0，1，2，3，0～9中除以4余0的数有3个，除以4余1的也有3个，除以4余2和3的各有2个．三个数的和要能被4整除，必须要求它们除以4的余数的和能被4整除，余数的情况有如下5种：0+0+0；0+1+3；0+2+2；1+1+2；2+3+3．（1）如果是0+0+0，即3个数除以4的余数都是0，则每位上都有3种选择，共有3×3×3=27种可能，但是注意到其中也包含了000这个数，应予排除，所以此时共有27−1=26(个);（2）如果是0+1+3，即3个数除以4的余数分别为0，1，3，而在3个位置上的排列有3!=6(种)，所以此时有3×3×2×6=108(个);（3）如果是0+2+2，即3个数除以4的余数分别为0，2，2，在3个位置上的排列有3种，所以此时有3×2×2×3=36(个);（4）如果是1+1+2，即3个数除以4的余数分别为1，1，2，在3个位置上的排列有3种，所以此时有3×3×2×3=54(个);（5）如果是2+3+3，即3个数除以4的余数分别为2，3，3，在3个位置上的排列有3种，此时有2×2×2×3=24(个).根据加法原理，共有26+108+36+54+24=248(个).19. 下列算式中，“迎”、“春”、“杯”、“数”、“学”、“花”、“园”、“探”、“秘”代表1~9 中的不同非零数字，那么，“迎春杯”所代表三位数的最大值是．1984−迎春杯=2015−数学−花园−探秘【答案】214【分析】（1）将等式整理得：迎春杯+31=数学+花园+探秘,等式两边除以9的余数相同，所以迎春杯除以9的余数只能为7，等式右侧除以9的余数为2；（2）要想迎春杯最大，则数学，花园，探秘应尽量的大，这3个数和最大为96+85+74=255,所以迎春杯最大不大于255−31=224，由于不同汉字代表不同非零数字，所以“迎”最大为2，“春”最大为1；（3）由于迎春杯除以9的余数为7，若“迎”取2，“春”取1，则“杯”为4，经尝试可得：214+31=97+85+67,所以迎春杯最大值为21420. 18＋28＋38＋…＋98除以3的余数是多少？【答案】0．【分析】根据等差数列求和列式：18＋28＋38＋…＋98=(18+98)×9÷2，整理可得58×9，因为58÷3⋯⋯1，9÷3⋯⋯0，根据余数定理，58×9除以3的余数等于1乘0除以3的余数，即1×0÷3⋯⋯0，所以18＋28＋38＋…＋98除以3的余数是0．21. 从1，2，3，4，⋯，2007中取N个不同的数，取出的数中任意三个的和能被15整除．N最大为多少？【答案】134【分析】取出的N个不同的数中，任意三个的和能被15整除，则其中任意两个数除以15的余数相同，且这个余数的3倍能被15整除，所以这个余数只能是0，5或者10．在1∼2007中，除以15的余数为0的有15×1,15×2,⋯,15×133,共有133个；除以15的余数为5的有15×0+5,15×1+5,⋯,15×133+5,共有134个；除以15的余数为10的有15×0+10,15×1+10,⋯,15×133+10,共有134个．所以N最大为134．22. 验算46876×9573=447156412这个算式是否正确？【答案】不正确．【分析】根据余数乘积性质，以及弃九法可知这个算式左边(46876×9573)÷9的余数为6，而右边447156412除以9的余数为7，所以这个算式不成立．23. 有如下图所示的十二张扑克牌．2点、6点、10点各四张，你能从中选出七张牌，使上面点数之和恰等于52吗？说明理由．【答案】不能【分析】因为每张牌除以4的余数均为2，7张牌除以4的余数仍为2，而52是4的倍数，矛盾，所以不能选出这样的7张牌．24. 若a为自然数，证明10∣∣(a2005−a1949)．【答案】见解析．【分析】10=2×5，由于a2005与a1949的奇偶性相同，所以2∣∣(a2005−a1949)．a2005−a1949=a1949(a56−1)，如果a能被5整除，那么5∣a1949(a56−1)；如果a不能被5整除，那么a被5除的余数为1、2、3或者4，a4被5除的余数为14、24、34、44被5除的余数，即为1、16、81、256被5除的余数，而这四个数除以5均余1，所以不管a为多少，a4被5除的余数为1，而a56=(a4)14，即14个a4相乘，所以a56除以5均余1，则a56−1能被5整除，有5∣a1949(a56−1)．所以5∣(a2005−a1949)．由于2与5互质，所以10∣(a2005−a1949)．25. 求644312÷19的余数．【答案】11【分析】本题为余数乘法定理的拓展模式，即数字的乘方与一个数相除的余数情况．由6443÷19余2，求原式的余数只要求212÷19的余数即可．但是如果用2÷19发现会进入一个死循环，因为这时被除数比除数小了，所以可以进行适当的调整，212=26×26=64×64，64÷19余数为7，那么求212÷19的余数就转化为求64×64÷19的余数，即49÷19的余数．49÷19余数为11，所以644312÷19的余数为11．26. 从1，2，3，4，⋯，200中取N个不同的数，取出的数中任意三个的和都不能被7整除．N最大为多少？【答案】60【分析】除以7的余数有：0、1、2、3、4、5、6，从余数看，能整除7的组合有：余数和为7：(0,0,0)、(0,1,6)、(0,2,5)、(0,3,4)、(1,1,5)、(1,2,4)、(1,3,3)、(2,2,3);余数和为14：(2,6,6)、(3,5,6)、(4,4,6)、(4,5,5).取1，则不能取6、5、3；取2，则不能取6、5、3；取1和2，则不能取4.1和2，与6、5、4、3选择，要选择取1和2．200÷7＝28⋯⋯4,取29个1，取29个2，2个0，共计：29+29+2＝60(个).27. 用自然数n去除63，91，129得到的三个余数之和为25，那么n=．【答案】43．【分析】n能整除63+91+129−25=258．因为25÷3=8...1，所以n是258大于8的约数．显然，n不能大于63．符合条件的只有43．28. 已知:a÷5=⋯⋯3，b÷5=⋯⋯2且a>b那么：（1）(a+b)÷5⋯⋯；（2）(a−b)÷5⋯⋯；（3）(a×b)÷5⋯⋯．【答案】（1）0；（2）1；（3）1．【分析】（1）(3+2)÷5⋯⋯0；（2）(3−2)÷5⋯⋯1；（3）(3×2)÷5⋯⋯1．29. 1＋2＋3＋…＋2000除以19的余数是多少？【答案】15．【分析】根据等差数列求和列式：1＋2＋3＋…＋2000=(1+2000)×2000÷2，整理可得2001×1000，因为2001÷19⋯6，1000÷19⋯12，根据余数定理，2001×1000除以19的余数等于6×12除以19的余数，即6×12÷19⋯15，所以1＋2＋3＋…＋2000除以19的余数是15．30. 如果a+b+c是5的倍数，2a+3b+4c也是5的倍数，求证a−c是5的倍数．（a、b、c都是自然数）【答案】见解析【分析】a−c=3(a+b+c)−(2a+3b+4c)，所以a−c能被5整除．31. 有一串数：1，1，2，3，5，8，……，从第三个数起，每个数都是前两个数之和，在这串数的前2014个数中，有几个是5的倍数？【答案】402【分析】先观察规律可知这组数从第三个开始，每个数都等于与它相邻的前面两个数的和，所以根据余数的加法性质得出如下表格：数112358⋯⋯⋯⋯⋯⋯⋯⋯⋯除以5的余数112303314044320从上表可知这组自然数除以5的余数是每5个就有一个余数为0，所以2014÷5=402⋯⋯4所以，在这串数的前2014个数中，有402个是5的倍数．32. 六名小学生分别带着14元、17元、18元、21元、26元、37元钱，一起到新华书店购买《数学的发现》．一看定价才发现有5个人带的钱不够，但是其中甲、乙、丙3人的钱凑在一起恰好可买2本，丁、戊2人的钱凑在一起恰好可买1本．这本《数学的发现》的定价是多少元？【答案】32【分析】六名小学生共带钱133元．133除以3余1，因为甲、乙、丙、丁、戊的钱恰好能买3本，所以他们五人带的钱数是3的倍数，另一人带的钱除以3余1．易知，这个钱数只能是37元，所以每本《数学的发现》的定价是(14+17+18+21+26)÷3=32元．33. 六位数20▫▫08能被49整除，▫▫中的数是多少？【答案】05或54．【分析】设六位数为20ab08，则20ab08=200008+ab00=200008+ab×100．因为200008÷49=4081⋯⋯39，所以(ab×100)÷49的余数为49−39=10．又因为100÷49=2⋯⋯2，所以ab÷49的余数为5．则ab可以是05或54．34. 在所有由1、3、5、7、9中的3个不同数字组成的三位数中，有多少个是3的倍数？【答案】24【分析】除以3余0的数有3,9，除以3余1的数有1,7，除以3余2的数有5，三个数字之和为3的倍数，本题只能从除以3余0,1,2的数中各取一个，每个三位数交换位置又可以变换出6个，因此共有2×2×1×6=24(个)．35. （1）123+456+789的结果除以111的余数是多少？（2）224468−6678的结果除以22的余数是多少？【答案】（1）36；（2）12【分析】简答：利用替换求余法计算．36. 已知98个互不相同的质数p1，p2，⋯，p98，记N=p12+p22+⋯+p982，问：N被3除的余数是多少？【答案】1或2．【分析】（1）这些质数中不含质数3，所以该数平方后被3除的余数就是1，所以N被3除的余数就是98被3除的余数，是2；（2）如果有3，那么剩下97个除以3余1．3的平方除以3余数是０，那么N除以3的余数1．37. 已知n!+4等于两个相邻自然数的乘积，试确定自然数n的值．（n!=1×2×3×⋯×n）【答案】2【分析】注意到两个相邻自然数的乘积除以3只能余0或余2．因为当n⩾3时，n!+4除以3余1，所以n<3，尝试n取0、1、2后得n为2．38. 从1，2，3，⋯⋯49，50这50个数中取出若干个数，使其中任意两个数的和都不能被7整除，则最多能取出多少个数？【答案】23【分析】将1至50这50个数，按除以7的余数分为7类：[0]，[1]，[2]，[3]，[4]，[5]，[6]，所含的数的个数分别为7，8，7，7，7，7，7．被7除余1与余6的两个数之和是7的倍数，所以取出的数只能是这两种之一；同样的，被7除余2与余5的两个数之和是7的倍数，所以取出的数只能是这两种之一；被7除余3与余4的两个数之和是7的倍数，所以取出的数只能是这两种之一；两个数都是7的倍数，它们的和也是7的倍数，所以7的倍数中只能取1个．所以最多可以取出8+7+7+1=23个39. （1）21100的个位数字是多少？32014除以10的余数是多少？（2）32014除以7的余数是多少？【答案】（1）6；9（2）4【分析】详解：（1）2n的个位数字依次是2、4、8、6、⋯每四个数为一个周期．100除以4的余数是0，那么2100的个位数字是周期中的第四个数6．3n的个位数字依次是3、9、7、1、⋯每四个数为一个周期．2014除以4的余数是2，那么32014的个位数字是周期中的第二个数9．（2）3n除以7的余数依次是3、2、6、4、5、1、⋯每六个数为一个周期．2014除以6的余数是4．所以32014除以7的余数是周期中的第四个数4．40. 甲、乙两个天平上都放着一定重量的物体，问：哪—个是平衡的？【答案】天平乙是平衡的．【分析】考虑除以3，所得的余数．因为478除以3余1，9763除以3也余1（只要看4+7+8，9+7+6+3除以3的余数），所以478×9763除以3余1×1=1，而4666514除以3余2（即4+6+6+6+5+1+4除以3余2），因此478×9763≠4666514，从而天平甲不平衡．天平乙是平衡的．41. 有6个密封的盒子，分别装有红球、白球和黑球，每个盒子里只有一种颜色的球，且球的个数分别是15，16，18，19，20，31，已知黑球的个数是红球个数的两倍，装白球的盒子只有1个，问：（1）装有15个球的盒子里装的是什么颜色的球？（2）有多少个盒子里装的是黑球？【答案】（1）红球；（2）3【分析】（1）所有球的个数：15+16+18+19+20+31=119(个).黑球的个数是红球的2倍，黑球加红球的个数是红球的2+1=3倍119÷3=39⋯⋯2根据余数的可加可减性，白球的个数除以3也是余2，白球的个数只能是20．黑球和红球共：119−20=99(个).红球：99÷3=33(个)只能是15+18=33(个).答：装有15个球的盒子里装的是红球．（2）还剩下16，19，31的盒子里装的是黑球，即有3个盒子．答：有3个盒子里装的是黑球．42. 如果(3a+b)是7的倍数，求证(2b−a)也是7的倍数．（a、b都是自然数）．【答案】见解析【分析】方法一：因为(3a+b)是7的倍数，所以(6a+2b)也是7的倍数，所以(6a+2b−7a)即(2b−a)，也是7的倍数．方法二：设3a+b=7k，那么a=7k−b3，所以2b−a=7b−7k3也是7的倍数．43. 11+22+33+44+⋯+20052005除以10所得的余数为多少？【答案】3【分析】求结果除以10的余数即求其个位数字．从1到2005这2005个数的个位数字是10个一循环的，而对一个数的幂方的个位数，我们知道它总是4个一循环的，因此把所有加数的个位数按每20个（20是4和10的最小公倍数）一组，则不同组中对应的个位数字应该是一样的．首先计算11+22+33+44+⋯+2020的个位数字，为1+4+7+6+5+6+3+6+9+0+1+6+3+6+5+6+7+4+9+0=94的个位数字，为4，由于2005个加数共可分成100组另5个数，100组的个位数字和是4×100=400的个位数即0，另外5个数为20012001、20022002、20032003、20042004、20052005，它们和的个位数字是1+4+7+6+5=23的个位数3，所以原式的个位数字是3，即除以10的余数是3．44. 今天是星期四，101000天之后将是星期几？【答案】星期一【分析】先求较小的n，使10n除以7的余数为1．10除以7余3，102除以7余2，103=10×102除以7余3×2=6，104=102×102除以7余2×2=4，106=103×103除以7的余数等于6×6=36除以7的余数等于1，所以，101000除以7的余数等于104×106×166除以7的余数等于4×1=4故101000天后为星期一．45. 在小于1000的自然数中，分别除以18及33所得余数相同的数有多少个？（余数可以为0）【答案】99【分析】我们知道18，33的最小公倍数为[18,33]=198，所以每198个数一次．1～198之间只有1，2，3，⋯，17，198（余0）这18个数除以18及33所得的余数相同，而999÷198=5⋯⋯9，所以共有5×18+9=99个这样的数．46. 如果六位数1992▫▫能被105整除，那么它的最后两位数是多少？【答案】90【分析】方法一：利用整除特征．因为105=3×7×5，所以这个六位数同时满足能被3、7、5整除的数的特征即可．末位只能为0或5．①如果末位填入0，那么数字和为1+9+9+2+▫+0=21+▫，要求数字和是3的倍数，所以▫可以为0，3，6，9，验证200−199=1，230−199=31，260−199=61，290−199=91，有91是7的倍数，即199290是7的倍数，所以题中数字的末两位为90．②如果末位填入5，同上解法，验证没有数同时满足能被3、7、5整除的特征．所以，题中数的末两位只能是90．方法二：采用试除法用199200试除，199200÷105=1897⋯⋯15，余15可以看成不足，105−15=90．所以补上90，即在末两位的方格内填入90即可．47. 22008+20082除以7的余数是多少？【答案】3【分析】23=8除以7的余数为1，2008=3×669+1，所以22008=23×669＋1=(23)669×2，其除以7的余数为：1669×2=2；2008除以7的余数为6，则20082除以7的余数等于62除以7的余数，为1；所以22008+20082除以7的余数为：2+1=3．48. 甲、乙、丙三数分别为603，939，393．某数A除甲数所得余数是A除乙数所得余数的2倍，A除乙数所得余数是A除丙数所得余数的2倍．求A等于多少？【答案】17【分析】设这个数为M，则603÷M=A1⋯⋯r1，939÷M=A2⋯⋯r2，393÷M=A3⋯⋯r3，r1=2×r2，r2=2×r3，要消去余数r1,r2,r3，我们只能先把把余数处理成相同的，再两数相减．这样我们先把第二个式子乘以2，这样被除数和余数都扩大2倍，同理，第三个式子乘以4．这样我们可以得到下面的式子：603÷M=A1…r1，(939×2)÷M=2A2…(r2×2)，(393×4)÷M=4A3⋯⋯(r3×4)这样余数就处理成相同的．最后两两相减消去余数，意味着能被M整除．939×2−603=1275，393×4−603=969，1275−969= 306，(1275,306)=51=3×17．603,939,393这三个数有公约数3．51÷3=17．则A等于17．49. 如果(a+2b)被5除余数为2，(3a−b)被5除所得的余数为3，求证：(a−b)能被5整除．（a、b都是自然数）．【答案】证明见解析【分析】方法一：设a+2b=5k+2，3a−b=5l+3，解方程组 $\left\{ \begin{gathered}a + 2b = 5k +2 \hfill \\3a - b = 5l +3 \hfill \\\end{gathered} \right.$ 得到 $\left\{ \begin{gathered}a = \dfrac{{10l+ 5k + 8}}{7} \hfill \\b = \dfrac{{3 +15k - 5l}}{7} \hfill \\\end{gathered} \right.$，所以a−b=15l−10k+57能被5整除．方法二：由题目条件2(3a−b)−3(a+2b)能被5整除，即3a−8b能被5整除，继而得到3a−3b能被5整除，所以a−b能被5整除．50. 在六位数11▫▫11中的两个方框内各填入一个数字，使此数能被17和19整除，那么方框中的两位数是多少？【答案】53【分析】采用试除法．设六位数为11ab11，则11ab11=11×10000+ab00+11=110011+ab00如果一个数能同时被17和19整除，那么一定能被323整除．110011÷323=340⋯⋯191,余191也可以看成不足323−191=132．所以当ab00=132+323n时，即ab00是100的倍数时，六位数才是323的倍数．所以有323n的末位只能是10−2=8，所以n只能是6，16，26，⋯验证有n=16时，132+ 323×16=5300，所以原题的方框中填入5，3得到的115311满足题意．−1的个位数字是多少？51. 自然数2×2×2×...×2⏟67个2【答案】7．的个数数字，再减去1即为所求（特别的如果是0，【分析】我们先计算2×2×2×...×2⏟67个2那么减去1后的个位数字因为借位为9）．将一个数除以10，所得的余数即是这个数的个位数字．而积的余数，等于同余余数的积．2除以10的余数为2，2×2除以10的余数为4，2×2×2除以10的余数为8，2×2×2×2除以10的余数为6；2×2×2×2×2除以10的余数为2，2×2×...×2除以10的余数为4，⏟6个22×2×...×2除以10的余数为8，⏟7个22×2×...×2除以10的余数为6；⋯⋯⏟8个2也就是说，n个2相乘所得的积除以10的余数每4个数一循环．除以10的余数同余与2×2×2，即余数为8，因为67÷4=16⋯⋯3，所以2×2×2...×2⏟67个2−1除以10的余数为7．所以2×2×2...×2⏟67个2−1的个位数字为7．即2×2×2...×2⏟67个2评注：n个相同的任意整数相乘所得积除以10的余数每4个数一循环．52. 11+22+33+44+⋯⋯+20132013+20142014除以10所得的余数为多少？【答案】3【分析】求结果除以10的余数即求其个位数字．从1到2014这2014个数的个位数字是10个一循环的，而对一个数的幂方的个位数，我们知道它总是4个一循环的，因此把所有加数的个位数按每20个（20是4和10的最小公倍数）一组，则不同组中对应的个位数字应该是一样的．首先计算11+22+33+44+⋯⋯+2020的个位数字，为1+4+7+6+5+6+3+6+9+0+1+6+3+6+5+6+7+4+9+0=94结果的个位数字为4，由于2014个加数共可分成100组另14个数，100组的个位数字和是4×100=400的个位数即0，另外5个数为20012001、20022002、20032003、20042004、20052005、…… 20142014，它们和的个位数字是1+4+7+6+5+6+3+6+9+0+1+6+3+6=63，63的个位数3，所以原式的个位数字是3，即除以10的余数是3．53. 求证：可以找到一个各位数字都是4的自然数，它是1996的倍数．【答案】见解析．【分析】1996÷4=499，下面证明可以找到1个各位数字都是1的自然数，它是499的倍数．取500个数：1，11，111，⋯⋯，111⋯⋯1（500个1）．用499去除这500个数，得到500个余数a1，a2，a3，⋯，a500．由于余数只能取0，1，2，⋯，498这499个值，所以根据抽屉原则，必有2个余数是相同的，这2个数的差就是499的倍数，差的前若干位是1，后若干位是0：11⋯100⋯0．又499和10是互质的，所以它的前若干位由1组成的自然数是499的倍数，将它乘以4，就得到一个各位数字都是4的自然数，这是1996的倍数．54. 已知n!+3是一个完全平方数，试确定自然数n的值．（n!=1×2×3×⋯×n）【答案】0、1或3【分析】枚举验证n为0、1、2、3、4、…，得到n为0、1或3时满足．因为当n⩾4时，n!+3除以4余3，根据完全平方数除以4只能余0或余1，可知当n⩾4时，n!+1不可能是完全平方数．55. 算式188+288+388+⋯+1988+2088的结果除以9、13的余数分别是多少？【答案】8；10【分析】188+288+388+⋯+1988+2008=(188+2088)×10然后利用替换求余法计算．56. （1）87784+49235×81368除以4、9的余数分別是多少？（2）365366+367368×369370除以7、11、13的余数分别是多少？【答案】（1）0；2（2）2；2；2【分析】 详解：提示，特性求余法和替换法结合使用．57. 用 0 至 9 这十个数字各 1 次，组成四位数、三位数、两位数和一位数各 1 个，并使这四个数两两互质．已知组成的四位数是 1860，那么其他的三个数是多少？【答案】 7；43；529【分析】 1860=22×3×5×31，一位数只能是 7，另外两个数的末位只能是 3 和 9．剩下的数字之和除以 3 余 2，只能拆成两个数除以 3 余 1 的组合，所以 4 和 2、5 是分成两组，49 是 7 的倍数，所以两位数只能是 43，259 是 7 的倍数，所以三位数只能是 529．58. 在任意的四个自然数中，是否其中必有两个数，它们的差能被 3 整除？【答案】 是．【分析】 因为任何整数除以 3，其余数只可能是 0，1，2 三种情形．我们将余数的这三种情形看成是三个“抽屉”．一个整数除以 3 的余数属于哪种情形，就将此整数放在那个“抽屉”里．将四个自然数放入三个抽屉，至少有一个抽屉里放了不止一个数，也就是说至少有两个数除以 3 的余数相同，所以这两个数的差必能被 3 整除．59. 一个大于 1 的数去除 290，235，200 时，得余数分别为 a ，a +2，a +5，则这个自然数是多少？【答案】 19【分析】 设这个数为 x ，则有{290÷x =m ⋯⋯a235÷x =n ⋯⋯a +2200÷x =p ⋯⋯a +5可以转化为：{290÷x =m ⋯⋯a233÷x =n ⋯⋯a 195÷x =p ⋯⋯a即有 290≡233(modx)≡195(modx)，根据同余性质，可知 x 为它们两两差的约数，又290−233=57，290−195=95，233−195=38，(38,57,95)=19，所以这个自然数为 19．60. 算式 2009×2009+2010×2010+2011×2011 除以 31 的余数是多少？【答案】 15【分析】 简答：利用替换求余法计算．61. 已知60，154，200被某自然数除所得的余数分别是a−1，a2，a3−1，求该自然数的值．【答案】29【分析】根据题意可知，自然数61，154，201被该数除所得余数分别是a，a2，a3．由于a2=a×a，所以自然数612=3721与154同余；由于a3=a×a2，所以61×154=9394与201同余，所以除数是3721−154=3567和9394−201=9193的公约数，运用辗转相除法可得到(3567,9193)=29，该除数为29．经检验成立．62. 一个自然数除429、480所得的余数相等，求这个自然数的值．【答案】3，17或51．【分析】这两个数除以该自然数的余数相同，也就是同余，那么这两个数的差除以该自然数就除得开，也就是(480−429)能够除得开，即51．51=3×17，这个数可以是3，17或51．63. 请问至少出现一个数码3，并且是3的倍数的五位数共有多少个？【答案】12504【分析】五位数共有90000个，其中3的倍数有30000个．可以采用排除法，首先考虑有多少个五位数是3的倍数但不含有数码3．首位数码有8种选择，第二、三、四位数码都有9种选择．当前四位的数码确定后，如果它们的和除以余数为0，则第五位数码可以为0、6、9；如果余数为1，则第五位数码可以为2、5、8；如果余数为2，则第五位数码可以为1、4、7．可见只要前四位数码确定了，第五位数码都有3种选择，所以五位数中是3的倍数但不含有数码3的数共有8×9×9×9×3=17496(个).所以满足条件的五位数共有30000−17496=12504(个).64. (3130+3031)被13除所得的余数是多少？【答案】3【分析】31被13除所得的余数为5，当n取1，2，3，⋯，时5n被13除所得余数分别是5，12，8，1，5，12，8，1，⋯，以4为周期循环出现，所以530被13除的余数与52被13除的余数相同，余12，则3130除以13的余数为12；30被13除所得的余数是4，当n取1，2，3，⋯，时，4n被13除所得的余数分别是4，3，12，9，10，1，4，3，12，9，10，⋯，以6为周期循环出现，所以431被13除所得的余数等于41被13除所得的余数，即4，故3031除以13的余数为4；所以(3130+3031)被13除所得的余数是12+4−13=3．65. 求1∼2013的自然数中最多可以取出多少个数，使得任意两数之和不能被两数之差整除？。
带余数的除法奥数题道 带余数的除法奥数题及答案
带余数的除法奥数题道带余数的除法奥数题及答案题目1小明手上有45个苹果，要均分给他的3个朋友。
请问小明每人能分到几个苹果，还有剩余几个苹果？解答将45除以3得到商15，余数为0。
小明每人能分到15个苹果，没有剩余。
题目2小红收到了30本书，想要将它们平均分成4堆。
请问每堆书有几本，还有剩余几本书？解答将30除以4得到商7，余数2。
小红每堆书有7本，还剩下2本。
题目3小华手上有65只纸鹤，他想把它们放在3本相同大小的笔记本中。
请问每本笔记本里有几只纸鹤，还有剩余几只？解答将65除以3得到商21，余数2。
每本笔记本里有21只纸鹤，还剩下2只。
题目4有100个学生参加足球比赛，要将他们平均分到10个队中。
请问每个队有几个学生，还有剩余几个学生？解答将100除以10得到商10，余数0。
每个队有10个学生，没有剩余。
题目5小李有17本漫画书，要将它们分成5堆。
请问每堆有几本书，还有剩余几本？解答将17除以5得到商3，余数2。
每堆有3本书，还剩下2本。
题目6小明买了23根铅笔，要均分给他的4个朋友。
请问每人能分到几根铅笔，还有剩余几根？解答将23除以4得到商5，余数3。
每人能分到5根铅笔，还剩下3根。
题目7小华有98个糖果，他想将它们平均分给他的7个同学。
请问每个同学能分到几个糖果，还有剩余几个糖果？解答将98除以7得到商14，余数0。
每个同学能分到14个糖果，没有剩余。
题目8小红有53块巧克力，她想将它们分成4堆。
请问每堆有几块巧克力，还有剩余几块？解答将53除以4得到商13，余数1。
每堆有13块巧克力，还剩下1块。
题目9小李有63颗石头，他想将它们放在4个箱子中。
请问每个箱子里有几颗石头，还有剩余几颗？解答将63除以4得到商15，余数3。
每个箱子里有15颗石头，还剩下3颗。
题目10有30个学生参加篮球比赛，要将他们平均分到6个队中。
请问每个队有几个学生，还有剩余几个学生？解答将30除以6得到商5，余数0。
六年级下册数学试题-小升初提升：余数问题(无答案)全国通用
余数问题（1）本讲重点余数综合应用——“物不知数”。
【例1】(★★)不足100名同学跳集体舞时有两种组合：一种是中间一组5人，其他人按8人一组围在外圈；另一种是中间一组8人，其他人按5人一组围在外圈。
问最多有多少名同学?【例2】(★★★)试证不小于5的质数的平方与1的差必能被24整除。
【例3】(★★★) (北京市迎春杯决赛试题)有5000多根牙签，按以下6种规格分成小包：如果10根一包，最后还剩9根；如果9根一包，最后还剩8根；如果依次以8、7、6、5根为一包，最后分别剩7、6、5、4根。
原来一共有牙签多少根？【例4】(★★★☆)在200至300之间，有三个连续的自然数，其中，最小的能被3整除，中间的能被7整除，最大的能被13整除，那么这样的三个连续自然数分别是多少？【巩固】(★★☆)有连续的三个自然数a、a＋1、a＋2，它们恰好分别是9、8、7的倍数，求这三个自然数中最小的数至少是多少？【例5】(★★★)请找出所有的四位数，使它除以7、11、13的余数之和尽可能大。
【本讲要点回顾】物不知数——通过不同除数下的余数找满足条件的被除数：1．去同余，添同补；2．和谐法(调系法)——除与被除双等差数列；3．中国剩余定理——逐级满足法。
余数问题（2）本讲重点余数问题——综合应用（俗称大杂烩）【例1】(★★★)(南京市“兴趣杯”少年数学邀请赛决赛)现有糖果254粒，饼干210块和桔子186个。
某幼儿园大班人数超过40，每人分得一样多的糖果，一样多的饼干，也分得一样多的桔子。
余下的糖果、饼干和桔子的数量的比是1∶3∶2，这个大班有名小朋友，每人分得糖果粒，饼干块，桔子个。
【例2】(★★☆)桌上有111根火柴，甲乙两人轮流取火柴，每人每次可以取一根或质数根，取到最后一根者为胜方，问甲应如何取才能取得胜利？【巩固】(★★☆)请你参加一种游戏：有1996个棋子，两人轮流取棋子，每次允许取其中2个、4个或8个，谁最后把棋子取完，就算获胜。
小学六年级奥数题大全：余数问题
小学六年级奥数题大全：余数问题1.1111+2×1111+3×1111+…+1111×1111被7除所得的余数是 . ?2.在所有的两位数中，用较大的自然数除以较小的自然数，得到的余数能够达到 .??3.一个自然数被9除余1，所得的商被8除也余1.再把第2次所得的商除以8得商为a余7.又知这个自然数被17除余4，所得的商被17除余15，商是a的2倍，这个自然数是 .4.除以3余1，除以4，5，7不足2的三位数是 .??5.用某自然数a去除2002，得到的商是46，余数是r.则a= ，r= .??6.除以3余1，除以5余2，除以7余4的最小三位数是 .??7.两数相除商5余5，如果被除数扩大5倍，除数不变，则商是27，余数是3，原被除数是，除数是 .??8.7599除以一个质数，所得余数是9，这个质数最小是 .??9.678除以一个数，不完全商是13，并且除数与余数的差是8，除数是，余数是 .??10.一个三位数除以9余6，除以4余2，除以5余1，这样的数中的一个是 .11.某三位数的各位数字都不为零，并且这个三位数被它的各位数字之和除，所得的商最小可能是 .??12.8.77÷5.3除到一位小数时，商是1.6，余数是___________.??13.在下面算式的方框内填数，使带余数的除法的余数.?□÷78=245…□14.一个数能被3、5、7整除，若用11去除则余1.这个数最小是 .?15.某校五年级有学生若干人.?(1)若3人一行最后余2人，7人一行最后余2人，11人一行最后也余2人，五年级最少有学生多少人???(2)若3人一行最后余1人，7人一行最后余5人，11人一行最后余9人，五年级最少有学生多少人?。
小学奥数数论专题--余数(六年级)竞赛测试.doc
小学奥数数论专题--余数（六年级）竞赛测试姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题评卷人得分（每空xx 分，共xx分）【题文】号码分别为101，126，173，193的4个运动员进行乒乓球比赛，规定每两人比赛的盘数是他们号码的和被3除所得的余数．那么打球盘数最多的运动员打了多少盘?【答案】5【解析】因为两个数和的余数同余与余数的和．有101，126，173，193除以3的余数依次为2，0，2，1．则101号运动员与126，173，193号运动员依次进行了2，1，0盘比赛，共3盘比赛；26号运动员与101，173，193号运动员依次进行了2，2，1盘比赛，共5盘比赛；173号运动员与101，126，193号运动员依次进行了1，2，0盘比赛，共3盘比赛；193号运动员与101，126，173号运动员依次进行了0，1，0盘比赛，共1盘比赛．所以，打球盘数最多的运动是126号，打了5盘．【题文】自然数－1的个位数字是多少?【答案】7【解析】我们先计算出的个数数字，再减去1即为所求．(特别的如果是0，那么减去1后的个位数字因为借位为9)将一个数除以10，所得的余数即是这个数的个位数字．而积的余数等于余数的积．有2除以10的余数为2，2×2除以10的余数为4，2×2×2除以10的余数为8，2×2×2×2除以10的余数为6；2×2×2×2×2除以10的余数为2，除以10的余数为4，除以10的余数为8，除以10的余数为6；…… ……也就是说，n个2相乘所得的积除以10的余数每4个数一循环．因为67÷4＝16……3，所以除以10的余数同余与2×2×2，即余数为8，所以－1除以8的余数为7．即－1的个位数字为7．评注：n个相同的任意整数相乘所得积除以10的余数每4个数一循环．【题文】算式7+7×7+…+计算结果的末两位数字是多少?【答案】56【解析】我们只用算出7+7×7+…+的和除以100的余数，即为其末两位数字．7除以100的余数为7，7×7除以100的余数为49，7×7×7除以100的余数为43，7×7×7×7除以100的余数等于43×7除以100的余数为1；而除以100的余数等于×7的余数，即为7，……这样我们就得到一个规律除以100所得的余数，4个数一循环，依次为7，49，43，1．1990÷4＝497……2，所以7+7×7+…+的和除以100的余数同余与：497×(7+49+43+1)+7+49＝49756，除以100余56．所以算式7+7×7+…+计算结果的末两位数字是56．【题文】除以9的余数是多少?【答案】2【解析】能被9整除的数的特征是其数字和能被9整除，如果这个数的数字和除以9余a，那么我们在减去a而得到的新数一定能被9整除，那么这个新数加上a后再除以9，所得的余数一定为a，即一个数除以9的余数等于其数字和除以9的余数．的数字和为20×(1+9+9+0)＝380，380的数字和又是3+8＝11，11除以9的余数为2，所以除以9的余数是2．【题文】将1，2，3，…，30从左往右依次排列成一个5l位数，这个数被11除的余数是多少?【答案】8【解析】1，2，3，...，30这30个数从左往右依次排列成一个51位数为：123456...910...17...192021...25 (2930)记个位为第1位，十位为第2为，那么：它的奇数位数字和为：0+9+8+7+6+…+1+9+8+7+6+…+1+9+7+5+3+1＝115；它的偶数位数字和为：3+++8+6+4+2＝53；它的奇数位数字和与偶数位数字和的差为115－53＝62.而62除以11的余数为7．所以将原来的那个51位数增大4所得到的数123456…910…17…192021…25…2934就是11倍数，则将123456…910…17…192021…25…2934减去4所得到数除以11的余数为7．即这个51位数除以11的余数是7．评注：如果记个位为第1位，十位为第2位，那么一个数除以11的余数为其奇数位数字A和减去偶数位数字和B的差A－B＝C，再用C除以11所得的余数即是原来那个数的余数．(如果减不开可将偶数位数字和B 减去奇数位数字和A，求得B－A＝C，再求出C除以11的余数D，然后将11－D即为原来那个数除以11的余数) ．如：123456的奇数位数字和为6+4+2＝12，偶数位数字和为5+3+1＝9，奇数位数字和与偶数位数字和的差位12－9＝3，所以123456除以11的余数为3．又如：654321的奇数位数字和为1+3+5＝9，偶数位数字和位2+4+6＝12，奇数位数字和减不开偶数位数字和，那么先将12－9＝3，显然3除以11的余数为3，然后再用11－3＝8，这个8即为654321除以11的余数．【题文】一个1994位的整数，各个数位上的数字都是3．它除以13，商的第200位(从左往右数)数字是多少?商的个位数字是多少?余数是多少?【答案】2,7【解析】这个数即为，而整除13的数的特征是将其后三位与前面的数隔开而得到两个新数，将这两个新数做差，这个差为13的倍数．显然有能够被13类整除，而1994÷6＝332……2，即＝＝+33，而是13的倍数，所以除以13的余数即为33除以13的余数为7．有÷13＝25641，而÷13＝25641025641，所以除以13所得的商每6个数一循环，从左往右依次为2、5、6、4、1、0．200÷6＝33……2，所以除以13所得商的第23位为5．除以13的个位即为33除以13的个位，为2．即商的第23位(从左往右数)数字是5，商的个位数字是2，余数是7．【题文】己知：a＝．问：a除以13的余数是几？【答案】8【解析】因为199119911991能被13整除，而1991÷3＝663……2．有a＝＝199119911991×+199119911991×+199119911991×++199119911991×+…+199119911991×+19911991．所以a除以13的余数等于19911991除以13的余数8．【题文】有一个数，除以3余数是2，除以4余数是1．问这个数除以12余数是几?【答案】5【解析】我们将这个数加上7，则这个数能被3整除，同时也能被4整除，显然能被12整除，所以原来这个数除以12的余数为12－7＝5．【题文】某个自然数被247除余63，被248除也余63．那么这个自然数被26除余数是多少?【答案】11【解析】我们将这个数减去63，则得到的新数能被247整除，也能被248整除，而相邻的两个整数互质，所以得到的新数能被247×248，显然能被26整除．于是将新数加上63除以26的余数等于63除以26的余数为11．所以这个自然数被26除余数是11．【题文】一个自然数除以19余9，除以23余7．那么这个自然数最小是多少?【答案】237【解析】这个自然数可以表达为19m+9，也可以表达为23n+7，则有19m+9＝23n+7，即23n－19m＝2，将未知数系数与常数对19取模，有4n≡2(mod 19) ．n最小取10时，才有4n≡2(mod 19) ．所以原来的那个自然数最小为23×10+7＝237．评注：有时往往需要利用不定方程来清晰的表示余数关系，反过来不定方程往往需要利用余数的性质来求解．【题文】如图，在一个圆圈上有几十个孔(不到100个)．小明像玩跳棋那样从A孔出发沿着逆时针方向，每隔几个孔跳一步，希望一圈以后能跳回到A孔．他先试着每隔2孔跳一步，结果只能跳到B孔．他又试着每隔4孔跳一步，也只能跳到B孔．最后他每隔6孔跳一步，正好回到A孔．问这个圆圈上共有多少个孔？【答案】91【解析】设这个圆圈有n个圆孔，那么有n除以3余1，n除以5余1，n能被7整除．则将n－1是3、5的倍数，即是15的倍数，所以n＝15t+1，又因为n是7的倍数，即15t+1＝7A，将系数与常数对7取模，有t－1≡0(mod 7)，所以t取6或6与7的倍数和．对应孔数为15×6+1＝91或91与105的倍数和，满足题意的孔数只有91．即这个圆圈上共有91个孔．【题文】某住宅区有12家住户，他们的门牌号分别是l，2，3，…，12．他们的电话号码依次是12个连续的六位自然数，并且每家的电话号码都能被这家的门牌号码整除．已知这些电话的首位数字都小于6，并且门牌号码是9的这一家的电话号码也能被13整除，问这一家的电话号码是什么数?【答案】388089【解析】设这12个连续的自然数为n+1，n+2，n+3，…，n+12，那么有它们依次能被1，2，3，…，12整除，显然有n能同时被1，2，3，…，12整除．即为1，2，3，…，12的公倍数．[1，2，3，…，12]＝23×32×5×7×11＝27720，所以n是27720的倍数，设为27720k．则有第9家的门牌号码为27720k+9为13的倍数，即27720k+9＝13A，将系数与常数对13取模有：4k+9≡0(mod 13)，所以k可以取1或1与13的倍数和．有要求n+1，n+2，n+3，…，n+12，为六位数，且首位数字都小于6，所以k只能取14，有n＝27720×14＝388080．那么门牌号码是9的这一家的电话号码是388080+9＝388089．【题文】有5000多根牙签，可按6种规格分成小包．如果10根一包，那么最后还剩9根．如果9根一包，那么最后还剩8根．第三、四、五、六种的规格是，分别以8，7，6，5根为一包，那么最后也分别剩7，6，5，4根．原来一共有牙签多少根?【答案】5039【解析】设这包牙签有n根，那么加上1根后为n+1根，此时有n+1根牙签即可以分成10根一包，又可以分成9根一包，还可以分成8、7、6、5根一包．所以，n+1是10、9、8、7、6、5的倍数，即它们的公倍数．[10，9，8，7，6，5]＝23×32×5×7＝2520，即n+1是2520的倍数，在满足题意下只能是2520×2＝5040，所以n＝5039．即原来一共有牙签5039根．【题文】有一个自然数，用它分别去除63，90，130都有余数，3个余数的和是25．这3个余数中最大的一个是多少?【答案】20【解析】设这个自然数为☆，设它除63，90，130所得的余数依次为a，b，c，商依次为A，B，C．显然有63+90+130＝☆×(A+B+C)+(a+b+c)＝☆×(A+B+C)+25，所以☆×(A+B+C)＝(63+90+130)－25＝258，所以☆是258的约数．258＝2×3×43，显然当除数☆为2、3、6时，3个余数的和最大为3×(2－1)＝3，3×(3－1)＝6，3×(6－1)＝15，所以均不满足．而当除数☆为43×2，43×3，43×2×3时，它除以63的余数均是63，所以也不满足．那么除数☆只能是43，它除以63，90，130的余数依次为20，4，1，余数的和为25，满足．显然这3个余数中最大的为20．【题文】一个数去除55l，745，1133，1327这4个数，余数都相同．问这个数最大可能是多少?【答案】194【解析】这个数A除55l，745，1133，1327，所得的余数相同，所以有55l，745，1133，1327两两做差而得到的数一定是除数A的倍数．1327－1133＝194，1133－745＝388，745－551＝194，1327－745＝582，1327－551＝776，1133－551＝582．这些数都是A的倍数，所以A是它们的公约数，而它们的最大公约数(194，388，194，582，776，582)＝194．所以，这个数最大可能为194．【题文】用某自然数去除，得到商是46，余数是，求和．【答案】43,14【解析】因为是的倍还多,得到，得，所以，．【题文】甲、乙两数的和是，甲数除以乙数商余，求甲、乙两数．【答案】1000,88【解析】(法1)因为甲乙，所以甲乙乙乙乙；则乙，甲乙．(法2)将余数先去掉变成整除性问题，利用倍数关系来做：从中减掉以后，就应当是乙数的倍，所以得到乙数，甲数．【题文】一个两位数除310，余数是37，求这样的两位数。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
余数问题【求余数】（1990年江苏宜兴市第五届小学生数学竞赛试题）一组，就可得到331组，尚余4个6。
而6666÷7=952……2。
所以，原式的余数是2。
例2 9437569与8057127的乘积被9除，余数是__。
（《现代小学数学》邀请赛试题）讲析：一个数被9除的余数与这个数各位数字之和被9除的余数是一样的。
9437569各位数字之和除以9余7；8057127各位数字之和除以9余3。
7×3=21，21÷9=2……3。
所以，9437569与8057127的乘积被9除，余数是3。
例3 在1、2、3、4、……、1993、1994这1994个数中，选出一些数，使得这些数中的每两个数的和都能被26整除，那么这样的数最多能选出_______个。
（1994年全国小学数学奥林匹克初赛试题）讲析：可将1、2、3、……、1994这1994个数，分别除以26。
然后，按所得的余数分类。
要使两个数的和是26的倍数，则必须使这两个数分别除以26以后，所得的余数之和等于26。
但本题要求的是任意两个数的和都是26的倍数，故26的倍数符合要求。
这样的数有1994÷26=76（个）……余18（个）。
但被26除余13的数，每两个数的和也能被26整除，而余数为13的数共有77个。
所以，最多能选出77个。
【同余问题】例1 一个整数，除300、262、205，得到相同的余数（余数不为0）。
这个整数是_____。
（全国第一届“华杯赛”初赛试题）讲析：如果一个整数分别除以另两个整数之后，余数相同，那么这个整数一定能整除这两个数的差。
因此，问题可转化为求（300—262）和（262—205）的最大公约数。
不难求出它们的最大公约数为19，即这个整数是19。
例2 小张在计算有余数的除法时，把被除数113错写成131，结果商比原来多3，但余数恰巧相同。
那么该题的余数是多少？（1989年上海市小学数学竞赛试题）讲析：被除数增加了131-113=18，余数相同，但结果的商是3，所以，除数应该是18÷3=6。
又因为113÷6的余数是5，所以该题的余数也是5。
例3 五只猴子找到一堆桃子，怎么也平分不了，于是大家同意去睡觉，明天再说。
夜里，一只猴子偷偷起来，吃掉一只桃子，剩下的桃子正好平分五等份，它拿走自己的一份，然后去睡觉；第二只猴子起来，也吃掉一只桃子，剩下的桃子也正好分成五等份，它也拿走了自己的一份，然后去睡觉。
第三、四、五只猴子也都这样做。
问：最初至少有______个桃子。
（哈尔滨市小学数学竞赛试题）讲析：因为第一只猴子把桃5等分后，还余1个桃；以后每只猴子来时，都是把前一只猴子剩下的4等份再分成5等份，且每次余1个桃子。
于是，我们可设想，如果另加进4个桃子，则连续五次可以分成5等份了。
加进4个桃之后，这五只猴每次分桃时，不再吃掉一个，只需5等份后，拿走一份。
因为4与5互质，每次的4份能分成5等份，这说明每次等分出的每一份桃子数，也能分成5等份。
这样，这堆桃子就能连续五次被5整除了。
所以，这堆桃子至少有5×5×5×5×5-4=3121（个）。
例4 在1、2、3、……、30这30个自然数中，最多能取出______个数，使取出的这些数中，任意两个不同的数的和都不是7的倍数。
（上海市第五届小学数学竞赛试题）讲析：我们可将1到30这30个自然数分别除以7，然后按余数分类。
余数是0：7、14、21、28余数是1：1、8、15、22、29余数是2：2、9、16、23、30余数是3：3、10、17、24余数是4：4、11、18、25余数是5：5、12、19、26余数是6：6、13、20、27要使两数之和不是7的倍数，必须使这两个数分别除以7所得的余数之和不等于7。
所以，可以取余数是1、2、3的数，不取余数是4、5、6的数。
而余数为0的数只取一个。
故最多可以取15个数。
有关数的法则或方法【数的读写方法】（整数中多位数的读写方法，以及小数、分数、百分数的读、写方法，见小学数学课本，此处略。
）“成数”、“折数”即“十分数”，它们常用中国数字和文字“七成”、“二成五”、“八折”、“九五折”等表示，并根据其文字去读。
它们也常用分母为十的分数，或者用百分数去表示，这时便可按分数、百分数的方法去读。
“千分数”是表示一个数是另一个数的千分之几的分数，它常用“千分号”--“‰”来写千分数，如某地人口出生率为千分之七，写作“7‰”，读作“千分之七”。
【科学记数法】用带一位整数的小数，去乘以10的整数次幂来表示一个数的方法，叫做“科学记数法”。
利用小数点移动的规律，很容易把一个数用“科学记数法”表达为“a×10n （1≤a≤10，n是整数）”的形式。
例如：25700，把小数点向左移动四位，得1＜2.57＜10，但2.57比25700小了10000倍，所以25700=2.57×104。
0.00867，把小数点向右移动三位，得1＜8.67＜10，但8.67比0.00867大了1000倍，所以【近似数截取方法】截取近似数的方法，一般有四舍五入法、去尾法和进一法三种。
四舍五入法──省略一个数的一部分尾数，取它的近似数的时候，如果要舍去的尾数的最高位上的数是4，或者是比4小的数，就把尾数舍去；如果要舍去的尾数的最高位上的数是5，或者是比5大的数，把尾数舍去以后，要向它的前一位进一。
这种求近似数的方法叫做“四舍五入法”。
例如，把8，654，000四舍五入到万位，约等于865万；把7.6239四舍五入保留两位小数约等于7.62；把2，873，000，000四舍五入到亿位，约等于29亿；把32.99506四舍五入精确到百分位约等于33.00。
去尾法──要省略的尾数不论是多少，一律舍去不要，这种求近似数的方法叫做“去尾法”。
进一法──省略某一个数某一位后面的尾数时，不管这些尾数的大小，都向它的前一位进一。
这种求近似数的方法，叫做“进一法”。
显然，用“进一法”和“五入”方法截取的近似值，叫做“过剩近似值”，而用“去尾法”和“四舍”方法截取的近似值，叫做“不足近似值”。
值得注意的是：在近似数的取舍结果中，小数点后最右一位上的零必须写上。
例如，把1.5972四舍五入，保留两位小数得1.60，即1.5972≈1.60，最后的“0”不可去掉，否则，它只精确到十分位了。
【质数判定方法】判定一个较大的数是不是质数，一般有两种方法。
（1）查表法。
用查质数表的方法，可以较快地判断一个数是否为质数：质数表上有的是质数，同一范围内的质数表上没有这个数，那它便是个合数。
（2）试除法。
如果没有质数表，也来不及制作一个质数表，可以用试除来判断。
例如，要判定161和197是不是质数，可以把这两个数依次用2、3、5、7、11、13、17、19……等质数去试除。
这是因为一个合数总能表示成几个质因数的乘积，若161或197不能被这个合数的质因数整除，那么也一定不能被这个合数整除。
所以，我们只要用质数去试除就可以了。
由161÷7=23，可知161的约数除了1和它本身外，至少还有7和23。
所以，161是合数，而不是质数。
由197依次不能被2、3、5、7、11、13整除，而197÷17=11……10，这时的除数17已大于不完全商11，于是可以肯定：197是质数，而不是合数。
因为197除了它本身以外，不可能有比17大的约数。
假定有，商也一定比11小。
这就是说，197同时还要有比11小的约数。
但经过试除，比11小的质数都不能整除197，这说明比11小的约数是不存在的，所以197是质数，不是合数。
【最大公约数求法】最大公约数的求法，一般可用下面四种方法。
（1）分解质因数法。
先把各数分解质因数，再把各数公有的一切质因数连乘起来，就是所求的最大公约数。
例如，求2940、756和168的最大公约数：∵ 2940=22×3×5×72，756=22×33×7，168=23×3×7；∴（2940，756，168）=22×3×7=84。
注：“（2940，756，168）=84”的意思，就是“2940、756和168的最大公约数是84”。
（2）检验公约数法。
“检验公约数法”即“试除法”，也是小学数学课本介绍的那一种一般的求法，此处略。
（3）辗转相减法。
较大的两个数求最大公约数，可以用“辗转相减法”：用大数减小数，如果减得的差与较小的数不相等，便再以大减小求差，直到出现两数相等为止。
这时，相等的数就是这两个数的最大公约数。
例如，求792和594的最大公约数。
∵（792，594）=（792-594，594）=（198，594）=（594-198，198）=（198，396）=（198，396-198）=（198，198）=198，∴（792，594）=198。
用辗转相减法求两个数的最大公约数，可以推广到求n个数的最大公约数，具体做法是：可以不拘次序地挑选最方便的，从较大的数里减去较小的数。
这样逐次做下去，直到所得的差全部相等为止。
这个相等的差，就是这些数的最大公约数。
例如，求1260、1134、882和1008的最大公约数。
∵（1260，1134，882，1008）=（1260-1134，882，1008-882，1134-882）=（126，126，882，252）=（126，126，882-126×6，252-126）=（126，126，126，126）=126，∴（1260，1134，882，1008）=126。
（4）辗转相除法（欧几里得算法）。
用辗转相除法求两个数的最大公约数，步骤如下：光用较小数去除较大的数，得到第一个余数；再用第一个余数去除较小的数，得到第二个余数；又用第二个余数去除第一个余数，得到第三个余数；这样逐次用后一个余数去除前一个余数，直到余数是0为止。
这时，余数“0”前面的那个余数，便是这两个数的最大公约数。
求两个较大的数的最大公约数，用上面的第一、二种方法计算，是相当麻烦的，而采用“辗转相除法”去求，就简便、快速得多了。
例如，求437和551的最大公约数。
具体做法是：先将437和551并排写好，再用三条竖线把它们分开。
然后依下述步骤去做：（1）用较小数去除较大数把商数“1”写在较大数的线外，并求得余数为114。
（2）用余数114去除437，把商数“3”写在比114大的数（437）的线外，并求得余数为95。
（3）用余数95去除114，把商数“1”写在114右边的直线外，并求得余数为19。
（4）用余数19去除95，把商数“5”写在95左边的直线外面，并求得余数为0。