华中科技大学《量子力学》20讲-量子跃迁

合集下载

量子力学第9章-含时微扰

ˆ ˆ H(t) = H0 + H′(t)
量与时间有关，因为 Hamilton 量与时间有关，所以体系波函数须由含时方程解出。但是精确求解这种问题通常是很困难的， Schrodinger 方程解出。但是精确求解这种问题通常是很困难的，而定态微扰法在此又不适用，而定态微扰法在此又不适用，这就需要发展与时间有关的微扰理论。含时微扰理论可以通过含时微扰理论可以通过 H0 的定态波函数近似地求出微扰存在情况下的波函数，从而可以计算无微扰体系在加入含时微扰后，在情况下的波函数，从而可以计算无微扰体系在加入含时微扰后，体系由一个量子态到另一个量子态的跃迁几率。体系由一个量子态到另一个量子态的跃迁几率。
比较等式两边得
(0 (1 δnk = an )(0) +λan )(0) +⋯
(0 an )(0 =δnk ) (1 (2 an )(0 = an )(0 =⋯ 0 ) ) =
n
幂次项得：比较等号两边同 λ 幂次项得：
不随时间变化，所以a 因 an(0)不随时间变化，所以an(0)(t) = an(0)(0) = δnk。后加入微扰，则第一级近似： t ≥ 0 后加入微扰，则第一级近似：
(0 (1 (2 an = an ) +λan ) +λ2an ) +⋯
∑
n
n
n
n
m n
零级近似波函数 am 不随时 d m) a(0 间变化， = 0 间变化，它由未微扰时体系 (4)解这组方程解这组方程， (4)解这组方程，我们可得到关于所处的初始状态所决定。所处的初始状态所决定。 t d 的各级近似解， an 的各级近似解，从而得到波函 d (1) am (0 ˆ ′ 的近似解。实际上，数 Ψ 的近似解。实际上，大多数 iℏ n = ∑ an )H neiωm t m d t 情况下，只求一级近似就足够了。情况下，只求一级近似就足够了。 n a(2 1，（最后令 λ = 1，即用 H’mn代替 d m) (1 ˆ ′ n iℏ = ∑ an )H neiωm t m d t n λ H’mn，用a m (1)代替 λa m (1)。） ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ = ⋯ ⋯

量子跃迁

n
Cnk (t) e−iEn t/ |ψn ⟩
Cnk (t) = ⟨ψn |ψ (t)⟩
我们增加k 的指标是为了表明扰动之前是处在|ψk ⟩这个本征态上，出现跃迁是从Ek 这个能级上跃迁出来的。按照统计诠释，t时刻测量力学量F ，得到Fn 的几率应该为 Pnk (t) = |Cnk (t)| = |⟨ψn |ψ (t)⟩|
) ′ ′ eiωmk t ∂Hmk (t′ ) ′ + dt |m⟩ e−iEm t/ = δmk − ωmk ωmk ∂t′ −∞ m ) ( ′ ∑ e−iEm t/ ∫ t ∂H ′ (t′ ) ∑ ′ Hmk ′ ′ mk |m⟩ e−iEk t/ − eiωmk t dt′ |m⟩ = |k ⟩ + ′ Ek − Em Ek − Em −∞ ∂t m m ∑ ( t) ∫
t > t0 t < t0
ˆ 0 ，在某个时刻开始加上一个扰也就是说，在无外界相互作用的时候，体系Hamiltonian 为不含时的H ˆ ′ (t)。动H ˆ 0 本征态|ψk ⟩上， t < t0 时是定态问题，系统处于H ˆ 0 |ψn ⟩ = En |ψn ⟩ H |ψk (t)⟩ = e−iEk t/ |ψk ⟩ (t < t0 )
t iωmk t′ ′ Hmk ′ ′
∫
(1) Cmk
(t)
当t < 0，H 有加上微扰，量子态随时间的演化只是一个非定态的不含时问题，各成分保持不变。从另一个角度也可以理解为跃迁出去多少，从所有别的态跃迁回来也是多少。当0 < t < T ， Cmk (t) = −
(1) ′ eiωmk t Hmk ( t) + ωmk
∫

曾谨言《量子力学教程》(第3版)配套题库【课后习题-量子跃迁】

第11章量子跃迁11.1 荷电q的离子在平衡位置附近作小振动（简谐振动），受到光照射而发生跃迁，设照射光的能量密度为ρ（w），波长较长．求：（a）跃迁选择定则；（b）设离子原来处于基态，求每秒跃迁到第一激发态的概率．解：（a）具有电荷为q的离子，在波长较长的光的照射下，从n→n'的跃迁速率为而根据谐振子波函数的递推关系（见习题2.7）可知跃迁选择定则为（b）设初态为谐振子基态（n＝0），利用可求出而每秒钟跃迁到第一激发态的概率为11.2 氢原子处于基态，受到脉冲电场的作用．试用微扰论计算它跃迁到各激发态的概率以及仍然处于基态的概率（取E0沿z轴方向来计算）．【解答与分析见《量子力学习题精选与剖析》[上]，10.2题，l0.3题】10.2 氢原子处于基态，受到脉冲电场作用，为常数．试用微扰论计算电子跃迁到各激发态的概率以及仍停留在基态的概率．解：自由氢原子的Hamilton量记为H0，能级记为E n，能量本征态记为代表nlm 三个量子数），满足本征方程如以电场方向作为Z轴，微扰作用势可以表示成在电场作用过程中，波函数满足Schr6dinger方程初始条件为令初始条件（5）亦即以式（6）代入式（4），但微扰项（这是微扰论的实质性要点!）即得以左乘上式两端，并对全空间积分，即得再对t积分，由即得因此t＞0时（即脉冲电场作用后）电子已经跃迁到态的概率为根据选择定则终态量子数必须是即电子只跃迁到各np态（z＝1），而且磁量子数m＝0．跃迁到各激发态的概率总和为其中a o为Bohr半径．代入式（9）即得电场作用后电子仍留在基态的概率为10.3 氢原子处于基态，受到脉冲电场作用，为常数．求作用后（t ＞0）发现氢原子仍处于基态的概率（精确解）．解：基态是球对称的，所求概率显然和电场方向无关，也和自旋无关．以方向作z 轴，电场对原子的作用能可以表示成以H0表示自由氢原子的Hamilton量，则电场作用过程中总Hamilton量为电子的波函数满足Schr6dinger方程初始条件为为了便于用初等方法求解式（3），我们采取的下列表示形式：的图形如下图所示．注意图11-1式（5）显然也给出同样的结果．利用式（5）．，可以将式（1）等价地表示成下面将在相互作用表象中求解方程（3），即令代入式（3），并用算符左乘之，得到其中一般来说，H'和H0不对易，但因H'仅在因此一H'，代入式（8）即得再利用式（1'），即得初始条件（4）等价于方程（11）满足初始条件的解显然是代入式（7），即得这是方程（3）的精确解．t＞0时（电场作用以后）发现电子仍处于基态的概率为计算中利用了公式利用基态波函数的具体形式容易算出a o为Bohr半径．将上式代入式（15），即得所求概率为这正是上题用微扰论求得的结果，为跃迁到各激发态的概率总和．11.3 考虑一个二能级体系，Hamilton量H0表示为（能量表象）设t＝0时刻体系处于基态，后受到微扰H'作用（α，β，γ为实数）求t时刻体系跃迁到激发态的概率．【解答与分析见《量子力学习题精选与剖析》[上]，10.4题】10.4 有一个二能级体系，Hamilton量记为H0，能级和能量本征态记为E1，。

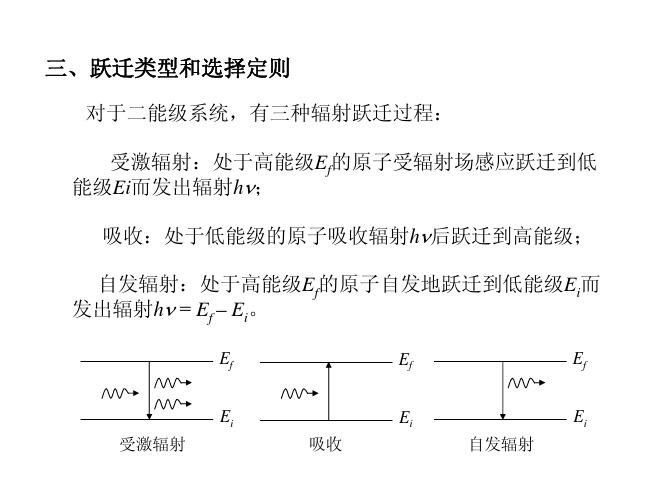
跃迁类型和选择定则

λm1 1 μ ⎛ Z μ B ⎞ ⎛ Zα ⎞ ≈ 2 ≈⎜ =⎜ ≈ 10−5 ⎟ ⎟ λE1 c er ⎝ ea0 c ⎠ ⎝ 2 ⎠
2 2 2
电四极跃迁的跃迁速率与电偶极跃迁速率之比为
λE2 3 ⎛ ω r ⎞ 3 ⎛ Zα ⎞ ≈ ⎜ = ⎜ ≈ 10−6 λE1 40 ⎝ c ⎟ 40 ⎝ 2 ⎟ ⎠ ⎠
λif =
( Ei − E f
3πε 0 c
)
3
4 3
∫ψ
* f
(-er )ψ i dτ (nk,ε + 1)
2
式中Ei – Ef = hν，上式已对k和ε的各个方向取了平均，相当于原子与各向同性的非偏振辐射的相互作用。
跃迁速率包括两项：第一项对应于受激辐射，在通常光源作用下可以忽略，只有在较强光场中才明显出现。第二项对应于自发辐射，即外界不存在辐射 (nk,ε= 0)时的辐射速率。如果存在简并态，自发辐射的速率变为
磁偶极跃迁M1
0→0
电四极跃迁E2
ΔJ = 0, ±1, ±2 0 → 0,1
1 2
0 → 0 ΔJ = 0, ±1,
→
1 2
ΔM=0,±1 宇称改变有单电子跃迁 Δl = ±1 ΔS=0
ΔL = 0, ±1, 0→0
ΔM=0,±1 宇称不变无单电子跃迁 Δl = 0, Δn = 0 ΔS=0 ΔL=0
j = 0 (无辐射) 的跃迁，称为单极跃迁，只能通过电子碰撞或其他无辐射方式跃迁。
定则2同样来自角动量守恒以及原子波函数相对量子化轴的角向对称性。定则3来自宇称守恒。电偶极辐射的宇称：
λif
( Ei − E f ) =
3πε 0 c
4 3

量子力学课件(完整版)

Light beam
metal
electric current
11
能量量子化的假设
造成以上难题的原因是经典物理学认为能量永远是连续的。
如果能量是量子化的，即原子吸收或发射电磁波，只能以“量子”的方式进行，那末上述问题都能得到很好的解释。
12
能量量子化概念对难题的解释
原子寿命 ①原子中的电子只能处于一系列分立的能级之中。
18
当 kT hc（高频区）
E(, T)

2hc2 5
e hc
kT
Wein公式
当 kT hc（低频区）
E(, T)

2c 4
kT
Rayleigh–Jeans公式
19
能量量子化概念对难题的解释
对光电效应的解释
如果电子处于分立能级且入射光的能量也是量子化的，那么只有当光子的能量（E =hυ）大于电子的能级差，即E =hυ > En－Em时，光电子才会产生。如果入射光的强度足够强，但频率υ足够小，光电子是无法产生的。
2 , k 2 / ,
得到 d 2 0,所以，t x(t)
dk 2 m
物质波包的观点夸大了波动性的一面，抹杀了粒子性的一面，与实际不符。
45
（2）第二种解释：认为粒子的衍射行为是大量粒子相互作用或疏密分布而产生的行为。然而，电子衍射实验表明，就衍射效果而言，弱电子密度＋长时间＝强电子密度＋短时间由此表明，对实物粒子而言，波动性体现在粒子在空间的位置是不确定的，它是以一定的概率存在于空间的某个位置。
2
这面临着两个问题：
1、信号电磁波所覆盖的区域包括大量的元件，每个元件的工作状态有随机性，但器件的响应具有统计性；

能级跃迁课件

能级跃迁课件
• 能级跃迁理论概述 • 能级跃迁的分类 • 能级跃迁的实例 • 能级跃迁的影响因素 • 能级跃迁的实现路径 • 能级跃迁的未来展望
目录
Part
01
能级跃迁理论概述
能级跃迁的定义
能级跃迁
原子中的电子在不同的能级上运动，当电子从高能级向低能级跃迁时，会释放出一定频率的光子。反之，当电子从低能级向高能级跃迁时，需要吸收一定频率的光子。
压力
压力变化会影响气体分子的密度和碰撞频率，从而影响能级跃迁的概率。
电磁场
电磁场可以与分子产生相互作用，影响分子的能级分布，从而影响能级跃迁。
内部因素
分子结构
分子内部的结构决定了分子的振动和转动能级，从而影响能级跃迁。
量子力学效应
在微观尺度上，量子力学效应对能级跃迁有重要影响。
多能级体系
Part
05
能级跃迁的实现路径
提升自我认知
STEP 01
自我认知
STEP 02
职业定位
了解自己的优势、劣势、价值观、兴趣和目标，以便更好地规划职业发展。
STEP 03
行业洞察
了解所在行业的发展趋势和未来方向，以便更好地把握机会和应对挑战。
明确自己的职业定位，了解自己在职场中的价值和位置。
02
智能化水平提升
未来能级跃迁将进一步提高智能化水平，利用人工智能、大数据等技术
手段实现能源系统的智能化管理和调控，提高能源利用效率和安全性。
03
可持续发展
未来能级跃迁将更加注重可持续发展，推动能源行业与生态环境、社会
经济的协调发展，为实现全球可持续发展目标作出贡献。
增强自我能力
专业技能

量子跃迁的微扰理论

物理跃迁知识点总结高中

物理跃迁知识点总结高中一、跃迁的基本概念1.1 跃迁的定义在物理学中，跃迁指的是原子或分子内部的电子在不同能级之间的转移过程。

这种转移可能会伴随着能量的吸收或释放。

跃迁是量子力学的重要概念之一，它揭示了微观世界中粒子的行为规律。

1.2 能级的概念在原子或分子中，电子围绕原子核运动，形成了离散的能级。

每个能级对应着一定的能量，电子只能处于这些能级中的某一个，而不能处于中间状态。

当电子从一个能级跃迁到另一个能级时，它会吸收或释放一定量的能量。

1.3 跃迁的方式跃迁可以分为辐射跃迁和非辐射跃迁两种方式。

在辐射跃迁中，电子吸收或释放能量的同时会辐射出光子；而在非辐射跃迁中，电子的能级发生改变，但并不伴随着光子的发射或吸收。

1.4 能级图为了直观地展示原子或分子内部的能级结构和跃迁过程，物理学家们常常会绘制出相应的能级图。

能级图通过图形的方式清晰地展示了跃迁的过程和能级之间的相对关系，有利于学生的理解和记忆。

二、原子的跃迁2.1 原子的能级原子内部的电子绕原子核运动，形成了一系列的能级。

这些能级是分立的，即电子只能处于某一个能级中，而不能处于中间状态。

当电子跃迁时，它会吸收或释放能量，从而使得它的能级发生改变。

2.2 能级的量子化原子的能级是量子化的，这意味着电子只能处于能级的某个离散取值上，而不能处于其他能级上。

这种量子化现象是量子力学的基本内容，它揭示了微观世界中粒子的奇特行为。

2.3 能级的转移原子的能级之间存在着一些转移的规律。

譬如，当电子从高能级跃迁到低能级时，它会释放能量，并且发射出光子；相反地，当电子从低能级跃迁到高能级时，它会吸收能量。

这些跃迁过程构成了原子光谱的基础。

2.4 光谱线原子的能级转移会伴随着光子的辐射或吸收，从而产生出特定的光谱线。

这些光谱线对应着原子的不同能级转移过程，它们的波长、强度和数量都可以为物理学家们提供重要的信息。

2.5 光谱分析通过对原子的光谱线进行精密的分析，物理学家可以了解原子内部的能级结构以及电子的跃迁规律。

量子跃迁中的选择定则

量子跃迁中的选择定则张扬威（华中师范大学物理学院2008级基地班，武汉，430079）摘要本文根据量子跃迁过程中遵从的角动量守恒和宇称守恒运用量子化概念，推导出电偶极近似条件下，在不同的外场中单电子原子以及多电子原子辐射跃迁时的选择定则，并结合具体实例，说明这些规律的实质。

关键词辐射跃迁选择定则角动量守恒宇称守恒原子态电偶极近似 1 、引言推微观粒子在不同的量子化状态间变化，称为跃迁。

跃迁有很多种，不同跃迁遵从不同的跃迁选择定则。

原子辐射跃迁的选择定则是原子能级之间发生跃迁所满足的条件，它对于研究光的吸收和发射具有很重要的意义。

由于电偶极矩跃迁强度比其它形式的跃迁强度大很多（倍），原子的辐射跃迁选择定则是指电偶极辐射跃迁选择定则。

它是从大量光谱的观察分析和研究中总结出来的，本文则运用量子力学的理论对它进行推导研究。

510~1082、入射光为单色偏振光引入周期性微扰下的跃迁概率的基本知识：设微扰Hamilton 算符为（式中为与无关的厄米算符）'0(0)A cos ()(0)i t i t H t t F e e t ωωω∧∧∧−=<=+≥或（1）体系在处于'0t =(0)n ϕ态，跃迁到态的概率为't =t (0)m ϕ22(0)(0)2()()n m m mn m n W a t F E E πδω→==−±h h（2）若该单色偏振光是沿x 轴方向传播，偏振方向沿z 轴，在电偶极近似条件下，它的电场为0cos z t εεω= 0x ε= 0y ε= （3）电子的电偶极矩为 D er ex =−=−r（4）微扰作用势为 '00cos ()2i t i tz ez H D ez ez t e e ωωεεεεω∧−=−===+r uv （5）对比（1）式可得 02ez F ε∧=（6）带入（2）式可得 222(0)(0)0()2n m mn m n e W z E E πεδω→=−h h±（7）由（7）式可以得出，原子能否由n 态跃迁到m 态，决定于电子位矢的z 分量在这两个态之间的矩阵元mn z 是否为零。

量子力学+周世勋(全套课件)

H
（2）光电效应理论
用光子的概念，Einstein 成功地解释了光电效应的规律。当光照射到金属表面时，能量为 hν的光子被电子所吸收，电子把这份能量的一部分用来克服金属表面对它的吸引，另一部分用来提供电子离开金属表面时的动能。其能量关系可写为：
1V2 h A
2
•从上式不难解释光电效应的两个典型特点：
(2) 光的波动性在1803年由杨的衍射实验有力揭示出来，麦克斯韦在1864年发现的光和电磁现象之间的联系把光的波动性置于更加坚实的基础之上。
H
（二）经典物理学的困难
但是这些信念，在进入20世纪以后，受到了冲击。经典理论在解释一些新的试验结果上遇到了严重的困难。
（1）黑体辐射问题（2）光电效应（3）氢原子光谱
§2 量子论的诞生
（一）Planck 黑体辐射定律（二）光量子的概念和光电效应理论（四）波尔（Bohr）的量子论
（三）Compton 散射 ——光的粒子性的H进一步证实
（一）Planck 黑体辐射定律
究竟是什么机制使空腔的原子产生出所观察到的黑体辐射能量分布，对此问题的研究导致了量子物理学的诞生。
“ 总而言之，我们可以说，在近代物理学结出硕果的那些重大问题中，很难找到一个问题是爱因斯坦没有做过重要贡献的，在他的各种推测中，他有时可能也曾经没有射中标的，例如，他的光量子假设就是如此，但是这确实并不能成为过分责怪他的理由，因为即使在最精密的科学中，也不可能不偶尔冒点风险去引进一个基本上全新的概念 ”
2
n
于是得光子的能动系量：关 E pC 或 p E/ C
把光子的波动性和粒子性联系了起来
H
• 虽然爱因斯坦对光电效应的解释是对Planck量子概念的极大支持，但是Planck不同意爱因斯坦的光子假设，这一点流露在Planck推荐爱因斯坦为普鲁士科学院院士的推荐信中。

《量子力学》教学大纲

《量子力学》课程教学大纲一、课程基本信息英文名称 Quantum Mechanics 课程代码 PHYS3004课程性质专业必修课程授课对象物理学学分 4学分学时 72学时主讲教师修订日期 2021.9指定教材曾谨言，《量子力学教程》，科学出版社，2000年二、课程目标（一）总体目标：本课程的知识目标：了解量子力学的实验基础和发展史、应用和前沿，及其对现代科学技术的支撑作用；系统掌握量子力学的基本概念、基本原理及处理量子系统实际问题的计算方法。

能力目标：掌握微观体系的物理研究方法和前沿进展，提高解决交叉学科领域量子问题的能力，锤炼科学思维能力和科研创新能力。

素质目标：掌握辩证唯物主义基本原理，建立科学的世界观和方法论；富有科学精神，勇于在物理学前沿及交叉领域探索、创新与攀登。

（二）课程目标：课程目标1：了解量子力学的发展简史，量子力学理论发展中的著名物理实验及其地位和作用；了解量子力学的诠释及适用范围；了解量子力学实验和理论研究的前沿进展和应用前景；使学生认识到量子力学理论在现代科学研究领域的重要性，掌握辩证唯物主义基本原理，建立科学的世界观和方法论。

课程目标2：掌握量子力学基本原理和基本计算方法，学会运用量子力学理论对一维定态若干问题，以及中心力场氢原子等问题的分析和处理；训练学生运用理论公式求解并分析量子系统的能力，培养和提高学生的抽象思维能力和解决交叉学科领域量子问题的能力。

课程目标3：掌握定态微扰论的近似计算方法，掌握利用含时微扰理论处理近代物理实验量子跃迁等的方法，掌握自旋及全同粒子体系的处理方法；培养和提高学生对非精确求解、自旋纠缠态等复杂系统的求解能力，掌握对近似解的误差分析和数据处理等基本技能，锤炼科学思维能力和科研创新能力。

（三）课程目标与毕业要求、课程内容的对应关系表1：课程目标与课程内容、毕业要求的对应关系表课程目标对应课程内容对应毕业要求课程目标1 第一章波函数和薛定谔方程第四章中心力场第六章自旋与全同粒子第七章微扰论与量子跃迁毕业要求3：了解物理学前沿和发展动态，新技术中的物理思想，熟悉物理学新发现、新理论、新技术对社会的影响。

量子跃迁的三种形式

量子跃迁的三种形式
量子跃迁是量子力学中重要的现象之一，它描述的是一个量子系统由一个能级向另一个能级的跃迁。

根据跃迁的方式不同，可将量子跃迁分为三种形式：
1. 自发跃迁：自发跃迁是指一个量子系统在没有外界干扰的情况下，由高能级向低能级跃迁的过程。

在这个过程中，量子系统会发出一个光子，能量等于能级差值。

自发跃迁是量子力学中最简单的一种现象，也是实验中最容易观测到的一种跃迁形式。

2. 受激跃迁：受激跃迁是指一个量子系统在外界干扰下，由低能级向高能级跃迁的过程。

这种干扰可以是光子、电磁波、粒子束等，只要它们的能量等于能级差值即可。

在受激跃迁中，输入的能量被转化为一个光子，能量等于能级差值。

受激跃迁是激光等技术的基础，也是量子光学领域中的重要现象。

3. 自发受激跃迁：自发受激跃迁是指一个量子系统在外界干扰下，由高能级向低能级跃迁，并且在这个过程中发射一个光子，同时另一个光子被输入到系统中，使得系统从低能级向高能级跃迁。

这种跃迁形式在量子光学中有广泛的应用，如拉曼散射、共振荧光等。

总之，量子跃迁是量子力学中重要的现象，它的三种形式分别是自发跃迁、受激跃迁和自发受激跃迁。

这些现象不仅在理论上有很重要的意义，还有广泛的应用价值。

- 1 -。

量子力学考研核心题库

一、填空题1．描述微观粒子运动状态的量子数有_____;具有相同n的量子态，最多可以容纳的电子数为_____个。

【答案】2．力学量算符必须是_____算符，以保证它的本征值为_____. 【答案】厄米；实数【解析】力学量的测量值必须为实数，即力学量算符的本征值必须为实数，而厄米算符的本征值为实数，于是量子力学中就有了一条基本假设——量子力学中所有力学量算符都是厄米算符.3．（1）自由粒子被限制在x和x+1处两个不可穿透壁之间，按照经典物理.如果没有给出其他资料，则粒子在 x和x+1/3之间的概率是_____. A.025 B.033 C.011 D.067（2）上题中，按照量子力学.处于最低能态的粒子在x和x+1/3之间被找到的概率是_____. A.019 B.072 C.033 D.050【答案】（1）B【解析】按照经典力学，粒子处于空间的概率密度为常数，故概率与体积成正比，即所求概率为（2）A【解析】取x为原点，则有波函数为所求概率即4．不确定关系是微观粒子_____性质的数学表述。

【答案】波粒二象性5．一维谐振子升、降算符、a的对易关系式为_____;粒子数算符N与、a的关系是;哈密顿量H 用N或、a表示的式子是_____；N（亦即H）的归一化本征态为_____。

【答案】6．—粒子的波函数为写出粒子位于间的几率的表达式_____。

【答案】二、选择题7．__________。

【答案】8．设粒子处于态为归一化波函数为归一化的球谐函数，则系数的取值为_____的可能值为_____的平均值为_____。

【答案】9．（1）_____；（2）_____。

【答案】10．下面关于厄米算符的定义式中.正确的为（）.【答案】A【解析】量子力学中力学量对应的算符必须为厄米算符，这是因为力学量算符的本征值必须为实数.厄米算符定义式为11．量子谐振子的能量是（）.【答案】A【解析】由于谐振子的哈密顿算符为而本征值为n，于是谐振子能量为第 4 页，共 47 页12．设粒子处于态为归一化的球谐函数，则的平均值为（）。

高等量子力学-理论方法-量子跃迁理论 ppt课件

ppt课件
11
2. 一阶常微扰
（1）含时 Hamilton 量
设 H’ 在 0 t t1 这段时间之内不为零，但与时间无关，
即： 0
t0
Hˆ

Hˆ
(r)
0
0 t t1 t t1
（2）一级微扰近似 am(1)
H’mk 与 t 无关 (0 t t1)
am(1)(t )

an (t )n
n

i t n
an (t )n Hˆ (t )
n
an (t )n
i
n

d dt
an
(t
)
n

i
n
an (t
)
t
n
i t
n

Hˆ 0n
相 an(t )Hˆ 0n an(t )Hˆ (t)n
n
m* Hˆ (t )nd
i n
d dt
an(t ) mn

n
an (t )

* m
Hˆ
(
t
)
ne
i[
m

n
]t
/
d
d
i dt am (t) n
an(t )Hˆ m neimn t
其中

Hˆ
m n

* m
Hˆ
(t
)
nd

ppt课件
4
含时微扰理论
i Hˆ (t ) t
Hˆ 0 n n n
i t
n

Hˆ 0n

量子力学讲义第1112章

第四篇跃迁问题和散射问题量子跃迁 ~ 初态 −→−'H末态：几率？弹性散射 ~ 初态 −−→−)(r U 末态：散射截面（几率）？第十一章量子跃迁量子态的两类问题：① 体系的可能状态问题，即力学量的本征态和本征值问题。

② 体系状态随时间演化问题ψψH ti =∂∂。

11.1 跃迁与跃迁几率设 )0().()(),()(0)0()0()0(00=∂∂='+=tH r E r H t H H t H n nnψψ → 定态波函数 ,......2,1,)(),()0()0()0(==-n e r t r t E in nn ψψ。

将)(t H ' 作微扰，t =0时加入。

本节讨论在)(t H '作用下，由初态)0(k ψ−→−'H末态)0(m ψ的几率?=→m k W一、体系由)0(k ψ→)0(m ψ的几率将),(t r ψ按}{)0(n ψ展开：)()(),()0(r t C t r n nn ψψ∑=。

由0H 的定态波函数知，0H 引起的变化由tE i n e )0(-反映，故可令t E i n n n et a t C )0()()(-=，)(t H '引起的变化由)}({t a n 反映。

),()()()(),()0()0()0(t r t a r e t a t r n nn n t E in n nψψψ∑∑==→-。

)(~)(2t a t a W m m m k =∴→称为几率幅。

二、)(t a n 的运动方程利用含时S-方程，有∑∑∑∑'+=∂∂+nnn n n n n n n n n n t r H t a t r H t a t r t t a i dt t da t r i ),()(),()(),()()(),()0()0(0)0()0(ψψψψ 由 ∑∑'=→=∂∂nn n n n n n n t r H t a dt t da t r i t r H t r t i ),()()(),(),(),()0()0()0(0)0(ψψψψ用),()*0(t r m ψ左乘，并积分得∑'=nt i mnn m mn e H t a dt t da i ω)()(，式中 )(1,)()()0()0()0()*0(n m mn n m mnE E d r H r H -='='⎰ωτψψ~玻尔频率。

量子力学知识：量子力学之电子跃迁

量子力学知识：量子力学之电子跃迁1906年，J·J·汤姆逊因为发现电子而被授予诺贝尔物理学奖，人类第一次知道，原子并不是组成世间万物的最小单位，原子里面还有电子。

但奇怪的是：电子是带负电荷的，而原子呈现电中性，那么一个合理的推测便是：原子中还存在带正电荷的物质，与带负电荷的电子进行中和，导致原子呈现电中性。

J·J·汤姆逊为原子构想了一个模型，我称之为西瓜模型：原子就像一个大西瓜，而电子就像西瓜籽，分散在原子内部，而正电荷物质就像西瓜瓤，均匀地分布在原子内部，将电子包裹着，所以原子呈现电中性。

另一个物理学家，名叫卢瑟福，他用α粒子轰击原子，结果发现偶尔会有α粒子被反弹回来。

这说明什么呢？说明原子里面有个硬东西，α粒子撞上了这个硬东西，才会反弹。

这就说明，J·J·汤姆逊的西瓜模型是错误的。

因为如果正电荷物质是均匀地分布在原子体内，就像西瓜瓤一样，那么它的硬度就不够，不可能把α粒子反弹回来。

卢瑟福认为，真实的原子模型，应该是正电荷物质集中成一团，位于原子的核心，卢瑟福将之命名为：原子核。

α粒子正是撞上了原子核，才会被反弹回来。

原子核带正电荷，电子带负电荷，电子绕着原子核转圈圈，所以原子呈现电中性。

卢瑟福的原子模型有一个致命问题：缺乏稳定性。

电子是带电的，所有带电的事物，在运动的时候，都会进行电磁辐射，而电磁辐射会损失能量。

电子的能量很小，如果它持续进行辐射，很快能量就会耗尽，电子将不可能绕着原子核旋转，而会被原子核直接吸进去。

卢瑟福解决不了这个问题，按照他的原子模型，电子一定会掉入原子核，这个原子是不稳定的。

这个时候，卢瑟福新招了一名学生，于是卢瑟福就让这名学生帮他想办法，看看怎样才能使电子不掉入原子核之中。

这个学生的名字，就叫尼尔斯·玻尔。

玻尔一开始也解决不了这个问题，但很快，他看到了普朗克为了解决黑体辐射而发明出来的普朗克常数h，一个大胆的想法，从他的大脑中冒了出来。

量子运动规律

量子运动规律量子运动规律是指微观粒子在量子力学框架下的运动方式和规律。

量子力学是描述微观世界的物理理论，它与经典力学有着本质的区别，其中最显著的就是量子力学中存在着不确定性原理和波粒二象性。

量子力学中的不确定性原理指出，无法同时准确测量一个粒子的位置和动量。

这是由于粒子在量子力学中被描述为波函数，波函数的平方模表示了粒子出现在空间中的概率分布。

根据不确定性原理，当我们试图准确测量一个粒子的位置时，其波函数会被坍缩到一个很小的空间范围内，从而导致我们对其动量的测量变得不确定。

反之亦然，当我们试图准确测量一个粒子的动量时，其波函数会被坍缩到一个较大的波包范围内，从而使我们对其位置的测量变得不确定。

这种不确定性的存在使得量子粒子的运动具有一定的随机性。

量子力学中的波粒二象性表明，微观粒子既可以表现为粒子，又可以表现为波动。

这一概念最早由德布罗意在1924年提出，并由实验证实。

根据波粒二象性，微观粒子具有粒子的局部性和波动的干涉性。

在实验中，我们可以观察到电子和光子等微观粒子的干涉和衍射现象，这是波动性的直接证据。

而在其他实验中，我们又可以观察到微观粒子在碰撞过程中的粒子特性，这是粒子性的体现。

量子力学中还存在着量子纠缠和量子跃迁等现象。

量子纠缠是指当两个或多个粒子处于一种特殊状态时，它们之间的状态是相互依赖、相互联系的，无论它们之间的距离有多远。

这种相互依赖关系导致了一些非经典的现象，例如“量子纠缠隐形传态”和“量子纠缠纳米通信”。

量子跃迁是指量子粒子在量子态之间的跳跃现象，这是由于量子力学中存在着量子态之间的非平凡演化导致的。

量子跃迁在原子和分子能级之间的转变中起着重要作用，也是激光、核反应和量子计算等领域的基础。

总的来说，量子运动规律是基于量子力学的，它描述了微观粒子在量子世界中的运动方式和规律。

不确定性原理和波粒二象性是量子运动规律的核心概念，它们揭示了微观粒子的运动具有一定的随机性和波动性。

此外，量子纠缠和量子跃迁等现象进一步丰富了量子运动规律的内容。

量子跃进原理

量子跃迁原理引言量子跃迁是量子力学中的一个基本现象，描述了微观粒子从一个能级到另一个能级的跃迁过程。

这一现象是量子力学中独特的，与经典物理学中的连续能量变化不同，量子跃迁是不连续的，只允许粒子在离散的能级之间进行跃迁。

量子跃迁原理是描述量子系统中粒子跃迁的基本原理。

它包括了量子力学的波函数演化、能级结构和跃迁概率等关键概念。

在本文中，我们将详细解释与量子跃迁原理相关的基本原理，并努力使其易于理解。

波函数演化量子系统中的粒子状态可以用波函数来描述。

波函数是一个复数函数，它包含了粒子在不同位置和能级上的概率幅。

根据薛定谔方程，波函数在时间演化中会发生变化。

这个变化可以通过薛定谔方程的求解来描述。

薛定谔方程是量子力学中的基本方程，描述了波函数随时间的演化。

它可以写成如下的形式：iℏ∂Ψ∂t=ĤΨ其中，i是虚数单位，ℏ是约化普朗克常数，Ψ是波函数，Ĥ是哈密顿算符。

波函数的演化可以通过薛定谔方程的解来求得。

解薛定谔方程可以得到波函数在不同时间的表达式，从而揭示了粒子在不同能级上的概率分布和演化规律。

能级结构量子系统中的能级结构是指粒子在不同能级上的分布和能量差距。

能级结构决定了粒子在不同能级之间的跃迁方式和概率。

在量子力学中，能级结构可以通过求解薛定谔方程得到。

对于一个特定的势能场，薛定谔方程的解可以给出粒子在不同能级上的波函数和能量。

能级结构通常是离散的，只允许粒子在特定的能级之间跃迁。

这是量子力学与经典物理学的一个重要区别，经典物理学中的能量是连续的，而量子力学中的能量是分立的。

能级结构的描述可以用能级图来表示。

能级图是一个横轴表示能级，纵轴表示能量的图像。

能级图可以帮助我们理解粒子在不同能级上的分布和跃迁方式。

跃迁概率量子跃迁是粒子在不同能级之间的跃迁过程。

跃迁概率描述了粒子从一个能级到另一个能级的概率。

根据量子力学的基本原理，跃迁概率与波函数的叠加有关。

当粒子处于一个能级上时，它同时也具有在其他能级上的概率幅。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。