高中数学 第1章 数列 3.1 等比数列 第2课时 等比数列的性质教案 高二数学教案
4.3.1等比数列的概念(第二课时)课件——高二上学期数学人教A版选择性必修第二册

是函数
f x a1
q
qx x R
当 x n 时的函数值,即 an = f n .
a4
(4, a4 )
反之:任给指数函数f(x)=kax ( k, a为常数, k≠0 , a>0, 且 a≠1 ), 则f(1)=ka, f(2)=ka2 , …, f(n)=kan…构成一个等比数列 {kan},其首项为ka,公比为a.
是否一定是等比数列?如果数列{an}是各项均为正的等比数列, 那么数列{logb an}是否一定是等差数列?
➯ an1
b an1-an
d
b b b an
性质1:数列{an}是等差数列 ⇔数列{ban }是等比数列.
➯ logban1
logban
logb
an1 an
logbq
性质2:数列{an}是正项等比数 列⇔数列{logban}是等差数列.
∴a1=-12. 当n≥2时, an=Sn-Sn-1=13(an-1)-13(an-1-1),
得aan-n 1=-12.又 a1=-12, 所以{an}是首项为-12,公比为-12的等比数列.
已知数列{an}的前n项和为Sn,且对任意的n∈N*有an+Sn= n.
设bn=an-1,求证:数列{bn}是等比数列;
判断一个数列是等比数列的常用方法 (1)定义法:若数列{an}满足aan+n1 =q(q 为常数且不为零)或aan-n1 =q(n≥2,q 为常数且不为零),则数列{an}是等比数列. (2)通项公式法:若数列{an}的通项公式为 an=a1qn-1(a1≠0,q≠0),则数列 {an}是等比数列. (3)等比中项法:若 a2n+1 =anan+2(n∈N*且 an≠0),则数列{an}为等比数列. 说明:证明一个数列是等比数列,只能用定义法或等比中项法.
等比数列的性质及应用(课件)高二数学(人教A版2019选择性必修第二册)

息不少于按月结算的利息(精确到10−5 )?
分析:
复利是把前一期的利息与本金之和算作本金,再计算下一期的利息,所以若
原始本金为a元,每期的利率为r,则从第一期开始,各期的本利和.
解:(1)设这笔钱存n个月以后的本利和组成一个数列 { } ,则 { } 是等比数列,
首项 1 = 104 (1 + 0.400%),
价格为8 100元的计算机3年后的价格可降为(
A.300元
B.900元
C.2 400元
公比q=1+0.400% ,所以
12 = 104 (1 + 0.400%)12 ≈ 10 490.7
所以, 12个月后的利息为10 490.7 − 104 ≈ 491(元)
(2)设季度利率为r,这笔钱存n个季度以后的本金和组成一个数列{ },
则{ }也是一个等比数列,
首项 1 = 104 (1 + ),公比为1+r,于是
数列.
( 2 ) 若 数 列 { } , { } 均 为 等 比 数 列 , c 为 不 等 于 0 的 常 数 , 则 数 列
,
2
, ∙
, { }
也为等比数列.
【典例 3】在等差数列{an}中,公差 d≠0,a1,a2,a4 成等比数列,已知数列 a1,
a3,ak1,ak2,…,akn,…也成等比数列,求数列{kn}的通项公式.
2
【解析】由题意得a2
=a1a4,即(a1+d)2=a1(a1+3d),
得d(d-a1)=0,又d≠0,所以a1=d.
又a1,a3,ak1,ak2,…,akn,…成等比数列,
a3 3d
所以该数列的公比q=a = d =3,
高中数学选择性必修二 4 3 1(第2课时)等比数列的性质及应用 教案
重点
等比数列的性质、等比数列的应用
难点
等比数列的运算、等比数列的性质及应用
教学过程
教学环节
教师活动
学生活动
设计意图
导入新课
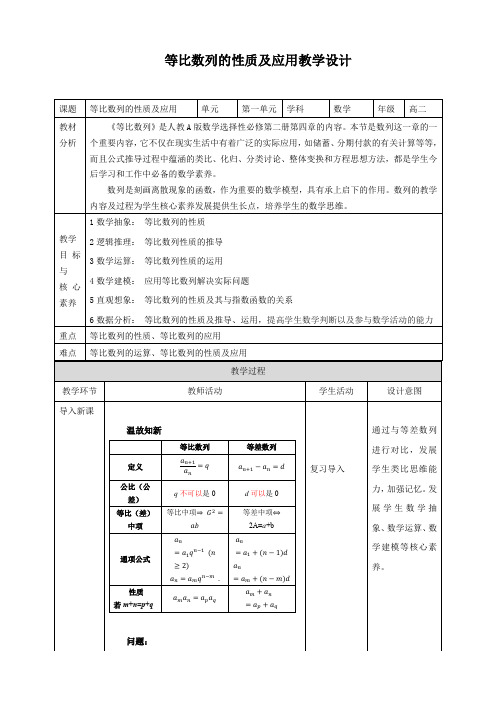
温故知新
等比数列
等差数列
定义
公比(公差)
q不可以是0
d可以是0
等比(差)中项
等比中项
等差中项 2A=a+b
等比数列的性质及应用教学设计
课题
等比数列的性质及应用
单元
第一单元
学科
数学
年级
高二
教材分析
《等比数列》是人教A版数学选择性必修第二册第四章的内容。本节是数列这一章的一个重要内容,它不仅在现实生活中有着广泛的实际应用,如储蓄、分期付款的有关计算等等,而且公式推导过程中蕴涵的类比、化归、分类讨论、整体变换和方程思想方法,都是学生今后学习和工作中必备的数学素养。
分析:复利是把前一期的利息与本金之和算作本金,再计算下一期的利息,所以若原始本金为a元,每期的利率为r,则从第一期开始,各期的本利和 构成等比数列.
解:(1)设这笔钱存n个月以后的本利和组成一个数列 ,则 是等比数列,
首项 ,
公比q=1+0.400%,所以
所以,
12个月后的利息为 (元)
(2)设季度利率为r,这笔钱存n个季度以后的本金和组成一个数列 ,则 也是一个等比数列,首项 ,公比为1+r,于是
因此,以季度复利计息,存4个季度后的利息为 元.
解不等式 ,得
所以,当季度利率不小于1.206%时,按季结算的利息不少于按月结算的利息.
例5已知数列Байду номын сангаас的首项 .
第2课时等比数列的判定与性质2023-2024学年高二上学期数学人教A版(2019)选择性必修第二册

结题总结: 三个数成等比数列的设法: 设为aq,a,aq. 推广到一般:奇数个数成等比数列设为…, qa2,aq,a,aq,aq2,…
三、课堂练习
1.已知{an},{bn}都是等比数列,那么( C )
A.{an+bn},{anbn}都一定是等比数列 B.{an+bn}一定是等比数列,但{anbn}不一定是等比数列 C.{an+bn}不一定是等比数列,但{anbn}一定是等比数列 D.{an+bn},{anbn}都不一定是等比数列
二、讲授新知
(四)等比数列性质的简单应用
例 4 有四个实数,前三个数成等比数列,且它们的乘积为 216,后三个数成等差
数列,且它们的和为 12,求这四个数.
解 方法一:设前三个数分别为aq,a,aq,则aq·a·aq=216, 所以 a3=216.所以 a=6. 因此前三个数为6q,6,6q.由题意知第 4 个数为 12q-6. 所以 6+6q+12q-6=12,解得 q=23.故所求的四个数为 9,6,4,2.
二、讲授新知
(1)解 由 S1=13(a1-1),得 a1=13(a1-1),
(一)等比数列的判定与证明
∴a1=-12.又 S2=13(a2-1),
例 1 已知数列{an}的前 n 项和为 Sn, 即 a1+a2=13(a2-1),得 a2=14.
Sn=13(an-1)(n∈N*).
(2)证明 当 n≥2 时,
第2课时 等比数列的判定与性质
一、复习引入
1.等比数列的定义; 2.等比中项; 3.等比数列的通项公式(含推广公式).
二、讲授新知
(一)等比数列的判定与证明 1.定义法: an =q(n∈N*且n≥2,常数q 不为0); an-1 2.等比中项法:a2n=an-1an+1(n∈N*且 n≥2); 3.通项公式法:an=a1qn-1=aq1·qn=A·qn(A≠0).
§3 3.1 第2课时 等比数列的性质

(1)如果以每时平均毁林约48hm2计算,剩下的森林经过 如果以每时平均毁林约48hm 计算, 多少年将被毁尽? 多少年将被毁尽? (2)根据(1)计算的年数n,如果以每年3.6%~3.9% 根据( 计算的年数n 如果以每年3.6%~3.9% 3.6%~3.9 的速度减少,计算n年后的毁林情况; 的速度减少,计算n年后的毁林情况; (3)若按3.6%的速度减少,估算经过150年后、经过200 若按3.6%的速度减少,估算经过150年后、经过200 3.6 150年后 年后、经过250年后及经过300年后森林面积的情况, 年后、经过250年后及经过300年后森林面积的情况,经过 250年后及经过300年后森林面积的情况 多少年森林将被毁尽? 多少年森林将被毁尽?
第2课时
等比数列的性质
1.知识目标:灵活应用等比数列的定义及通项公式; 1.知识目标:灵活应用等比数列的定义及通项公式;深刻 知识目标 理解等比中项概念;熟悉等比数列的有关性质, 理解等比中项概念;熟悉等比数列的有关性质,并系统了 解判断数列是否成等比数列的方法. 解判断数列是否成等比数列的方法.
a2 ; p 2p时,有am·an=________; 时
末两项的积; 末两项的积;
在有穷等比数列中, 在有穷等比数列中,与首末两项等距离的二项的积等于首
(3)等比数列中每隔一定项取出一项按原来顺序排列构成 (3)等比数列中每隔一定项取出一项按原来顺序排列构成 也成等比数列; 的数列仍为等比数列. 的数列仍为等比数列.例如am,a2m,a3m也成等比数列; ≠0), |}皆为等比数列 皆为等比数列, (4){λan}(λ≠0),{|an|}皆为等比数列,公比分别为
2 解析:(1)由等比数列性质得 解析:(1)由等比数列性质得 a2a4=a3,a4a6=a2, 由等比数列性质 5
第二课时 等比数列的性质

错因分析: 在使用等比数列前 n 项和公式表示 S3,
(C)既是等差数列又是等比数列 (D)既不是等差数列也不是等比数列
例2:设Sn为等比数列{an}的前n项和,已知 3S3=a4-2, 3S2=a3-2,则公比q= 解: 3S3=a4-2 ① 3S2=a3-2 ② 两式相减得3a3=a4-a3, a4=4a3 ,即q=4
例3:等比数列1,a, a2, a3, · · · 的前nቤተ መጻሕፍቲ ባይዱ和为________
1 1 1 1 例4:数列: 1 3 5 15 2 4 8 256
a1 1-q3 a1 1-q6 a1 1-q9 所以 + =2× . 1-q 1-q 1-q 因为 q≠ 0, q≠ 1, 所以可得 2q3+ 1= 0.所以 q
4 =- . 2 3
纠错心得:在解题时要认真思考,培养细心的 良好习惯.
例4.若数列{an}中前n项和Sn=3n+1,则数列{an}是( D ). (A)等差数列 (B)等比数列
答案:S30=260
4.若正项等比数列{an}的前n项和Sn, S2=7,S6=91,则S4= 解:∵正项等比数列{an}中,若S2=7,S6=91,由于每相 邻两项的和也成等比数列, ∴S2、S4﹣S2、S6﹣S4成等比数列,即7,S4﹣7, 91﹣S4 成等比数列. ∴(S4﹣7)2=7(91﹣S4),解得 S4=28, 故答案为:28. 5.若{an}为等比数列,a1=1,项数为偶数,S奇=85,S偶=170, 则求这个数列的项数. 解:设等比数列项数为2n项,所有奇数项之和为S奇,
新教材人教B版高中数学选择性必修第三册教案设计-等比数列的性质

第2课时等比数列的性质学习目标核心素养1.理解等比中项的概念.(易错点)2.掌握等比数列的性质及其应用.(重点)3.熟练掌握等比数列与等差数列的综合应用.(难点、易错点) 1.通过等比数列性质的学习,培养逻辑推理的素养.2.通过等比数列与等差数列的综合应用的学习,提升数学运算素养.在等差数列{a n}中,通项公式可推广为a n=a m+(n-m)d,并且若m+n=p+q,则a m+a n=a p+a q(n,m,p,q∈N+),特别地,若m+n=2p,则a m+a n=2a p.问题:在等比数列中有无类似的性质?1.等比中项定义如果x,G,y是等比数列,那么称G为x与y的等比中项关系式G2=xy结论在等比数列中,中间每一项都是它的前一项与后一项的等比中项[提示]不是.若G是x与y的等比中项,则G2=xy,反之不成立.2.等比数列的性质在等比数列{a n}中,若s+t=p+q(s,t,p,q∈N+),则a s·a t=a p·a q.(1)特别地,当2s=p+q(s,p,q∈N+)时,a p·a q=a2s.(2)对有穷等比数列,与首末两项“等距离”的两项之积等于首末两项的积,即a1·a n=a2·a n-1=…=a k·a n-k+1=….拓展:(1)“子数列”性质对于无穷等比数列{a n},若将其前k项去掉,剩余各项仍为等比数列,首项为a k+1,公比为q;若取出所有的k的倍数项,组成的数列仍为等比数列,首项为a k,公比为q k.(2)两个等比数列合成数列的性质若数列{a n},{b n}均为等比数列,c为不等于0的常数,则数列{ca n},{a n·b n},⎩⎨⎧⎭⎬⎫a nb n 也为等比数列.1.思考辨析(正确的画“√”,错误的画“×”) (1)任意两个实数都有等比中项. ( ) (2)在等比数列{a n }中,a 2·a 8=a 10.( ) (3)若{a n },{b n }都是等比数列,则{a n +b n }是等比数列.( )(4)若数列{a n }的奇数项和偶数项分别成等比数列,且公比相同,则{a n }是等比数列.( )[答案] (1)× (2)× (3)× (4)×2.已知等比数列{a n },a 1=1,a 3=19,则a 5等于( ) A .±181 B .-181 C.181 D .±12 C[在等比数列中,a 23=a 1·a 5,所以a 5=a 23a 1=181.]3.(教材P 34练习AT3改编)等比数列{a n }中,a 4=4,则a 2·a 6等于( ) A .4 B .8 C .16 D .32 C [∵{a n }是等比数列, ∴a 2·a 6=a 24=16.]4.在等比数列{a n }中,已知a 7a 12=5,则a 8a 9a 10a 11=________. 25 [∵{a n }是等比数列, ∴a 8·a 11=a 9·a 10=a 7·a 12,∴a 8a 9a 10a 11=(a 9a 10)2=(a 7a 12)2=52=25.]等比中项的应用A .b =3,ac =9B .b =-3,ac =9C .b =3,ac =-9D .b =-3,ac =-9(2)在等差数列{a n }中,公差d ≠0,且a 1,a 3,a 9成等比数列,则a 1+a 3+a 9a 2+a 4+a 10=________.(1)B(2)1316 [(1)因为b 2=(-1)×(-9)=9,a 2=-1×b =-b >0,所以b <0,所以b =-3,且a ,c 必同号.所以ac =b 2=9.(2)由题意知a 3是a 1和a 9的等比中项,∴a 23=a 1a 9,∴(a 1+2d )2=a 1(a 1+8d ),得a 1=d ,∴a 1+a 3+a 9a 2+a 4+a 10=13d 16d =1316.]由等比中项的定义可知:G a =bG ⇒G 2=ab ⇒G =±ab .这表明只有同号的两项才有等比中项,并且这两项的等比中项有两个,它们互为相反数.反之,若G 2=ab ,则G a =bG ,即a ,G ,b 成等比数列.所以a ,G ,b 成等比数列⇔G 2=ab (ab ≠0).[跟进训练]1.已知等比数列的前三项和为168,a 2-a 5=42,求a 5,a 7的等比中项. [解] 设该等比数列的公比为q ,首项为a 1, ∵⎩⎨⎧a 1+a 1q +a 1q 2=168,a 1q -a 1q 4=42, ∴⎩⎨⎧a 1(1+q +q 2)=168,a 1q (1-q 3)=42. ∵1-q 3=(1-q )(1+q +q 2). 上述两式相除,得q (1-q )=14⇒q =12. ∴a 1=42q -q 4=4212-⎝ ⎛⎭⎪⎫124=96.若G 是a 5,a 7的等比中项,则应有G 2=a 5·a 7=a 1q 4·a 1q 6=a 21q 10=962·⎝ ⎛⎭⎪⎫1210=9. ∴a 5,a 7的等比中项是±3.等比数列性质的应用【例2】 (1)已知数列{a n }为等比数列.若a n >0,且a 2a 4+2a 3a 5+a 4a 6=36,则a 3+a 5=________.(2)在2和8之间插入三个数,使这五个数成等比数列,则中间三个数的积等于________.(1)6 (2)64 [(1)∵a 2a 4+2a 3a 5+a 4a 6=36,∴a 23+2a 3a 5+a 25=36,∴(a 3+a 5)2=36,又∵a n >0,∴a 3+a 5=6. (2)设a 1=2,a 5=8, ∴a 3=a 1a 5=4,∴a 2·a 3·a 4=a 23·a 3=a 33=43=64.]在等比数列的有关运算中,常常涉及到次数较高的指数运算.若按常规解法,往往是建立a 1,q 的方程组,这样解起来很麻烦.通过本例可以看出:结合等比数列的性质进行整体变换,会起到化繁为简的效果.[跟进训练]2.在等比数列{a n }中,已知a 4+a 7=2,a 5a 6=-8,求a 1+a 10. [解] 因为数列{a n }为等比数列,所以a 5a 6=a 4a 7=-8. 联立⎩⎨⎧ a 4+a 7=2,a 4a 7=-8.可解得⎩⎨⎧ a 4=4,a 7=-2或⎩⎨⎧a 4=-2,a 7=4.当⎩⎨⎧a 4=4,a 7=-2时,q 3=-12,故a 1+a 10=a 4q 3+a 7q 3=-7; 当⎩⎨⎧a 4=-2,a 7=4时,q 3=-2,同理,有a 1+a 10=-7. 即a 1+a 10的值为-7.等比数列的设法与求解1.类比等差数列中相邻三项的设法,想一想:等比数列中的相邻三项如何设运算更方便?[提示] 可设为aq ,a ,aq 或a ,aq ,aq 2(q ≠0). 2.如果四个数成等比数列,如何设更方便运算? [提示] 可设为a q ,a ,aq ,aq 2或a q 3,aq ,aq ,aq 3(q ≠0).【例3】 有四个数,其中前三个数成等差数列,后三个数成等比数列,并且第一个数与第四个数的和是16,第二个数与第三个数的和是12,求这四个数.[解] 法一:设四个数依次为a -d ,a ,a +d ,(a +d )2a , 由条件得⎩⎪⎨⎪⎧a -d +(a +d )2a =16,a +(a +d )=12,解得⎩⎨⎧ a =4,d =4,或⎩⎨⎧a =9.d =-6.所以,当a =4,d =4时,所求四个数为0,4,8,16; 当a =9,d =-6时,所求四个数为15,9,3,1. 故所求四个数为0,4,8,16或15,9,3,1.法二:设四个数依次为2a q -a ,aq ,a ,aq (a ≠0), 由条件得⎩⎪⎨⎪⎧2a q -a +aq =16,aq +a =12.解得⎩⎨⎧a =8,q =2,或⎩⎪⎨⎪⎧a =3,q =13.当a =8,q =2时,所求四个数为0,4,8,16; 当a =3,q =13时, 所求四个数为15,9,3,1.故所求四个数为0,4,8,16或15,9,3,1.合理地设出所求数中的三个数,根据题意再表示出另一个数是解决这类问题的关键,一般地,三个数成等比数列,可设为aq ,a ,aq ;三个数成等差数列,可设为a -d ,a ,a +d .[跟进训练]3.三个数成等比数列,其积为512,如果第一个数与第三个数各减去2,则这三个数成等差数列,求这三个数.[解] 设三个数依次为aq ,a ,aq , ∵a q ·a ·aq =512,∴a =8. ∵⎝ ⎛⎭⎪⎫a q -2+(aq -2)=2a , ∴2q 2-5q +2=0, ∴q =2或q =12,∴这三个数为4,8,16或16,8,4.1.在数列{a n }中,a 2n =a n -k ·a n +k (n ,k ∈N +,n >k )是{a n }成等比数列的必要不充分条件.2.等比数列的常用性质:(1)如果m +n =k +l ,则有a m a n =a k a l ; (2)如果m +n =2k ,a m ·a n =a 2k ;(3)若m ,n ,p 成等差数列,a m ,a n ,a p 成等比数列;(4)在等比数列{a n }中,每隔k 项(k ∈N +)取出一项,按原来的顺序排列,所得的新数列仍为等比数列;(5)如果{a n },{b n }均为等比数列,且公比分别为q 1,q 2,那么数列⎩⎨⎧⎭⎬⎫1a n ,{a n ·b n },⎩⎨⎧⎭⎬⎫b n a n ,{|a n |}仍是等比数列,且公比分别为1q 1,q 1q 2,q 2q 1,|q 1|;(6)等比数列的项的对称性:在有穷等比数列中,与首末两项“等距离”的两项之积等于首末两项的积,即a 1·a n =a 2·a n -1=a 3·a n -2=….3.根据等比中项和等比数列的性质巧设等比数列中的项:当三个数成等比数列且知这三个数的积时,一般将这三个数设为aq ,a ,aq ;当有五个数成等比数列时,常设为a q 2,aq ,a ,aq ,aq 2.1.对任意等比数列{a n },下列说法一定正确的是( ) A .a 1,a 3,a 9成等比数列 B .a 2,a 3,a 6成等比数列 C .a 2,a 4,a 8成等比数列 D .a 3,a 6,a 9成等比数列D [因为a 26=a 3a 9,所以a 3,a 6,a 9成等比数列.]2.等比数列{a n }中,a 1=18,q =2,则a 4与a 8的等比中项为( ) A .±4 B .4 C .±14 D.14 A [a 4=a 1q 3=18×23=1,a 8=a 1q 7=18×27=16,∴a 4与a 8的等比中项为±16=±4.]3.在等比数列{a n }中,各项都是正数,a 6a 10+a 3a 5=41,a 4a 8=4,则a 4+a 8=________.7 [∵a 6a 10=a 28,a 3a 5=a 24,∴a 24+a 28=41. 又a 4a 8=4,∴(a 4+a 8)2=a 24+a 28+2a 4a 8=41+8=49.∵数列{a n }各项都是正数,∴a 4+a 8=7.]4.在递增等比数列{a n }中,a 1a 9=64,a 3+a 7=20,求a 11的值. [解] 在等比数列{a n }中, ∵a 1·a 9=a 3·a 7,∴由已知可得a 3·a 7=64且a 3+a 7=20. 联立得⎩⎨⎧ a 3=4,a 7=16,或⎩⎨⎧a 3=16,a 7=4.∵{a n }是递增等比数列,∴a 7>a 3. ∴取a 3=4,a 7=16, ∴16=4q 4,∴q 4=4. ∴a 11=a 7·q 4=16×4=64.。
高中数学等比数列教案

高中数学等比数列教案
一、教学目标:
1. 掌握等比数列的定义及判断方法;
2. 掌握等比数列的通项公式及前 n 项和公式;
3. 能够灵活应用等比数列解决实际问题。
二、教学重点:
1. 等比数列的定义及判断方法;
2. 等比数列的通项公式及前 n 项和公式。
三、教学难点:
1. 灵活运用等比数列解决复杂问题;
2. 培养学生数学思维和逻辑推理能力。
四、教学内容:
1. 等比数列的定义及性质;
2. 等比数列通项公式及前 n 项和公式的推导;
3. 等比数列的应用实例。
五、教学过程:
1. 引入:通过生活中的实例引入等比数列的概念,让学生了解等比数列的特点和应用场景。
2. 学习等比数列的性质和判断方法,让学生能够判断一个数列是否为等比数列。
3. 学习等比数列的通项公式及前 n 项和公式的推导,让学生掌握这两个公式的用法和计算
方法。
4. 练习与巩固:让学生通过练习题巩固所学知识,培养他们的解题能力和推理思维。
5. 应用实例:通过一些实际问题,让学生运用等比数列解决实际问题,培养他们的数学建
模能力。
六、作业布置:
1. 课后练习:布置一些等比数列相关的习题,巩固学生所学知识。
2. 探究性问题:布置一些拓展性问题,让学生能够进一步应用所学知识解决问题。
七、课堂反馈:
1. 通过课堂讨论和作业批改,及时纠正学生的错误,加深他们对等比数列的理解和掌握。
八、教学总结:
1. 总结本节课所学知识,梳理等比数列的性质和应用场景,巩固学生的学习成果。
2. 展望下一节课内容,引导学生进行自主学习和提前预习。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第2课时 等比数列的性质阅读教材P 23思考交流以下P 24例3以上部分,完成下列问题.对于等比数列{a n },通项公式a n =a 1·q n -1=a 1q·q n.根据指数函数的单调性,可分析当q >0时的单调性如下表:思考:(1)若等比数列{a n }中,a 1=2,q =2,则数列{a n }的单调性如何?[提示] 递减数列.(2)等比数列{a n }中,若公比q <0,则数列{a n }的单调性如何? [提示] 数列{a n }不具有单调性,是摆动数列. 2.等比中项阅读教材P 25练习2以上最后两段部分,完成下列问题. (1)前提:在a 与b 中间插入一个数G ,使得a ,G ,b 成等比数列.(2)结论:G 叫作a ,b 的等比中项. (3)满足关系式:G 2=ab .思考:(1)任意两个数都有等差中项,任意两个数都有等比中项吗?[提示] 不是,两个同号的实数必有等比中项,它们互为相反数,两个异号的实数无等比中项.(2)两个数的等差中项是唯一的,若两个数a ,b 存在等比中项,唯一吗?[提示] 不唯一,如2和8的等比中项是4或-4.1.已知{a n }是等比数列,a 2=2,a 5=14,则公比q 等于( )A .-12B .-2C .2D .12D [由a 5=a 2q 3,得q 3=a 5a 2=142=18,所以q =12,故选D .]2.将公比为q 的等比数列{a n }依次取相邻两项的乘积组成新的数列a 1a 2,a 2a 3,a 3a 4,…,则此数列是( )A .公比为q 的等比数列B .公比为q 2的等比数列 C .公比为q 3的等比数列 D .不一定是等比数列B [由于a n a n +1a n -1a n =a n a n -1×a n +1a n=q ·q =q 2,n ≥2且n ∈N +,所以{a n a n +1}是以q 2为公比的等比数列,故选B .]3.等比数列{a n }中,若a 1=2,且{a n }是递增数列,则数列{a n }的公比q 的取值范围是________.(1,+∞) [因为a 1=2>0,要使{a n }是递增数列,则需公比q >1.]4.4-23与4+23的等比中项是________. 2或-2 [由题意知4-23与4+23的等比中项为 ±4-234+23=±16-12=±2.]等比中项及应用x =_____________.(2)设a ,b ,c 是实数,若a ,b ,c 成等比数列,且1a ,1b ,1c成等差数列,则c a +ac的值为________.(1)-4 (2)2 [(1)由题意得(2x +2)2=x (3x +3),x 2+5x +4=0,解得x =-1或x =-4,当x =-1时,2x +2=0,不符合题意,舍去, 所以x =-4.(2)由a ,b ,c 成等比数列,1a ,1b ,1c成等差数列,得⎩⎪⎨⎪⎧b 2=ac ,2b =1a +1c,即4ac =⎝ ⎛⎭⎪⎫1a +1c 2,故(a -c )2=0, 则a =c ,所以c a +ac=1+1=2.]应用等比中项解题的两个注意点(1)要证三数a ,G ,b 成等比数列,只需证明G 2=ab ,其中a ,b ,G 均不为零.(2)已知等比数列中的相邻三项a n -1,a n ,a n +1,则a n 是a n -1与a n +1的等比中项,即a 2n =a n -1·a n +1,运用等比中项解决问题,会大大减少运算过程.1.(1)已知1既是a 2与b 2的等比中项,又是1a 与1b的等差中项,则a +ba 2+b2的值是( ) A .1或12B .1或-12C .1或13D .1或-13(2)已知等比数列{a n }的前三项依次为a -1,a +1,a +4,则a n =________.(1)D(2)4×⎝ ⎛⎭⎪⎫32n -1[(1)由题意得,a 2b 2=(ab )2=1,1a +1b=2,所以⎩⎪⎨⎪⎧ab =1,a +b =2或⎩⎪⎨⎪⎧ab =-1,a +b =-2.因此a +b a 2+b 2的值为1或-13.(2)由已知可得(a +1)2=(a -1)(a +4), 解得a =5,所以a 1=4,a 2=6,所以q =a 2a 1=64=32,所以a n =4×⎝ ⎛⎭⎪⎫32n -1.]等比数列的设法与求解【例2】 已知四个实数,前三个数依次成等比数列,它们的积是-8,后三个数依次成等差数列,它们的积是-80,则这四个数为________.1,-2,4,10或-45,-2,-5,-8 [由题意设此四个数分别为b q,b ,bq ,a ,则b 3=-8,解得b =-2,q 与a 可通过解方程组⎩⎪⎨⎪⎧2bq =a +b ,ab 2q =-80求出,即为⎩⎪⎨⎪⎧a =10,b =-2,q =-2或⎩⎪⎨⎪⎧a =-8,b =-2,q =52,所以此四个数为1,-2,4,10或-45,-2,-5,-8.]灵活设项求解等比数列的技巧(1)三个数成等比数列设为aq,a ,aq .(2)四个符号相同的数成等比数列设为a q 3,a q,aq ,aq 3.(3)四个数成等比数列,不能确定它们的符号相同时,可设为:a ,aq ,aq 2,aq 3.2.已知三个数成等比数列,其积为1,第2项与第3项之和为-32,则这三个数依次为________.-25,1,-52 [设这三个数分别为aq,a ,aq ,则⎩⎪⎨⎪⎧a 3=1,a +aq =-32,解得a =1,q =-52,所以这三个数依次为-25,1,-52.]等比数列的性质及应用[探究问题]1.在等差数列{a n }中,a n =a m +(n -m )d ,类比等差数列中通项公式的推广,你能得出等比数列通项公式推广的结论吗?[提示] a n =a m ·qn -m.2.在等差数列{a n }中,由2a 2=a 1+a 3,2a 3=a 2+a 4,…我们推广得到若2p =m +n ,则2a p =a m +a n ,若{a n }是等比数列,我们能得到什么类似的结论.[提示] 若2p =m +n ,则a 2p =a m ·a n .3.在等差数列{a n }中,若m +n =p +q ,则a m +a n =a p +a q ,类比这个性质,若{a n }是等比数列,有哪个结论成立?[提示] 若m +n =p +q ,则a m ·a n =a p ·a q .【例3】 (1)在等比数列{a n }中,a n >0,若a 3·a 5=4,则a 1a 2a 3a 4a 5a 6a 7=________.(2)设{a n }为公比q >1的等比数列,若a 2 018和a 2 019是方程4x 2-8x +3=0的两根,则a 2 030+a 2 031=________.(3)在等比数列{a n }中,已知a 4a 7=-512,a 3+a 8=124,且公比q 为整数,则a n =________.思路探究:利用等比数列的性质求解.(1)128 (2)2·312 (3)-(-2)n -1[(1)a 3a 5=a 24=4,又a n>0,所以a 4=2,a 1a 2a 3a 4a 5a 6a 7=(a 1·a 7)·(a 2·a 6)·(a 3·a 5)·a 4=a 24·a 24·a 24·a 4=a 74=27=128.(2)解方程4x 2-8x +3=0得x 1=12,x 2=32,因为q >1,故a 2 019=32,a 2 018=12,故q =3, ∴a 2 030+a 2 031=a 2 018q 12+a 2 019·q 12=(a 2 018+a 2 019)q 12=2·312.(3)在等比数列{a n }中,由a 4a 7=-512得a 3a 8=-512, 又a 3+a 8=124,解得a 3=-4,a 8=128或a 3=128,a 8=-4,因为公比q 为整数,所以q =5a 8a 3=-51284=-2, 故a n =-4×(-2)n -3=-(-2)n -1.]1.(变条件)将例3(3)中等比数列满足的条件改为“a 4+a 7=2,a 5a 6=-8”,求a 1+a 10.[解] 因为{a n }是等比数列,所以a 5a 6=a 4a 7=-8, 又a 4+a 7=2,解得a 4=4,a 7=-2或a 4=-2,a 7=4, 当a 4=4,a 7=-2时,q 3=-12,a 1+a 10=a 4q3+a 7q 3=-7,当a 4=-2,a 7=4时,q 3=-2,a 1+a 10=a 4q3+a 7q 3=-7.故a 1+a 10=-7.2.(变结论)例3(3)题的条件不变,求log 4|a 2|+log 4|a 3|+log 4|a 8|+log 4|a 9|.[解] 因为a 4a 7=-512,所以a 2a 9=a 3a 8=-512, 故log 4|a 2|+log 4|a 3|+log 4|a 8|+log 4|a 9| =log 4(|a 2a 9|·|a 3a 8|)=log 45122=log 229=9.等比数列的常用性质性质1:通项公式的推广:a n =a m ·qn -m(m ,n ∈N +).性质2:若{a n }为等比数列,且k +l =m +n (k ,l ,m ,n ∈N +),则a k ·a l =a m ·a n .特别的,若k +φ=2m (m ,k ,φ∈N +),则a k ·a φ=a 2m .性质3:若{a n },{b n }(项数相同)是等比数列,则{λb n },⎩⎨⎧⎭⎬⎫1a n ,{a 2n },{a n ·b n },⎩⎨⎧⎭⎬⎫a nb n 仍是等比数列.性质4:在等比数列{a n }中,序号成等差数列的项仍成等比数列.性质5:⎩⎪⎨⎪⎧a 1>0,q >1或⎩⎪⎨⎪⎧a 1<0,0<q <1⇔{a n }递增;⎩⎪⎨⎪⎧a 1>0,0<q <1或⎩⎪⎨⎪⎧a 1<0,q >1⇔{a n }递减;q =1⇔{a n }为常数列;q<0⇔{a n }为摆动数列.1.解题时,应该首先考虑通式通法,而不是花费大量时间找简便方法.2.所谓通式通法,指应用通项公式,前n 项和公式,等差中项,等比中项等列出方程(组),求出基本量.3.巧用等比数列的性质,减少计算量,这一点在解题中也非常重要.1.判断正误(正确的打“√”,错误的打“×”)(1)数列-1,-2,-4,-8,-16是递减数列.( ) (2)等比数列{a n }中,a 1>1,q <0,则数列|a 1|,|a 2|,|a 3|,…,|a n |,…是递增数列.( )(3)若G 是a ,b 的等比中项,则G 2=ab ,反之也成立.( ) [答案] (1)√ (2)× (3)× [提示] (1)正确;(2)不正确,如a 1=2,q =⎝ ⎛⎭⎪⎫-12,则|a n |=2×12n -1=12n -2是递减数列;(3)不正确,当G 是a ,b 的等比中项时,G 2=ab 成立,但当G 2=ab 时,G 不一定是a ,b 的等比中项,如G=a =b =0.2.在等比数列{a n }中,a 4=6,则a 2a 6的值为( ) A .4 B .8 C .36D .32C [因为{a n }是等比数列,所以a 2a 6=a 24=36.]3.在等比数列{a n }中,a 888=3,a 891=81,则公比q =_____________.3 [因为a 891=a 888q891-888=a 888q 3,所以q 3=a 891a 888=813=27.所以q =3.]4.在等比数列{a n }中,a 3a 4a 5=8,求a 2a 3a 4a 5a 6的值.[解] 在等比数列{a n }中,由a 3a 4a 5=a 34=8,得a 4=2,又因为a2a6=a3a5=a24,所以a2a3a4a5a6=a54=25=32.。
