3、3 正弦电路中的电阻、电感、电容元件
电工电子教案之 3.3-纯电感和电容电路

纯电感和电容电路(80分钟)本次课的教学内容属于课程标准中工作任务2:交流电路。
一、教学说明1、要完成本次课的教学,教师应准备如下材料:教材、多媒体课件。
2、学生应具备的基础:1)掌握正弦交流电的相量概念;2)掌握电阻电路在交流电路中的计算。
二、教学目的通过本次课的学习,要求学生达到以下知识和能力目标。
1、知识目标1)能描述纯电感电路的电流、电压、功率等参数的测量方法和分析方法;2)能描述纯电容电路的电流、电压、功率等参数的测量方法和分析方法。
2、能力目标1)能比较三种元件在交流电中的电压电路大小、方向关系。
3、素质目标1)具备查阅资料的能力;2)具备独立工作或团队合作的能力;3)具备精益求精、严谨求实的工作态度;4)具备良好的职业道德和素质。
三、教学重点和难点分析1、教学重点纯电感和电容在正弦交流电路中的电压电流关系。
正弦交流电的电压和电流是用相量来表示的,对于电阻电路来说在交直流电路中都适用欧姆定律,没有特别大的区别。
电感和电容这两种元件属于储能元件,电压电流的关系不是比例关系,而是求导和积分的关系,这样导致在计算电压电流关系时出现一个相位差的问题,这个是需要特别注意的,对于电感来说电压超前电流九十度,对于电容来说电流超前电压九十度。
2、教学难点三种元件的比较。
电阻、电感和电容是在交流电路中主要出现的元件,这三种元件由于本身性能的不一样,导致在相同的交流电源作用下有不一样的电压电流,这个是学生非常容易搞混的内容,需要学生对这三种元件有一个清晰的概念,为后续的完整电路计算打好基础。
四、教学思想本次课程是交流电路的第四次课程,在前几次的课程已经详细介绍了交流电的概念,电阻在交流电中的表现,以及电容器的基本功能等内容,为本次课程做好了充分的准备,在此次课程中主要介绍学生电感和电容在交流电路中的表现,这个知识点对于学生来说是比较抽象的,需要反复强调前面的基础知识,以加深理解。
五、教学安排通过六、教学过程和教学方法设计教学过程采用“讲授、演示、讨论”的方式开展,辅以多媒体课件、分析讨论等教学手段。
12.元件伏安特性相量形式
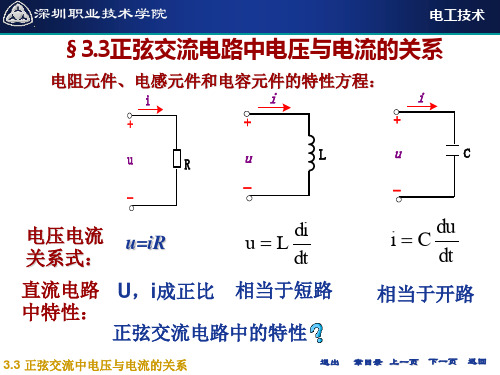
U
返回
章目录 上一页 下一页
深圳职业技术学院
电工技术
2. 电容元件的功率
u 2Usi nω t i 2Uω C si n( ω t 90)
i
u
ωt
瞬时功率:
p i u UI si n2 ω t
o平均功率:P =0u Nhomakorabeap+
i
+ u
i
-
u
+
i
u
+
i
无功功率:
Q UI I X C
90
相位差
ψu ψi 90
退出 章目录 上一页 下一页 返回
2.1 正弦交流中电压与电流的关系
深圳职业技术学院
电工技术
u 2Usinω t i 2Uω C sin( ω t 90)
有效值
I U ω C 或 1 1 定义: XC 容抗(Ω ) ωC 2 π f C
返回
深圳职业技术学院
电工技术
§3.3.3 纯电容电路
1. 电压电流关系
du 基本关系式: i C dt 设:u 2 U sin ω t
2 U ωC sin( ω t 90) u i
du dt 2 UC ω cos ω t
i
+ u _
C
则: i C
u
i
ωt
1) 频率关系: 频率相同 2)大小关系: I =UC 3)相位关系 : 电流超前电压90
退出
章目录 上一页 下一页
返回
深圳职业技术学院
电工技术
§ 3.3.1 纯电阻电路
1.电压与电流的关系 根据欧姆定律:
第二章 正弦稳态电路

3
已知正弦电压u1(t)=141 sin(ωt+π/3) V,u2(t)=70.5 sin(ωt-π/6) V 写出u1和u2的相量, 并画出相量图。
解: u1 U 1 141 100 V 3 3 2 70.5 50 V u2 U 2 6 6 2
阻抗的另一形式
Z R jX
Z R2 X 2 X arctan R
.
+ . U I N
Z的实部为R, 称为“电阻”, Z的虚部为X, 称为“电抗”
3
2. 阻抗的串并联
n个阻抗串联的电路
I
+ . .
Z1
Z2
Z3
+ . -+ . - . - + + U1 U2 U3 .
U
Un
Zn
【例2.5.1】图所示正弦稳态电路中,交流电压表V1、V2、V3的读数分别 为30V、60V和20V,求交流电压表V的读数。
1
R
2
L C
I1
3
Z1
V
US
求图所示二端网络的戴维南等效电路。 【例2.6.3】已知 us 10 2 sin10000tV , R1 R2 R3 1 , R4 4 , C 400F , L 0.4mH 求电阻R4两端的电压。
L
品质因数
Q 0C G 1 ( 0 LG )
并联谐振电路的特点:阻抗最大;电流源一定时,电压 最大;电流谐振,能量互换仅在LC之间。
i
N
有功功率P、功率因数
P UI cos
无功功率Q
视在功率S 复功率S
cos
电工学考试答案

1. 下列关于正弦量之间的相位关系的说法中错误的是(BCD )。
( )。
(4 分)A . 同频率的两正弦量的相位差与计时起点无关。
B .两个正弦量的相位差与它们的参考方向的选择无关。
C . 任意两个正弦量的相位差都等于其初相之差。
D . u1、u2、u3为同频率正弦量,若u1超前u2,u2超前u3,则u1一定超前u3。
2. 下列说法中正确的是( BCD )。
( )。
(4 分)A .三相正弦电路中,若负载的线电压对称,则其相电压也一定对称。
B . 三相正弦电路中,若负载的相电流对称,则其线电流也一定对称。
C . 对称三相正弦交流电路中各组电压和电流都是对称。
D . 三相三线制正弦交流电路中,若三个线电流IU =IV =IW ,则这三个线电流一定对称。
3.下列关于无功率功率的说法中错误的是(ACD )。
( )。
(4 分)A . 正弦交流电路中,电感元件或电容元件的瞬时功率的平均值称为该元件的无功功率。
B . 正弦交流电路中任一无源二端网络所吸收的无功功率等于其瞬时功率的无功分量的最大值。
C . 在正弦交流电路中任一个无源二端网络所吸收的无功功率,一定等于网络中各元件无功功率的数值(指绝对值)之和。
D . 无功功率就是无用(对电气设备的工作而言)的功率。
4. 下列关于RLC 串联的正弦电路的电压的说法中错误的是(AC )( )。
(4 分) A. 电路的总电压U 可能比UL 、UC 都小。
B . 电路的总电压U 一定大于UR 。
C . 在各电压参考方向一致的情况下,电路总电压一定超前Uc ,但不一定超前UR 。
D . 在各电压参考方向一致的情况下,电路总电压一定滞后Uc ,但不一定滞后UR 。
5.下列关于电阻、电感、电容元件(指线性定常元件)的电压与电流的关系的说法中错误的是(ACD )。
( )。
(4 分)A . 无论电压和电流的参考方向如何,uR =RiR ,uL =L(diL/dt),iC =C(duC/dt)总是成立。
正弦电路中的电阻、感抗、容抗

3.3.1电阻元件的正弦交流电路
一、电阻元件基本关系:
根据 欧姆定律
u iR
u 2 U sin t i u 2 U sin t 2 I sin t
RR
电阻电路中电流、电压的关系
1. 频率相同
2. 相位相同
3. 有效值关系: U IR
4. 相量关系:设 U U 0
I
则 I U 0 R
dt
2 I L sin(t 90 ) 2 U sin(t 90 )
电感电路中电流、电压的关系
设:
u 2 I L sin( t 90 )
i 2I sin t
2U sin( t 90 )
1. 频率相同
2. 相位相差 90° (u 超前i 90 °)
3. 有效值 U IL
定义: X L L 感抗(Ω) U
内容简介
本教材理论推导从简,计算思路交待详细,概念述明 来龙去脉,增加例题数量和难度档次,章节分 “重计算 ”及“重概念”两类区别对待,编排讲究逐步引深的递进 关系,联系工程实际,训练动手能力,尽力为后续课程铺 垫。借助类比及对偶手法,语言朴实简练,图文印刷结合 紧密,便于自学与记忆,便于节省理论教学时数。适用于 应用型本科及高职高专电力类、自动化类、机电类、电器 类、仪器仪表类、电子类及测控技术类专业。
则: U I X L
I
相量图
4. 相量关系
设: I I 0
超前!
U U 90 I L90
U
I
U I L 90 I ( jX L )
电感电路中复数形式的欧姆定律
U I j X L
其中含有幅度和相位信息
I
+
U-
jL
有效值关系 U IL
第三章 正弦交流电路-1

一.电阻元件
i
根据欧姆定律,线性电阻上的电压与电流
成正比关系,即 i u R
图3-10
当电压和电流均用相量表示时,欧姆定律
的相量表示式为 第(23)页
•
•
I
U
R
u
R
电阻元件
上式表明,电阻元件上电压和电流的相位相同,
如图3-11所示。
设 i 2ISint
u 2USint 图3-11
电阻元件吸收的瞬时功率为
方法二: 运用矢量运算
Y I2m B
C I3m
10 50
I1m
A
5
0 60 30
X
i1 I1m OA矢量 i2 I2m OB矢量 i3 I3m OC矢量
根据矢量图
I3m 14.6
3 50 于是i3 14.6CoS(t 50)
+j
I3m
方法三.运用复数运算:
11.16
I1m 5e j30
只要有幅值与初相位两个要素就足以表示各电压 与电流之
间的关系,因此我们约定:用式(3-1)中的复常数 Ie ji 表
示正弦电流 i 2ISint i ,并用下列记法
•
I Ie ji I i
(3-2)
上式中I• m不仅是一个复数,而且表示了一个正弦量,所以给它
一个专有名称——相量。代表正弦电流的相量称之为电流相量,
U
的正方向如图3-13(a)所示。
u,i
(b) 0
u
i
t
i ii
i
+ -- +
p- + + 储能 放能 储能 放能
根据楞次定律得出
u
eL
03-1正弦交流

3.1
正弦交流电的基本概念
正弦交流电的方向
交流电路进行计算时,首先也要规定物理量 的参考方向,然后才能用数字表达式来描述。
i
u
R
i
0
实际方向和参考方向一致
t
实际方向和参考方向相反
3.1
正弦交流电的基本概念
二、正弦量的三要素
Im
0
i
i I m sin t
t
瞬时表达式
Instantaneous Expression
i2
0
i1
t
i1
1 2
i2
0
1 2 0
1 2
t
i1
0
i1 超前 i2
1 2 0
2 1
i2
t
i1 滞后 i2
3.1
正弦交流电的基本概念
三相交流电路:三种电压初相位各差120。
uA
uB
uC
0
t
3.1
正弦交流电的基本概念
在工程应用中常用有效值表示幅度。常用交流电表指示的电 压、电流读数,就是被测物理量的有效值。标准电压220V,也 是指供电电压的有效值。
I m I me j
i I m sin( t )
3.2
正弦量的相量表示方法
复指数函数虚轴投影和正弦函数间对应关系示意图: 一个正弦量的瞬时值可以用一个旋转的有向线 段在纵轴上的投影值来表示。 +j u
u U m sin t
ω
0
+1
Um
0
t
3.2
I
Im 2
3.1
(完整版)纯电阻、电感、电容电路
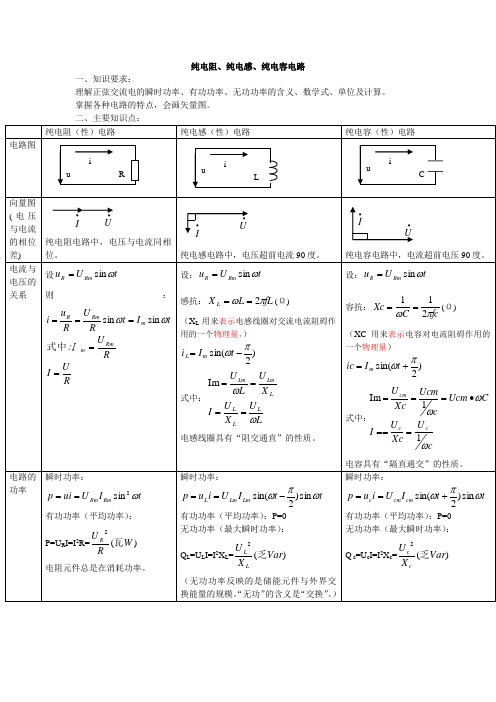
纯电阻、纯电感、纯电容电路一、知识要求:理解正弦交流电的瞬时功率、有功功率、无功功率的含义、数学式、单位及计算。
掌握各种电路的特点,会画矢量图。
三、例题:1.已知电阻R=10Ω,其两端电压V t t u R )30314sin(100)(︒+=,求电流i R(t ).、电路消耗的功率。
解:由于电压与电流同相位,所以 i R(t )=10)(=Rt u R )30314sin(︒+t A 电路消耗的功率P=U R I=W X Um 5002101002Im 2==• 2、已知电感L=0.5H ,其两端电压V t t u L )301000sin(100)(︒+=,求电流i L(t ). 解:L X L ω==1000X0.5=500Ω由于纯电感电路中,电流滞后电压90°,所以:A t t X t i LL )601000sin(2.0)90301000sin(100)(︒-=︒-︒+=3.已知电容C=10μF ,其两端电压V t t u c )301000sin(100)(︒+=,求电流i c (t ).. 解: Ω===-10010101000116X X C X c ω 由于电流超前电压90°,所以:A t t Xct i c )1201000sin()90301000sin(100)(︒+=︒+︒+=四、练习题: (一)、填空题1、平均功率是指( ),平均功率又称为( )。
2、纯电阻正弦交流电路中,电压有效值与电流有效值之间的关系为( ),电压与电流在相位上的关系为( )。
纯电感正弦交流电路中,电压有效值与电流有效值之间的关系为( ),电压与电流在相位上的关系为( )。
纯电容正弦交流电路中,电压有效值与电流有效值之间的关系为( ),电压与电流在相位上的关系为( )。
3、在纯电阻电路中,已知端电压V t u )30314sin(311︒+=,其中R=1000Ω,那么电流i=( ),电压与电流的相位差=( ),电阻上消耗的功率P=( )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
= U = 220∠60 = 3.5∠ 30 A I jX L j 62.8
Q L = IU = 3.5 × 220 = 770 var
(2)f=5000Hz时 X L = ωL = 2π × 5000 × 0.2 = 6.28 × 103
= U = 220∠60 = 3.5 × 10 2 ∠ 30 A I jX L j 6.28 × 10 3
(d)
电感的功率: 电感的功率: 设 i=
2 I sin ωt
u O
P.u.i p i
u = 2U sin(ωt + 90 ) = 2U cos ωt
p = u i = 2UI sin ωt cos ωt = UI sin 2ωt
π
2
ωt
1 P= T
∫
1 pdt = T
∫
T
0
UI sin 2ωtdt = 0
i 电流、 电流、电压的瞬时值为 : = 0.984 2 sin( 314t 33.4 ) A
u R = 98.4 2 sin( 314t 33.4 )V u L = 196.8 2 sin( 314t + 56.6 )V
UR I
3、5 阻抗与导纳
一、 阻抗 一个包含电阻、电感、电容的无源二端电路N, 一个包含电阻、电感、电容的无源二端电路 ,定义其等效阻抗为 U I Z= I I
3 、3
正弦电路中的电阻、电感、 正弦电路中的电阻、电感、电容元件
i
U = RI ψ u = ψ i
u
一、 电阻元件的交流电路
i = 2 I sin(ωt + ψ i ) u = 2 RI sin(ωt + ψ i ) = 2U sin(ωt +ψ u ) I = I∠ψ U = U∠ψ
i
u, i i
③ U = U∠θ u → u ( t ) ④必要时作相量图
I = I∠θ i → i( t )
例: 在图3.4.2(a)所示电路中 已知 u S = 220 2 sin( 314t + 30 )V 所示电路中,已知 在图 所示电路中 R=100 ,L=0.639H,求电流 i、uR及uL。 , 、 解:先画出电路的相量模型 先画出电路的相量模型
3 、4
基尔霍失定律的相量形式
一、 KCL的相量形式 n 的相量形式 对某一结点, 对某一结点,有 ik = 0
∑ i = ∑ I [ 2I e
h n k m k k =1 k =1
j (ωt +ψ k )
∑ ]= ∑ I [ 2 I e ] =
k =1
n m k jω t k =1
i k = I m [ 2 I k e j (ωt +ψ k ) ]
∑
k =1
n k =1
n
Ik = U
+j
∑Y
k =1
n k =1
k
Yk = G k + jBk
4.导纳的串联 导纳的串联
1 1 1 1 = + + + = Y Y1 Y2 Yn
Y=
∑G
I
k
∑B
Z2
k
∑
1 Y k =1 k
n
a +
U
Z1
Zn
计算等效阻抗和导纳, 计算等效阻抗和导纳,串联时使 用阻抗, 用阻抗,并联时使用导纳较方便
2Im e
[
jω t
ΣI k
]
∑i
k =1
n
k
=0
∑
k =1
n
Ik = 0
二、KVL的相量形式 的相量形式 设对某一回路, 设对某一回路,有
∑u
∑
k =1
n
k
=0
k =1 n
同理可得
Uk = 0
三、相量分析法 1.条件:线性电路在同频率正弦量激励下的稳态响应 条件: 条件 2.方法 ①电路中所有正弦量用其对应的相量表示 方法: 方法
i = 3.5 × 10 2 2 sin(3.14 × 10 4 t 30 ) A
QL = IU = 3.5 × 10 2 × 220 = 7.7 var
三、 电容元件的交流电路
u = 2U sin(ωt + ψ u )
i C
ψu ψi
i
du + = 2ωCU cos(ωt + ψ u ) i=C u dt = 2ωCU sin(ωt + ψ u + 90 )
i
+
u
L
u,i i
ψi ψu
u
-
电感电压的相位超前电流90° 电感电压的相位超前电流 ° = U∠ψ = ωLI∠(ψ + 90 ) = ωLI∠90° (a) U u i
+ U -
I
(b)
U I
jωL 令 XL=ωL 则 U=XLI XL称为电感元件的电抗,简称感抗 称为电感元件的电抗,简称感抗 (c) ω→∞时,XL→∞,电感相当于开路 时 , ω=0时,XL=0,电感相当于短路, 时 ,电感相当于短路, 对直流电, 对直流电,电感相当于短路 1 1 感抗的倒数称为感纳 感纳, 感抗的倒数称为感纳,用BL表示 B L = X = ωL L
1 YR = G = R
YL = 1 jω L
1 I Y= = Z U
Y = G + jB
Y的实部 称为电导,Y的虚部 称为电纳 的实部G称为电导, 的虚部 称为电纳 的虚部B称为 的实部 称为电导
= jB L YC = jωC = jBC
三、 阻抗与导纳的串并联 1.阻抗的串联 Z = Z1 + Z 2 + + Z n = ∑ Z k 阻抗的串联
U s = 220∠30 V X L = ωL = 314 × 0.639 = 200
+
i
I
+
R L
uR
+
uS
-
UR +UL = US U R = RI = 100I U L = jωLI = j 200 I 得
100I + j 200I = 220∠30
由
uL
-
+ US -
QC = UI = I 2 X C
的电容。 例: 一正弦电流 i = 2 2 sin( 314t + 60 ) A 通过 ,通过10F的电容。 的电容 (1)求电容电压及电容的无功功率; )求电容电压及电容的无功功率; (2)当电流频率提高一倍时,电容电压的有效值如何改变? )当电流频率提高一倍时,电容电压的有效值如何改变? 解:(1)
u
π
2π
ωt
+
u
(a)
R
O
(b)
U = RI∠ψ i = RI
电阻元件的瞬时功率为
+ p = u i = 2UI sin(ωt + ψ u ) sin(ωt + ψ i ) U 1 T 1 T P= pdt = UI [1 cos 2(ωt + ψ i )]dt = UI
T
I I
R (c) (d)
+ R UR + jω L U L -
220∠30 220∠30 = I= 100 + j 200 5 × 100∠63.4
U R = 100 I = 98.4∠ 33.4 V
= 0.984∠ 33.4 A UL US
U L = j 200I = 196.8∠(90 33.4 ) = 196.8∠56.6 V
jψ z
+ U -
=| Z | ∠ψ Z 极坐标形式为 Z =| Z | e Z的模 称为阻抗模,Z的辐角 Z称为阻抗角 的模|z|称为阻抗模 的辐角ψ 的模 称为阻抗模, 的辐角 U | z |= , ψ Z = ψ u ψ i I Z的直角坐标形式为 Z=R+jX 的直角坐标形式为
电阻 Z R = R 电感 Z L = jωL = jX L 1 = jX C 电容 Z C = j ωC
+
N
U
Z
-
R称为电阻或交流电阻;X称为电抗 阻抗三角形 称为电阻或交流电阻; 称为电抗 称为电阻或交流电阻 称为 对Z X=0,电阻性 电阻性 X>0, 电感性 X<0,电容性 电容性
对R、L、C串联电路 串联电路 U 1 Z = = R + j ( X L X C ) = R + j (ωL ) ωC I 二端电路是电阻性的; 当XL=XC时,二端电路是电阻性的; 二端电路是电感性的,简称感性; 当XL>XC时,二端电路是电感性的,简称感性; 二端电路是电容性的, 当XL<XC时,二端电路是电容性的,简称容性 二、 导纳 阻抗Z的倒数为导纳, 阻抗 的倒数为导纳,用Y表示 的倒数为导纳 表示
电感是储能元件, 电感是储能元件,它在电路中的作用与电源或外电路进行能量 变换,这种能量交换规模的大小, 变换,这种能量交换规模的大小,我们用瞬时功率的最大值来 衡量并称为无功功率 无功功率, 衡量并称为无功功率,用QL表示
Q L = UI = I 2 X L
单位是乏 var
的电感线圈, 例:一个0.2H的电感线圈,电阻忽略不计,将它接在电压 一个 的电感线圈 电阻忽略不计, u = 220 2 sin(314t + 60 ) 的交流电源上。 的交流电源上。 (1)求线圈中的电流相量和无功功率 L )求线圈中的电流相量和无功功率Q (2)若将电源的频率改变为 )若将电源的频率改变为5000Hz,其它不变,求i和QL。 ,其它不变, 和 解:(1) X L = ωL = 314 × 0.2 = 62.8
