20170403-三个基本功率变换器的CCM-DCM边界条件
20170403-三个基本功率变换器在DCM下的稳态关系

iL (t )
AS
ILP
DTs
D′Ts
IL
D′′Ts
Ts
M=
Vo 1 + 1 + 4 D 2 / K 2 Lfs ,其中: K = = Vg 2 R
3:Buckboost 变换器在 DCM 下的稳态电压增益:
AS PS
IoL
C
iL (t )
Vg
ILP
Vo
DTs
D′Ts
L
IL
D′′TsILTsM =,得到:
M =
2 1 + 1 + 4(1 − D) / D 2
=
2 =D 1 + (2 − D) / D
2
在 Boost 变换器中,将边界关系 K = D (1 − D ) 代入 M =
1 + 1 + 4D 2 / K , 得到: 2
2 2 1 1 + 1 + 4 D 2 / K 1 + 1 + 4 D / D(1 − D) = = M = 1− D 2 2
2 Lfs Vo D ,其中: K = = R Vg K
用得到的 DCM 下之输出电压与输入电压的稳态增益关系, 再将各变换器的 CCM/DCM 边界条件代进去,会发现得到的关系,即是对应变换器在 CCM 下的稳态增益关系。 在 Buck 变换器中:将边界关系 K = 1 − D 代入 M =
2 1 + 1 + 4K / D 2
在 Buckboost 变换器中,将边界关系 K = (1 − D ) 2 代入 M =
D K
, 得到:
M =
D K
=
D (1 − D) 2
开关电源CCM和DCM工作模式
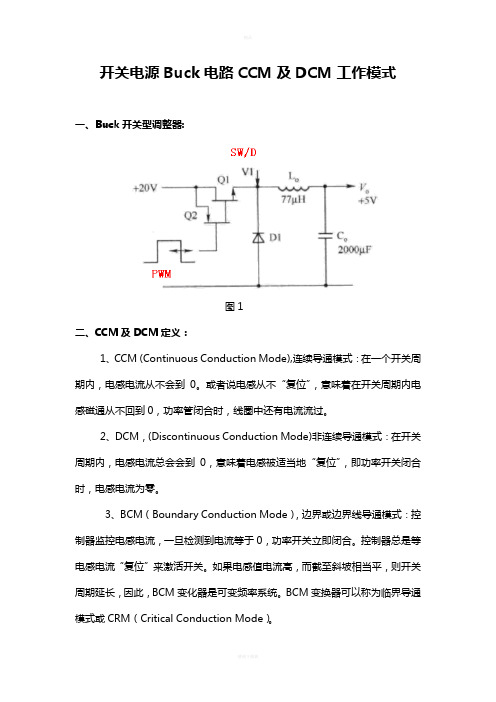
开关电源Buck电路CCM及DCM工作模式一、Buck开关型调整器:图1二、CCM及DCM定义:1、CCM (Continuous Conduction Mode),连续导通模式:在一个开关周期内,电感电流从不会到0。
或者说电感从不“复位”,意味着在开关周期内电感磁通从不回到0,功率管闭合时,线圈中还有电流流过。
2、DCM,(Discontinuous Conduction Mode)非连续导通模式:在开关周期内,电感电流总会会到0,意味着电感被适当地“复位”,即功率开关闭合时,电感电流为零。
3、BCM(Boundary Conduction Mode),边界或边界线导通模式:控制器监控电感电流,一旦检测到电流等于0,功率开关立即闭合。
控制器总是等电感电流“复位”来激活开关。
如果电感值电流高,而截至斜坡相当平,则开关周期延长,因此,BCM变化器是可变频率系统。
BCM变换器可以称为临界导通模式或CRM(Critical Conduction Mode)。
图1通过花电感电流曲线表示了三种不同的工作模式。
图2 电感工作的三种模式电流斜坡的中点幅值等于直流输出电流I的平均值,峰值电流Ip与谷值电o流I之差为纹波电流。
V三、CCM工作模式及特点根据CCM定义,测试出降压变换器工作于连续模式下的波形,如下图3所示。
图3波形1表示PWM 图形,将开关触发成导通和截止。
当开关SW 导通时,公共点SW/D 上的电压为Vin 。
相反,当开关断开时,公共点SW/D 电压将摆到负,此时电感电流对二极管D 提供偏置电流,出现负降压——续流作用。
波形3描述了电感两端电压的变化。
在平衡点,电感L 两端的平均电压为0,及S1+S2=0。
S1面积对应于开关导通时电压与时间的乘积,S2面积对应于开关关断时电压与时间的乘积。
S1简单地用矩形高度(in V -out V )乘以D sw T ,而S2也是矩形高度-out V t 乘以(1-D )sw T 。
连续(CCM)及非连续(DCM)导通模式

CCM Continuous Conduction Mode 连续导通模式DCM Discontinuous Conduction Mode 非连续导通模式CCM连续模式:变压器磁能尚未释放完毕,或激磁电流未下降到零时开关管再次导通,开关管电流从这个还未下降到零的激磁电流开始上升,即开关管电流不是锯齿波,是侧梯形波,因全过程中没有前后级同时关断的时刻,VDS波形后肩没有低频波。
90V输入,IPK波形 90V输入,VDS波形DCM断续模式:变压器磁能释放完毕,或激磁电流下降到零,再延时后开关管导通。
开关管电流从零开始上升,开关管电流为锯齿波。
在中间的延时段,前后级同时关断,因输出电压门槛,关断后还有少量能量未释放完,在变压器内部形成振荡波,即VDS波形后肩低频波(由于是分布电容与变压器激磁电感与漏感的和形成的,故频率较低。
而尖峰电压为分布电容与漏感形成的,频率高)。
264V输入,IPK波形 264V输入,VDS波形临界模式:即DCM模式中的激磁电流下降到零点时开关管马上再次导通,没有延时,开关管电流为锯齿波,VDS波形后肩没有低频波。
(其实也有类似DCM 模式下的输出门槛电压造成磁能未完全释放,但能量很低,开关管再次导通时起始电流基本接近零,可以忽略)即激磁电流还未下降到零时,开关管再次导通为CCM模式;下降到零时马上导通为临界模式;下降到零再延时开关管才导通为DCM 模式。
锯齿波电流起始端的电流尖峰是寄生电容对开关管充放电引起的,电容中的电流能突变,电压不能突变;电感上的电压能突变,电流不能突变。
相对来说,MOS管关断后无电流通过(绝对来说,还是有很微弱的电流振荡),变压器的储能通过次级及外围分布参数续流释放能量,分布参数形成尖峰冲击振荡。
由于开关管引脚D还“挂靠”在上面,能感受到其压力即电压。
上图电流波形上的,那个尖峰是由哪产生的,有的电流波形朝也也会有这个尖,开通瞬间的电流尖峰是次级二极管的反向恢复以及分布电容放电产生的。
Buck 电路中的CCM和DCM
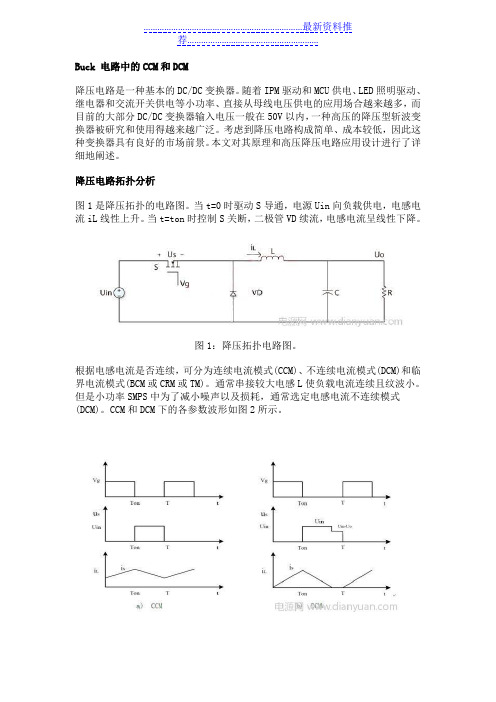
Buck 电路中的CCM和DCM降压电路是一种基本的DC/DC变换器。
随着IPM驱动和MCU供电、LED照明驱动、继电器和交流开关供电等小功率、直接从母线电压供电的应用场合越来越多,而目前的大部分DC/DC变换器输入电压一般在50V以内,一种高压的降压型斩波变换器被研究和使用得越来越广泛。
考虑到降压电路构成简单、成本较低,因此这种变换器具有良好的市场前景。
本文对其原理和高压降压电路应用设计进行了详细地阐述。
降压电路拓扑分析图1是降压拓扑的电路图。
当t=0时驱动S导通,电源Uin向负载供电,电感电流iL线性上升。
当t=ton时控制S关断,二极管VD续流,电感电流呈线性下降。
图1:降压拓扑电路图。
根据电感电流是否连续,可分为连续电流模式(CCM)、不连续电流模式(DCM)和临界电流模式(BCM或CRM或TM)。
通常串接较大电感L使负载电流连续且纹波小。
但是小功率SMPS中为了减小噪声以及损耗,通常选定电感电流不连续模式(DCM)。
CCM和DCM下的各参数波形如图2所示。
图2:CCM和DCM下主要参数波形。
1. BCM和CCM设IL为iL的平均值,△iL是iL的纹波值。
则在BCM和CCM模式下:稳态时:又从(3)和(4)得:从(1)、(2)和(5)得:在CCM下, (5)取>号在BCM下, (5)取等号, ==> L=R*Ts*(1-D)/22. DCM设图2中t1处iL=0,且a=(t1-ton)/Ts=t1/Ts-D。
则稳态时 L上电压开关周期平均值为0:C在开关周期内电流平均值为0:iL的平均值:IL=△iL*(D+a)/2<△iL/2Load电流: Io=Uo/R根据(7)、(8)和(4)得: 0.5*[(Uin-Uo)/L]*D*Ts*[Uin*D/Uo]=Uo/R且: K=2*L/(D2*Ts*R)=2/(D2*x), x=Ts*R/L, y=Uo/Uin。
图3:各模式下Uo/Uin的比值变化图。
DCM-CCM 临界控制的APFC电路设计规范

DCM/CCM 临界控制的APFC电路设计规范2000年6月22日发布 2000年6月22日实施深圳市安圣电气有限公司前言本规范于2000年6月22日首次发布。
本规范起草单位:二次/工业电源研究部、研究管理部技术管理处本规范执笔人:高拥兵本规范主要起草人:赵林冲、朱品华、李晓、董晓鹏本规范标准化审查人:刘善中本规范批准人:华麟本规范修改记录:更改信息登记表目录摘要 (5)缩写词/关键词/解释 (5)1.来源 (5)2.适用范围 (5)3.规范满足的技术指标(特征指标) (5)4.详细电路图 (5)5.工作原理简介 (6)6.设计、调试要点 (7)7.局部PCB版图(可选项) (11)8.元器件明细表(详见附录) (11)9.附录 (13)附录1.元器件明细表 (13)附录2.应用反例(可选项) (15)摘要:本规范介绍了一种DCM/CCM临界连续控制方式的APFC电路,该电路一般应用于中小功率AC/DC电源整流模块中(75W-1000W),作为前置变换器,起输入功率因数校正作用。
关键词:DCM/CCM 临界控制,APFC缩略词解释CCM:Continuous Current Mode,电感电流连续模式DCM:Discontinuous Current Mode ,电感电流断续模式APFC:Active Power Factor Correction,有源功率因数校正1.来源本规范中的电路来源于GSM3.0 AC/DC模块S2T24M1M1单板,已经在GSM3.0 AC/DC模块中得到的批量使用验证,与之相关的外围单元电路有输入EMI电路、后级双管正激DC/DC变换电路。
2.适用范围该单元电路可用于交流输入的中小功率整流模块中(75-1000W),如一次电源10A整流模块,工业电源的GSM3.0和HR项目,UPS的充电器等。
3.规范满足的技术指标(特征指标)本单元电路在GSM3.0 AC/DC电源的PFC 电路得到验证。
ccm dcm 纹波系数

ccm dcm 纹波系数
在CCM(连续导通模式)和DCM(非连续导通模式)中,纹波系数是一个重要的参数。
纹波系数定义为电感电流的纹波与平均电感电流的比值。
在电感电流波形中,由于电压波形是脉动矩形,电感电流将呈三角形,具有一定的直流电平。
当纹波系数小于2时,转换器以连续导通模式(CCM)运行,否则以非连续导通模式(DCM)运行。
在合适的降压转换器设计中,CCM工作在满载时更为理想,因为它在功率半导体中具有较低的电流应力。
对于CCM模式反激变换器,设计时KRF(电流纹波系数)<1,此时,KRF 的取值会影响到初级电流的均方根值(RMS)。
对于DCM模式变换器,设计时KRF=1。
此外,在经验上,电感的电流纹波总是设计为平均电感电流的30%左右。
如需更多关于CCM和DCM的信息,建议请教电子工程专家或查阅相关文献资料。
PFC电路的分类

PFC电路的分类PFC电路按照输入电流的工作情况分为三种模式:CCM电流连续型,DCM电流不连续性和介于两者之间的是TCM临界性。
1.CCM(continuouscurrentmode)电流连续型如下图所示为连续模式的一种类型:平均电流型。
平均连续性PFC变换器开关频率固定,周期T不变,占空比随着输入电压的变化而变化,通过PFC电感器和开关MOSEFT的电流在AC线路电压的半个周期内任何时刻都不为零,而是时刻跟随电压的变化轨迹,其平均电流IAC呈正弦波,且保持和AC输入电压同相位。
根据控制方式不同,除了平均电流型以外,CCM模式还分为峰值电流控制和滞后电流控制,共同的特点就是电流连续,不存在断点。
一般CCM的PFC变换器可以用于250瓦以上的开关电源,工作在CCM模式的PFC变换器有很低的谐波失真度.THD可达到5%以下。
由于其电感电流不会降到零,电感电压变化较小,谐波IIR热损耗较小,有较小的电磁干扰,由于电流的变化幅度小,相比也有较小的磁芯损耗。
同DCM方式相比.CCM模式电路相对复杂,而且由于MOSEFT 导通不在电感电流为零的时候,二极管的反向恢复电流会产生很大的开关应力,损耗不容忽视,因此需要使用价格较高的快速反向恢复二极管以减小损耗。
2.DCM(discontinuouscurrentmode)电流不连续性如下图所示为电流不连续性PFC电路的模式.DCM的特点是利用两个开关周期之间的电感电流存在死区。
和连续性模式相比,电路设计更容易实现,由于其导通的时候电流为零,所以不必考虑升压二极管的反向恢复电流,对二极管的要求比较低。
显而易见,在同样的平均输入电流下,DCM需要较高的峰值电感电流,因而需要选用大的功率器件。
由于其电流变化幅度较大,峰值较高,电感有较大的磁芯.I2R热损耗较大。
谐波失真度THD也比连续型模式的要大,所以电流不连续模式一般只用于相对较小功率的开关电源。
和后面提到的CRM临模式相比,其主要优点是可以固定开关频率以限制最大开关频率.使前端EMI滤波器设计简单化。
20170402-三个基本功率变换器在CCM下的稳态关系
普高(杭州)科技开发有限公式 张兴柱 博士
最基本的 DC-DC 变换器有三个,它们是 Buck 变换器、Boost 变换器和 Buckboost 变换 器。根据电感上电压的稳态伏秒平衡定律,可以方便地推导出这三个基本变换器在 CCM 工 作模式下的稳态输入输出关系。 1:Buck 变换器的稳态电压增益:
1− D
从得到的输出电压与输入电压之稳态增益关系中,可以看出: Buck 变换器最基本的特 性是降压;Boost 变换器最基本的特性是升压;Buckboost 变换器最基本的特性是升降压, 且其输出与输入的极性相反。
这三种稳态电压增益关系,分别代表了三种类别的功率变换器,由它们延伸的各种功 率变换器拓扑,基本上也可以归结为这三大类,即降压型变换器;升压型变换器;升降压型 变换器。
1
为 1 时,且是可以稳定工作的,其原因是在稳态时,因为输出电压和输入电压的相同,导致 每一个开关周期内,在电感上既没有激磁,也没有去磁,所以可以长期稳定工作。
不过在实际的产品应用中,一般都会对其控制的最大占空比设一个限制。目的是防止 元器件的应力过高,和实现变换器的性能最优。
另外当负载为空载时,这三个基本变换器,在某一占空比控制下的工作均是不可能的, 原因是这种情况下的输出电容只有充电,没有放电,导致其安秒的不平衡,结果是使输出电 容上的电压不断升高,最终导致输出电容因电压超过额定值而损坏。
2Ig ASVg NhomakorabeaPS
L
IL
C
2:Boost 变换器的稳态电压增益:
Ig
L
PS
Vg
AS
C
3:Buckboost 变换器的稳态电压增益:
AS
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三个基本功率变换器的CCM/DCM 边界条件
普高(杭州)科技开发有限公式 张兴柱 博士
对于Buck 变换器、Boost 变换器和Buckboost 变换器,在工作点发生变化时,其工作模式也会跟着发生变化,这种变化可用下图来表示:
边界
LP
L I I 21=CCM/DCM
边界
LP L I I 21>
CCM LP
L I I 2
1<DCM
随着负载电流的减小,三个变换器中的电感电流会从黄色的波形,变化到红色的波形。
黄色波形的工作模式,在一个开关周期内只有两个工作间隔,称为CCM ;红色波形的工作模式在一个开关周期内有三个工作间隔,称为DCM 。
在这两个波形之间,有一个兰色的电感电流波形,它的上方是CCM ,它的下方是DCM ,因此兰色波形所对应的工作点,叫做CCM/DCM 的边界工作点。
在CCM/DCM 边界上的这些工作点,是两种模式工作点的特例,因此它们既可以被当作CCM 工作点来看待,也可以被当作DCM 工作点来看待。
1:三个基本变换器的CCM/DCM 边界条件:
L
2: CCM/DCM 边界条件的示意图:
用CCM/DCM 边界波形和电感电压的伏秒平衡定律,可以推导出三个基本变换器的CCM/DCM 边界关系,如上图所示。
从获得的CCM/DCM 边界关系,可以看出,这是一个
方程,方程的左边是占空比的函数,方程的右边是随负载电阻变化而变化的一个变量,与占空比无关,在数学上,可将这三个基本变换器的CCM/DCM 边界方程写成下面的一般形式:
crit K D K =)( (1)
其中R
Lf K s
crit 2=
,是与负载和功率级参数有关的变量; D D K −=1)(,Buck 变换器; 2)1()(D D D K −=,Boost 变换器;
2)1()(D D K −=,Buckboost 变换器。
这个函数与具体的拓扑结构和占空比有关。
如将方程(1)中的两边,均看成是占空比D 的函数,并画在同一张坐标中,则CCM/DCM 边界就可以被理解为是这两个函数的交点,下面是三个基本变换器的这种边界示意图:
D K −=1(
1()(D D K =
1()
(D K −=
Buck 变换器 Boost 变换器 Buckboost 变换器
在CCM/DCM 边界示意图上,如两根曲线有交点,则这个交点(图中红色的点)就是CCM/DCM 边界工作点,而CCM 区间及DCM 区间则可用下面的不等式来判断。
crit K D K >)( 为DCM ; crit K D K <)( 为CCM
非常有趣的是在Boost 变换器中,有两个交点,它们对应了两个CCM/DCM 边界点,这与Buck 变换器和Buckboost 变换器中的情况不同。
在Buck 变换器或者Buckboost 变换器中,当输出电压已经稳定后,输入电压越高(占空比越小),就越容易进入DCM ,反之亦然。
而在Boost 变换器中,随着输入电压的提高(占空比的减小),先会从CCM ,通过CCM/DCM 的第一个边界点进入DCM ,在DCM 工作一段时间后,又会通过CCM/DCM 的第二个边界点进入CCM 。
