有限元分析及应用例子FEM14
CEM_8_FEM_14 频域有限元
CEM-Finite Element Method - 6
8.1.3 Development of FEM (1) • 1851/52: Karl Schellbach, Variational Calculus; Solution of the problem of minimal area • 1868: Kirsch, Modelling of a 3D-continuum with cuboids and beam elements • 1908/09: Walter Ritz, new methods to solve a variational problem (Ritz’ method) • 1915: Boris G. Galerkin, Method of weighted residuals • 1940/41: Alexander Hrennikoff, Beam models, Replacement of plates by lattice • 1956: M. J. Turner, Ray W. Clough, H. C. Martin, L. J. Topp, Stiffness and deflection analysis of complex structures (first structural calculation of airplane wings at Boing, first computer aided application of FEM) Larissa Vietzorreck CEM-Finite Element Method - 7
Computational Methods for Electromagnetics Chapter 8: Finite Element Method (FEM)
2-杆系统-FEM2012本科双语有限元法PPT-2014(哈工程中文版)
2.2 有限元表达式
T 1 cos sin 0 0 sin cos 0 0 0 0 cos sin 0 0 sin cos
f u T 1 F KT 1U
F TKT 1U
sin cos sin 2 sin cos sin 2 cos2 sin cos cos2 sin cos sin cos U iX sin 2 U iY sin cos U jX 2 U sin jY
整体坐标下的载荷和局部坐标下的载荷同理:
FiX f ix cos f iy sin
FiY f ix sin f iy cos
FjX f jx cos f jy sin
F Tf
FjY f jx sin f jy cos
Harbin Engineering University
K (G )
0 0 0 1.49
0 1.49 1.49 0 0 0 0 0 4.22 0 1.49 1.49 0 1.49 1.49
5. 施加载荷和约束条件
约束条件: 载荷:
U1X 0 U1Y 0 U 3 X 0 U 3Y 0
F4Y 500lb, F5Y 500lb
前处理
1. 离散化成节点和单元
单元element 单元节点Element nodes 整体节点System nodes
(1) i, j 1, 2 0
(2) i, j 2, 3 135
(3) i, j 3, 4 0
(4) i, j 2, 4 90
(5) i, j 2, 5 45
(6) i, j 4, 5 0
通过FEM分析找出圆形自由锻造的最优方法
通过FEM分析找出圆形自由锻造的最优方法S.K.Choi,M.S.Chun,C.J.Van Tyne,Y.H. Moon摘要：三维刚塑性有限元分析法FEM分析法已经被用来优化圆形制品的自由铸造。
当自由铸造圆形制品时，我们很难在工业环境中通过反复试验的方法获取最佳的工艺参数。
在本课题中，我们用FEM分析法来分析测试的自由铸造，我们应该关注通过设计实验何种进料速率和旋转角能得到最优铸造。
进料速率和旋转角的最优组合取决于制品的纵向方向和圆度上的量化圆径剖面。
通过对实验结果的分析，通过自由铸造法可以使最佳的工艺条件被用来获得圆形制品的最好的尺寸精度。
关键词：FEM；自由锻造；圆棒料；进给率；旋转角度1.引言自由铸造是一种金属成型工艺，是当成型毛坯介于平的和一系列简单的褶皱毛边时使用的一种工艺手法。
工件在碰撞间中旋转着打磨着，特别是大型钢型制品中的小件圆柱形刚性制品,如涡轮机转子、轴承、需求量比较大。
为了尽量减小后续加工量,这些大的组件需要在自由锻造的压力下最终变形几何近似。
为了获得满意的变形,在制造这样的大件产品时候，自由铸造工艺只是初始制造步骤。
自由铸造使制品在反复的挤压和交替乱换中减少了制品横截面积并增加了工件的长度。
此工艺是逐步增加式的完成的;每个阶段只有一小部分的工件被处理变化。
这个工具的变形压力的设置时更具制品的弹性模量和弯曲模量来设定的,相比较于大型的批量型生产工艺模具，此工具是比较小的。
在同一时间里段里，部分工件铸造比完全工件铸造负荷小，这种减小负荷量的方法可以让更多的低功能的机械用于处理某些既定的工件部分。
这是一个渐进的工艺过程，最终目标是通过反复的压缩和铸造形成最终的符合要求的形状。
自由锻造质量取决于几个控制参数;例如,模具宽度、模具构型、模具重叠区及模具交错区、钢锭的形状、温度梯度、设计方案,完成时间等。
在先前，已有大量的自由锻造模具的研究课题。
Kiefer和Shah分析了模具宽度比例和高度减少之间的对使用模具的影响。
有限元法(FEM)简介
EA ( − cosθ sin θ u1 − sin 2 θ v1 + cosθ sin θ u2 + sin 2 θ v2 ) + EA ( v2 − v3 ) l1 l2
节点3的x方向 节点3的y方向
Fx 3 = Rx23 = 0 EA 2 Fy 3 = Ry 3 = ( −v2 + v3 ) l2
u12=1，u11= v11= v12= 0
EA R = k13 = − cos 2 θ l1
1 x1
v12=1，u11= v11= u12= 0
R11 = k14 = − x R11 = k24 = − y
1 Rx 2 = k34 =
EA cos θ sin θ l1 EA 2 sin θ l1
EA R = k23 = − cos θ sin θ l1
写成矩阵形式
R11 cos 2 θ x 1 Ry1 EA cos θ sin θ 1 = Rx 2 l1 − cos 2 θ R1 2 − cos θ sin θ y cos θ sin θ sin 2 θ − cos θ sin θ − sin 2 θ − cos 2 θ − cos θ sin θ cos 2 θ cos θ sin θ
EA ( cosθ sin θ u1 + sin 2 θ v1 − cosθ sin θ u2 − sin 2 v2 ) l1
EA ( − cos2 θ u1 − cosθ sin θ v1 + cos2 θ u2 + cosθ sin θ v2 ) l1
节点2的y方向
2 Fy 2 = R1 2 + Ry 2 = y
92049-有限元法-FEM1404
(1)
(2)
Fig.2.13 A triangle and the area coordinate system
2
General Procedure of Finite Element Method
Definition of Area Coordinates
i - the area of triangle formed by the points p, j and m j - the area of triangle formed by the points p, m and i
also the shape functions, i.e.,
Li Ni (i, j, m)
(2.54)
Shape Function Matrix for a 3-node triangle element
N
Ni 0
0 Ni
Nj 0
0 Nj
Nm 0
0 Nm
Li
0
0 Li
Lj 0
0 Lj
i will vary from zero to as point p moves from side jm to
node i. In other words, the ratio Li varies from 0 to 1.
4
General Procedure of Finite Element Method
a) Integration over the area of a triangle ( )
Lai Lbj LcmdA
(a
a!b!c! bc
2 2)!
(2.59)
where a, b and c are constant integers(整常数) and a! is a
有限元分析在工程设计中的应用案例分析
有限元分析在工程设计中的应用案例分析有限元分析，简称FEA（Finite Element Analysis），是一种利用数值计算方法对复杂结构进行力学分析的技术。
它基于物理学原理，利用离散化方法将连续的结构在有限元上分解成多个互相联系但是局部地独立的单元，再通过数学算法进行求解，最终得到整个结构的力学行为。
因为它可以减少试错周期、降低开发成本和提高产品性能，所以有限元分析已经成为当今工程设计和生产领域一项非常重要的技术。
本文将介绍一些有限元分析在工程设计中的具体应用案例。
1.汽车发动机壳体优化汽车发动机壳体是承载引擎所有关键部件的重要结构，其制造复杂度很高。
为了减少开发过程中的试验成本和时间,一家风机厂专门利用有限元分析技术对汽车发动机壳体进行优化设计。
更改前发动机壳体在经过一定的较高频振动时会存在密封性能下降的现象，需要进行加强设计。
利用有限元分析技术，他们对发动机壳体进行了动力学分析，并计算了各部位的振动位移和应力分布，通过不断地修改控制点的位置和形状来提高振动阻尼性能和密封性能。
最终确定了优化方案，成功地减少了振动，提高了发动机壳体的防震性能和密封性能。
2.建筑物钢框架分析建筑物钢框架是建筑结构的重要组成部分，其承载能力和组装结构设计都需要严格控制。
如何选取更好的工艺和材料来设计出更安全可靠的钢框架结构，被许多建筑设计公司所思考。
有限元分析技术的应用可以帮助工程师确定结构的承载能力，最大应力极限和变形情况，进而实现结构的优化。
一家建筑设施的设计公司利用有限元分析技术来优化钢框架的结构，计算具体承载状况，最终确定钢框架结构的有效设计方案。
这一个优化设计方案进一步增强了建筑物钢框架的承载能力，提高了项目的整体优势性。
3.飞机负荷分析航空工业是重要的现代国家产业之一。
飞机设计、测试和生产都需要极高的准确性，而这需要大量的场地、人力和物资投入。
一家工程公司成功地利用有限元分析技术对飞机进行负荷分析并评估整体结构的强度和刚度。
有限元分析实例
有限元分析实例引言有限元分析（Finite Element Analysis，简称FEA）是一种工程分析方法，能够将连续体结构分割成有限个小单元，通过在每个小单元内建立方程模型，最终求解整个结构的力学行为。
本文将以一个实例来介绍有限元分析的基本过程和步骤。
实例背景我们将以一个简单的杆件弯曲问题为例来进行有限元分析。
假设有一根长度为L、截面积为A的杆件，材料的弹性模量为E，截面的转动惯性矩为I。
我们希望通过有限元分析来计算杆件在一定加载条件下的弯曲变形。
有限元网格的划分首先，我们需要将杆件划分成有限个小单元，即有限元网格。
常用的网格划分方法有三角形划分、四边形单元划分等。
根据具体问题的要求和复杂度，选择合适的划分方法。
单元的建立划分好网格后，我们需要在每个小单元内建立方程模型。
在弯曲问题中，常见的单元模型有梁单元、壳单元等。
在本实例中，我们选择梁单元作为杆件的单元模型。
对于梁单元，我们需要定义每个节点的位移和约束条件。
根据杆件的几何尺寸和材料属性，可以利用应变能量原理和几何相似原理，得到每个节点的位移和约束条件。
材料特性和加载条件的定义在进行有限元分析之前，我们需要定义材料的特性和加载条件。
对于本实例中的杆件，我们需要定义弹性模量E、截面积A和转动惯性矩I。
加载条件可以包括集中力、均布力、弯矩等。
在本实例中，假设杆件受到均布力，即沿杆件轴向的受力分布是均匀的。
单元方程的建立和求解在定义了材料特性和加载条件之后，我们可以根据每个梁单元的位移和约束条件，建立每个单元的方程模型。
常见的方程模型有刚度矩阵方法、位移法等。
根据所选的单元模型，选择合适的方程模型进行计算。
通过对每个单元的方程模型进行组装，我们可以得到整个结构的方程模型。
将加载条件带入，可以求解出整个结构在给定加载条件下的位移、应力等参数。
结果分析根据求解得到的位移信息，我们可以绘制出结构的变形图。
通过变形图，可以直观地观察到结构在弯曲条件下的变形情况。
有限元分析及应用例子FEM14
有限元分析及应用例子FEM14有限元分析及应用例子FEM14有限元分析（Finite Element Analysis, FEA）是一种数值计算的方法，用于求解工程结构中的各种物理问题。
它将结构分割成有限个小单元，通过计算每个单元的行为来推断整体结构的行为。
下面将介绍有限元分析的原理，并举例说明其在实际应用中的使用情况。
有限元分析的原理是将复杂的结构问题转化为一系列简单的数学模型，通过数学方法求解这些模型的行为来预测整体结构的行为。
具体而言，有限元分析的步骤包括对结构进行离散化、建立有限元模型、确定边界条件、计算求解和分析结果。
举例来说，假设我们希望研究一根悬臂梁的变形和应力分布。
首先，我们将梁划分成若干个小单元，如梁单元。
然后，我们需要为每个单元定义适当的数学模型来描述其行为。
对于梁单元而言，可以使用简化的梁理论或柔性梁解来建立数学模型。
接下来，我们需要确定边界条件，如悬臂梁的杆端固定，另一端加载一定的力。
然后，通过求解各个单元的行为，并结合边界条件，我们可以计算整个梁的变形和应力分布。
最后，我们可以根据求解结果，分析梁的承载能力，优化设计以及进行结构改进。
1.结构力学：有限元分析可用于预测建筑物、桥梁、飞机和汽车等结构的应力分布和变形情况，以评估结构的安全性和稳定性。
例如，可以通过有限元模拟来确定一个钢梁在承受一定荷载后的变形和应力情况，以保证其设计的合理性。
2.流体力学：有限元分析可以用于模拟流体在管道、容器或其他结构中的流动情况。
例如，可以通过有限元分析预测液体或气体在流体力学系统中的流动速度和压力分布，并优化系统设计。
3.热传导：有限元分析可以用于计算热传导过程中的温度分布和热流情况。
例如，可以通过有限元分析来优化热交换器的设计，以提高传热效率。
4.振动分析：有限元分析可以用于模拟结构在受到激励时的振动情况。
例如，可以通过有限元分析来研究机械系统中的固有频率和模态形状，以减少振动和噪声。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
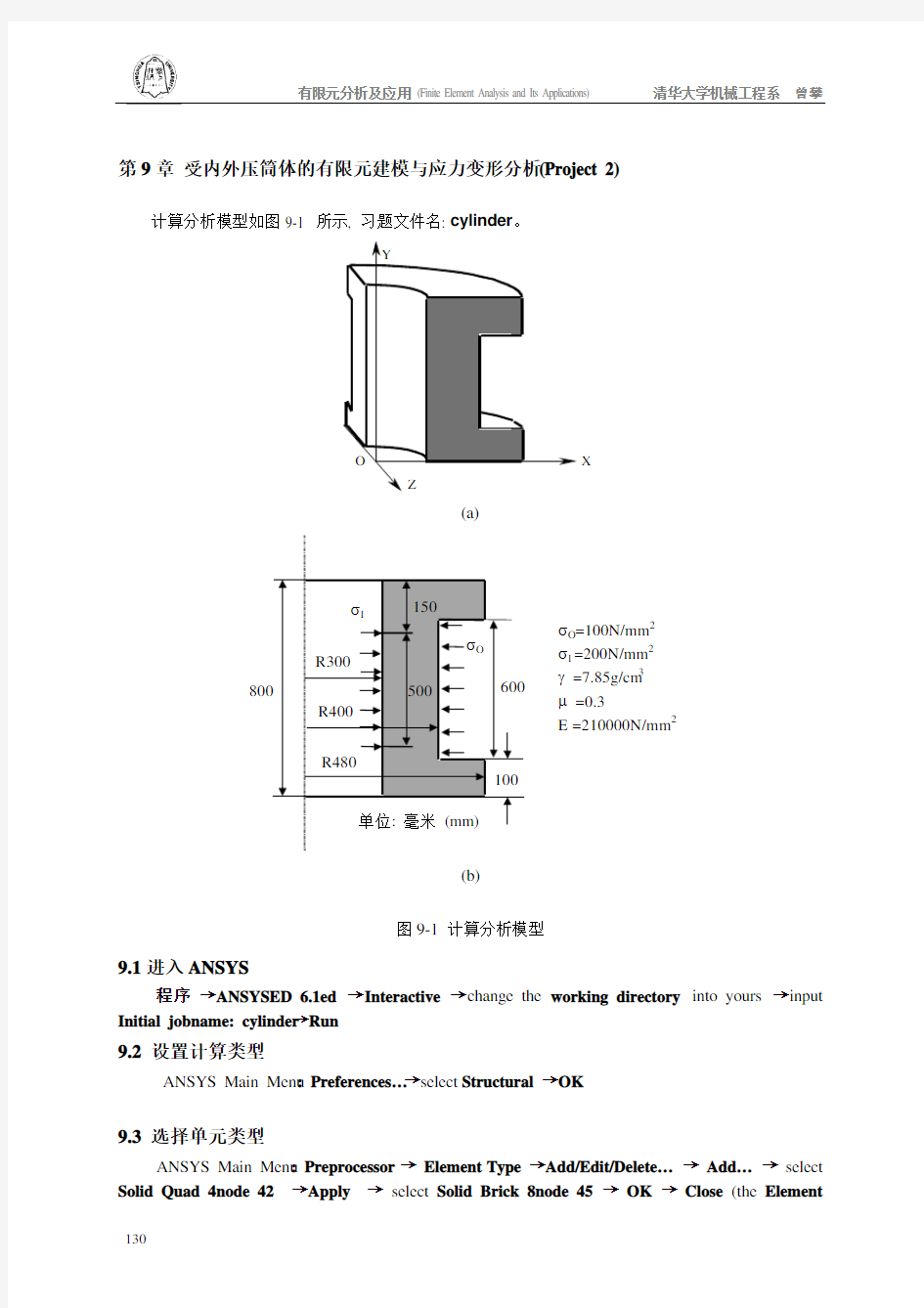
第9章受内外压筒体的有限元建模与应力变形分析(Project 2)计算分析模型如图9-1 所示, 习题文件名: cylinder。
X(a)σO=100N/mm2σI =200N/mm2γ =7.85g/cm3µ =0.3E =210000N/mm2(b)图9-1 计算分析模型9.1进入ANSYS程序→ANSYSED 6.1ed →Interactive →change the working directory into yours→input Initial jobname: cylinder→Run9.2 设置计算类型ANSYS Main Menu: Preferences…→select Structural →OK9.3 选择单元类型ANSYS Main Menu: Preprocessor → Element Type →Add/Edit/Delete… → Add… →select Solid Quad 4node 42 →Apply →select Solid Brick 8node 45 → OK → Close (the ElementTypes window)9.4定义材料参数ANSYS Main Menu: Preprocessor →Material Props →Materials Models →Structural→Lineal →Elastic→Isotropic…→input EX:2.1e5, PRXY:0.3→ OK 关闭材料定义窗口9.5构造筒体模型➊生成模型截平面ANSYS Main Menu: Preprocessor →Modeling→Create →Keypoints →In Active CS… →按次序输入横截平面的十个特征点和旋转对称轴上两点坐标（十个特征点：(300,0,0), (480,0,0), (480,100,0), (400,100,0), (400,700,0), (480,700,0), (480,800,0), (300,800,0), (300,650,0), (300,150,0)，对称轴上两点：(0,0,0), (0,800,0)）（每次输入完毕，用Apply结束，0可以不输入）→Cancel (back to Create window) →-Areas- Arbitrary → Through KPs →依次连接截面边线上的十个特征点(注意在选完第10点后结束，不要再选第1点)→ OK➋对平面进行网格划分ANSYS Main Menu: Preprocessor →Meshing→Mesh Tool →(Size Controls) Globl: Set →input SIZE (element edge length): 50 →OK (back to MeshTool window)→Mesh → Pick All (in Picking Menu) → Close( the MeshTool window)➌用旋转法生成筒体模型ANSYS Main Menu: Preprocessor →Modeling→Operate →Extrude→Elem Ext Opts→select TYPE:SOLID 45→Element sizing options for extrusion No. Elem divs: 1→OK (back to Extrude window)→Areas →About Axis →Pick All(in Picking Menu)→OK→Pick the two keypoints (11,12) of the Symmetrical Axis → OK→input ARC: 90; NSEG: 3→ OK9.6 模型加位移约束ANSYS Main Menu: Solution→Define Loads →Apply→Structural→Displacement➊两截面分别加Z, X方向的约束ANSYS Utility Menu: Select → Entities…→Nodes → By Location →select X coordinates →input 0→ OK (back to Displacement window)→On Nodes → Pick All(in Picking Menu) → select Lab2:UX →OK →ANSYS Utility Menu: Select → EverythingANSYS Utility Menu: Select → Entities…→ Nodes → By Location →select Z coordinates →input 0→ OK (back to Displacement window)→On Nodes →Pick All(in Picking Menu) → select Lab2:UZ →OK →ANSYS Utility Menu: Select →Everything➋底面加Y方向的约束ANSYS Utility Menu: Select → Entities… → Nodes → By Location →select Y coordinates →input 0→ OK (back to Displacement window)→On Nodes →Pick All(in Picking Menu) →select Lab2:UY → OK →ANSYS Utility Menu: Select →Everything9.7 模型加载荷ANSYS Main Menu: Solution→ Define Loads→Apply→Structural→Pressure →On Areas →pick the Internal Load Surface of model (Total 6 areas) → OK→input V ALUE:200 → Apply →(忽略警告信息)pick the External Load Surface of model → OK→input V ALUE:100→ OK9.8 分析计算ANSYS Main Menu: Solution→ -Solve- Current LS→OK (to close the Solve Current Load Step window)9.9 结果显示ANSYS Main Menu: General Postproc →Plot Results→Deformed Shape…→select Def + Undeformed→OK (back to Plot Results window)→ -Contour Plot- Nodal Solu…→select: Stress, Von Mises, Def + Undeformed→OK9.10 退出系统ANSYS Utility Menu: File→Exit…→ Save Everything→OK9.11完全的直接命令输入方式操作finish !finish the last case/clear,start !restart/prep7 !preprocessoret,1,plane42 !define the elementset,2,solid45mp,ex,1,210000 !define materials parametersmp,prxy,1,0.3k,1,300,,, !define key points of section framek,2,480,,,k,3,480,100,,k,4,400,100,,k,5,400,700,,k,6,480,700,,k,7,480,800,,k,8,300,800,,k,9,300,650,,k,10,300,150,,k,11,,,, !define key points of revolving axisk,12,,800,0a,1,2,3,4,5,6,7,8,9,10 !link the key points to an areaesize,50,, !define element edge lengthamesh,all !meshing the areatype,2 !define the following element typeextopt,esize,1,0 !define element division number when extruding vrotat,all,,,,,,11,12,90,3 !extrude (sweep) the area with meshes/solution !define the load and run this casensel,s,loc,x,0 !select all nodes whose x coordinate are 0d,all,ux,0 !constrain the node's x DOFallsel,allnsel,s,loc,z,0 !select all nodes whose z coordinate are 0d,all,uz,0 !constrain the node's z DOFallsel,allnsel,s,loc,y,0 !select all nodes whose y coordinate are 0d,all,uy,0 !constrain the node's y DOFallsel,allsfa,10,1,pres,200 !define pressure on the inner area of cylinder sfa,21,1,pres,200sfa,32,1,pres,200sfa,5,1,pres,100 !define pressure on the outter area of cylinder sfa,16,1,pres,100sfa,27,1,pres,100solve !runfinish/view,1,1,2,3/post1 !postprocessorplnsol,s,eqv,0,1 !plot the contour of von-Mises stressfinish !end。