年四川省对口高考数学试题
四川省2024年普通高校对口招生统一考试数学试卷(含答案) (6)
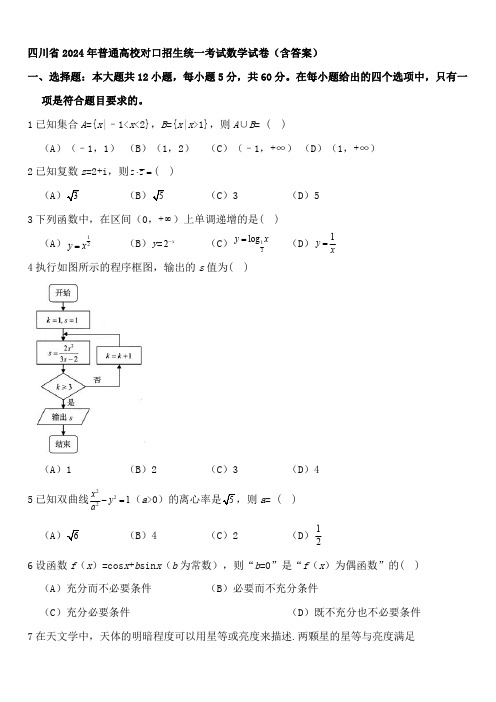
四川省2024年普通高校对口招生统一考试数学试卷(含答案)一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1已知集合A ={x |–1<x <2},B ={x |x >1},则A ∪B =()(A)(–1,1)(B)(1,2)(C)(–1,+∞)(D)(1,+∞)2已知复数z =2+i,则z z ⋅=()(C)3(D)53下列函数中,在区间(0,+∞)上单调递增的是()(A)12y x=(B)y =2x-(C)12log y x=(D)1y x=4执行如图所示的程序框图,输出的s 值为()(A)1(B)2(C)3(D)45已知双曲线2221x y a-=(a ,则a =()(B)4(C)2(D)126设函数f (x )=cos x +b sin x (b 为常数),则“b =0”是“f (x )为偶函数”的()(A)充分而不必要条件(B)必要而不充分条件(C)充分必要条件(D)既不充分也不必要条件7在天文学中,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足212152–lg E m m E =,其中星等为k m 的星的亮度为k E (k =1,2).已知太阳的星等是–26.7,天狼星的星等是–1.45,则太阳与天狼星的亮度的比值为()(A)1010.1(B)10.1(C)lg10.1(D)10.110-8如图,A ,B 是半径为2的圆周上的定点,P 为圆周上的动点,APB ∠是锐角,大小为β.图中阴影区域的面积的最大值为()(A)4β+4cos β(B)4β+4sin β(C)2β+2cos β(D)2β+2sin β9.已知各项均为正数的等比数列{a n }的前4项和为15,且a 5=3a 3+4a 1,则a 3=()A.16B.8C.4D.210.已知曲线e ln xy a x x =+在点(1,a e)处的切线方程为y =2x +b ,则()A.a=e,b =-1B.a=e,b =1C.a=e -1,b =1D.a=e -1,1b =-11.(5分)已知椭圆C:=1(a>b>0)的左、右顶点分别为A 1,A 2,且以线段A 1A 2为直径的圆与直线bx﹣ay+2ab=0相切,则C 的离心率为()A.B.C.D.12.(5分)已知函数f(x)=x 2﹣2x+a(e x﹣1+e ﹣x+1)有唯一零点,则a=()A.﹣B.C.D.1二、填空题13.(5分)已知向量=(﹣2,3),=(3,m),且,则m=.14.(5分)双曲线(a>0)的一条渐近线方程为y=x,则a=.15.(5分)△ABC 的内角A,B,C 的对边分别为a,b,c,已知C=60°,b=,c=3,则A=.16.(5分)设函数f (x)=,则满足f (x)+f (x﹣)>1的x 的取值范围是.三、解答题17.(本题满分12分)已知函数)1,0()(≠>+=b b b a x f x的图象过点)4,1(和点)16,2(.(1)求)(x f 的表达式;(2)解不等式23)21()(xx f ->;(3)当]4,3(-∈x 时,求函数6)(log )(22-+=x x f x g 的值域.18.(本题满分12分)设)(x f 是定义在),0(+∞上的增函数,当),0(,+∞∈b a 时,均有)()()(b f a f b a f +=⋅,已知1)2(=f .求:(1))1(f 和)4(f 的值;(2)不等式2()2(4)f x f <的解集.19.(12分)如图四面体ABCD 中,△ABC 是正三角形,AD=CD.(1)证明:AC⊥BD;(2)已知△ACD 是直角三角形,AB=BD,若E 为棱BD 上与D 不重合的点,且AE⊥EC,求四面体ABCE 与四面体ACDE 的体积比.20.(12分)在直角坐标系xOy 中,曲线y=x 2+mx﹣2与x 轴交于A、B 两点,点C 的坐标为(0,1),当m 变化时,解答下列问题:(1)能否出现AC⊥BC 的情况?说明理由;(2)证明过A、B、C 三点的圆在y 轴上截得的弦长为定值.21.(12分)已知函数f(x)=lnx+ax 2+(2a+1)x.(1)讨论f(x)的单调性;(2)当a<0时,证明f(x)≤﹣﹣2.[选修4-4:坐标系与参数方程]22.(10分)在直角坐标系xOy 中,直线l 1的参数方程为,(t 为参数),直线l 2的参数方程为,(m 为参数).设l 1与l 2的交点为P,当k 变化时,P 的轨迹为曲线C.(1)写出C 的普通方程;(2)以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,设l 3:ρ(cosθ+sinθ)﹣=0,M 为l 3与C 的交点,求M 的极径.[选修4-5:不等式选讲]23.已知函数f(x)=|x+1|﹣|x﹣2|.(1)求不等式f(x)≥1的解集;(2)若不等式f(x)≥x 2﹣x+m 的解集非空,求m 的取值范围.四川省2024年普通高校对口招生统一考试数学试卷(含答案)一、选择题:本大题共12小题,每小题5分,共60分。
2018-2021四川对口升学数学历年真题(含部分答案)

四川省2018年普通高校职教师资班和高职班对口招生统一考试数 学本试题卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)㊂第Ⅰ卷1 3页,第Ⅱ卷3 4页,共4页㊂考生作答时,须将答案答在答题卡上,在本试题卷㊁草稿纸上答题无效㊂满分150分㊂考试时间120分钟㊂考试结束后,将本试题卷和答题卡一并交回㊂第Ⅰ卷(共60分)注意事项:1.必须使用2B 铅笔在答题卡上将所选答案对应的标号涂黑㊂2.第Ⅰ卷共1大题,15小题,每小题4分,共60分㊂一㊁选择题(本大题共15小题,每小题4分,共60分㊂在每小题列出的四个选项中,只有一个是符合题目要求的)1.设集合A ={a ,b },B ={b ,c },则A ɘB =A.⌀B .{b }C .{a ,c } D.{a ,b ,c }2.s i n 2π+π6æèçöø÷=A.32B .-32C .12D.-123.函数f (x )=1x -1的定义域是A.(1,+ɕ)B .(-ɕ,1)C .(-ɕ,1)ɣ(1,+ɕ) D.(-ɕ,+ɕ)4.已知平面向量a =(2,0),b =(1,-1),则a ㊃b =A.2B .1C .0 D.-15.函数y =s i n x c o s 2x2-s i n x 2æèçöø÷的最小正周期是A.2πB .πC .π2D.π46.一元二次不等式x 2-1<0的解集为A.(-ɕ,-1)ɣ(1,+ɕ)B .(-ɕ,-1]ɣ[1,+ɕ)C .(-1,1) D.[-1,1]7.过点(2,0)且与直线2x +y -2=0平行的直线方程是A.2x +y -4=0B .2x -y +4=0C .x +2y -4=0D.x -2y +4=08.双曲线x 24-y 29=1的渐近线方程是A.y =ʃ49xB .y =ʃ94xC .y =ʃ23x D.y =ʃ32x9.设a ,b 均为大于0且不等于1的常数,对数函数f (x )=l o g a x 与g (x )=l o g bx 在同一直角坐标系中的大致图象如图所示,则下列结论正确的是A.0<b <1<a B .0<a <1<b C .0<b <a <1 D.1<b <a 10.某商场对使用移动支付的客户发放问卷,调查用户偏好等内容,共有2000名使用移动支付的客户参与了本次调查.用x (单位:岁)表示客户的年龄,参与了本次调查的客户中,x ɤ30的有1600人,30<x ɤ40的有300人,40<x ɤ50的有60人,x >50的有40人.采用分层抽样的方法,从参与了本次调查的客户中抽取容量为500的样本,则x ɤ30的客户应抽取的人数为A.100B .200C .300 D.40011.某公司销售一种商品的利润L (单位:百元)是销售量x (件)的函数,且L (x )=-x 2+200x -100(0<x <190),则该公司销售这种商品的最大利润是A.900百元B .990百元C .9900百元D.9990百元2.设a ,b ,c ɪR ,则a >b 是a c 2>b c 2的A.充分且不必要条件B .必要且不充分条件C .充要条件 D.既不充分又不必要条件13.l o g 33+l o g 71+2l g 2+l g 25=A.1B .2C .3 D.514.设α,β是两个不同的平面,l ,m 是两条不同的直线.给出下列三个命题:①若l ʅα,m ʅα,则l ʊm ;②若αʊβ,l ʊα,m ʊβ,则l ʊm ;③若l ʊm ,l ʊα,m ʊβ,则αʊβ.其中正确命题的个数是A.0B .1C .2 D.315.若将函数y =s i n 2x -π3æèçöø÷的图象变为函数y =s i n 2x +π2æèçöø÷的图象,则需将第一个函数的图象A.向左平移5π12个单位B .向左平移π12个单位C .向右平移5π12个单位 D.向右平移π12个单位第Ⅱ卷(共90分)注意事项:1.必须使用0.5毫米黑色墨迹签字笔在答题卡上题目所指示的答题区域内作答㊂作图题可先用铅笔绘出,确认后再用0.5毫米黑色墨迹签字笔描清楚㊂答在试题卷㊁草稿纸上无效㊂2.第Ⅱ卷共2大题,11小题,共90分㊂二㊁填空题(本大题共5小题,每小题4分,共20分)16.已知平面向量a=(-1,2),b=(4,2),则|a+b|=.17.二项式(x+2)6展开式中含有x5项的系数为.18.抛物线y2=-4x的准线方程为.19.某变速箱的第1个到第9个齿轮的齿数成等差数列,其中第1个齿轮的齿数是25,第9个齿轮的齿数是57,则第5个齿轮的齿数是.20.已知函数f(x)是定义在R上的奇函数,且对任意xɪR都有(x+2)=f(x).当0<x<1时,f(x)=x+1,则f(-1)+f(0)+f92æèçöø÷=.(用数字作答)三㊁解答题(本大题共6小题,共70分,解答应写出文字说明㊁证明过程或演算步骤) 21.(本小题满分10分)某工厂生产一批商品,其中一等品占45,每件一等品获利20元;二等品占320,每件二等品获利10元:次品占120,每件次品亏损10元.设ξ为任一件商品的获利金额(单位:元) (Ⅰ)求随机变量ξ的概率分布;(Ⅱ)求随机变量ξ的均值.12.(本小题满分12分)在等比数列{a n}中,a6-a4=a5+a4=24,求数列{a n}的通项公式及前n项和S n.23.(本小题满分12分)如图,已知四棱锥P A B C D的底面为正方形,P Dʅ底面A B C D,P D=A D=1,E为线段P B的中点.(Ⅰ)求四棱锥P A B C D的体积;(Ⅱ)证明:B DʅC E.24.(本小题分12分)已知直线l1:x+2y-2=0与直线l2垂直,且直线l2与y轴的交点为A(0,4) (Ⅰ)求直线l2的方程;(Ⅱ)设直线l1与x轴的交点为B,求以A B的中点为圆心并与x轴相切的圆的标准方程.25.(本小题满分12分)已知b,c为实数,函数f(x)=14x2+b x+c,对一切实数x都有f(x-2)=f(x)成立. (Ⅰ)求b的值;(Ⅱ)设F(x)=f(x)-x,不等式f(x)ȡ0与2F(x)ɤ(x-1)2对一切实数x都成立,求c的值.26.(本小题满分12分)在әA B C中,内角A,B,C所又对的边分别为a,b,C.(Ⅰ)设әA B C的面积为S,证明:S=12a b s i n C;(Ⅱ)已知әA B C的面积是1.记u=a2+b2-a b c o s C,证明:uȡ23.四川省2019年普通高校职教师资和高职对口招生统一考试数学试题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
数学2024四川对口升学数学试题

数学2024四川对口升学数学试题数学2024四川对口升学数学试题2024年四川对口升学数学试题,是四川省教育考试院组织命题的一张综合性数学试卷,旨在全面考察学生的数学基础知识和应用能力。
该试卷不仅注重基础知识的掌握,还强调数学应用能力的培养,对于学生的数学思维和解题能力都有一定的要求。
该试卷的命题范围涵盖了初中和高中数学的主要内容,包括数与代数、几何与三角、概率与统计等方面。
其中,数与代数部分主要考察学生的计算能力、方程求解能力、代数式变形能力等;几何与三角部分主要考察学生的几何图形认知能力、三角形性质应用能力等;概率与统计部分主要考察学生的概率计算能力、统计图表解读能力等。
该试卷的题型多样,包括选择题、填空题、计算题、证明题等。
其中,选择题和填空题主要考察学生的基础知识掌握情况,计算题和证明题则注重学生的数学应用能力和思维能力。
以下是根据2024年四川对口升学数学试题的关键词和内容进行撰写的一篇文章:2024年四川对口升学数学试题分析与对策2024年四川对口升学数学试题是四川省教育考试院组织命题的一张综合性数学试卷,旨在全面考察学生的数学基础知识和应用能力。
通过对该试卷的分析,我们可以发现其命题特点、考察重点和应对策略。
首先,该试卷注重基础知识的掌握,几乎涵盖了初中和高中数学的所有内容。
无论是数与代数、几何与三角还是概率与统计,都要求学生扎实掌握基础知识,才能顺利解答题目。
因此,学生在备考过程中要注重对基础知识的复习和巩固。
其次,该试卷强调数学应用能力的培养,通过各种题型的设计,让学生在解题过程中运用数学知识解决实际问题。
这就要求学生在掌握基础知识的同时,还要学会将所学知识应用于实际问题的解决中。
因此,学生在备考过程中要多做练习,提高数学应用能力。
最后,该试卷的难度适中,既考察了学生的基础知识,又充分考虑了学生的实际水平。
因此,学生在备考过程中要认真对待每一道题目,做到举一反三,理解解题思路和方法。
2022-2023学年四川省达州市普通高校对口单招数学自考真题(含答案)

2022-2023学年四川省达州市普通高校对口单招数学自考真题(含答案)班级:________ 姓名:________ 考号:________一、单选题(10题)1.下列命题正确的是()A.若|a|=|b|则a=bB.若|a|=|b|,则a>bC.若|a|=|b丨则a//bD.若|a|=1则a=12.不等式组的解集是()A.{x|0<x<2}B.{x|0<x<2.5}C.{x|0<x<}D.{x|0<x<3}3.设集合,则MS等于()A.{x|x>}B.{x|x≥}C.{x|x<}D.{x|x≤}4.设AB是抛物线上的两点,O为原点,OA丄OB,A点的横坐标是-1,则B点的横坐标为()A.lB.4C.8D.165.已知拋物线方程为y2=8x,则它的焦点到准线的距离是()A.8B.4C.2D.66.已知集合A={1,2,3,4,5,6,7},B={3,4,5},那么=()A.{6,7}B.{1,2,6,7}C.{3,4,5}D.{1,2}7.函数f(x)的定义域是()A.[-3,3]B.(-3,3)C.(-,-3][3,+)D.(-,-3)(3,+)8.若f(x)=4log2x+2,则f⑵+f⑷+f(8)=()A.12B.24C.30D.489.已知等差数列的前n项和是,若,则等于()A.B.C.D.10.下列立体几何中关于线面的四个命题正确的有()(1)垂直与同一平面的两个平面平行(2)若异面直线a,b不垂直,则过a的任何一个平面与b都不垂直(3)垂直与同一平面的两条直线一定平行(4)垂直于同一直线两个平面一定平行A.1个B.2个C.3个D.4个二、填空题(10题)11.12.13.若x<2,则_____.14.15.已知拋物线的顶点为原点,焦点在y轴上,拋物线上的点M(m,-2)到焦点的距离为4,则m的值为_____.16.在锐角三角形ABC中,BC=1,B=2A,则=_____.17.已知一个正四棱柱的底面积为16,高为3,则该正四棱柱外接球的表面积为_____.18.19.在△ABC中,AB=,A=75°,B=45°,则AC=__________.20.等差数列中,a1>0,S4=S9,S n取最大值时,n=_____.三、计算题(5题)21.近年来,某市为了促进生活垃圾的分类处理,将生活垃圾分为“厨余垃圾”、“可回收垃圾”、“有害垃圾” 和“其他垃圾”等四类,并分别垛置了相应的垃圾箱,为调查居民生活垃圾的正确分类投放情况,现随机抽取了该市四类垃圾箱总计100吨生活垃圾,数据统计如下(单位:吨):(1) 试估计“可回收垃圾”投放正确的概率;(2) 试估计生活垃圾投放错误的概率。
2024年四川省对口升学数学试题 以及解析

四川省2024年普通高校对口招生统一考试数学试题第Ⅰ卷(选择题共60分)一、选择题(本大题共15个小题,每小题4分,共60分。
在每小题给出的四个选项中,只有一个是符合题目要求的)1.已知集合{}2,1,0,1,2M =--,{}0,1,2N =,则=M N ⋂().A {}2,1,0--.B {}1,0,1-.C {}0,1,2.D {}2,1,0,1,2--2.函数()()2333x f x log x -=--的定义域是().A ()3,-+¥.B [)3,-+¥.C ()3,+¥.D [)3,+¥3.3090cos cos +=o o ().A 2-.B 12-.C 12.D 24.已知平面向量()2,3=-a ,()2,1=--b ,则=×a b ().A 2-.B 1-.C 1.D 25.不等式122x <-<的解集为().A ()0,4.B (-∞,1)È(4,+∞).C ()1,3.D ()()0,13,4È6.过点()11,且与直线20x y -=垂直的直线的方程是().A 230x y +-=.B 210x y +-=.C 230x y --=.D 210x y --=7.224lg 22lg 4lg 25lg 25++=().A 1.B 2.C 4.D 258.函数()2sin y x ωϕ=+的部分图象如图所示,其中0ω>,2πϕ<,则().A 2sin 26x y π⎛⎫=- ⎪⎝⎭.B 2sin 23x y π⎛⎫=- ⎪⎝⎭.C 2sin 26y x π⎛⎫=- ⎪⎝⎭.D 2sin 23y x π⎛⎫=- ⎪⎝⎭9.已知椭圆()2222103x y m m m+=>的左焦点为()4,0-,则m 的值为().A .B .C 3.D 410.某保险公司为了解购买某险种的1000名投保人的出险次数情况,随机调查了其中100名投保人的出险次数,得到如下表格:出险次数01234³投保人数a 292583则下列结论中正确的是().A 表中a 的值为25.B 调查的这100名投保人的出险次数的均值大于1.C 购买该险种的100名投保人的出险次数是总体.D 估计购买该险种的所有投保人中,出险次数不低于3次的人数为1111.已知0.22a =,0.33b =,20.2c =,则a b c 、、的大小关系为().A a b c >>.B a c b >>.C b a c>>.D b c a >>12.设a R Î,则“1tan α=-”是“34πα=”的().A 充分不必要条件.B 必要不充分条件.C 充要条件.D 既不充分也不必要条件13.一个温度为0T C o 的物体移入恒温a C o 的室内,t 分钟后该物体的温度为T C o .已知T 与t 的关系可以表示为()0kt T a T a e -=+-,其中0k >.现将温度为90C o 的该物体移入恒温10C o 的室内,20分钟后该物体的温度为50C o ,则再过20分钟该物体的温度为.A 10C o .B 20C o .C 30C o .D 40Co 14.设αβγ、、是三个不同的平面,l m 、是两条不同的直线.给出下列四个命题:①若∥a g ,∥b g ,则a b ∥;②若a g ^,b g ^,则a b ∥;③若l ∥a ,m ∥b ,l m ∥,则a b ∥;④若l a g Ç=,m b g Ç=,l m ∥,则a b ∥.其中正确命题的个数是().A 1.B 2.C 3.D 415.已知定义在R 上的函数()f x 满足()()66f x f x -=+.当31x -£<时,()22f x x x =--;当19x £<时,()4f x x =-.则()()()()1232024f f f f +++⋅⋅⋅+=().A 328.B 332.C 336.D 340第Ⅱ卷(非选择题共90分)二、填空题(本大题共5个小题,每小题4分,共20分)16.已知抛物线22y px =过点()3,6,则p =.17.若5(2+)x a 的展开式中2x 的系数为320-,则a =.18.某植物的快速生长期约有10天,在此期间该植物每天结束时的高度都为前一天结束时的高度的2倍.已知在快速生长期的第4天结束时,该植物的高度是20毫米,那么它在第7天结束时的高度为毫米.19.已知函数()()ln 11b f x x a x ⎛⎫=++ ⎪+⎝⎭是偶函数,其中,a b ∈R ,则a b -=.20.已知平面向量,a b 满足3=a ,1=b ,则++-a b a b 的最大值是.三、解答题(本大题共6个小题,共70分.解答应写出文字说明、证明过程或演算步骤)21.(本小题满分10分)为弘扬中华优秀传统文化,某学校将开展传统文化知识竞赛.已知该学校的文学、朗诵、书画、戏曲4个社团的人数分别为140,112,56,28,且每个社团的成员都只参加了1个社团.竞赛组委会拟采用分层抽样的方法从以上4个社团中抽取12名同学担任志愿者.(1)求应从这4个社团中分别抽取的志愿者人数;(2)若从抽取的12名志愿者中随机抽取3名担任竞赛分数统计员,求抽取的3名统计员中恰有2名来自同一社团的概率.22.(本小题满分12分)已知ABC ∆的内角,,A B C 的对边分别为,,a b c ,且23sin sin 2122A A π⎛⎫++= ⎪⎝⎭.(1)求角A 的大小;(2)若cos sin c b A B =+,证明:ABC ∆为直角三角形.23.(本小题满分12分)如图,已知四棱锥P ABCD -的底面为长方形,PA ABCD ⊥底面,1AB PA ==,AD =E 为BC 的中点.(1)证明:PE BD ⊥;(2)求二面角P BD A --的正切值.24.(本小题满分12分)设数列{}n a 的前n 项和n S 满足:()121n n S n a +=+,且321S =.(1)求数列{}n a 的通项公式;(2)求数列12n S n ⎧⎫⎨⎬+⎩⎭的前n 项和n T .25.(本小题满分12分)设a ∈R ,函数()2335f x x ax a =-+-.(1)设函数()f x 的图象与x 轴相交于A B 、两点,且2153AB =,求a 的值;(2)若()0f x <对任意的[]1,1a ∈-恒成立,求实数x 的取值范围.26.(本小题满分12分)设k ∈R ,过定点A 的动直线240kx y k --+=和过定点B 的动直线0x ky +=相交于点M .(1)求定点A B 、的坐标,并求点M 的轨迹方程;(2)求MA +的最大值.四川省2024年普通高校对口招生统一考试数学试题相关解析第Ⅰ卷(选择题共60分)一、选择题(本大题共15个小题,每小题4分,共60分。
2020年四川对口升学数学样题3

2020年四川普通高校职教师资和高职班对口招生统一考试数学样题(3)本试题卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷第1~2页,第Ⅱ卷第3~4页,共4页。
考生作答时,须将答案答在答题卡上,在本试题卷、草稿纸上答题无效。
满分150分,考试时间120分钟。
考试结束后,将本试题卷和答题卡一并交回。
第Ⅰ卷(选择题 共60分)注意事项:1.选择题必须使用2B 铅笔在答题卡上将所选答案对应的标号涂黑。
2.第I 卷共1个大题,15个小题。
每个小题4分,共60分。
一、选择题:(本大题共15个小题.每小题4分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1. 已知R U =,{}|||1A x x =<,{}032|2<--=x x x B ,则A B I = ( ) A.{}31|≥<x x x 或 B.{}11|<<-x x C. {}31|≤≤-x x D. {}11|≤<-x x2.已知θθ2cos ,21cos 则== ( ) A .21- B .23- C .23 D .21 3.在等比数列{}n a 的前n 项的和n S ,2112s s =,则公比q= ( ) A. 5.0 B. 5.0- C. 2 D. 2-4.在直角坐标系中,直线033=--y x 的倾斜角是 ( )A .030B .060C .0120D .0150 5.已知53cos -=α,且α是第三象限角,则=-)2cos(απ ( ) A .53 B .54- C .54 D .53- 6.已知)(x f 1()42x =+(R x ∈),则(2)f -= ( ) A .8- B .0 C .4 D .8 7.已知向量)1 ,5( ),3 ,3(--=-=则=21 ( ) A .)2,1( B .)2,1(-C .)1,4(-D .)1,4(- 8.在等差数列{n a }中,4a 、10a 是方程0462=--x x 的两根,则7a = ( )A .6B .3C .6-D .3-9.若直线0=++m y x 与圆122=+y x 相切,则m 为 ( )A .2B . 2±C . 2-D .210.双曲线2213x y m m-=的一个焦点是(2,0),则m 的值是 ( ) A .1 B .1- C .2 D .2-11.在ABC ∆中,的长为则边c A b a ,30,15 ,5 === ( )A .52B .5C .52或5D .以上都不对 12.下列命题正确的是 ( )A .函数x y -=3在),(+∞-∞上是增函数B .函数x xy -+=11的定义域为x≤1 C .函数x x y sin =是奇函数 D .函数)32sin(π+=x y 的最小正周期为л13.四名学生报名参加三个项目的比赛,每项只准一人参加,则不同报名方法数为 ( )A .34CB .34AC .43D .3414.若抛物线()220y px p =>过点M )(4,4,F 是焦点,则=MF ( ) A .5 B .4 C .3 D .215.二项式n x )2(+的展开式中所有项的系数和是729,此展开式中含4x 的系数是 ( )A .30B . 60C .120D . 240 第Ⅱ卷(非选择题 共90分)注意事项:1.非选择题必须使用0.5毫米黑色墨迹签字笔在答题卡上题目所指示的答题区域内作答。
四川省中职类2024单招数学试题以及参考答案

四川省2024年普通高等学校高职教育单独招生文化考试(中职类)·数学试题第Ⅰ卷(选择题共50分)一、单项选择题(本大题共10小题,每小题5分,共50分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其选出。
错选、多选或未选择均无分。
1.已知集合{}4224M ,,,=--,N 为自然数集,则M N Ç=().A Æ.B {}2,4.C {}4,2--.D {}4,2,2,4--2.已知平面向量()3,2a =-,()2,4b =-,则a b +=().A ()1,0-.B ()1,2-.C ()1,0.D ()1,23.函数12y x =+的定义域是().A ()2,-+∞.B ()(),22,-∞-⋃-+∞.C ()2,+∞.D ()(),22,-∞⋃+∞4.不等式()()530x x -+£的解集为().A []3,5-.B (][),35,-∞-⋃+∞.C ()3,5-.D ()(),35,-∞-⋃+∞5.在等差数列{}n a 中,12=a ,2414+=a a ,则6=a ().A 13.B 14.C 15.D 166.已知453=a ,2527=b ,159=c ,则a b c 、、之间的大小关系是().A a b c <<.B b a c <<.C a c b<<.D c a b<<7.已知角α的顶点为坐标原点,始边与x 轴非负半轴重合,终边经过点),则sin α=().A 73-.B 34-.C 34.D 738.已知椭圆方程为2213620+=x y ,则该椭圆的离心率为().A 16.B 12.C 23.D 539.已知,R a b Î,则“0a >且0b >”是“0a b +>”的().A 充分且不必要条件.B 必要且不充分条件.C 充要条件.D 既不充分又不必要条件10.函数()sin 2y x p =+在[],p p -上的图象大致为().A .B .C .D 第Ⅱ卷(共50分)二、填空题(本大题共3小题,每小题4分,共12分)请在每小题的空格中填上正确答案。
四川对口高考2023年数学试卷

四川对口高考2023年数学试卷四川对口高考2023年数学试卷一、选择题下列函数中,最小值为4的是 ( )A. y = x + 4/xB. y = √(x^2 + 2) + √[(4 - x)^2 + 1]C. y = 3^x + 3^(-x)D. y = |x - 2| + |x + 3|下列四个命题:① "若 x^2 + y^2 = 0,则 xy = 0" 的否命题;② "若 x > y,则 x^3 > y^3" 的逆命题;③ "若 a ≠ b,则 a^2 ≠ b^2" 的逆命题;④ "若 x > 1,则 x^2 > 1" 的逆否命题。
其中真命题的个数是 ( )A. 1B. 2C. 3D. 4下列函数中,既是偶函数又在区间(0, +∞)上单调递减的是 ( )A. y = x^3B. y = ln xC. y = x/2D. y = e^x若复数 z 满足 (1 - i)z = i,其中 i 为虚数单位,则复数 z = ( )A. -1/2 - i/2B. -1/2 + i/2C. 1/2 - i/2D. 1/2 + i/2∈,则∠BAC最大时点C的坐标是已知△ABC中,A(-3,0),B(0,3),C(m,m + 3),m R( )A. (0,3)B. (9/4,9/4)C. (3,6)D. (9/2,9/2)下列函数中,在区间(0,1)上单调递减的是 ( )A. y = e^xB. y = (1/3)^xC. y = log_2xD. y = arctan x下列四个命题:① "若 xy = 0,则 x = 0 或 y = 0" 的否命题;② "若 x > y,则 x^2 > y^2" 的逆命题;③ "若 a < b,则 a^3 < b^3" 的逆命题;④ "若 x > y,则 x^4 > y^4" 的逆否命题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
机密★启用前
四川省2015年普通高校职教师资班和高职班对口招生统一考试
一口口数学
本试题卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第1卷第1-2页,第Ⅱ卷第3-4页,共4页,考生作答时,须将答案在答题卡上,在本试题卷、草稿纸上答题无效.满分150分.考试时间120分钟,考试结束后,将本试题卷和答题卡一并交回.
第1卷(选择题共60分)
注意事项:
1.选择题必须使用2B铅笔在答题卡上将所选答案对应的标号涂黑.
2.第1卷共1个大题,15个小题,每个小题4分,共60分.
一、选择题:(每小题4分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.设集合A={}3,21,,B={4,5,6},则A B= ( )
A.φ
B.{3}
C.{1,2}
D.{1,2,3,4,5}
2.与340°角终边相同的时 ( )
A.-160°
B.-20°
C.20°
D.160°
3.函数f(x)=
2
-x 1
的定义域为 ( ) A.{}2≠∈x R x B.{}2<∈x R x C. {}2≥∈x R x D.{}2>∈x R x
4.已知甲、乙两组数据的平均数都是10,甲组数据的方差为0.5,乙组数据的方差为0.8,则 ( ) A .甲组数据比乙组数据的波动大 B .甲组数据比乙组数据的波动小 C .甲组数据与乙组数据的波动一样大 D .甲、乙两组数据的波动大小不能比较 数学试卷第1页(共4页)
5.抛物线y 2 =4x 的准线为
A.x=2
B.x=-2
C.x=l
D.x=-1
6.已知y=f(x)是R 上的奇函数,且f(1)=3,f(-2)=-5,则,f (-1)+f(2)=( )
A. -2
B. -1
C.l
D. 2
7.已知直线x+5y -1 =0与直线ax -5y+3 =30平行,则a=( )
A. -25
B. -1
C.l
D. 25
8.已知正四棱锥的高为3,底面边长为2,则该棱锥的体积为
A. 6
B. 32
C. 2 D .2
9.如果在等差数列{}n a 中,a 3 +a 4 +a 5 =6,那么a 1 +a 2=( )
A. 2
B. 4
C. 6
D. 8
10.从10人的学习小组中选正、副组长各一人,选法共有( )
A .30种
B .45种
C .90种 D.100种
11.“x<2”是“022<--x x ”的
A .必要不充分条件
B .充分不必要条件
C .充要条件
D .既不充分也不必要条件 12.以点(1,-2)为圆心,且与直线x-y -1 =0相切的圆的方程是 A. (x -1)2 +(y+2)2 =2 B. (x-l)2 +(y+2)2=1 C. (x+l)2 +(y-2)2 =2 D. (x+l)2 +(y-2)2=1 13.某函数的大致图像如右图所示,则该函数可能是 ( ) A .x y -=3 B. x y 3= C .x y 3-= D. x y -=3- 14.已知a∈[ππ
,2
],cos =α5
3
,则tan =α( )
A .2 B. 21 C.2
1
- D. -2
15.设a 为非零向量,λ为非零实数,那么下列结论正确的是
A.a 与-λa 方向相反 B .a ≥λα- C.a 与λ2a 方向相同 D. αλλα=- 数学试卷第2页(共4页)
第二部分(非选择题 共90分)
注意事项:
1.非选择题必须用0.5毫米黑色墨迹签字笔在答题卡上题目所指示的答题区域内作
答,答在试题卷上无效。
2.本部分共2个大题,11个小题,共90分。
二、填空题:(本大题共5个小题,每小题4分,共20分) 16.已知向量a=(l ,2),那么=a . 17. Log 228的值为 .
18.二项式6)1x
x +(展开式中的常数项为 .
(用数字作答) 19.已知双曲线)0,0(122
22>>=-b a b
y a x 的左焦点为F (一2,0),离心率
为2,则a=
20.已知某电影院放映厅共有6排座位,第1排座位数为10,后面每排座位数比前面一
排多2,则该电影院放映厅的座位总数为 .
三、解答题:(本大题共6个小题,共70分。
解答应写出文字说明、证明过程或演算步骤) 21.(本小题满分10分)
已知数列{}n a 中,n n a a a 2,211==+,求数列{}n a 的通项公式及前n 项和Sn .
22.(本小题满分10分
已知向量a=(2,3),b=(2,-10). (I)求2a +b ;
(Ⅱ)证明:a ⊥(2a +b).
数学试卷第3页(共4页) 23.(本小题满分12分) 已知点A(O ,2),B( -2,2). (I)求过A ,B 两点的直线l 的方程;
(Ⅱ)已知点A 在椭圆C :)0(12
222>>=+b a b
y
a x 上,且(I)中的直线l
过椭圆C 的左
焦点.求椭圆C 的标准方程.
24.(本小题满分12分)
某商品的进价为每件50元.根据市场调查,如果售价为每件50元时,每天可卖出
400件;商品的售价每上涨1元,则每天少卖10件,设每件商品的售价定为x 元(x ≥50,x∈N).
(I)求每天销售量与自变量x 的函数关系式; (Ⅱ)求每天销售利润与自变量x 的函数关系式;
(Ⅲ)每件商品的售价定为多少元时,每天可获得最大利润?最大的日利润是多少元?
25.(本小题满分13分)
如图,直三棱柱ABC -A1B1C l的侧棱长为3,底面Rt△ABC中,AC ⊥AB,AB =AC一2,D为BC的中点.
(I)证明:AB⊥平面BCC l B1;
(Ⅱ)求二面角C1 -AD -C的大小.
A
26.(本小题满分13分)
已知△ABC三个内角A,B,C所对的边分别为a,b,c,且a=5,c=23,2π
A=
3
(I)求sinC的值;
π).
(Ⅱ)求5sin2C+2sin(C+
4
数学试卷第4页(共4页)。
