第6次作业题和参考答案 正弦稳态电路
电路分析正弦稳态电路考题

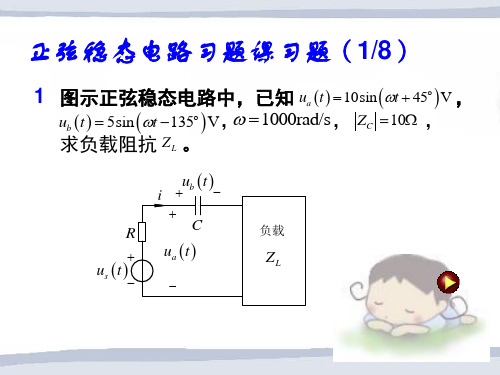
7. 在图示所示电路中ZL= R + jX,R、X都可变, 求 ZL= ? 时获得最大功率。
10 1 0 A 10 -j10
解: Z 10 ( j10) 5 j5 Ω 0
ZL
10 j10
Z L 5 j5 Ω
。(15分) 和电压 U 8. 求电路中电流 I
Zab= 。 (1 j2)( j) 2 j j 解:Z ab j 1 j2 j 1 j
a b
j −j
j2 1
(2 j)(1 j) 1 j3 1 2 j j ( 1 j) 45 Ω ( 1 j)(1 j) 2 2 2
七、正弦稳态电路如图所示,已知iS(t)=10cos(1000t) mA; (1) 求自ab端向左看戴维南等效电路时域模型; (2) 若负载A是1/4F电容,求它两端的电压u(t)。
u1
iS
2k 0.5F
2k 2H
a + u(t) A – b a
解 :(1) I sm 100 mA
列网孔电流方程 1 (4 j2 j2) I ( j2) 0 I
(1)
1 ( j2) I (1 j2) j5 1 50 (2) I 1 j0.5I 1 j2 I 0 由 (1) 得 I 4I
代入 (2) 得
I j2 I 5(1 j) I
uOC – 4k
+
1/4 F 2H b
–
u
Z0为4k电阻和2H电感的串联。
uOC ( t ) 20 cos(1000t ) V
时域模型
七、正弦稳态电路如图10所示,已知iS(t) = 10cos(1000t) mA; (1) 求自ab端向左看戴维南等效电路时域模型; (2) 若负载A是 1/4F电容,求它两端的电压 u(t)。
正弦稳态电路习题课
⇒ Z1 = Z 2
2 2 2 2
Z2 = R + X
X1 = X 2
性质相反,一个 为感性,另一个 为容性
⇒
U1 = U 2 = 50 2V>U = 50V ⇒
X1 = − X 2
Z = Z1 + Z 2 = R1 + jX 1 + R2 + jX 2 = R1 + R2 = 2 R1
端口电压、电流 同相
B0 = −0.1S < 0
1 1 =− = 1H L0 = − −0.1× 10 B0ω
B0 = −0.1S < 0
⇒
5Ω
1H
正弦稳态电路习题课习题(3/8) )
图示正弦交流电路中,已知电流表的示数为2A, 3 图示正弦交流电路中,已知电流表的示数为 ,电 压表1的示数为 的示数为17V,2的示数为 的示数为10V。求电源电压 压表 的示数为 , 的示数为 。 的有效值。 的有效值。
正弦稳态电路习题课习题(6/8) )
U 图示电路中,ɺ = 50∠0o V,每一阻抗部分消耗的功 6 图示电路中, 率均为250W,且电压的峰值为 率均为 ,且电压的峰值为100V。求(1)阻抗 。 ) Z1 和 Z 2 ;( )若 ω = 800π rad/s ,求电路可能含有 ;(2) 的元件及其数值。 的元件及其数值。
jω L2
R1
ɺ Us −
+
ɺ IC
jω L1
1 jωC
ɺ IC
R2
ZL
7 解(1) 求开路电压
Z L 2 = jω L2 = j100Ω
1 ZC = = − j100Ω + jωC ɺ Us ɺ = − I R = −100 I − ɺ ɺ ⇒U
正弦交流电路 习题参考答案

正弦交流电路 习题参考答案一、填空题:1. 表征正弦交流电振荡幅度的量是它的 最大值 ;表征正弦交流电随时间变化快慢程度的量是 角频率ω ;表征正弦交流电起始位置时的量称为它的 初相 。
三者称为正弦量的 三要素 。
2. 电阻元件上任一瞬间的电压电流关系可表示为 u = iR ;电感元件上任一瞬间的电压电流关系可以表示为dtdi Lu =L ;电容元件上任一瞬间的电压电流关系可以表示为dtdu Ci CC =。
由上述三个关系式可得, 电阻 元件为即时元件; 电感 和 电容 元件为动态元件。
3. 在RLC 串联电路中,已知电流为5A ,电阻为30Ω,感抗为40Ω,容抗为80Ω,那么电路的阻抗为 50Ω ,该电路为 容 性电路。
电路中吸收的有功功率为 450W ,吸收的无功功率又为 600var 。
二、 判断题:1. 正弦量的三要素是指最大值、角频率和相位。
(错)2. 电感元件的正弦交流电路中,消耗的有功功率等于零。
(对)3. 因为正弦量可以用相量来表示,所以说相量就是正弦量。
(错)4. 电压三角形是相量图,阻抗三角形也是相量图。
(错)5. 正弦交流电路的视在功率等于有功功率和无功功率之和。
(错)6. 一个实际的电感线圈,在任何情况下呈现的电特性都是感性。
(错)7. 串接在正弦交流电路中的功率表,测量的是交流电路的有功功率。
(错)8. 正弦交流电路的频率越高,阻抗越大;频率越低,阻抗越小。
(错)三、选择题:1. 某正弦电压有效值为380V ,频率为50Hz ,计时始数值等于380V ,其瞬时值表达式为( B )A 、t u 314sin 380=V ;B 、)45314sin(537︒+=t u V ;C 、)90314sin(380︒+=t u V 。
2. 一个电热器,接在10V 的直流电源上,产生的功率为P 。
把它改接在正弦交流电源上,使其产生的功率为P /2,则正弦交流电源电压的最大值为( D )A 、7.07V ;B 、5V ;C 、14V ;D 、10V 。
第6章 正弦稳态电路分析 (2)

Q = IS 2 Im[Z ] = 52 × (1 / 3) = 8.3(Var)
S = IS 2 | Z | = 52 × 32 + (1 / 3)2 = 75.5(VA) cos φ = P / S = 0.993 也可以电阻,电抗分别计算。
第6章 正弦稳态电路分析
§6-8 功率因数的提高
一、提高功率因数的意义 设备容量 S (额定)向负载送多少有功要由负载的阻抗角决定。
从能量的角度,并联电容后,电容可以补偿电感的无功;
并联电容后,电路有功功率没有发生变化。
第6章 正弦稳态电路分析
补偿容量的确定:
I
IC
ϕ1 ϕ2 I
U
+
R
I L
U
C
IC I L 有功功率没有发生变化:
_L
P = U IL cosφ1 = UI cosφ2
由相量关系: IC = IL sinφ1 - I sin φ2
R、L、C元件的瞬时功率 i
+
R元件(ϕ =0),pR =UI(1-cos2ωt)
u -
R pR对总大于零,电阻消耗能量。
i
+
L元件(ϕ = 90°),pL =-UIsin2ωt
u -
L pL时正时负,和外界交换能量。
i
+
C元件(ϕ =- 90°),pC =UIsin2ωt
u -
C pC时正时负,和外界交换能量。
| Z |2 −R2
=1 314
502 − 302 = 0.127(H)
第6章 正弦稳态电路分析
三、无功功率 (reactive power) Q p(t) = UI[cos φ − cos(2ωt − φ)] = UI cos φ(1− cos 2ωt) −UI sinφ sin 2ωt UIcosϕ(1-cos2ω t)表示网络中电阻所消耗的功率; UIsinϕ sin2ω t表示电抗与电源的能量交换。
第6章 正弦交流电路的分析练习题及答案

第6章 正弦交流电路的分析习题答案6-1 在RL 串联的交流电路中,R 上端电压为16V ,L 上端电压为12V ,则总电压为多少?解:V 2012162222=+=+=L R U U U6-2 RL 串联电路接到220V 的直流电源时功率为1.2kW ,接在220V 、50Hz 的电源时功率为0.6kW ,试求它的R 、L 值。
解:接直流电源时,电感元件相当于短路,只有电阻作用,因此Ω===3.40k 2.122022P U R ,接交流电源时,A 86.33.40k6.0===R P I , 由此得707.086.3220k 6.0cos =⨯==UI P φ,所以阻抗角︒=45φ, 感抗Ω=︒⨯=⋅=3.4045tan 3.40tan φR X L ,H 13.05014.323.402=⨯⨯==∴f X L L π6-3 已知交流接触器的线圈电阻为200Ω,电感量为7H ,接到工频220V 的交流电源上,求线圈中的电流I 。
如果误将此接触器接到220V 的直流电源上,线圈中的电流又为多少?如果此线圈允许通过的电流为0.2A ,将产生什么后果?解:线圈接工频交流电时,Ω=⨯+=+=+=2207)7314(200)(222222L R X R Z L ω,由此得线圈中电流A 1.02207220≈==Z U I 。
如果将该线圈接到直流电源上,A 1.1200220≈==R U I 如果此线圈允许通过的电流为0.2A ,在直流电中线圈将烧毁,在工频交流电中可以正常使用。
6-4 在RLC 串联电路中,已知R =10Ω,L =1H ,C =0.005F ,电源电压V 20sin 2100t u =,计算:(1)X C 、X L 、Z ;(2)I &、R U &、LU &、C U &,并画出相量图; (3)写出i 、u R 、u L 、u C 的表达式。
解:(1)X C =1/(ωC )=1/(20×0.005)=10Ω,X L =ωL =20×1=20Ω,Z=R+j(X L -X C )=10+ j10=102∠45°。
第6章稳态作业参考答案

选择电容器组的容量为15Mvar
电压校验。将k和Qc代回方程组中,求出最大负荷和最小 符合情况下的低压母线的电压U2max和U2min:
12 19.32 (8 0) 80 117 10.5U 2 min 10.5U 2 min 30 19.32 (18 Qc ) 80 117 10.5U 2 max 10.5U 2 max
Us
L 110kV
Z1 17 j 40
T
D
S
Smin 12 j8MVA
ZT 2.23 j 40
Smax 30 j18MVA
求解:
线路和变压器的总阻抗为:
Z Z L ZT (17 j 40) (2.32 j 40) 19.32 j80
第六章作业一
第六章作业一
第六章作业一
第六章作业一
第六章作业二
2.如下图所示网络,线路和变压器归算至高压 u 侧的阻抗已经标注图中。供电点电压 s 117 kv 恒 定。如变压器低压母线要求保持10.4KV恒定 ,试配合变压器分接头( 2 2.5% )的选择确定并 联补偿设备的容量:a)采用电容器;b)采用调 相机。
U 2 min 10.38kV U 2 max 10.43kV
3.
采用调相机进行调压,则有方程
1 12 19.32 (8 Qc ) 80 2 117 10.4k 10.4k 30 19.32 (18 Qc ) 80 117 10.4k 10.4k
10.4k 117 10.4k 30 19.32 (18 Qc ) 80 10.4k
电力系统稳态分析第六次作业参考答案可编辑

电力系统稳态分析第六次作业参考答案可编辑 Document serial number【KK89K-LLS98YT-SS8CB-SSUT-SST108】第五次作业1、造成电力系统电压水平波动的原因是什么2、电力系统的电压调整与电力系统的频率调整相比较有那些特点3、在常用的无功补偿设备中,那些无功补偿设备具有正的调节效应那些具有负的调节效应4、什么叫电力系统的电压中枢点电压中枢点的电压调整方式有那几种5、常用的调压措施有那些对于由于无功缺乏造成电压水平下降的电力系统应优先采取何种调压措施对于无功功率并不缺乏,但局部电网电压偏低的电力系统应优先采用何种调压措施6、电力系统无功电源最有分布的目的是什么无功电源最优分布的原则是什么7、电力系统无功最优补偿的目的是什么无功最优补偿的原则是什么8、某降压变电所由110kV 线路供电,变电所装有一台40MVA 普通变压器,如图三所示。
110kV 送端电压U1保持115kV 不变。
若要求变电所10kV 母线电压U2变化范围不超出~,试选择变压器分接头。
9、电力网接线如下图所示,已知Ω=70ij X ,变电所低压母线要求逆调压(最小负荷时电压为额定电压,最大负荷时电压为105%U N ),低压母线额定电压为10KV ,变压器额定电压为KV 11/%5.22110⨯±。
最大负荷及最小负荷时,归算到高压侧的实际电压分别为:KV U KV U j j 2.110;1.101min .max .='='。
若i U 不变,求应选择的变压器分接头和并联电容器的容量。
电力系统稳态分析第五次作业参考答案1、造成电力系统电压水平波动的原因是什么压分别为:KV U KV U j j 2.110;1.101min .max .='='。
若i U 不变,求应选择的变压器分接头和并联电容器的容量。
解:1、根据最小负荷时的调压要求选择变压器的变比22.12111102.110min .min .=⨯='=iN j j tJ U U U U 取KV U tJ 5.11505.0110110=⨯+=变压器变比为5.10115.115==K 2、根据最大负荷时的调压要求选择补偿电容器的容量var 41.145.10)5.101.10105.110(7005.110)(22max .max .max .M K K U U x U Q j jc ij jc C =⨯-⨯⨯='-= 答:变压器变比应选5.10115.115==K ;补偿电容器容量MVAR Q C 41.14=。
正弦稳态电路习题

正弦稳态电路习题1、图示正弦稳态电路,已知R=3Ω、L=1H 、C=0.25F 、u s (t)=32cos4t V 。
(1)、用相量分析法求i(t)、u R (t)、u L (t)、u C (t)。
(2)、求ab 右侧单口网络的平均功率P 、无功功率Q 、视在功率S 、功率因数λ。
(3)、当电压源角频率ω为多少时,ab 右侧单口网络发生谐振。
2、电路如图(a )所示,求 Z L =? 时能获得最大功率,并求最大功率。
3、已知对称三相电路,电源电压︒∠=∙0220A U ,)(6.0cos ,1011感性=Ω=ϕZ ,Ω+=Ω-=j Z j Z N 21,502求A 相的线电流∙A I 及负载上的相电流∙'A I ,∙''A I 。
4、图示电路中M=1,求电路的谐振频率。
5、图示电路,求i 1(t),i 2(t).1H7H 5H姓名 专业 学号 级 班正弦稳态电路习题参考答案1、(1) ∙I =Z Us ∙=0.5︒-∠452 A ∙R U =R ∙I =︒-∠4525.1 V∙L U =Z L ∙I =︒∠4522 V ∙C U =Z C ∙I =︒-∠13525.0 Vi(t)=cos(4t-︒45) Au r (t)=3cos(4t-︒45) Vu L (t)=4cos(4t+︒45) Vu C (t)=cos(4t-︒135) V(2)P=UIcos φ=3*0.52*cos ︒45=1.5 WQ=UIsin φ=3*0.52*sin ︒45=1.5 var S=UI=3*0.52=1.52 V ∙A λ=COS φ= cos ︒45=0.52 (3) 225.0*1110====LC ωω rad/s2、当时,负载获得最大功率3、4、ω0=10rad/s.5、 A 6.17j 13.2A 13.532213.53100220'o o o1AN A -=-∠=∠∠==∙∙Z U I j13.2A 3/50j 0220''o 2AN A =-∠==∙∙Z U I A 4.189.13'''o A A A -∠=+=∙∙∙I I I A t t i )2.402cos(247.0)(1︒-=A t t i )8.42cos(2498.0)(2︒+=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5. 一阻抗 Z 接到正弦电压U& 。求在下列两种情况下,电路的功率因数及功率。
(1) U& = 220∠0°V , I& = 5∠ − 30°A ; (2) U = 220V , Z = 100∠45°Ω ; (3) Z = 40 + j20Ω ,I=5A。
答案: (1) P = 953W,Q = 550var, cosϕ = cos30o = 0.86(6 滞后)
Z3=20-j20Ω。求两电源各自发出的功率。 Z2
Z4
I&S
Z1
Z3
+
U& S
−
答案: S IS − 3.187 − j0.777 VA, SUS = 185.6 − j182.66 VA
7. 电压为 220V 的工频电源供给一组动力负载,负载电流 I=318A,功率 P=42kW。现在要在此电源上 再接一组功率为 20kW 的照明设备(白炽灯),并希望照明设备接入后电路总电流不超过 325A,为此便需再 并联电容。计算所需电容的无功量、电容值,并计算此时电路的总功率因数。
=
− μU& 5 R6
⎪ ⎪⎪I&1
=
U& S1 − U& n1 R1
⎪⎪U& 5 = U& n3
⎪⎩
2. 电路如图所示。已知 U=220V,Z2=15+j20Ω,Z3=20Ω, I&2 = 4∠0°A ,且 I&2 滞后U& 30°。求 Z1。 I&1 Z1
+ + U&1 − I&2 I&3+
U&
第六次作业和参考答案 ——正弦稳态电路
1. 用节点法列写下图所示电路的相量方程。 R6
+ μU& 5 −
I&1 U& n1
R1
U& S1 +
−j 1 ωC2
−
U& n2
jωL3
R4−
βI&1
U&
+
5
−
U& n3
−j 1 ωC5
答案:
⎧1
⎪( ⎪
R1
+
1 R6
−
1 j ω L3
+
jωC2 )U& n1
答案:
C
=
1 2.38× ω
= 1338.1μF ,QC=源自−20319.9var ,
cosϕ
= cos 29.9o
= 0.867(感性)
3
Z2
Z3 U& 2
−
A
−
答案: Z1 = 16.62∠ −16.8o = 15.9 − j4.8Ω
1
3. 如图所示电路中,已知 U=100V,R3=6.5Ω,可调变阻器 R 在 R1=4Ω,R2=16Ω的位置时,电压表 的读数最小为 30V。求阻抗 Z。
+
R1
R3
U& R
V
R2
Z
−
答案: Z = 3.50 + j15.0Ω ,或 Z = 3.50 − j15.0Ω
(2) P = 342W,Q = 342var , cosϕ = cos 45o = 0.70(7 滞后)
(3) P = 1000W , Q = 500var , cosϕ = cos 26.6o = 0.89(4 滞后)
2
6. 如图所示电路中,已知U& S = 100∠ − 120°V , I&S = 1∠30°A ,Z1=3Ω, Z2=10+j5Ω,Z3=-j10Ω,
4. 电路如图所示。已知 I&S = 1∠30°A ,U& S = 50∠ − 60°V ,Z1=20Ω,Z2=15-j10Ω,Z3=5+j7Ω,Z4=
-j20Ω。求 ab 端接上多大阻抗 Z 时,此阻抗中有最大电流?此最大电流为多大?
Z4
a
Z3
Z2
I&S
Z1
+
Z
−U& S
b
答案: Z = j3.61Ω时,电流I& 最大 , I&max = 3.42∠ − 35.5o A
−
(−
j
1 ωL3
)U&
n
2
−
1 R4
U& n3
=
U& I&A S1 R1
+
μU& 5 R6
⎪ ⎪− ⎪
(−
j
1 ωL3
)U&
n1
+ (− j 1 ωL3
+
1 R6
)U& n2
−
1 R4
U& n3
=
βI&1
⎪⎪⎨− ⎪
1 R6
U&
n1
−
1 R4
U&
n
2
+( 1 R4
+
1 R6
+
jωC5 )U& n3
