电路分析正弦稳态电路考题
电路分析正弦稳态电路考题

7. 在图示所示电路中ZL= R + jX,R、X都可变, 求 ZL= ? 时获得最大功率。
10 1 0 A 10 -j10
解: Z 10 ( j10) 5 j5 Ω 0
ZL
10 j10
Z L 5 j5 Ω
。(15分) 和电压 U 8. 求电路中电流 I
Zab= 。 (1 j2)( j) 2 j j 解:Z ab j 1 j2 j 1 j
a b
j −j
j2 1
(2 j)(1 j) 1 j3 1 2 j j ( 1 j) 45 Ω ( 1 j)(1 j) 2 2 2
七、正弦稳态电路如图所示,已知iS(t)=10cos(1000t) mA; (1) 求自ab端向左看戴维南等效电路时域模型; (2) 若负载A是1/4F电容,求它两端的电压u(t)。
u1
iS
2k 0.5F
2k 2H
a + u(t) A – b a
解 :(1) I sm 100 mA
列网孔电流方程 1 (4 j2 j2) I ( j2) 0 I
(1)
1 ( j2) I (1 j2) j5 1 50 (2) I 1 j0.5I 1 j2 I 0 由 (1) 得 I 4I
代入 (2) 得
I j2 I 5(1 j) I
uOC – 4k
+
1/4 F 2H b
–
u
Z0为4k电阻和2H电感的串联。
uOC ( t ) 20 cos(1000t ) V
时域模型
七、正弦稳态电路如图10所示,已知iS(t) = 10cos(1000t) mA; (1) 求自ab端向左看戴维南等效电路时域模型; (2) 若负载A是 1/4F电容,求它两端的电压 u(t)。
正弦稳态电路的分析

14、如图所示14正弦稳态电路,R=XL=5Ω,I1=10A,
UC=100V,XC=10Ω,
试求U和I。
解:设 2=I2 A
=50 V
=100 2=10 A 1=10 A
所以,I= =10 AI12+I2=I22
易知 与 同相
U= UC=100 V
15、如图15a所示正弦稳态电路,R1=1KΩ,R2=2KΩ,L=1H,求Ucd=Uab时C的值。
解:电路的总阻抗为
Z=-jXC+ = +j( -XC)
当XC=1Ω和XC=2Ω,可以列出如下两个方程
(1)
(2)
解(1)、(2)得,R=2 Ω,XL=2Ω
4、图4所示工频正弦电流电路中,U=100V,感性负载Z1的电流I1=10A,功率因数λ1=0.5,R=20Ω。
(1)求电源发出的有功功率、电流I、功率因数λ
(3)u= u1+u2+u3的表达式
解:(1)将 , 写成标准指数形式,即
=-100∠150°V=100∠-30°V
=-100+j100 V=100 ∠135°V
根据相量和正弦量的关系,可得
u1=50 cos(314t+60°) V,u2=100 cos(314t-30°) V
u3=200cos(314t+135°) V
解: =Y =( ) = 45°
I= A
11、列出图11所示电路相量形式的回路方程和结点方程。
解:设各回路方向如图所示。
回路方程如下:
(1)
(2)
(3)
(4)
- = S(5)
选结点0作为参考结点,结点方程如下:
课件-第4章 正弦稳态电路分析--例题

第4章 正弦稳态电路分析--例题√【例4.1】已知两个同频正弦电流分别为()A 3314cos 2101π+=t i ,()A 65314cos 2222π-=t i 。
求(1)21i i +;(2)dt di 1;(3)⎰dt i 2。
【解】 (1)设()i t I i i i ψω+=+=cos 221,其相量为i I I ψ∠=∙(待求),可得:()()()()A54.170314cos 224.14A54.17014.24A 34.205.14 A1105.19A j8.665 A15022A 601021︒-=︒-∠=--=--++=︒-∠+︒∠=+=∙∙t i j j I I I(2)求dtdi 1可直接用时域形式求解,也可以用相量求解()()︒+︒+=︒+⨯-=9060314cos 23140 60314sin 3142101t t dt di用相量形式求解,设dt di 1的相量为K K ψ∠,则有 )9060(31406010314K 1K ︒+︒∠=︒∠⨯==∠∙j I j ωψ两者结果相同。
(3)⎰dt i 2的相量为︒∠=︒∠︒-∠=∙12007.0903********ωj I【例4.2】 图4-9所示电路中的仪表为交流电流表,其仪表所指示的读数为电流的有效值,其中电流表A 1的读数为5 A ,电流表A 2的读数为20 A ,电流表A 3的读数为25 A 。
求电流表A 和A 4的读数。
图4-9 例4.2图【解】 图中各交流电流表的读数就是仪表所在支路的电流相量的模(有效值)。
显然,如果选择并联支路的电压相量为参考相量,即令V 0︒∠=∙S S U U ,根据元件的VCR 就能很方便地确定这些并联支路中电流的相量。
它们分别为:A 25 ,A 20 ,A 05321j I j I I =-=︒∠= 根据KCL ,有:()A095A 5A 457.07A 55324321︒∠==+=︒∠=+=++=j I I I j I I I I 所求电流表的读数为:表A :7.07 A ;表A 4:5 A【例4.3】 RLC 串联电路如图4-12所示,其中R =15Ω,L =12mH ,C =5μF ,端电压u =1002cos (5000t )V 。
电路分析 选择题题库 第11章 正弦稳态功率和三相电路

第11章正弦稳态的功率和三相电路1、在三相交流电路中,负载对称的条件是()。
(a)Z Z ZA B C==(b)ϕϕϕA B C==(c)Z Z ZA B C==答案:(c)2、某三角形连接的三相对称负载接于三相对称电源,线电流与其对应的相电流的相位关系是()。
(a)线电流导前相电流30︒(b)线电流滞后相电流30︒(c)两者同相答案:(b)3、三角形连接的三相对称负载,接于三相对称电源上,线电流与相电流之比为()。
(a)3(b)2(c)1答案:(a)4、作星形连接有中线的三相不对称负载,接于对称的三相四线制电源上,则各相负载的电压()。
(a)不对称(b)对称(c)不一定对称答案:(b)5、对称三相电路的有功功率P U I l l=3λ,功率因数角ϕ为()。
(a)相电压与相电流的相位差角(b)线电压与线电流的相位差角(c)阻抗角与30︒之差答案:(a)6、对称三相电路的无功功率Q U I l l=3sinϕ,式中角ϕ为()。
(a)线电压与线电流的相位差角(b)负载阻抗的阻抗角(c)负载阻抗的阻抗角与30︒之和答案:(b)7、有一对称星形负载接于线电压为380V的三相四线制电源上,如图所示。
当在M点断开时,U1为()。
(a)220V (b)380V (c)190VABCNM答案:(a)18、一对称三相负载接入三相交流电源后,若其相电压等于电源线电压,则此三个负载是( )接法。
(a)Y (b)Y 0 (c)∆答案:(c)9、作三角形连接的三相对称负载,均为RLC 串联电路,且R =10Ω,X L =X C =5Ω,当相电流有效值为I P =1A 时,该三相负载的无功功率Q =( )。
(a)15Var (b)30Var (c)0Var答案:(c)10、正弦交流电路的视在功率定义为( )。
(a)电压有效值与电流有效值的乘积 (b)平均功率(c)瞬时功率最大值答案:(a)11、正弦交流电路的无功功率表征该电路中储能元件的( )。
第9章 正弦稳态电路的分析(答案)

第9章 正弦稳态电路的分析 答案例 如图所示正弦稳态电路,已知I1=I2=10A,电阻R 上电压的初相位为零,求相量•I 和•S U 。
解: 电路中电阻R 和电容C 并联,且两端电压的初相为0。
由电阻和电容傻姑娘的电压与电流的相位关系可知:电阻电流•1I 与电压•R U 同相,电容电流•2I 超前电压•R U 相角90○,故ο0101∠=•I A ο90102∠=•I A由KCL 方程,有 ()101021j I I I +=+=•••A由KVL 方程,有 ︒•••∠==++-=+=9010010010010010010101j j I I j U S V例 如图所示正弦稳态电路,R 1=R 2=1Ω。
(1)当电源频率为f 0时,X C2=1Ω,理想电压表读数V 1=3V ,V 2=6V ,V 3=2V,求I S 。
(2)电路中电阻、电容和电感的值不变,现将电源的频率提高一倍,即为2 f 0,若想维持V 1的读数不变,I S 问应变为多少如果把电源的频率提高一倍,而维持V1的读数不变,即R1上的电压有效值U R1=3V,那么R1上的电流的有效值I也不变,此时仍把•I设置为参考相量,故︒•∠=03I A。
由于L和C1上的电流•I不变,根据电感和电容上电压有效值与频率的关系,电源的频率提高一倍,电感上电压表的读数增大一倍,而电容上电压表的读数降为原来的一半,故电源得频率提高一倍,X C2也降为原来得一半,即所以例如图所示正弦稳态电路,已知I1=10A,I2=20A,R2=5Ω,U=220V,并且总电压•U与总电流•I同相。
求电流I和R,X2,X C的值。
例 如图所示正弦稳态电路,已知有效值U 1=1002V, U=5002V ,I 2=30A ,电阻R=10Ω,求电抗X 1,X 2和X 3的值。
由电路可得两边取模得已知2550=U V ,所以6002=U V ,故有。
电路分析II复习题(有解答)

M=
3Ω 1Ω
1H
2H
10V
L1
1H
L2
6Ω 解:去耦等效变换,并将串联电阻合并为一个
R 31 6 10
L (L1 M ) (L2 M ) 5H
L / R 0.5s
21.图示正弦稳态单口的端口等效电感是:( )
L1=2H
L0 1H
M 0.5H
L2=1H
解:去耦等效变换,
L L0 //[(L1 M ) (L2 M )] 0.667 H
i(t) 10 cos(t 60 o) 2 cos(3t 135 o) ( A)
求单口网络吸收的平均功率 P 及电流和电压的有效值。
解:单口网络吸收的平均功率 P 110010cos60 1 30 2cos135 228.8W
2
2
电流的有效值
U 1 1002 1002 502 302 76.49(V ) 2
可将图示正弦稳态单口的功率因数提高到1的
电容是:( )
1Ω
C
1H
解答
12.对称Y-Y三相电路,线电压为208V,
负载吸收的平均功率共为12kW,λ=0.8(感性),
求负载每相的阻抗
A
+.
UA
.
N-
UC -
-
.
UB
+
+
C
B
.
IA
.
IN
.
IB
.
IC 图15
Z1
N'
Z2 Z3
解答
13.Y-Y三相四线电路,相电压为200V,
解答
25.图示电路,求i
12Ω 2:1 i
18V
电路分析试题和答案(全套)

电路分析试题(Ⅰ)二. 填空(每题1分,共10分)1.KVL体现了电路中守恒的法则。
2.电路中,某元件开路,则流过它的电流必为。
3.若电路的支路数为b,节点数为n,则独立的KCL方程数为。
4.在线性电路叠加定理分析中,不作用的独立电压源应将其。
5.若一阶电路电容电压的完全响应为uc(t)= 8 - 3e-10t V,则电容电压的零输入响应为。
7.若一个正弦电压的瞬时表达式为10cos(100πt+45°)V,则它的周期T 为。
8.正弦电压u1(t)=220cos(10t+45°)V, u2(t)=220sin(10t+120°)V,则相位差φ12=。
9.若电感L=2H的电流i =2 cos(10t+30°)A (设u ,i为关联参考方向),则它的电压u为。
三.求下图单口网络的诺顿等效电路,并画等效电路图。
(15分)ab四.用结点分析法,求各结点电位和电压源功率。
(15分)1 2五.一阶电路如图,t = 0开关断开,断开前电路为稳态,求t ≥0电感电流i L(t) ,并画出波形。
(15分)电路分析试题(Ⅱ)二. 填空(每题1分,共10分)1.电路的两类约束是。
2.一只100Ω,1w的电阻器,使用时电阻上的电压不得超过V。
3.含U S和I S 两直流电源的线性非时变电阻电路,若I S单独作用时,R 上的电流为I′,当U S单独作用时,R上的电流为I",(I′与I"参考方向相同),则当U S和I S 共同作用时,R上的功率应为。
4.若电阻上电压u与电流i为非关联参考方向,则电导G的表达式为。
5.实际电压源与理想电压源的区别在于实际电压源的内阻。
6.电感元件能存储能。
9.正弦稳态电路中, 某电感两端电压有效值为20V,流过电流有效值为2A,正弦量周期T =πS , 则电感的电感量L=。
10.正弦稳态L,C串联电路中, 电容电压有效值为8V , 电感电压有效值为12V , 则总电压有效值为。
最全第九章(正弦稳态电路分析)习题解答打印版.doc
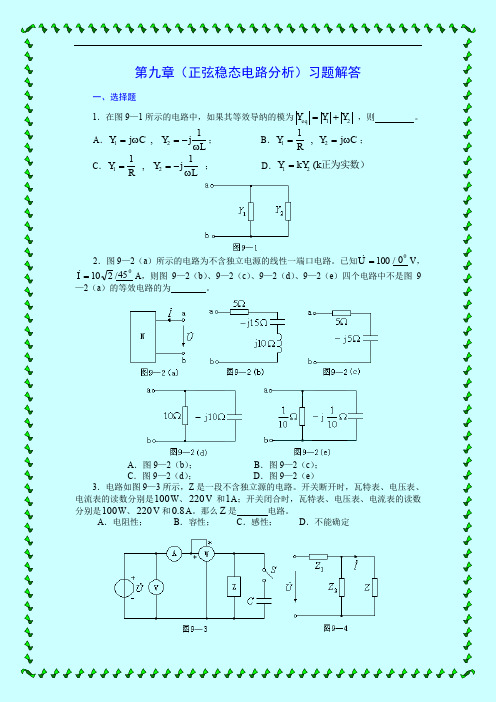
第九章(正弦稳态电路分析)习题解答一、选择题1.在图9—1所示的电路中,如果其等效导纳的模为21Y Y Y eq += ,则 。
A .L Y C Y ω-=ω=1j, j 21; B .C Y RY ω==j , 121;C .L Y R Y ω-==1j , 121 ;D .正为实数)k kY Y ( 21=2.图9—2(a )所示的电路为不含独立电源的线性一端口电路。
已知00 /100=UV ,045 /210=I A ,则图9—2(b )、9—2(c )、9—2(d )、9—2(e )四个电路中不是图9—2(a )的等效电路的为 。
A .图9—2(b );B .图9—2(c );C .图9—2(d );D .图9—2(e )3.电路如图9—3所示,Z 是一段不含独立源的电路。
开关断开时,瓦特表、电压表、电流表的读数分别是100W 、220V 和1A ;开关闭合时,瓦特表、电压表、电流表的读数分别是100W 、220V 和8.0A 。
那么Z 是 电路。
A .电阻性;B .容性;C .感性;D .不能确定4.电路如图9—4所示,U固定不变。
如果 ,则改变Z (Z 不等于无限大)时,I不变。
A .21Z Z =; B .21Z Z -=; C .21Z Z =; D .)Arg()Arg(21Z Z =5.Ω=10R 的电阻,F 1μ=C 的电容与电感L 串联,接到频率1000Hz 的正弦电压源上。
为使电阻两端的电压达到最高,电感应取 。
A .1H ;B .π21H; C .21H ; D .241πH二、填空题1.若Ω=3R ,Ω=ω6L ,Ω=ω2011C ,Ω=ω2012C ,则图9—5所示电路的输入阻抗为 j4)3(-Ω。
.2.线性一端口电路如图9—6所示,A /02 V ,30/5000=-=I U。
则此一端口电路吸收的复功率,有功功率、无功功率分别为V A 30/1000、W 350、50Var 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2k 2H
a
+ u(t) A – b
sm 100 mA 解 :(1)I
L =2000 1/ C = 2000
1/ CA = 4000
iS
0.5F
20V U OCm
a
U OCm
Z 0 4000 j2000 Ω
+
– Z0
A U m
+
OCm ( j4000) U 20 ( j4000) m (2) U Z 0 ( j4000) 4000 j2000 j4000 40 (1 2 j) 17.8 63.4 V 5
5(1 j) 2(1 j) I
5∠0 V – + −j2 1 j
2.50 A I j j5 ( I j5) 1 U
5 2.5 j5 2.5 j5
1 I
4
j2
I
+ U
–
j5A
5.59116.56 V U
Zab= 。 (1 j2)( j) 2 j j 解:Z ab j 1 j2 j 1 j
a b
j −j
j2 1
(2 j)(1 j) 1 j3 1 2 j j ( 1 j) 45 Ω ( 1 j)(1 j) 2 2 2
《电路分析基础 》部分试题及解答三
( 10t 30 ) V, 1. 元件两端电压 u( t ) 100cos ( 10 t 120 )mA 电流 i ( t ) 0.1 cos 此元件为 电容 元件,其值为 0.1 F 。
i
+
u
90º 电容元件 超前 U 解: I
Im 0.1 10 C 0.1 μF U m 100 10
2. 电路的开路电压Uab = 2090 V 。
3
−
ab j L2 I 2 j M I 1 解: U
2 0 I ab j2 100 U
2090 V
1 I
j3
j2 j5
2 I
a
10∠0º A
b
3. 单口网络的输入阻抗
0.707 45 Ω
2k
0.5F 2k
a
sm 100 mA 解 :( 1) I
L =2000 1/ C = 2000
1/ CA = 4000
+ A 2H u ( t ) Z0 – a b +
20V U OCm
求 Z0 = Zab
j2000( 2000 j2000) Z 0 2000 2000 j2000 j2000 2000 j( 2000 j2000) 4000 j2000 Ω
uOC – 4k
+
1/4 F 2H b
–
u
Z0为4k电阻和2H电感的串联。
uOC ( t ) 20 cos(1000t ) V
时域模型
七、正弦稳态电路如图10所示,已知iS(t) = 10cos(1000t) mA; (1) 求自ab端向左看戴维南等效电路时域模型; (2) 若负载A是 1/4F电容,求它两端的电压 u(t)。
L =2000 1/ C = 2000
求开路电压
j2000( 2000 j2000) Z 000 j2000 j2000 j2000 2000 Ω
u1
iS
Z
2k 0.5F
2k 2H
uOC(t) – b
+
1m I sm Z 10( 2 j2)V U
Z L 4 (1 j) 4 2 45 Ω
。 6. 求图示电路中开路电压 U j8 解:
I1 3
+ –
300°V j4
j8 U –
+
30 30 I1 6 53 . 13 A 3 j4 553.13
j8 I 4836.7 V U 1
列网孔电流方程 1 (4 j2 j2) I ( j2) 0 I
(1)
1 ( j2) I (1 j2) j5 1 50 (2) I 1 j0.5I 1 j2 I 0 由 (1) 得 I 4I
代入 (2) 得
I j2 I 5(1 j) I
–
b
u( t ) 17.8 cos(1000t 63.4 ) V
1m j U 1m j10 ( 2 j2) 20 ( j 1) j 2000 U OCm U 20V 2000 j2000 1 j 1 j j1
七、正弦稳态电路如图,已知 iS(t) = 10cos(1000t) mA; (1) 求自ab端向左看戴维南等效电路时域模型; (2) 若负载A是 1/4F电容,求它两端的电压 u(t)。
4. GCL并联电路中,R = 1k,L = 0.5H,C = 50F,则此电路 的谐振频率f0 = 31.83 Hz ,谐振时品质因数Q = 10 。
1 1 解: f 0 31.83 Hz 5 2π LC 2π 0.5 5 10
1 LG C 5 10 5 Q 10 2 2 6 0 LG LG LG 0.5 10
七、正弦稳态电路如图所示,已知iS(t)=10cos(1000t) mA; (1) 求自ab端向左看戴维南等效电路时域模型; (2) 若负载A是1/4F电容,求它两端的电压u(t)。
u1
iS
2k 0.5F
2k 2H
a + u(t) A – b a
解 :(1) I sm 100 mA
5. 电路中ZL= 4 2 45 Ω ,
1:2
获得最大功率。
IS
2
j2
ZL
解:
j4 4 Z 0 2 // j2 45 245Ω 2 j2 2 2
1 1 ZL ZL ZL n2 4 1 ZL ZL 1 j 4
* Z0 获得最大功率 当 ZL 时,Z L
7. 在图示所示电路中ZL= R + jX,R、X都可变, 求 ZL= ? 时获得最大功率。
10 1 0 A 10 -j10
解: Z 10 ( j10) 5 j5 Ω 0
ZL
10 j10
Z L 5 j5 Ω
。(15分) 和电压 U 8. 求电路中电流 I
