电路 第9章习题2 正弦稳态电路的分析
第九章正弦稳态电路分析

矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。
如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。
㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。
(2 列出开发利用方案编制所依据的主要基础性资料的名称。
如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。
对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。
二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。
2、国内近、远期的需求量及主要销向预测。
㈡产品价格分析
1、国内矿产品价格现状。
2、矿产品价格稳定性及变化趋势。
三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。
2、矿区矿产资源概况。
3、该设计与矿区总体开发的关系。
㈡该设计项目的资源概况
1、矿床地质及构造特征。
2、矿床开采技术条件及水文地质条件。
电路第9章 正弦稳态电路的分析

I 1 Y G jC j G jB Y y U L
§9-1
阻抗和导纳
Y—复导纳;|Y| —复导纳的模;y—
导纳角; G —电导(导纳的实部);
B —电纳(导纳的虚部);
| Y | G 2 B 2 转换关系: 或 B y arctan G
I
相量图:选电压为参考向量,
u 0
y
IG
.
IB U
I I G2 I B2 I G2 (I C I L )2
注意
RLC并联电路会出现分电流大于总电流的现象
§9-1
阻抗和导纳
+ I R U -
等效电路
IR
1 jC eq
I B
(3)wC<1/wL,B<0,y<0,电路为感性,电流落后电压;
1 Y 0.0128 50.20 Z 78.150.20 0.0082 j0.0098 S 1
R’
L’
1 1 1 0.102mH R 122 L 0.0098 G 0.0082
§9-1
阻抗和导纳
① 一端口N0的阻抗或导纳是由其内部的参数、
y
IG
I
.
U
.
I I I I (I L IC )
2 G 2 B 2 G
2
IC .
IL
§9-1
阻抗和导纳
I
+
IR
R
j Leg
等效电路
I B
U -
(4)wC=1/wL,B=0,j y =0,电路为电阻性, 电流与电压同相。
I
C
IL
I IG
最全第九章(正弦稳态电路分析)习题解答打印版.doc
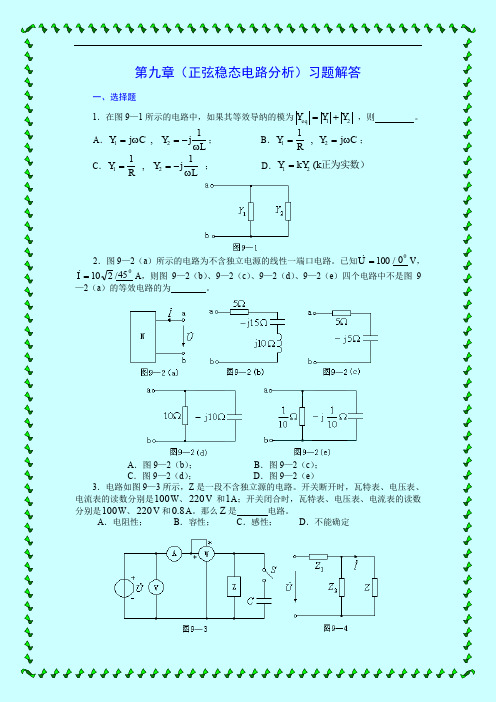
第九章(正弦稳态电路分析)习题解答一、选择题1.在图9—1所示的电路中,如果其等效导纳的模为21Y Y Y eq += ,则 。
A .L Y C Y ω-=ω=1j, j 21; B .C Y RY ω==j , 121;C .L Y R Y ω-==1j , 121 ;D .正为实数)k kY Y ( 21=2.图9—2(a )所示的电路为不含独立电源的线性一端口电路。
已知00 /100=UV ,045 /210=I A ,则图9—2(b )、9—2(c )、9—2(d )、9—2(e )四个电路中不是图9—2(a )的等效电路的为 。
A .图9—2(b );B .图9—2(c );C .图9—2(d );D .图9—2(e )3.电路如图9—3所示,Z 是一段不含独立源的电路。
开关断开时,瓦特表、电压表、电流表的读数分别是100W 、220V 和1A ;开关闭合时,瓦特表、电压表、电流表的读数分别是100W 、220V 和8.0A 。
那么Z 是 电路。
A .电阻性;B .容性;C .感性;D .不能确定4.电路如图9—4所示,U固定不变。
如果 ,则改变Z (Z 不等于无限大)时,I不变。
A .21Z Z =; B .21Z Z -=; C .21Z Z =; D .)Arg()Arg(21Z Z =5.Ω=10R 的电阻,F 1μ=C 的电容与电感L 串联,接到频率1000Hz 的正弦电压源上。
为使电阻两端的电压达到最高,电感应取 。
A .1H ;B .π21H; C .21H ; D .241πH二、填空题1.若Ω=3R ,Ω=ω6L ,Ω=ω2011C ,Ω=ω2012C ,则图9—5所示电路的输入阻抗为 j4)3(-Ω。
.2.线性一端口电路如图9—6所示,A /02 V ,30/5000=-=I U。
则此一端口电路吸收的复功率,有功功率、无功功率分别为V A 30/1000、W 350、50Var 。
电路原理:第9章 正弦稳态电路的分析

1000 166.99 52.3
0.652.3
A
I2
j
1 C
1 R1 j C
I1
j318.47 1049.5 17.7
0.652.3
0.181 20
A
I3
R1
R1 j 1
C
I1
1000 1049.5 17.7
0.652.3
0.5770
A
例2.
_
列写电路的回路电流方程和节点电压方程
Z Z1Z2 Z1 Z2
例 求图示电路的等效阻抗, =105rad/s 。
解 感抗和容抗为:
X L L 105 1103 100
1
1
XC C 105 0.1106 100
R1
30 1mH
R2 100 0.1F
Z
R1
jX L (R2 jX C ) jX L R2 jX C
U I
j
L
jX L
Z可以是实数,也可以是虚数
2. RLC串联电路
iR
L
+ + uR - + uL - +
u
C uC
-
-
.
IR
j L
+
+
.
U
-
R
+
.
U
L
-
.
1
U -
jω C
+. -U C
..
由KVL: U UR
[R j(L 1 C
.
U
)]
.
L UC
I [R
.
RI
j( X
.
jL I j
9章_正弦稳态电路的分析n

9-1 阻抗和导纳 9-2 电路的相量图 9-3 正弦稳态电路的分析 9-4 正弦稳态电路的功率 9-5 复功率 9-6 最大功率传输
一、复阻抗Z
9-1 阻抗和导纳
I
+
U
无源 线性
-
I
+
U
Z
-
正弦激励下的无独立源线性网络,定义其入端等效复阻抗Z:
Z
UI
U I
(u
Z 2Ω I=8A ?
两个阻抗并联时,在什么情况下:
1 1 1 成立。
Z Z1 Z2
1. 图示电路中,已知 X L XC R 2Ω 电流表A1的读数为3A,
试问(1)A2和A3的读数为多少? + A1 A2 A3 (2)并联等效阻抗Z为多少? U L R C -
2. 如果某支路的阻抗 Z (8 j6)Ω, 则其导纳
阻抗三角形(impedance triangle)
|Z|
z
R
z > 0
X或
R
z
X |Z|
z < 0
| Z |
R2 X 2
φ arctan X R
R = |Z|cos z X = |Z|sin z
阻抗Z可以用加压求流法计算(含受控源),也可以用复阻 抗的串并联等效计算。
UL超 前I90°
由相量图可求得:
V 读数为141V
UL
100I1 10
U
45°I 45°
100UAB
10 2 I2
练习题
一、 如图电路中,已知:
i
u(t) 10cos(400π t 60o) V
第九章 正弦稳态电路的分析

第九章正弦稳态电路的分析 §9-1阻抗和导纳§9-2阻抗(导纳)的串联和并联§9-3正弦稳态电路的分析§9-4正弦稳态电路的功率§9-5复功率§9-6最大传输功率§9-7串联电路的谐振§9-8并联电路的谐振串、并联谐振的特性比较§9-1阻抗和导纳一、阻抗1、阻抗的定义无源线性一端口网络等效电路§9-1阻抗和导纳2、单个元件的阻抗电阻电容电感§9-1阻抗和导纳3、RLC 串联电路的阻抗或§9-1阻抗和导纳对于RLC 串联电路:(1)当ωL >1/ωC 时§9-1阻抗和导纳(2)当ωL <1/ωC时§9-1阻抗和导纳(3)当ωL =1/ωC时§9-1阻抗和导纳二、导纳1、导纳的定义无源线性一端口网络等效电路§9-1阻抗和导纳2、单个元件的导纳电阻电容电感§9-1阻抗和导纳3、RLC 并联电路的导纳或§9-1阻抗和导纳对于RLC 并联电路:(1)当ωL >1/ωC时§9-1阻抗和导纳(2)当ωL <1/ωC 时§9-1阻抗和导纳(3)当ωL = 1/ωC时§9-1阻抗和导纳三、复阻抗和复导纳的等效互换同一个两端口电路阻抗和导纳可以互换,互换的条件为:即:§9-1阻抗和导纳串联电路和其等效的并联电路它的阻抗为:其等效并联电路的导纳为:即等效电导和电纳为:§9-1阻抗和导纳同理,对并联电路,它的导纳为其等效串联电路的阻抗为:即等效电阻和电抗为:§9-1阻抗和导纳)60sin(25 +=t u ωHz f 4103⨯=例9-1电路如图(a)所示,已知:R =15Ω,L =0.3mH,C =0.2μF, ,。
求i ,u R ,u L ,u C 。
VU 605∠=•解:电路的相量模型如图(b )所示,其中:§9-1阻抗和导纳C j L j R Z ωω1-+=A Z U I 4.3149.04.6354.33605-∠=∠∠==••V I L j U L 4.8642.84.3149.0905.56∠=-∠⨯∠==••ωV I R U R 4.3235.24.3149.015-∠=-∠⨯==••V I Cj U C 4.9395.34.3149.0905.261-∠=-∠⨯-∠==••ω因此总阻抗为总电流为电感电压为电阻电压为电容电压为相量图如图(c )所示,各量的瞬时式为:§9-1阻抗和导纳例9-2 RL 串联电路如图(a )所示,求在ω=106rad/s 时的等效并联电路图(b )。
正弦稳态电路的分析

I Y U i u
导纳三角形
|Y|
2019/2/26
B G
12/71
分析 R、L、C 并联电路得出:
(1)Y=G+j(C-1/L)=|Y|∠为复数,故称复导纳; (2)C > 1/L ,B>0, ‘>0,电路为容性,电流超前电压
C<1/L ,B<0, ‘<0,电路为感性,电流落后电压; C=1/L ,B=0, =0,电路为电阻性,电流与电压同相
2019/2/26
22/71
例5 已知:R1 1000 , R2 10 , L 500mH , C 10F ,
U 100V , 314rad / s , 求:各支路电流。
R1 i2 i1 i3 + _ u
I 1
C R2 L + U _
I 2
R1
j 1 C
k 1 k 1 n n
分流公式
Yi Ii I Y
两个阻抗Z1、Z2的并联等效阻抗为:
2019/2/26
Z1 Z 2 Z Z1 Z 2
18/71
例3 求图示电路的等效阻抗, =105rad/s 。 解 感抗和容抗为:
X L L 105 1 103 100
20/71
9. 3
正弦稳态电路的分析
正弦电路相量分析: KCL : I 0 KVL : U 0 元件约束关系: U Z I 或 I YU
电阻电路与正弦电流电路的分析比较:
电阻电路 : KCL : i 0 KVL : u 0 元件约束关系: u Ri 或 i Gu
第九章 正弦稳态电路的分析
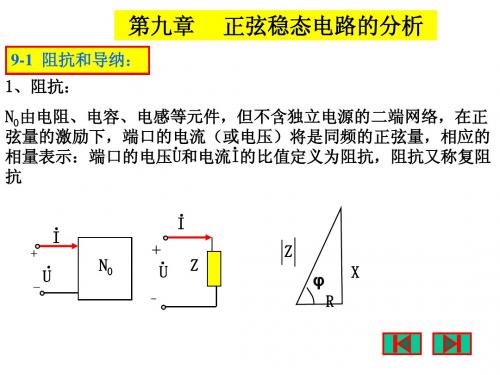
依据上述数据,还可求出 依据上述数据,还可求出R1、L1: :
& Us Z1 = = 38∠ 75 0 & I1 Z 1 = R 1 + j ωL 1 R 1 = 9.84 36.71 L1 = = 116.9mH 314
9-5
正弦稳态电路的功率 。 i u -。
+
设一端口N内部不含独立源,仅有 、 、 设一端口 内部不含独立源,仅有R、L、C 内部不含独立源 吸收的功率: 吸收的功率:p=ui(关联方向) (关联方向) i = 2I cos(ωt + Ψi ) 设u = 2U cos(ωt + Ψu )
u
ϕ = Ψu − Ψi )
) − UIsin(-ϕ ) sin( 2ωt + 2Ψ ) = UI cos ϕ{1 + cos[2( ωt + Ψ ]} + UI sin ϕ sin[2(ωt + Ψ )]
u u
平均功率又称有功功率 一周期内的平均值 1T 1T p = ∫ pdt = ∫ UI[ cos ϕ + cos( 2ωt + Ψu + Ψi )]dt =UI cos ϕ T0 T0 功率因数 cosϕ用λ = cosϕ 无功功率 ϑ = UIsinϕ 视在功功率 S = UI
& 1 I I 导纳:阻抗Z的倒数定义为导纳 Y 的倒数定义为导纳: 导纳:阻抗 的倒数定义为导纳: = = = ∠ψ i − ψ u = Y ∠ϕ y & Z U U Y的代数式可写为: 的代数式可写为: 的代数式可写为 Y = G + jB ← 电纳 ↑ 电导 电阻YR =
单个元件的导纳: 单个元件的导纳:
单个元件的阻抗: 单个元件的阻抗:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
9-001、 已知图示正弦电路中,电压表的读数为V 1 :6V ;V 2 :2V ;U S =10V 。
求:(1)、图中电压表V 3、V 4的读数; (2)、若A I 1.0=,求电路的等效复阻抗; (3)、该电路呈何性质? 答案(1)V U U U 32.622214=+= V 4的读数为 6.32V ; 23221)(U U U U S -+=64)(212232=-=-U U U U s832±=-U U 取 V U 10823=+=,所以V 3的读数为10 V 。
(2)、A I 1.0=,电路的等效复阻抗: Ω===1001.010I U Z ︒-=-=-=1.5368arctan arctan132U U U ϕ Ω-=︒-+︒=)8060()1.53sin(1.53cos 100j j Z (3)、由于复阻抗虚部为负值,故该电路呈电容性。
9-002、答案V 1 -R V 3Lu s V 2 +CV 49-003、求图示电路的等效阻抗,已知ω=105 rad/s 。
例9 — 3 图解:感抗和容抗为:所以电路的等效阻抗为9-004、例9-4图示电路对外呈现感性还是容性?例9 — 4 图解: 图示电路的等效阻抗为:所以 电路对外呈现容性。
9-005、3-9日光灯电源电压为V 220,频率为Hz 50,灯管相当于Ω300的电阻,与灯管串联的镇流器(电阻忽略不计)的感抗为Ω500,试求灯管两端电压与工作电流的有效值。
解:电路的总阻抗为 Ω≈+=58350030022Z 此时电路中流过的电流:A Z U I 377.0583220===灯管两端电压为: V RI U R 113377.0300=⨯==9-006、5、 与上题类似今有一个40W 的日光灯,使用时灯管与镇流器(可近似把镇流器看作纯电感)串联在电压为220V ,频率为50Hz 的电源上。
已知灯管工作时属于纯电阻负载,灯管两端的电压等于110V ,试求镇流器上的感抗和电感。
这时电路的功率因数等于多少?解:∵P =40W U R =110(V) ω=314rad/s ∴36.011040====R L R U P I I (A) ∵U U U L R 222+=∴5.1901102202222=-=-=U U U R L (V) ∴52936.05.190===I U X LL L (Ω)69.1314529===ωX L L (H)这时电路的功率因数为: 5.0220110cos cos ===U U R ϕ9-007、日光灯电路在正常工作时可等效为R 、L 串联电路(灯管等效为电阻R )(镇流器可近似把镇流器看作纯电感L)。
今测其实际工作电压U=220V ,电流I=0.36A ,功率P=44.6,电源频率为50Hz 。
试求:灯管的R ,镇流器的感抗和电感。
这时电路的功率因数等于多少? 解:Ω===34436.06.4422I P R 563.052206.44cos =⨯==UI P ϕ又22cos LXR R +=ϕΩ==505L X L ωH X L L61.1314505===ω(344, 505,1.61 0.563)9-008、图示正弦交流电路,当开关K 打开或闭合时,电流表、功率表的读数均不变。
已知:正弦交流电源的频率为50HZ ,U= 250V ,I=5A ,P=1000W ,试求R 、X L 和C 。
解:当开关K 闭合时Ω===405100022I P R Ω===505250I U Z RLΩ=-=30405022L X 当开关K 打开时Ω===505250I U Z 5022=-+=)(C L X X R Z 求得 Ω=60c XF X C C μω536031411=⨯==9-201、1、例题3-13 (书中80页)图示正弦交流电路,已知:Ω=281R ,Ω=96L ω,Ω=482R ,Ω=641Cω,V 240=U ,求电路及各支路的有功功率,无功功率及视在功率。
解Ω︒∠=+=+=74.73100962811J JX R Z L Ω︒-∠=-=-=13.5380644822J JX R Z CA Z U I ︒-∠=︒∠︒∠==74.734.274.73100024011&& A Z U I ︒∠=︒-∠︒∠==13.53313.538002022&& AJ J Z U I I I ︒∠=++-=︒∠+︒-∠==+=22.2274.24.28.1304.2672.013.53374.734.2121&&&&支路W UI P 3.16174.73cos 4.2240cos 111=︒⨯⨯==ϕvar 55374.73sin 4.2240sin 111=︒⨯⨯==ϕUI Q支路2 W UI P 432)13.53cos(3240cos 222=︒-⨯⨯==ϕvar 576)13.53sin(3240sin 221-=︒-⨯⨯==ϕUI Q总功率W UI P 3.593)22.2cos(474.2240cos =︒-⨯⨯==ϕ(W P P P 3.59321=+=var 55374.73sin 4.2240sin 11=︒⨯⨯==ϕUI Q(或 var 2321-=+=Q Q Qvar 23)22.2sin(474.2240sin -=︒-⨯⨯==ϕUI Q2、 与上题类似 图示电路中,已知R 1=40Ω,X L =30Ω,R 2=60Ω,X c =60Ω,接至220V 的电源上.试求各支路电流及总的有功功率、无功功率和功率因数。
解:设︒=0/220.U (V)则︒-=+︒=+=9.36/4.430400/22011j X j R U I L&& (A) 同理︒=-︒=-=45/59.260600/22022j X j R U I C && (A)∵ ︒-=︒+︒-=+=61.8/41.545/59.29.36/4.421I I I &&&(A) ∴18.161.8cos 41.5220cos =︒⨯⨯==ϕUI P (KW)2.17861.8sin 41.5220sin =︒⨯⨯==ϕUI Q (Var)3、 3-8 一个电阻和电感串联的无源二端网络,当外加电压V )15100sin(311︒+=t u 时,电流为 A )45100sin(14.14︒-=t i 。
求:该网络中的电阻R 和电感L.解:对应的电压、电流相量为:V 152********︒∠=︒∠=U &,A 4510︒-∠=I &Ω+=Ω︒∠=︒-∠︒∠==)19j 11(6022451015220eqIU Z && Ω=11R H X L L 19.010019===ω9-301、例9-5 图示为 RC 选频网络,试求 u 1 和 u 0 同相位的条件及?01=U U&&解:设输出电压输出电压和输入电压的比值例 9 — 5 图因为当,上式比值为实数,则u1和u0同相位,此时有9-302、例9-11已知图示电路:Z =10+j50Ω,Z1=400+j1000Ω,问:β等于多少时,相位差90°?例9 — 11 图解:根据KVL 得所以令上式的实部为零,即得: ,即电压落后电流90°相位。
9-303、例9-12已知图(a)所示电路中,U =115V , U1=55.4V , U2= 80V , R1=32W , f=50Hz ,求:电感线圈的电阻R2和电感L2。
例9 — 12 (a)(b)解:方法-、画相量图分析。
相量图如图(b)所示,根据几何关系得:代入数据得因为所以方法二、列方程求解,因为令上式等号两边实部、虚部分别相等得:解得其余过程同方法一。
9-304、例9-14图示电路,已知:f =50Hz, U =220V, P =10kW, 线圈的功率因素cosφ=0.6 ,采用并联电容方法提高功率因素,问要使功率因数提高到0.9, 应并联多大的电容C,并联前后电路的总电流各为多大?例9—14 图解:所以并联电容为:未并电容时,电路中的电流为:并联电容后,电路中的电流为:9-142答案电压表读数为2V或者18V。
9-172、答案9-143、答案电流表读数为5A 9-148、答案9-153、答案9-150答案9-155答案9-151答案9-98答案9-156三.典型例题例8-1 写出图示电路的输入阻抗ab Z 表达式,ω已知,不必化简。
(a) (b)图8-6 例8-1图解:(a))j (j 1)j (j 1221ab L R C L R CR Z ωωωω+++⨯+=;(b))j 1()j ()j 1()j (2121ab CR L R CR L R Z ωωωω++++⨯+=例8-2 RLC 串联电路,已知:Ω=15R ,m H 12=L ,F μ5=C , 端电压V )5000cos(2100t u =。
求:电流i 及各元件的电压相量,并画相量图。
解:用相量法解题时,可先写出已知相量和设定待求相量。
已知相量V 0100︒∠=U &,待求相量是I &,R U &,L U &和C U &各部分阻抗:Ω=15R Z , Ω==60j j L L Z ω,Ω-==j40j 1CZ C ω 图8-7 例8-2图 Ω+=-+=++=j2015j4060j 15C L R eq Z Z Z ZΩ︒∠=13.5325 A 13.53413.53250100eq ︒∠=∠∠==οο&&Z U I 各元件电压相量:V 13.5360R ︒-∠==I R U &&V 87.36240j ︒∠==I L U L &&ω 图8-8 例8-2相量图V 13.143160j 1︒-∠==I CU C &&ω 正弦电流i 为:A )13.535000cos(24︒-=t i例8-3 图示电路,已知:Ω=51R ,Ω=22R ,Ω=35L ω,Ω=381Cω,A 155S ︒-∠=I &,求等效阻抗eq Z 及1I &、2I &,并画出电流相量图。
图8-9 例8-3图 图8-10 例8-3相量图解:Ω+=+=j355j 11L R Z ω;Ω-=+=j382j 122CR Z ω Ω︒∠=+++=+=08.187.176j38-2j355j38)-j35)(2(5 2121eq Z Z Z Z Z分流公式:A 79.7898.24155j38-2j355j38-2 S 2121︒-∠=︒-∠⨯++=+=I Z Z Z I &&; A 26.9020.23155j38-2j355j355 S2112︒∠=︒-∠⨯+++=+=I Z Z Z I && 相量图见图8-10例8-4 图8-11所示电路,试列出该电路的节点电压方程及网孔电流方程。
