LINGO练习题复习资料
Lingo作业练习

Lingo作业1 、用长度500cm的钢条,截成长度为98和78cm的两种毛坯,要求截出长度98cm的毛坯10000根,78cm的毛坯20000根,问怎么样截法,才使所用原材料最少。
2、某钢管零售商从钢管厂进货,将钢管按照顾客的要求切割后售出,从钢管厂进货时得到的钢管都是19m.(1)现有一客户需要50根4m、20根6m和15根8m的钢管,应如何下料最节省?(2)零售商如果采用的不同切割模式太多,将会导致生产过程的复杂化,从而增加生产和管理成本,所以该零售商规定采用的不同切割模式不能超过3种。
此外该客户需要(1)中的三种钢管外,还需要10根5m的钢管,应如何下料最省?3、电视台为某个广告公司特约播放两套片集,其中片集甲播映时间为20min,广告时间为1min,收视观众60万;片集乙播映时间10min,广告时间1min,收拾观众20万,广告公司规定每周至少有6min广告,而电视台每周只能为该公司提供不多于80min的节目时间。
电视台每周播映两套片集各多少次,才能获得最高的收视率?4、某公司计划在A,B,C三个区建立销售部,确定了7个位置M1-M7可供选择,并且规定:(1)在A区,从M1,M2,M3中至多选两个;(2)在B区,M4,M5中至少选一个;(3)在C区,M6,M7中至少选一个;已知:如果选择M1-M7,则分别投资为200,300,350,250,350,200,400万元,预计每年可以获利50,80,120,70,100,60,120万元,现在公司可用于投资的资金是1200万元,问应如何建立销售部?5、有4名同学到一家公司参加三个阶段的面试:公司要求每个同学都必须首先找公司秘书处初试,然后到部门主管处复试,最后到经理处参加面试,并且不允许插队(即在任何一个阶段4名同学的顺序是一样的)。
由于4名同学的专业背景不同,所以每个人在三个阶段的面试时间也不同,如下表所示(单位:min):这4名同学约定他们全部面试完以后一起离开公司。
专题资料(2021-2022年)lingo学习教程

例3.7
sets:
days /MO,TU,WE,TH,FR,SA,SU/:needs,cost;
endsets
data:
needs cost = 20 100;
enddata
3.1.5 数据部分的未知数值
有时只想为一个集的部分成员的某个属性指定值,让其余成员的该属性保持未知,以 便让LINGO去求出它们的最优值。 在数据声明中输入两个相连的逗号表示该位置对应的集成员的属性值未知。两个逗号 间可以有空格。
• Setname是你选择的来标记集的名字,最好具有较强的 可读性。集名字必须严格符合标准命名规则:以拉丁字 母或下划线(_)为首字符,其后由拉丁字母(A—Z)、 下划线、阿拉伯数字(0,1,…,9)组成的总长度不 超过32个字符的字符串,且不区分大小写。
• 注意:该命名规则同样适用于集成员名和属性名等的命 名。
!产量约束;
@for(warehouses(I):
@sum(vendors(J):
volume(I,J))<=capacity(I));
• !这里是数据;
• data:
• capacity=60 55 51 43 41 52;
• demand=35 37 22 32 41 32 43 38;
• cost=6 2 6 7 4 2 9 5
• LINGO有两种类型的集:原始集(primitive set)和 派生集(derived set)。
• 一个原始集是由一些最基本的对象组成的。 • 一个派生集是用一个或多个其它集来定义的,也
就是说,它的成员来自于其它已存在的集。
2.3 模型的集部分
• 集部分是LINGO模型的一个可选部分。在 LINGO模型中使用集之前,必须在集部分事 先定义。集部分以关键字“sets:”开始,以 “endsets”结束。一个模型可以没有集部分, 或有一个简单的集部分,或有多个集部分。 一个集部分可以放置于模型的任何地方,但 是一个集及其属性在模型约束中被引用之前 必须定义了它们。
Lingo精选题目及参考答案

Lingo 精选题目及答案答题要求:将Lingo 程序复制到Word 文档中,并且附上最终结果。
1、简单线性规划求解(目标函数)2134maxx x z += s.t.(约束条件)⎪⎪⎩⎪⎪⎨⎧≥≤≤+≤+0,781022122121x x x x x x x2、整数规划求解219040Max x x z +=⎪⎩⎪⎨⎧≥≤+≤+0,702075679212121x x x x x x 3、0-1规划求解Max 432215.18.04.0x x x x f +++=10106234321≤+++x x x x10,,,4321或=x x x x4、非线性规划求解||4||3||2||min 4321x x x x z +++=s.t. ⎪⎪⎩⎪⎪⎨⎧-=+--=-+-=+--2132130432143214321x x x x x x x x x x x x5、集合综合应用产生一个集合5052--=x x y ,(10,...,2,1=x ),求y 前6个数的和S 1,后6个数的和S 2,第2~8个数中的最小值S 3,最大值S 4。
6、综合题要求列出具体的目标函数和约束条件,然后附上Lingo 程序和最终结果。
6.1 指派问题有四个工人,要指派他们分别完成4项工作,每人做各项工作所消耗的时间如下表:问指派哪个人去完成哪项工作,可使总的消耗时间为最小?6.2 分配问题某两个煤厂A1,A2每月进煤数量分别为60t和100t,联合供应3个居民区B1,B2,B3。
3个居民区每月对煤的需求量依次分别为50t,70t,40t,煤厂A1离3个居民区B1,B2,B3的距离依次分别为10km,5km,6km,煤厂A2离3个居民区B1,B2,B3的距离分别为4km,8km,12km。
问如何分配供煤量使得运输量(即t·km)达到最小?1、model:max=4*x1+3*x2;2*x1+x2<10;x1+x2<8;x2<7;end2、model:max=40*x1+90*x2;9*x1+7*x2<56;7*x1+20*x2<70;@gin(x1);@gin(x2);end3、model:max=x1^2+0.4*x2+0.8*x3+1.5*x4;3*x1+2*x2+6*x3+10*x4<10;@bin(x1); @bin(x2);@bin(x3); @bin(x4);end4、model:max=@abs(x1)+2*@abs(x2)+3*@abs(x3)+4*@abs(x4);x1-x2-x3+x4=0;x1-x2+x3-3*x4=1;x1-x2-2*x3+3*x4=-1/2;end5、model:sets:jihe/1..10/:y;ss/1..4/:S;endsets!由于y和s中部分有负数,所以要先去掉这个约束;@for(jihe:@free(y));@for(ss(i):@free(S));!产生元素;@for (jihe(x):y(x)=x^2-5*x-50); S(1)=@sum (jihe(i)|i#le#6:y(i)); S(2)=@sum (jihe(i)|i#ge#5:y(i));S(3)=@min (jihe(i)|i#ge#2 #and# i#le#8:y(i)); S(4)=@max (jihe(i)|i#ge#2 #and# i#le#8:y(i)); end6.1、设:第i 个工人做第j 项工作用时ij t ,标志变量ij f 定义如下:⎩⎨⎧=其他件工作个工人去做第指派第01j i f ijmin∑∑==⨯4141i j ij ijt fs.t. 141=∑=i ijf()4,3,2,1=j 每份工作都有一人做∑==411j ijf()4,3,2,1=i 每人都只做一项工作model : sets :work/A B C D/;worker/jia yi bing ding/; time(worker,work):t,f; endsets!目标函数可以用[obj]标志出,也可以省略;[obj] min =@sum (time(i,j):t(i,j)*f(i,j)); data :!可以直接复制表格,但是在最后要有分号; t=; e !每份工作都有一人做;@for (work(j):@sum (time(i,j):f(i,j))=1); !每人都只做一项工作;@for (worker(i):@sum (time(i,j):f(i,j))=1); !让f 取0-1值,此条件可以省略;!@for(time(i,j):@bin(f(i,j))); end6.2设:煤厂进煤量i s ,居民区需求量为i d ,煤厂i 距居民区j 的距离为ij L ,煤厂i 供给居民区j 的煤量为ij g那么可以列出如下优化方程式∑∑==⨯=3121min j i ij ij L gs.t ()3,2,121==∑=j d gi jij()2,131=≤∑=i s gj iijmodel : sets :supply/1,2/:s; demand/1,2,3/:d;link(supply,demand):road,sd; endsets data :road=10 5 6 4 8 12; d=50 70 40; s=60 100; enddata[obj] min =@sum (link(i,j):road(i,j)*sd(i,j)); @for (demand(i):@sum (supply(j):sd(j,i))=d(i)); @for (supply(i):@sum (demand(j):sd(i,j))<s(i));end1.线性规划模型。
Lingo精选题目及答案

Lingo 精选题目及答案答题要求:将Lingo 程序复制到Word 文档中,并且附上最终结果。
1、简单线性规划求解(目标函数)2134maxx x z += s.t.(约束条件)⎪⎪⎩⎪⎪⎨⎧≥≤≤+≤+0,781022122121x x x x x x x2、整数规划求解219040Max x x z +=⎪⎩⎪⎨⎧≥≤+≤+0,702075679212121x x x x x x 3、0-1规划求解Max 432215.18.04.0x x x x f +++=10106234321≤+++x x x x10,,,4321或=x x x x4、非线性规划求解||4||3||2||min 4321x x x x z +++=s.t. ⎪⎪⎩⎪⎪⎨⎧-=+--=-+-=+--2132130432143214321x x x x x x x x x x x x5、集合综合应用产生一个集合5052--=x x y ,(10,...,2,1=x ),求y 前6个数的和S 1,后6个数的和S 2,第2~8个数中的最小值S 3,最大值S 4。
6、综合题要求列出具体的目标函数和约束条件,然后附上Lingo 程序和最终结果。
6.1 指派问题6.2 分配问题某两个煤厂A1,A2每月进煤数量分别为60t和100t,联合供应3个居民区B1,B2,B3。
3个居民区每月对煤的需求量依次分别为50t,70t,40t,煤厂A1离3个居民区B1,B2,B3的距离依次分别为10km,5km,6km,煤厂A2离3个居民区B1,B2,B3的距离分别为4km,8km,12km。
问如何分配供煤量使得运输量(即t·km)达到最小?1、model:max=4*x1+3*x2;2*x1+x2<10;x1+x2<8;x2<7;end2、model:max=40*x1+90*x2;9*x1+7*x2<56;7*x1+20*x2<70;@gin(x1);@gin(x2);end3、model:max=x1^2+0.4*x2+0.8*x3+1.5*x4;3*x1+2*x2+6*x3+10*x4<10;@bin(x1); @bin(x2);@bin(x3); @bin(x4);end4、model:max=@abs(x1)+2*@abs(x2)+3*@abs(x3)+4*@abs(x4);x1-x2-x3+x4=0;x1-x2+x3-3*x4=1;x1-x2-2*x3+3*x4=-1/2;end5、model:sets:jihe/1..10/:y;ss/1..4/:S;endsets!由于y和s中部分有负数,所以要先去掉这个约束;@for(jihe:@free(y));@for(ss(i):@free(S));!产生元素;@for (jihe(x):y(x)=x^2-5*x-50); S(1)=@sum (jihe(i)|i#le#6:y(i)); S(2)=@sum (jihe(i)|i#ge#5:y(i));S(3)=@min (jihe(i)|i#ge#2 #and# i#le#8:y(i)); S(4)=@max (jihe(i)|i#ge#2 #and# i#le#8:y(i)); end6.1、设:第i 个工人做第j 项工作用时ij t ,标志变量ij f 定义如下:⎩⎨⎧=其他件工作个工人去做第指派第01j i f ijmin∑∑==⨯4141i j ij ijt fs.t. 141=∑=i ijf()4,3,2,1=j 每份工作都有一人做∑==411j ijf()4,3,2,1=i 每人都只做一项工作model : sets :work/A B C D/;worker/jia yi bing ding/; time(worker,work):t,f; endsets!目标函数可以用[obj]标志出,也可以省略;[obj] min =@sum (time(i,j):t(i,j)*f(i,j)); data :!可以直接复制表格,但是在最后要有分号; t=; e !每份工作都有一人做;@for (work(j):@sum (time(i,j):f(i,j))=1); !每人都只做一项工作;@for (worker(i):@sum (time(i,j):f(i,j))=1); !让f 取0-1值,此条件可以省略;!@for(time(i,j):@bin(f(i,j))); end6.2设:煤厂进煤量i s ,居民区需求量为i d ,煤厂i 距居民区j 的距离为ij L ,煤厂i 供给居民区j 的煤量为ij g那么可以列出如下优化方程式∑∑==⨯=3121min j i ij ij L gs.t ()3,2,121==∑=j d gi jij()2,131=≤∑=i s gj iijmodel : sets :supply/1,2/:s; demand/1,2,3/:d;link(supply,demand):road,sd; endsets data :road=10 5 6 4 8 12; d=50 70 40; s=60 100; enddata[obj] min =@sum (link(i,j):road(i,j)*sd(i,j)); @for (demand(i):@sum (supply(j):sd(j,i))=d(i)); @for (supply(i):@sum (demand(j):sd(i,j))<s(i));end1.线性规划模型。
LINGO练习

∑=nj i ijij xc1,1 解非线性方程组⎪⎩⎪⎨⎧=+++=+4222222y y x x y x2 装配线平衡模型 一条装配线含有一系列的工作站,在最终产品的加工过程中每个工作站执行一种或几种特定的任务。
装配线周期是指所有工作站完成分配给它们各自的任务所化费时间中的最大值。
平衡装配线的目标是为每个工作站分配加工任务,尽可能使每个工作站执行相同数量的任务,其最终标准是装配线周期最短。
不适当的平衡装配线将会产生瓶颈——有较少任务的工作站将被迫等待其前面分配了较多任务的工作站。
问题会因为众多任务间存在优先关系而变得更复杂,任务的分配必须服从这种优先关系。
这个模型的目标是最小化装配线周期。
有2类约束:① 要保证每件任务只能也必须分配至一个工作站来加工; ② 要保证满足任务间的所有优先关系。
例 有11件任务(A —K )分配到4个工作站(1—4),任务的优先次序如下图。
每件任务所花费的时间如下表。
3 旅行售货员问题(又称货郎担问题,Traveling Salesman Problem )有一个推销员,从城市1出发,要遍访城市2,3,…,n 各一次,最后返回城市1。
已知从城市i 到j 的旅费为ij c,问他应按怎样的次序访问这些城市,使得总旅费最少?可以用多种方法把TSP 表示成整数规划模型。
这里介绍的一种建立模型的方法,是把该问题的每个解(不一定是最优的)看作是一次“巡回”。
在下述意义下,引入一些0-1整数变量:ij x ⎩⎨⎧≠=其它情况,且到巡回路线是从,0,1j i j i 其目标只是使为最小。
这里有两个明显的必须满足的条件:访问城市i 后必须要有一个即将访问的确切城市;访问城市j 前必须要有一个刚刚访问过的确切城市。
用下面的两组约束分别实现上面的两个条件。
ni xnj ij,,2,1,11 ==∑=nj xni ij,,2,1,11==∑=到此我们得到了一个模型,它是一个指派问题的整数规划模型。
lingo题目与答案(附程序)

Lingo软件题目与答案1.一奶产品加工厂用牛奶生产A1,A2两种奶产品,1桶牛奶可以在甲类设备上用12h加工,成3kg A1,或者在乙类设备上用8h加工成4kg A2。
根据市场需求,生产的A1,A2全部能售出,且每千克A1获利24元,每千克A2获利16元。
现在加工厂每天能得到50桶牛奶供应,每天正式工人的劳动时间为480h,并且甲类设备每天最多加工100kg A1,乙类设备的加工时间没有限制,讨论以下问题1)若35元可以买一桶牛奶,做这项投资是否值得?若投资,每天最多购买多少桶牛奶?2)若聘用临时工人以增加劳动时间,付给临时工人的工资最多是多少?3)由于市场需求变化,每千克A1的获利增加到30元,是否改变原有的生产计划?Lingo程序:model:max=72*x+64*y;x+y<50;12*x+8*y<480;3*x<100;end2.一汽车厂生产小、中、大三种类型的的汽车,已知各类型每辆车对钢材、劳动时间的需求,利润以及每月工厂钢材、劳动时间如下表。
1)制定生产计划,使工厂利润最大;2)若生产某类型车,则至少需生产80辆,求改变后的生产计划。
3.建筑工地的位置(a,b)和水泥日用量d如下表,目前有两个临时料场位于P(5,1),Q(2,7),日储量各有20t。
1)求从P,Q两料场分别向各工地运送多少吨水泥,使总的吨公里数最小;2)现打算舍弃原有料场,新建两个料场A,B,求新料场的位置,使新的吨公里数最小,此时与P,Q相比能节省多少吨公里。
4.设从4个产地Ai往3个销地Bj运送物资,产量、销量和单位运费如下表,求总运费最少的运输方案和总运费。
Lingo程序:Model:sets:warehouse/1..3/:a;customer/1..4/:b;link(warehouse,customer):c,x;endsetsdata:a=30,25,21;b=15,17,22,12;c=6,2,6,7,4,9,5,3,8,8,1,5;enddata[OBJ]min=@sum(link:c*x);@for(warehouse(i): @sum(customer(j):x(i,j))<a(i));@for(customer(j):@sum(warehouse(i):x(i,j))=b(j));end5.求下图中v1到v11的最短路Lingo程序:Model:sets:cities/1..11/;roads(cities,cities):p,w,x; endsetsdata: !半连通图和权图;p=0 1 1 1 0 0 0 0 0 0 00 0 1 0 1 0 0 0 0 0 0 0 1 0 1 1 1 1 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 0 1 0 1 0 1 0 1 0 0 0 0 1 1 0 1 0 0 1 1 0 0 0 0 0 1 0 0 0 1 0 10 0 0 0 1 1 1 1 0 1 10 0 0 0 0 0 1 0 1 0 10 0 0 0 0 0 0 1 1 1 0;w=0 2 8 1 0 0 0 0 0 0 02 0 6 0 1 0 0 0 0 0 08 6 0 7 5 1 2 0 0 0 01 0 7 0 0 0 9 0 0 0 00 1 5 0 0 3 0 2 9 0 00 0 1 0 3 0 4 0 6 0 00 0 2 9 0 4 0 0 3 1 00 0 0 0 2 0 0 0 7 0 90 0 0 0 9 6 3 7 0 1 20 0 0 0 0 0 1 0 1 0 40 0 0 0 0 0 0 0 9 2 4;enddatan=@size(cities);min=@sum(roads:w*x);@for(cities(i)|I # ne # 1 # and # I # ne # n: @sum(cities(j):p(i,j)*x(i,j))=@sum(cities(j):p(j,i)*x(j,i)));@sum(cities(j):p(1,j)*x(1,j))=1;end6.露天矿里有若干个爆破生成的石料堆,每堆称为一个铲位,每个铲位已预先根据铁含量将石料分成矿石和岩石。
Lingo考试
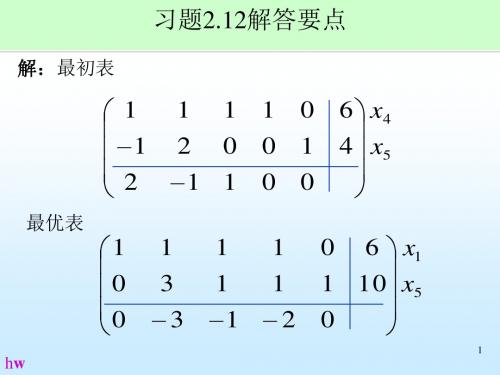
解:最初表
1 1 1 1 2 0 2 1 1
最优表
1 0 0 1
0 1 0 0
6 x4 4 x5 6 x1 1 10 x5 0
1
1 0 0
hw
1 3 3
1
1 1 1 2
习题2.12(a)
1 0 1 0 1 最优基 B 1 1 , 其逆 B 1 1 (a) 因x1是基变量,由最优表可得
5
0 2/3 0 2/3 1 1/ 3 0 5/3
*
新的最优值
z 28 / 3
习题2.16(a)
解:最初表
3 5 1 0 450 x4 6 3 4 5 0 1 300 x 5 30 10 40 0 0 最优表 1 1/ 3 0 1/ 3 1/ 3 50 x1 1 1 1/ 5 2 / 5 30 x3 0 0 20 0 2 6
1 50 b1 3 1 B b 0 30 1 b 1 5 得 150 b1 150,所以雇佣150h为宜。
hw
9
最优生产计划:A、C分别生产50、30件,不生产B 最大利润为2700元
6
hw
习题2.16(b)
因x1是基变量,由最优表可得
1 1 1 20 1 2 1 6 1 0 3 3 3
从而
6 1 18
即当 24 C1 48 时, 上述最优计划不变;
当 C3 (, 2] 时,问题的最优解不变 。
hw
2
习题2.12(b)
6 1 0 1 6 1 由 10 1 1 0 10 0 1 得 1 6
上机练习题目(LINGO部分)

表
料场 a b d
工地的位置(a,b)及水泥日用量d 1 2 3 4 5 6 1.25 8.75 0.5 5,75 3 7.25 1.25 0.75 4.75 5 6.5 7.75 3 5 4 7 6 11
十一、某厂生产的一种产品有甲、乙两个牌号,讨论在产 销平衡的情况下如何确定各自的产量,使总的利润最大。 所谓产销平衡指工厂的产量等于市场上的销量,没有卖不 出去的产品的情况。显然,销售总利润既取决于两种牌号 产品的销量和(单件)价格,也依赖于产量和(单件)成 本。按照市场经济规律,甲的价格p1固然会随其销量x1的 增长而降低,同时乙的销量x2的增长也会使甲的价格有稍 微的下降。可以简单地假设价格与销量成线性关系,即 p1=b1-a11x1-a12x2,b1,a11,a12>0,a11>a12;类似地,乙的 价格p2遵循同样的规律,即有p2=b2-a21x1-a22x2,b2,a21, a22>0,a22>a21。例如,假定实际中b1=100,a11=1, a12=0.1,b2=280,a21=0.2,a22=2。此外,假设工厂的生 产能力有限,两种牌号产品的产量之和不可能超过100件, 且甲的产量不可能超过乙的产量的两倍,甲、乙的单件生 产成本分别是q1=2和q2=3(假定为常数)。求甲、乙两个 牌号的产量x1、x2,使总利润最大。
十、某公司有6个建筑工地要开工,每个工地的位置(用平面坐标a, b表示,距离单位:km)及水泥日用量d(单位:t)由下表给出。 目前有两个临时料场位于P(5, 1),Q(2, 7),日储量各有20t,请回答 以下两个问题: (1)假设从料场到工地之间均有直线道路相连,试制定每天的供 应计划,即从A,B两料场分别向各工地运送多少吨水泥,使总的 顿公里数最小。 (2)为了进一步减少顿公里数,打算舍弃目前的两个临时料场, 改建两个新的料场,日储量仍各为20t,问应建在何处,与目前相 比节省的顿公里数有多大下线性规划(LP)问题:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、用LINGO 软件解方程组221212222359x x x x ⎧+=⎪⎨-=-⎪⎩。
2、用LINGO 软件解方程组1211221222/64x x x x x ⎧⎪-=-⎨⎪=⎩。
3、用LINGO 软件解线性规划问题4、用LINGO 软件解二次规划问题且12,x x 都是整数5、用LINGO 软件解下列问题(1)max 12z=x x +12121212..26,4520,,0,,s tx x x x x x x x +≤+≤≥为整数(2) min 2212z=x -3-2x +()() 22121212..-50,24,,0s tx x x x x x +≤+≤≥。
(3) min 2212z=x ++x +(1)(1) 22122..-20,1s tx x x +≤≥。
max 23,..4310,3512,,0.z x y s t x y x y x y =++≤+≤≥22121122121212max 982770.32,..100,2,,0,x x x x x x s t x x x x x x +---+≤≤≥6、用LINGO软件分别产生序列(1){1,3,5,7,9,11};(2){1,4,9,16,25,36};(3)1111 {1,,,,}6122030.7、已知向量c={1,3,0.5,7,5,2},用LINGO软件解答下列问题。
(1)求向量c前5个数中的最大值;(2)求向量c后4个数平方中的最小值;(3)求向量c 中所有数的和。
8、某学校游泳队要从5名队员中选4名参加4乘100米混合泳接力赛。
5名队员4种泳姿的百米成绩(单位:秒)-----------------------------------------------------------------------------------李王张刘赵蝶泳66.8 57.2 78 70 67.4仰泳75.6 66 67.8 74.2 71蛙泳87 66.4 84.6 69.6 83.8自由泳58.6 53 59.4 57.2 62.4-----------------------------------------------------------------------------------如何选拔?(1)请建立“0----1规划”模型;(2)用Lingo求解。
9、某帆船制造公司要决定下两年八个季度的帆船生产量。
八个季度的帆船需求量分别是40条、60条、75条、25条、30条、65条、50条、20条,这些需求必须按时满足,既不能提前也不能延后。
该公司每季度的正常生产能力是40条帆船,每条帆船的生产费用为400美圆。
如果是加班生产的,则每条生产费用为450美圆。
帆船跨季度库存的费用为每条20美圆。
初始库存是10条帆船。
如何生产?10、现要将8名同学分成4个调查队(每组2人)前往4个地区进行社会调查。
假设他们任意两人组成一队的工作效率为已知,见下表(由于对称性,只须列出上三角部分):任意两人组成一队的工作效率学生S1 S2 S3 S4 S5 S6 S7 S8S1 9 3 4 2 1 5 6S2 1 7 3 5 2 1S3 4 4 2 9 2S4 1 5 5 2S5 8 7 6S6 2 3S7 4问如何组队可以使总效率最高?参考答案1、MODEL:X1^2+2*X2^2=22;3*X1-5*X2=-9; @gin(x1);@gin(x2);END2、MODEL:X1^0.5-2*x1*X2=-2;X1^2=64*X2; END3、MODEL:max=2*x+3*y;4*x+3*y<=10;3*x+5*y<=12;END4、MODEL:max=98*x1+277*x2-x1^2-0.3*x1*x2-2*x2^2; x1<=2*x2;x1+x2<=100;@gin(x1); @gin(x2);END5、(1) MODEL:max=x1+x2;2*x1+x2<=6;4*x1+5*x2<=20;@gin(x1); @gin(x2);END(2) MODEL:min=(x1-3)^2+(x2-2)^2;x1^2+x2^2<=5;x1+2*x2<=4;@gin(x1); @gin(x2);END(3)MODEL:min=(x1+1)^2+(x2+1)^2;x1^2+x2^2<=2;x2>=1;END6、(1)model:sets:number/1..6/:x;endsets@for(number(I): x(I)=2*I-1);end(2)model:sets:number/1..6/:x;endsets@for(number(I): x(I)=I^2);end(3)model:sets:number/1..5/:x;endsets@for(number(I): x(I)=1/(I*(I+1)));end7、(1)model :data :N=6;enddatasets :number/1..N/:x;endsetsdata :x=1 3 0.5 7 5 2;enddatamaxc=@max (number(I)| I#le#5:x);end(2) model :data :N=6;enddatasets :number/1..N/:x;endsetsdata :x=1 3 0.5 7 5 2;enddataminc=@min (number(I)| I#ge#N-3:x^2);end(3) model :data :N=6;enddatasets :number/1..N/:x;endsetsdata :x=1 3 0.5 7 5 2;enddatas=@sum (number(I)| I#le#N:x);end8、解:若第i 名队员参加第j 种泳姿比赛,则令1=ij x ;否则令0=ij x ;共有20个决策变量ij x 。
第i 名队员的第j 种泳姿成绩记为ij c ,则目标函数为:∑∑==5141min i j ij ij xc约束条件有:每名队员顶多能参加一种泳姿比赛5,4,3,2,1,141=≤∑=i x j ij ;每种泳姿有且仅有一人参加 .4,3,2,1,151==∑=j xi ij这样就能建立如下“0----1规划”模型:∑∑==5141min i j ij ij xcs.t.5,4,3,2,1,141=≤∑=i x j ij .4,3,2,1,151==∑=j xi ij.4,3,2,1,5,4,3,2,1,10===j i x ij 或Lingo 程序如下:sets :row/1..4/;col/1..5/;links(row,col):c,x;endsetsdata :c=66.8 57.2 78 70 67.475.6 66 67.8 74.2 7187 66.4 84.6 69.6 83.858.6 53 59.4 57.2 62.4;enddatamin =@sum (links:c*x);@for (col(j):@sum (row(i):x(i,j))<=1);@for (row(i):@sum (col(j):x(i,j))=1);@for (links:@bin (x));答:14433221,,,x x x x 均等于1,即,依次取第2个人王、第3个人张、第4个人刘、第1个人李参加蝶泳、仰泳、蛙泳、自由泳,成绩为253.2秒。
9、解:八个季度的需求量数组记为xq ,则 xq=[40,60,75,25,30,65,50,20]. 类似地,用数组zc, jb, kc 分别表示八个季度的正常生产量、加班生产量、季度末库存量。
目标函数是全部费用之和:.))(20)(450)(400(min 81∑=++i i kc i jb i zc约束条件:生产能力 8,...,2,1,40)(=≤i i zc ;数量平衡 .8,...,3,2),()()()1()(),1()1()1(10)1(=-++-=-++=i i xq i jb i zc i kc i kc xq jb zc kc 以上是模型。
怎样用Lingo 编程呢? 把下标的范围当作集合,本题的集合是{1,2,3,4,5,6,7,8};定义在集合上的一个个数组,都分别称为该集合的属性,本题这个集合有四个属性,分别是xq,zc,jb,kc .先看本题的Lingo 程序,再看注解:model:sets:jihe/1..8/:xq,zc,jb,kc;endsetsdata:xq=40,60,75,25,30,65,50,20;enddatamin=@sum(jihe:400*zc+450*jb+20*kc);@for(jihe:zc<=40);kc(1)=10+zc(1)+jb(1)-xq(1);@for(jihe(i)|i#gt#1:kc(i)=kc(i-1)+zc(i)+jb(i)-xq(i));end10、解:构造一个效率集合xljh ,其属性xl 就是上表中那28个数据,如:xl(S1,S5)=2, xl(S3,S7)=9。
用y(Si,Sj)=1表示Si 与Sj 组成一个队;用y(Si,Sj)=0表示Si 与Sj 不是一个队。
目标函数:∑≤<≤⋅81),(),(maxj i Sj Si y Sj Si xl约束条件:每名学生必须且只能参加某一个队,即,对于第k 名同学而言,他与其他人所组成的队的个数必须等于1,故有1),(81=∑≤<≤==j i k j k i Sj Si y 或, k=1,2,3,…,8另外,10),(或=Sj Si y(以上就是本题的优化模型,是“0----1线性规划”)model:sets:xsjh/1..8/;xljh(xsjh,xsjh)|&2#gt#&1:xl,y;endsetsdata:xl=9,3,4,2,1,5,6,1,7,3,5,2,1,4,4,2,9,2,1,5,5,2,8,7,6,2,3,4;enddatamax=@sum(xljh(i,j):xl(i,j)*y(i,j));@for(xsjh(k): @sum(xljh(i,j)|(i#eq#k)#or#(j#eq#k):y(i,j))=1);@for(xljh(i,j):@bin(y(i,j)));end注解:(1)根据基本集合xsjh构造效率集合xljh时,我们只需要二元对(i,j) 中那些当i<j时的元素对,即第2个下标j必须大于第1个下标i,相应的“元素过滤”命令为&2#gt#&1 。
