2010数学建模与计算机模拟题目
2010年全国数学建模B题答案

2010年上海世博会对居民消费结构影响力的定量评估摘要本文从世博会的筹备期间(2003年---2009年)对上海居民消费结构的影响进行定量评估研究。
消费结构是一项反映居民消费水平的重要指标,包含居民的收入水平、消费支出、消费分类三部分[1]。
为了全面反映和研究居民的生活消费状况,我们采取了一系列相互联系的统计指标对上海居民的消费结构进行定量研究。
在对大量的数据分析基础上,研究了上海市居民的收入水平的变化;并且从上海市的几个主要消费群体来分析上海市居民的收入与支出的变化情况;对消费分类的研究,我们选取了食品、衣着、居住、家庭设备用品及服务、交通和通信、文教娱乐用品及服务、医疗保健、商品和服务作为消费分类的八项指标,利用主成分分析的方法对各个主成分进行了详细的定量分析,并运用matlab编程利用曲线拟合的方法做了假设不存在世博会时的预测,再将所搜集到的实际值与预测值作差,我们定义该差值为影响力指数,通过影响力指数的大小来说明上海世博会对上海市居民消费分类的影响,影响力指数越大,说明世博会对上海居民消费结构的影响越深,进而定量评估了上海世博会对上海市居民的消费结构的影响情况。
消费结构的升级产生的经济势力是持久强大的,了解了上海世博会的对上海居民消费结构的影响后,若能顺势调控,则能充分带动经济的发展,为支撑我国国民经济的稳定快速发展提供动力。
关键词:消费结构主成分分析定量评估预测曲线拟合 matlab一 问题的提出2010年上海世博会是首次在中国举办的世界博览会.从1851年伦敦的“万国工业博览会”开始,世博会正日益成为各国人民交流历史文化、展示科技成果、体现合作精神、展望未来发展等的重要舞台.请你们选择感兴趣的某个侧面,建立数学模型,利用互联网数据,定量评估2010年上海世博会的影响力.二 符号说明np x 第n 个样品的第p 个指标 X标准化数据矩阵R 变量的关系矩阵p λ 关系矩阵的特征值p μ p λ所对应的单位特征向量i y 第i 个主成分y 1995年到2002年dy 影响力指数三 模型的假设1、本文所作的影响力评估是针对上海市居民的消费结构.2、本文所作的影响力评估仅限于世博会筹备期间及召开期间的居民消费结构.3、消费结构是一项反映居民消费水平的重要指标,要全面反映和研究居民的生活消费状况,包含居民的收入水平、消费支出、消费分类三部分.4、上海居民消费由食品、衣着、居住、家庭设备用品及服务、交通和通信、文教娱乐用品及服务、医疗保健、商品和服务八部分组成.5、居民的收入是决定居民的消费水平和消费结构的主要因素,收入水平的高低直接决定消费水平的高低.四 模型的建立及求解上海是我国最大的经济中心城市,随着2010年上海世博会的日益临近,将对上海经济发展发挥巨大的作用.投资、消费和出口被称为经济发展的三架马车,2010年的世博会为上海经济发展提供了会前的投资拉动和会后的需求拉动两个方面的刺激,消费是需求的基础,有效地投资必须准确的把握需求的变化.消费是人们为了满足生活需要而消耗产品和服务的行为和过程, 是满足人们生存、发展和生活享受所必需的行为.人们基本的消费状况, 既能反映需求规律, 又成为其他需求的基础,因此, 评估消费状况和需求趋向便成为政府和企业了解市场的起点.据中国社科院的研究, 2001年投资、消费和出口对国内GDP 增长的贡献分别是77%、34%和-11%. 从2002 年上海的统计数据来看, 同样是外需下降、出口下滑, 依靠增幅达31.7%的社会固定资产投资和9.8%的社会消费品零售总额的增长, 才保证了上海经济10.4%的高速增长.由此也可以看到投资和消费是推动上海经济发展的两个最基本因素。
2010数学建模与计算机模拟题目

数学建模与计算机模拟题目8、政府中的腐败与一宗重大的政府丑闻的有牵连人数的增加率与早已牵连进去的人数和有关而尚未牵连进去的人数的乘积成正比。
假设当华盛顿的报纸将这一丑闻公诸于众时,有牵连人数为7人,3个月后有牵连人数增加了9人,又过了3个月后有牵连人数增加了12人。
与该丑闻有关的人数大概有多少人?请写出建立的模型及用matlab或者公式推导出来的结果。
9、某城市1990年的人口密度近似为,表示距市中心r公里区域内的人口数,单位为每平面公里10万人。
(1)试求距市中心2km区域内的人口数。
写出建立的模型,并用matlab算出最终答案。
(2)若人口密度近似为(单位不变),试求距市中心2km区域内的人口数。
写出建立的模型,并用matlab算出最终答案。
10、梵塔问题:传说中认为是世界中心的现印度北方邦瓦拉西纳县的一座大庙的穹顶的下面放有一个黄铜盘子,盘子上有三根钻石柱子,在其中一根柱子上套有64个大小不同的中空的纯金盘子(称为梵塔),且按上小下大的次序排列。
该庙的和尚按梵天(印度教大神之一)的法令昼夜不停地、每秒把一个盘子移到没有盘子的柱子上去,或者放到比它大的盘子的上面,传说,如果一旦把64个纯金盘子组成的梵塔按原样移到另两根钻石柱子中的任意一根时,世界末日就要到了,问和尚们要用多少时间才能完成,世界末日会来临吗?11、在市场经济中存在这样的循环现象,若去年的猪肉生产量供过于求,猪肉的价格就会降低,价格降低会使今年养猪者减少,使今年猪头供不应求,于是肉价上扬,价格上扬又使明年猪肉产量增加造成新的供过于求。
据统计,某城市1991年的猪头产量为30万吨,肉价为6.00元/公斤,1992年生产猪肉25万吨,肉价为8.00元/公斤,已知1993年的猪肉产量为28万吨。
若维持目前的消费水平与生产模式,并假定猪肉产量与价格之间是线性关系,问若干年以后猪肉的生产量与价格是否会趋于稳定?若能够稳定,请求出稳定的生产量和价格。
2010全国数学建模d题

承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): D我们的参赛报名号为(如果赛区设置报名号的话):20101219所属学校(请填写完整的全名):淮安信息职业技术学院参赛队员(打印并签名) :1. 王姚2. 杨彬3. 黄影影指导教师或指导教师组负责人(打印并签名):刘嘉日期: 2010 年 9月 13 日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号)对学生宿舍设计方案的评价摘 要本文主要采用层次分析法对四种学生宿舍的设计进行评价。
首先,根据调查我们得到经济性、舒适性、安全性的一组正互反对比矩阵,见(矩阵一),然后可以根据这组矩阵得出特征向量w ,然后根据调查得出【建设成本、运行成本、收费标准】、【人均面积 使用方便 互不干扰 采光 通风】、【人员疏散、防盗】得出这样的3组矩阵,见(矩阵二到四),应用MATLAB 并分别可得出对应的特征向量。
然后,我们根据每种学生宿舍设计方案的楼层平面图,可以计算各个指标的数值,接着根据这些指标我们根据假设对这些指标量化。
根据量化的指标值,将每种数值归类,便可以得出一组四行十列的矩阵,根据每种方案的条件又可以得出10组四乘四的矩阵,便可以得出相应的的特征向量,以此作依据,计算出最终的权重,然后比较权重即得出最佳方案。
数学建模试卷2010(答案)

华中科技大学《数学建模》考试卷(半开卷)2010~2011学年度第一学期成绩学号专业班级姓名一、怎样解决下面的实际问题,包括需要哪些数据资料,要作些什么观察、试验以及建立什么样的数学模型等。
(10分)(1)估计一批电饭煲的寿命;(2)一高层办公楼有四部电梯,早晨上班时间非常拥挤,试制订合理的运行计划。
解:(1)从一批电饭煲中取一定数量的样本,测得其平均寿命,可作为该批电饭煲寿命的估计值。
为衡量估计的精度,需要从样本寿命确定该批电饭煲寿命的概率分布,即可得到估计值的置信区间。
还可试验用提高电压的办法加速寿命测试,以缩短测量时间。
⑤(2)统计在各层上班的人数,通过数据或计算确定电梯运行时间,以等待的人数与时间乘积为目标,建立优化模型,确定每部电梯运行的楼层(有的从大厅直接运行到高层)。
⑤二、学校共有1000名学生,235人住在A 宿舍,333人住在B 宿舍,432人住在C 宿舍。
学生们要组织一个10人的委员会,试用以下方法分别分配各宿舍的委员数。
(10分) 1.Hamilton 方法 2.Q 值方法3.其它方法或你自己提出的方法解:1.Hamilton 方法:③2.Q 值法: 先按比例计算结果将整数部分的9席分配,123n 2,n 3,n 4=== ①再用Q 值法分配第十席:()()()()()()221111222222223333p 235Q 9204.17n n 1221p 333Q 9240.75n n 1331p 432Q 9331.20n n 1441===++===++===++ ③Q 3最大,第十席分配给C 宿舍,即:123n 2,n 3,n 5===。
①3.略 ②三、人体注射葡萄糖溶液时,血液中葡萄糖浓度g (t )的增长率与注射速率r 成正比,与人体血液容积V 成反比,而由于人体组织的吸收作用,g (t )的减少率与g (t )本身成正比。
分别在以下假设下建立模型,并讨论稳定情况。
2010高教社杯全国大学生数学建模竞赛C题

同上的解法求得方案一最佳。
问题一的解答:
2、当共用管线和非共用管线费用不相同时要考
虑方案二中的各部分管线的总费用并与方案一
中的费用对比,得出最优方案。经过查阅资料
得知某非共用管道5万元/千米;共用管道8万 元/千米;方案一的费用为
C1 5 l 2 (a b 方案二的费用为:) 2
;
2010高教社杯全国大学生数学建模 竞赛 C题 输油管线设计的数学模型
阐述的主要问题
某油田计划在铁路线一侧建造两家炼油厂,同 时在铁路线上增建一个车站,用来运送成品油。 由于这种模式具有一定的普遍性,油田设计院 希望建立管线建设费用最省的模型。
针对这个问题,通过三个小问题 进行解答:
1.针对两炼油厂到铁路线距离和两炼油厂间距离的各种不同情形, 提出设计方案。若有共用管线,考虑其共用管线费用与非共用管 线费用相同或不同的情形。 B 2. 两炼油厂的具体位置其中A厂位于郊区(Ⅰ), 厂位于城区 Ⅱ (Ⅱ),两个区域有明显的分界线。若所有管线的铺设费用均相 同, 铺设在城区的管线还需增加拆迁和工程补偿等附加费用, 根据三家工程咨询公司对此项附加费用的估计,为设计院给出管 线布置方案及相应的费用。 3. 为进一步节省费用,炼油厂根据生产能力,选用相适应的油管。 这时的管线铺设费用就各不相同,拆迁等附加费用同上。给出管 线最佳布置方案及相应的费用。
,
2 3 l ,解得 C1 C2 3
问题一的解答:
2)同理:当 a b
当 a b 时,解得C1 C 2。当 a
3 10 3 3a 3b l 时, 2 C l 3 3 3
3l
8
b时,解得
C1 C 2。即方案一最佳。
问题二的解答:
2010高教社杯全国大学生数学建模竞赛官方题目(含ABCD)
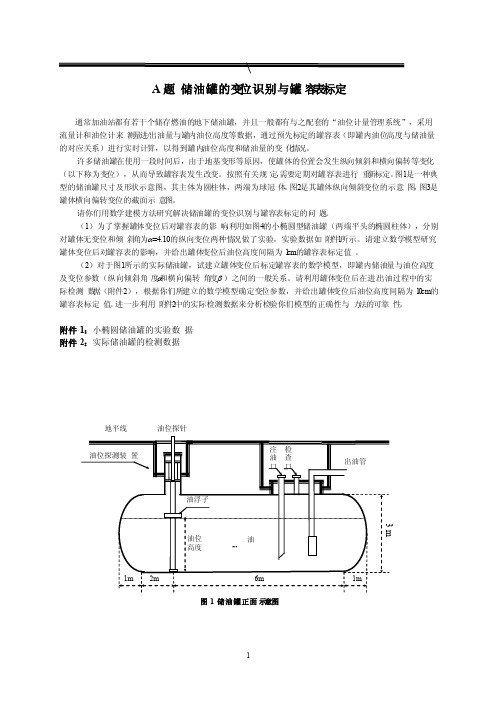
\A 题 储油罐的变位识别与罐容表标定通常加油站都有若干个储存燃油的地下储油罐,并且一般都有与之配套的“油位计量管理系统”,采用流量计和油位计来测量进/出油量与罐内油位高度等数据,通过预先标定的罐容表(即罐内油位高度与储油量的对应关系)进行实时计算,以得到罐内油位高度和储油量的变化情况。
许多储油罐在使用一段时间后,由于地基变形等原因,使罐体的位置会发生纵向倾斜和横向偏转等变化(以下称为变位),从而导致罐容表发生改变。
按照有关规定,需要定期对罐容表进行重新标定。
图1是一种典型的储油罐尺寸及形状示意图,其主体为圆柱体,两端为球冠体。
图2是其罐体纵向倾斜变位的示意图,图3是罐体横向偏转变位的截面示意图。
请你们用数学建模方法研究解决储油罐的变位识别与罐容表标定的问题。
(1)为了掌握罐体变位后对罐容表的影响,利用如图4的小椭圆型储油罐(两端平头的椭圆柱体),分别对罐体无变位和倾斜角为α=4.10的纵向变位两种情况做了实验,实验数据如附件1所示。
请建立数学模型研究罐体变位后对罐容表的影响,并给出罐体变位后油位高度间隔为1cm 的罐容表标定值。
(2)对于图1所示的实际储油罐,试建立罐体变位后标定罐容表的数学模型,即罐内储油量与油位高度及变位参数(纵向倾斜角度α和横向偏转角度β )之间的一般关系。
请利用罐体变位后在进/出油过程中的实际检测数据(附件2),根据你们所建立的数学模型确定变位参数,并给出罐体变位后油位高度间隔为10cm 的罐容表标定值。
进一步利用附件2中的实际检测数据来分析检验你们模型的正确性与方法的可靠性。
附件1:小椭圆储油罐的实验数据 附件2:实际储油罐的检测数据油油浮子出油管油位探测装置注油口 检查口地平线 2m6m1m1m3 m油位高度图1 储油罐正面示意图油位探针油位探针α地平线 图2 储油罐纵向倾斜变位后示意图油油浮子出油管油位探测装置注油口 检查口水平线(b) 小椭圆油罐截面示意图α油油浮子出油管油位探针注油口水平线2.05mcm 0.4m1.2m1.2m1.78m(a) 小椭圆油罐正面示意图图4 小椭圆型油罐形状及尺寸示意图图3 储油罐截面示意图(b )横向偏转倾斜后正截面图地平线β地平线垂直线油位探针(a )无偏转倾斜的正截面图油位探针油位探测装置地平线油3m油B题2010年上海世博会影响力的定量评估2010年上海世博会是首次在中国举办的世界博览会。
数学与统计学学院2010年数学建模竞赛试题

数学与统计学学院2010年数学建模竞赛试题(请先仔细阅读竞赛要求)A题、武汉房地产价格问题房地产价格是一个备受关注的问题。
现在请你就以下几个方面的问题进行讨论1.给出你的房地产价格指标的定义(考虑房子所处的位置(交通,学校,医院,商场…),房子的户型,房子的楼层,房子的朝向,小区的内环境(绿化,容积率…等等),房子的开发商,物业,房子的质量,小区的大小,噪音大小,空气等等…);2.请搜集武汉近两年来的房子日销售情况表(至少搜集10天的武汉的房子日销售情况表);对你的上述房地产价格指标的定义做简化,给出一个简化的武汉的房地产价格指标的定义;并且假设:以你搜集到的10天的武汉的房子日销售情况表中时间最早的那一天武汉的房地产价格指标为100,利用你的简化的武汉的房地产价格指标的定义,计算其他天的武汉的房地产价格指标;3.请搜集相应10天的武汉(或者全国)的物价指标,请你建立武汉的房地产价格指标与武汉(或者全国)的物价指标的关系模型,并假设有一天武汉(或者全国)的物价指标,是你搜集到的10天的武汉的房子日销售情况表中时间最早的那一天的武汉(或者全国)的物价指标的100倍,请你预测那一天的武汉的房地产价格指标;4.如果某人准备在武汉买房,请你给他买房的时机的建议。
中南民族大学数学与统计学学院2010年首届数学建模竞赛要求1、参赛者为中南民族大学任意在校本科生, 以队为单位参赛。
学生自愿组队,每队有且仅有三人,鼓励学生跨院系组队。
比赛开始后不允许更换队员。
2、竞赛时间为:2010年4月9日16时至4月14日16时。
3、竞赛按照甲、乙组分别命题,甲组(参加对象为2007,2008级学生)分为A,B两题,乙组(2009级学生)分为C,D两题,每个参赛队可任选一题,4月9日16时起可在院网页上下载试题。
4、竞赛采取开放的竞赛方式,竞赛期间参赛队员可以使用各种图书资料、计算机和软件,在国际互联网上浏览,但不得与队外任何人(包括在网上)讨论。
2010东北三省数学建模

周游先生退休后想到各地旅游。计划走遍全国 的省会城市、直辖市、香港、澳门、台北。请 你为他按下面要求制定出行方案: 1.按地理位置(经纬度)设计最短路旅行方案; 2.如果2010年5月1日周先生从哈尔滨市出发, 每个城市停留3天,可选择航空、铁路(快车卧 铺或动车),设计最经济的旅行互联网上订票 方案; 3. 要综合考虑省钱、省时又方便,设定你的评 价准则,建立数学模型,修订你的方案; 4.对你的算法作复杂性、可行性及误差分析; 5.关于旅行商问题提出对你自己所采用的算法 的理解及评价。
最省钱的路径
周游先生引发的思考
最短路
最经济
综合考虑 省时、省钱
旅网的拓扑结构指的是组成网络的基本单元之间 的相互连接关系,网络的衔接结构包括任何一个 基本单元和其他基本单元之间的关系和整个网络 之间的关系所呈现的路线特性。
旅游低碳是指旅行商在综合考虑省钱、省时因素, 所最终达到让旅行商满意的状态。该项指标对于 整个旅网线路的选择有着较大的意义。 旅游网络领域内很多是解决最短路的问题,对低 碳的研究还处于表面阶段。该模型提出旅网拓扑 低碳评价准则,利用该准则界定旅网中的关键线 路,与此该准则也可以评价整个网络的低碳评价 准则。
模拟退火
最优化三大理论 经典算法
遗传算法
神经网络
TSP问题
旅行商问题TSP (Traveling Salesman Problem) 是指 已知n 个城市之间的相互距离,现有一推销员必须 遍访n 个城市,并且每个城市只能访问一次,最后 又必须返回出发城市。如何安排访问次序,才可 以使其旅行路线的总长度最短 ,这是一个典型的 组合优化问题,并且是一个NP 难题,所以一般很难 精确的求出其最优解。而1983 年由Kirkpatrick 等 人提出的按统计方式工作的机器与组合最佳化问 题有着深刻意义的联系 ,这成功的将退火思想引 入了组合最优领域。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学建模与计算机模拟题目
8、政府中的腐败
与一宗重大的政府丑闻的有牵连人数的增加率与早已牵连进去的人数和有关而尚未牵连进去的人数的乘积成正比。
假设当华盛顿的报纸将这一丑闻公诸于众时,有牵连人数为7人,3个月后有牵连人数增加了9人,又过了3个月后有牵连人数增加了12人。
与该丑闻有关的人数大概有多少人?请写出建立的模型及用matlab或者公式推导出来的结果。
9、某城市1990年的人口密度近似为,表示距市中心r公里区域内的人口数,单位为每平面公里10万人。
(1)试求距市中心2km区域内的人口数。
写出建立的模型,并用matlab算出最终答案。
(2)若人口密度近似为(单位不变),试求距市中心2km区域内的人口数。
写出建立的模型,并用matlab算出最终答案。
10、梵塔问题:传说中认为是世界中心的现印度北方邦瓦拉西纳县的一座大庙的穹顶的下面放有一个黄铜盘子,盘子上有三根钻石柱子,在其中一根柱子上套有64个大小不同的中空的纯金盘子(称为梵塔),且按上小下大的次序排列。
该庙的和尚按梵天(印度教大神之一)的法令昼夜不停地、每秒把一个盘子移到没有盘子的柱子上去,或者放到比它大的盘子的上面,传说,如果一旦把64个纯金盘子组成的梵塔按原样移到另两根钻石柱子中的任意一根时,世界末日就要到了,问和尚们要用多少时间才能完成,世界末日会来临吗?
11、在市场经济中存在这样的循环现象,若去年的猪肉生产量供过于求,猪肉的价格就会降低,价格降低会使今年养猪者减少,使今年猪头供不应求,于是肉价上扬,价格上扬又使明年猪肉产量增加造成新的供过于求。
据统计,某城市1991年的猪头产量为30万吨,肉价为6.00元/公斤,1992年生产猪肉25万吨,肉价为8.00元/公斤,已知1993
年的猪肉产量为28万吨。
若维持目前的消费水平与生产模式,并假定猪肉产量与价格之间是线性关系,问若干年以后猪肉的生产量与价格是否会趋于稳定?若能够稳定,请求出稳定的生产量和价格。
12、某饮料厂使用同一条生产线轮流生产多种饮料。
若某周开工生产某种饮料, 需支出生产准备费8千元。
存贮费:每周每千箱饮料 0.2千元。
且某种饮料4周的需求量、生产能力和成本如下表:
周次需求量(千箱)生产能力(千箱)成本(千元/千箱)
1 15 30 5.0
2 25 40 5.1
3 35 45 5.4
4 2
5 20 5.5
合计 100 135
问:安排生产计划, 满足每周的需求, 使4周总费用最小。
13、在按年龄分组的种群增长模型中,设一群动物最高年龄为15岁,每5岁一组,分成3个年龄组,各组的繁殖率为b1 =0,b2 =4,b3 =3,存活率为s1 =1/2,s2 =1/4,开始时3组各有1000只。
求15年后各组有多少只,以及时间充分长后种群的增长率(即固有增长率)和按年龄组的分布。
14为减少层次分析法中的主观成份,可请若干专家没人构造成对比较矩阵。
试给出一种有若干个成对比较矩阵确定权向量的方法。
15下图是5位网球选手循环赛的结果。
作为竞赛图,它是双向连通的吗?找出几条完全路径,用适当方法排出5为选手的名次。
16某甲(农民)有一块土地,若从事农业生产可收入1万元;若将土地租给某乙(企业家)用于工业生产,可收入2万元;若租给某丙(旅店老板)开发旅游业,可收入3万元;当旅店老板要求企业家参与经营时,收入达4万元。
为促成最高收入的实现,试用Shapley值方法分配各人的所得。
17、〔借款选择〕建立下列问题的线性规划数学模型.
陈先生是一家服装连锁店的主管,他希望开办三家新商店:一家在椒江,一家在路桥,一家在黄岩.开办这些商店分别需要250万、100万和170万元.为对此进行融资,陈先生与三家银行进行了联系.根据商店的位置和对相关风险的评估,每家银行都决定至多提供8年期总值为300万元的贷款,但对不同商店项目的利率各不相同(见下表).请制定从这些银行借款的方案,以使每个商店都能得到所需的资金,并且使总支出最小.
椒江的商店路桥的商店黄岩的商店
银行1 5% 6.5% 6.1%
银行2 5.2% 6.2% 6.2%
银行3 5.5% 5.8% 6.5%
18、营养学家指出,成人良好的日常饮食应该至少提供0.075 kg的碳水化合物,0.06 kg的蛋白质,0.06 kg的脂肪。
1 kg食物A含有0.105 kg碳水化合物,0.07 kg蛋白质,0.14 kg脂肪,花费28元;而1 kg 食物B含有0.105 kg碳水化合物,0.14 kg蛋白质,0.07 kg脂肪,花费21元。
假如你是一个主妇你会如何合理的购买食用食物A和食物B多少kg呢?
19、有四个工人,要指派他们分别完成4项工作,每人做各项工作
问指派哪个人去完成哪项工作,可使总的消耗时间为最小?
20、有两个煤场A 、B,每月进煤不少于60t、100t,他们担负三个居民区的运煤任务,这三个居民区每月需要用煤分别为45t 、 75t 、 40t ,A厂距离着三个居民区为10km、5km、6km,B 厂距离这三个居民区分别为4km、8km、15km,问这两煤矿厂如何分配供煤,才能使总运输量最小
21、电视台为某个广告公司特约播放两套片集。
其中片集甲播映时间为20分钟,广告时间为1分钟,收视观众为60万;片集乙播映时间为10分钟,广告时间为1分钟,收视观众为20万。
广告公司规定每周至少有6分钟广告,而电视台每周只能为该公司提供不多于80分钟的节目时间。
电视台每周应播映两套片集各多少次,才能获得最高的收视率?
22、有高为1m的半球形容器,水从它的底部小孔流出,小孔截面面积为1cm2.开始时容器内充满了水,求水从小孔流出过程中容器里水面的高度h(水面与孔口之间的距离)随时间t的变化规律,并求水流完所需的时间.
23、镭的衰变有如下规律:
镭的衰变速度与它的现存量R成正比
由经验材料得知,镭经过1 600年后,只余原始量R0的一半.试求镭的现存量R与时间t的函数关系.
24、森林救火问题
根据导数的物理意义,给出森林失火面积的变化率,依据火势蔓延速度和灭火速度的关系,建立由损失费和救援费组成的总费用的数学模型,求出时总费用最小的派出灭火人员的数量.
25、手表时针与分针何时重合问题
研究手表时针与分针何时重合问题,定义每个整点时间段内的时针与12:00的时针夹角w,通过建立夹角w与该时间段内的任意时刻t的函数关系,分别求出12小时内分针与时针12次重合的具体时刻.
26、预报人口的增长
认识人口数量的变化规律,建立人口模型,作出较准确的预报,是有效控制人口增长的前提.试根据表1建立人口模型,并由此预报2010年美国的人口.
(注:表1为近两个世纪美国人口的统计数据(以百万为单位))
27、牛顿冷却定律的应用
牛顿冷却定律:当系统与环境的温度差不大时,系统温度的变化率与系统温度与环境温度之差成正比.
实例:某被害者的尸体于晚上7:30被发现,法医于晚上8:20赶到暗杀现场,测的尸体温度为32.6度;一小时后,当尸体即将被抬走时,测的尸体温度为31.4度,室内温度几小时内始终保持在21.1度.此案最大嫌疑犯是张某,但张某声称自己无罪,并有证人说:“下午张某一直在办公室上班,5:00时打了一个电话后离开办公室”.从张某办公室被害者家步行需要5分钟,根据上述信息判断张某是否有杀人嫌疑. 如果张某的律师出示了一份证据:被害者于当天下午去医院看过病,病历纪录被害者发烧到38.3度,而且在死者体内未发现阿司匹林或者类似药物,问张某是否有杀人嫌疑?
28、鉴定物品
根据碳-14会发生放射性衰变的规律,建立木炭制品所含碳-14数量的微分方程,并且得到木炭制品中碳-14的衰变速率,将碳-14的半衰变期5568年作为方程的初始条件,求解微分方程,结合初始速率这一条件,确定木炭制品的年代.
实例:马王堆一号墓于1972年8月出土,出土时测的木炭标本的碳-14的平均原子衰变速率为29.78次/分,而新砍伐烧成的木炭原子衰变速率为38.37次/分.试估算马王堆一号墓大致年代.
29、举出几个差分形式阻滞增长模型的应用实例。
