离散数学期末复习(一)
离散数学期末复习

离散数学内容总结大纲第一篇 数理逻辑第1章 命题逻辑求命题公式的主析取范式及主合取范式例 求()()p r q p ∨⌝∧∨的主析取范式及主合取范式。
例 求(P →Q)∧R 的主析取范式及主合取范式。
例 求命题公式R Q P ∨∧)(的主析取范式和主合取范式。
例 求公式A =(p →⌝q )→r 的主析取范式与主合取范式。
例 求()r q p →→的主析取范式。
判断公式类型例 用等值演算法判断公式q ∧⌝ (p →q )的类型例 判断下列命题公式的类型(永真式、永假式、可满足式),方法不限。
(1)(2)证明例 证明:()()()r q r p r q p →∧→⇔→∨ 例 证明:r q p r q p →∧⇔→→)()( 例 推证:⌝Q ∧(P →Q)⇒⌝P例 前提:q p s q r p ∨→→,,,结论:s r ∨。
该结论是否有效?请说明原因。
在命题逻辑中构造下面推理的证明:例 如果小张守第一垒并且小李向B 队投球,则A 队获胜。
或者A 队未获胜,或者A 队成为联赛的第一名。
小张守第一垒。
A 队没有成为联赛的第一名。
因此小李没有向B 队投球。
解:先将简单命题符号化。
P:小张守第一垒;Q:小李向B队投球;R:A队取胜;S:A 队成为联赛第一名。
前提:(P∧Q)→R,R∨S,P,S结论:Q证明:(1) R∨S 前提引入(2) S 前提引入(3) R (1)(2)析取三段论(4) (P∧Q)→R 前提引入(5) (P∧Q) (3)(4)拒取式(6) P∨Q (5)置换(7) P 前提引入(8) Q (6)(7)析取三段论例一个公安人员审查一件盗窃案,已知下列事实:(1)甲或乙盗窃了录像机;(2)若甲盗窃了录像机,则作案时间不能发生在午夜前;(3)若乙的证词正确,则午夜时屋里灯光未灭;(4)若乙的证词不正确,则作案时间发生在午夜前;(5)午夜时屋里灯光灭了。
根据以上事实,推断谁是盗窃犯。
(在命题逻辑中构造推理证明。
离散期末考试题

离散期末考试题一、选择题(每题3分,共30分)1. 在离散数学中,以下哪个概念用于描述两个集合之间的一一对应关系?A. 并集B. 交集C. 映射D. 子集2. 以下哪个命题的否定是正确的?A. 如果今天是周一,那么明天是周二。
B. 如果下雨,那么地面会湿。
C. 如果x > 0,则x² > 0。
D. 所有的鸟都会飞。
3. 在图论中,一个连通图是指图中任意两个顶点之间都存在一条路径。
以下哪个选项描述的不是连通图?A. 完全图B. 树C. 环D. 星形图4. 以下哪个逻辑运算符表示逻辑“或”?A. ∧B. ∨C. ¬D. →5. 在集合论中,以下哪个符号表示集合的差集?A. ∪B. ∩C. -D. ×6. 以下哪个命题是永真命题?A. p ∧ ¬pB. p ∨ ¬pC. p → ¬pD. ¬(p → ¬p)7. 在关系R中,如果对于任意的a, b ∈ A,都有(a, b) ∈ R和(b,a) ∈ R,则称R是对称的。
以下哪个关系不是对称的?A. 等价关系B. 子集关系C. 整除关系D. 朋友关系8. 在命题逻辑中,以下哪个等价于“p且q”?A. ¬p ∨ ¬qB. p ∧ qC. ¬p → ¬qD. ¬(p → ¬q)9. 在图论中,以下哪个术语描述的是一个图中没有环的子图?A. 路径B. 连通图C. 树D. 环10. 在集合论中,以下哪个符号表示集合的笛卡尔积?A. ×B. ∪C. ∩D. -二、填空题(每题2分,共20分)11. 如果集合A有n个元素,那么集合A的子集个数是________。
12. 在逻辑中,一个命题的________是当原命题为真时,它为假;当原命题为假时,它为真的命题。
13. 如果一个图的每个顶点的度数都是偶数,则该图一定存在________。
离散数学期末复习题(6套)

《离散数学》期末考试题(A)一、填空题(每小题3分,共15分)1.设}}{},,{{c b a A =,}}{},,{},{{c c b a B =,则)(=⋃B A ,)(=⋂B A ,)()(=A P .2.集合},,{c b a A =,其上可定义( )个封闭的1元运算,( )个封闭的2元运算,( )个封闭的3元运算.3.命题公式1)(↑∧q p 的对偶式为( ).4.所有6的因数组成的集合为( ).5.不同构的5阶根树有( )棵.二、单选题(每小题3分,共15分)1.设A , B 是集合,若A B A =-,则(A)B = ∅ (B) A = ∅ (C)=⋂B A ∅ (D)A B A =⋂2.谓词公式)())()((x R y yQ x P x ∧∃→∀中量词x ∀的辖域为(A))())()((x R y yQ x P x ∧∃→∀ (B))()(y yQ x P ∃→(C))())()((x R y yQ x P ∧∃→ (D))()(y yQ x P ∃→和)(x R3.任意6阶群的子群的阶一定不为(A)4 (B)6 (C)2 (D)34.设n 是正整数,则有限布尔代数的元素个数为(A)2n (B)4n (C)n 2 (D)2n5.对于下列序列,可构成简单无向图的度数序列为(A)3, 3, 4, 4, 5 (B)0, 1, 3, 3, 3 (C)1, 1, 2, 2, 3 (D)1, 1, 2, 2, 2三、判断题(每小题3分,共15分): 正确打“√”,错误打“×”.1. 设N N N :⨯→f ,)1,()(+=x x x f ,则f 是满射. () 2. 5男5女圆桌交替就座的方式有2880种. () 3. 设),(≤L 是格,对于L z y x ∈,,,若z x y x ⋅=⋅且z x y x +=+,则z y =. () 4. 任何树都至少2片树叶. ()5. 无向图G 有生成树的充要条件是G 为连通图. ( )四、(10分)设C B A ,,和D 是集合,证明)()()()(D B C A D C B A ⨯-⨯⊆-⨯-,并举例说明上式中不能将⊆改为 = .五、(15分)设N 是自然数集合,定义N 上的关系R 如下:y x R y x +⇔∈),(是偶数,1.证明R 是N 上的等价关系.2.求出N 关于等价关系R 的所有等价类.3.试求出一个N 到N 的函数f ,使得)}()(,N ,|),{(y f x f y x y x R =∈=.六、(10分)在实数集合R 中证明下列推理的有效性:因为R 中存在自然数,而所有自然数是整数,所以R 中存在整数.七、(10分)设R 是实数集合,令}0,R ,|),{(≠∈=a b a b a G ,定义G 上的运算如下: 对于任意G d c b a ∈),(),,(,),(),(),(b ad ac d c b a +=⋅,证明),(⋅G 是非Abel 群.八、(10分)若简单平面图G 的节点数7=n 且边数15=m ,则G 是连通图,试证明之.《离散数学》期末考试题(B)一、填空题(每小题3分,共15分)1.设,,},,{{b a b a A =∅},则-A ∅ = ( ),-A {∅} = ( ),)(A P 中的元素个数=|)(|A P ( ).2.设集合A 中有3个元素,则A 上的二元关系有( )个,其中有( )个是A 到A 的函数.3.谓词公式))()(())()((y P y Q y x Q x P x ⌝∧∃∧→∀中量词x ∀的辖域为( ), 量词y ∃的辖域为( ).4.设}24,12,8,6,4,3,2,1{24=D ,对于其上的整除关系“|”,元素( )不存在补元.5.当n ( )时,n 阶完全无向图n K 是平面图,当n 为( )时,n K 是欧拉图.二、单选题(每小题3分,共15分)1.设R 是集合A 上的偏序关系,1-R 是R 的逆关系,则1-⋃R R 是A 上的(A)偏序关系 (B)等价关系 (C)相容关系 (D)以上结论都不成立2.由2个命题变元p 和q 组成的不等值的命题公式的个数有(A)2 (B)4 (C)8 (D)163.设p 是素数且n 是正整数,则任意有限域的元素个数为(A)n p + (B)pn (C)n p (D)pn4.设R 是实数集合,≤是其上的小于等于关系,则(R, ≤)是(A)有界格 (B)分配格 (C)有补格 (D)布尔格5.3阶完全无向图3K 的不同构的生成子图有(A)2 (B)3 (C)4 (D)5 三、判断题(每小题3分,共15分): 正确打“√”,错误打“×”.1.若一个元素a 既存在左逆元l a ,又存在右逆元r a ,则r l a a =. ( )2.命题联结词→不满足结合律. ( )3.在Z 8 = {0,1,2,3,4,5,6,7}中,2关于“⋅8”的逆元为4. ( )4.整环不一定是域. ( )5.任何),(m n 平面图的面数2+-=n m r . ( )四、(10分)设B A f →:且C B g →:,若g f 是单射,证明f 是单射,并举例说明g 不一定是单射.五、(15分)设},,,{d c b a A =,A 上的关系)},(),,(),,(),,(),,(),,(),,(),,(),,{(c d b d a d c c b c a c c a b a a a R =,1.画出R 的关系图R G .2.判断R 所具有的性质.3.求出R 的关系矩阵R M .六、(10分)利用真值表求命题公式))(())((p q r r q p A →→↔→→=的主析取范式和主合取范式.七、(10分) 边数30<m 的简单平面图G ,必存在节点v 使得4)deg(≤v .八、(10分) 有六个数字,其中三个1,两个2,一个3,求能组成四位数的个数.《离散数学》期末考试题(C)一、填空题(每小题3分,共15分)1. 若n B m A ==||,||,则=⨯||B A ( ),A 到B 的2元关系共有( )个,A 上的2元关系共有( )个.2. 设A = {1, 2, 3}, f = {(1,1), (2,1), (3, 1)}, g = {(1, 1), (2, 3), (3, 2)}和h = {(1, 3), (2, 1), (3,1)},则( )是单射,( )是满射,( )是双射.3. 下列5个命题公式中,是永真式的有( )(选择正确答案的番号).(1)q q p p →→∧)(;(2))(q p p ∨→;(3))(q p p ∧→;(4)q q p p →∨∧⌝)(;(5)q q p →→)(.4. 设D 24是24的所有正因数组成的集合,“|”是其上的整除关系,则3的补元( ),4的补元( ),6的补元( ).5. 设G 是(7, 15)简单平面图,则G 一定是( )图,且其每个面恰由( )条边围成,G 的面数为( ).二、单选题(每小题3分,共15分)1. 设A , B , C 是集合,则下述论断正确的是( ).(A)若A ⊆ B , B ∈ C ,则A ∈ C . (B)若A ⊆ B , B ∈ C ,则A ⊆ C .(C)若A ∈ B , B ⊆ C ,则A ∈ C . (D)若A ∈ B , B ⊆ C ,则A ⊆ C .2. 设R ⊆ A ⨯ A ,S ⊆ A ⨯ A ,则下述结论正确的是( ).(A)若R 和S 是自反的,则R ⋂ S 是自反的.(B)若R 和S 是对称的,则S R 是对称的.(C)若R 和S 是反对称的,则S R 是反对称的.(D)若R 和S 是传递的,则R ⋃ S 是传递的.3.在谓词逻辑中,下列各式中不正确的是( ).(A))()())()((x xB x xA x B x A x ∀∨∀=∨∀(B))()())()((x xB x xA x B x A x ∀∧∀=∧∀(C))()())()((x xB x xA x B x A x ∃∨∃=∨∃(D)),(),(y x xA y y x yA x ∀∃=∃∀4. 域与整环的关系为( ).(A)整环是域 (B)域是整环 (C)整环不是域 (D) 域不是整环5.设G 是(n , m )图,且G 中每个节点的度数不是k 就是k + 1,则G 中度数为k 的节点个数为( ). (A)2n . (B)n (n + 1). (C)nk . (D)m k n 2)1(-+. 三、判断题(每小题3分,共15分): 正确打“√”,错误打“×”.1.设f : Z → Z ,x x x f 2||)(-=,则f 是单射. ( )2.设ϕ是群G 1到群G 2的同态映射,若G 1是Abel 群,则G 2是Abel 群. ( )3.设),(≤L 是格,对于L z y x ∈,,,若z x y x ⋅=⋅且z x y x +=+,则z y =. ( )4.元素个数相同的有限布尔代数都是同构的. ( )5.设G 是n (n ≥ 11)阶简单图,则G 或G 是非平面图. ( )四、(15分)设A 和B 是集合,使下列各式(1)A B A =⋂; (2)A B B A -=-;(3)A A B B A =-⋃-)()(成立的充要条件是什么,并给出理由.五、(10分) 设S 是实数集合R 上的关系,其定义如下∈=y x y x S ,|),{(R 且是3y x -是整数}, 证明: S 是R 上的等价关系. 六、(10分) 求谓词公式)))()(()(()(x xD y yC y B x xA ∀→∃⌝→→∃的前束范式.七、(10分) 若n 个人,每个人恰有3个朋友,则n 必为偶数,试证明之.八、(10分) 利用生成函数求解递归关系⎩⎨⎧=-+=-2)1(211a n a a n n .《离散数学》期末考试题(D)一、填空题(每小题3分,共15分)1. 设|A | = 5, |B | = 2, 则可定义A 到B 的函数( )个,其中有( )单射,( )个满射.2. 令G (x ): x 是金子,F (x ): x 是闪光的,则命题“金子都是闪光的,但闪光的未必是金子”符号化为( ).3. 设X 是非空集合,则X 的幂集P (X )关于集合的⋃运算的单位元是( ),零元是( ),P (X )关于集合的⋂运算的单位元是( ).4. 不同构的5阶无向树有( )棵.5. 对于n 阶完全无向图K n , 当n 为( )时是Euler 图,当n ≥ ( )时是Hamilton 图,当n ( )时是平面图.二、单选题(每小题3分,共15分)1. 幂集P (P (P (∅))) 为( )(A){{∅}, {∅, {∅}}}. (B){∅, {∅, {∅}}, {∅}}.(C){ ∅, {∅, {∅}}, {{∅}}, {∅}} (D){ ∅, {∅, {∅}}}.2. 设R 是集合A 上的偏序关系,则1-⋃R R 是( ).(A)偏序关系 (B)等价关系 (C)相容关系 (D)以上答案都不对3. 下列( )组命题公式是不等值的.(A))(B A →⌝与B A ⌝∧. (B) )(B A ↔⌝与)()(B A B A ∧⌝∨⌝∧.(C))(C B A ∨→与C B A →⌝∧)(. (D))(C B A ∨→与)(C B A ∨∧⌝.4.下列代数结构(G , *)中,( )是群.(A)G = {0, 1, 3, 5}, “*”是模7加法. (B) G = Q , “*”是数的乘法.(C)G = Z , “*”是数的减法. (D) G = {1, 3, 4, 5, 9}, “*”是模11乘法.5.4阶完全无向图4K 中含3条边的不同构的生成子图有(A)3 (B)4 (C)5 (D)2三、判断题(每小题3分,共15分): 正确打“√”,错误打“×”.1.函数的复合运算“ ”满足结合律. ( )2. {→⌝,}是最小功能完备联结词集合. ( )3. 实数集R 关于数的乘法运算“⋅”阿贝尔群. ( )4. 任意有限域的元素个数为2n . ( )5. 设G 是n (n 为奇数)简单图,则G 与G 中度数为奇数的节点个数相同. ( )四、(10分)设A 和B 是集合,使B B A =-成立的充要条件是什么,并给出理由.五、(10分) 设R 和S 是集合A 上的对称关系,证明S R 对称的充要条件是R S S R =.六、(15分)分别利用(1)等值演算法和(2)真值表求命题公式))(())((r q p p q r A ∨→→→∨⌝=的主析取范式和主合取范式.七、(10分) 设G 是(n , m )无向图,若n m ≥,证明G 中必存在圈.八、(10分) 在初始条件f (1) = c 下,求解递归关系bn n f n f +⎪⎭⎫ ⎝⎛=22)(,其中b ,c 为常数且kn 2=,k 为正整数.《离散数学》期末考试题(E)一、填空题(每小题3分,共15分)1.设A = {2, {3}, 4, a }, B = {1, 3, 4, {a }}, 则{3}( )A ,{a }( )B ,{{a }}( )B .2. 设A = {1, 2, 3, 4, 5}上的关系R = {(1, 2), (3, 4), (2, 2)}, S = {(4, 2), (2, 5), (3, 1), (1, 3)}, 则=S R { }, =R S { }, =R R { }.3. gcd(36, 48) = ( ),lcm(36, 48) = ( ).4.任意有限布尔代数)1,0,,,,(⋅+B 均与集合代数( )同构,其元素个数为( ).5. 不同构的5阶无向树有( )棵,不同构的5阶根树有( )棵.二、单选题(每小题3分,共15分)1. 在有理数集合Q 上定义运算“*”如下:对于任意x , y ∈ Q ,y x * = x + y – xy ,则Q 关于*的单位元是( ).(A)x . (B)y . (C)1. (D)0.2. 设A = {1, 2, 3}, 下图分别给出了A 上的两个关系R 和S ,则S R 是( )关系.(A)自反. (B)对称. (C)传递. (D)等价.3.令T (x ): x 是火车,B (x ): x 是汽车,F (x , y ): x 比y 快,则“某些汽车比所有的火车慢”符号化为( ).(A)()()),()()(y x H x T x y B y →∀∧∃.(B)()()),()()(y x H x T x y B y ∧∀→∃.(C)()()),()()(y x H x T y B y x ∧→∃∀.(D)()()),()()(y x H x T x y B y →∀→∃.4. 整数集合Z 关于数的加法“+”和数的乘法“⋅”构成的代数结构(Z, +, ⋅)是( ). 1 1 22 3 3G S G R(A)域(B)域和整环(C)整环(D) 有零因子环G≅,则称G为自补图. 5阶不同构的自补图5.设G是简单图,G是G的补图,若G个数为( ).(A)0. (B)1. (C)2. (D)3.三、判断题(每小题3分,共15分): 正确打“√”,错误打“×”.1. { ∅, {∅}} ∉P(P({∅})). ( )2. 非空1元及2元联结词集合的个数为29-1. ( )3. 群可分为Abel群和非Abel群. ( )4. 元素个数相同的有限域都是同构的. ( )5. 设G是简单图,则G或G是连通图. ( )四、(15分)设C,:, 若gf 是单射,证明f是单射,并举例说明g→:f→gBBA不一定是单射.五、(10分)设A = {a, b, c, d}上的关系R = {(a, b), (b, d), (c, c), (a, c)}, 画出R的关系图,并求出R的自反闭包r(R)、对称闭包s(R)和传递闭包t(R).六、(10分)用CP规则证明下列推理.⌝∨→∨(.⇒),(⌝),→pqssrqrqp→七、(10分)求谓词公式))xyByAxA∀→∨∀∧⌝∃的前束范式.zC((x()))(z(()八、(10分)任意6个人中,一定有3个人彼此认识或有3个人彼此不认识.《离散数学》期末考试题(F)一、填空题(每小题3分,共15分)1. 设A = {1, 2, 3, {1, 2}, {3}}, B = {2, {2,3}, {1}} , 则A–B = { }, B–A = { }, A⊕B = { }.2. 实数集合R关于加法运算“+”的单位元为( ), 关于乘法运算“⋅”的单位元为( ), 关于乘法运算“⋅”的零元为( ).3. 令Z(x): x是整数,O(x): x是奇数,则“不是所有整数都是奇数”符号化为( ).4. 有限域的元素个数为( ), 其中( )且( ).5. 设G 是(7, 15)简单平面图,则G 一定 ( )连通图,其每个面恰由( )条边围成,G 的面数为( ).二、单选题(每小题3分,共15分)1. 函数的复合运算“ ”满足( )(A)交换律. (B)结合律. (C)幂等律. (D)消去律.2. 设集合A 中有4个元素,则A 上的等价关系共有( )个.(A)13 (B)14 (C)15 (D)163.下列代数结构(G , *)中,( )是群.(A)G = {0, 1, 3, 5}, “*”是模7加法. (B) G = Q , “*”是数的乘法.(C)G = Z , “*”是数的减法. (D) G = {1, 3, 4, 5, 9}, “*”是模11乘法.4. 下列偏序集,( )是格.5. 不同构的(5, 3)简单无向图有( )个.(A)4 (B)5 (C)3 (D)2三、判断题(每小题3分,共15分): 正确打“√”,错误打“×”.1. 设A ,B ,C 是集合,若C A B A ⊕=⊕, 则B = C . ( )2. 逻辑联结词“→”满足结合律. ( )3. 设 (L , ≤)是偏序集,若L 的任意非空子集均存在上确界和下确界,则(L , ≤)是格.( )4. 在同构意义下,有限布尔代数只有,,,),((⋂⋃X P ∅, X ). ( )5. 设G 是简单图,则G 与G 中度数为奇数的节点个数相同. ( )四、(15分) 设C B g B A f →→:,:, 若g f 是满射,证明g 是满射,并举例说明f 不一定是满射.五、(10分) 在整数集合Z 上定义关系R 如下:对于任意∈y x , Z ,y y x x R y x +=+⇔∈22),(.判断R 是否具有自反性、反自反性、对称性、反对称性及传递性.六、(10分)利用真值表求命题公式)())(q p q p A ⌝→↔→⌝=的主析取范式和主合取范式.七、(10分)证明:在至少两个人的人群中,必有两个人有相同个数的朋友.八、(10分)将6阶完全无向图K 6的边随意地涂上红色或蓝色,证明:无论如何涂法,总存在红色的K 3或蓝色的K 3.(ps :答案见离散数学期末复习题(6套)答案文档)。
离散数学期末考试复习题及参考答案

参考答案: B
6、 设 A. 代数系统 B. 半群 C. 群
,*为普通乘法,则<S,*>是( )
D. 都不是
参考答案: A
7、 设S={0,1},*为普通乘法,则< S , * >是( ) A. 半群,但不是独异点 B. 只是独异点,但不是群 C. 群 D. 环,但不是群
参考答案: B
A. B. C. D.
参考答案: B
3、 命题“有的人喜欢所有的花”的逻辑符号化为( ) 设D:全总个体域,F(x):x是花,M(x) :x是人,H(x,y):x喜欢y
A. B. C. D.
参考答案: D
4、 下列等价式成立的有( )
A. B. C. D.
参考答案: D
5、 下列公式是重言式的有( )
5、 ( )设S={1,2},则S在普通加法和乘法运算下都不封闭。 参考答案: 正确
8、 谓词公式
中的x是( )
A. 自由变元
B. 约束变元
C. 既是自由变元又是约束变元
D. 既不是自由变元又不是约束变元
参考答案: C
9、 设
是一个有界格,如果它也是有补格,只要满足( )
A. 每个元素都至少有一个补元
B. 每个元素都有多个补元
C. 每个元素都无补元
D. 每个元素都有一个补元
参考答案: A
10、 一棵无向树T有4度、3度、2度的分枝点各1个,其余顶点均为树叶,则T中有( )片树叶
A. 3 B. 4 C. 5 D. 6
参考答案: C
11、 设
A. {{1,2}} B. {1,2 } C. {1} D. {2}
参考答案: A
,则有( )
北邮离散数学期末复习题

北邮离散数学期末复习题 第一章集合论 一、判断题(1)空集是任何集合的真子集. ( 错 )(2){}φ是空集. ( 错 ) (3){}{}a a a },{∈ ( 对 ) (4)设集合{}{}{}{}AA 22,1,2,1,2,1⊆=则. ( 对 ) (5)如果B A a ⋃∉,则A a ∉或B a ∉. ( 错 )解 B A a ⋃∉则B A B A a ⋂=⋃∈,即A a ∈且B a ∈,所以A a ∉且B a ∉(6)如果A ∪.,B A B B ⊆=则 ( 对 )(7)设集合},,{321a a a A =,},,{321b b b B =,则},,,,,{332211><><><=⨯b a b a b a B A ( 错 )(8)设集合}1,0{=A ,则}1},0{,0},0{,1,,0,{><><><><=φφρ是A2到A 的关系. ( 对 )解 A 2}},1{},0{,{A φ=, =⨯A A 2}1,,0,,1},1{,0},1{,1},0{,0},0{,1,,0,{><><><><><><><><A A φφ(9)关系的复合运算满足交换律. ( 错 )(10).条件具有传递性的充分必要上的关系是集合ρρρρA =ο ( 错 )(11)设.~,上的传递关系也是则上的传递关系是集合A A ρρ ( 对 ) (12)集合A 上的对称关系必不是反对称的. ( 错 )(13)设21,ρρ为集合A 上的等价关系, 则21ρρ⋂也是集合A 上的等价关系( 对 )(14)设ρ是集合A 上的等价关系, 则当ρ>∈<b a ,时, ρρ][][b a = ( 对 )(15)设21,ρρ为集合 A 上的等价关系, 则 ( 错 )二、单项选择题(1)设R 为实数集合,下列集合中哪一个不是空集 ( A )A. {}R x x x ∈=-且,01|2 B .{}R x x x ∈=+且,09|2C. {}R x x x x ∈+=且,1|D. {}R x x x ∈-=且,1|2(2)设B A ,为集合,若φ=B A \,则一定有 ( C )A. φ=B B .φ≠B C. B A ⊆ D. B A ⊇(3)下列各式中不正确的是 ( C )A. φφ⊆ B .{}φφ∈ C. φφ⊂ D. {}}{,φφφ∈ (4)设{}}{,a a A =,则下列各式中错误的是 ( B )A. {}A a 2∈ B .{}A a 2⊆ C. {}A a 2}{∈ D. {}Aa 2}{⊆ (5)设{}2,1=A ,{}c b a B ,,=,{}d c C ,=,则)(C B A I ⨯为 ( B ) A. {}><><c c ,2,1, B .{}><><c c ,2,,1C. {}><><2,,,1c cD. {}><><2,,1,c c(6)设{}b A ,0=,{}3,,1b B =,则B A Y 的恒等关系为 ( A ) A. {}><><><><3,3,,,1,1,0,0b b B .{}><><><3,3,1,1,0,0C. {}><><><3,3,,,0,0b bD. {}><><><><0,3,3,,,1,1,0b b(7)设{}c b a A ,,=上的二元关系如下,则具有传递性的为 ( D )A. {}><><><><=a b b a a c c a ,,,,,,,1ρB . {}><><=a c c a ,,,2ρC. {}><><><><=c b a b c c b a ,,,,,,,3ρD. {}><=a a ,4ρ(8)设ρ为集合A 上的等价关系,对任意A a ∈,其等价类[]ρa 为 ( B )A. 空集; B .非空集; C. 是否为空集不能确定; D. }|{A x x ∈.(9)映射的复合运算满足 ( B )A. 交换律 B .结合律 C. 幂等律 D. 分配律(10)设A ,B 是集合,则下列说法中( C )是正确的.A .A 到B 的关系都是A 到B 的映射B .A 到B 的映射都是可逆的C .A 到B 的双射都是可逆的D .B A ⊂时必不存在A 到B 的双射(11)设A 是集合,则( B )成立.A .A A #22#=B .A X X A⊆↔∈2 C .{}A2∈φ D .{}AA 2∈ (12)设A 是有限集(n A =#),则A 上既是≤又是~的关系共有(B ).A .0个B .1个C .2个D .n 个三、填空题1. 设}}2,1{,2,1{=A ,则=A2____________.填}}},2,1{,2{}},2,1{,1{},2,1{}},2,1{{},2{},1{,{2A A φ=2.设}}{,{φφ=A ,则A 2= . 填}}},{{},{,{2A A φφφ=3.设集合B A ,中元素的个数分别为5#=A ,7#=B ,且9)(#=⋃B A ,则集合B A ⋂中元素的个数=⋂)(#B A .34.设集合}4,1001|{Z x x x x A ∈≤≤=的倍数,是,}5,1001|{Z x x x x B ∈≤≤=的倍数,是,则B A Y 中元素的个数为 .405.设 },{b a A =, ρ 是 A2 上的包含于关系,,则有ρ= .},,},{,}{},{,},{,}{},{,,,}{,,}{,,,{><><><><><><><><><A A A b b b A a a a A b a φφφφφ6.设21,ρρ为集合 A 上的二元关系, 则=21ρρο .~1~2ρρο7.集合A 上的二元关系ρ为传递的充分必要条件是 .ρρρ⊆ο8. 设集合{}{}><><==0,2,2,02,1,01ρ上的关系A 及集合A 到集合{}4,2,0=B 的关系=2ρ{><b a ,|><b a ,A b a B A ∈⨯∈,且∩}=21,ρρο则B ___________________.填 }2,2,0,2,2,0,0,0{><><><><四、解答题1. 设 A d c b a A },,,,{=上的关系 },,,,,,,,,,,,,,,{><><><><><><><><=c d d c a b b a d d c c b b a a ρ(1)写出ρ的关系矩阵;(2)验证ρ是A 上的等价关系;(3)求出A 的各元素的等价类。
离散数学总复习题(选择填空) (1)
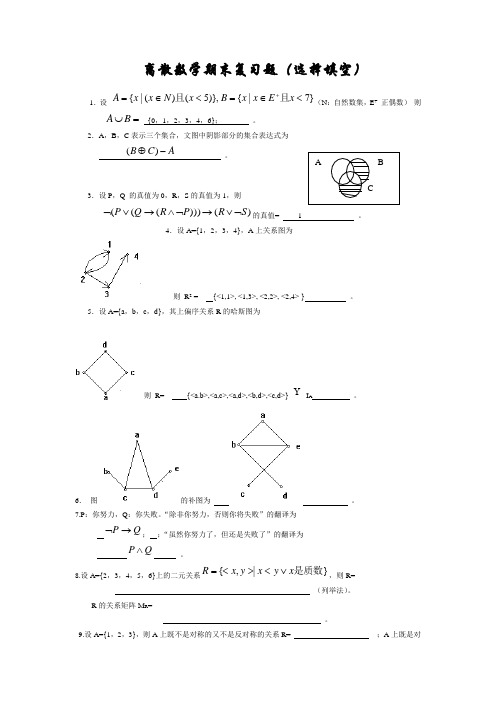
离散数学期末复习题(选择填空)1.设 }7|{)},5()(|{<∈=<∈=+x E x x B x N x x A 且且(N :自然数集,E + 正偶数) 则 =⋃B A {0,1,2,3,4,6}; 。
2.A ,B ,C 表示三个集合,文图中阴影部分的集合表达式为A CB -⊕)( 。
3.设P ,Q 的真值为0,R ,S 的真值为1,则 )()))(((S R P R Q P ⌝∨→⌝∧→∨⌝的真值= 1 。
4.设A={1,2,3,4},A 上关系图为则 R 2 = {<1,1>, <1,3>, <2,2>, <2,4> } 。
5.设A={a ,b ,c ,d},其上偏序关系R 的哈斯图为则 R= {<a.b>,<a,c>,<a,d>,<b,d>,<c,d>}I A 。
6. 图的补图为 。
7.P :你努力,Q :你失败。
“除非你努力,否则你将失败”的翻译为Q P →⌝; ;“虽然你努力了,但还是失败了”的翻译为Q P ∧ 。
8.设A={2,3,4,5,6}上的二元关系}|,{是质数x y x y x R∨<><=,则R= (列举法)。
R 的关系矩阵M R =。
9.设A={1,2,3},则A 上既不是对称的又不是反对称的关系R= ;A 上既是对AB C称的又是反对称的关系R= 。
10.n 个结点的无向完全图K n 的边数为 )1(21-n n ,欧拉图的充要条件是:图中无奇度结点且连通11.设A={a ,b ,c},A 上二元关系R={< a, a > , < a, b >,< a, c >, < c, c>} ,则s (R )=}a , c ,a , b ,c , c ,c , a ,b , a ,a , a {><><><><><>< 。
离散数学(1)复习笔记
离散数学(1)复习笔记Ch1 命题逻辑的基本概念1.1 命题命题:能判断真假且⾮真即假的陈述句。
命题的真值,真命题,假命题。
* 真值待定 *简单命题 | 原⼦命题,复合命题。
1.2 常⽤的5个命题联结词否定,合取,析取,蕴涵,双蕴涵。
* 异或 | 排斥或 | 不可兼或 * 注意语义判断。
* p→q = ﹁ p∨q ** 必要条件 * 只有……才……;仅当……,……;……,仅当……。
注意命题符号化的蕴涵⽅向。
* domain * A horse is white. (×)联结词集,⼀元联结词,⼆元联结词。
* 优先顺序 * (),﹁,∧,∨,→,↔1.3 合式公式及其赋值命题常项 | 命题常元(值是确定的),命题变项 | 命题变元(真值可以变化的陈述句)。
合式公式 | 命题公式 | 命题形式 | 公式(wff)(well formed formulas),原⼦命题公式(单个命题变项),⼦公式。
* 单个命题变项是合式公式,没说命题常项。
*赋值 | 解释,成真赋值,成假赋值。
真值表。
* 真值表要点:赋值从00…0开始,按照⼆进制加法,直到11…1为⽌;按照运算的优先次序写出各⼦公式。
*命题公式的分类:重⾔式 | 永真式,⽭盾式 | 永假式,可满⾜式。
1.4 重⾔式与代⼊规则代⼊规则。
* 1. 公式中被代换的只能是命题变项(原⼦命题),⽽不能是复合命题。
2.对公式中某命题变项施以代⼊,必须对该公式中出现的所有同⼀命题变项施以相同的代换。
* 1.5 命题形式化命题形式化 | 符号化。
* 注意充分条件和必要条件的区别 ** 注意语义是否考虑完整 *1.6 波兰表达式中置式 | 中缀式,前置式 | 前缀式 | 波兰式,后置式 | 后缀式 | 逆波兰式。
Ch2 命题逻辑的等值和推理演算2.1 等值定理等值 | 等价,等值定理:设A,B为两个命题公式,A = B的充分必要条件是 A↔B为⼀个重⾔式。
离散数学期末考试试题(有几套带答案)
离散数学试题(A 卷及答案)一、证明题(10分)1)(⌝P ∧(⌝Q ∧R))∨(Q ∧R)∨(P ∧R)⇔R证明: 左端⇔(⌝P ∧⌝Q ∧R)∨((Q ∨P)∧R)⇔((⌝P ∧⌝Q)∧R))∨((Q ∨P)∧R)⇔(⌝(P ∨Q)∧R)∨((Q ∨P)∧R)⇔(⌝(P ∨Q)∨(Q ∨P))∧R ⇔(⌝(P ∨Q)∨(P ∨Q))∧R ⇔T ∧R(置换)⇔R2)∃x(A(x)→B(x))⇔ ∀xA(x)→∃xB(x)证明 :∃x(A(x)→B(x))⇔∃x(⌝A(x)∨B(x))⇔∃x ⌝A(x)∨∃xB(x)⇔⌝∀xA(x)∨∃xB(x)⇔∀xA(x)→∃xB(x) 二、求命题公式(P ∨(Q ∧R))→(P ∧Q ∧R)的主析取范式和主合取范式(10分)证明:(P ∨(Q ∧R))→(P ∧Q ∧R)⇔⌝(P ∨(Q ∧R))∨(P ∧Q ∧R))⇔(⌝P ∧(⌝Q ∨⌝R))∨(P ∧Q ∧R) ⇔(⌝P ∧⌝Q)∨(⌝P ∧⌝R))∨(P ∧Q ∧R)⇔(⌝P ∧⌝Q ∧R)∨(⌝P ∧⌝Q ∧⌝R)∨(⌝P ∧Q ∧⌝R))∨(⌝P ∧⌝Q ∧⌝R))∨(P ∧Q ∧R) ⇔m0∨m1∨m2∨m7 ⇔M3∨M4∨M5∨M6三、推理证明题(10分)1) C ∨D, (C ∨D)→ ⌝E, ⌝E →(A ∧⌝B), (A ∧⌝B)→(R ∨S)⇒R ∨S证明:(1) (C ∨D)→⌝E(2) ⌝E →(A ∧⌝B)(3) (C ∨D)→(A ∧⌝B) (4) (A ∧⌝B)→(R ∨S) (5) (C ∨D)→(R ∨S)(6) C ∨D(7) R ∨S2) ∀x(P(x)→Q(y)∧R(x)),∃xP(x)⇒Q(y)∧∃x(P(x)∧R(x))证明(1)∃xP(x) (2)P(a)(3)∀x(P(x)→Q(y)∧R(x)) (4)P(a)→Q(y)∧R(a) (5)Q(y)∧R(a) (6)Q(y) (7)R(a) (8)P(a) (9)P(a)∧R(a) (10)∃x(P(x)∧R(x)) (11)Q(y)∧∃x(P(x)∧R(x))四、设m 是一个取定的正整数,证明:在任取m +1个整数中,至少有两个整数,它们的差是m 的整数倍证明 设1a ,2a ,…,1+m a 为任取的m +1个整数,用m 去除它们所得余数只能是0,1,…,m -1,由抽屉原理可知,1a ,2a ,…,1+m a 这m +1个整数中至少存在两个数s a 和t a ,它们被m 除所得余数相同,因此s a 和t a 的差是m 的整数倍。
离散数学期末复习题
离散数学期末复习题第一章集合论一、判断题(1)空集是任何集合的真子集. ( 错 )(2){}φ是空集. ( 错 ) (3){}{}a a a },{∈ ( 对 ) (4)设集合{}{}{}{}AA 22,1,2,1,2,1⊆=则. ( 对 ) (5)如果B A a ⋃∉,则A a ∉或B a ∉. ( 错 )解 B A a ⋃∉则B A B A a ⋂=⋃∈,即A a ∈且B a ∈,所以A a ∉且B a ∉(6)如果A ∪.,B A B B ⊆=则 ( 对 )(7)设集合},,{321a a a A =,},,{321b b b B =,则},,,,,{332211><><><=⨯b a b a b a B A ( 错 )(8)设集合}1,0{=A ,则}1},0{,0},0{,1,,0,{><><><><=φφρ是A2到A 的关系. ( 对 )解 A 2}},1{},0{,{A φ=, =⨯A A 2}1,,0,,1},1{,0},1{,1},0{,0},0{,1,,0,{><><><><><><><><A A φφ(9)关系的复合运算满足交换律. ( 错 )(10).条件具有传递性的充分必要上的关系是集合ρρρρA = ( 错 )(11)设.~,上的传递关系也是则上的传递关系是集合A A ρρ ( 对 ) (12)集合A 上的对称关系必不是反对称的. ( 错 )(13)设21,ρρ为集合A 上的等价关系, 则21ρρ⋂也是集合A 上的等价关系( 对 )(14)设ρ是集合A 上的等价关系, 则当ρ>∈<b a ,时, ρρ][][b a = ( 对 )(15)设21,ρρ为集合 A 上的等价关系, 则 ( 错 )二、单项选择题(1)设R 为实数集合,下列集合中哪一个不是空集 ( A )A. {}R x x x ∈=-且,01|2 B .{}R x x x ∈=+且,09|2C. {}R x x x x ∈+=且,1|D. {}R x x x ∈-=且,1|2(2)设B A ,为集合,若φ=B A \,则一定有 ( C )A. φ=B B .φ≠B C. B A ⊆ D. B A ⊇(3)下列各式中不正确的是 ( C )A. φφ⊆ B .{}φφ∈ C. φφ⊂ D. {}}{,φφφ∈ (4)设{}}{,a a A =,则下列各式中错误的是 ( B )A. {}A a 2∈ B .{}A a 2⊆ C. {}A a 2}{∈ D. {}Aa 2}{⊆ (5)设{}2,1=A ,{}c b a B ,,=,{}d c C ,=,则)(C B A ⨯为 ( B ) A. {}><><c c ,2,1, B .{}><><c c ,2,,1C. {}><><2,,,1c cD. {}><><2,,1,c c(6)设{}b A ,0=,{}3,,1b B =,则B A 的恒等关系为 ( A ) A. {}><><><><3,3,,,1,1,0,0b b B .{}><><><3,3,1,1,0,0C. {}><><><3,3,,,0,0b bD. {}><><><><0,3,3,,,1,1,0b b(7)设{}c b a A ,,=上的二元关系如下,则具有传递性的为 ( D )A. {}><><><><=a b b a a c c a ,,,,,,,1ρB . {}><><=a c c a ,,,2ρC. {}><><><><=c b a b c c b a ,,,,,,,3ρD. {}><=a a ,4ρ(8)设ρ为集合A 上的等价关系,对任意A a ∈,其等价类[]ρa 为 ( B )A. 空集; B .非空集; C. 是否为空集不能确定; D. }|{A x x ∈.(9)映射的复合运算满足 ( B )A. 交换律 B .结合律 C. 幂等律 D. 分配律(10)设A ,B 是集合,则下列说法中( C )是正确的.A .A 到B 的关系都是A 到B 的映射B .A 到B 的映射都是可逆的C .A 到B 的双射都是可逆的D .B A ⊂时必不存在A 到B 的双射(11)设A 是集合,则( B )成立.A .A A #22#=B .A X X A⊆↔∈2 C .{}A2∈φ D .{}AA 2∈ (12)设A 是有限集(n A =#),则A 上既是≤又是~的关系共有(B ).A .0个B .1个C .2个D .n 个三、填空题1. 设}}2,1{,2,1{=A ,则=A2____________.填}}},2,1{,2{}},2,1{,1{},2,1{}},2,1{{},2{},1{,{2A A φ=2.设}}{,{φφ=A ,则A 2= . 填}}},{{},{,{2A A φφφ=3.设集合B A ,中元素的个数分别为5#=A ,7#=B ,且9)(#=⋃B A ,则集合B A ⋂中元素的个数=⋂)(#B A .34.设集合}4,1001|{Z x x x x A ∈≤≤=的倍数,是,}5,1001|{Z x x x x B ∈≤≤=的倍数,是,则B A 中元素的个数为 .405.设 },{b a A =, ρ 是 A2 上的包含于关系,,则有ρ= .},,},{,}{},{,},{,}{},{,,,}{,,}{,,,{><><><><><><><><><A A A b b b A a a a A b a φφφφφ6.设21,ρρ为集合 A 上的二元关系, 则=21ρρ .~1~2ρρ7.集合A 上的二元关系ρ为传递的充分必要条件是 .ρρρ⊆8. 设集合{}{}><><==0,2,2,02,1,01ρ上的关系A 及集合A 到集合{}4,2,0=B 的关系=2ρ{><b a ,|><b a ,A b a B A ∈⨯∈,且∩}=21,ρρ 则B ___________________. 填 }2,2,0,2,2,0,0,0{><><><><四、解答题1. 设 A d c b a A },,,,{=上的关系 },,,,,,,,,,,,,,,{><><><><><><><><=c d d c a b b a d d c c b b a a ρ(1)写出ρ的关系矩阵;(2)验证ρ是A 上的等价关系;(3)求出A 的各元素的等价类。
大学《离散数学》期末考试试卷及答案(1)
大学《离散数学》期末考试试卷及答案(1)一、选择题1. 离散数学的主要研究对象是()。
A. 连续的数学结构B. 有限的数学结构C. 数学的综合应用D. 数学的哲学思考2. 命题逻辑是离散数学的一个重要组成部分,它主要研究()。
A. 命题之间的真假关系B. 变量之间的关系C. 函数之间的关系D. 集合之间的关系3. 集合的基本运算包括()。
A. 并、交、差、补B. 加、减、乘、除C. 包含、相等、不等、自反D. 大于、小于、等于、不等于二、填空题1. 若集合A={m|2m-1>3},则A中的元素为______。
2. 有一个集合A={1,2,3},则集合A的幂集为______。
3. 若命题p为真,命题q为假,则复合命题“p∧q”的真值为______。
三、解答题1. 请写出离散数学中常用的数学符号及其含义。
2. 请解释命题逻辑中的充分必要条件及其符号表示,并给出一个例子。
3. 请定义集合的笛卡尔积,并给出两个集合进行笛卡尔积运算的例子。
四、问答题1. 离散数学在计算机科学中有着重要的应用,请列举三个与计算机科学相关的离散数学应用领域并简要介绍。
2. 请简要解释归纳法在离散数学中的作用,并给出一个使用归纳法证明的例子。
3. 什么是有向图?请给出一个有向图的例子,并解释该图中的关系。
参考答案:一、选择题1. B2. A3. A二、填空题1. A={m|2m-1>3}2. {{}, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}}3. 假三、解答题1. 常用数学符号及含义:- ∪:并,表示集合的合并操作。
- ∩:交,表示集合的交集操作。
- ∖:差,表示减去一个集合中的元素。
- ⊆:包含,表示一个集合包含于另一个集合。
- =:相等,表示两个集合具有相同的元素。
2. 充分必要条件是指一个命题的成立与另一个命题的成立互为必要条件,若A是B的充分必要条件,那么当A成立时B一定成立,且当A不成立时B也一定不成立。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• • • • •
• • • •
给定群<G,⊙>及非空子集HG,则 <H,⊙>是<G,⊙>的子群 (a)(b)(a,b∈H→ a⊙b∈H)∧(a)(a∈H→a-1∈H) 即<H,⊙>为<G,⊙>的子群的充要条件是 H对于⊙封闭及H中每个元素存在逆元。 因为: (a ⊙ a-1)=e∈H 又⊙继承了<G,⊙>的可结合性 于是<H,⊙>满足群的定义,而HG 所以<H,⊙>是<G,⊙>的子群.
• 4-7设f1和f2都是从代数系统<S1,*>到<S2,◦> 的同态映射,这里*和◦都是二元运算,并 且◦满足交换律和结合律。定义函数h: S1→S2,使得对于任意 • x∈S1, h(x)=f1(x)◦f2(x) • 试证明h也是从<S1,*>到<S2,◦>的同态映射。 • 证明:由于f1和f2都是从代数系统<S1,*>到 <S2,◦>的同态映射,因此<S1,*>和<S2,◦> 满足同态的基本条件,即是同类型的。只 用证明函数h满足运算的像等于像的运算。
• • • • • • •
•
• 这部分的练习题 4-1通常数的减法运算能否和下列集合构成一个代 数系统. (N ) (1)非负整数集Z (Y) (2)整数集I (Y) (3)有理数集Q 4-2设代数系统V=<I,+,•>,其中I表示整数集,+ 和· 分别表示通常的加法和乘法运算,下面的各个 子集,它是否能构成V的子代数? (1) H1={2n+1| n∈I} N (2) H2={2n | n∈I} Y 4-3设代数系统V=<{1,2,3},◦>,其中二元运算◦定 义为x◦y=x与y中较大的数, 则V有()个子代数。 A.3 B.6 C.7 D.8
• 4-9给定代数系统Um=<Nm,+m>,其中Nm 是 模m同余关系划分自然数集合造成的商集, +m是模m加法,试证U2ΧU3和U6同构 • 解:首先求U2和U3及U2ΧU3 • U2=< N2,+2 >= < {[0],[1]},+2 > • U3=< N3,+3>= < {[0],[1],[2]},+3 > U2ΧU3=<{ <[0],[0]>, <[0],[1]>, <[0],[2]>, <[1],[0]> ,<[1],[1]>, <[1],[2]> },Δ> U6=<{[0],[1],[2],[3],[4],[5]}, +6 >
• Δ <[0],[0]> <[0],[1]> <[0],[2]> <[1],[0]> <[1],[1]> <[1],[2]> <[0],[0]> <[0],[0]> <[0],[1]> <[0],[2]> <[1],[0]> <[1],[1]> <[1],[2]> <[0],[1]> <[0],[1]> <[0],[2]> <[0],[0]> <[1],[1]> <[1],[2]> <[1],[0]> <[0],[2]> <[0],[2]> <[0],[0]> <[0],[1]> <[1],[2]> <[1],[0]> <[1],[1]> <[1],[0]> <[1],[0]> <[1],[1]> <[1],[2]> <[0],[0]> <[0],[1]> <[0],[2]> <[1],[1]> <[1],[1]> <[1],[2]> <[1],[0]> <[0],[1]> <[0],[2]> <[0],[0]> <[1],[2]> <[1],[2]> <[1],[0]> <[1],[1]> <[0],[2]> <[0],[0]> <[0],[1]>
令f: N2 Χ N3→ {[0],[1],[2],[3],[4],[5]}, 并且:f(<[0],[0]> )=[0] ,f(<[0],[1]> )=[4] f(<[0],[2]> )=[2] ,f(<[1],[0]> )=[3] f(<[1],[1]> )=[1] ,f(<[1],[2]> )=[5] 显然f是个双射,而且满足运算的象等于象的运算, 两代数系统同构。
• 对于任意x,y∈S1,因为f1和f2都是从代数系 统<S1,*>到<S2,◦>的同态,因此 • f1(x*y)=f1(x)◦f1(y) • f2(x*y)=f2(x)◦f2(y) • 则h(x*y)=f1(x*y)◦f2(x*y)= (f1(x)◦f1(y))◦( f2(x)◦f2(y)) • 由于◦满足交换律和结合律,故 • h(x*y)= (f1(x)◦f1(y))◦( f2(x)◦f2(y)) • =(f1(x)◦f2(x))◦(f1(y)◦f2(y)) =h(x)◦h(y) • 由x,y取值的任意性可知,h也是从<S1,*>到 <S2,◦>的同态映射。
• 4-6给定集合E={a,b,c},ρ(E)为E的幂集, • < ρ(E),∪>为代数系统,在ρ(E)上定义二 元关系R如下: • XRY当且仅当{b}∩X= {b}∩Y • 其中X,Y∈ρ(E), ∩,∪为集合上的交和并运 算. • 1)证明R是ρ(E)上的等价关系 • 2)证明R是ρ(E)上关于∪ 的同余关系 • 3)求商代数
• • • • • • • • • •
我们来证X1 ∪ X2和Y1 ∪ Y2 也有R的关系 即证{b}∩( X1 ∪ X2)= {b}∩(Y1∪Y2) 而上式({b}∩X1) ∪ ({b}∩ X2) =({b}∩Y1)∪({b}∩Y2) 由已知条件知上式成立,即R为同余关系. 3) ρ(E)/R={ {{b}, {b,c}, {a,b}, {a,b,c}}, {Φ,{a}, {a,c},{c}}} 商代数为<ρ(E)/R,Δ>,对仸意 [X]R,[Y]R ∈ ρ(E)/R, [X]RΔ[Y]R=[X∪Y]R
• 从表中可以看出该代数系统有四个子代数即 U1=<{0},*, Δ >, U2=<{0,3},*, Δ >, U3=<{0,1,2},*, Δ >,和它本身。 • 4-5设U=<I,+,*>,其中I为整数集合,+和*分别是 普通意义下的加和乘,对于I的以下子集,能构成 U的子代数吗?说明理由 • U1=<{-1,0,1}, +,*> • U2=<S1, +,*>, S1={x|x∈Ix≤0} • U3=<S2, +,*>, S2={2x|x∈I} • 解: U1不能,因为1+1=2,不封闭 • U2也不能,因为两个负数相乘为正数,不封闭。 • U3可以。
4-4设U=<{0,1,2,3},*,Δ>为代数系统,其中运 算*,Δ的定义为: x*y=min{x,y} x Δy=(x+y)(mod3) 试给出U的运算表,并求出它的所有子代数. 解:* 0 1 2 3 Δ 0 1 2 3 00 000 0 0 1 2 0 10 111 1 1 2 0 1 20 122 2 2 0 1 2 30 123 3 0 1 2 0
• U=<S,*>及S上的同余关系E,其商代 数为:V= =<S/E, Δ>,对任意x,y ∈S, • [x]E ,[y]E ∈ S/E, • [x]E Δ[y]E= [x*y]E • 群是每一个元素均有逆元的含幺半群。 • 设<S,*>,为群,S´⊆ S,并且<S’,*>为群, 则称<S ´,*>为<S,*>的子群。
• 证明:因为h是从S1到S2的函数,所以 h(S1)⊆S2。由S1非空可知,h(S1)也非空。 • 对任意的y1,y2∈h(S1),必有x1,x2∈S1,使 得h(x1)=y1,h(x2)=y2,于是 • y1*2y2=h(x1)*2h(x2)=h(x1*1x2)=h(x) ∈h(S1) • 对任意的y∈h(S1),必有x∈S1,使得 h(x)=y,于是~2(y)=~2(h(x))=h(~1(x))=h(x’) ∈h(S1)。 • 由y1,y2和y的任意性可知,运算*2和~2在子 集h(S1)上是封闭的,故<h(S1),*2,~2>是V2 的子代数。
• 5、 群中方程解是惟一的。
• • • • • • 6、 ① a∈G,(a-1)-1 = a ② a, b∈G,(a⊙b) -1 = b-1⊙a-1 ③ a∈G,m,n∈Z,有am⊙an = a m+n ④ a∈G,m,n∈Z,有(am)n = amn ⑤ 若<G,⊙>为Abel群(可交换群),则 (a⊙b)n = an⊙bn
• 概念回顾 • 设U=<S,F>,其中 • S是非空元素的集合,F是运算的集合,对 任何fi∈F和任意xi,xj ∈S,有xi fi xj ∈S, 则称U=<S,F>为代数系统。 • 对代数系统U´=<S´,F>,若S´⊆S,F在 S´封闭,则称U´=<S´,F>为 • U=<S,F>的子代数系统。 • 设U=<S,F>和V= < S´,F´ >是两个同型 的代数系统,若存在
