立体几何证明平行专题.doc

合集下载

立体几何(平行线的证明)

立体几何(平行线的证明)在立体几何中，平行线是一种非常重要的概念。

平行线可以定义为在同一个平面内没有交点的两条直线。

证明两条直线平行的方法有很多种，下面将介绍一种简单而常用的方法。

方法一：使用平行线的性质平行线有很多性质，其中一个性质是平行线与横截线之间的夹角相等。

根据这个性质，我们可以通过检查两条线的夹角来证明它们是否平行。

具体步骤如下：1. 给定两条直线AB和CD，我们要证明这两条直线平行。

2. 构建一条横截线EF，该直线与AB和CD相交于点E和F。

3. 使用量角器或直尺测量∠AED和∠CFD的夹角。

如果这两个夹角相等，即∠AED = ∠CFD，那么我们可以得出结论AB与CD平行。

这种方法的好处是简单直观，只需要测量夹角即可。

然而，这种方法并不适用于所有情况，因为有些情况下无法构建合适的横截线。

方法二：使用等边三角形的性质等边三角形是一个有趣的几何形状，所有边都相等。

在等边三角形中，对角线之间的直线也是平行线。

具体步骤如下：1. 给定两条直线AB和CD，我们要证明这两条直线平行。

2. 构建一个等边三角形BCD，在这个等边三角形中，BC = CD。

3. 连接线段AD，我们可以发现线段AD与线段BC平行。

这种方法的好处是不需要测量夹角，只需要利用等边三角形的性质即可。

然而，这种方法也有局限性，因为有些情况下无法构建等边三角形。

综上所述，证明平行线的方法有很多种，其中一些常用的方法是使用平行线的性质和使用等边三角形的性质。

选择合适的方法取决于具体的几何形状和问题要求。

立体几何平行垂直的证明

平行、垂直的证法方法归纳总结
一、平行问题的证明方法
平行问题证明的基本思路：平面平行线面平行线线平行.
1.线线平行的证明方法：
①利用平面几何中的定理：三角形（或梯形）的中位线与底边平行；
平行四边形的对边平行；
利用比例、……；
②三线平行公理：平行于同一条直线的两条直线互相平行；
③线面平行的性质定理：如果一条直线平行于一个平面，经过这条直线的平面和这个平面相交，则这条直线和
垂直问题证明的基本思路：面面垂直线面垂直线线垂直.
1.线线垂直的证明方法：
①利用平面几何中的定理：勾股定理、等腰三角形，三线合一、菱形对角线、直径所对的圆周角是直角、点在
线上的射影。
②线面垂直的定义：如果一条直线和一个平面垂直，那么这条直线就和这个平面内任意的直线都垂直；
③三垂线定理或三垂线逆定理：如果平面内的一条直线和斜线的射影垂直，则它和斜线垂直；反之亦成立。
交线行；
④面面平行的性质定理：如果两个平行平面同时和第三个平面相交，那么它们的交线平行；
⑤线面垂直的性质定理：垂直于同一个平面的两条直线平行。
2.线面平行的证明方法：
①线面平行的定义：直线与平面没有公共点；
②线面平行的判定定理：如果平面外一条直线和这个平面内的一条直线平行，那么这条直线和这个平面平行；
④如果两条平行线中的一条垂直于一条直线，则另一条也垂直于这条直线。
2.线面垂直的证明方法：
①线面垂直的定义：直线与平面内任意直线都垂直；
②线面垂直的判定定理：如果一条直线和一个平面内的两条相交直线垂直，那么这条直线垂直于这个平面；
③线面垂直的性质定理：两条平行直线中的一条垂直于平面，则另一条也垂直于这个平面；
1.如图，四棱锥中，四边形为矩形，为等腰三角形，，平面平面，且．分别为和的中点．

立体几何证明方法——证线线平行

A D1 A1 B1 D B C1
C

a：
方法三：同垂直于一个平面的两条直线互相平行。
a
b

a 推理过程： a // b b
一如何证明直线与直线平行：
方法四：同平行于一条直线的两条直线互相平行。
a b c
a // c 推理过程： a // b b // c
方法演练1：
一如何证明直线与直线平行：
方法一：线面平行则线线平行；
a // 平面推理过程： a 平面 a // b b

b
a

一如何证明直线与直线平行：

方法二：面面平行则线线平行；
// 推理过程： a b // a b
P
已知：四边形 ABCD 是平行四边形，点 P 是平面 ABCD 外一点， M 是 PC 的中点，在 DM 上取一点 G，过 AP 和 G 作平面交平面 BDM 于 GH，A 求证：AP∥GH （提示：线面平行则线线平行）
M D H G C
O
B
方法演练2：
在长方体 ABCD A1 B1C1 D1 中，证明 BD // B1 D1 。（面面平行）

方法技巧专题05立体几何中平行与垂直证明

方法技巧专题05立体几何中平行与垂直证明平行与垂直证明是立体几何中的重要内容之一，本文将介绍一些方法和技巧用于解决平行与垂直的证明问题。

一、平行性的证明方法：1.公共光线法：如果两条直线分别与第三条直线相交，在相交点处的两个对应的内角相等，则这两条直线是平行的。

例如，如果直线AB和CD都与直线EF相交，在交点F处的∠AFC=∠DFB，则AB，CD。

2.反证法：假设AB和CD不平行，然后通过构造形式，证明得到矛盾。

例如，如果直线AB和CD不平行，则可以证明存在一条直线EF与这两条直线分别相交于F和G，且所形成的内角∠FAG=π/2-∠DAF≠π/2，则与直线EF平行，这是与已知条件矛盾的，所以AB，CD。

3.平行线性质法：利用平行线的性质来证明其他线段平行。

例如，根据平行线的交角性质可证明，如果一条直线与一对平行线之一形成等于直角的角，则与另一条平行线也形成等于直角的角。

二、垂直性的证明方法：1.垂直线性质法：利用垂直线的性质来证明其他线段垂直。

例如，如果直线AB与直线CD相交于点E，且∠AED=∠BEC=π/2，则直线AB垂直于直线CD。

2.垂直线段法：如果两条线段的斜率之积为-1，则这两条线段垂直。

例如，如果直线AB和直线CD的斜率之积为-1，则AB⊥CD。

3.反证法：假设AB和CD不垂直，然后通过构造形式，证明得到矛盾。

例如，如果直线AB和CD不垂直，则可以证明存在一条直线EF与这两条直线相交于点G，且所形成的两个内角∠GAC和∠GDB之和小于π/2，这与直线EF垂直的性质矛盾，所以AB⊥CD。

综上所述，平行与垂直证明可以通过公共光线法、反证法、平行线性质法、垂直线性质法、垂直线段法等方法和技巧来解决。

在实际问题中，可以根据已知条件选择合适的方法和技巧，灵活运用来解决平行与垂直的证明问题。

立体几何线面平行证明

立体几何线面平行证明要证明两个线面平行，一般可以通过以下几种方法来进行证明：方法一：使用平行线的性质假设我们有线面A和线面B，要证明A和B平行，可以通过以下步骤进行证明：1.假设线面A和线面B不平行，即存在一条线a与线面A不平行，又与线面B相交于一点P。

2.假设在线面A上存在一点Q，它与直线a上相交于一点R。

3.由于线a与线面B相交于P，所以线段PR必然属于线面B。

4.由于线a与线面A相交于R，所以线段PR必然属于线面A。

5.由于线面A和线面B都包含线段PR，所以它们必然相交。

6.这与我们的假设相矛盾，因此假设不成立，即线面A和线面B是平行的。

方法二：使用支撑面的性质假设我们有线面A和线面B，要证明A和B平行，可以通过以下步骤进行证明：1.假设在线面A上存在一条直线a，它与线面B相交于一点P。

2.过直线a作平行于线面B的平面，该平面与线面A相交于线段QR。

3.由于直线a与线面B相交于点P，所以线段PR必然属于线面B。

4.由于平面上的任意两点可以确定一条直线，所以线段QR也属于线面B。

5.因此，线段QR同时属于线面A和线面B，所以它们不是平行的。

6.这与我们的假设相矛盾，因此假设不成立，即线面A和线面B是平行的。

方法三：使用平行四边形的性质假设我们有线面A和线面B，要证明A和B平行1.假设在线面A上存在一条直线a，它与线面B相交于一点P。

2.在线面A上选择一点Q，并通过P点作一条平行于线面A的直线b。

3.连接直线a和直线b，得到平行四边形PQRD。

4.由于平行四边形的特性，相邻两边平行且长度相等，所以线段PD也是平行于线面A的，并且它必然属于线面B。

5.因此，线段PD同时属于线面A和线面B，所以它们不是平行的。

6.这与我们的假设相矛盾，因此假设不成立，即线面A和线面B是平行的。

以上三种方法是一些常用的证明线面平行的方法，根据实际问题的具体情况，可以选择适合的方法进行证明。

专题01 平行问题的证明(原卷版)

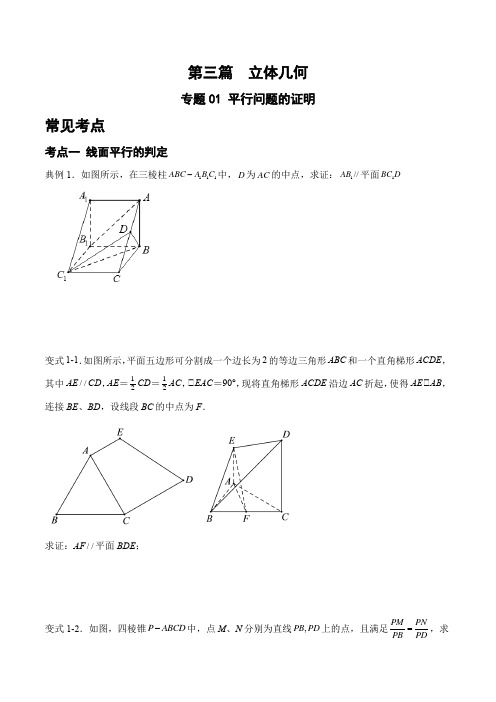
第三篇立体几何专题01 平行问题的证明常见考点考点一线面平行的判定典例1．如图所示，在三棱柱111ABC A B C -中，D 为AC 的中点，求证：1//AB 平面1BC D变式1-1．如图所示，平面五边形可分割成一个边长为2的等边三角形ABC 和一个直角梯形ACDE ，其中AE //CD ，AE ＝12CD ＝12AC ，∠EAC ＝90°，现将直角梯形ACDE 沿边AC 折起，使得AE ∠AB ，连接BE 、BD ，设线段BC 的中点为F ．求证：AF //平面BDE ；变式1-2．如图，四棱锥P ABCD -中，点M 、N 分别为直线,PB PD 上的点，且满足PM PN PB PD=，求证：//MN 平面ABCD .变式1-3．如图所示，已知正方形ABCD .E 、F 分别是AB 、CD 的中点，将ADE 沿DE 折起.证明//BF 平面ADE .考点二面面平行的判定典例2．如图，在四棱锥P －ABCD 中，E ，F ，G 分别是PC ，PD ，BC 的中点，DC //AB ，求证：平面P AB //平面EFG .变式2-1．已知棱长为1的正方体ABCD －A 1B 1C 1D 1中，E ，F ，M 分别是A 1C 1，A 1D 和B 1A 上任意一点．求证：平面1//A EF 平面1B MC .变式2-2．如图，在斜三棱柱ABC A 1B 1C 1中，点D ， D 1分别在AC ， A 1C 1上，那么当点D 在什么位置时，平面BC 1D ∠平面AB 1D 1变式2-3．如图为一简单组合体，其底面ABCD 为正方形，棱PD 与EC 均垂直于底面ABCD ，2PD EC =，求证：平面//EBC 平面PDA .考点三线面平行的性质典例3．如图，在四棱锥P ABCD -中，PA ⊥平面ABCD ，四边形ABCD 是正方形，24AB PA ==，点E 在棱PA 上，//PC 平面BDE ．求证：E为PA的中点；变式3-1．四面体ABCD如图所示，过棱AB的中点E作平行于AD，BC的平面，分别交四面体的棱，，于点F G H，，．证明：四边形EFGH是平行四边形．BD DC CA变式3-2．如图所示，已知三棱柱ABC-A'B'C'中，D是BC的中点，D'是B'C'的中点，设平面A'D'B∩平面ABC=a，平面ADC'∩平面A'B'C'=b，判断直线a，b的位置关系，并证明．被一平面所截，截面为平行四边形EFGH，求证：CD∥平面EFGH．变式3-3．如图，三棱锥A BCD考点四面面平行的性质典例4．如图，在三棱锥P －ABC 中，D ，E ，F 分别是PA ，PB ，PC 的中点．M 是AB 上一点，连接MC ，N 是PM 与DE 的交点，连接FN ，求证：FN∠CM ．变式4-1．如图，在棱锥中，:1:3AE AB =，截面EFG ∥底面BDC ．已知BDC 的周长是18，求EFG的周长．变式4-2．如图，已知平面//α平面β，点P 是平面α，β外一点，且直线PB ，PD 分别与α，β相交于点A ，B 和点C ，D ．如果4cm PA =，5cm AB =，3cm PC =，求PD 的长．变式4-3．如图所示，两条异面直线BA，DC与两平行平面α，β分别交于点B，A和D，C，点M，MN平面αN分别是AB，CD的中点，求证：//巩固练习练习一线面平行的判定1．如图，四棱锥A DBCE-中，O为底面平行四边形DBCE对角线的交点，F为AE的中点．求证：AB∥平面DCF．2．如图所示，在棱长为2的正方体ABCD-A1B1C1D1中，E，F分别为DD1，DB的中点.求证：EF//平面ABC1D1.3．如图所示，在四棱锥P ABCD -中，22PA AD CD AB ====，AB AD ⊥，CD AD ⊥，PA ⊥底面ABCD ， M 为PC 的中点。

专题20立体几何中的平行与垂直问题(解析版)

专题20 立体几何中的平行与垂直问题一、题型选讲题型一、线面平行与垂直知识点拨：证明直线与平面的平行与垂直问题，一定要熟练记忆直线与平面的平行与垂直判定定理和性质定理，切记不可缺条件。

直线与平面的平行有两种方法：一是在面内找线；二是通过面面平行转化。

直线与平面垂直关键是找两条相交直线例1、（2019南通、泰州、扬州一调）如图，在四棱锥PABCD中，M, N分别为棱PA, PD的中点.已知侧面PAD丄底面ABCD,底面ABCD是矩形，DA=DP.求证：（1）MN〃平面PBC；MD丄平面PAB.【证明】（1）在四棱锥P-ABCD中，M, N分别为棱PA, PD的中点，所以MN〃AD.（2分）又底面ABCD是矩形，所以BC〃AD.所以MN〃BC.（4分）又BC U平面PBC，MN Q平面PBC，所以MN〃平面PBC. （6分）（2）因为底面ABCD是矩形，所以AB丄AD.又侧面PAD丄底面ABCD，侧面PAD n底面ABCD=AD, AB U底面ABCD，所以AB丄侧面PAD.（8分）又MD U侧面PAD，所以AB丄MD.（10分）因为DA=DP,又M为AP的中点，从而MD丄PA. （12分）又PA，AB在平面PAB内，PA n AB=A，所以MD丄平面PAB.（14分）例2、（2019扬州期末）如图所示，在三棱柱ABCA1B1C1中，四边形AA1B1B为矩形，平面AA1B1B丄平面ABC,点E，F分别是侧面AA1B1B，BB1C1C对角线的交点.（1）求证：EF〃平面ABC；（2）求证：BB］丄AC.规范解答（1）在三棱柱ABCA1B1C1中，四边形AA1B1B,四边形BB1C1C均为平行四边形，E, F分别是侧面AA1B1B, BB1C1C对角线的交点，所以E, F分别是AB1，CB1的中点，所以EF〃AC.（4分）因为EF Q平面ABC, AC U平面ABC，所以EF〃平面ABC.（8分）（2）因为四边形AA1B1B为矩形，所以BB1丄AB.因为平面AA1B1B丄平面ABC,且平面AA1B1B n平面ABC=AB, BB1U平面AA1B1B, 所以BB1丄平面ABC.（12分）因为AC U平面ABC，所以BB1丄AC.（14分）例3、（2019南京、盐城二模）如图，在三棱柱ABCA1B1C1中，AB=AC, A1C丄BC］, AB］丄BC1，D, E 分别是AB1和BC的中点.求证：（1）DE〃平面ACC1A1；（2）AE丄平面BCC1B1.A _________ c,规范解答⑴连结A1B，在三棱柱ABCA1B1C1中，AA1#BB1且AA1=BB1，所以四边形AA1B1B是平行四边形．又因为D是AB1的中点，所以D也是BA1的中点.（2分）在厶BA1C中，D和E分别是BA1和BC的中点，所以DE〃A］C.又因为DE G平面ACC1A1，A1C U平面ACC1A1，所以DE〃平面ACC1A1.（6分）（2）由（1）知DE〃A］C，因为A1C丄BC” 所以BC］丄DE.（8 分）又因为BC］丄AB1，AB1H DE=D，AB1，DE U平面ADE，所以BC1丄平面ADE.又因为AE U平在ADE,所以AE丄BC1.（10分）在厶ABC中，AB=AC，E是BC的中点，所以AE丄BC.（12分）因为AE丄BC1，AE丄BC，BC1H BC=B，BC1，BC U平面BCC1B1，所以AE丄平面BCC1B1. （14 分）例4、（2019苏锡常镇调研）如图，三棱锥DABC中，已知AC丄BC，AC丄DC，BC=DC，E，F 分别为BD，CD 的中点．求证：（1）EF〃平面ABC；（2）BD丄平面ACE.所以EF 〃平面ABC.（6分）（2）因为AC丄BC，AC丄DC，BC H DC = C，BC，DC U平面BCD所以AC丄平面BCD，（8分）因为BD U平面BCD，所以AC丄BD，（10分）因为DC=BC，E为BD的中点，所以CE丄BD，（12分）因为AC n CE = C, AC，CE U平面ACE，所以BD丄平面ACE.（14分）例5、（2019苏州三市、苏北四市二调）如图，在直三棱柱ABCA1B1C1中，侧面BCC1B1为正方形，A1B1 丄B1C1•设A1C与AC1交于点D, B1C与BC1交于点E.求证：（1） DE〃平面ABB1A1；（2） BC］丄平面A1B1C.规范解答（1）因为三棱柱ABCA1B1C1为直三棱柱，所以侧面ACC1A1为平行四边形．又A1C 与AC1 交于点D,所以D为AC]的中点，同理，E为BC]的中点•所以DE〃AB.（3分）又AB U平面ABB]A], DE G平面ABB]A], 所以DE〃平面ABB]A].（6分）（2）因为三棱柱ABCA]B]C]为直三棱柱，所以BB]丄平面A]B]C]. 又因为A]B]U平面A]B]C],所以BB]丄A]B i.（8分）又A]B]丄B]C], BB], B]C] U 平面BCC]B], BB]n B]C1=B1，所以A]B]丄平面BCC]B].（10 分）又因为BC]U平面BCC]B1，所以A]B丄BC].（12分）又因为侧面BCC]B1为正方形，所以BC]丄BQ.又A1B1n B1C=B1，A1B1，B1C U平面A1B1C, 所以BC1丄平面A1B1C.（14分）例6、（2017苏北四市一模）如图，在正三棱柱ABCA1B1C1中，已知D, E分别为BC, B1C1的中点，点F 在棱CC1上，且EF丄CD.求证：（1）直线A1E〃平面ADC1；⑴证法1连结ED,因为D, E分别为BC, B1C1的中点，所以B&/BD且B1E=BD, 所以四边形BBDE是平行四边形，（2分）所以BB/DE且BB1=DE. 又BB]〃AA]且BB]=AA], 所以AA/DE且AA1=DE, 所以四边形AA]ED是平行四边形，所以A]E〃AD.（4分）又因为AE G平面ADC, AD U平面ADC，所以直线AE〃平面ADC.（7分）1 1 1畀 ------ 1B证法2连结ED,连结A1C, EC分别交AC” DC1于点M, N,连结MM,则因为D, E分别为BC,B1C1的中点，所以C1E^CD且C、E=CD,所以四边形C1EDC是平行四边形，所以N是CE的中点.（2分）因为A1ACC1为平行四边形，所以M是A1C的中点，（4分）所以MN//A\E.又因为A]E G平面ADC，MN U平面ADC，，所以直线Af〃平面ADC、.（7分）（2）在正三棱柱ABCA1B1C1中，BB]丄平面ABC.又AD U平面ABC，所以AD丄BB、.又A ABC是正三角形，且D为BC的中点，所以AD丄BC.（9分）又BB，，BC U 平面BBCC，，BB1A BC=B，所以AD丄平面B,BCC,，又EF U平面BBCC，所以AD丄EF.（11分）又EF丄CD，CD，AD U平面ADC,，C,D A AD=D，所以直线EF丄平面ADC,.（14分）题型二、线面与面面平行与垂直证明平面与平面的平行与垂直问题，一定要熟练记忆平面与平面的平行与垂直判定定理和性质定理，切记不可缺条件。

完整版)立体几何中平行与垂直证明方法归纳

完整版)立体几何中平行与垂直证明方法归纳本文系统总结了立体几何中平行与垂直证明方法，适合高三总复时学生构建知识网络、探求解题思路、归纳梳理解题方法。

以下是常见证明方法：一、“平行关系”常见证明方法一）直线与直线平行的证明1.利用平行四边形的对边互相平行的特性；2.利用三角形中位线性质；3.利用空间平行线的传递性（即公理4）；4.利用直线与平面平行的性质定理；5.利用平面与平面平行的性质定理；6.利用直线与平面垂直的性质定理；7.利用平面内直线与直线垂直的性质；8.利用定义：在同一个平面内且两条直线没有公共点。

二）直线与平面平行的证明1.利用直线与平面平行的判定定理；2.利用平面与平面平行的性质推论；3.利用定义：直线在平面外，且直线与平面没有公共点。

三）平面与平面平行的证明1.利用平面与平面平行的判定定理；2.利用某些空间几何体的特性；3.利用定义：两个平面没有公共点。

二、“垂直关系”常见证明方法一）直线与直线垂直的证明1.利用直角三角形的两条直角边互相垂直的特性；2.看夹角：两条共（异）面直线的夹角为90°，则两直线互相垂直；3.利用直线与平面垂直的性质：如果一条直线与一个平面垂直，则这条直线垂直于此平面内的所有直线。

1.利用空间几何体的特性：例如长方体侧棱垂直于底面。

2.观察直线与平面所成角度：若直线与平面所成角为90度，则该直线垂直于平面。

3.利用直线与平面垂直的判定定理：若一条直线与一个平面内的两条相交直线垂直，则该直线垂直于此平面。

4.利用平面与平面垂直的性质定理：若两个平面互相垂直，则在这两个平面内分别作垂直于交线的直线，则这两条直线互相垂直。

5.利用常用结论：例如若一条直线平行于一个平面的垂线，则该直线也垂直于此平面。

高中立体几何证明线面平行的常见方法

高中立体几何证明线面平行的常见方法1.通过“平移”再利用平行四边形的性质题目1：四棱锥P-ABCD的底面是平行四边形，点E、F分别为棱AB、PD的中点。

证明AF∥平面PCE。

证明：将四棱锥P-ABCD平移，使其底面平移到平面PCE上，得到四棱锥P'-A'B'C'D'，其中A'B'C'D'与ABCD平行，且P'、E'、F'分别为A'B'、C'D'、A'D'的中点。

因为AF∥PD，所以AF'=PD'=C'F'，又因为AD'=C'D'/2=AB'/2=AF'/2，所以AD'∥B'C'。

因此，根据平行四边形的性质，AF'∥B'C'，即AF∥CE。

题目3：四棱锥P-ABCD底面是直角梯形，BA⊥AD，CD⊥AD，CD=2AB，E为PC的中点，证明EB∥平面PAD。

证明：连接PE，因为E为PC的中点，所以PE∥AD。

又因为CD⊥AD，所以CD∥PE。

又因为CD=2AB，所以AB∥PE。

因此，根据平行四边形的性质，EB∥PA，即EB∥平面PAD。

2.利用三角形中位线的性质题目4：四面体ABCD中，E、F、G、M分别是棱AD、CD、BD、BC的中点，证明AM∥平面EFG。

证明：连接EF、EG、FG，因为E、F、G分别为三角形BCD、ACD、ABD的中点，所以EF、EG、FG分别是这三个三角形的中位线。

因此，EF∥AD，EG∥BD，FG∥AC。

又因为M为BC的中点，所以AM∥FG。

因此，AM∥平面EFG。

3.利用平行四边形的性质题目7：正方体ABCD-A' B' C' D'中O为正方形ABCD的中心，M为B'B的中点，求证D'O∥平面A'BC'。

空间立体几何中的平行、垂直证明

l ml m
☺ 简称：线面垂直，线线垂直.
精选ppt
15
复习定理
空间中的垂直
3．平面与平面垂直判定
判定：如果一个平面经过另一个平面的一条垂线,则这两个平面互相垂直.
b
b
b
☺ 简称：线面垂直，面面垂直.
精选ppt
16
复习定理
空间中的垂直
4．平面与平面垂直性质
性质：如果两个平面互相垂直，则其中一个平面内垂直于交线的直线必垂直于另一个平面.
13
复习定理
空间中的垂直
1．直线与平面垂直判定
判定：如果一条直线和一个平面内的两条相交直线都垂直,则称这条直线和这个平面垂直.
l P mn
m
n m
n
P
l .
l m
l n
☺ 简称：线线垂直，线面垂直.
精选ppt
14
复习定理
空间中的垂直
2．直线与平面垂直性质
判定：如果一条直线和一个平面垂直,则称这条直线和这个平面内任意一条直线都垂直.
分析： (1)证明线面平行只需在平面内找一条和该直线平行的直线即可，也可转化为经过这条直线的平面和已知平面平行；(2)证明面面垂直，只需在一个平面内找到另一个平面的垂线.
精选ppt
21
(1) 证明如图所示，取线段 BC 的中点 F，
连接 EF、FD.
在△PBC 中，E、F 分别为 PC、CB 的中点，
∵AA1C1C为矩形，则E为AC1的中点．又D是AB的中点，
∴在△ABC1中，DE∥BC1.
E
又DE⊂平面CA1D，
BC1⊄平面CA1D，
∴BC1∥平面CA1D.
精选ppt

立体几何中的向量方法——证明平行及垂直

立体几何中的向量方法(一)——证明平行与垂直1．直线的方向向量与平面的法向量确实定(1)直线的方向向量：在直线上任取一非零向量作为它的方向向量．(2)平面的法向量可利用方程组求出：设a ，b 是平面α两不共线向量，n 为平面α的法向量，则求法向量的方程组为⎩⎨⎧n ·a ＝0，n ·b ＝0.2．用向量证明空间中的平行关系(1)设直线l 1和l 2的方向向量分别为v 1和v 2，则l 1∥l 2(或l 1与l 2重合)⇔v 1∥v 2.(2)设直线l 的方向向量为v ，与平面α共面的两个不共线向量v 1和v 2，则l ∥α或l ⊂α⇔存在两个实数*，y ，使v ＝*v 1＋y v 2.(3)设直线l 的方向向量为v ，平面α的法向量为u ，则l ∥α或l ⊂α⇔v ⊥u .(4)设平面α和β的法向量分别为u 1，u 2，则α∥β⇔u 1∥u 2.3．用向量证明空间中的垂直关系(1)设直线l 1和l 2的方向向量分别为v 1和v 2，则l 1⊥l 2⇔v 1⊥v 2⇔v 1·v 2＝0.(2)设直线l 的方向向量为v ，平面α的法向量为u ，则l ⊥α⇔v ∥u .(3)设平面α和β的法向量分别为u 1和u 2，则α⊥β⇔u 1⊥u 2⇔u 1·u 2＝0.【思考辨析】判断下面结论是否正确(请在括号中打"√〞或"×〞)(1)直线的方向向量是唯一确定的．()(2)平面的单位法向量是唯一确定的．()(3)假设两平面的法向量平行，则两平面平行．()(4)假设两直线的方向向量不平行，则两直线不平行．()(5)假设a ∥b ，则a 所在直线与b 所在直线平行．()(6)假设空间向量a 平行于平面α，则a 所在直线与平面α平行．()1．以下各组向量中不平行的是()A ．a ＝(1,2，－2)，b ＝(－2，－4,4)B ．c ＝(1,0,0)，d ＝(－3,0,0)C ．e ＝(2,3,0)，f ＝(0,0,0)D ．g ＝(－2,3,5)，h ＝(16,24,40)2．平面α有一点M (1，－1,2)，平面α的一个法向量为n ＝(6，－3,6)，则以下点P 中，在平面α的是()A ．P (2,3,3)B ．P (－2,0,1)C ．P (－4,4,0)D ．P (3，－3,4)3．AB →＝(1,5，－2)，BC →＝(3,1，z )，假设AB →⊥BC →，BP →＝(*－1，y ，－3)，且BP ⊥平面ABC ，则实数*，y ，z 分别为______________．4．假设A (0,2，198)，B (1，－1，58)，C (－2,1，58)是平面α的三点，设平面α的法向量n ＝(*，y ，z )，则*∶y ∶z ＝________.题型一证明平行问题例1(2013·改编)如图，在四面体A －BCD 中，AD ⊥平面BCD ，BC ⊥CD ，AD ＝2，BD ＝22，M 是AD 的中点，P 是BM 的中点，点Q 在线段AC 上，且AQ ＝3QC .证明：PQ ∥平面BCD .如图，在棱长为2的正方体ABCD －A 1B 1C 1D 1中，E ，F ，M ，N 分别是棱AB ，AD ，A 1B 1，A 1D 1的中点，点P ，Q 分别在棱DD 1，BB 1上移动，且DP ＝BQ ＝λ(0<λ<2)．(1)当λ＝1时，证明：直线BC 1∥平面EFPQ ；(2)是否存在λ，使平面EFPQ 与平面PQMN 所成的二面角为直二面角？假设存在，求出λ的值；假设不存在，说明理由．题型二证明垂直问题例2 如下图，正三棱柱(底面为正三角形的直三棱柱)ABC —A 1B 1C 1的所有棱长都为2，D 为CC 1的中点．求证：AB 1⊥平面A 1BD .如下图，在四棱锥P －ABCD 中，PC ⊥平面ABCD ，PC ＝2，在四边形ABCD 中，∠B ＝∠C ＝90°，AB ＝4，CD ＝1，点M 在PB 上，PB ＝4PM ，PB 与平面ABCD 成30°角．(1)求证：CM ∥平面PAD ；(2)求证：平面PAB ⊥平面PAD .题型三解决探索性问题例3 如图，棱柱ABCD－A1B1C1D1的所有棱长都等于2，∠ABC和∠A1AC均为60°，平面AA1C1C⊥平面ABCD.(1)求证：BD⊥AA1；(2)求二面角D－A1A－C的余弦值；(3)在直线CC1上是否存在点P，使BP∥平面DA1C1，假设存在，求出点P的位置，假设不存在，请说明理由．如下图，四棱锥S—ABCD的底面是正方形，每条侧棱的长都是底面边长的2倍，P为侧棱SD上的点．(1)求证：AC⊥SD.(2)假设SD⊥平面PAC，则侧棱SC上是否存在一点E，使得BE∥平面PAC.假设存在，求SE∶EC的值；假设不存在，试说明理由．利用向量法解决立体几何问题典例：如图，四棱锥P－ABCD中，底面ABCD为矩形，PA⊥平面ABCD，E为PD的中点．(1)证明：PB∥平面AEC；(2)设二面角D－AE－C为60°，AP＝1，AD＝3，求三棱锥E－ACD的体积．A组专项根底训练1．假设直线l的方向向量为a＝(1,0,2)，平面α的法向量为n＝(－2,0，－4)，则()A．l∥αB．l⊥αC．l⊂αD．l与α相交2．假设AB→＝λCD→＋μCE→，则直线AB与平面CDE的位置关系是()A．相交B．平行C．在平面D．平行或在平面3．A(4,1,3)，B(2，－5,1)，C(3,7，－5)，则平行四边形ABCD的顶点D的坐标是() A．(2,4，－1) B．(2,3,1)C．(－3,1,5) D．(5,13，－3)4．a＝(2，－1,3)，b＝(－1,4，－2)，c＝(7,5，λ)，假设a，b，c三向量共面，则实数λ等于()A.627B.637C.607D.6575．如图，在长方体ABCD —A 1B 1C 1D 1中，AB ＝2，AA 1＝3，AD ＝22，P 为C 1D 1的中点，M 为BC 的中点．则AM 与PM 所成的角为()A ．60°B ．45°C ．90°D ．以上都不正确6．平面α的三点A (0,0,1)，B (0,1,0)，C (1,0,0)，平面β的一个法向量n ＝(－1，－1，－1)，则不重合的两个平面α与β的位置关系是________．7．设点C (2a ＋1，a ＋1,2)在点P (2,0,0)、A (1，－3,2)、B (8，－1，4)确定的平面上，则a ＝________.8．如图，在正方体ABCD —A 1B 1C 1D 1中，棱长为a ，M 、N 分别为A 1B 和AC 上的点，A 1M ＝AN ＝2a 3，则MN 与平面BB 1C 1C 的位置关系是________． 9．如图，四边形ABCD 为正方形，PD ⊥平面ABCD ，PD ∥QA ，QA ＝AB＝12PD .证明：平面PQC ⊥平面DCQ . 10．如图，在底面是矩形的四棱锥P －ABCD 中，PA ⊥底面ABCD ，E ，F 分别是PC ，PD 的中点，PA ＝AB ＝1，BC ＝2.(1)求证：EF ∥平面PAB ；(2)求证：平面PAD ⊥平面PDC .B 组专项能力提升11．如图，正方形ABCD 与矩形ACEF 所在平面互相垂直，AB ＝2，AF ＝1，M 在EF 上，且AM ∥平面BDE ，则M 点的坐标为()A ．(1,1,1)B ．(23，23，1) C ．(22，22，1) D ．(24，24，1)12．设u ＝(－2,2，t )，v ＝(6，－4,4)分别是平面α，β的法向量，假设α⊥β，则t 等于()A ．3B ．4C ．5D ．613．在正方体ABCD —A 1B 1C 1D 1中，P 为正方形A 1B 1C 1D 1四边上的动点，O 为底面正方形ABCD 的中心，M ，N 分别为AB ，BC 的中点，点Q 为平面ABCD 一点，线段D 1Q 与OP 互相平分，则满足MQ →＝λMN→的实数λ有________个．14．如下图，直三棱柱ABC —A 1B 1C 1中，△ABC 为等腰直角三角形，∠BAC ＝90°，且AB ＝AA 1，D 、E 、F 分别为B 1A 、C 1C 、BC 的中点．求证：(1)DE ∥平面ABC ；(2)B 1F ⊥平面AEF .15．在四棱锥P —ABCD 中，PD ⊥底面ABCD ，底面ABCD 为正方形，PD ＝DC ，E 、F 分别是AB 、PB 的中点．(1)求证：EF ⊥CD ；(2)在平面PAD 求一点G ，使GF ⊥平面PCB ，并证明你的结论．。

立体几何线面面面平行的证明

立体几何线面面面平行的证明要证明两个面是平行的，首先要明确面的定义。

在几何学中，面是一个二维的几何概念，它由至少三个非共线的点所确定。

这三个点可以通过线段相连，并且所构成的平面是无限延伸的。

一个典型的例子是平面镜子的表面，它可以反射光线。

现在，我们假设有两个面α和β。

要证明这两个面是平行的，需要证明它们的法线向量是平行的。

法线向量是垂直于面的向量，它指向面的外部。

如果两个面的法线向量平行，那么这两个面就是平行的。

我们先来介绍一些与线面相交相关的概念。

1.线面交点：线与面的交点是线的一部分在面上的投影，我们用P表示线的交点。

2.线面距离：线与面的距离是从线上一点到面的垂直距离，我们用d 表示线与面的距离。

3.线面垂足：线与面的垂足是从线上一点到面的垂直线与面的交点，我们用H表示线面的垂足。

现在，我们来证明线面的性质。

1.性质1：直线与平行的平面不相交。

证明：设平面α和β平行且有交点P。

由于α和β平行，所以可以在平面α上找到一条直线和线段以及线面相交所需的点H（线段PH与线段PA平行于面β）。

然而，平面β与线段PH垂直，因此线段相交于点H，与α平行。

根据定义，线面的交点是线的一部分在面上的投影，并且直线和平行的平面不相交,矛盾。

2.性质2：线面垂直的直线是线在面上的最短路径。

证明：设直线L和平面α相交于点P，PL是直线L上的线段，L上的其他点Q到α的距离大于P到α的距离。

我们可以在平面α上找到一点H，使得PH与线段PL垂直。

连接PH，并延长PH到与α的交点为K。

根据定义，线面距离是从线上一点到面的垂直距离，因此PK是从L到α的最短路径，与已知矛盾。

现在，我们来证明两个面是平行的。

设α和β是两个面，它们分别由点A、B、C和D、E、F确定。

我们要证明α和β是平行的，需要证明它们的法线向量平行。

首先，我们可以找到一条直线L，通过点A且与α和β都不平行。

连接线段AD和线段AF，并找到线段AD和α的垂直线段AH。

立体几何证明方法——证面面平行

立体几何证明方法——证面面平行立体几何中，证明面面平行是一个常见的问题，可以通过多种方法进行证明。

下面将介绍几种常用的证明方法。

1.使用直线面法相交性质证明：设空间中有两个平面ABCD和EFGH，要证明这两个平面平行。

首先，选择平面ABCD上的两条相交直线AE和BF，然后分别在这两条直线上选择两个点C和D。

根据直线面法相交性质，直线AE与平面ABCD相交于点E，直线AE与平面CDH相交于点C，同理，直线BF与平面ABCD相交于点F，直线BF与平面CDH相交于点D。

连接线段AD和BC，可以得到四边形ABCD。

然后，考察四边形ABCD，如果四边形ABCD是平行四边形，则线段AD与线段BC互相平行。

由直线平行与面平行的性质可知，平面ABCD与平面EFHG平行。

因此，我们只需要证明四边形ABCD为平行四边形即可。

接下来，通过证明线段AD与线段BC互相平行来证明四边形ABCD为平行四边形。

可采用向量法、等距向量法等方法进行证明，具体方法根据题目要求来选择。

2.使用距离法证明：设空间中有两个平面ABCD和EFGH，要证明这两个平面平行。

首先，在平面ABCD上选择一点P，在平面EFGH上选择一点Q。

然后，构造线段PQ，并将其延长，过点P和Q分别作平行于平面ABCD和EFGH的直线。

两条直线与平面ABCD和EFGH的交点分别为A、B和E、F。

由于点P、Q到平面ABCD的距离相等，点A、B到平面EFGH的距离相等，利用距离的定义可以推出直线AE与直线BF互相平行。

同理可以证明直线BE与直线AF互相平行。

因此，根据平行四边形的性质可知线段AD与线段BC平行。

由于线段AD与线段BC平行，所以平面ABCD与平面EFGH平行。

3.使用垂线法证明：设空间中有两个平面ABCD和EFGH，要证明这两个平面平行。

首先，选择平面ABCD上的两条垂线，可以是两个相交直线的垂线或两个平行直线的垂线。

然后，在平面EFGH中分别找到与这两条垂线相交的直线段，并将其延长。

立体几何-线面、面面平行的证明

QDCBAP理科数学复习专题立体几何线面平行与面面平行专题复习【题型总结】题型一小题：判断正误1. a 、b 、c 是直线，,,αβγ是平面，下列命题正确的是_____________ααββααβαβαγαγββααα////a ,//a //a //,//a ////a ,//a ////,////a //,//a //a //,//a b b b b c c b b 则⑥则⑤则④则③则②则①归纳：_______________________________________ 题型二线面平行的判定1、如图，在四棱锥P —ABCD 中，底面ABCD 是矩形，E 、F 分别是ＰＢ，ＰＣ的中点，求证：EF//面P ＡＤ归纳 3、已知：点是平行四边形ABCD 所在平面外一点， Q 是PA 的中点,求证：PC//平面BQD.归纳：C 1B 1A 1D 1DCDA 1C 1CB 1B3、在正方体中，Ｅ，Ｆ分别为C1D1和BC 的中点，求证：FE//面BB1DD1归纳：小结1：证明线面平行的方法常常转化为面外线与面内线平行，而证明两线平行的方法常有：，，题型二、面面平行的判定1、1111111//.ABCD A B C D AB D C BC -在正方体中，求证：平面平面11111111111,,:(1)//;(2)//.ABC A B C D AC BC AB D D AC B DA BC D -2、如图已知正三棱柱中，点为的中点求证平面为的中点，求证：平面平面题型四面面平行的应用：用面面平行证线面平行1、如图，在直三棱柱111ABC A B C -中，已知AB AC =，,,M N P 分别为11,,BC CC BB 的中点，求证： 1//A N 平面AMP .【综合练习】一、选择题1、直线和平面平行是指该直线与平面内的（）(A)一条直线不相交 (B)两条直线不相交 (C)无数条直线不相交(D)任意一条直线都不相交 2、已知a b ||,αα⊂，则必有（）()||(),A a b B a b 异面 (),C a b 相交 (),D a b 平行或异面3、若直线a,b 都与平面平行，则a 和b 的位置关系是（） (A)平行 (B)相交 (C)异面 (D)平行或相交或是异面直线4.已知平面α、β和直线m ，给出条件：①m ∥α；②m ⊥α；③m ⊂α；④α⊥β；⑤α∥β.为使m ∥β，应选择下面四个选项中的 ( )A ．①④B ．①⑤C ．②⑤D ．③⑤5．下列命题正确的是（） A 一直线与平面平行，则它与平面内任一直线平行B 一直线与平面平行，则平面内有且只有一个直线与已知直线平行C 一直线与平面平行，则平面内有无数直线与已知直线平行，它们在平面内彼此平行D 一直线与平面平行，则平面内任意直线都与已知直线异面 6. 以下命题（其中a ，b 表示直线，a 表示平面）①若a ∥b ，b Ìa，则a ∥a ②若a ∥a ，b ∥a ，则a ∥b ③若a ∥b ，b ∥a ，则a ∥a ④若a ∥a ，b Ìa，则a ∥b 其中正确命题的个数是（）A.0个B.1个C.2个D.3个二、解答题1．如图，E D ,分别是正三棱柱111ABC A B C -的棱1AA 、11B C 的中点，求证：1//A E 平面1BDC ；2、如图，在四棱锥P-ABCD 中，底面ABCD 是正方形，侧棱PD ⊥底面ABCD ，PD=DC=1，点E 是PC 的中点，作EF PB 交PB 于点F.求证：PA ∥平面EBD ；3、在正方体ABCD —A1B1C1D1中，O 为面ABCD 的中心，P ，Q 分别为DD1和CC1的中点，证明：面PAO//面BQD14、如图，在三棱柱ABC﹣A1B1C1中，侧面ABB1A1，ACC1A1均为正方形，AB=AC=1，∠BAC=90°，点D是棱B1C1的中点．求证：AB1∥平面A1DC；。

高中立体几何证明平行的专题

FGG A B CD ECA BDE F DE B 1A 1C 1CM 立体几何——平行的证明【例1】如图，四棱锥P －ABCD 的底面是平行四边形，点E 、F 分别为棱AB 、 PD 的中点．求证：AF ∥平面PCE ；分析：取PC 的中点G ，连EG.，FG ，则易证AEGF 是平行四边形'【例2】如图，已知直角梯形ABCD 中，AB ∥CD ，AB ⊥BC ，AB ＝1，BC ＝2，CD ＝1＋3，过A 作AE ⊥CD ，垂足为E ，G 、F 分别为AD 、CE 的中点，现将△ADE 沿AE 折叠，使得DE ⊥EC 。

（Ⅰ）求证：BC ⊥面CDE ；（Ⅱ）求证：FG ∥面BCD ； &分析：取DB 的中点H ，连GH,HC 则易证FGHC 是平行四边形；【例3】已知直三棱柱ABC －A 1B 1C 1中，D, E, F 分别为AA 1, CC 1, AB 的中点， M 为BE 的中点, AC ⊥BE. 求证：（Ⅰ）C 1D ⊥BC ；（Ⅱ）C 1D ∥平面B 1FM. 分析：连EA ，易证C 1EAD 是平行四边形，于是MF -,,AD CD AD BA ⊥⊥//EB PAD 平面E F GM AD CD BD BC AM EFG 求证：E F BACDP （第1题图）AE;PEDCBAAB 1ABEF ⊥ABCD ABEF ABCD 090,BAD FAB BC ∠=∠=//=12AD BE //=12AF,G H ,FA FD BCHG ,,,C D F E ）利用平行四边形的性质【例9】正方体ABCD —A 1B 1C 1D 1中O 为正方形ABCD 的中心，M 为BB 1的中点，求证： D 1O21中点为PD E 求证：AE ∥平面PBC ； ~分析：取PC 的中点F ，连EF 则易证ABFE 是平行四边形【例11】在如图所示的几何体中，四边形ABCD 为平行四边形，∠ ACB=90︒，ＥＡ⊥平面ＡＢＣＤ，EF ∥ＡＢ，ＦＧ∥ＢＣ，ＥＧ∥ＡＣ.ＡＢ=２ＥＦ。

专题08 立体几何垂直平行的证明(原卷版)

专题8 立体几何平行垂直的证明一、解答题1．（2022·全国·高考真题（理））如图，四面体ABCD 中，,,AD CD AD CD ADB BDC ⊥=∠=∠，E 为AC 的中点．(1)证明：平面BED ⊥平面ACD ；(2)设2,60AB BD ACB ==∠=︒，点F 在BD 上，当AFC △的面积最小时，求CF 与平面ABD 所成的角的正弦值．2．（2022·全国·高考真题）如图，PO 是三棱锥P ABC -的高，PA PB =，AB AC ⊥，E 是PB 的中点．(1)证明：//OE 平面PAC ；(2)若30ABO CBO ∠=∠=︒，3PO =，5PA =，求二面角C AE B --的正弦值．3．（2022·全国·高考真题（理））在四棱锥P ABCD -中，PD ⊥底面,,1,2,ABCD CD AB AD DC CB AB DP =====∥(1)证明：BD PA ⊥；(2)求PD 与平面PAB 所成的角的正弦值．4．（2022·青海·海东市第一中学模拟预测（理））如图，在三棱柱111ABC A B C -中，11222AC AA AB AC BC ====，160BAA ∠=︒．原创精品资源学科网独家享有版权，侵权必究！ 2(1)证明：平面ABC ⊥平面11AA B B ．(2)设P 是棱1CC 的中点，求AC 与平面11PA B 所成角的正弦值．5．（2022·青海·海东市第一中学模拟预测（文））如图，在四棱锥P ABCD -中，平面PCD ⊥平面ABCD ，PCD 为等边三角形，22CD AB ==，AD 90BAD ADC ∠=∠=︒，M 是棱PC 上一点．(1)若2MC MP =，求证：//AP 平面MBD ．(2)若MC MP =，求点P 到平面BDM 的距离．6．（2021·上海市建平中学模拟预测）如图，三棱锥P ABC -，侧棱2PA =，底面三角形ABC 为正三角形，边长为2，顶点P 在平面ABC 上的射影为D ，有AD DB ⊥，且1DB =.(1)求证：//AC 平面PDB ；(2)求二面角P AB C 的余弦值.7．（2022·内蒙古·赤峰红旗中学松山分校模拟预测（理））如图，在四棱锥P —ABCD 中，底面ABCD 为正方形，PD ⊥底面ABCD ，M 为线段PC 的中点，PD AD =，N 为线段BC 上的动点．(1)证明：平面MND ⊥平面PBC(2)当点N 在线段BC 的何位置时，平面MND 与平面P AB 所成锐二面角的大小为30°？指出点N 的位置，并说明理由．8．（2022·四川·成都七中模拟预测（理））如图1，在边上为4的菱形ABCD 中，60DAB ∠=︒，点M ，N 分别是边BC ，CD 的中点，1AC BD O ⋂=，AC MN G ⋂=．沿MN 将CMN △翻折到PMN 的位置，连接PA ，PB ，PD ，得到如图2所示的五棱锥P ABMND -．(1)在翻折过程中是否总有平面PBD ⊥平面PAG ？证明你的结论；(2)当四棱锥P MNDB -体积最大时，求直线PB 和平面MNDB 所成角的正弦值；(3)在（2）的条件下，在线段PA 上是否存在一点Q ，使得二面角Q MN P --存在，试确定点Q 的位置；若不存在，请说明理由．9．（2022·全国·模拟预测）在四棱锥P ABCD -中，PA ⊥平面ABCD ，四边形ABCD 是矩形，1,,2AB AP AD E F ==分别是AP BC ，的中点．原创精品资源学科网独家享有版权，侵权必究！ 4(1)求证：//EF 平面PCD ；(2)求二面角C EF D --的余弦值．10．（2022·内蒙古·乌兰浩特一中模拟预测（文））如图在梯形中，//BC AD ，22AB AD BC ===，23ABC π∠=，E 为AD 中点，以BE 为折痕将ABE △折起，使点A 到达点P 的位置，连接,PD PC ，(1)证明：平面PED ⊥平面BCDE ；(2)当2PC =时，求点D 到平面PEB 的距离.11．（2022·全国·南京外国语学校模拟预测）如图，在三棱台111ABC A B C -中，AB AC ⊥，4AB AC ==，1112A A A B ==，侧棱1A A ⊥平面ABC ，点D 是棱1CC 的中点．(1)证明：平面1BB C ⊥平面1AB C ；(2)求二面角C BD A --的正弦值．12．（2022·青海·模拟预测（理））如图，在四棱锥A -BCDE 中，底面BCDE 为矩形，M 为CD 中点，连接BM ，CE 交于点F ，G 为△ABE 的重心．(1)证明：//GF 平面ABC(2)已知平面ABC △BCDE ，平面ACD △平面BCDE ，BC =3，CD =6，当平面GCE 与平面ADE 所成锐二面角为60°时，求G 到平面ADE 的距离．13．（2022·北京市第九中学模拟预测）如图，在四棱锥P ABCD -中，底面ABCD 是边长为2的正方形，△P AB 为正三角形，且侧面P AB △底面ABCD ，M 为PD 的中点．(1)求证：PB //平面ACM ；(2)求直线BM 与平面P AD 所成角的正弦值；(3)求二面角C PA D --的余弦值．14．（2022·浙江·三模）如图，四面体ABCD 的棱AB 平面,CD α=，23,cos cos 3AB AC AD BAC BAD ===∠=∠=．(1)证明：平面ABC ⊥平面ABD ；(2)若平面ABC 与平面α所成锐二面角的正切值为12，线段CD 与平面α相交，求平面ACD 与平面α所成锐二面角的正切值．15．（2022·内蒙古·海拉尔第二中学模拟预测（理））已知四棱锥S ABCD -中，四边形ABCD 为菱形，SAB SBA ∠=∠，.SD AB ⊥(1)求证：ABD △是等边三角形；(2)2SD AD ===，求SC 与平面SAD 所成角的正弦值.原创精品资源学科网独家享有版权，侵权必究！6 16．（2022·宁夏中卫·三模（理））如图1，菱形ABCD 中，60A ∠=︒，4AB =，DE AB ⊥于E ，将AED 沿DE 翻折到A ED '，使A E BE '⊥，如图2．(1)求三棱锥C A BD -'的体积；(2)在线段A D '上是否存在一点F ，使EF △平面A BC '？若存在，求DF FA '的值；若不存在，说明理由． 17．（2022·广东茂名·二模）如图，四棱锥P ﹣ABCD 的底面是等腰梯形，AD △BC ，BC =2AD ，60ABC ∠=︒ ，E 是棱PB 的中点，F 是棱PC 上的点，且A 、D 、E 、F 四点共面．(1)求证：F 为PC 的中点；(2)若△P AD 为等边三角形，二面角P AD B -- 的大小为120︒ ，求直线BD 与平面ADFE 所成角的正弦值． 18．（2022·安徽省舒城中学三模（理））在四棱锥P ABCD -中，PAB △为正三角形，四边形ABCD 为等腰梯形，M 为棱AP 的中点，且2224AB AD BC CD ====，DM =14AO AB =.(1)求证：平面ODM ⊥平面ABCD ；(2)求直线AP 与平面PBC 所成角的正弦值.19．（2022·广东·大埔县虎山中学模拟预测）如图，在四棱台1111ABCD A B C D -中，2AB =，111A B =，四边形ABCD 为平行四边形，点E 为棱BC 的中点．(1)求证：1//D E 平面11ABB A ；(2)若四边形ABCD 为正方形，1AA ⊥平面ABCD ，12A A AB ==，求二面角1A DE C --的余弦值． 20．（2022·全国·模拟预测）如图所示，四棱台1111ABCD A B C D -的上下底面均为正方形，侧面11ADD A 与底面垂直，11113BB CC B C BC ===．(1)求证：平面11ADD A ⊥平面11ABB A ；(2)已知四棱台1111ABCD A B C D -的体积为 △求异面直线BC 和1AA 的距离△求1A 到平面11CDD C 的距离．请从以上两个问题中选取一道进行求解．注：若两个问题均求解，则按第一个问题计分．。

立体几何线面平行-题型全归纳(解析版)

立体几何线面平行-题型全归纳题型一利用三角形中位线例题1、如图所示，在三棱柱ABC-111C B A 中，侧棱⊥1AA 底面ABC ，AB ⊥BC ，D 为AC 的中点。

求证：1AB //平面DBC 1证明：连接C B 1，交1BC 于点Ｏ，再连接ＯＤ，平面11B BCC 是平行四边形，∴Ｏ是1BC 的中点，又Ｄ是ＡＣ的中点，∴ＯＤ是1ACB ∆的中位线，1//AB OD ∴，⊂OD 平面D BC 1，⊄1AB 平面D BC 1，//OD ∴平面D BC 1。

解题步骤（1）把直线通过平移到平面上，得到线线平行的初步形状；（2）连接平行四边形的对角线，再连接两个中点，恰好为平移所得到的线段；（3）通过延长两条线段的端点，构成一个三角形，即可得到三角形的中位线。

变式训练1、如图，在直四棱柱ABCD-1111D C B A 中，底面ABCD 为菱形，E 为1DD 中点。

求证：1BD //平面ACE ；证明：连接ＢＤ，交ＡＣ于点Ｏ，再连接ＯＥ，在直四棱柱ABCD-1111D C B A 中，Ｏ为ＢＤ的中点，且Ｅ为1DD 的中点，∴ＯＥ是1BDD ∆的中位线，1//BD OE ∴，又ＯＥ⊂平面ＡＣＥ，⊄1BD 平面ＡＣＥ，∴1BD //平面ACE 。

变式训练2、如图，在斜三棱柱ABC-111C B A 中，CA=CB ，D 、E 分别是AB ，C B 1的中点，求证：DE//平面11A ACC ；证明：连接1BC ，连接1AC ，在斜三棱柱ABC-111C B A 中，∴点Ｅ在线段1BC 上，∴点Ｅ是1BC 的中点，又点Ｄ是ＡＢ的中点，∴ＤＥ是1ABC ∆的中位线，∴ＤＥ//1AC ，⊄DE 平面11A ACC ，⊂1AC 平面11A ACC ∴DE//平面11A ACC 变式训练3、如图所示，正三棱柱ABC-111C B A 的高为2，点D 是B A 1的中点，点E 是11C B 的中点，求证：DE//平面11A ACC证明：连接1AB ，连接1AC ，在正三棱柱ABC-111C B A 中，∴点Ｄ在线段1AB 上，∴点Ｄ是1AB 的中点，又点Ｅ是11C B 的中点，∴ＤＥ是11C AB ∆的中位线，∴ＤＥ//1AC ，⊄DE 平面11A ACC ，⊂1AC 平面11A ACC ∴DE//平面11A ACC题型二利用平行四边形的对边平行例题2、如图，在多面体ABCDE 中，AEB 为等边三角形，AD//BC ，BC AD 21=，F 为EB 的中点。

立体几何线面平行证明

立体几何线面平行证明立体几何是数学中的一个重要分支，研究的是空间中点、线、面的相互关系和性质。

在立体几何中，平行是一个基本的概念，它描述了两个或多个线或面在空间中不相交且始终保持相同的间距。

本文将从线面平行的定义、性质和应用等方面进行阐述，以展示立体几何中线面平行的证明方法。

一、线面平行的定义在立体几何中，我们常常会遇到线和面的关系。

当一个线和一个面的方向相同，并且线上的任意一点到面的距离保持不变时，我们称这个线和面是平行的。

具体来说，设有一条直线l和一个平面P，如果直线l上的任意一点到平面P的距离d保持不变，那么我们就说直线l和平面P是平行的。

二、线面平行的性质线面平行具有以下性质：1. 平行线和同一平面内的直线没有交点；2. 平行线和同一平面内的直线的距离是恒定的；3. 平行线在同一平面内的投影线也是平行的；4. 平行线和平行面之间的角度为零。

三、线面平行的证明方法证明线面平行的方法有多种，下面列举几种常用的证明方法：1. 利用垂直关系证明：若直线和平面是平行的，那么直线上的任意一条垂线和平面垂直。

2. 利用距离关系证明：若直线和平面是平行的，那么直线上的任意一点到平面的距离是恒定的。

3. 利用投影关系证明：若直线和平面是平行的，那么直线在平面上的投影线也是平行的。

四、线面平行的应用线面平行在实际生活和科学研究中有着广泛的应用，下面列举几个常见的应用场景：1. 建筑工程：在建筑设计中，我们常常需要考虑墙壁和地面的平行关系，以保证建筑的稳定和美观。

2. 几何光学：在光学中，光线和镜面的关系是平行的，这是实现反射现象和成像的基础。

3. 地理测量：在地理测量中，为了计算地球上两点之间的距离，我们需要考虑经线和纬线的平行关系。

4. 电磁学：在电磁学中，电场线和等势面的关系是平行的，这是电场分布和电势分布的重要性质。

线面平行是立体几何中一个重要的概念。

通过定义、性质、证明方法和应用等方面的介绍，我们可以更深入地理解和应用线面平行的概念。