卧式容器容积计算
椭圆形封头卧式容器不同液面高度的容积计算

椭圆形封头卧式容器不同液面高度的容积计算新疆工学院孟永彪在设计卧式容器时,常常要计算不同液面高度所对应的容积,有时还需列出容积—液位高度对照表或图。
例如,在盛装有毒有害介质的卧式储罐设计中,要根据体积充装系数确定最高液面高度并加以标识。
在一般资料中仅能查到容器的全容积计算公式,而要计算不同液面高度下的容积则需设计者自行推导公式计算。
本文以标准椭圆形封头卧式容器为例介绍不同液面高度下的容积计算方法,并以液化石油气储罐为例编制了QUICK BASIC程序,此法仅供大家参考。
1卧式容器的组成卧式容器是由筒体和两封头组焊而成(如图1),常用的封头为标准椭圆封头。
2卧式容器2.1计算简图及说明计算简图如图2。
L———筒体长度(两封头切线间的距离,含直边段长度)D i———封头及筒体内直径h i———封头曲面深度2.2不同液面高度下封头的容积计算如图2,可假想将卧式容器两端的曲面部分合并,则形成一个完整的椭球面。
2==i ih R c a 122222=++cz a y x )(21222y x a z +-=dxy x a dy h a y a )(2222022+-=⎰⎰--)323(23331a h h a V +-=π其中,a=b=R i因此,椭球面的方程为:推导出: 当容器内的液面高度为h 时(如图3所示)。
封头的容积公式推导:对其积分得从上式可看出,h 变化,V 1也随之变化。
2.3 不同液面高度筒体的容积计算在计算筒体的容积时,忽略尺寸公差及制造误差等因素,可将其断面方程为x 2+y 2=a 2的一圆柱体进行计算,那么如图3所示液面高度的筒体容积为:令:y=acos θ dy=-asin θd θdxdy y x a V s )(2122221+-=⎰⎰dx y x a dy h a y a y a )(2122222222+-=⎰⎰----dy y a L V h a⎰--=2222dy y a L h -=222当 y=-a 时,θ=π;当y=h 时,代入公式积分得:2.4 卧式容器在不同液面高度下的容积通过以上V 1,V 2的计算公式,可计算出卧式容器在不同液面高度下的容积之和V :3 利用QUICK BASIC 语言进行卧式容器的容积计算要计算不同液位高度下的容积以表格、曲线的形式列出是很麻烦的,因此本文利用简便易行的QB 编制程序,当然编程语言可以有多种,本文愿起到抛砖引玉的作用。
卧式储罐不同液位下的容积(质量)计算

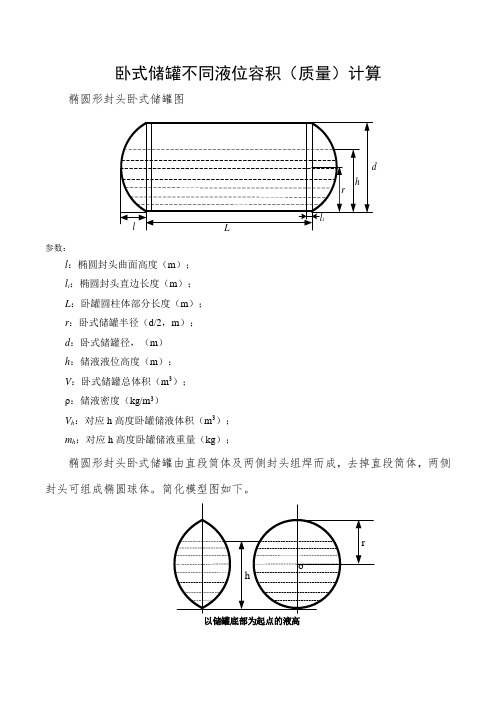
卧式储罐不同液位下的容积(质量)计算卧式储罐不同液位容积(质量)计算椭圆形封头卧式储罐图h drl Ll i参数:l:椭圆封头曲面高度(m);l i:椭圆封头直边长度(m);L:卧罐圆柱体部分长度(m);r:卧式储罐半径(d/2,m);d:卧式储罐内径,(m)h:储液液位高度(m);V:卧式储罐总体积(m3);ρ:储液密度(kg/m3)V h:对应h高度卧罐内储液体积(m3);m h:对应h高度卧罐内储液重量(kg);椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
简化模型图如下。
以储罐底部为起点的液高卧式储罐内储液总体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=表1 卧式储罐不同液位下容积(重量)该计算公式推导过程如下卧式储罐不同液位下的容积简化计算公椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
以储罐中心为起点的液高(1)椭圆球体部分该椭圆球体符合椭圆球体公式:2222221x y z a b c ++= 其中a=b=r ,则有222221x y z a c++= 垂直于y 轴分成无限小微元,任一微元面积为:22()yi cS a y aπ=-当液面高度为h 时,椭圆球体内液氨容积为 V1=hyi a S dy -⎰ 22()haca y dy aπ-=-⎰3322()33ch a a h a π=-+ (2)直段筒体部分:筒体的纵断面方程为222x y a += 任一微元的面积为222yj S a y dy =- 则筒体部分容积为:2hyj a V S -=⎰222ha L a y dy -=-⎰22222(arcsin )2h h La a h a aπ=+-(arcsin)22h a ππ-≤≤ (3)卧式储罐储液总体积总容积为V=V1+V2,V=23242()33ch a a h a π-++2(arcsin )2h La a π+此公式中液位高度h 是以储罐内径中心为原点,其中a=b=r 化简后卧式储罐储液总体积为:⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2-arcsin 3212222πh r r h r h Lr L r V h若液位高度h 以卧罐底部为起点,如下图则卧式储罐内储液总体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=其它方法如下:第一种方法卧式储罐不同液位下的容积简化计算公卧式储罐内储液总体积计算公式:)]arcsin(2)[(]3)(1)[(222232rr h r h hr r h L r r h r h l V V h -+--+---+=π若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=此方式用到参数较多ρ、V 、r 、l 、L 、h 。
卧式储罐不同液位下地容积(高质量)计算
卧式储罐不同液位容积(质量)计算椭圆形封头卧式储罐图参数:l:椭圆封头曲面高度(m);l i:椭圆封头直边长度(m);L:卧罐圆柱体部分长度(m);r:卧式储罐半径(d/2,m);d:卧式储罐径,(m)h:储液液位高度(m);V:卧式储罐总体积(m3);ρ:储液密度(kg/m3)V h:对应h高度卧罐储液体积(m3);m h:对应h高度卧罐储液重量(kg);椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
简化模型图如下。
以储罐底部为起点的液高卧式储罐储液总体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h若密度为ρ,则卧式储罐储液总重量为:hh V m ρ=表1 卧式储罐不同液位下容积(重量)该计算公式推导过程如下卧式储罐不同液位下的容积简化计算公椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
以储罐中心为起点的液高(1)椭圆球体部分该椭圆球体符合椭圆球体公式:2222221x y z a b c ++= 其中a=b=r ,则有222221x y z a c++= 垂直于y 轴分成无限小微元,任一微元面积为:22()yi cS a y aπ=-当液面高度为h 时,椭圆球体液氨容积为 V1=hyi a S dy -⎰ 22()haca y dy aπ-=-⎰3322()33ch a a h a π=-+ (2)直段筒体部分:筒体的纵断面方程为222x y a +=任一微元的面积为yj S = 则筒体部分容积为:2hyj a V S -=⎰ha L -=⎰2(arcsin )2h La a π=+(arcsin)22h a ππ-≤≤ (3)卧式储罐储液总体积总容积为V=V1+V2,V=23242()33ch a a h a π-++2(arcsin )2h La a π+ 此公式中液位高度h 是以储罐径中心为原点,其中a=b=r 化简后卧式储罐储液总体积为:⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2-arcsin 3212222πh r r h r h Lr L r V h若液位高度h 以卧罐底部为起点,如下图则卧式储罐储液总体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h若密度为ρ,则卧式储罐储液总重量为:hh V m ρ=其它方法如下:第一种方法卧式储罐不同液位下的容积简化计算公卧式储罐储液总体积计算公式:)]arcsin(2)[(]3)(1)[(222232rr h r h hr r h L r r h r h l V V h -+--+---+=π若密度为ρ,则卧式储罐储液总重量为:hh V m ρ=此方式用到参数较多ρ、V 、r 、l 、L 、h 。
卧(立)式容器容积计算

直径D 直边高度h 液面高度
筒体长度 L
直径 D
筒体长度 L
计算结果(m3): 全容积: 液体容积:
计算结果(m3): 全容积: 液体容积: 97.05 52.44 上部空间 44.60
注:筒体部分参考文献的公式有误。这里采用的是另外一个公式: r^2arccos[(r-h)/r] - (r-h)*SQRT(2rh-h^2)/2
筒体长度 L 直边高度 h
输入数据(mm): 直径D 直边高度h 3200 筒体长度L 40 封头深度 10920 800
液面高度
1700
直径 D
注1:这里的封头为标准椭圆封头,即长半轴:短半轴=1:2 注2:这种封头都有直边。在输入时注意,筒体长度不包含封头直边(如图)
直边高度 h
输入数据(mm):
即长半轴:短半轴=1:2
注意,筒体长度不包含封头直边(如图)
500 筒体长度L 40 封头深度 1400
1250 125
0.29
卧式储罐不同液位下的容积(质量)计算

卧式储罐不同液位容积(质量)计算椭圆形封头卧式储罐图参数:l:椭圆封头曲面高度(m);l i:椭圆封头直边长度(m);L:卧罐圆柱体部分长度(m);r:卧式储罐半径(d/2,m);d:卧式储罐内径,(m)h:储液液位高度(m);V:卧式储罐总体积(m3);ρ:储液密度(kg/m3)V h:对应h高度卧罐内储液体积(m3);m h:对应h高度卧罐内储液重量(kg);椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
简化模型图如下。
以储罐底部为起点的液高卧式储罐内储液总体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=表1 卧式储罐不同液位下容积(重量)该计算公式推导过程如下卧式储罐不同液位下的容积简化计算公椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
以储罐中心为起点的液高(1)椭圆球体部分该椭圆球体符合椭圆球体公式:2222221x y z a b c ++= 其中a=b=r ,则有222221x y z a c++= 垂直于y 轴分成无限小微元,任一微元面积为:22()yi cS a y aπ=-当液面高度为h 时,椭圆球体内液氨容积为V1=h yi a S dy -⎰ 22()haca y dy aπ-=-⎰3322()33ch a a h a π=-+ (2)直段筒体部分:筒体的纵断面方程为222x y a +=任一微元的面积为yj S = 则筒体部分容积为:2hyj a V S -=⎰ha L -=⎰2(arcsin )2h La a π=+(arcsin)22h a ππ-≤≤ (3)卧式储罐储液总体积总容积为V=V1+V2,V=23242()33ch a a h a π-++2(arcsin )2h La a π+ 此公式中液位高度h 是以储罐内径中心为原点,其中a=b=r 化简后卧式储罐储液总体积为:⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2-arcsin 3212222πh r r h r h Lr L r V h若液位高度h 以卧罐底部为起点,如下图则卧式储罐内储液总体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=其它方法如下:第一种方法卧式储罐不同液位下的容积简化计算公卧式储罐内储液总体积计算公式:)]arcsin(2)[(]3)(1)[(222232rr h r h hr r h L r r h r h l V V h -+--+---+=π若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=此方式用到参数较多ρ、V 、r 、l 、L 、h 。
卧式储罐不同液位下的容积(质量)计算

卧式储罐不同液位容积(质量)计算椭圆形封头卧式储罐图参数:l:椭圆封头曲面高度(m);l i:椭圆封头直边长度(m);L:卧罐圆柱体部分长度(m);r:卧式储罐半径(d/2,m);d:卧式储罐内径,(m)h:储液液位高度(m);V:卧式储罐总体积(m3);ρ:储液密度(kg/m3)V h:对应h高度卧罐内储液体积(m3);m h:对应h高度卧罐内储液重量(kg);椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
简化模型图如下。
以储罐底部为起点的液高卧式储罐内储液总体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=表1 卧式储罐不同液位下容积(重量)该计算公式推导过程如下卧式储罐不同液位下的容积简化计算公椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
以储罐中心为起点的液高(1)椭圆球体部分该椭圆球体符合椭圆球体公式:2222221x y z a b c ++= 其中a=b=r ,则有222221x y z a c++= 垂直于y 轴分成无限小微元,任一微元面积为:22()yi cS a y aπ=-当液面高度为h 时,椭圆球体内液氨容积为V1=h yi a S dy -⎰ 22()haca y dy aπ-=-⎰3322()33ch a a h a π=-+ (2)直段筒体部分:筒体的纵断面方程为222x y a +=任一微元的面积为yj S = 则筒体部分容积为:2hyj a V S -=⎰ha L -=⎰2(arcsin )2h La a π=+(arcsin)22h a ππ-≤≤ (3)卧式储罐储液总体积总容积为V=V1+V2,V=23242()33ch a a h a π-++2(arcsin )2h La a π+ 此公式中液位高度h 是以储罐内径中心为原点,其中a=b=r 化简后卧式储罐储液总体积为:⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2-arcsin 3212222πh r r h r h Lr L r V h若液位高度h 以卧罐底部为起点,如下图则卧式储罐内储液总体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=其它方法如下:第一种方法卧式储罐不同液位下的容积简化计算公卧式储罐内储液总体积计算公式:)]arcsin(2)[(]3)(1)[(222232rr h r h hr r h L r r h r h l V V h -+--+---+=π若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=此方式用到参数较多ρ、V 、r 、l 、L 、h 。
卧式储罐不同液位下的容积(质量)计算

卧式储罐不同液位容积(质量)计算椭圆形封头卧式储罐图参数:l:椭圆封头曲面高度(m);l i:椭圆封头直边长度(m);L:卧罐圆柱体部分长度(m);r:卧式储罐半径(d/2,m);d:卧式储罐内径,(m)h:储液液位高度(m);V:卧式储罐总体积(m3);ρ:储液密度(kg/m3)V h:对应h高度卧罐内储液体积(m3);m h:对应h高度卧罐内储液重量(kg);椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
简化模型图如下。
以储罐底部为起点的液高卧式储罐内储液总体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h 若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=表1 卧式储罐不同液位下容积(重量)该计算公式推导过程如下卧式储罐不同液位下的容积简化计算公椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
以储罐中心为起点的液高(1)椭圆球体部分该椭圆球体符合椭圆球体公式:2222221x y z a b c ++= 其中a=b=r ,则有222221x y z a c++= 垂直于y 轴分成无限小微元,任一微元面积为:22()yi cS a y aπ=-当液面高度为h 时,椭圆球体内液氨容积为 V1=hyi a S dy -⎰ 22()haca y dy aπ-=-⎰3322()33ch a a h a π=-+ (2)直段筒体部分:筒体的纵断面方程为222x y a += 任一微元的面积为yj S = 则筒体部分容积为:2hyj a V S -=⎰ha L -=⎰2(arcsin )2h La a π=+(arcsin)22h a ππ-≤≤ (3)卧式储罐储液总体积总容积为V=V1+V2,V=23242()33ch a a h a π-++2(arcsin )2h La a π+ 此公式中液位高度h 是以储罐内径中心为原点,其中a=b=r 化简后卧式储罐储液总体积为:⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2-arcsin 3212222πh r r h r h Lr L r V h若液位高度h 以卧罐底部为起点,如下图则卧式储罐内储液总体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h 若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=其它方法如下:第一种方法卧式储罐不同液位下的容积简化计算公卧式储罐内储液总体积计算公式:)]arcsin(2)[(]3)(1)[(222232rr h r h hr r h L r r h r h l V V h -+--+---+=π若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=此方式用到参数较多ρ、V 、r 、l 、L 、h 。
卧式储罐不同液位下的容积(质量)计算精选全文

可编辑修改精选全文完整版卧式储罐不同液位容积(质量)计算椭圆形封头卧式储罐图参数:l:椭圆封头曲面高度(m);l i:椭圆封头直边长度(m);L:卧罐圆柱体部份长度(m);r:卧式储罐半径(d/2,m);d:卧式储罐内径,(m)h:储液液位高度(m);V:卧式储罐整体积(m3);ρ:储液密度(kg/m3)V h:对应h高度卧罐内储液体积(m3);m h:对应h高度卧罐内储液重量(kg);椭圆形封头卧式储罐由直段筒体及双侧封头组焊而成,去掉直段筒体,双侧封头可组成椭圆球体。
简化模型图如下。
以储罐底部为起点的液高卧式储罐内储液整体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h 假设密度为ρ,那么卧式储罐内储液总重量为:hh V m ρ=表1 卧式储罐不同液位下容积(重量)该计算公式推导进程如下卧式储罐不同液位下的容积简化计算公椭圆形封头卧式储罐由直段筒体及双侧封头组焊而成,去掉直段筒体,双侧封头可组成椭圆球体。
以储罐中心为起点的液高(1)椭圆球体部份该椭圆球体符合椭圆球体公式:2222221x y z a b c ++= 其中a=b=r ,那么有222221x y z a c++= 垂直于y 轴分成无穷小微元,任一微元面积为:22()yi cS a y aπ=-当液面高度为h 时,椭圆球体内液氨容积为 V1=hyi a S dy -⎰ 22()haca y dy aπ-=-⎰3322()33ch a a h a π=-+ (2)直段筒体部份:筒体的纵断面方程为222x y a +=任一微元的面积为yj S = 那么筒体部份容积为:2hyj a V S -=⎰ha L -=⎰2(arcsin )2h La a π=+(arcsin)22h a ππ-≤≤ (3)卧式储罐储液整体积总容积为V=V1+V2,V=23242()33ch a a h a π-++2(arcsin )2h La a π+ 此公式中液位高度h 是以储罐内径中心为原点,其中a=b=r 化简后卧式储罐储液整体积为:⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2-arcsin 3212222πh r r h r h Lr L r V h假设液位高度h 以卧罐底部为起点,如以下图那么卧式储罐内储液整体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h 假设密度为ρ,那么卧式储罐内储液总重量为:hh V m ρ=其它方式如下:第一种方式卧式储罐不同液位下的容积简化计算公卧式储罐内储液整体积计算公式:)]arcsin(2)[(]3)(1)[(222232rr h r h hr r h L r r h r h l V V h -+--+---+=π假设密度为ρ,那么卧式储罐内储液总重量为:hh V m ρ=此方式用到参数较多ρ、V 、r 、l 、L 、h 。
