探索三角形全等的条件练习题38题
三角形全等测试题及答案

三角形全等测试题及答案一、选择题1. 两个三角形全等的条件是()A. 有两条边和它们的夹角对应相等B. 三条边对应相等C. 有两条边和其中一条边的对角对应相等D. 有两条边和其中一条边的邻角对应相等答案:B2. 如果两个三角形的对应角相等,那么这两个三角形()A. 一定全等B. 可能相似C. 一定相似D. 无法确定答案:B二、填空题3. 已知三角形ABC与三角形DEF全等,且∠A=∠D,AB=DE,那么AC=______。
答案:EF4. 如果两个三角形的两边和夹角对应相等,那么这两个三角形是______。
答案:全等三、判断题5. 如果两个三角形的对应边成比例,那么这两个三角形一定全等。
()答案:错误6. 如果两个三角形的两边和夹角对应相等,那么这两个三角形一定相似。
()答案:正确四、解答题7. 如图所示,已知三角形ABC与三角形DEF全等,且AB=5cm,BC=7cm,∠A=∠D=90°,求DE的长度。
答案:DE=7cm8. 已知三角形ABC与三角形DEF相似,且AB=3cm,BC=4cm,DE=6cm,求AC的长度。
答案:AC=8cm五、证明题9. 已知三角形ABC与三角形DEF全等,且∠A=∠D,AB=DE,证明:AC=EF。
证明:由于三角形ABC与三角形DEF全等,根据全等三角形的性质,对应边相等,所以AC=EF。
10. 已知∠A=∠D,AB=DE,AC=DF,求证:三角形ABC≌三角形DEF。
证明:根据SAS(边角边)判定方法,已知∠A=∠D,AB=DE,AC=DF,所以三角形ABC≌三角形DEF。
全等三角形证明经典45题及答案
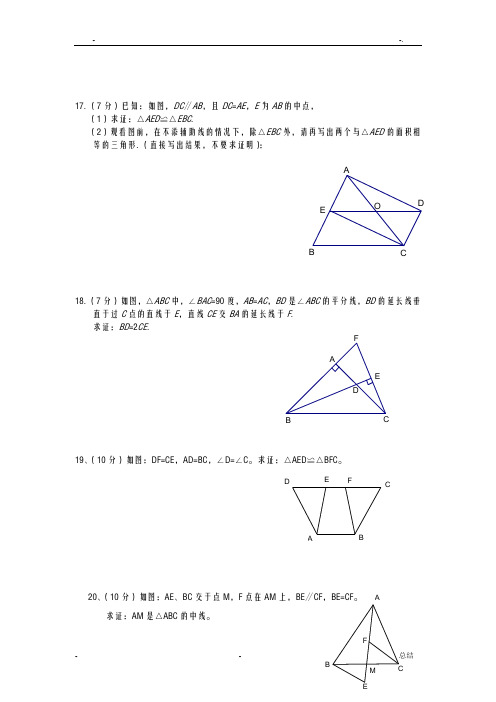
17.(7分)已知:如图,DC ∥AB ,且DC =AE ,E 为AB 的中点, (1)求证:△AED ≌△EBC .(2)观看图前,在不添辅助线的情况下,除△EBC 外,请再写出两个与△AED 的面积相等的三角形.(直接写出结果,不要求证明):18.(7分)如图,△ABC 中,∠BAC =90度,AB =AC ,BD 是∠ABC 的平分线,BD 的延长线垂直于过C 点的直线于E ,直线CE 交BA 的延长线于F . 求证:BD =2CE .19、(10分)如图:DF=CE ,AD=BC ,∠D=∠C 。
求证:△AED ≌△BFC 。
20、(10分)如图:AE 、BC 交于点M ,F 点在AM 上,BE ∥CF ,BE=CF 。
求证:AM 是△ABC 的中线。
O ED C B A FE D C B AFAFE DCBA21、(10分)如图:在△ABC中,BA=BC,D是AC的中点。
求证:BD⊥AC。
22、(10分)AB=AC,DB=DC,F是AD的延长线上的一点。
求证:BF=CF23、(12分)如图:AB=CD,AE=DF,CE=FB。
求证:AF=DE。
DCBAF DCBAF BA24.公园里有一条“Z ”字形道路ABCD ,如图所示,其中AB ∥CD ,在AB ,CD ,BC 三段路旁各有一只小石凳E ,F ,M ,且BE =CF ,M 在BC 的中点,试说明三只石凳E ,F ,M 恰好在一条直线上.25.已知:点A 、F 、E 、C 在同一条直线上, AF =CE ,BE ∥DF ,BE =DF .求证:△ABE ≌△CDF .26.已知:如图所示,AB =AD ,BC =DC ,E 、F 分别是DC 、BC 的中点,求证: AE =AF 。
27.如图,在四边形ABCD 中,E 是AC 上的一点,∠1=∠2,∠3=∠4,求证: ∠5=∠6.D A FE 654321E DCADCBAE28.已知AB ∥DE ,BC ∥EF ,D ,C 在AF 上,且AD =CF ,求证:△ABC ≌△DEF .29.已知:如图,AB =AC ,BD ⊥AC ,CE ⊥AB ,垂足分别为D 、E ,BD 、CE 相交于点F ,求证:BE =CD .30如图,△ABC 中,AD 是∠BAC 的平分线,DE ⊥AB 于E ,DF ⊥AC 于F .求证:(1)AD ⊥EF ;(2)当有一点G 从点D 向A 运动时,GE ⊥AB 于E ,GF ⊥AC 于F ,此时上面结论是否成立?31.已知:如图, AC ⊥BC 于C , DE ⊥AC 于E , AD ⊥AB 于A , BC =AE .若AB = 5 ,求AD 的长?AC B DEF AEBF32.如图:AB=AC ,ME ⊥AB ,MF ⊥AC ,垂足分别为E 、F ,ME=MF 。
全等三角形的判定练习题

全等三角形的判定练习题全等三角形在几何学中是一个重要的概念。
判定两个三角形是否全等是解决几何问题的基础,也是推导其他几何性质的前提。
本文将提供一些全等三角形的判定练习题,以帮助读者巩固和加深对该概念的理解。
练习题1:已知三角形ABC和DEF,判定它们是否全等。
已知如下条件:1. ∠A = ∠D,∠B = ∠E,∠C = ∠F;2. AB = DE,BC = EF,AC = DF。
解析:根据题目给出的条件,我们可以得出以下结论:1. 两个三角形的对应角度相等(∠A = ∠D,∠B = ∠E,∠C =∠F);2. 两个三角形的对应边长相等(AB = DE,BC = EF,AC = DF)。
由于两个三角形的对应角度和对应边长都相等,因此可以判定三角形ABC和DEF全等。
练习题2:已知三角形ABC和DEF,判定它们是否全等。
已知如下条件:1. ∠A = ∠D,∠B = ∠E;2. AB = DE,AC = DF。
解析:根据题目给出的条件,我们可以得出以下结论:1. 两个三角形的对应角度相等(∠A = ∠D,∠B = ∠E);2. 两个三角形的对应边长不全等(AB = DE,AC = DF)。
由于两个三角形仅仅只有两对对应角度相等且没有所有对应边长相等,因此无法判定三角形ABC和DEF全等。
练习题3:已知三角形ABC和DEF,判定它们是否全等。
已知如下条件:1. ∠A = ∠D,∠B = ∠E,∠C = ∠F;2. AB = DE,AC ≠ DF。
解析:根据题目给出的条件,我们可以得出以下结论:1. 两个三角形的对应角度相等(∠A = ∠D,∠B = ∠E,∠C =∠F);2. 两个三角形的对应边长不全等(AB = DE,AC ≠ DF)。
由于两个三角形仅仅只有三对对应角度相等且没有所有对应边长相等,因此无法判定三角形ABC和DEF全等。
通过以上练习题,我们可以发现判定两个三角形是否全等时,既需要考虑对应角度是否相等,又需要考虑对应边长是否相等。
直角三角形全等的判定练习题

直角三角形全等判定练习班级________ 学号 ______ 姓名 ___________ 评价___________ 课题 直角三角形全等的判定(一) 日期一、选择题1.△ABC 中,∠C=90°,AD 为角平分线,BC=32,BD ∶DC=9∶ 7, 则点D 到AB 的距离为( )A.18cmB.16cmC.14cmD.12cm2.在△ABC 内部取一点P 使得点P 到△ABC 的三边距离相等,则点P 应是△ABC 的哪三条线交点. ( )(A )高 (B )角平分线 (C )中线 (D )边的垂直平分线 3.已知,如图,△ABC 中,AB=AC ,AD 是角平分线,BE=CF ,则下列说法正确的有几个 ( )(1)AD 平分∠EDF ;(2)△EBD ≌△FCD ;(3)BD=CD ; (4)AD ⊥BC . (A )1个 (B )2个 (C )3个 (D )4个 二、填空题4.如图,在△ABC 和△ABD 中,∠C=∠D=90°,若利用“AAS ”证明△ABC ≌△ABD ,则需要加条件 _______或 ; 若利用“HL ”证明△ABC ≌△ABD ,则需要加条件 或 .第4题 第5题 第6题5.如图,有一个直角△ABC ,∠C=90°,AC=10,BC=5,一条线段PQ=AB ,P.Q 两点分别在AC 和过点A 且垂直于AC 的射线AX 上运动,当AP= 时,才能使ΔABC ≌ΔPQA.6.如图,在△ABC 中,∠C =90°,AC =BC ,AD 平分∠CAB ,交BC 于 D,DE ⊥AB 于E ,且AB =6 cm ,则△DEB 的周长为___________cm.三、解答题7.如图,在△ABC 中,已知D 是BC 中点,DE ⊥AB ,DF ⊥AC ,垂足分别是E 、F ,DE =DF . 求证:AB=ACP Q C A B x D C BA DB CA E F DBC A E F8.已知:如图,AC 平分∠BAD ,CE ⊥AB 于E ,CF ⊥AD 于F ,且BC =DC .你能说明BE 与DF 相等吗?9.已知:如图,在△ABC 中,∠ACB=90°,CD ⊥AB 于D ,∠A=30°.求证:BD=14AB10.如图,在△ABC 中,AB =AC ,DE 是过点A 的直线,BD ⊥DE 于D ,CE ⊥DE 于E .(1)若BC 在DE 的同侧(如图①)且AD =CE ,说明:BA ⊥A C .(2)若BC 在DE 的两侧(如图②)其他条件不变,问AB 与AC 仍垂直吗?若是请予证明,若不是请说明理由.A BC D E F 1 2 B A C D。
全等三角形的判定练习题

全等三角形的判定练习题一、选择题1. 下列哪组条件可以判定两个三角形全等?A. 两边和其中一边的对角相等B. 两角和其中一角的对边相等C. 两边和它们的夹角相等D. 两角和其中一边相等A. ∠A=∠DB. ∠B=∠EC. ∠C=∠FA. SAS(边角边)B. ASA(角边角)C. AAS(角角边)D. SSS(三边)二、填空题1. 若两个三角形的______相等,且它们的夹角相等,则这两个三角形全等。
2. 在全等三角形中,对应边______相等,对应角______相等。
3. 要判定两个三角形全等,至少需要知道它们的______个元素相等。
三、判断题1. 若两个三角形的两边和它们的夹角分别相等,则这两个三角形一定全等。
()2. 两个等腰三角形的底角相等,则这两个三角形全等。
()3. 两个等边三角形的边长相等,则这两个三角形全等。
()四、解答题1. 在△ABC中,AB=AC,∠B=∠C,求证:△ABC是等腰三角形。
2. 已知△ABC和△DEF,AB=DE,BC=EF,∠B=∠E,求证:△ABC≌△DEF。
3. 在△ABC中,AB=AC,∠A=40°,∠B=70°,求∠C的度数。
4. 已知△ABC和△DEF,AB=DE,BC=EF,AC=DF,求证:△ABC≌△DEF。
5. 在△ABC中,AB=8cm,AC=10cm,∠A=60°,求BC的长度。
五、作图题1. 请作出一个三角形,使其与给定三角形全等,已知条件是两边及其夹角。
2. 请作出一个三角形,使其与给定三角形全等,已知条件是两角及其夹边。
3. 请作出一个三角形,使其与给定三角形全等,已知条件是三边。
六、综合题1. 在平面直角坐标系中,点A(2, 3),点B(6, 3),点C和点D在x轴上,且△ABC≌△ABD,求点C和点D的坐标。
2. 在四边形ABCD中,AB=CD,AD=BC,且∠ABC=∠CDA=90°,证明:△ABC≌△CDA。
三角形全等判定专题训练题
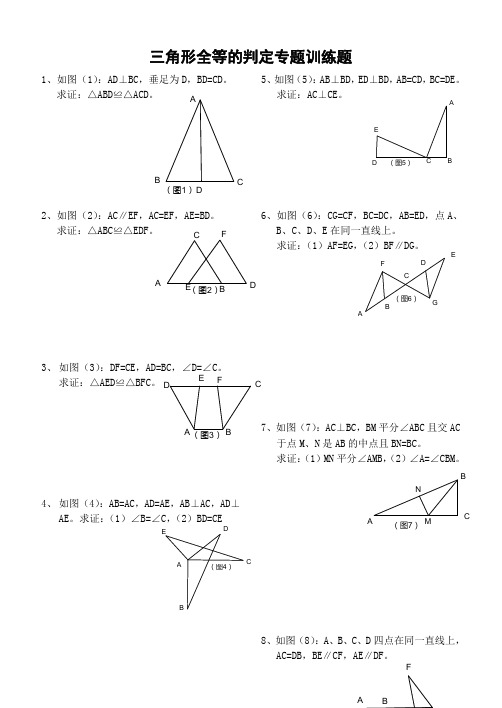
三角形全等的判定专题训练题1、如图(1):AD ⊥BC ,垂足为D ,BD=CD 。
求证:△ABD ≌△ACD 。
5、如图(5):AB ⊥BD ,ED ⊥BD ,AB=CD ,BC=DE 。
求证:AC ⊥CE 。
2、如图(2):AC ∥EF ,AC=EF ,AE=BD 。
求证:△ABC ≌△EDF 。
3、 如图(3):DF=CE ,AD=BC ,∠D=∠C 。
求证:△AED ≌△BFC 。
4、 如图(4):AB=AC ,AD=AE ,AB ⊥AC ,AD ⊥AE 。
求证:(1)∠B=∠C ,(2)BD=CE6、如图(6):CG=CF ,BC=DC ,AB=ED ,点A 、B 、C 、D 、E 在同一直线上。
求证:(1)AF=EG ,(2)BF ∥DG 。
7、如图(7):AC ⊥BC ,BM 平分∠ABC 且交AC 于点M 、N 是AB 的中点且BN=BC 。
求证:(1)MN 平分∠AMB ,(2)∠A=∠CBM 。
8、如图(8):A 、B 、C 、D 四点在同一直线上,(图1)DC B A F E (图2)D C BA FE (图3)D C B A E(图4)D CB A E (图5)DC B A G FE(图6)D C B AN M(图7)C BA求证:△ABE ≌△DCF 。
9、如图(9)AE 、BC 交于点M ,F 点在AM 上,BE ∥CF ,BE=CF 。
求证:AM 是△ABC 的中线。
10、如图(10)∠BAC=∠DAE ,∠ABD=∠ACE ,BD=CE 。
求证:AB=AC 。
11、如图(11)在△ABC 和△DBC 中,∠1=∠2,∠3=∠4,P 是BC 上任一点。
求证:PA=PD 。
12、如图(12)AB ∥CD ,OA=OD ,点F 、D 、O 、A 、E 在同一直线上,AE=DF 。
求证:EB ∥CF 。
13、如图(13)△ABC ≌△EDC 。
求证:BE=AD 。
全等三角形证明经典100题

1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD2. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D,F 是CD 中点,求证:∠1=∠24. 已知:∠1=∠2,CD=DE,EF//AB ,求证:EF=ACADBCBA CDF2 1 E5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C6. 已知:AC 平分∠BAD,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE7. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD8. 已知:D 是AB 中点,∠ACB=90°,求证:12CD ABADB CCDB A9. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠210. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC11. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C12. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BEBA CDF2 1 ECDB A12。
如图,四边形ABCD 中,AB ∥DC,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
求证:BC=AB+DC.13。
已知:AB//ED ,∠EAB=∠BDE ,AF=CD ,EF=BC ,求证:∠F=∠C14. 已知:AB=CD,∠A=∠D ,求证:∠B=∠CDCBAFEAB C D15. P 是∠BAC 平分线AD 上一点,AC>AB ,求证:PC —PB 〈AC-AB16. 已知∠ABC=3∠C ,∠1=∠2,BE ⊥AE ,求证:AC —AB=2BE17. 已知,E 是AB 中点,AF=BD ,BD=5,AC=7,求DC18.(5分)如图,在△ABC 中,BD =DC ,∠1=∠2,求证:AD ⊥BC . 19.(5分)如图,OM 平分∠POQ ,MA ⊥OP ,MB ⊥OQ ,A 、B 为垂足,AB 交OM 于点N .求证:∠OAB =∠OBAP D ACBFAED C B20.(5分)如图,已知AD ∥BC ,∠P AB 的平分线与∠CBA 的平分线相交于E ,CE 的连线交AP 于D .求证:AD +BC =AB .21.(6分)如图,△ABC 中,AD 是∠CAB 的平分线,且AB =AC +CD ,求证:∠C =2∠B22.(6分)如图①,E 、F 分别为线段AC 上的两个动点,且DE ⊥AC 于E,BF ⊥AC 于F ,若AB =CD ,AF =CE ,BD 交AC 于点M . (1)求证:MB =MD ,ME =MF(2)当E 、F 两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.23.(7分)已知:如图,DC ∥AB ,且DC =AE ,E 为AB 的中点, (1)求证:△AED ≌△EBC .P EDCBA D CBA(2)观看图前,在不添辅助线的情况下,除△EBC 外,请再写出两个与△AED 的面积相等的三角形.(直接写出结果,不要求证明):24.(7分)如图,△ABC 中,∠BAC =90度,AB =AC ,BD 是∠ABC 的平分线,BD 的延长线垂直于过C 点的直线于E ,直线CE 交BA 的延长线于F . 求证:BD =2CE .25、(10分)如图:DF=CE ,AD=BC,∠D=∠C.求证:△AED ≌△BFC 。
全等三角形的判定方法50道经典题

全等三角形的判定方法50道经典题以下是全等三角形判定的50道经典题:1. 给定两个三角形的三边长,判断它们是否全等。
2. 给定两个三角形的一个角和两个侧边,判断它们是否全等。
3. 给定两个三角形的两个角和一个侧边,判断它们是否全等。
4. 给定两个三角形的一个角和两个高,判断它们是否全等。
5. 给定两个三角形的两个角和一个高,判断它们是否全等。
6. 给定两个三角形的两个角和一个中线,判断它们是否全等。
7. 给定两个三角形的一个角和两个角平分线,判断它们是否全等。
8. 给定两个三角形的两个角和一个外接圆半径,判断它们是否全等。
9. 给定两个三角形的一个角和一个内切圆半径,判断它们是否全等。
10. 给定两个三角形的一个角和一个内心到边的距离,判断它们是否全等。
11. 给定两个三角形的两个角和一个重心到边的距离,判断它们是否全等。
12. 给定两个三角形的两个角和一个垂心到边的距离,判断它们是否全等。
13. 给定两个三角形的一个角和一个外心到边的距离,判断它们是否全等。
14. 给定两个三角形的两个角和一个外心到边的距离,判断它们是否全等。
15. 给定两个三角形的两个角和一个垂足到边的距离,判断它们是否全等。
16. 给定两个三角形的两个角和一个内心到边的角平分线的距离,判断它们是否全等。
17. 给定两个三角形的一个角和一个外心到边的角平分线的距离,判断它们是否全等。
18. 给定两个三角形的两个角和一个内角平分线的夹角,判断它们是否全等。
19. 给定两个三角形的一个角和两个角平分线的夹角,判断它们是否全等。
20. 给定两个三角形的两个角和一个内心到边的角平分线的夹角,判断它们是否全等。
21. 给定两个三角形的两个角和一个内心到边的角平分线的夹角,判断它们是否全等。
22. 给定两个三角形的一个角和两个角平分线的夹角之和,判断它们是否全等。
23. 给定两个三角形的两个角和一个内心到边的角平分线的夹角之和,判断它们是否全等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
探索三角形全等的条件练习题
1、已知AD 是⊿ABC 的中线,BE ⊥AD ,CF ⊥AD ,问BE =CF 吗?说明理由。
2、已知AC =BD ,AE =CF ,BE =DF ,问AE ∥CF 吗?
3、已知AB =CD ,BE =DF ,AE =CF ,问AB ∥CD 吗?
4、已知在四边形ABCD 中,AB =CD ,AD =CB ,
问AB ∥CD 吗?说明理由。
5、已知∠BAC =∠DAE ,∠1=∠2,BD =CE ,问ABD ≌⊿ACE .吗?为什么?
A B C D
F E A C B D E F D C F E A B
A D E
B
C 1 2
6、已知CD ∥AB ,DF ∥EB ,DF =EB ,问AF =CE 吗?说明理由。
7、已知BE =CF ,AB =CD , ∠B =∠C .问AF =DE 吗?
8、已知AD =CB , ∠A =∠C ,AE =CF ,问EB ∥DF 吗?说明理由。
9、已知,M 是AB 的中点,∠1=∠2,MC =MD ,问∠C =∠D 吗?说明理由。
10、已知,AE =DF ,BF =CE ,AE ∥DF ,问AB =CD 吗?说明理由。
A D C E F
B A C
D B
E
F B
A
D F
E C M A B C D 1 2 D C
F E A B
11、已知∠1=∠2,∠3=∠4,问AC =AD 吗?说明理由。
12、已知∠E =∠F ,∠1=∠2,AB =CD ,问AE =DF 吗?说明理由。
13、已知ED ⊥AB ,EF ⊥BC ,BD =EF ,问BM =ME 吗?说明理由。
14、在⊿ABC 中,高AD 与BE 相交于点H ,且AD =BD ,问⊿BHD ≌⊿ACD ,为什么?
15、已知∠A =∠D ,AC ∥FD ,AC =FD ,问AB ∥DE 吗?说明理由。
A C
D B 1 2 3 4 A B C
D E F 1 2 A B C E H D A
C M E F B
D A
B C E F D
16、已知CE ⊥AB ,DF ⊥AB ,AC ∥DB ,AC =BD ,问CE =DF 吗?说明理由。
17、已知EF ∥BC ,AF =CD ,AB ⊥BC ,DE ⊥EF ,问⊿ABC ≌⊿DEF 吗?说明理由。
18、已知AD =AE ,∠B =∠C ,问AC =AB 吗?说明理由。
19、已知AD ⊥BC ,BD =CD ,问AB =AC 吗?
20、已知∠1=∠2,BC =AD ,问⊿ABC ≌⊿BAD 吗?
A B C E D F A D E B C A
B C D
C A E
B
F D
21、已知AB =AC , ∠1=∠2,AD =AE ,问⊿ABD ≌⊿ACE .说明理由。
22、已知BE ∥DF ,AD ∥BC ,AE =CF ,问⊿AFD ≌⊿CEB 吗?
23、已知AD =AE ,BD =CE ,∠1=∠2,问⊿ABD ≌⊿ACE 吗?
24、已知AB =AC ,AD =AE ,∠1=∠2,问CE =BD 吗?
25、已知AC =AB ,AE =AD , ∠1=∠2,问∠3=∠4吗?
B A D F E
C A B C
D
E 1 2 A C D B E
F
G 1 2 A D B E C 1 2 A D E B C 1 2 3 4
26、如图,AD =BC ,AE =BE ,问∠C =∠D 吗?
27、已知∠1=∠2,AC =BD ,E ,F ,A ,B 在同一直线上,
问∠3=∠4吗?
28、已知D O ⊥BC ,O C =O A ,O B =O D ,问CD =AB 吗?
29、已知CE=DF ,AE =BF ,CE ⊥AB ,DF ⊥AB ,问⊿EAC ≌⊿FBD 吗?
30、已知AB 与CD 相交于点E ,EA =EC ,ED =EB ,问⊿AED ≌⊿CEB 吗?
A C D E
B A E D
C B O C
D A
E F
B 2 1 3
4 A C B D E C
A E
B F D
31、已知AB =AC ,D ,E 分别是AB ,AC 的中点。
问BE =CD 吗?说明理由。
32、已知DE =FE ,FC ∥AB ,问AE =CE 吗?
33、已知CE ⊥AB ,DF ⊥AB ,CE =DF ,AE =BF ,问⊿CEB ≌⊿DFA 吗?说明理由。
34、如图,D ,E ,F ,B 在一条直线上,AB =CD ,∠B =∠D ,BF =DE ,问(1)AE =CF (2)AE ∥CF 。
35、已知,点C 是AB 的中点,CD ∥BE ,且CD =BE ,问∠D =∠E 吗?说明理由。
B A
C
D
E F
C D E
F A B D A E C B 1 2 A D B E F C A C
B E D
36、已知,E 、F 是AB 上的两点,AE =BF ,又AC ∥DB ,AC =DB ,问CF =DE 吗?说明理由。
37、已知,AC ⊥CE ,AC =CE , ∠ABC =∠DEC =900,问BD =AB +ED 吗?
38、已知:⊿ABC ≌⊿A ′B ′C ′,AD 与A ′D ′分别是中线,问AD =A ′D ′吗?
39.如图,已知:OA=OB,OD=OC,∠AOC=∠BOD.
试说明:AD=BC
A
B C D E A B D A ′ B ′ C ′ D ′ B A D
F E C。
