13幅逻辑图,改变你的生活轨迹
13幅逻辑图

13幅逻辑图,领略杜克大学的经典思维杜克大学作为全球排名第7的大学在全球教育中有着巨大的影响力,今日借杜克大学的13幅逻辑图与您一块探讨关于生活的哲学,这13幅图将帮助您更清晰地了解自己的行为、目标及思考问题的方式,让你选择正确的方式去实现心中所想与所需。
No.1、什么是生活生活中我们往往因为缺乏对自我的认知而错过了我们很多原本属于自己的生活,生活总是在不经意间见错过了那些最美好的东西。
“Pay close attention. This is your life.”请留意生活中的细节,这是你的生活No.2、明天比今天更重要人们总是过于在意那些重要的决定 (比如接受什么样的工作或者职位) 但是实际上明天总是模糊的。
潜心规划,向你认为最好的目标大胆进发,要知道,很少有所谓完全“正确”或是“错误”的决定,因为它们只不过都是一个让你的生命进入下一个阶段的台阶。
认真地思考,清楚滴知道自己的追求及内心深处想要的东西是神马,这是航行中的灯塔,没有了这个灯塔,前行的路上就会有更多“错误”的选择,今天--->明天是一条不可逆转的路,珍惜每个当下及生命中的过客。
No.3、获得满足感和你得到的实物相比,你可以从和别人建立的关系中获得更多的满足。
在我们的现实生活中,我们总是错误地追求“物质”所带来的快感,就如我常说的,钱绝对不是我们人生的追求,它只不过是满足我们需求的工具而已,可是很多人只看了工具,却没有想清楚,努力获得这个工具用来干什么?在现实生活中往往会出现两种情况:(1)钱有了,却无所事事;(2)钱没了,所有的精力及焦点都陷入到“求生存”的状态,几乎没有心智考虑幸福的事情,然后越来越穷,越来越没有幸福感。
No.4、体现生命的价值在这里的“头衔”是指他人的评价,也就是所谓的面子,我们往往太在意他人的评价而忽略了自己最真实的需求,有一句话说的很好“外面只有自己,没有别人”;这句话反过来说也挺有意义:“里面只有别人,没有自己”,真正的忽略了别人的评价。
逻辑记忆的例子

逻辑记忆的例子逻辑记忆是人们用于处理和储存信息的一种记忆方式,它涉及到对信息进行组织、分类和排序的能力。
以下是一些逻辑记忆的例子,展示了在日常生活中如何运用逻辑思维来记忆和处理信息。
1. 购物清单:当我们需要去购物时,我们可以使用逻辑记忆来记住需要购买的物品。
我们可以将物品按照不同的类别进行分类,例如食品、生活用品和药品等。
在遵循逻辑的基础上,我们可以将每个类别中的具体物品列出来,并按照逻辑顺序记忆它们。
这样,我们可以避免忘记购买任何东西。
2. 地图导航:当我们需要前往一个陌生地点时,逻辑记忆可以帮助我们记住道路和方向。
我们可以根据地图上的标志物和建筑物来创建一个逻辑性的路径。
通过将街道名称、标志和地标按照逻辑顺序记忆,我们可以更容易地找到目的地。
3. 学习规则:学习新的知识或技能时,逻辑记忆可以帮助我们理解和记住规则。
例如,在学习语法规则时,我们可以将它们按照类别进行归类并创建逻辑性的顺序。
这样,我们可以更有效地记住不同的规则,并将它们应用到实际的写作或口语中。
4. 事务安排:逻辑记忆还可以帮助我们有效地安排日常事务。
我们可以使用逻辑记忆来记住重要的事情和任务,并将它们按照优先级进行排序。
这样,我们可以更好地管理时间和资源,确保任务按照逻辑步骤完成。
总之,逻辑记忆是一种重要的思维能力,可以帮助我们在各个方面更好地处理和记忆信息。
通过将信息组织成逻辑顺序,并利用分类和排序技巧来记忆,我们可以提高记忆力和信息处理的效率。
无论是在日常生活中的购物、导航,还是在学习和工作中的知识应用和事务管理,逻辑记忆都扮演着重要的角色。
15个经典思维模型,改变你的思考方式!

15个经典思维模型,改变你的思考方式!展开全文每个学科都是从一个独特的角度去切入了解这个世界,都是一个摸象的瞎子;要超越普通人的认知决策,就必须掌握多个核心思维模型。
以下内容是从查理·芒格的100种思维模型中提炼出的15个,让人受益终身。
01复利原理爱因斯坦说:复利是世界的第八大奇迹。
巴菲特说:人生就像滚雪球,关键是要找到足够湿的雪和足够长的坡。
查理·芒格说:同时理解复利的力量和获得它的困难,是理解许多事情的核心和灵魂。
在有限的时间,把有限的精力和财富,持续而反复地投入到某一领域,长期坚持下去,最终产生的积极影响,会如雪球越滚越大,它带来的回报一定超过你的想象。
这就是经济学中典型的复利思维。
大多数人终其一生都不会去运用复利,也体会不到复利的威力。
复利思维需要我们用发展和长远的眼光去看待事物。
02反熵增思维模型从一个系统、一个组织,再到一个星球,甚至我们每个人,都符合熵增定律。
我们会变得混乱、无序、僵化、没有活力,直至在这种混乱中走向消亡。
值得庆幸的是,宇宙是平衡的,在熵增的大前提下,给了我们一条不同的路,反熵增,也即自组织、生命化。
亚马逊的CEO贝佐斯对于反熵增的理解非常深刻。
他把亚马逊的服务做得足够开放,所以才有了亚马逊云;对于新生事物,哪怕是取得一点点的成绩,他都会大加赞赏,要求主管以上级别员工每周都要读一遍《创新者的窘境》。
反熵增就是重现生命。
行星从星云中诞生,行星上产生了岩石圈、大气、河流、季风、泉水、矿藏,这些都是组织化的过程,是对无序的反抗。
这种有序化、组织化进程的顶峰,便是生命的产生:DNA团块、单细胞生物、多细胞生物、植物和动物,一直到最精巧的组织化结构——人类。
人老后,最好的状态就是复归婴儿和自然。
一个企业,要让自己反熵增,就是让自己更有活力,更开放,更多地适应外部变化,让其在环境中自我进化。
同时,可以不断生出独立的新的业务,新的业务也可以不断进化。
从本质上来讲,延续的发展就是一个熵增的过程,而要想突破非连续性,必须要“生”出新的曲线,这才是对抗熵增最好的办法。
6步逻辑层次即可以改变我们的生活,又能让我们学会做

6步逻辑层次即可以改变我们的生活,又
能让我们学会做
《6步逻辑层次:改变我们的生活》人类的大脑是一个复
杂的系统,在解决问题时采用6步逻辑层次是其中一个有效的方法。
这6步逻辑层次被称为“改变我们的生活”,在以下6个
步骤中,介绍了我们如何利用逻辑层次改变我们的生活。
首先,我们需要认识到自身的问题。
因为我们面临的问题可能是复杂的,可能有多个不同的解决方案。
因此,我们要努力了解自身的问题,分析它,以便找出最佳的解决方案。
其次,我们要审视自身的理念和价值观。
这一步是非常重要的,因为它不仅影响我们对事物的看法,也影响我们最终做出的决定。
因此,我们要审视自身的理念和价值观,以便能够做出明智的决定。
三,我们要分析自身的能力和技能。
我们要知道自己有什么能力和技能,以便知道自己有什么可以拿来应对挑战的能力和技能。
四,我们要分析其他人的意见和想法。
沟通是解决问题的基础,因此,我们应该尊重他人的意见,深入了解他们的观点。
五,我们要分析可能的解决方案。
有了前面几步的准备,我们已经可以分析可能的解决方案,并作出正确的决定。
最后,我们要实施解决方案。
实施解决方案需要坚持不懈,但也要记住,坚持不懈是成功的前提。
从上面的说明可以看出,6步逻辑层次是一个有效的解决
问题的方法,它不仅可以帮助我们改变生活,还可以让我们学会如何正确地处理问题,并及时有效地解决问题。
而且,它还可以帮助我们培养独立思考的能力,提高自己的解决问题的能力,从而获得更好的生活。
13种逻辑思维开发性逻辑

13种逻辑思维开发性逻辑1、有个老人爱清静,可附近常有小孩玩,吵得他要命,于是他把小孩召集过来,说:我这很冷清,谢谢你们让这更热闹,说完每人发三颗糖。
孩子们很开心,天天来玩。
几天后,每人只给2颗,再后来给1颗,最后就不给了。
孩子们生气说:以后再也不来这给你热闹了。
老人清静了。
【逻辑思维】抓住人性的弱点,无事不成。
2. 两马各拉一货车。
一马走得快,一马慢吞吞。
于是主人把后面的货全搬到前面。
后面的马笑了:“切!越努力越遭折磨!”谁知主人后来想:既然一匹马就能拉车,干嘛养两匹?最后懒马被宰掉吃了。
这就是经济学中的懒马效应。
【逻辑思维】如果让你的老板觉得你已经可有可无,那你已经站在即将离去的边缘。
3. 夜市有两个面线摊位。
摊位相邻、座位相同。
一年后,甲赚钱买了房子,乙仍无力购屋。
为何?原来,乙摊位生意虽好,但刚煮的面线很烫,顾客要15分钟吃一碗。
而甲摊位,把煮好的面线在冰水里泡30秒再端给顾客,温度刚好。
【逻辑思维】为客户节省时间,钱才能进来快些。
4. 一禅师见一蝎子掉到水里,决心救它。
谁知一碰,蝎子蛰了他手指。
禅师无惧,再次出手,岂知又被蝎子狠狠蛰了一次。
旁有一人说:它老蜇人,何必救它?禅师答:蜇人是蝎子的天性,而善是我的天性,我岂能因为它的天性,而放弃了我的天性。
【逻辑思维】我们的错误在于,因为外界过多地改变了自己。
5. 曼德拉曾被关压27年,受尽虐待。
他就任总统时,邀请了三名曾虐待过他的看守到场。
当曼德拉起身恭敬地向看守致敬时,在场所有人乃至整个世界都静了下来。
他说:当我走出囚室,迈过通往自由的监狱大门时,我已经清楚,自己若不能把悲痛与怨恨留在身后,那么我仍在狱中。
【逻辑思维】原谅他人,其实是升华自己。
6. 有人问农夫:“种了麦子了吗?”农夫:“没,我担心天不下雨。
”那人又问:“那你种棉花没?”农夫:“没,我担心虫子吃了棉花。
”那人再问:“那你种了什么?”农夫:“什么也没种,我要确保安全。
”【逻辑思维】一个不愿付出、不愿冒风险的人,一事无成对他来说是再自然不过的事。
14个底层逻辑

14个底层逻辑在我们的生活和工作中,有一些底层逻辑思维对我们的思考和决策有着重要的影响。
在这篇文章中,我们将探讨14个底层的逻辑思维,帮助你更好地理解世界,提高决策质量,实现自我成长。
1.理解个体与整体的关系。
在分析问题时,我们不能仅仅看到个体,还要关注整体。
整体往往大于部分之和,因此理解整体与个体的关系有助于我们做出更为全面的判断。
2.把握事物的本质与现象。
很多时候,事物的表象会让我们产生误导。
学会挖掘事物的本质,帮助我们更好地认识世界,找到问题的根本原因。
3.学会批判性思维。
批判性思维是一种能力,它可以帮助我们发现问题、分析问题,并找到解决问题的方法。
在生活中,我们要学会用批判性思维来审视各种观点和论据。
4.运用概率思维。
概率思维使我们能够根据不确定事件的发生概率来做出决策。
学会用概率思维看待生活和工作中的事物,有助于我们提高决策的准确性。
5.掌握系统思维。
系统思维让我们看到事物之间的相互关联。
通过系统思维,我们可以更好地理解复杂问题,并找到解决问题的整体解决方案。
6.了解非线性关系。
在现实生活中,很多事物之间的关系并非线性,而是非线性的。
了解非线性关系有助于我们更好地把握事物的发展趋势。
7.运用边际思维。
边际思维是一种寻求事物最优解的思维方式。
通过边际思维,我们可以找到在特定条件下最优的决策。
8.理解时间价值。
时间价值意味着不同时间点的价值是不同的。
了解时间价值,可以帮助我们更好地利用时间资源,提高工作和生活的效率。
9.把握动态平衡。
动态平衡是指在事物发展过程中,各种因素之间不断调整和达到平衡的状态。
学会把握动态平衡,有助于我们在面对变化时做出合适的调整。
10.学会跨学科思考。
跨学科思考能帮助我们跳出思维定式,发现新的问题和解决方案。
在生活中,我们要学会运用不同学科的知识来解决问题。
11.运用复利思维。
复利思维让我们明白积累和持续努力的重要性。
通过复利思维,我们可以更好地规划自己的人生,实现财富和能力的积累。
儿童逻辑思维题
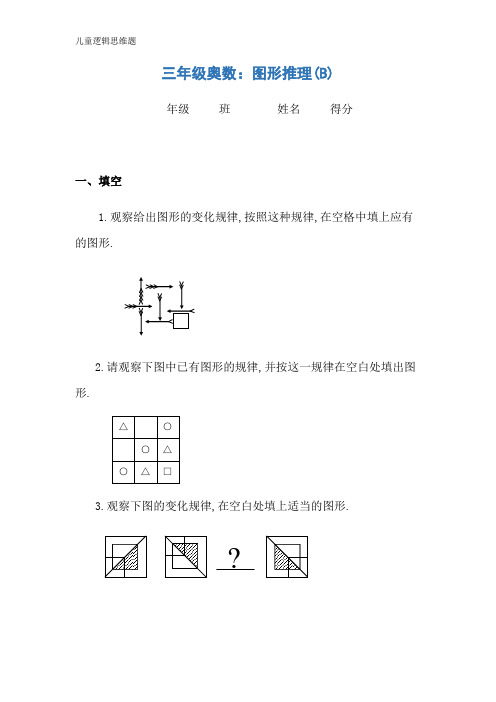
三年级奥数:图形推理(B)年级班姓名得分一、填空1.观察给出图形的变化规律,按照这种规律,在空格中填上应有的图形.2.请观察下图中已有图形的规律,并按这一规律在空白处填出图形.3.观察下图的变化规律,在空白处填上适当的图形.?4.下图的排列规律你发现了吗?请你根据这一规律,把第3幅图填出来.5.下图的变化很多,请你认真仔细地观察,画出第四幅图的答案.6.观察下面这组图形的变化规律,在标号处画出相应的图形.7.下图是由9个小人排列的方阵,但有一个小人没有到位,请你从右面的6个小人中,选一位小人放到问号的位置.你认为最合适的人选是 号.① ② ③?1 2 3 4 5 68.下图是用几何图形组成的小房子,请你根据组成的规律在标号处画出相应的图形.9.按规律填图.如果变成那么应变为10.按规律填画图.② ①③如果变成那么应变成二、解答题11.在下面图形中找出一个与众不同的.(1) (2) (3) (4) (5) 12.依照下面图中所给图形的变化规律,在空格中填图.13.正四面体分别写有1、2、3、4四个数字.现在有三个四面体,请问哪一个和其它两个不同?图(1) 图(2) 图(3)14.“兵”、“马”、“卒”如图所示占“田”字的四个小格,把它们不停的变换位置,第一次上下两排交换,第二次在第一次交换后左右两列交换,第三次再上下两排交换,第四次再左右两列交换……这样交换二十次位置后,“马”在几号小格内?兵 卒 卒 兵 3 4 兵 卒 车 马 马 车———————————————答 案——————————————————————……1. 观察这道题给出的八个图,形状都是箭,这使我们可以肯定空格处的图形也是箭.在这组图中,发生变化的有两点:一是箭的方向,二是箭尾的“羽毛”.首先我们看横行(从左到右),箭的方向是顺时针依次旋转得到的,所以空格处的箭应向上.再看箭尾的“羽毛”,每一行也是依次减少一对,所以空格处的箭箭笔没有“羽毛”.所以空格的图形为:2. 在这幅图中,都是△、○、□,所以我们可以确定空白处也应是△、○、□,中的一种.通过观察每一行,又可以发现每一行都没有重复的图形,这时,我们就可以根据这个规律填出空白处的图形了.第一横行中有△、○,少□,所以空白处应为□. 第二横行中也有△、○,所以空白处也为□.所以,最后这幅图应为:3. 这组图形不变的有两点,外面是一个大正方形,里面是一个小正方形.所以空白处也应是一个大正方形里面有一个小正方形.变化的有三点:一是大正方形一条对角线的方向.第1个图形是连接右上角和左下角,第2个图形是连接左上角和右下角,第4个图形还是连接左上角和右下角.可见对角线的方向是交替变化的,所以空白处的对角线应是连接右上角左下角的.二是圈住大正方形和小正方形的方形的位置.通过观察可得,它是按顺时针依次旋转得到下一图形的.所以空白处应在右上角.三是阴影部分的位置.阴影部分是按照逆时针方向依次旋转得到的,所以空白处的阴影部分应在小正方形的左上角.这样,我们就可以得到空白处的图形了:4. 在这道题中,不变的是用三角形组成图形,变化的是三角形的个数的颜色.从第一幅图到第二幅图是在图形的上、左、右,三个方向上各加了一个三角形,而且第4幅图比第二幅各方向上多了2个三角形,可见第四幅应比第三幅每个方向上各多1个,第三幅比第二幅每个方向上各多1个.所以第三幅图的横排应有7个三角形,竖排有5个三角形.三角形的颜色是黑白相间的,所以最后第三幅图为:5. 在这道题中,变化较多,我们一方面一方面的分开来看.①四个图形的位置.四个图形是按照顺时针旋转的.所以第四幅图内右上角应为三角形,右下角应为半圆形,左下角应为圆形,左上角应为正方形.②圆形阴影部分位置的变化.圆形的阴影部分是按顺时针方向依次旋转得到的,所以第四幅图中圆形阴影部分应在圆形的左上角.③正方形的阴影部分位置的变化.正方形的阴影部分是按逆时针方向依次旋转得到的,所以第四幅图中正方形的阴影部分应在它的上方.④三角形的方向变化.三角形是按逆时针方向依次旋转得到的,所以第四幅图中三角形应向右.⑤半圆形的方向变化.半圆形也是逆时针方向依次旋转得到的,所以第四幅图中半圆形向右.通过这样的分析,我们得到了第四幅图的画法:6. 这道题中的每一个图形是由里外两部分组成的,我们分开来看.先看外面的图形.外面的图形都是由△、□、○组成,并每一横行(或每一竖行)中都没有重复的图形.这样我们可以先确定①、②、③外面的图形.通过题目中给出的图形,我们不能确定出③的外部图形,因为不论③所在的横行还是③所在的竖行都只给出1个图形,所以我们应先确定出①和②的外部图形. ①所在的横行中只有○和△,所以①的外部图形是□, ②所在的竖行只有△和○,所以②的外部图形也是□, ③所在的横行只有□和○,所以③的外部图形是△.然后按照这种方法确定内部图形,可知①的内部图形是□,②的内部图形是△, ③的内部图形是○,形状确定好以后,我们还要注意各个图形的内部图形是有不同颜色的,分别由点状、斜线和空白三种组成,确定的方法和确定形状是完全相同的,请你自己把三个图的颜色确定出来.最后①、②、③应分别为:① ② ③7. 仔细观察,可发现图中小人的排列规律:即每行(列)的小人“手臂”(向上、水平、向下).“身腰”(三角形矩形、半圆),及“脚”(圆脚、方脚、平脚)各不相同.从中可知问号处的小人应是向上伸臂.矩形腰,圆脚的小人.即最合适的人选是6号.8. 这道题同(1)卷解答题第4题分析完全相同. ①、②、③图形分别如下:②①③9. 第1行图形由左向右变化的规律是左右颠倒,上下颠倒.(或旋转),然后将移到上面的图形以中线为对称轴做出另一半图形.根据这个变化规律,请你做出要求的图形.答案应为:10. 分析:先应找出变化的规律,然后再依规律,在空白处填画所缺的图形.从题图的第一行可以看到,当左边的图形变化成右边的图形时,图形外部的圆变为图形的下半部分,且圆变成半圆,白色变成灰色(画有斜线).也就是说,在变化过程中,原来图形的外部部分有形状、位置、颜色这三个方面的变化.再看原图形的内部部分:中间的灰色正方形变到了上半部分(位置变),成了白色的(颜色变化)斜放着的正方形(角度变化).根据这些规律可以知道,空白处的图形其下部分是由左边图形的外部大正方形变化而成的,半个大正方形,颜色为灰色;上半部分是由左边图形的中间部分变化而成的一个白色、正放着的小正方形,如图.解:在空白处的图形如图所示.11. 分析:很容易看出题目图中(1)逆时针旋转就是(4),但是这样一来,(2)、(3)、(5)都与它们不同了.题目上要求找出一个.所以放弃这种想法.图(2)顺时针旋转,且大、小两个矩形颜色互换一下就得到(5).而图(1)与(3)的变化规律也是这样:顺时针旋转,大小两部分颜色互换.因此(1)与(3)配对,(2)与(5)配对.解:与众不同的是题目图中的(4).12. 分析:我们分花盆、花茎、花叶、花朵四个部分逐步观察.(1)花盆:花盆的形状每一行都是由同样的三种形状组成,所以第三行所缺的形状便是应填的图案中的花盆形状;花盆的颜色在同一行中都是由黑、白、灰(画有斜线)三色组成,图中第三行已有白、灰二色,所以应填的花盆为黑色(如下图(1));(2)花茎:如同上面一样的分析.花茎的形状为鱼钩状,方向向右(如下图(2));(3)花叶:花叶数量为两朵,方向是向左、右平展(如下图(3));(4)花朵:形状为圆形(如下图(4)).(1) (2) (3) (4)解:依照所给图形的变化规律,空格中应填的图形如图(4).13. 图(1)和图(2)的底面号码都是3.把图(3)向左旋转,也把3做为底面,变为:将其它三面的号码按顺时针方向排起来,图(1)应为 图(2)应为图(3)应为 .由此可见图(1)和图(2)的顺序是一样的,图(3)和其它两个不同.14. 因为题目中只是问“马”所在的位置,所以我们只要考虑“马”的位置变化规律就可以了.“马”最开始在2号位置,我们记做②,那么变化规律为: ②④ ③ ① ② ……很容易看出,每交换一次位置,“马”就按顺时针方向转动一格,所以每交换四次,“马”就可以4 2 1 2 1 4回到原地.因为204=5正好整除,说明“马”正好转了5圈回到原地.所以交换二十次位置后,“马”仍在2号小格内.。
只需记住四张逻辑图,帮助你思考和说话,变得轻松自如(三维树)

只需记住四张逻辑图,帮助你思考和说话,变得轻松自如(三维树)很多的职场朋友,经常会遇到这样的情况:思考某个问题的时候,总是被问题中的各种内在关系,弄得晕头转向,越理越乱;或者阅读某本好书的时候,感觉内容很好,但不会梳理内在的结构,和别人分享的时候,说不清思想观点的所以然!正如一句俗语讲的“茶壶煮饺子--有料倒不出”。
怎么办呢?思考问题理不清晰内在的联系,有想法却没有表达的方式!这是因为缺乏经验使用逻辑这个工具,使你的思考没方法,表达时没有合适的输出通道。
就如农民在地里挖土一样,如果没有锄头等工具,在地里的红薯你也很难弄出来卖哈。
为此,很多人去阅读一些形式逻辑方面的书籍,但读着读着,感觉内容过于庞杂,看了几个月都难以消化。
其实,对于职场人士来讲,形式逻辑中很多的东西你不一定都用得上,学的太多估计对你的工作没有太大的帮助。
所以,你只需要搞清楚逻辑思维中“两关系和两结构”就够了,帮助你很好的思考和表达。
两关系和两结构是指:相互关系,因果关系,阶段图和过程图。
1,相互关系图:是指有多个主体之间的相互矛盾关系。
相互关系图,也称为关系图法,是指用连线图来表示事物想到关系的一种方法。
比如,你想搞清楚三国时期的纷争局面:曹操最强,刘备和孙权之间既竞争又合作,并且双方还是亲戚关系……。
你只需要一张相互关系图来表达,你思考起来就有顺序了。
2.因果关系图:是表达事物的原因与结果之间关系。
因果关系图是很复杂的,因为你需要将很多的事例列出来,进行有序的筛选之后,才能找出结果背后的原因。
如果我们简单来表达的话,就是事物由A点到B点,所发生的关系。
比如,为什么B小姐不愿意跟A先生约会呢?先画两个框,在B框上写结果:为什么B不喜欢A先生?再填写B框架,找出客观事实的原因。
经过这两步之后,你的思路的比较清晰了。
所以讲,思考问题没有头绪的时候,就用画这两张思考图试一试。
接下来,我们讨论常用于表达中的阶段图和过程图。
3.阶段图:是指将某个事物进行各阶段的划分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
“Never confuse being educated with being smart。”别把受到教育这件事和聪明这件事混为一个概念。
No.10 阅读能激发灵感
广泛的阅读,热情的阅读。创造力是一个必需的生存技能,而一些灵感就来自于你没有期待的来源。
No.11 诚实比什么都重要
“Be true to yourself. Be willing to learn and to be coachable.”诚实的对待自己,愿意学习,愿意被指导。
No.12 拥有感恩的心
“Give back—serve from a sense of gratitude.”回报用感恩的心,感恩身边的人和事。
No.13 坚持,坚持,再坚持
“Stick with it,and keep moving”坚持,坚持,再坚持。
水滴石穿,NO会变成另一个等待,学习和再次尝试的机会。
No.6 挑战自我
“Find a place where you can be challenged. Ask yourself: Am I proud of my work?”找到一个挑战自己 的事业。自省:“我是否为我的工作感到自豪”?
No.7 别害怕不确定性
13幅逻辑图,改变你的生活轨迹
杜克大学作为全球排名第7的大 学在全球教育中有着巨大的影响力, 今日借杜克大学的13幅逻辑图与您 一块探讨关于生活的哲学,这13幅 图将帮助您更清晰地了解自己的行为、 目标及思考问题的方式,让你选择正 确的方式去实现心中所想与所需。
No.1 什么是生活
“Payclose attention. This is your life.”请留意生活中的细节,这是你的生活。
别害怕偏离你的计划,勇敢的接受不确定性。那些在你感情,工作和生活上表现出不确定性和高风险的东西往往 都是很Cool而且很值得你尝试的。
No.8 回顾过去的经历
当你进入你人生的新阶段,别忘了停下来回头看看,去发现你过去经历的意义。它可以让你更好的了解你是谁, 将到哪里去,如何去那里。
No.9 受到教育不等于聪明
No.2 明天比今天更重要
人们总是过于在意那些重要的决定 (比如:接受什么样的工作或者职位) 但是实际上明天总是模糊的。
No.3 获得满足感
和你得到的实物相比,你可以从和别人建立的关系中获得更多的满足。
No.4 体现生命的价值
外面只有自己,没有别 不要轻易说“不”
