简谐运动的合成
合集下载
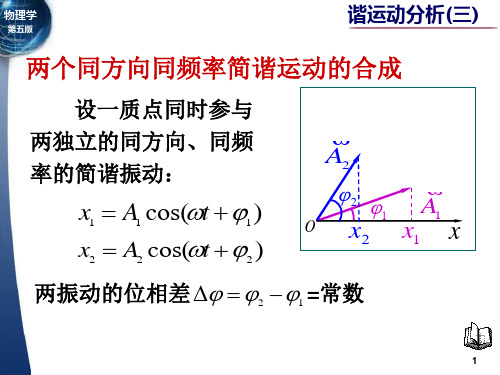
谐振动分析(三)两个同方向同频率简谐运动的合成
o
o
A1
A2
A
T
t
A A1 A2
x (A A )cos(t )
1
2
2 1 2k π
3
物理学
第五版
谐运动分析(三)
（2）相位差 (2k 1) π(k 0，1, )
2
1
x
x
A1
2 o
o
Tt
A
A2
A A1 A2
x (A2 A1)cos(t )
2
1
(2k
1)π
4
物理学
第五版
小结
（1）相位差
2
1
2k
π
A A1 A2
谐运动分析(三)
(k 0，1， ) 加强
（2）相位差
2
1
(2k 1) π
(k 0，1， )
A A A
1
2
减弱
（3）一般情况
A1 A2 A A1 A2
5
物理学
第五版
谐运动分析(三)
二 两个相互垂直的同频率的简谐
运动的合成 x A1 cos(t 1)
x 阻尼振动位移时间曲线
A
Ae t
Aet cost
O
T A
t
( 0)
21
物理学
第五版
三种阻尼的比较
谐运动分析(三)
(a)欠阻尼
2 0
2
(b)过阻尼
2 0
2
(c)临界阻尼
2 0
2
x
b
oc
t
a
22
物理学
第五版
谐运动分析(三)
例 有一单摆在空气（室温为 20C）中来 回摆动. 摆线长l 1.0 m，摆锤是半径r 5.0103 m 的铅球.求（1）摆动周期；（2）振幅减小 10％所需的时间；（3）能量减小10％所需 的时间；（4）从以上所得结果说明空气的 粘性对单摆周期、振幅和能量的影响.
简谐运动的合成
所以，拍频是振动 cos(
2
1 2 (
拍频（振幅变化的频率）
2 1
2 t)
的频率的两倍。
2 1
2
) 2 1
8.2
四
简谐运动的合成
第八章 机械振动
两个相互垂直的同频率简谐运动的合成 x A1 cos( t 1 )
y A 2 cos( t 2 )
( k 0 ， 1 ， 2, )
1）相位差 2 1 2 k π
x
o A
A2
x
o
T
1
t
x ( A1 A 2 ) cos( t )
A
A A1 A 2
2 1 2k π
8.2
简谐运动的合成
A
2 1 2 2
x n A n cos( t n )
A
1 A1
x x1 x 2 x n
x A cos( t )
2
A2
A3 3
o
x
多个同方
简谐运动的合成
第八章 机械振动
x 1 A 0 cos t x 2 A 0 cos( t )
2
T π
T
1
2 1
2 1
拍频（振幅变化的频率）
8.2
简谐运动的合成
第八章 机械振动
由于振幅是周期性变化的，所以合振动不再是 简谐振动。
当 与 都很大，且相差甚微时，可将 1 2 2 视为振幅部分，合成振动是以 为角频率的 ( 2 1 ) / 2 近似谐振动。 2 1 1 2
2
1 2 (
拍频（振幅变化的频率）
2 1
2 t)
的频率的两倍。
2 1
2
) 2 1
8.2
四
简谐运动的合成
第八章 机械振动
两个相互垂直的同频率简谐运动的合成 x A1 cos( t 1 )
y A 2 cos( t 2 )
( k 0 ， 1 ， 2, )
1）相位差 2 1 2 k π
x
o A
A2
x
o
T
1
t
x ( A1 A 2 ) cos( t )
A
A A1 A 2
2 1 2k π
8.2
简谐运动的合成
A
2 1 2 2
x n A n cos( t n )
A
1 A1
x x1 x 2 x n
x A cos( t )
2
A2
A3 3
o
x
多个同方
简谐运动的合成
第八章 机械振动
x 1 A 0 cos t x 2 A 0 cos( t )
2
T π
T
1
2 1
2 1
拍频（振幅变化的频率）
8.2
简谐运动的合成
第八章 机械振动
由于振幅是周期性变化的，所以合振动不再是 简谐振动。
当 与 都很大，且相差甚微时，可将 1 2 2 视为振幅部分，合成振动是以 为角频率的 ( 2 1 ) / 2 近似谐振动。 2 1 1 2
简谐运动的合成
x = ( 2 A1 cos 2 π
ν 2 −ν 1
2
t ) cos 2 π
ν 2 +ν1
2
t
振幅部分 振动频率 ν = (ν 1 + ν 2 ) 2 振幅 A = 2 A1 cos 2 π
合振动频率
ν 2 −ν 1
2
振 动
Amax = 2A1
t
Amin = 0
15
第九章
物理学
第五版
9-5
简谐运动的合成
y
ϕ （1） 2 −ϕ1 = 0或 2 π ） A2 y= x A1
A2
A1
o
x
ϕ （2） 2 − ϕ1 = π ） A2 y=− x A1
第九章 振 动
y
A2
A1
o
x
7
物理学
第五版
9-5
简谐运动的合成
x 2 y 2 2 xy 讨 + 2− cos(ϕ 2 − ϕ1 ) = sin 2 (ϕ 2 − ϕ1 ) 论 A12 A2 A1 A2
A
ϕ1
ϕ
A 1
O
x2
x1
xx
两个同方向同频率简谐运动合成后仍 两个同方向同频率简谐运动合成后仍 合成 频率的简谐 简谐运动 为同频率的简谐运动
第九章 振 动
2
物理学
第五版
9-5
简谐运动的合成
（1）相位差 ∆ϕ = ϕ 2 − ϕ1 = 2k π (k = 0，1，2,⋯ ） ± ± )
x
ϕ
A2
x
o
y = A2 cos(ωt + ϕ 2 )
椭圆方程） 质点运动轨迹 （椭圆方程）
x 2 y 2 2 xy + 2− cos(ϕ 2 − ϕ1 ) = sin 2 (ϕ 2 − ϕ1 ) 2 A1 A2 A1 A2
ν 2 −ν 1
2
t ) cos 2 π
ν 2 +ν1
2
t
振幅部分 振动频率 ν = (ν 1 + ν 2 ) 2 振幅 A = 2 A1 cos 2 π
合振动频率
ν 2 −ν 1
2
振 动
Amax = 2A1
t
Amin = 0
15
第九章
物理学
第五版
9-5
简谐运动的合成
y
ϕ （1） 2 −ϕ1 = 0或 2 π ） A2 y= x A1
A2
A1
o
x
ϕ （2） 2 − ϕ1 = π ） A2 y=− x A1
第九章 振 动
y
A2
A1
o
x
7
物理学
第五版
9-5
简谐运动的合成
x 2 y 2 2 xy 讨 + 2− cos(ϕ 2 − ϕ1 ) = sin 2 (ϕ 2 − ϕ1 ) 论 A12 A2 A1 A2
A
ϕ1
ϕ
A 1
O
x2
x1
xx
两个同方向同频率简谐运动合成后仍 两个同方向同频率简谐运动合成后仍 合成 频率的简谐 简谐运动 为同频率的简谐运动
第九章 振 动
2
物理学
第五版
9-5
简谐运动的合成
（1）相位差 ∆ϕ = ϕ 2 − ϕ1 = 2k π (k = 0，1，2,⋯ ） ± ± )
x
ϕ
A2
x
o
y = A2 cos(ωt + ϕ 2 )
椭圆方程） 质点运动轨迹 （椭圆方程）
x 2 y 2 2 xy + 2− cos(ϕ 2 − ϕ1 ) = sin 2 (ϕ 2 − ϕ1 ) 2 A1 A2 A1 A2
Ch6-2 简谐运动的合成
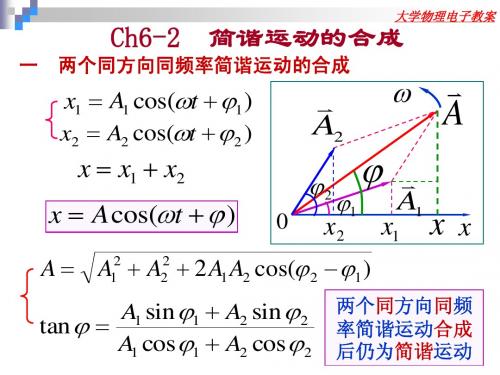
A = A + A + 2 A1 A2 cos(ϕ 2 − ϕ1 )
A1 sin ϕ 1 + A2 sin ϕ 2 tan ϕ = A1 cos ϕ 1 + A2 cos ϕ 2
两个同方向同 两个同方向同频 率简谐运动合成 率简谐运动合成 后仍为简谐 简谐运动 后仍为简谐运动
大学物理电子教案
A = A + A + 2 A1 A2 cos(ϕ 2 − ϕ1 ) ± ± 1）相位差 ∆ϕ = ϕ 2 − ϕ1 = 2k π (k = 0 ， 1， 2,L)
大学物理电子教案
x1 = A1 cos ω1t = A1 cos 2π ν 1t x2 = A2 cos ω 2t = A2 cos 2π ν 2t
讨论
x = x1 + x2
A1 = A2 , ν 2 − ν 1 << ν 1 + ν 2 的情况
方法一
x = x1 + x 2 = A1 cos 2π ν 1t + A2 cos 2π ν 2 t
π y = A2 cos(ωt + ) 2
A2 y
x = A1 cos ωt
o
A1
x
大学物理电子教案
用 旋 转 矢 量 描 绘 振 动 合 成 图
大学物理电子教案
两 相 互 垂 直 同 频 率 不 同 相 位 差
简 谐 运 动 的 合 成 图
大学物理电子教案
五
两相互垂直不同频率的简谐运动的合成 李 萨 如 图
讨论
2 1 2 2
x
o ϕ A
x
o
T
A = A1 + A2 x = ( A1 + A2 ) cos( ω t + ϕ ) ϕ = ϕ 2 = ϕ1 + 2 k π
简谐运动的合成和分解
2 A2 A12 A2 2 A1 A2 cos 2 1 2 2
A A 2 A1 A2 cos 2 1
2 1 2 2
A2
A1
A
A A A 2 A1 A2 cos y A1 sin 1 A2 sin 2 tan x A1 cos 1 A2 cos 2
π π 2 1 1 2 2 π π A2 cos 2 0 2 2
2
t
A2
2
2 1 π A A2 A1
A
x
2 π π (2) 由矢量图: 2 T 2π π x A2 A1 cos( t ) T 2
2
F0 k , 2 , f 0 m m m
驱动力
d x dx 2 2 0 x f 0 cos t 2 dt dt
方程的解：
2
x A0 e
t
2 2 cos 0 t 0 A cost
在阻尼较小时，其通解为对应齐次方程的通解加上一个特解，
2 1 t ) 随时间缓慢变化 振幅 2 A cos( 2
2 1 t ) 快速变化 谐振因子 cos( 2
第一项缓慢变化，第二项快速变化：“拍(beat)” 调制
拍现象的应用： 用音叉振动校准乐器 测定无线电频率 测定超声波 调制高频振荡的振幅和频率
3. 相互垂直的简谐运动的合成 x方向的谐振动 x A1 cos( t 1 )
A1
例12: 两个同方向、同频率的简谐运动,其合振动的 振幅为20cm,与第一个振动的相位差为 1 π 6 .若第 一个振动的振幅为 10 3 cm .则(1)第二个振动的振幅为多 少？(2) 两简谐运动的相位差为多少？ 解： A2 A2 A12 2 AA1 cos π 6
8-5简谐运动的合成
(1)相位差 2k π (k 0，1，)
A A1 A2
相互加强
(2)相位差 (2k 1) π (k 0，1，)
A A1 A2
(3)一般情况
相互削弱
A1 A2 A A1 A2
第八章 机械振5 动
8-5 简谐运动的合成
思考
例 图中所画的是两个简谐振动的振动曲线. 若这 两个简谐振动可叠加，则合成的余弦振动的初相为
arctan11rad
第八章 机械振8 动
O A1
O
A2
A
T t
A A1 A2
2 1 2kπ
x ( A1 A2 ) cos(t )
第八章 机械振3 动
8-5 简谐运动的合成
A A12 A22 2A1A2 cos(2 1)
(2)相位差 2 1 (2k 1)π (k 0，1, )
tan A1 sin 1 A2 sin 2 A1 cos1 A2 cos2
第八章 机械振2 动
8-5 简谐运动的合成
讨论 A A12 A22 2A1A2 cos(2 1) (1)相位差 2 1 2kπ (k 0，1， 2,)
xx
8-5 简谐运动的合成
两个同方向同频率简 当 t 0时
谐运动的合成
x1 A1 cos(t 1) x2 A2 cos(t 2 )
x x1 x2
A2
2 1
O x20
A1
x10
A x Acos(t )
两个同方向、同频率 简谐运动的合振动仍是简 谐运动，其频率与分振动
（A）3π / 2
大学物理(9.3.2)--简谐运动的合成
A2
2
o
1 A1
x
多个同方向同频率简谐运动合成仍为简谐
运动
东北大学 理学院 物理系
大学物理 第九单元 振动
第三讲 简谐运动的合成
* 四、两个同方向不同频率简谐运动的合成
x1
拍
t
x2 t
x t
拍 合振动振幅 随时间周期性加强与减弱的现
两 个 频 率 较 大 且 相 差 极 小 的象同 方 向 谐 振 动 合 成 形 成
东北大学 理学院 物理系
大学物理 第九单元 振动
第三讲 简谐运动的合成
3. 两种特殊情况
A
A2 1
A2 2
2 A1 A2
cos( 2
1 )
(1) 若两分振动同相
2 1=2k
(k=0,1,2,…)
则 A=A1+A2 , 两分振动相互加强
(2) 若两分振动反相
2 1=(2k+1)
第三讲 简谐运动的合成
* 三、多个同方向同频率简谐运动的合成
x1 A1 cos(t 1 ) x2 A2 cos(t 2 )
xn An cos(t n )
x x1 x2 xn
x A cos(t )
A
A3
3
A1 sin1 A2 sin2 Asin
A A12 A22 2 A1A2 cos(2 1)
tan
A1 sin1 A1 cos1
A2 A2
sin 2 cos2
x Acos cost Asin sint Acos( t )
相互垂直简谐运动合成
A1A 2
2
1
2 2 1
2 1 4
斜椭圆方程
x2 A2
1
y2 m A22
xy 2
AA 12
1 2
2 1 4
2
1
74
4
顺时针 逆时针
相互垂直的简谐运动的合成
2
1
3
4
x2 y2 A12 A22
2 xy 1 斜椭圆方程 A1A 2 2
2 1 3 4
顺时针
2
1
5434
逆时针
一般情况21====任意值任意值任意值任
意值,,都为椭圆方程都为椭圆方程都为椭 圆方程都为椭圆 方程..
相互垂直的简谐运动的合成
二、两个不同频率相互垂直简谐运动的合成 李萨如图形（Lissajou figure）
一般情况下, 合振动的轨迹是不稳定的. 当两个分振动 的频率成简单整数比时, 将形成稳定闭合曲线.
相互垂直的简谐运动的合成
不同频率相互垂直的简谐运动的合成
x A1 cost1 1 y A2 cost2 2
任意时刻 t::由坐标由坐标(x，y)确定质点的
位 置.确定质点的位置确定质点的位置确
定质点Ax22的 1
Ay位222 置 )y，A2，1xA，yx(由2 c坐os标由2 坐1标消si去n 2
t得2 (1
推导从略)
——轨迹方程（椭圆方程）
相互垂直的简谐运动的合成
大学物理
振动学基础
第8讲 相互垂直的简谐运动的合成
相互垂直的简谐运动的合成
相互垂直的简谐运动的合成
激光李萨如图形演示 两个相互垂直简谐运动的合运动仍是简谐运动吗?
相互垂直的简谐运动的合成
5-4一维简谐运动的合成
A(t) = 2Acos
ω2 −ω1
2 ω2 −ω1 t +π = 2Acos 2
(t +T)
比较
11
5-4 一维简谐运动的合成
第五章 机械振动
A(t) = 2Acos
ω2 −ω1
2 比较 ω2 −ω t +π 1 = 2Acos 2 ω2 −ω1 ω2 −ω1 1 T =π 或 =π 2 2 ν
快速在振动。 质点则按ω1快速在振动。
10
5-4 一维简谐运动的合成
第五章 机械振动
ω2 −ω1 tcos(ω t +ϕ) x = 2Acos 1 2 ω −ω 振幅 A(t) = 2Acos t 2
2 1
2.合振幅变化频率 拍频”。 合振幅变化频率—“拍频” 合振幅变化频率 拍频 由于余弦函数绝对值的周期为π。
1
5-4 一维简谐运动的合成
第五章 机械振动
一 两个同方向同频率简谐运动的合成 质点同时参与两个振动。 质点同时参与两个振动。两 个振动频率相同， 个振动频率相同，振动方向在同一 直线上。 直线上。 质点的振动是这两个振动的合成。 质点的振动是这两个振动的合成。 设两个分振动方程分别为： 设两个分振动方程分别为：
第五章 机械振动
ω2 −ω1 tcos(ω t +ϕ) x = 2Acos 1 2 ω −ω 振幅 A(t) = 2Acos t 2
2 1
1.振幅是周期变化的， 振幅是周期变化的， 振幅是周期变化的
ω1 ≈ ω2,
ω1 −ω2
2
很小， 很小，振幅 A（t）随时间 t 缓慢地变 （） 现象， 化—“拍”现象，最大值为 2A。 “ 。
高二物理竞赛两个同方向同频率简谐运动的合成PPT(课件)
x1 5 cos(20 t 2) cm
x2 5 cos(20 t ) cm
由旋转矢量法
4 -5 振动合成
A2 4
AOx
A A12 A22 5 2 cm
A1
5
4
x 5 2 cos (20 t 5 ) cm
4
11
物理学
第五版
4 -5 振动合成
两个简谐运动方向相同，频率相同，振
3
x A co t s ( ) n n 当木块位于平衡位置下方时，x>0
一 两个同方向同频率简谐运动的合成
n
A 例2 已知两谐振动的曲线(如图),它们是同频率的谐振动,求它们的合振动方程。
1、图示，木块上放置一质量为 m 的砝码，木块沿竖直方向作简谐运动，问砝码脱离木块的可能位置将发生在
2
x x x x 1 2 （b）在平衡位置上方（向上运动）（向下运动）
两振动步调反0 向,
1
12
2
（2）若另有一简谐运动
xAco t s() 多个同方向同频率简谐运动合成仍为简谐运动
例3、两个同方向、同频率简谐运动方程分别为
当 一
N两≥个0同时方，向砝同码2 频不率脱简离谐木运块动2 的合成
2
合位移 xx1x2
（SI）求：合成谐振动方程
（b）在平衡位置上方（向上运动）（向下运动）
0.4 （4）推广到 多个同方向同频率简谐运动的合成
（2）若另有一简谐运动
则合振幅为
则合振幅为
6
A2
x
0.12 x 0 .5 co 3 t s0 .1 ( 2 )
3
14
物理学
x 第五版 1
0.4cos3t()
3
x2 5 cos(20 t ) cm
由旋转矢量法
4 -5 振动合成
A2 4
AOx
A A12 A22 5 2 cm
A1
5
4
x 5 2 cos (20 t 5 ) cm
4
11
物理学
第五版
4 -5 振动合成
两个简谐运动方向相同，频率相同，振
3
x A co t s ( ) n n 当木块位于平衡位置下方时，x>0
一 两个同方向同频率简谐运动的合成
n
A 例2 已知两谐振动的曲线(如图),它们是同频率的谐振动,求它们的合振动方程。
1、图示，木块上放置一质量为 m 的砝码，木块沿竖直方向作简谐运动，问砝码脱离木块的可能位置将发生在
2
x x x x 1 2 （b）在平衡位置上方（向上运动）（向下运动）
两振动步调反0 向,
1
12
2
（2）若另有一简谐运动
xAco t s() 多个同方向同频率简谐运动合成仍为简谐运动
例3、两个同方向、同频率简谐运动方程分别为
当 一
N两≥个0同时方，向砝同码2 频不率脱简离谐木运块动2 的合成
2
合位移 xx1x2
（SI）求：合成谐振动方程
（b）在平衡位置上方（向上运动）（向下运动）
0.4 （4）推广到 多个同方向同频率简谐运动的合成
（2）若另有一简谐运动
则合振幅为
则合振幅为
6
A2
x
0.12 x 0 .5 co 3 t s0 .1 ( 2 )
3
14
物理学
x 第五版 1
0.4cos3t()
3
5-3 、 5-4 简谐振动的合成
ϕ
A2
x
O C A1
N −1 ∆ϕ ϕ = 合振动表达式 2 x ( t ) = A cos( ω t + ϕ ) sin(N∆ϕ / 2) N −1 = A0 cos(ω t + ∆ϕ ) sin(∆ϕ / 2) 2
讨论1： 讨论 ： 当 δ
= ±2kπ k = 0,1,2,L sin(N∆ϕ / 2) A = lim A0 = NA0 sin(∆ϕ / 2)
四、两个相互垂直的同频率简谐振动的合成
某质点同时参与两个同频率的互相垂直方向的简谐运动
x = A1 cos(ω t + ϕ 1 ) y = A2 cos(ω t + ϕ 2 )
合振动的轨迹方程为
x y 2 xy 2 cos(ϕ 2 − ϕ 1 ) = sin (ϕ 2 − ϕ 1 ) + 2− 2 A1 A2 A1 A2
'
各分振动矢量依次相接， 各分振动矢量依次相接，构 成闭合的正多边形， 成闭合的正多边形，合振动 的振幅为零。 的振幅为零。
三、同方向不同频率的简谐振动的合成
某质点同时参与两个不同频率且在同一条直线上的简谐振动
x1 = A1 cos(ω 1 t + ϕ 1 )
x 2 = A2 cos(ω 2 t + ϕ 2 )
A2 y=− x A1
y
x2 y2 2 xy + 2+ =0 2 A1 A2 A1 A2
x
合振动的轨迹是一条通过原点的直线
讨论3 讨论
∆ϕ = ϕ 2 − ϕ 1 = π / 2 x2 y2 合振动的轨迹是的椭圆 合振动的轨迹是的椭圆 + 2 =1 2 A1 A2 方程， 方程，且顺时针旋转
8.5 简谐运动的合成
ν 2 ν 1
2
t ) cos( 2 π
ν 2 +ν 1
2
t +)
振幅部分 振动频率 振幅
合振动频率
ν = (ν 1 + ν 2 ) 2
A = 2 A1 cos 2π
ν 2 ν 1
2
t
Amax = 2A1
Amin = 0
振幅是随时间变化的， 振幅是随时间变化的，由于振幅的改变也是周期 性的，因此就出现振动忽强忽弱的现象。 性的，因此就出现振动忽强忽弱的现象。
y A2
A2 y= x A1
o
A1
x
x 2 y 2 2 xy + 2 cos( 2 1 ) = sin 2 ( 2 1 ) 2 A1 A2 A1 A2
2） 2 1 = π
3） 2 1 = ± π 2
2 2
A2 y= x A1
o
y
A2
x y + 2 =1 2 A1 A2
π y = A2 cos(ωt + ) 2
合成振动为： 合成振动为： x = x1 + x2 = A1 cos(ω1t + ) + A2 cos(ω 2 t + ) 利用三角函数公式可得
x = 2 A cos(
ω2 ω1
2
t ) cos(
ω2 + ω1
2
t +)
= 2 A cos( 2 π
ν 2 ν 1
2
t ) cos( 2 π
ν 2 +ν 1
两个同方向不同频率简谐运动的合成
频率相近的两个同方向简谐振动的合振动是振幅随 频率相近的两个同方向简谐振动的合振动是振幅随 相近的两个同方向简谐振动的合振动是 时间周期性变化的特殊简谐振动 称为拍振动 的特殊简谐振动， 拍振动。 时间周期性变化的特殊简谐振动，称为拍振动。 单位时间内振动加强或减弱的周期数叫拍频。 单位时间内振动加强或减弱的周期数叫拍频。 拍频 由
大学物理简谐运动的合成
大学物理简谐运动的合 成
目录
• 简谐运动的定义与特性 • 简谐运动的合成原理 • 简谐运动的合成方法 • 简谐运动的合成应用 • 总结与展望
简谐运动的定义与特
01
性
简谐运动的定义
简谐运动
物体在平衡位置附近做往复运动，其位移、速度和加速度随时间按正弦或余弦 规律变化的运动。
简谐运动的数学描述
简谐运动可以用正弦或余弦函数表示，其数学表达式为 $x = Asin(omega t + varphi)$，其中 $A$ 是振幅，$omega$ 是角频率，$varphi$ 是初相。
简谐运动的特性
周期性
简谐运动具有周期性，即物体在每个周期内重复 相同的运动轨迹。
往复性
简谐运动是往复运动，即物体在平衡位置附近来 回振动。
能量守恒
简谐运动过程中，系统的动能和势能相互转化， 总能量保持不变。
简谐运动的分类
自由振动
不受外力作用的简谐运动。
受迫振动
受到周期性外力作用的振动，其振动频率与外力频率 相同或相近。
简谐运动的合成方法
03
旋转矢量法
总结词
旋转矢量法是一种直观且易于理解的方法，用于合成简谐运动。
详细描述
旋转矢量法是通过引入一个旋转矢量来表示简谐运动，该矢量在复平面内以角速 度旋转。通过旋转矢量的长度和角度变化，可以直观地理解简谐运动的合成过程 。
复数法
总结词
复数法是一种基于复数运算的方法，用于合成简谐运动。
自激振动
由系统内部激励产生的振动，不需要外部激励作用。
02
简谐运动的合成原理
线性合成原理
线性合成原理是指两个简谐运动的合成结果仍为简谐运动，其振幅和角频率分别为两个简谐运动振幅 和角频率的线性组合。
目录
• 简谐运动的定义与特性 • 简谐运动的合成原理 • 简谐运动的合成方法 • 简谐运动的合成应用 • 总结与展望
简谐运动的定义与特
01
性
简谐运动的定义
简谐运动
物体在平衡位置附近做往复运动，其位移、速度和加速度随时间按正弦或余弦 规律变化的运动。
简谐运动的数学描述
简谐运动可以用正弦或余弦函数表示，其数学表达式为 $x = Asin(omega t + varphi)$，其中 $A$ 是振幅，$omega$ 是角频率，$varphi$ 是初相。
简谐运动的特性
周期性
简谐运动具有周期性，即物体在每个周期内重复 相同的运动轨迹。
往复性
简谐运动是往复运动，即物体在平衡位置附近来 回振动。
能量守恒
简谐运动过程中，系统的动能和势能相互转化， 总能量保持不变。
简谐运动的分类
自由振动
不受外力作用的简谐运动。
受迫振动
受到周期性外力作用的振动，其振动频率与外力频率 相同或相近。
简谐运动的合成方法
03
旋转矢量法
总结词
旋转矢量法是一种直观且易于理解的方法，用于合成简谐运动。
详细描述
旋转矢量法是通过引入一个旋转矢量来表示简谐运动，该矢量在复平面内以角速 度旋转。通过旋转矢量的长度和角度变化，可以直观地理解简谐运动的合成过程 。
复数法
总结词
复数法是一种基于复数运算的方法，用于合成简谐运动。
自激振动
由系统内部激励产生的振动，不需要外部激励作用。
02
简谐运动的合成原理
线性合成原理
线性合成原理是指两个简谐运动的合成结果仍为简谐运动，其振幅和角频率分别为两个简谐运动振幅 和角频率的线性组合。
简谐运动的合成与分解
m
(
2 0
2
)2
4
2
2
共振
A
（1）位移共振（图1）
在一定条件下，振幅出现极大值，振动 剧烈的现象。
共振
2 0
2
2
（2）速度共振（图2）
0
一定条件下，速度幅A极大的现象。
vm
共振 0
即速度共振时，速度与策动力同相，一周期内策动力
总作正功，此时向系统输入的能量最大。
0
总结：
两个同方向频率相同的简谐振动的合成仍为简谐振动。 合振幅与两振动的相位差有关，可用旋转矢量图求得。
如果两振动的频率相差较大但有简单的整数比五谐振分析和频谱在自然界和工程技术中我们所遇到的振动大多不是简谐振动而是复杂的振动处理这类问题往往把复杂振动看成由一系列不同频率的间谐振动组合而成也就是把复杂振动分解为一系列不同频率的间谐振动这样分解在数学上的依据是傅立叶
本讲主要内容： 一、同方向同频率两个简谐振动的合成 二、同方向不同频率两个简谐振动的合成 三、两个互相垂直同频率简谐振动的合成 四、两个互相垂直不同频率简谐振动的合成 五、谐振分析和频谱
A1 sin10 A2 sin20 A1 cos10 A2 cos20
2010
x20
0
x10
AM
A1
x0
t o .P x
同方向同频率两个简谐振动的合成仍为简谐振动。
讨论两个特例 x
(1)两个振动同相
20 10 2k , k 0,1,2,...
合成振动
由 A A12 A22 2A1 A2 cos(20 10 ) o
解：
A A1 A2
A2
A1 A2 A
O
2
物理-相互垂直的简谐运动的合成
y A2 x A1
质点离开 平衡位置 的位移
r(t) A12 A22 cos(t 1 )
y
A2
o A1 x
合振动是与分振动同频率的简谐振动
一、两个相互垂直的谐振动的合成
x A1
2
y A2
2
2xy cos(2 A1 A2
1 )
s in2 ( 2
1 )
(3)
若
2
1
2
x2 A12
y2 A22
合运动的 轨道方程
( x )2 ( y )2 2xycos sin2
A1
A2
A1 A2
其中： (2 1 )t (2 1 ) ——随时间变化
一般情况下，合运动的轨迹是不稳定的。
一、两个相互垂直的谐振动的合成
分振动： x A1 cos(ω1t φ1 ) y A2 cos(ω2t φ2 )
二、振动频谱分析
数学上已经证明：
任意周期函数（周期为T）：x(ωt) 其中 ω 2π /T
均可展开为三角级数
基频
x(ωt ) a0 (ak cos kωt bk sin kωt )
k 1
k次谐频
1 T/2
a0 T
f (ωt )dt
T / 2
2
ak T
T /2
f (ωt)cos kωtdt (k 0)
x A1
2
y A2
2
2xy cos(2
A1 A2
1 )
s in2 ( 2
1 )
合运动一般是在 x A1, y A2 范围内的一个椭圆。
一、两个相互垂直的谐振动的合成
2
2
x A1
y A2
16-2简谐运动的合成
ϕ
v a2
a4 v a3 α
Q
α
2
α
x
Nα sin 2 ∴A= a α sin 2
16 – 2
简谐运动的合成
v M
1 1 Q∠ M = (π − Nα)， CO = (π −α) CO ∠ P 2 2
v a5
α
N −1 ∴ = ∠ P −∠ M = ϕ α CO CO 2
C
α
N α v α
所以合振动为
2π 2π ω= = = π s -1 T 2 -π ϕ= 2 )m
由旋转矢量图可知合振动的振幅及初相分别为
A = A2 − A1 = 0.08 − 0.04 = 0.04 m） （
所以合振动为
x = 0 . 04 cos( πt −
π 2
16 – 2 简谐运动的合成 二、N 二、N 个同方向同频率简谐运动的合成
简谐运动的合成
3．分振动方程分别为 x1 = 3 cos(50πt + 0.25π ) ． ) 制 和 x 2 = 4 cos(50πt + 0.75π （SI制） 则它们的合振动表达式为： 则它们的合振动表达式为： （ ） （A）x = 2 cos(50πt + 0.25π ) ） （B） x = 5 cos(50πt ) ） （C） = 5 cos(50πt + ） x （D） x ）
v A 2
ϕ2
0
ω
v A
xx
x = x1 + x2 x = A cos( ω t + ϕ )
2 1 2 2
ϕ1 x2 x1
ϕ
v A 1
A = A + A + 2 A1 A2 cos(ϕ 2 − ϕ1 ) A1 sin ϕ 1 + A2 sin ϕ 2 tan ϕ = A1 cos ϕ 1 + A2 cos ϕ 2
简谐运动的合成
(2)若另有一振动x3 0.07cos10t 0 ，问0为何值时，
x1 x3的振幅为最大；问0为何值时，x2 x3的振幅为最小。
解：根据题意，画出旋转矢量图
A A12 A22
0.052 0.062
A1
0.078(m)
0 10 0
0 =10
3 4
时，x1
x3的振幅最大
A
A2
tan
A1 sin 1 A1 cos1
A2 A2
sin 2 cos2
讨论 A A12 A22 2 A1A2 cos(2 1)
0，1， 2,)
合振幅最大
A A1 A2
xx
oo
A1 A2
t
A
A A12 A22 2 A1 A2 cos(2 1)
2、两个分振动的相位反相：
相位差 2 1 (2k 1)π (k 0，1,)
合振幅最小 A A1 A2
x
x
A1
2
o
o
t
A
A2
例题 有两个同方向、同频率的简谐振动，它们 的振动表式（SI制）为：
x1
0.05
cos
10t
3 4
x2
0.06 cos 10t
1 4
(1)求它们合成振动的振幅。
简谐运动的合成
一、同方向、同频率两个简谐运动的合成
x1 A1 cos( t 1 )
A2
Q
A
x2 A2 cos( t 2 )
用旋转矢量法求合运动
2 1
P A1
O x2
x1 x
X
合振动位移为： x x1 x2 两个同方向同频率简谐运
x A cos( t ) 动合成后仍为简谐运动
大学物理(工科) 4—1 简谐运动、旋转矢量简谐运动的合成
2
tan1( v0 ) 注意: 确定 的象限 x0
二、简谐运动的描述
x Acos(t )
1.解析法(由振动表达式)
A, T, , x, v, a
2.曲线法(由振动曲线)
x
x Acos(t )
A
►确定振幅A；
o
►确定周期T，ω；
►确定φ
-A
T
t
•根据图像判断速度的正负用斜率 •利用初始条件确定几个φ，再利用速度正负判断保留φ
3、掌握描述简谐波的各物理量及各量间的关系；
4、理解机械波产生的条件. 掌握由已知质点的简谐 运动方程得出平面简谐波的波函数的方法. 理解波函 数的物理意义. 了解波的能量传播特征及能流、能流密 度概念.
匀速直线运动
直线运动
匀变速直线运动
学
变速直线运动
过 的
变加速直线运动
运
动 形
平抛运动
式
抛体运动
例4.2: 已知一简谐振动的曲线如图所示，写出振动方程。
x （cm）5
6
2
3
p
O 1
t（s）
解: 已知振动方程表达式为：x Acos(t )，v Asin(t )
► 定振幅: A=0.06m
►定初相
x0 0.06cos 0.03
cos 0.5
利用斜率判断0时刻速度方向 0 0
晶格点阵
§4—1 简谐运动、旋转矢量、简谐运动的能量
一、简谐运动动力学 1.模型
2.定义 ►受力：F=-kx
►动力学微分方程：
d2 dt
x
2
2
x
0
令 2 k
m
►运动方程： x(t)=Acos( t + )
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
x
A A12 A22 2 A1 A2 cos( 2 1 )
A1 sin 1 A2 sin 2 tan A1 cos1 A2 cos 2
11
x
A1
x
反相
2
o
o
T
减弱
t
A
A2
A A1 A2
2 2
x ( A2 A1 ) cos( t )
A A1 A2 2 A1 A2 cos( 2 1 )
7
*三
多个同方向同频率简谐运动的合成
x1 A1 cos( t 1 )
x2 A2 cos( t 2 )
A2
2
x1 A1 cos( t 1 )
x2 A2 cos( t 2 )
0
x2
x
1
x1
A1
x
合振动：x x1 x2
o
？
t
3
x1 A1 cos( t 1 ) x2 A2 cos( t 2 )
2
x x1 x2
x A cos( t )
A4 A3 A5 A2 O A6 A x 1
10
小结：
x1 A1 cos( t 1 )
x2 A2 cos( t 2 )
2
A2
1
A
x x1 x2
x A cos( t )
0
A1
xn An cos( t n )
A3 A
1 A1
x x1 x2 xn
x A cos(t )
2
A2
3
o
x
多个同方向同频率简谐运动合成仍为 简谐运动 矢量合成2
8
x1 A0 cost x2 A0 cos( t ) x3 A0 cos( t 2 )
xN A0 cos[ t ( N 1) ]
O
合振动
A
An
M
a1
A2
P
x
x Acos(t )
9
x1 A0 cost x2 A0 cos( t ) x3 A0 cos( t 2 )
xN A0 cos[ t ( N 1) ]
矢量合成1
4
x A cos( t )
A A1 A2 2 A1 A2 cos( 2 1 )
2 2
A1 sin 1 A2 sin 2 tan A1 cos1 A2 cos 2
O
A2
A
1
2
A2
2
A2
A1
x
5
（1）相位差 2 1 2k π (k 0 ， 1， 2,)
9-5
示波器
简谐运动的合成
E
E
1
同振动方向的合成
e
E1 (1 )
E2 (2 )
e
x
x2 x 合振动 同振动方向、同频率的合成 1 2
x1
振动方向垂直的合成
x
E2 ( E1 )
eHale Waihona Puke E1yx y 合振动
2
一 两个同方向、同频率简谐振动的合成
设一质点同时参与 两独立的同方向、同频 率的简谐振动：
(1) 2kπ A NA0 (k 0,1,2,) 最强
(2) N 2k ' π
(k ' kN, k ' 1,2,)
2π k ' N
o A1 A2 A3 A4 A5 x
A
A Ai NA0
i
A0
2 平分：
两个同方向同频率 简谐运动合成后仍为同 频率的简谐运动
A A1 A2 2 A1 A2 cos( 2 1 )
2 2
A2
A
0
x2
1
x1
（ 2 1） A1
x
c 2 a 2 b 2 2ab cos
A2 A12 A22 2 A1 A2 cos[ (2 1 )]
x x
同相
o A
A2
o
加强
1
t
A
A A1 A2
2 2
x ( A1 A2 ) cos( t )
矢量合成1
6
A A1 A2 2 A1 A2 cos( 2 1 )
（2）相位差 2 1 (2k 1) π (k 0 ， 1, )