平行四边形的面积 练习题
平行四边形的面积_《平行四边形的面积》典型例题
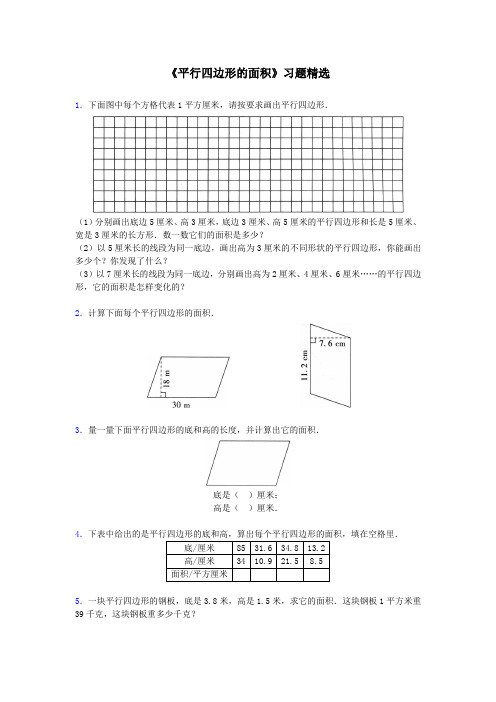
《平行四边形的面积》习题精选1.下面图中每个方格代表1平方厘米,请按要求画出平行四边形.(1)分别画出底边5厘米、高3厘米,底边3厘米、高5厘米的平行四边形和长是5厘米、宽是3厘米的长方形.数一数它们的面积是多少?(2)以5厘米长的线段为同一底边,画出高为3厘米的不同形状的平行四边形,你能画出多少个?你发现了什么?(3)以7厘米长的线段为同一底边,分别画出高为2厘米、4厘米、6厘米……的平行四边形,它的面积是怎样变化的?2.计算下面每个平行四边形的面积.3.量一量下面平行四边形的底和高的长度,并计算出它的面积.底是()厘米;高是()厘米.4.底/厘米85 31.6 34.8 13.2高/厘米34 10.9 21.5 8.5面积/平方厘米5.一块平行四边形的钢板,底是3.8米,高是1.5米,求它的面积.这块钢板1平方米重39千克,这块钢板重多少千克?6.一块平行四边形菜地,底是18.4米,高是9.2米.在这块地种茄子,每棵苗占地0.18平方米,这块地可种茄子多少棵?(得数保留整数)7.一块六边形水泥砖(如图),由三个面积相同的平行四边形组成.要铺300平方米地面大约需要多少块这样的水泥砖?参考答案1.(1)15平方厘米 15平方厘米 15平方厘米(2)无数个它们面积都相等(3)14平方厘米 28平方厘米 42平方厘米2.540m2 85.12cm23.略4.2890 344.44 748.2 112.25.5.7平方米 222.3千克6.169.28 ≈940棵7.≈2858块《平行四边形的面积》习题精选一、填空.1.4.5平方米=()平方分米 2400平方厘米=()平方分米2.一个平行四边形的底是9分米,高是底的2倍,它的面积是()平方分米.3.一个平行四边形的底是12厘米,面积是156平方厘米,高是()厘米.4.一块平行四边形钢板,底是1.5米,高是1.2米,如果每平方米钢板重23.5千克,这块钢板重()千克.二、判断题.1.平行四边形的面积等于长方形面积.()2.一个平行四边形的底是5分米,高是20厘米,面积是100平方分米.()3.一个平行四边形面积是42平方米,高是6米,底是7米.()三、选择题.1.下面的长方形和平行四边形面积()a.相等b.不相等2.用木条钉成的长方形拉成一个平行四边形,它的高和面积()a.都比原来大b.都比原来小c.都与原来相等3.平行四边形的底扩大3倍,高缩小3倍,面积()a.扩大3倍b.缩小3倍c.不变d.不好判断四、评议.下面是四个平行四边形,小红认为它们的面积都是6平方厘米,你认为对吗?(单位:厘米)23323232五、已知下图中正方形的周长为36厘米,求平行四边形的面积.参考答案一、填空1.450 24 2.162 3.13 4.42.3二、判断题.1.(×) 2.(×) 3.(√)三、选择题.1.a 2.b 3.c四、评议.2332(√)(×)3232(√)(×)五、已知下图中正方形的周长为36厘米,求平行四边形的面积.36÷4=9(厘米) 9×9=81(平方厘米)《平行四边形的面积》典型例题例.求下面平行四边形的面积.分析:图中给出的两个已知条件并不是一组相对应的底和高,要根据平行四边形“对边相等”的特性可以得出和高(6厘米)相对应的底也是4厘米,利用平行四边形的面积公式可以求出它的面积.解:2464=⨯(平方厘米)答:这个平行四边形的面积是24平方厘米.《平行四边形的面积》典型例题例.在两条平行线间画出两个平行四边形(如下图),试判断甲和乙谁的面积大?乙甲CB EFDA分析:平行四边形ABCD 和BCEF 是画在两条平行线之间,那么这两个平行四边形的高相等,因为两条平行线间的距离处处相等.这两个平行四边形都是以BC 为底,所以说这两个平行四边形的底也相等的.4厘米6厘米底和高都分别相等,那么底和高的乘积(面积)也相等,从两个面积相等的平行四边形中减去同样的一个三角形,剩下的面积也相等,所以甲和乙的面积是一样大的.解答:一样大.《平行四边形的面积》典型例题例.如图,正方形BDEC 周长是24厘米,平行四边形ADEB 面积是多少平方厘米?分析:从图上可以看出,平行四边形的底和高,都与正方形的边长相等.而正方形的边长是 (24÷4)厘米,所以平行四边形ADEB 的面积就是(24÷4)×(24÷4)=6×6=36(平方厘米)答:平行四边形ADEB 面积是36平方厘米.《平行四边形的面积》典型例题例.求下面平行四边形的周长(单位:分米)1267分析:已知平行四边形的一组底和高分别是12分米和7分米,可以求出它的面积是84712=⨯(平方分米),通过“平行四边形面积=底×高”,可以逆推出:底=平行四边形面积÷高,已知面积是84平方分米,高是6分米,可以求出和6分米相对应的底,用14684=÷(分米),平行四边形对边相等,已知平行四边形相邻的两条边分别是12分米和14分米,就可以求出它的周长.解:5221412=⨯+)((分米)答:这个平行四边形的周长是52分米.《平行四边形的面积》典型例题例.一个平行四边形,若底增加2厘米,高不变,则面积增加6平方厘米;若高增加1厘米,底不变,则面积增加4平方厘米,原平行四边形的面积是多少?分析:要求原平行四边形的面积,必须知道原平行四边形的底和高.根据第一组条件,增加部分是一个底是2厘米,面积是6平方厘米的平行四边形,根据平行四边形的面积公式可以求出这个平行四边形的高,即求出原平行四边形的高.根据第二组条件,,增加部分是一个高为1厘米,面积为4平方厘米的平行四边形,由此可以求出增加部分的底,即求出原平行四边形的底.解:12)14()26(=÷⨯÷(平方厘米)答:原平行四边形的面积是12平方厘米.《平行四边形的面积》典型例题例.在一块长80米,宽35米的长方形地上,修了两条宽分别为3米和2米的通道,其余的地方铺上草皮(如图).问:应铺多少平方米的草皮?分析:很显然,铺草皮的面积等于长方形的面积减去两条通道的面积,问题的关键是这两条 通道是什么图形?因为两条通道都是四边形,且两组对边分别平行,所以两条通道都是平行四边形.要求出这两个平行四边形的面积,底边分别是3米和2米,高是多少呢?这恐怕是个难点,你发现了吗?它们的高就是长方形的宽35米,问题得解.解:80×35-(3×35+2×35) =2800-175=2625(平方米)答:应铺2625平方米的草皮.《平行四边形的面积》典型例题例.如图,平行四边形的面积是150平方米,它的阴影部分的面积是多少平方米?分析:平行四边形的面积为已知,底边长已知,所以平行四边形的高可求出,由观察知阴影部分是一个直角梯形,这个直角梯形的上底为15米,下底为15-4=11(米),高就是平行四边形的高,问题得解.解:[15+(15-4)]×(150÷15)÷2=26×10÷2=130(平方米)答:阴影部分的面积是130平方米.。
平行四边形 面积练习题

平行四边形面积练习题平行四边形是几何学中的一个重要概念,它具有独特的性质和特点。
在学习平行四边形的面积计算时,我们需要掌握一些基本的公式和方法。
下面我将通过一些练习题来帮助大家更好地理解和应用这些知识。
练习题一:已知平行四边形ABCD的底边AB的长度为8cm,高为6cm,求其面积。
解析:根据平行四边形的面积公式,面积等于底边乘以高,即S = 底边× 高。
将已知数据代入公式,可得S = 8cm × 6cm = 48cm²。
所以平行四边形ABCD的面积为48平方厘米。
练习题二:已知平行四边形EFGH的两条邻边EF和FG的长度分别为5cm和7cm,夹角EFG为60°,求其面积。
解析:首先,我们可以根据三角函数的知识计算出平行四边形EFGH的高。
根据正弦定理,我们可以得到sin60° = 高 / 7cm。
解方程可得高≈ 6.08cm。
然后,根据平行四边形的面积公式,面积等于底边乘以高,即S = 底边× 高。
将已知数据代入公式,可得S = 5cm × 6.08cm ≈ 30.4cm²。
所以平行四边形EFGH的面积约为30.4平方厘米。
练习题三:已知平行四边形IJKL的对角线IK和JL的长度分别为10cm和8cm,夹角IKJ为120°,求其面积。
解析:与练习题二类似,我们可以先计算出平行四边形IJKL的高。
根据正弦定理,我们可以得到sin120° = 高 / 8cm。
解方程可得高≈ 6.93cm。
然后,根据平行四边形的面积公式,面积等于底边乘以高,即S = 底边× 高。
由于平行四边形IJKL的底边长度未知,我们可以利用余弦定理计算出底边的长度。
根据余弦定理,我们可以得到底边² = 10cm² + 8cm² - 2 × 10cm × 8cm × cos120°。
平行四边形面积的计算练习题

平行四边形面积的计算练习题一、填空(1)4.5平方米()平方分米2400平方厘米()平方分米(2)一个平行四边形的底是9分米,高是底的2倍,它的面积是()平方分米。
(3)一个平行四边形的底是12厘米,面积是156平方厘米,高是()厘米。
(4)一块平行四边形钢板,底是1.5米,高是1.2米,如果每平方米钢板重23.5千克,这块钢板重()千克。
二、判断题。
(1)平行四边形的面积等于长方形面积。
()(2)一个平行四边形的底是5分米,高是20厘米,面积是100平方分米。
()(3)一个平行四边形面积是42平方米,高是6米,底是7米。
()三、选择题。
(1)下面的长方形和平行四边形面积()a.相等b.不相等(2)用木条钉成的长方形拉成一个平行四边形,它的高和面积()a.都比原来大b.都比原来小c.都与原来相等(3)平行四边形的底扩大3倍,高缩小3倍,面积()扩大3倍b.缩小3倍c.不变d.不好判断2. 一块平行四边形木板, 它的底是12分米, 高是8分米, 这块木板的面积是多少平方分米?3. 一块平行四边形的草坪, 已知它的面积是1050平方米, 高是25米, 这块草坪的底边长是多少米?4. 一块平行四边形地, 底23米, 高15米, 如果每平方米栽瓜秧9棵, 共栽多少棵?5. 平行四边形的高是70.2厘米, 是底的2倍, 平行四边形的面积是多少?2. 一个平行四边形, 底是1.2米, 高是底的1.5倍, 求它的面积.3. 一块平行四边形钢板, 底5米, 高3米, 如果1平方米钢重39千克, 这块钢板重多少千克?4. 下图中的正方形周长为28厘米, 求平行四边形的面积.5. 一个平行四边形的底是9.6分米, 高2.5分米, 它的面积是多少平方分米?1、填空:(1)把一个平行四边形转化成一个(),它的面积和原来的平行四边形(),平行四边形的底是长方形的(),长方形的宽和平行四边形的()相等。
(2)平行四边形面积的计算公式是(),用含有字母的式子表示是()。
小学数学五年级上册《平行四边形的面积》精编练习题

五年级数学上册平行四边形面积练习题班级考号姓名总分一、填空题。
1、把一个平行四边形沿其中一条高剪开,可以平移拼成一个(),这个图形的()相当于原平行四边形的底,它的()相当于原平行四边形的高,它的面积和原平行四边形的面积()。
平行四边形的面积=,用字母表示是S=。
2、一个平行四边形的底是1.2厘米,面积是1.56平方厘米,高是()厘米。
3、一块平行四边形钢板,底是6米,高是0.2米,如果每平方米钢板重1.3千克,这块钢板共重()千克。
4、同底等高的平行四边形面积都()。
一个平行四边形的周长为46厘米,一边的长为14厘米,另外三边的长分是()、()、()。
6、填表:底高平行四边形面积0.7cm 50cm8dm 9.6dm20.02m 6m2二、选择题。
1、用木条钉成的长方形拉成一个平行四边形,它的高和面积()①不变②都比原来大③都比原来小④只有高变小2、下面图中长方形和平行四边形的面积相比,()①长方形大②同样大③平行四边形大三、计算下面各个平行四边形的面积。
四、应用题1、有一块平行四边形的玻璃,底是2.8米,高是2.4米。
这块玻璃的面积是多少?2、一块平行四边形钢板,面积8平方分米,高是1.6分米。
它的底是多少?3、一平行四边形钢板,底0.8m,高6m,它的面积多少?如果每平方米的钢板重0.038吨,这块钢板重多少千克?4、一个边长为8厘米的正方形,与一个高为5厘米的平行四边形的面积相等,这个平行四边形的底是多少?5、有两块面积相同的平行四边形地,一块地的的底是6米,高是3米,另一块地的底是9米,高是多少米?6、已知正方形周长为4.8cm,求下面平行四边形的面积。
7、如果用铁丝围成下图一样的平行四边形,需要多长的铁丝?米)8、一个平行四边形的周长是78cm(如图),以CD为底时,它的高是18cm,又BC是24cm,求它的面积。
平行四边形的面积计算练习题

平行四边形的面积计算练习题面积是几何学中一个重要的概念,常用于计算各种图形的大小。
其中,平行四边形是一种常见的图形,它具有四条边两两平行的特点。
在本文中,我们将通过几个面积计算练习题来深入理解平行四边形的面积计算方法。
练习题一:一个平行四边形的底长为8cm,高为5cm,求其面积。
解析:根据平行四边形的面积公式:面积 = 底长 ×高,将已知数据带入计算:面积 = 8cm × 5cm = 40平方厘米。
因此,这个平行四边形的面积为40平方厘米。
练习题二:一个平行四边形的底长为12cm,高为7cm,求其面积。
解析:同样利用平行四边形的面积公式进行计算:面积 = 12cm × 7cm = 84平方厘米。
所以,这个平行四边形的面积为84平方厘米。
练习题三:一个平行四边形的一边长为10cm,高为6cm,求其面积。
解析:在此题中我们不知道底长,但我们可以通过利用平行四边形的性质进行计算。
由于平行四边形的对角线相等,我们可以根据高与对角线之间的关系求出底长。
通过画图可知,高与对角线、底边构成一个直角三角形,利用勾股定理:对角线的平方 = 底长的平方 + 高的平方。
将已知数据带入计算:10cm的平方 = 底长的平方 + 6cm的平方,计算可得:100cm² = 底长的平方 + 36cm²,进一步计算得:底长的平方 = 64cm²,因此底长= √64cm = 8cm。
现在我们已经得到了平行四边形的底长和高,可以利用面积公式进行计算:面积 = 8cm × 6cm = 48平方厘米。
所以,这个平行四边形的面积为48平方厘米。
练习题四:一个平行四边形的对角线长分别为6cm和8cm,求其面积。
解析:在此题中我们同样不知道底长,但我们可以利用对角线的关系求出底长。
由于平行四边形的对角线相等,我们可以根据对角线与底边之间的关系计算底长。
根据平行四边形的性质,两条对角线互相平分,同时对角线相交处形成的四个三角形相似。
人教版五年级数学上册 平行四边形的面积练习题

人教版五年级数学上册平行四边形的面积练习题题目一:计算平行四边形的面积已知平行四边形的底边长为10 cm,高度为8 cm,请计算该平行四边形的面积。
解答:根据平行四边形的面积公式:面积 = 底边长 ×高度,将已知数据代入公式,得到面积 = 10 cm × 8 cm = 80 平方厘米。
题目二:求平行四边形的面积比已知两个平行四边形,其底边长度分别为12 cm和8 cm,高度分别为6 cm和4 cm,请计算这两个平行四边形的面积比。
解答:分别计算两个平行四边形的面积,平行四边形A的面积为 12 cm × 6 cm = 72 平方厘米,平行四边形B的面积为 8 cm × 4 cm = 32 平方厘米。
将平行四边形A的面积除以平行四边形B的面积,得到面积比为 72 平方厘米 / 32 平方厘米 = 2.25。
题目三:计算不规则图形的面积已知一个不规则图形如下所示,请计算其面积。
----\ | /\ | /\---\解答:可以将不规则图形划分为两个平行四边形和一个三角形。
先计算平行四边形的面积,假设底边长度为6 cm,高度为4 cm,面积为 6 cm × 4 cm = 24 平方厘米。
再计算三角形的面积,假设底边长度为6 cm,高度为2 cm,面积为 6 cm × 2 cm ÷ 2 = 6 平方厘米。
最后将两个平行四边形的面积加上三角形的面积,得到不规则图形的面积为 24 平方厘米 + 6 平方厘米 = 30 平方厘米。
以上为人教版五年级数学上册平行四边形的面积练习题。
建议同学们多加练习,熟练掌握计算平行四边形面积的方法和公式。
五年级数学 平行四边形的面积 练习题(含答案)

人教版数学五年级上册6.1 平行四边形面积练习卷一、选择题1.将一个长方形拉成平行四边形,它的面积().A.不变B.变大C.变小2.下列说法正确的是()。
A.平行四边形是特殊的长方形B.平行四边形易变形C.梯形两组对边分别平行3.如图,已知“4,7,20,35”(单位:厘米)是一个平行四边形的两条底和两条高的长度,这个平行四边形的面积是()平方厘米。
A.245B.140C.80D.284.把一个长方形拉成一个平行四边形(如图),拉成后的平行四边形与长方形相比,它的周长(),面积()。
A.变小;变小B.变大;变大C.不变;变小二、图形计算5.求图中阴影部分的面积(单位:cm)三、填空题6.一块平行四边形草地,底是3.6米,对应的高是2米,它的面积是( )平方米。
7.如图,M、N分别是平行四边形ABCD两边上的中点,三角形AMN的面积是7.2平方厘米,平行四边形ABCD的面积是平方厘米.8.一个平行四边形相邻的两条边分别是4厘米和6厘米,如果较长边上的高是2厘米,那么这个平行四边形的面积是( ).9.如图,正方形ABCD的边长为4厘米,EF和BC平行,ECH的面积是7平方厘米,EG的长为( )。
10.把一个木条做成的长方形框架沿着对角拉成一个平行四边形,拉成后的平行四边形与原长方形比较,周长( )。
11.一个边长5厘米的正方形木框,拉成一个平行四边形后,面积减少了5平方厘米.拉成的平行四边形的高是厘米.四、判断题12.在平行四边形内画一个最大的三角形,三角形的面积一定等于平行四边形面积的一半。
( )13.两个平行四边形的面积相等,这两个平行四边形的形状也一定相同._____.(判断对错)14.计算组合图形面积时,常用的方法有分割法和添补法..15.一个平行四边形的高和底都扩大到原数的4倍,那么这个平行四边形的面积也要扩大到原数的4倍。
( )16.把平行四边形割补成一个长方形后,面积变小。
( )五、解答题17.植物园里有一个平行四边形的玫瑰园,玫瑰园的底是120m,高是60m,如果每平方米种8株玫瑰,这个玫瑰园一共能种多少株玫瑰?18.河西村有一块平行四边形的实验田,底长600米,高250米.平均每公顷收稻谷1.2吨,这块田可收稻谷多少吨?19.一个平行四边形,若底增加2厘米,高不变,则面积增加6平方厘米;若高增加1厘米,底不变,则面积增加4平方厘米,原平行四边形的面积是多少?参考答案:1.C【详解】2.B(1)平行四边形的两组对边平行且相等,长方形不仅两组对边平行且相等,四个角均为直角。
平行四边形面积练习题

《平行四边形的面积计算》练习
一、基础型:
1.求下面平行四边形的面积。
2.要求下图的平行四边形面积,以DC边为底,应取哪一条高?并求图形ABCD的面积。
3.下面两个平行四边形面积都是3×2=6(厘米)。
•对吗?为什么?
二、拓展型:
4.选择条件,用两种方法算出平行四边形的面积,看看是否相等。
(单位:米)
5.把正确答案的编号填有括号里。
(1)计算下图平行四边形的面积,算式是()
A.7.5×4 B.7.5×6 C.6×4
(2)下图平行四边形的面积是()
A.12厘米B.12平方米C.12平方厘米
三、提高型:
6.下面两个平行四边形的面积相等吗?为什么?每个平行四边形的面积是多少?
7.小区物业要给一块底边长35米,高20米的平行四边形草坪重新铺草皮,每平方米需要6 元,铺这块地面一共需要多少元?要在这片地里种冬青,每4平方米种一棵,可以种多少棵?师:解决这两个问题时都要先求出平行四边形的面积,再根据题中的数量关系用不同的方法来解决,看来同学们对平行四边形的面积确实掌握的不错,下面这道题目看看谁能灵活的运用知识来解决。
8.猜一猜,哪个平行四边形的面积大?
得出结论:等底等高的平行四边形面积相等
师:你能用好办法,很快再画一个和他们面积相等的平行四边形吗?(画完展示)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平行四边形的面积练习题
一、填空。
1、把一个平行四边形转化成一个长方形,它的面积与原来的平行四边形()。
这个长方形的长与平形四边形的底(),宽与平行四边形的高()。
平行四边形的面积等于(),用字母表示是()。
2、一个平行四边形的底是12厘米,面积是156平方厘米,高是()厘米。
3、一块平行四边形钢板,底是6米,高是2米,如果每平方米钢板重13千克,这块钢板重()千克。
4、等底等高的平行四边形面积都()。
一个平行四边形的周长为46厘米,一边的长为14厘米,另外三边的长分是()、()、()。
6、填表:
二、选择题。
1、用木条钉成的长方形拉成一个平行四边形,它的高和面积()
①不变②都比原来大③都比原来小④只有高变小
2
①长方形大②同样大
③平行四边形大
三
五、应用题
1、一块平行四边形钢板,面积800平方厘米,高是16厘米。
它的底是多少?
3、一块平行四边形钢板,底8m,高6m,如果每平方米的钢板重38千克,这块钢板重多少千克?
5、有两块面积相同的平行四边形地,一块地的的底是6米,高是3米,另一块地的底是9米,高是多少米?
6、已知正方形周长为48cm,求下面平行四边形的面积。
7、如果用铁丝围成下图一样的平行四边形,需要多长的铁丝?米)
8、一个平行四边形的周长是78cm(如图),以CD为底时,它的高是18cm,又BC是24cm,求它的面积。
D
B 24 C
7.5cm。
