计量经济学的三种检验
计量经济学的各种检验
主分量回归是将具有多重相关的变量集综合得出少数几个互不相关的主分量.两步:(1)找出自变量集的主分量,建立y与互不相关的前几个主分量的回归式.(2)将回归式还原为原自变量结果.详见,<<实用多元统计分析>>,方开泰;
主分量回归结果
Obs _MODEL_ _TYPE_ _DEPVAR_ _PCOMIT_ _RMSE_ Intercept x1 x2 x3 y 1 MODEL1 PARMS y 0.48887 -10.1280 -0.05140 0.58695 0.28685 –1 2 MODEL1 IPCVIF y 1 0.25083 1.00085 0.25038 –1 3 MODEL1 IPC y 1 0.55001 -9.1301 0.07278 0.60922 0.10626 –14 MODEL1 IPCVIF y 2 0.24956 0.00095 0.24971 -15 MODEL1 IPC y 2 1.05206 -7.7458 0.07381 0.08269 0.10735 -1
多重共线性检验方法（3）样本相关系数检验法
FG test results
fg=20.488013401 p=0.0001344625；拒绝零假设，认为存在多重共线性。具体那些变量之间存在多重共线性，除了上面提到的辅助回归的方法外，还有以下提到的条件数检验和方差膨胀因子法。
多重共线性检验方法：（4）特征值分析法所用的检验统计指标
补救措施
增加样本;岭回归或主分量回归;至少去掉一个具有多重共线性的变量;对具有多重共线性的变量进行变换.对所有变量做滞后差分变换(一般是一阶差分),问题是损失观测值,可能有自相关.采用人均形式的变量（例如在生产函数估计中）在缺乏有效信息时,对系数关系进行限制,变为有约束回归(Klein,Goldberger,1955),可以降低样本方差和估计系数的标准差,但不一定是无偏的(除非这种限制是正确的).对具有多重共线性的变量,设法找出其因果关系,并建立模型和原方程构成联立方程组.
Eviews计量经济学三大检验讲解学习
E v i e w s计量经济学三大检验作业1我们有1978-2007年我国财政收入,国内生产总值,财政支出和商品零售价格指数的年度数据。
请用Eview 进行回归分析。
（1） 根据回归结果分析模型的经济意义（包含模型的显著性，拟合优度，系数的显著性，系数的经济意义）建立模型，做OLS 估计，得结果图一，列表如下：43283175.57898859.0003271.0558.6399X X X Y ++--=∧)0636.20)(065848.0)(012559.0)(836.2132(SE )882456.2)(65061.13)(260476.0-)(000492.3-(t =997046.02=R 996705.02=R 845.2924=F模型整体显著性较高（F 检验十分显著），可决系数2R 和调整的可决系数较大，即样本回归方程对样本观测值拟合较好。
t 检验显示2X 的系数不显著（p 值>0.05,不能拒绝β=0的原假设）,3X 和4X 的系数显著（p值<0.05，拒绝β=0的原假设）。
从模型的经济意义来看，财政支出、商品零售价格指数与财政收入成正相关，国内生产总值与财政收入成负相关,不符合客观经济规律，可能与模型变量的选取有关。
考虑对模型进行对数变换，结果为图二。
432ln 128427.1ln 631090.0ln 448496.0946444.6ln X X X Y +++-=∧)610249.0)(160929.0)(141418.0)(853146.2(SE)849127.1)(921549.3)(171412.3)(434662.2(t -=987673.02=R 986251.02=R 3969.694=F对数变换后模型整体显著性较高（F 检验十分显著，p 值=0.00<<0.05），可决系数2R 和调整的可决系数略有下降，模型可解释98.63%的因变量变化。
所有计量经济学检验方法
所有计量经济学检验方法
1、回归分析：回归分析是用来确定两个变量之间相关关系的一种统计方法，它能够推断出一个变量对另一个变量的影响程度。
常用的回归检验包括偏直斜率检验、R平方检验、Durbin-Watson检验、自相关检验、Box-Cox检验等。
2、主成分分析：主成分分析（PCA）是一种统计分析方法，用于消除随机变量之间的相关性，从而简化数据分析过程。
常用的方法有二元主成分分析（BPCA）、多元主成分分析（MPCA）
3、因子分析：因子分析是一种统计学方法，用于确定从多个离散观测变量中提取的隐含变量。
常用的因子分析检验包括KMO检验、Bartlett 统计量检验、条件双侧门限统计量检验等。
4、多元分析：多元分析是一种统计学方法，用于探索随机变量之间的关系，常用的多元分析检验包括多元弹性网络（MANOVA）、多元回归（MR）以及结构方程模型（SEM）。
5、聚类分析：聚类分析是一种用于探索研究数据中的结构和特征的统计学方法。
它主要是将数据集分组，以便对数据集中的每组信息单独进行分析。
常用的聚类分析检验有K均值聚类、层次聚类、嵌套聚类等。
6、特征选择：特征选择是一种数据分析技术，用于从大量可能的特征中，选择有效的特征变量。
计量经济学的三种检验PPT文档146页
谢谢！
146
Байду номын сангаас
26、要使整个人生都过得舒适、愉快，这是不可能的，因为人类必须具备一种能应付逆境的态度。——卢梭
▪
27、只有把抱怨环境的心情，化为上进的力量，才是成功的保证。——罗曼·罗兰
▪
28、知之者不如好之者，好之者不如乐之者。——孔子
▪
29、勇猛、大胆和坚定的决心能够抵得上武器的精良。——达·芬奇
▪
30、意志是一个强壮的盲人，倚靠在明眼的跛子肩上。——叔本华
45、法律的制定是为了保证每一个人 自由发 挥自己 的才能 ，而不 是为了 束缚他 的才能 。—— 罗伯斯 庇尔
▪
计量经济学的三种检验
41、实际上，我们想要的不是针对犯 罪的法 律，而 是针对 疯狂的 法律。 ——马 克·吐温 42、法律的力量应当跟随着公民，就 像影子 跟随着 身体一 样。— —贝卡 利亚 43、法律和制度必须跟上人类思想进 步。— —杰弗 逊 44、人类受制于法律，法律受制于情 理。— —托·富 勒
期末精华：计量经济学针对三种误差检验方法
2、近似共线性下普通最小二乘法参数估计量 非有效
在一般共线性（或称近似共线性）下，虽然可以得 到OLS法参数估计量，但是由参数估计量方差的表达 式为
Cov(ˆ ) 2 (XX)1
RESET 检验是 Regression Specification Error Test （回归设定误差检验）的简写。
设 y x β zc ε 设定误差检验是检验上式中 c 是否为零。 但关键哪些变量应该进入 z 呢？ （1）在缺失变量的情况下，那些缺失变量将构成 z。 （2）在方程设定有误时，应如何处理呢？
第五章 计量经济学检验 ——违背基本假设的情况
❖ 一方面，建立一个计量经济学模型要经过四 重检验，其中经济意义检验、统计检验、预 测检验已讲，这一章主要讲计量经济学检验 的范畴。
❖ 另一方面，前面讨论了最小二乘估计的优良 性质，但都是基于经典假设。如果这些假设 不满足，会出现什么问题呢？这一章对其进 行分析。
(3) 用F检验比较两个方程的拟合情况（类似于上一章中 联合假设检验采用的方法），如果两方程总体拟合情况 显著不同，则我们得出原方程可能存在误设定的结论。 使用的检验统计量为：
F (RSSM RSS ) / M RSS /(n k 1)
其中：RSSM为第一步中回归（有约束回归）的残差 平方和，RSS为第二步中回归（无约束回归）的残差 平方和，M为约束条件的个数，这里是M=3。
四、 解决解释变量误设定问题的原则
在模型设定中的一般原则是尽量不漏掉有关的解 释变量。因为估计量有偏比增大误差更严重。但如 果方差很大，得到的无偏估计量也就没有多大意义 了，因此也不宜随意乱增加解释变量。
在回归实践中，有时要对某个变量是否应该作为 解释变量包括在方程中作出准确的判断确实不是一 件容易的事，因为目前还没有行之有效的方法可供 使用。尽管如此，还是有一些有助于我们进行判断 的准则可用，它们是：
计量经济学
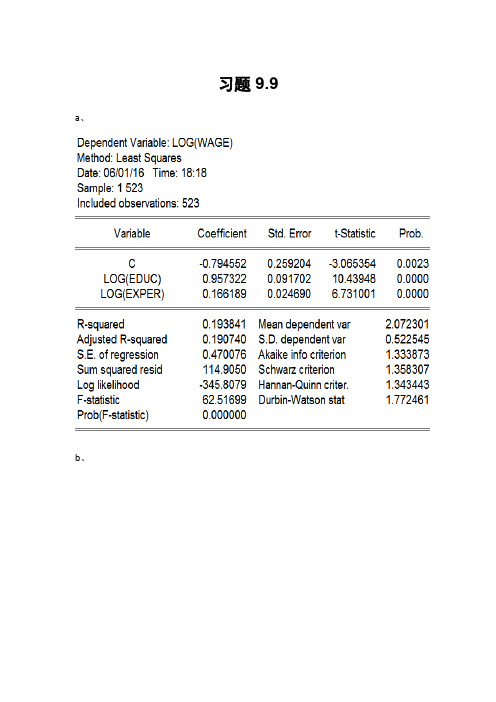
习题9.9 a、b、两者均可能存在异方差。
C、帕克检验三种帕克检验的p值都大于0.05，因此不拒绝原假设，即没有证据表明自变量系数为0；实质上帕克检验表明的是残差的平方并不体现出所假定的变化模式，残差的平方仍然可能存在其他形式的变化模型。
所以尚不能肯定一定不存在异方差。
格莱泽检验模型：ln（ei 2）=B1+B2ln(ln(educ))+vi格莱泽检验的第三种形式：残差的绝对值和1/educ显著相关，可能存在异方差问题。
怀特检验P=0.0004，拒绝原假设，即可能存在异方差问题。
帕克检验和格莱泽检验对异方差的形式要做出特殊的假定，要对不同的函数形式进行多次尝试，即便是自变量的系数不显著，也不態断定一定不存在异方差问题，因为可能是假定的函数形式不正确。
而怀特一般异方差检验采用了最为全面的函数形式，建议采用怀特一般异方差检验。
d、使用加权最小二乘法，选择权重是首要解决的问题。
权重选择得不恰当，异方差问题仍然会存在。
事实上，加权最小二乘法在使用过程中，需要经过多次尝试，多次检验，才可能找到一个合适的权重，因此在运用中这是比较不方便的。
本题样本容量为523，是个大样本，适合用怀特异方差校正。
其结果如下：e、选择不存在异方差的模型，即双对数模型。
因为异方差的存在会导致OLS估计量不再有效，其方差通常也会出现有偏性，在这种情况下，常用的假设检验都不再可靠，有可能出现错误的结论。
f、不能，因为两个模型的因变量形式不同。
习题9.28a、回归结果表明：小轿车的最高时速每提高1个百分点，耗油量平均下降1.27个百分点；马力每提高1个百分点，耗油量平均上升0.39个百分点；车重每提高1个百分点，耗油量平均下降1.90个百分点。
b、因为这是关于轿车耗油量的截面数据，因此预计存在异方差问题。
c、p值近似等于0，则拒绝原假设，即可能存在异方差问题。
d、校正后的值与OLS的结果比较发现：两者的估计系数的值是相同的,但是他们的方差和标准误差是不同的。
计量经济学中的各种检验
线性回归模型的各种检验
计量经济学线性回归模型的各种检验
对计量经济学模型的检验包括对回归模型的理论检 验（经济意义检验）、统计检验、计量经济学检验、 预测检验等。 理论检验（经济意义检验）指的是依据经济理论来 判断估计参数的正负号是否合理、大小是否适当。 经济意义检验是第一位的。如果模型不能够通过经 济意义检验，则必须找出原因，在找出原因的基础 上对模型进行修正或重新估计模型。如果通过了经 济意义检验，则可进行下一步的统计检验。
=
分子 分母
1 RSS n =
i
2
1 1 TSS RSS n n
i
=
RSS = TSS
R
2
ρ
2 ˆ y, y
和 R 一样，也是说明拟合的
2
ˆ y 与实际的 y 的相关程度的，
说明
ˆ y 拟合得约好。
i
修正的决定系数
在应用过程中人们发现，随着模型中解释变量的增多，多重 决定系数的值往往会变大，从而增加模型的解释功能。这给 人一个错觉，即要使模型拟合得好，就必须增加解释变量。 但是另一方面，在样本容量一定的情况下，增加解释变量必 然会使得待估参数的个数增加，从而损失自由度；而且在实 际中，有些解释变量的增加根本就是不必要的。对于这些不 必要的解释变量的引入不仅对于估计结果无益，同时还意味 着预测的精确度的降低。也就是说，不应该仅根据决定系数 是否增大来决定某解释变量是否应引入模型。 事实上，研究模型的拟合优度时，常常并不简单地仅依靠多 重决定系数，更常考虑的是修正的决定系数。
线性回归模型的各种检验
理论检验（经济意义检验） 统计检验 计量经济学检验 预测检验 这一节主要讨论各种统计检验
回归模型的统计检验
所有计量经济学检验方法(全)
所有计量经济学检验方法(全)计量经济学所有检验方法一、拟合优度检验 可决系数TSSRSSTSS ESS R -==12 TSS 为总离差平方和，ESS为回归平方和，RSS 为残差平方和该统计量用来测量样本回归线对样本观测值的拟合优度。
该统计量越接近于1，模型的拟合优度越高。
调整的可决系数)1/()1/(12----=n TSS k n RSS R 其中：n-k-1为残差平方和的自由度，n-1为总体平方和的自由度。
将残差平方和与总离差平方和分别除以各自的自由度，以剔除变量个数对拟合优度的影响。
二、方程的显著性检验(F 检验)方程的显著性检验，旨在对模型中被解释变量与解释变量之间的线性关系在总体上是否显著成立作出推断。
原假设与备择假设：H 0:β1=β2=β3=…βk =0 H 1:βj 不全为0 统计量)1/(/--=k n RSS kESS F 服从自由度为(k , n-k-1)的F分布，给定显著性水平α，可得到临界值Fα(k,n-k-1)，由样本求出统计量F的数值，通过F>Fα(k,n-k-1)或F≤Fα(k,n-k-1)来拒绝或接受原假设H，以判定原方程总体上的线性关系是否显著成立。
三、变量的显著性检验（t检验）对每个解释变量进行显著性检验，以决定是否作为解释变量被保留在模型中。
原假设与备择假设：H0：βi=0 （i=1,2…k）；H1：βi≠0给定显著性水平α，可得到临界值tα/2(n-k-1)，由样本求出统计量t的数值，通过|t|> tα/2(n-k-1) 或|t|≤tα/2(n-k-1)来拒绝或接受原假设H0，从而判定对应的解释变量是否应包括在模型中。
四、参数的置信区间参数的置信区间用来考察：在一次抽样中所估计的参数值离参数的真实值有多“近”。
统计量)1(~1ˆˆˆ----'--=k n t k n c S t iiii iiie e βββββ在(1-α)的置信水平下βi 的置信区间是( , ) ββααββi i t s t s ii-⨯+⨯22，其中，t α/2为显著性水平为α、自由度为n-k-1的临界值。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
• 非完全共线性是指变量不能完全表示为 其他变量的完全线性函数。
• 违反假定：多重共线性
8
完全多重共线性
• 完全共线性(Perfect collinearity)的例子 ：
– X1 X2 X3 – 10 50 52 – 15 75 75 – 18 90 97 – 24 120 129 – X1 和 X2 是完全线性相关的：
计量经济学检验
一、多重共线性 二、异方差 三、自相关
1
一：多重共线性 • 多重共线性的性质 • 多重共线性的原因 • 多重共线性的后果 • 多重共线性的诊断 • 多重共线性的补救措施
2
回顾多元线性回归模型的若干假定 • 零均值假定 • 同方差假定 • 无自相关假定 • 随机项与自变量不相关 • 非多重共线性
• X2 = 5X1
9
完全多重共线性
• 若X2 = 5X1 • 将其代入Y’=b0 ’ +b1 ’ X1+b2 ’ X2 +b3 ’ X3
Y’=b0 ’ +b1 ’ X1 +b2 ’ * 5X1 +b3 ’ X3 = b0 ’ +（b1 ’ + 5b2 ’ ） X1 +b3 ’
X3 = b0 ’ +A X1 +b3 ’ X3
• 三变量模型 • 无法从A值中得到b1 ’ 、b2’的值
10
接近完全多重共线性的情形 • 多重共线性是一个极端的情形 • 在实际中，很少遇到完全多重共线性的情
况，常常是接近或高度多重共线性。亦即 解释变量是接近线性相关的。 • 例：《widget》教科书
11
问题
• 多重共线性的性质是什么？ • 多重共线性产生的原因是什么？ • 多重共线性的理论后果是什么？ • 多重共线性的实际后果是什么？ • 在实际中，如何发现多重共线性？ • 消除多重共线性的弥补措施有哪些？
• 置信区间变宽。 • t值不显著， R2较高。 • OLS估计量及其标准差对数据的微小变
化非常敏感，也就是说它们趋于不稳定。 • 回归系数符号有误。 • 难以衡量各个解释变量对回归平方和
（ESS）或R2的贡献。
21
例：消费函数
• 消费函数的结果：
– Y = 24.77 + 0.94X1 - 0.04X2 – t (3.67) (1.14) (-0.53) – R2=0.96, F = 92.40 – X1 是收入 – X2 是财富 – 高的 R2 表明收入和财富可以解释消费变化
的96%
22
结果分析
• 没有任何一个斜率系数是显著的。 • 财富变量的符号是错误的。 • 高的 F 值意味着系数都等于0的联合假设不
成立
– 两个变量是如此地高度相关，以至于不能将二 者的效应分离出来。
23
例：消费函数 • 如果将 X2 对 X1 回归，得到：
17
注意
• 无偏性是一个重复抽样的性质，即：保持X 不变，如果得到一些样本并用OLS计算这 些样本估计量，则其平均值收敛于估计量 的真实值。但这并不是某个样本估计值的 性质，在现实中，我们经常无法得到大量 的重复样本。
18
注意 • 接近共线性并未破坏最小二乘估计量的最
小方差性：在所有线性无偏估计量中， OLS估计量的方差最小。 • 最小方差并不意味着方差值本身也比较小。
5
假定3
• 无自相关假定： • Cov(ui, uj)=0, i ≠ j, i,j=1,2…..n • 表明任意两次观测的ui, uj是不相关的，
即u在某次的观测值与任何其它次观测中 的值互不影响，称为无序列相关性。 • 等方差性和无序列相关性称为高斯—马 尔柯夫（Gauss-Markov）假定。 • 违反假定：自相关
19
注意
• 即使变量总体之间不线性相关，但却可 能与某一样本线性相关
• 多重共线性本质上是一个样本（回归） 现象。
• 原因：大多数经济数据不是通过试验获 得。如：国民生产总值、价格、失业率、 利润、红利等，是以其实际发生值为依 据，而并非试验得到。
20
多重共线性的实际后果
• OLS估计量的方差和标准差较大。也就 是说，OLS估计量的精确度下降。
12
多重共线性的性质
• 可以获得原始系数的一个线性组合的估 计值。
• 当解释变量之间存在完全线性相关或完 全多重共线性时，不可能获得所有参数 的唯一估计值。
• 既然我们不能获得它们的唯一估计值， 也就不能根据某一样本做任何统计推论 （也即假设检验）
13
多重共线性的原因
• 例：消费函数 • Y = b0 + b1X1 + b2X2 • X1 = income ； X2 = wealth
6
假定4 • 随机项与自变量不相关： • Cov(ui, x1i)=0； Cov(ui, x2i)=0 • 区分随机项u与每个自变量各自对y的影响。 • 如果x是非随机变量，即x是在重复抽样中
取某固定值，该条件自然满足。
7
假定5
• 解释变量之间不存在线性相关关系，即 任意两个解释变量之间线性的原因
• 模型设定:
– 例： 在模型中加入多项式项，特别是当X的取 值范围很小的时候。
• 变量之间有共同的时间趋势 • 模型的过定（ overdetermined）
– 解释变量的数目多于观测的数目。
16
多重共线性的理论后果 • 在存在高度多重共线性的情形下，即使多
元回归方程的一个或者多个偏回归系数是 统计不显著的，普通最小二乘估计量仍然 是最优线性无偏估计量。
3
假定1 • 零均值假定：E(ui)=0,i=1,2,….n • 对X1 ，X2的每个观测值，u可以取不同的值，
考虑u的所有可能值，它们的总体平均值 （期望值）等于0。
4
假定2 • 同方差假定：Var(ui)= σ u 2, i=1,2,…n • 上式表明，各次观测值中u具有相同的方差，
即各次观测所受到的随机影响的程度相同， 称为等方差性。 • 违反假定：异方差
X2 = 5X1 Y = b0 + b1X1 + b2 5X1 Y = b0 + (b1 + 5b2)X1
14
多重共线性的原因
• 所用的数据收集方法
– 例：在X的一个限定的范围内抽样
• 有关被抽样总体的约束：
– 例：具有高收入的人倾向于有更多的财富
• 也许有关低收入的富有的人和高收入的没钱人的 数据不够充足。