人口预测中线性回归分析简单步骤

人口预测的数学模型与预测方法分析

人口预测的数学模型与预测方法分析人口预测是对未来一定时期内人口数量和结构的变动进行估计和预测的过程。

人口预测在社会经济发展规划、城市规划、教育医疗资源配置等方面具有重要的参考价值。

为了准确预测人口的变动趋势，需要建立合理的数学模型和选择适当的预测方法。

人口预测的数学模型主要包括线性回归模型、指数模型、Logistic模型等。

线性回归模型是一种用来描述两个变量之间线性关系的统计模型，可以用来预测人口随时间的变化。

指数模型假设人口数量按照指数规律增长或减少，适用于人口增长较快的情况。

Logistic模型则适用于人口增长速度放缓后的情况，它是一种描述增长速度逐渐趋近于饱和的模型。

在选择数学模型时，需要综合考虑以下几个因素：人口历史变动趋势、人口自然增长率、人口迁移和流动情况、政策调控等因素。

同时，还需根据实际情况对模型的参数进行合理的设定和修正，以提高预测的准确性。

在预测方法上，常用的有趋势线法、复合增长率法、比较推理法、时间序列分析法和系统动力学方法等。

趋势线法是基于历史数据的发展趋势来进行预测，适用于人口变动趋势比较稳定的情况。

复合增长率法是将历史数据中的增长率按一定规则进行加权平均，再用来推算未来人口的增长率。

比较推理法通过对不同因素的比较和推理，来估计未来人口的变化。

时间序列分析法是根据时间序列数据的历史模式来预测未来的变化趋势。

系统动力学方法则是通过对不同因素的动态关系建立模型，用来探索人口变动的内在机制和规律。

在具体应用时，可以结合不同的数学模型和预测方法，进行多角度的分析和预测。

同时，还需要不断对模型进行修正和优化，以适应不断变化的人口变动趋势和社会经济背景。

此外，还应该注意对预测结果的不确定性进行评估和把握，提供多种可能性的预测结果，为决策者提供科学的参考依据。

线性回归方程解题步骤

线性回归方程解题步骤引言：线性回归是一种常见的统计分析方法，用于建立自变量与因变量之间的关系。

在许多实际问题中，我们需要通过线性回归方程来预测因变量的值。

本文将介绍线性回归方程的解题步骤，帮助读者更好地理解和应用这一方法。

一、收集数据：在开始解决线性回归方程问题之前，我们首先需要收集相关的数据。

这些数据应包含两个变量：自变量和因变量。

自变量是我们希望用来预测因变量的变量，而因变量是我们希望预测的变量。

例如，我们希望通过一个人的年龄来预测其收入，那么年龄就是自变量，收入就是因变量。

二、绘制散点图：收集到数据后，我们需要绘制散点图来观察自变量和因变量之间的关系。

散点图是一种将自变量和因变量的取值用点标出的图表，可以直观地反映二者之间的关系。

通过观察散点图，我们可以初步判断自变量和因变量之间是否存在线性关系。

三、确定最佳拟合直线：在线性回归中，我们希望找到一组参数，使得自变量和因变量之间的线性关系最好地被拟合。

最常用的拟合方法是最小二乘法，即通过最小化误差平方和来确定最佳拟合直线。

误差是指实际观测值与拟合值之间的差异。

通过最小二乘法，我们可以得到最佳拟合直线的参数，也就是线性回归方程的系数。

四、求解线性回归方程：得到最佳拟合直线的参数后，我们就可以得到线性回归方程。

线性回归方程的一般形式为：Y = aX + b，其中Y是因变量，X是自变量，a和b分别是线性回归方程的系数。

我们可以根据最佳拟合直线的参数来确定线性回归方程的具体形式。

五、进行预测：有了线性回归方程后，我们可以通过输入自变量的取值来预测因变量的值。

通过代入自变量的值到线性回归方程中，我们可以得到对应的因变量的预测值。

这样，我们就可以利用线性回归方程进行预测和分析。

六、评估回归模型：在进行线性回归分析后，我们需要对回归模型进行评估，以确定其在实际应用中的有效性和准确性。

常用的评价指标包括残差分析、确定系数（R²）和假设检验等。

残差分析用于检验回归模型是否符合一些基本的假设，如误差项的正态性和方差齐性。

线性回归分析的基本步骤

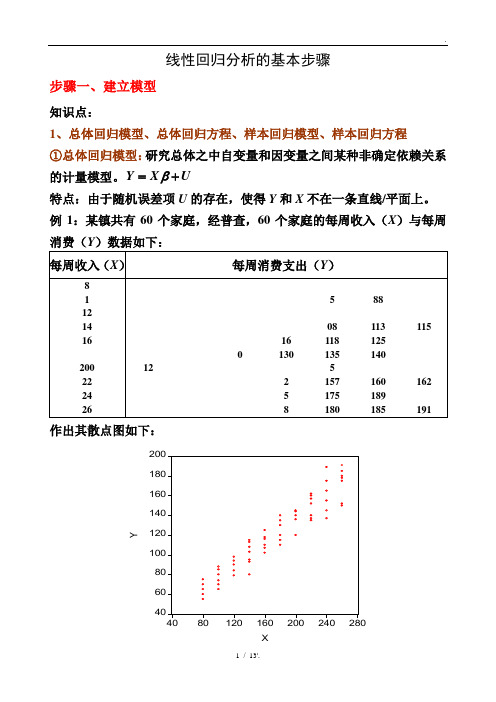
线性回归分析的基本步骤步骤一、建立模型知识点：1、总体回归模型、总体回归方程、样本回归模型、样本回归方程 ①总体回归模型：研究总体之中自变量和因变量之间某种非确定依赖关系的计量模型。

Y X U β=+特点：由于随机误差项U 的存在，使得Y 和X 不在一条直线/平面上。

例1：某镇共有60个家庭，经普查，60个家庭的每周收入（X ）与每周消费（Y ）数据如下：作出其散点图如下：②总体回归方程（线）：由于假定0EU =，因此因变量的均值与自变量总处于一条直线上，这条直线()|E Y X X β=就称为总体回归线（方程）。

总体回归方程的求法：以例1的数据为例由于01|i i i E Y X X ββ=+，因此任意带入两个X i 和其对应的E (Y |X i )值，即可求出01ββ和，并进而得到总体回归方程。

如在例1中，通过抽样考察，我们得到了20个家庭的样本数据：那么描述样本数据中因变量Y 和自变量X 之间非确定依赖关系的模型ˆY X e β=+就称为样本回归模型。

④样本回归方程（线）：通过样本数据估计出ˆβ，得到样本观测值的拟合值与解释变量之间的关系方程ˆˆY X β=称为样本回归方程。

如下图所示：⑤四者之间的关系：ⅰ：总体回归模型建立在总体数据之上，它描述的是因变量Y 和自变量X 之间的真实的非确定型依赖关系；样本回归模型建立在抽样数据基础之上，它描述的是因变量Y 和自变量X 之间的近似于真实的非确定型依赖关系。

人口增长趋势预测数据分析

人口增长趋势预测数据分析
首先，需要收集历史上的人口数据。

这些数据通常包括每年的人口数量、出生率、死亡率和迁移率等指标。

可以通过查阅历史文献、民政统计年鉴等途径获取这些数据。

接下来，可以利用统计学方法分析这些数据。

常见的方法包括线性回归、指数平滑、时间序列分析等。

线性回归可以用来研究人口数量与时间的关系，从而预测未来的人口数量。

指数平滑则可以通过对历史数据的平滑处理，得到未来人口数量的估计。

时间序列分析结合历史数据和时间的相关性，可以对未来的人口增长进行模型建立和预测。

在进行数据分析时，还需要考虑一些其他因素的影响。

例如，经济发展、社会政策、教育水平等都可能对人口增长有重要的影响。

因此，需要综合考虑这些因素，并在模型中加以考虑。

此外，为了得到更准确的结果，可以采用多种方法进行验证和比较。

例如，可以将数据分为训练集和测试集，使用训练集建立模型，然后用测试集验证模型的预测效果。

还可以使用多个不同的模型进行比较，选择最合适的模型。

最后，通过对人口增长趋势进行数据分析，可以得到未来人口数量的预测结果。

这些预测结果可以提供给政府部门和决策者，以指导人口政策的制定和实施。

需要注意的是，人口增长趋势预测是一个复杂的问题，受到多种因素的影响。

因此，在进行数据分析和预测时，需要慎重考虑，综合利用多种方法和数据，以提供尽可能准确和可靠的结果。

此外，还需要不断更新数据和模型，以应对社会和经济变化对人口增长趋势的影响。

人口预测中线性回归分析简单步骤

人口预测中线性回归分析简单步骤：
一、进行回归分析
SPSS-regression-linear
Dependent ——因变量这里应该为人口
Independent ——自变量这里可以为年份，也可以为GDP或其他认为可以引起人口变动的自变量
用箭头添加到相应的框中，然后点击ok，生成结果。

二、结果检验
Model Summary
a Predictors: (Constant), V1
R2=0.11，模型拟合效果不好（此数应该越接近1越好，如果在0.7以上均可认为模型拟合效果较好）
ANOVA(b)
a Predictors: (Constant), V1
b Dependent Variable: V2
sig=0.771，模型线性特征不显著（如果该值小于0.05，可认为线性关系较为显著）
Coefficients(a)
a Dependent Variable: V2
每个参数的sig分别为0.772和0.771，表示参数也不显著（如果该值小于0.05，可认为线性关系较为显著）
列出的一元一次方程为y=88.709x-176626.982。

将x=？？带入方程，得到y=？？，则？？年人口为？？。

但由于未通过显著性检验，模型拟合效果也不好，所以该方法预测的结果应当去掉。

（这里如果前面的拟合度和显著性检验效果均较好的话，就应当保留该方法预测的结果。

线性回归分析步骤

线性回归分析步骤线性回归分析是一种统计学方法，用于确定两个变量之间的线性关系。

它可以用于预测特定的变量，并估计它们之间的关系。

它也可以用于识别影响变量的其他因素，以验证假设。

线性回归是定量分析的一个重要方面，可以帮助研究人员更好地理解数据，并从中得出有意义的结论。

本文将介绍线性回归分析的基本步骤，包括数据收集、数据分析、回归分析和结果解释。

首先，在进行线性回归分析之前，需要收集数据。

这可通过实验、观察、实地考察或从其他人获得这些资料。

通常，数据收集者需要有清晰的研究目的，确定有关数据的变量类型和范围，以及所涉及的样本大小。

收集的数据需要记录，以便进行数据分析的第二步。

接下来，需要对收集的数据进行分析。

其核心方法是计算两个变量之间的相关系数，以确定它们之间的线性关系。

如果两个变量之间呈线性关系，那么可以使用线性回归分析，以估计它们之间的相关性。

同时，在样本内可以应用其他技术，比如回归的分类、因变量的探索和多变量的线性回归分析，以帮助调查人员更好地理解数据。

第三步是实施回归分析，以估计变量之间的关系。

回归分析的过程包括选择回归模型、计算参数、检验模型好坏和比较模型之间的区别。

需要注意的是，计算参数时，应该考虑到所采用的统计方法，以确保结果的准确性。

最后，还需要解释结果，以获得有意义的结论。

结果解释可以采用模型诊断和参数检验的结果，以识别模型的弱点，并根据结果对结论进行调整。

另外，也可以检查预期的变量之间的联系，以及其他变量对模型结果的影响。

最后，可以利用结果改善和解释过程中的假设，以验证研究的可行性。

综上所述，线性回归分析是一种重要的定量分析技术，可以帮助研究人员更好地理解数据，以及从中得出有意义的结论。

它的基本步骤包括数据收集、数据分析、回归分析和结果解释。

在收集数据时，应记录所涉及的变量类型、范围和样本大小的信息；在进行数据分析时，要计算变量之间的相关系数；在运行回归分析时，应考虑回归模型、计算参数和检验模型的好坏；在解释结果时，应诊断模型弱点、检查预期变量及其他变量对模型结果的影响，以及利用结果改善和验证假设。

总结线性回归分析的基本步骤

总结线性回归分析的基本步骤线性回归分析是一种统计方法，用于研究两个或更多变量之间的关系。

它的基本思想是通过构建一个线性函数来描述因变量与自变量之间的关系，并使用最小二乘法估计未知参数。

下面是线性回归分析的基本步骤：1.收集数据：首先，我们需要收集有关自变量和因变量的数据。

这些数据可以通过实验、观察或调查获得。

数据应该涵盖自变量和因变量的所有可能值，并且应该尽可能全面和准确。

2.绘制散点图：一旦我们收集到数据，我们可以使用散点图来可视化自变量和因变量之间的关系。

散点图展示了每个观测值的自变量与相应因变量的值之间的关系图形。

通过观察散点图，我们可以初步判断变量之间的关系类型，如直线、曲线或没有明显关系。

3.选择模型：在进行线性回归分析之前，我们需要选择适当的模型。

线性回归模型的形式为Y=β0+β1X1+β2X2+...+βnXn+ε，其中Y是因变量，X1,X2,...Xn是自变量，β0,β1,β2,...βn是未知参数，ε是误差项。

我们假设因变量与自变量之间的关系是线性的。

4.估计参数：在线性回归模型中，我们的目标是估计未知参数β0,β1,β2,...βn。

我们使用最小二乘法来估计这些参数，最小二乘法的目标是通过最小化残差平方和来选择最佳拟合直线，使预测值与观测值之间的差异最小化。

5.评估模型：一旦我们估计出参数，我们需要评估模型的拟合程度。

常见的评估指标包括残差分析、方差分析、回归系数的显著性检验、确定系数和调整确定系数。

这些指标可以帮助我们判断模型的有效性和可靠性。

6.解释结果：在得到合理的回归模型之后，我们可以使用回归方程来进行预测和解释结果。

通过回归系数可以了解自变量对因变量的影响程度和方向。

同时，我们可以进行假设检验，确定哪些自变量对因变量是显著的。

7.模型修正和改进：一旦我们获得了回归模型，我们可以进一步修正和改进模型。

这可以通过添加更多的自变量或删除不显著的自变量来完成。

同时，我们还可以使用交互项、多项式项或转换变量来探索更复杂的关系。

总结：线性回归分析的基本步骤

线性回归分析的基本步骤步骤一、建立模型知识点：1、总体回归模型、总体回归方程、样本回归模型、样本回归方程①总体回归模型：研究总体之中自变量和因变量之间某种非确定依赖关系的计量模型。

Y X Uβ=+特点：由于随机误差项U 的存在，使得Y 和X 不在一条直线/平面上。

例1：某镇共有60个家庭，经普查，60个家庭的每周收入（X ）与每周消费（Y ）数据如下：每周收入（X ）每周消费支出（Y ）805560657075　100657074808588　1207984909498　140809395103108113115160102107110116118125　180110115120130135140　200120136140144145　220135137140152157160162240137145155165175189　260150152175178180185191作出其散点图如下：②总体回归方程（线）：由于假定，因此因变量的均值与自变0EU =量总处于一条直线上，这条直线就称为总体回归线（方()|E Y X X β=程）。

总体回归方程的求法：以例1的数据为例1）对第一个X i ，求出E (Y |X i )。

每周收入（X ）每周消费支出（Y ）E (Y |X i )805560657075　65100657074808588　771207984909498　89140809395103108113115101160102107110116118125　113180110115120130135140　125200120136140144145　137220135137140152157160162149240137145155165175189　161260150152175178180185191173由于()01|i i i E Y X X ββ=+，因此任意带入两个X i 和其对应的E (Y |X i )值，即可求出01ββ一，并进而得到总体回归方程。

简单线性回归的分析步骤

简单线性回归的分析步骤简单线性回归是一种统计分析技术，通常用于确定两个变量之间的相关性和影响，以及预测一个变量响应另一个变量的变化。

这种分析技术可以帮助组织分析影响某个变量的原因，以更好地开发这些变量之间的关系。

简单线性回归分析可以帮助组织采取有效的管理和决策措施。

本文将介绍简单线性回归分析的六个步骤：第一步：定义回归模型简单线性回归中有两个变量：自变量（X）和因变量（Y），并假设存在线性关系。

变量之间的关系可以表示为方程：Y = +X+εα要求估计的参数，ε模型中的噪声。

第二步：收集数据简单线性回归的第二步是收集数据。

数据收集是回归分析的核心，是建立回归模型的基础，决定了估计参数的准确性。

因此，在收集数据的时候需要注意数据的准确性，也要注意数据量。

数据量越大，分析结果越准确。

第三步：检查数据在收集数据之后，需要检查数据，检查数据中是否存在缺失值，异常值等情况。

缺失值可能影响数据分析的准确性，而异常值可能会降低模型的准确性和复杂度。

此外，还需要检查自变量和因变量之间是否存在多重共线性。

第四步：拟合模型简单线性回归的第四步是拟合模型。

在拟合模型的时候，可以使用最小二乘法或最小平方根法来拟合模型。

最小二乘法可以获得最佳拟合参数，而最小平方根法可以获得更准确的拟合参数。

第五步：诊断模型简单线性回归的第五步是诊断模型。

诊断模型旨在检测模型的正确性。

此时，可以检查不变的残差、残差的自相关性、残差的正态性、残差的均值和方差，以及多元共线性、自变量的偏性和因变量的偏性等。

这些检查有助于验证模型的准确性和可靠性。

第六步：模型检验最后一步是模型检验。

模型检验旨在测试模型的可靠性。

模型检验可以使用拟合优度检验、显著性检验或者F-检验来完成。

拟合优度检验用于测量模型中变量的可预测性，而显著性检验用于检验参数的显著性，而F-检验用于检验拟合的精确度。

综上所述，简单线性回归分析有六个步骤：定义回归模型，收集数据，检查数据，拟合模型，诊断模型，以及模型检验。

报告中使用线性回归分析的步骤和解释

报告中使用线性回归分析的步骤和解释导言：在现代社会中，数据分析在决策制定和问题解决中扮演着重要的角色。

线性回归分析作为一种常用的统计方法，被广泛应用于商业、金融、医疗等各个领域。

本文将介绍报告中使用线性回归分析的步骤和解释，以帮助读者理解并正确运用该方法。

一、确定研究目的在使用线性回归分析之前，首先需要明确研究目的。

例如，我们想研究广告投入与销售额之间的关系，我们的目标是通过分析广告投入对销售额的影响来优化公司的广告策略。

二、收集数据接下来，需要收集与研究目的相关的数据。

这些数据可以来自内部的企业数据库，也可以通过市场调研等手段获取。

以广告投入与销售额的例子来说，我们需要收集每个时间段的广告投入和相应销售额的数据。

三、数据预处理在进行数据分析之前，需要对数据进行预处理。

这包括数据清洗、数据缺失值处理、异常值处理等步骤。

确保数据的准确性和完整性对于分析结果的可靠性至关重要。

四、变量选择在线性回归分析中，需要选择自变量和因变量。

自变量是研究目的中需要分析的影响因素，而因变量是我们希望了解其受自变量影响程度的变量。

在广告投入与销售额的例子中，广告投入是自变量，销售额是因变量。

五、模型建立在确定了自变量和因变量后，可以建立线性回归模型。

线性回归模型的基本形式为：Y = β0 + β1*X1 + β2*X2 + ... + βn*Xn + ε，其中Y表示因变量，X1、X2...表示自变量，β0、β1、β2...表示回归系数，ε表示误差项。

回归系数反映了自变量对因变量的影响程度。

六、模型诊断建立模型后，需要对模型进行诊断。

诊断的目的是检验模型的合理性和可靠性。

常用的诊断方法包括检验回归模型的显著性、检验残差的正态分布性、检验多重共线性等。

如果模型存在问题，需要进行进一步修正和优化。

七、解释回归结果最后，需要解释回归结果。

这包括解释回归系数的含义和统计显著性，解释模型的拟合度，比较不同自变量对因变量的影响程度等。

人口增长的Logistic模型分析及其应用资料讲解

人口增长的L o g i s t i c模型分析及其应用人口增长的Ｌｏｇｉｓｔｉｃ模型分析及其应用作者：熊波来源：《商业时代》2008年第27期◆中图分类号：C923 文献标识码：A内容摘要：本文运用迭代的方法计算出人口极限值xm和人口增长率r，用 Logistic模型预测了我国人口未来的发展趋势，并根据预测的结果提出了相应的对策与建议。

关键词：人口 Logistic模型迭代人口增长问题相关研究最早注意人口问题的是英国经济学家马尔萨斯，他在1798 年提出了人口指数增长模型。

这个模型的基本假设是：人口的增长率是一个常数。

记t时刻的人口总数为x(t)。

初始时刻t=0时的人口为x0。

人口增长率为r，r表示单位时间内x(t)的增量与x(t)的比例系数。

那么，时刻t到时刻t+Δt内人口的增量为x(t+Δt)-x(t)=rx(t)Δt。

于是x(t)满足下列微分方程的初值问题，他的解为x(t)=x0ert。

在r>0时，人口将按指数规律增长。

但是不管生物是按算术级数、几何级数还是按指数曲线变化，随着时间增长生物数量将趋于无穷大。

然而，实际情况却不然，实验指出在有限的空间内，一开始生物以较快速度增长，到一定时期生物增长量就会减缓，生物数量趋于稳定。

历史上的人口统计数据也表明，当一个国家的社会稳定时，一定时期内马尔萨斯模型是符合实际的，但是如果时间比较长或社会发生动荡时，马尔萨斯模型就不能令人满意了。

原因是随着人口的增加，自然资源、环境条件等因素对人口增长开始起阻滞作用，因而人口增长率不断下降。

基于以上考虑荷兰生物学家Verhaust对原人口发展模型进行了改造，于1838 年提出了以昆虫数量为基础的Logistic 人口增长模型。

这个模型假设增长率r是人口的函数，它随着x的增加而减少。

最简单的假定是r是x的线性函数，其中r称为固有增长率，表示x→0时的增长率。

由r（x）的表达式可知，x=xm时r=0。

xm表示自然资源条件能容纳的最大人口数。

基于线性回归模型的人口增长预测研究

基于线性回归模型的人口增长预测研究随着人类社会的发展和进步，人口增长成为许多国家和地区面临的重要问题之一。

对于政府和决策者而言，准确预测人口增长趋势至关重要，以便采取相应的政策和措施。

在这篇文章中，我们将探讨如何通过基于线性回归模型的方法，对人口增长进行预测研究。

线性回归模型是一种常见的统计学方法，用于分析两个或多个变量之间的关系。

在人口增长预测中，我们需要找到一个或多个自变量，例如时间、经济发展水平、教育水平等，来预测人口数量的变化。

通过收集历史数据并进行分析，我们可以建立一个可靠的线性回归模型，以预测未来人口的增长趋势。

首先，我们需要选择合适的自变量。

在人口增长预测中，时间是最常用的自变量之一。

通过将时间作为自变量，我们可以观察到人口数量随着时间的推移而发生的变化。

其他自变量如经济发展水平、教育水平等也可以在模型中加入，以更准确地预测人口增长。

通过收集这些自变量的历史数据，我们可以建立一个包含多个自变量的线性回归模型。

其次，在收集自变量的历史数据之后，我们需要进行数据的处理和分析。

数据处理的过程包括数据清洗、缺失值填充等，以确保数据的准确性和完整性。

然后，我们可以通过计算自变量与因变量（即人口数量）之间的相关系数，来确定自变量对人口增长的影响程度。

相关系数越大，说明自变量对人口增长的影响越大。

接下来，在建立线性回归模型之前，我们需要对数据进行拟合和验证。

通过拟合数据，我们可以确定模型的合适参数，从而使得模型可以准确地预测未来的人口增长趋势。

同时，我们还可以通过验证数据的方法，来检查模型的准确性和稳定性。

只有在模型经过充分验证后，才可以用于未来的人口增长预测。

最后，我们可以利用建立好的线性回归模型来进行人口增长的预测研究。

通过将未来的自变量输入到模型中，我们可以得到未来人口数量的预测结果。

这些预测结果可以为政府和决策者提供重要的参考，以制定相应的人口政策和措施。

当然，在使用预测结果时，我们也需要考虑模型的不确定性和误差范围，以避免过于依赖预测结果所带来的风险。

线性回归的求解过程

线性回归的求解过程线性回归是一种用于预测连续数值的机器学习算法。

在机器学习中，梯度下降法是一种常用的求解最优解的方法。

在线性回归中，梯度下降法被用来找到使得损失函数最小化的参数。

下面将详细介绍线性回归的求解过程。

线性回归模型的目标是找到一条直线，最小化真实值与预测值之间的差距。

我们以一个简单的二维线性回归问题为例，假设给定一个数据集，包含了m个样本数据和n个特征。

对于每个样本数据，我们有一个真实值y和n个特征值x。

我们的目标是找到最佳的线性模型:y = b + w1 * x1 + w2 * x2 + ... + wn * xn，其中b为偏置，w为权重。

梯度下降法是一种迭代的优化算法，通过逐步调整模型参数的值，最终找到损失函数最小的参数。

梯度下降法的核心思想是沿着损失函数的负梯度方向迭代更新参数。

以下是线性回归求解过程的具体步骤：Step 1: 初始化参数首先，我们需要初始化模型的参数，包括偏置b和权重w。

通常情况下，我们可以将它们初始化为0或者一个较小的随机数。

Step 2: 计算预测值使用当前的参数，我们可以计算出每个样本的预测值。

对于第i个样本，其预测值为：y_pred = b + w1 * x1 + w2 * x2 + ... + wn * xn。

Step 3: 计算损失函数损失函数是用来衡量真实值与预测值之间差异的函数。

在线性回归中，常用的损失函数是平方损失函数：Loss = (1/2m) * Σ(y_pred - y)^2 Step 4: 计算梯度梯度是损失函数对参数的偏导数，用来衡量损失函数沿着每个参数的变化率。

对于线性回归模型，我们需要计算每个参数的偏导数，即：∂Loss/∂b和∂Loss/∂w。

Step 5: 更新参数接下来，我们使用梯度下降法来更新参数的值。

参数的更新公式为：b = b - learning_rate * ∂Loss/∂b，w = w - learning_rate *∂Loss/∂w，其中learning_rate为学习率，表示每次参数更新的步长。

多元线性回归分析在人才需求预测中的应用

多元线性回归分析在人才需求预测中的应用一、本文概述随着全球化和科技进步的加速，人才需求预测已成为企业和政策制定者面临的重要任务。

在人才市场中，准确预测未来的人才需求不仅有助于企业和组织制定合理的人力资源规划，还可以优化招聘流程，提高招聘效率，降低招聘成本。

本文旨在探讨多元线性回归分析在人才需求预测中的应用，分析其有效性及可能面临的挑战。

多元线性回归分析是一种常用的统计分析方法，它通过建立多个自变量与因变量之间的线性关系模型，来预测因变量的变化趋势。

在人才需求预测中，多元线性回归分析可以通过分析历史数据，找出影响人才需求的关键因素，如行业发展趋势、技术进步、人口结构变化等，从而构建一个预测模型，对未来的人才需求进行预测。

本文首先将对多元线性回归分析的基本原理进行简要介绍，然后阐述其在人才需求预测中的具体应用方法。

接着，通过案例分析或实证研究，探讨多元线性回归分析在人才需求预测中的实际效果，并分析其可能存在的局限性。

本文将对多元线性回归分析在人才需求预测中的前景进行展望，提出改进建议和未来研究方向。

通过本文的研究，我们期望能够为企业和政策制定者提供一种有效的人才需求预测工具，帮助他们更好地了解未来的人才市场变化，制定更合理的人力资源规划，以应对日益复杂的人才市场挑战。

二、多元线性回归分析的基本原理多元线性回归分析是一种统计分析方法，用于研究多个自变量（也称为预测变量或解释变量）与一个因变量（也称为响应变量或依赖变量）之间的线性关系。

其基本原理基于最小二乘法，通过最小化残差平方和来估计回归系数，从而建立最优的线性预测模型。

在多元线性回归分析中，假设因变量与自变量之间存在线性关系，并且这种关系可以通过一个线性方程来表示。

这个方程通常表示为：Y = β0 + β11 + β22 + ... + βpp + ε，其中Y是因变量，1, 2, ..., p是自变量，β0是截距项，β1, β2, ..., βp是自变量的回归系数，ε是随机误差项。

常用方法预测城市人口规模的原理及实例

常用方法预测城市人口规模的原理及实例方法一：线性回归模型常用方法之一是线性回归模型。

线性回归模型基于统计学原理，通过分析城市人口规模与其它相关因素的关系来预测城市人口规模。

线性回归模型的基本原理是假设人口规模与一些自变量（如城市面积、GDP、人口密度等）之间存在线性关系，然后通过拟合这些自变量的数值来预测人口规模。

例如，我们可以收集一组城市的数据，包括城市的面积、GDP、人口密度等自变量，以及对应的城市人口规模。

然后，我们可以使用线性回归模型来拟合这些数据，并得到一个线性方程，例如：人口规模=a*面积+b*GDP+c*人口密度。

最后，我们可以使用这个线性方程来预测其他城市的人口规模。

方法二：人口增长模型另一种常用方法是人口增长模型，这些模型基于城市人口增长的趋势和模式来预测城市人口规模。

人口增长模型可以分为几种类型，例如指数增长模型、递减增长模型、饱和增长模型等。

以指数增长模型为例，这种模型假设城市的人口增长速度与当前的人口规模呈正比。

根据这个假设，我们可以使用历史数据来预测未来的人口规模。

例如，如果一个城市的人口规模在过去几年里呈指数增长，我们可以使用这个增长趋势来预测未来的人口规模。

方法三：地理信息系统（GIS）另一个常用方法是使用地理信息系统（GIS）来预测城市人口规模。

GIS是一种将地理数据和空间分析技术相结合的工具，可以帮助我们分析城市的空间分布和人口规模。

使用GIS方法预测城市人口规模的一种实例是基于空间插值技术。

这种方法通过收集已知地理位置和人口规模的点数据，然后使用插值算法来推断其他地区的人口规模。

插值算法可以基于点数据的空间分布规律来推测未知地区的人口规模。

例如，我们可以使用GIS收集一组城市的地理位置和人口规模的数据。

然后，我们可以使用空间插值技术来推断未知地区的人口规模，例如使用反距离加权法或克里金插值法来预测其他地区的人口规模。

综上所述，常用方法预测城市人口规模的原理可以是基于线性回归模型、人口增长模型或地理信息系统等。

人口数量spss线性回归模型建模步骤

人口数量spss线性回归模型建模步骤线性模式
线性模式不仅处理线性问题，主要是处理线性化的非线性模型:
线性模式是简单的比例关系，要求各个自变量彼此独立，才能利用最小二乘技术求线性模型的参数;而非线性则是对简单比例关系的偏离，各变量相互作用。

指数模型、对数模型、幂指数模型、双曲线模型、抛物线模型、正态分布模型等常用的非线性数学模型，也可以借助不数变换或者是变量替换表示为线性函数形式:此次实验主要利用线性
函数、指数函数、双曲线函数和Logistic增长函数的线性化模型预
测中国人口。

开展一般的回归分析，首先要作散点图(scatterplot)，然后选择表达式，最后采用适当的拟合方法。

预测结果不能出现违背基本逻辑的结论，同时预测结果要有现实意义。

如何进行简单线性回归和预测

如何进行简单线性回归和预测1、以下图是甲醛含量与对应测量得到的吸光度数据。

要求根据这一系列数据，得到由吸光度求甲醛含量的回归方程，在实验室也称为求标准曲线。

这就是简单的线性回归。

2、为了说明如何进行简单的回归分析，我们使用盈质统计分析软件打开一个以上例子的Excel文件。

3、我们注意到，该文件第一行不是标题行，选中行，勾选重置表头选项，点击确定。

4、然后在回归菜单下，点击拟合回归模型。

5、响应变量为甲醛含量，吸光度为自变量，所以在响应旁选择“甲醛含量”，在连续预测变量旁点击添加“吸光度”，点击确定。

6、会生成回归分析结果和相应图表。

7、我们先进行回归诊断，再看回归分析的结果。

回归诊断主要是看右边的甲醛含量残差图，左上的正态概率图表明残差符合正态性假设；右上的残差与拟合值的散点基本位于一条以0为中线的水平带中间，表明基本符合误差的均值为0的假设；左下的直方图虽然数据不多，但也能看出基本是符合正态分布的；右下的与顺序图可以看出散点是随机散布在以0为中线的水平带中间，可见误差服从独立性假设。

8、以上回归诊断都通过了，我们再来看左边的回归分析结果，先进行模型的有效性检验，在方差分析表中，回归对应的F统计量的P值为0，小于显著性水平0.05，说明所有的斜率系数不全为0，模型是有效的。

9、其次看拟合优度，在模型汇总栏中相关系数的R-sq为0.999，可见拟合效果非常好。

最后需要检验系数的显著性，在系数栏里，截距的P值为0.001，在5%的显著性水平上，拒绝了截距为0的原假设，说明截距显著不为0；吸光度的斜率系数P值为0，在5%的显著性水平上，拒绝了斜率为0的原假设，说明吸光度与甲醛含量有显著的线性关系。

10、综上所述，通过回归分析得到的结果是有效的，拟合效果很好。

可以看到最终软件分析给出的回归方程是：甲醛含量(ug)=-0.066 +2.852吸光度(A)11、得到该回归方程后，就可以进行预测了。

比如某样品通过该分析方法测得吸光度为0.453，求该样品的甲醛含量。

基于线性回归的人口增长趋势预测模型

基于线性回归的人口增长趋势预测模型人口增长趋势是人口学研究的重要课题之一，预测人口增长趋势对于社会发展和政策制定具有重要的意义。

线性回归是一种常用的预测模型，可用于预测人口增长趋势。

本文将基于线性回归模型，利用历史数据，预测未来的人口增长趋势。

首先，我们需要收集相关的历史数据来建立预测模型。

可以使用公开可获取的数据源，如国家统计局、联合国人口部等来获取历史的人口数据。

确保数据的准确性和全面性是建立可靠模型的基础。

接下来，我们需要对数据进行预处理，包括数据清洗和特征提取。

数据清洗可以包括去除异常值和缺失值处理。

特征提取可以将人口增长对应的时间作为自变量，人口数量作为因变量，构建出适合线性回归的数据集。

在进行线性回归建模之前，我们可以先进行数据可视化分析，了解历史人口增长趋势。

可以使用折线图或柱状图对历史人口数据进行可视化展示。

从可视化的结果中可以发现人口增长的趋势和周期性。

然后，我们可以使用线性回归模型对历史人口数据进行拟合。

线性回归建模的核心是通过最小二乘法来拟合出一条直线，使得拟合直线和实际数据之间的误差最小化。

通过对拟合直线进行分析，我们可以得到直线的斜率和截距，进而推断人口的增长率和初始数量。

在建立线性回归模型之后，我们可以进行模型的评估。

常用的评估指标包括残差分析、决定系数和平均绝对值误差等。

残差分析可以用来检验模型的拟合效果，决定系数可以衡量模型对数据的解释程度，平均绝对误差可以衡量模型的预测准确度。

最后，我们可以利用建立好的线性回归模型来预测未来的人口增长趋势。

根据模型的拟合直线，可以预测出未来一段时间内人口的增长数量。

然而，需要注意的是，线性回归模型是利用过去的数据来进行预测，未来的人口增长趋势可能会受到各种社会经济因素的影响，预测结果可能存在一定的偏差。

在实际应用中，该模型可以为政府部门和决策者提供参考，用于制定相关的人口政策和社会发展规划。

同时，基于线性回归模型的人口增长趋势预测也可以提供给研究者，并为社会科学研究提供数据支持。

线性回归分析方法

线性回归分析方法
线性回归是一种基本的统计分析方法，它可以用来研究两个或多个变量之间的线性关系。

线性回归的基本思想是通过一组数据点来拟合一条直线，以最小化数据点与拟合直线之间的距离。

线性回归可以用来预测一个自变量的取值对应的因变量的取值。

在数据分析和机器学习领域，线性回归是一种常见的分析方法，它可以被应用于多个领域，如金融、市场营销、健康保险、政治选举，等等。

下面是一些线性回归分析方法的基本步骤：
1. 定义问题：确定要研究的自变量和因变量，并确立研究目的。

2. 收集数据：收集和记录研究问题所需的数据。

3. 绘制散点图：将数据点绘制在一个平面直角坐标系上，并进行可视化展示。

4. 计算相关系数：通过计算自变量和因变量之间的相关系数，来判断两个变量之间的线性关系程度。

5. 拟合回归线：通过最小二乘法拟合一条直线，使数据点到拟合直线的距离最小。

6. 评估模型：计算误差大小和置信水平，以评估拟合直线的准确性及可靠性。

7. 应用模型：将模型应用到实际问题中，进行预测和统计分析。

基于线性回归分析的人口变化曲线拟合

基于线性回归分析的人口变化曲线拟合摘要：线性回归分析可以把工程和科学实验数据拟合为线性函数，以反映变量间的相互关系。

本文中，将实现非线性回归线性化的方法进行分析，对中国历年人口变化进行曲线拟合。

本文中利用Matlab编制相关程序进行曲线拟合，并可以根据拟合得到的曲线预测未来的人口数目。

关键词：线性回归分析；线性化；Matlab；曲线拟合1.引言在科学与工程计算中，为了把握某些规律，经常需要研究和探寻一些变量之间的关系。

而变量之间的关系有时是确定的，有时又是不确定的。

我们对这些不确定关系的变量进行分析就需要借助一些工具，回归分析方法就是一种研究确定性与不确定性之间关系的重要方法。

回归分析是数理统计的重要部分，而非线性回归在科学实验、建立数学模型、决策预测以及自动控制中都有着广泛的应用。

通过曲线拟合和回归分析，在一定条件下（如误差允许下），可以将无规律的数据拟合成最佳的函数表达式。

运用曲线拟合和回归分析将使得数据的处理和分析变得迅速而容易。

2.算法分析所谓回归分析法，是在掌握大量观察数据的基础上，利用数理统计方法建立因变量与自变量之间的回归关系函数表达式（称回归方程式）。

回归分析中，当研究的因果关系只涉及因变量和一个自变量时，叫做一元回归分析；当研究的因果关系涉及因变量和两个或两个以上自变量时，叫做多元回归分析。

此外，回归分析中，又依据描述自变量与因变量之间因果关系的函数表达式是线性的还是非线性的，分为线性回归分析和非线性回归分析。

处理非线性回归的基本方法是，通过变量变换，将非线性回归化为线性回归，然后用线性回归方法处理。

假定根据理论或经验，已获得输出变量与输入变量之间的非线性表达式，但表达式的系数是未知的，要根据输入输出的n 次观察结果来确定系数的值。

按最小二乘法原理来求出系数值，所得到的模型为非线性回归模型(nonlinear regression model)。

非线性回归的线性化需要进行配曲线。