哈夫曼树实验报告
哈弗曼树编码实验报告
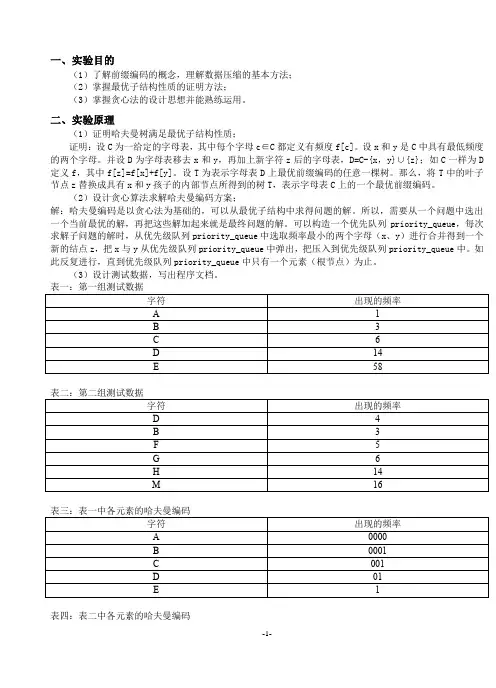
一、实验目的(1)了解前缀编码的概念,理解数据压缩的基本方法;(2)掌握最优子结构性质的证明方法;(3)掌握贪心法的设计思想并能熟练运用。
二、实验原理(1)证明哈夫曼树满足最优子结构性质;证明:设C为一给定的字母表,其中每个字母c∈C都定义有频度f[c]。
设x和y是C中具有最低频度的两个字母。
并设D为字母表移去x和y,再加上新字符z后的字母表,D=C-{x,y}∪{z};如C一样为D 定义f,其中f[z]=f[x]+f[y]。
设T为表示字母表D上最优前缀编码的任意一棵树。
那么,将T中的叶子节点z替换成具有x和y孩子的内部节点所得到的树T,表示字母表C上的一个最优前缀编码。
(2)设计贪心算法求解哈夫曼编码方案;解:哈夫曼编码是以贪心法为基础的,可以从最优子结构中求得问题的解。
所以,需要从一个问题中选出一个当前最优的解,再把这些解加起来就是最终问题的解。
可以构造一个优先队列priority_queue,每次求解子问题的解时,从优先级队列priority_queue中选取频率最小的两个字母(x、y)进行合并得到一个新的结点z,把x与y从优先级队列priority_queue中弹出,把压入到优先级队列priority_queue中。
如此反复进行,直到优先级队列priority_queue中只有一个元素(根节点)为止。
(3)设计测试数据,写出程序文档。
表四:表二中各元素的哈夫曼编码三、实验设备1台PC及VISUAL C++6.0软件四、代码#include <iostream>#include <queue>#include <vector>#include <iomanip>#include <string>#include<cctype>using namespace std;structcodeInformation{double priority;charcodeName;intlchild,rchild,parent;bool test;bool operator < (constcodeInformation& x) const {return !(priority<x.priority);} };bool check(vector<codeInformation>qa,const char c){for (int i=0 ;i<(int)(qa.size());i++){if(qa[i].codeName==c) return true;} return false;}voidaline(char c,int n){for (int i=0;i<n;i++)cout<<c;}intInputElement(vector<codeInformation>* Harffcode,priority_queue<codeInformation>* pq) {int i=1,j=1;codeInformation wk;while(i){aline('-',80);cout<<"请输入第"<<j<<"个元素的字符名称(Ascll码):"<<flush;cin>>wk.codeName;while(check(* Harffcode,wk.codeName)){cout<<"字符已存在,请输入一个其他的字符:";cin>>wk.codeName;}cout<<"请输入第"<<j<<"个元素的概率(权值):"<<flush;cin>>wk.priority;wk.lchild=wk.rchild=wk.parent=-1;wk.test=false;Harffcode->push_back(wk);pq->push(wk);j++;cout<<"1…………继续输入下一个元素信息!"<<endl;cout<<"2…………已完成输入,并开始构造哈夫曼树!"<<endl;cin>>i;if (i==2) i=0;}int count=1;j=Harffcode->size();int selectElement(vector<codeInformation>*,priority_queue<codeInformation>*);for (int k=j;k<2*j-1;k++){aline('*',80);cout<<"第"<<count<<"次合并:"<<endl;int i1=selectElement(Harffcode,pq);int i2=selectElement(Harffcode,pq);(*Harffcode)[i1].parent=(*Harffcode)[i2].parent=k;wk.lchild=wk.rchild=wk.parent=-1;wk.codeName='#';(*Harffcode).push_back(wk);wk.priority=(*Harffcode)[k].priority=(*Harffcode)[i1].priority+(*Harffcode)[i2].priority;(*Harffcode)[k].lchild=i1;(*Harffcode)[k].rchild=i2;wk.test=false;pq->push(wk); c ount++;cout<<"所合成的节点名称:#(虚节点)\t"<<"概率(权值):"<<(*Harffcode)[k].priority<<endl;}aline('*',80);return j;}voidshowChar(const char c){if(isspace(c))cout<<"#";cout<<c;}int selectElement(vector<codeInformation>*Harffcode,priority_queue<codeInformation>*qurgh){for (int i=0;i<(int)(*Harffcode).size();i++){if (((*Harffcode)[i].priority==(*qurgh).top().priority)&&((*Harffcode)[i].test==false)){cout<<"所选择的节点的信息:"<<"频率(权值):"<<setw(5)<<(*qurgh).top().priority<<"\t 名为:";showChar((*qurgh).top().codeName);cout<<endl;(*qurgh).pop();(*Harffcode)[i].test=true;return i;}}}voidhuffmanCode(vector<codeInformation>Harffcode,int n){for (int i1=0;i1<(int)Harffcode.size();i1++){cout<<"array["<<i1<<"]的概率(权值):"<<Harffcode[i1].priority<<"\t"<<"名为:";showChar(Harffcode[i1].codeName);cout<<"\t父节点的数组下标索引值:"<<Harffcode[i1].parent<<endl;}aline('&',80);for (int i=0;i<n;i++){string s=" "; int j=i;while(Harffcode[j].parent>=0){if (Harffcode[Harffcode[j].parent].lchild==j) s=s+"0";else s=s+"1";j=Harffcode[j].parent;}cout<<"\n概率(权值)为:"<<setw(8)<<Harffcode[i].priority<<" 名为:";showChar(Harffcode[i].codeName);cout<<"的符号的编码是:";for (int i=s.length();i>0;i--)cout<<s[i-1];}}voidchoise(){cout<<endl;aline('+',80);cout<<"\n1……………………继续使用该程序"<<endl;cout<<"2……………………退出系统"<<endl;}void welcome(){cout<<"\n"<<setw(56)<<"欢迎使用哈夫曼编码简易系统\n"<<endl;}int main(){welcome();system("color d1");int i=1,n;vector<codeInformation>huffTree; priority_queue<codeInformation>qpTree;while(i!=2){n=InputElement(&huffTree,&qpTree);huffmanCode(huffTree, n);choise();cin>>i;huffTree.clear();while(qpTree.empty()) qpTree.pop();}return 0;}五、实验过程原始记录( 测试数据、图表、计算等)程序测试结果及分析:图(2)输入第一组测试数据开始输入第一组测试数据,该组数据信息如表一所示。
数据结构(C语言版)实验报告(哈夫曼树)

《数据结构与算法》实验报告一、需求分析1.问题描述:利用哈夫曼编码进行通信可以大大提高信道利用率,缩短信息传输时间,降低传输成本。
但是,这要求在发送端通过一个编码系统对待传数据预先编码,在接收端将传来的数据进行译码(复原)。
对于双工通道(及可以双向传输信息的通道),每端都需要一个完整的编/译码系统。
试为这样的信息收发站写一个哈夫曼的编/译码系统。
2.基本要求一个完整的系统应具有以下功能:(1)I:初始化(Initialization)。
从终端读入字符集大小n,以及n个字符和n个权值,建立哈夫曼树,并将它存于文件hfmTree中。
(2)E:编码(Encoding)。
利用已建好的哈夫曼树(如不在内存,则从文件hfmTree中读入),对文件ToBeTran中的正文进行编码,然后将结果存入文件CodeFile中。
(3)D:译码(Decoding)。
利用已建好的哈夫曼树将文件CodeFile中的代码进行译码,结果存入文件TextFile中。
(4)P:印代码文件(Print)。
将文件CodeFile以紧凑格式显示在终端上,每行50个代码。
同时将此字符形式的编码文件写入文件CodePrin中。
(5)T:印哈夫曼树(Tree printing)。
将已在内存中的哈夫曼树以直观的方式(树或凹入表形式)显示出,同时将此字符形式的哈夫曼树写入文件TreePrint中。
3.测试数据(1)利用教科书例6-2中的数据调试程序。
(2)用下表给出的字符集和频度的实际统计数据建立哈夫曼树,并实现以下报文的编码和译码:“THIS PROGRAM IS MY FAVORITE”。
4,实现提示(1)编码结果以文本方式存储在文件CodeFile中。
(2)用户界面可以设计为“菜单”方式:显示上述功能符号,再加上“Q”表示退出运行Quit。
请用户键入一个选择功能符。
此功能执行完毕后再显示此菜单,直至某次用户选择了“Q”为止。
(3)在程序的一次执行过程中,第一次执行I、D或C命令之后,哈夫曼树已经在内存了,不必再读入。
数据结构哈夫曼树编码及译码的实现实验报告

实验:哈夫曼树编码及译码的实现一.实验题目给定字符集的HUFFMANN编码与解码,这里的字符集及其字符频数自己定义,要求输出个字符集的哈夫曼编码及给定的字符串的哈夫曼码及译码结果。
二.实验原理首先规定构建哈夫曼树,然后进行哈夫曼树的编码,接着设计函数进行字符串的编码过程,最后进行哈夫曼编码的译码。
首先定义一个结构体,这个结构体定义时尽可能的大,用来存放左右的变量,再定义一个地址空间,用于存放数组,数组中每个元素为之前定义的结构体。
输入n个字符及其权值。
构建哈夫曼树:在上述存储结构上实现的哈夫曼算法可大致描述为:1.首先将地址空间初始化,将ht[0…n-1]中所有的结点里的指针都设置为空,并且将权值设置为0.2.输入:读入n个叶子的权值存于向量的前n个分量中。
它们是初始森林中n个孤立的根结点上的权值。
3.合并:对森林中的树共进行n-1次合并,所产生的新结点依次放入向量ht的第i个分量中。
每次合并分两步:①在当前森林ht[0…i-1]的所有结点中,选取权最小和次小的两个根结点[s1]和 [s2]作为合并对象,这里0≤s1,s2≤i-1。
②将根为ht[s1]和ht[s2]的两棵树作为左右子树合并为一棵新的树,新树的根是新结点ht[i]。
具体操作:将ht[s1]和ht[s2]的parent置为i,将ht[i]的lchild和rchild分别置为s1和s2 .新结点ht[i]的权值置为ht[s1]和ht[s2]的权值之和。
4.哈夫曼的编码:约定左子为0,右子为1,则可以从根结点到叶子结点的路径上的字符组成的字符串作为该叶子结点的编码。
当用户输入字母时。
就在已经找好编码的编码结构体中去查找该字母。
查到该字母就打印所存的哈夫曼编码。
接着就是完成用户输入0、1代码时把代码转成字母的功能。
这是从树的头结点向下查找,如果当前用户输入的0、1串中是0则就走向该结点的左子。
如果是1这就走向该结点的右结点,重复上面步骤。
哈夫曼树的实验报告1
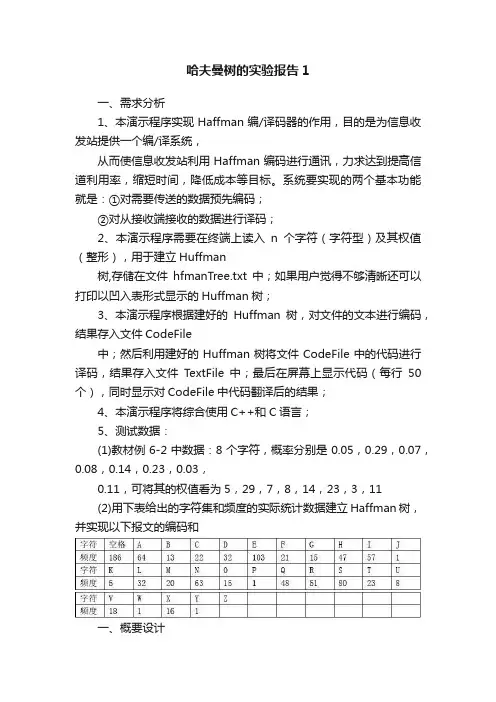
哈夫曼树的实验报告1一、需求分析1、本演示程序实现Haffman编/译码器的作用,目的是为信息收发站提供一个编/译系统,从而使信息收发站利用Haffman编码进行通讯,力求达到提高信道利用率,缩短时间,降低成本等目标。
系统要实现的两个基本功能就是:①对需要传送的数据预先编码;②对从接收端接收的数据进行译码;2、本演示程序需要在终端上读入n个字符(字符型)及其权值(整形),用于建立Huffman树,存储在文件hfmanTree.txt中;如果用户觉得不够清晰还可以打印以凹入表形式显示的Huffman树;3、本演示程序根据建好的Huffman树,对文件的文本进行编码,结果存入文件CodeFile中;然后利用建好的Huffman树将文件CodeFile中的代码进行译码,结果存入文件TextFile中;最后在屏幕上显示代码(每行50个),同时显示对CodeFile中代码翻译后的结果;4、本演示程序将综合使用C++和C语言;5、测试数据:(1)教材例6-2中数据:8个字符,概率分别是0.05,0.29,0.07,0.08,0.14,0.23,0.03,0.11,可将其的权值看为5,29,7,8,14,23,3,11(2)用下表给出的字符集和频度的实际统计数据建立Haffman树,并实现以下报文的编码和一、概要设计1、设定哈夫曼树的抽象数据类型定义ADT Huffmantree{数据对象:D={a i| a i∈Charset,i=1,2,3,……n,n≥0}数据关系:R1={< a i-1, a i >| a i-1, a i∈D, i=2,3,……n}基本操作:Initialization(&HT,&HC,w,n,ch)操作结果:根据n个字符及其它们的权值w[i],建立Huffman树HT,用字符数组ch[i]作为中间存储变量,最后字符编码存到HC中;Encodeing(n)操作结果:根据建好的Huffman树,对文件进行编码,编码结果存入到文件CodeFile 中Decodeing(HT,n)操作结果:根据已经编译好的包含n个字符的Huffman树HT,将文件的代码进行翻译,结果存入文件T extFile中} ADT Huffmantree1)主程序模块void main(){输入信息,初始化;选择需要的操作;生成Huffman树;执行对应的模块程序;输出结果;}2)编码模块——根据建成的Huffman树对文件进行编码;3)译码模块——根据相关的Huffman树对编码进行翻译;各模块的调用关系如图所示二、详细设计1、树类型定义typedef struct {unsigned int weight; //权值char ch1; //储存输入的字符unsigned int parent,lchild,rchild;}HTNode,*HuffmanTree;2、编码类型定义typedef char **HuffmanCode;哈夫曼编译器的基本操作设置如下Initialization(HuffmanTree &HT,HuffmanCode &HC,int *w,int &n,char *ch) //根据输入的n个字符及其它们的权值w[i],建立Huffman树HT,用字符数组ch[i]作为中间存储变量存储编码,最后转存到HC中;Encodeing(int n)//根据建好的包含n个字符的Huffman树,对文件进行编码,编码结果存入到文件CodeFile中Decodeing(HuffmanTree HT,int n)//根据已经编译好的包含n个字符的Huffman树HT,对文件的代码进行翻译,结果存入文件TextFile中基本操作操作的算法主函数及其他函数的算法void select(HuffmanTree HT,int n,int &s1,int &s2){ //依次比较,从哈夫曼树的中parent为0的节点中选择出两个权值最小的if(!HT[i].parent&&!HT[S1]&&!HT[S2]){if(HT[i].weight<ht[s1].weight){< p="">s2=s1; s1=i;}else if(HT[i].weight<ht[s2].weight&&i!=s1)< p=""> s2=i;}3、函数的调用关系图三、调试分析Encodeing Decoding Print PrintTreeInitialization1、本次实习作业最大的难点就是文件的读和写,这需要充分考虑到文件里面的格式,例如空格,换行等等,由于不熟悉C++语言和C语言的文件的输入和输出,给编程带来了很大的麻烦;2、原本计划将文本中的换行格式也进行编码,也由于设计函数比较复杂,而最终放弃;3、一开始考虑打印哈夫曼树的凹入表时是顺向思维,希望通过指针的顺序变迁来实现打印,但问题是从根结点到叶子结点的指针不是顺序存储的,所以未能成功,后来查找相关资料,最终利用递归的方法解决问题;4、程序中的数组均采用了动态分配的方法定义,力求达到减少空间的浪费;5、时间的复杂度主要是由查树这个步骤决定,因为无论是编码还是译码都需要对Huffman树进行查找和核对,但考虑到英文字母和空格也就是27个字符,影响不是很大;6、程序无论在屏幕显示还有文件存储方面都达到了不错的效果;7、程序不足的地方就是在文件文本格式方面处理得还是不够,或许可以通过模仿WORD的实现来改善。
哈夫曼树_实验报告

一、实验目的1. 理解哈夫曼树的概念及其在数据结构中的应用。
2. 掌握哈夫曼树的构建方法。
3. 学习哈夫曼编码的原理及其在数据压缩中的应用。
4. 提高编程能力,实现哈夫曼树和哈夫曼编码的相关功能。
二、实验原理哈夫曼树(Huffman Tree)是一种带权路径长度最短的二叉树,又称为最优二叉树。
其构建方法如下:1. 将所有待编码的字符按照其出现的频率排序,频率低的排在前面。
2. 选择两个频率最低的字符,构造一棵新的二叉树,这两个字符分别作为左右子节点。
3. 计算新二叉树的频率,将新二叉树插入到排序后的字符列表中。
4. 重复步骤2和3,直到只剩下一个节点,这个节点即为哈夫曼树的根节点。
哈夫曼编码是一种基于哈夫曼树的编码方法,其原理如下:1. 从哈夫曼树的根节点开始,向左子树走表示0,向右子树走表示1。
2. 每个叶子节点对应一个字符,记录从根节点到叶子节点的路径,即为该字符的哈夫曼编码。
三、实验内容1. 实现哈夫曼树的构建。
2. 实现哈夫曼编码和译码功能。
3. 测试实验结果。
四、实验步骤1. 创建一个字符数组,包含待编码的字符。
2. 创建一个数组,用于存储每个字符的频率。
3. 对字符和频率进行排序。
4. 构建哈夫曼树,根据排序后的字符和频率,按照哈夫曼树的构建方法,将字符和频率插入到哈夫曼树中。
5. 实现哈夫曼编码功能,遍历哈夫曼树,记录从根节点到叶子节点的路径,即为每个字符的哈夫曼编码。
6. 实现哈夫曼译码功能,根据哈夫曼编码,从根节点开始,按照0和1的路径,找到对应的叶子节点,即为解码后的字符。
7. 测试实验结果,验证哈夫曼编码和译码的正确性。
五、实验结果与分析1. 构建哈夫曼树根据实验数据,构建的哈夫曼树如下:```A/ \B C/ \ / \D E F G```其中,A、B、C、D、E、F、G分别代表待编码的字符。
2. 哈夫曼编码根据哈夫曼树,得到以下字符的哈夫曼编码:- A: 00- B: 01- C: 10- D: 11- E: 100- F: 101- G: 1103. 哈夫曼译码根据哈夫曼编码,对以下编码进行译码:- 00101110111译码结果为:BACGACG4. 实验结果分析通过实验,验证了哈夫曼树和哈夫曼编码的正确性。
(完整word版)哈夫曼树实验报告

实验报告1、实验目的:(1)理解哈夫曼树的含义和性质。
(2)掌握哈夫曼树的存储结构以及描述方法。
(3)掌握哈夫曼树的生成方法。
(4)掌握哈夫曼编码的一般方法,并理解其在数据通讯中的应用.2、实验内容:哈夫曼树与哈弗曼编码、译码a。
问题描述:哈夫曼问题的提出可以参考教材P。
145。
利用哈弗曼编码进行通信可以大大提高通信利用率,缩短信息传输时间,降低传输成本。
但是,这要求在发送端通过一个编码系统对待传数据预先编码,在接收端将传来的数据进行译码.b。
算法提示:参见教材P.147—148算法6.12、6。
13的描述.3、实验要求:建立哈夫曼树,实现编码,译码。
错误!.初始化(Initialization)。
从终端读入字符集大小n,以及n个字符和n个权值,建立哈夫曼树,并将它存于文件hfmTree中。
○2。
编码(Encoding).利用已建好的哈夫曼树(如不在内存,则从文件hfmTree中读入),对文件ToBeTran 中的正文进行编码,然后将结果存入文件CodeFile中。
○3.译码(Decoding ).利用已建好的哈夫曼树将文件CodeFile中的代码进行译码,结果存入文件T extFile 中。
错误!.输出代码文件(Print).将文件CodeFile以紧凑格式显示在终端上,每行50个代码。
同时将此字符形式的编码文件写入文件CodePrint中。
错误!。
输出哈夫曼树(TreePrinting).将已在内存中的哈夫曼树以直观的方式(树或凹入表形式)显示在终端上,同时将此字符形式的哈夫曼树写入文件TreePrint中。
测试数据:设权值c= (a,b, c, d , e, f,g,h)w=(5,29,7,8,14,23,3,11),n=8。
按照字符‘0’或‘1’确定找左孩子或右孩子,则权值对应的编码为:5:0001,29:11,7:1110,8:111114:110,23:01,3:0000,11:001。
哈夫曼树实验报告
哈夫曼树实验报告一、问题描述利用哈夫曼编码进行通信可以大大提高信道利用率,缩短信息传输时间,降低传输成本。
但是,这要求在发送端通过一个编码系统对待传数据预先编码,在接收端将穿来的数据进行译码,此试验即设计这样的一个简单的编/译码系统。
系统应该具有如下的几个功能。
1. 接受原始数据从终端任意读入字母,求出其各自的权重值,建立哈夫曼树,并将它存于hfmtree.dat文件中。
2. 编码利用已建好的哈夫曼树,对文件中的正文进行编码,然后将结果存入codefile.dat中。
3. 译码利用已建好的哈夫曼树将文件codefile.dat中的代码进行译码,结果存入文件textfile.dat中。
4. 打印编码规则即字符与编码的一一对应关系。
5. 打印哈夫曼树将已存在内存中的哈夫曼树以直观的方式显示在终端上。
二、数据结构设计1. 构造哈夫曼树时使用静态量表作为哈夫曼树的存储。
在构造哈夫曼树时,设计一个结构体数组HuffNode保存哈夫曼树中各节点的信息,根据二叉树的性质可知,具有n个叶子节点的哈夫曼树共有2n-1个结点,所以数组HuffNode的大小设置为2n-1,描述节点的数据类型为:typedef struct{int weight; //结点权值int parent;int lchild;int rchild;}HNodeType;2. 求哈夫曼编码时使用一位结构数组HuffCode作为哈腹满编码信息的存储。
求哈夫曼编码,实质上就是在以建立的哈夫曼树中,从叶子结点开始,沿结点的双亲链域退到根结点,每退回一步,就走过了哈夫满树的一个分支,从而得到一位哈夫曼码值,由于一个字符的哈夫曼编码是从根结点到相应叶子结点所经过的路径上各分支所组成的0、1序列,因此先得到的分支代码为所求编码的低位码,后得到的分支代码为所求编码的高位码,所以设计如下数据类型:typedef struct{int bit[26];int start;}HCodeType;3. 文件hfmtree.dat、codefile.dat、和textfile.dat。
哈夫曼树编码实训报告
一、实训目的本次实训旨在通过实际操作,让学生掌握哈夫曼树的基本概念、构建方法以及编码解码过程,加深对数据结构中树型结构在实际应用中的理解。
通过本次实训,学生能够:1. 理解哈夫曼树的基本概念和构建原理;2. 掌握哈夫曼树的编码和解码方法;3. 熟悉Java编程语言在哈夫曼树编码中的应用;4. 提高数据压缩和传输效率的认识。
二、实训内容1. 哈夫曼树的构建(1)创建叶子节点:根据给定的字符及其权值,创建叶子节点,并设置节点信息。
(2)构建哈夫曼树:通过合并权值最小的两个节点,不断构建新的节点,直到所有节点合并为一棵树。
2. 哈夫曼编码(1)遍历哈夫曼树:从根节点开始,按照左子树为0、右子树为1的规则,记录每个叶子节点的路径。
(2)生成编码:将遍历过程中记录的路径转换为二进制编码,即为哈夫曼编码。
3. 哈夫曼解码(1)读取编码:将编码字符串按照二进制位读取。
(2)遍历哈夫曼树:从根节点开始,根据读取的二进制位,在哈夫曼树中寻找对应的节点。
(3)输出解码结果:当找到叶子节点时,输出对应的字符,并继续读取编码字符串。
三、实训过程1. 准备工作(1)创建一个Java项目,命名为“HuffmanCoding”。
(2)在项目中创建以下三个类:- HuffmanNode:用于存储哈夫曼树的节点信息;- HuffmanTree:用于构建哈夫曼树、生成编码和解码;- Main:用于实现主函数,接收用户输入并调用HuffmanTree类进行编码和解码。
2. 编写代码(1)HuffmanNode类:```javapublic class HuffmanNode {private char data;private int weight;private HuffmanNode left;private HuffmanNode right;public HuffmanNode(char data, int weight) {this.data = data;this.weight = weight;}}```(2)HuffmanTree类:```javaimport java.util.PriorityQueue;public class HuffmanTree {private HuffmanNode root;public HuffmanNode buildHuffmanTree(char[] data, int[] weight) {// 创建优先队列,用于存储叶子节点PriorityQueue<HuffmanNode> queue = new PriorityQueue<>();for (int i = 0; i < data.length; i++) {HuffmanNode node = new HuffmanNode(data[i], weight[i]);queue.offer(node);}// 构建哈夫曼树while (queue.size() > 1) {HuffmanNode left = queue.poll();HuffmanNode right = queue.poll();HuffmanNode parent = new HuffmanNode('\0', left.weight + right.weight);parent.left = left;parent.right = right;queue.offer(parent);}root = queue.poll();return root;}public String generateCode(HuffmanNode node, String code) {if (node == null) {return "";}if (node.left == null && node.right == null) {return code;}generateCode(node.left, code + "0");generateCode(node.right, code + "1");return code;}public String decode(String code) {StringBuilder result = new StringBuilder();HuffmanNode node = root;for (int i = 0; i < code.length(); i++) {if (code.charAt(i) == '0') {node = node.left;} else {node = node.right;}if (node.left == null && node.right == null) { result.append(node.data);node = root;}}return result.toString();}}```(3)Main类:```javaimport java.util.Scanner;public class Main {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);System.out.println("请输入字符串:");String input = scanner.nextLine();System.out.println("请输入字符及其权值(例如:a 2 b 3 c 5):"); String[] dataWeight = scanner.nextLine().split(" ");char[] data = new char[dataWeight.length / 2];int[] weight = new int[dataWeight.length / 2];for (int i = 0; i < dataWeight.length; i += 2) {data[i / 2] = dataWeight[i].charAt(0);weight[i / 2] = Integer.parseInt(dataWeight[i + 1]);}HuffmanTree huffmanTree = new HuffmanTree();HuffmanNode root = huffmanTree.buildHuffmanTree(data, weight); String code = huffmanTree.generateCode(root, "");System.out.println("编码结果:" + code);String decoded = huffmanTree.decode(code);System.out.println("解码结果:" + decoded);scanner.close();}}```3. 运行程序(1)编译并运行Main类,输入字符串和字符及其权值。
哈夫曼树上机实验报告
霍夫曼树实验目的:掌握结构体、指针及二叉树的生成、遍历等操作掌握霍夫曼编码/译码的原理。
基本要求:熟练掌握树的操作。
程序实现:程序第一遍统计原数据中各字符出现的频率,利用得到的频率值创建哈夫曼树,并把树的信息保存起来,以便解压时创建同样的哈夫曼树进行解压;第二遍,根据第一遍扫描得到的哈夫曼树进行编码,并把编码后的码字存储。
要点分析:题目中涉及的主要知识点:1、本程序参考霍夫曼算法(由给定的权值构造赫夫曼树):(1) 由给定的n个权值{wθ, w1, w2, … , Wn-I},构造具有n棵二叉树的集合F二{TO, T1, T2, ”,Tn-I},其中每一棵二叉树Ti只有一个带有权值VVi 的根结点,其左、右子树均为空。
(2) 重复以下步骤,直到F中仅剩下一棵树为止:①在F中选取两棵根结点的权值最小的二叉树,做为左、右子树构造一棵新的二叉树。
置新的二叉树的根结点的权值为其左、右子树上根结点的权值之和。
② 在F中删去这两棵二叉树。
③ 把新的二叉树加入F。
2、用构造赫夫曼树以完成赫夫曼编码:把d1,d2,,z , dn作为叶子.word资料. 结点,把Wl, w2, … , Wn作为叶子结点的权,构造赫夫曼树。
在赫夫曼树中结点的左分支赋0,右分支赋1,从根结点到叶子结点的路径上的数字拼接起来就是这个叶子结点字符的编码。
3、译码的过程是分解电文中的字符串,从根出发,按字符'0'或'1' 确定找左孩子或右孩子,直至叶子节点,便求得该子串相应的字符。
心得体会:通过本次实验,我熟练掌握了结构体、指针及二叉树的生成、遍历等操作,掌握了霍夫曼编码和译码的原理,熟练掌握树的操作,尤其是对霍夫曼树有了更深刻的理解。
同时,在编写代码的过程中方,对字符串的相关知识进行了回顾。
代码#include<std io.h>#include<stdlib.h># i ncIude<st r i ng.h>typedef struet{int Weight;int Parent, IChi Id,rchiId;int sign;}HTNode, *HuffmanTree;typedef Char * *HuffmanCode;VOid HUffmanCOding(HUffmanTree &HT, HUffmanCOde &HC, int *w, int n, Char *s); VOid SeIect (HUffmanTree &HT, int i, int &s1, int &s2);VOid CreatHuffmanTree(int *w, Char *s,Char *r);VOid Pr (HUffmanCode &HC,Char r [],Char s,Char a[]);VOid HUffmanYM(HUffmanCOde &HC,Char r [],Char a[], int n, HUffmanTree &HT);VOid HUffmanPaSS(HUffmanCOde &HC,Char r [], int n, HUffmanTree &HT);int mainO{Char s[100];Char r[100];Char a[100]="aπ Jint w[100];int n,p;HUffmanTree HTJHUffmanCOde HC;Printf C,请输入进行编码的字符串∖rΓ);SCanf ("%s", S);P=Strien(s);if (p!=1)CreatHuffmanTree (w, s, r);Pr i ntf ("进行编码 ...... ∖nπ);if(p!=DHUffmanCOd i ng (HT, HC, w, Str Ien (r) -1, r);else Pr intf (,,%c 的霍夫曼编码是:⅜c∖nπ, s[0], ,0,);Printf C,霍夫曼码序列为:∖n");if(p!=Dfor (i rτt i=0; i <str Ien (S) ; i ÷+)Pr (HC, r, s[i], a);Printf ("∖n");n=s tCe n( r)-1;if(p==1)printfC l0∖n,i);Pr intf (”霍夫曼编码进行译码:∖r√);if(P==I)Pr intf (Π%C M, S[0]);e I Se HUffmanYM (HC, r, a, n, HT);Printf ("∖n");Pr i ntf ("先序遍历输出叶子节点∖n");if(P==I){Pr intf(u%c∖nπ,S[0]);}e I Se HUffmanPaSS (HCJ r, n, HT);retUrn 0;}VOid HUffmanCOding(HUffmanTree &HT,HUffmanCOde &HC, int w[], int n,Char s[]) { int s1,s2,f,c;int m, i, I;int start;Char cd[101] Jif (n<1)return;I=Stτ Ien (S);m=2*n-1;HT= (HUffmanTree)ma I IOC((m+1)*s iZeOf(HTNOde));HT[0].weight=10000;for (i=1;i<=n;++i){HT [ i ]. v/e i ght=w[i-l];HT[i].Parent=0;HT[i].IchiId=O;HT[i].rchild=O;HT [ i].Sign=O;}for (;i<=m+1;++i){HT[i]. v∕eight=O;HT [ i].Parent=0;HT[i].IchiId=O;HT[i].rchild=O;HT [ i].Sign=O;}for (i=n+1;i<=m;i++)}Se I ect (HT, i-1, s1, s2);//选择最小的两个结点HT[s1]. Parent=i ;HT[s2]. Parent=i;//将它们的父节点赋值HT[i].IChild=S1;HT[i].rchild=s2;HT[i]. v∕eight=HT[sl]. Weight÷HT[s2]. weight;HC= (HUffmanCOde) ma Iloc((n+1)*s i ZeOf(Char *)); cd[n-1]=,∖0,;for (i=1;i<=n;i++){Start=n;C= i ;for (f=HT[i]. Parent;f!=Ojf=HT[f].Parent){if (HT[f]. IChiId==C){Start—; cd[start]='O';}else{Start—; cd[start] = ' 1';}C=f;}HC[i] = (Char *)ma Iloc( (n~start)*s iZeOf(Char));for (int a=O;a<n-start;a++){HC[i] [a]=Cd[start+a];}HC[i][a] = ,∖O,;Pr i ntf (π%c 的霍夫曼编码是: %s∖n u, s [ i ], HC [ i ]);}}VOid Se Iect (HUffmanTree &HT, int i, int &s1, int &s2)s1=0;s2=0;for (int j=1;j<=i;j++)if (HT[j]. Parent==O)}i f(HT[j]. we i ght<=HT[s1]. We i ght) s1=j; else continue;else continue;}for(j=1;j<=i;j++){if (j==s1)corτt inue;elseif (HT[j]. Parent=O){if(HT[j]. we ight<=HT[s2]. Weight) s2=j;else COntinue;}else continue;}}VOid CreatHUffmanTree (int w[], Char s[], Char r[]) {int g=1;int q=0;r[0]=,0,;r[1]=s[0];w[0]=1;for (int e=1 ;e<str len(s) ;e++){for (int k=1;k<=g;k++){if (r [k]=s[e]){w[k~1]++;q=1;}else COntinue;1if (q==0){r[++g]=s[β] Jw[g-1]=1;} q=0;r[÷÷g]=,∖O∙;}VOid Pr (HUffmanCode &HC,Char r [],Char s,Char a[]) {for (int i=1;i<strIen(r) ;i++){if (r[i]==s){Printf (n%s,,,HC[i]); StrCat (a, HC[i]);}else COrTtinue;}}VOid HUffmanYM(HUffmanCOde &HC,Char r [],Char a [], int n, HUffmanTree &HT) { int e=st门en(a);int k=0;int f=2*n-1;Char b[10] = ,,Γ,;for (int j=1;j<=e;j++){if (HT[f]. IChild!=O∣∣HT[f]. rchi ld!=O){b[k]=a[j]Jk++;if(a[j] = ,Γ)仁HT[f]. rchiId;else if (a[j]==,O,)仁HT[f]. IChi Id;}else{for (int S=I;s<=n;s++){if (strcmp(HC[s], b) ==0){Pr intf("%cπ, r[s]);break;else COntinue;for (int u=0;u<10;u++) b[u]=,∖O,;k=0; f=2*n-1;j=j-1;}}}n,HUffmanTree &HT) VOid HUffmanPaSS(HUffmanCOde &HC, Char r[], in {int f,k=0;Ohar b[10]=,,a∙,;f=2*n-1;HT [f].Sign=O;if (HT[f]. IChi Id=O&&HT[f]. rchi Id=O) return;do{if (HT[f]. IChi Id==O&&HT[f]. rchi Id=0) {for (int S=I;s<=n;s++){if (strcmp(HC[s], b) ==0){Pr i ntf C%c,t9 r [s]); break;}else COntinue;}b[k-] = ,∖O,; HT[f]. S i gn=2; 仁HT[f]. parent;}if (HT[f]. Sign==O){b[k]=,O'; HT[f].S i gn++; 仁HT[f]. IChi Id; k+÷;elseif (HT[f]. sign=!){b[k]=∙Γ; HT[f].sign++; 仁HT[f]. rchiId; k++;elseif (HT [f].si gn==2){f=HT[f]. parent; b[k-]=,∖O,;}whi le(f !=0); Pr intf (π%∖n u);。
哈夫曼树 实验报告
哈夫曼树实验报告哈夫曼树实验报告引言:哈夫曼树是一种经典的数据结构,广泛应用于数据压缩、编码和解码等领域。
本次实验旨在通过构建哈夫曼树,探索其原理和应用。
一、哈夫曼树的定义和构建方法哈夫曼树是一种特殊的二叉树,其叶子节点对应于待编码的字符,而非叶子节点则是字符的编码。
构建哈夫曼树的方法是通过贪心算法,即每次选择权值最小的两个节点合并,直到构建出完整的哈夫曼树。
二、哈夫曼编码的原理和实现哈夫曼编码是一种可变长度编码,即不同字符的编码长度不同。
其原理是通过构建哈夫曼树来确定字符的编码,使得频率较高的字符编码较短,频率较低的字符编码较长。
这样可以有效地减少编码的长度,从而实现数据的压缩。
三、实验过程和结果在本次实验中,我们选择了一段文本作为输入数据,通过统计每个字符的频率,构建了对应的哈夫曼树。
然后,根据哈夫曼树生成了字符的编码表,并将原始数据进行了编码。
最后,我们通过对编码后的数据进行解码,验证了哈夫曼编码的正确性。
实验结果显示,通过哈夫曼编码后,原始数据的长度明显减少,达到了较好的压缩效果。
同时,解码后的数据与原始数据完全一致,证明了哈夫曼编码的可靠性和正确性。
四、哈夫曼树的应用哈夫曼树在实际应用中有着广泛的用途。
其中,最典型的应用之一是数据压缩。
通过使用哈夫曼编码,可以将大量的数据压缩为较小的存储空间,从而节省了存储资源。
此外,哈夫曼树还被广泛应用于网络传输、图像处理等领域,提高了数据传输的效率和图像的质量。
五、对哈夫曼树的思考哈夫曼树作为一种经典的数据结构,其优势在于有效地减少了数据的冗余和存储空间的占用。
然而,随着技术的不断发展,现代的数据压缩算法已经不再局限于哈夫曼编码,而是采用了更为复杂和高效的算法。
因此,我们需要在实际应用中综合考虑各种因素,选择合适的压缩算法。
六、总结通过本次实验,我们深入了解了哈夫曼树的原理和应用。
哈夫曼编码作为一种重要的数据压缩算法,具有广泛的应用前景。
在实际应用中,我们需要根据具体情况选择合适的压缩算法,以达到最佳的压缩效果和性能。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数据结构实验报告实验名称:实验三哈夫曼树学生姓名:班级:班内序号:学号:日期:程序分析:存储结构:二叉树程序流程:template <class T>class BiTree{public:)1.初始化链表的头结点2.获得输入字符串的第一个字符,并将其插入到链表尾部,n=1(n记录的是链表中字符的个数)3.从字符串第2个字符开始,逐个取出字符串中的字符将当前取出的字符与链表中已经存在的字符逐个比较,如果当前取出的字符与链表中已经存在的某个字符相同,则链表中该字符的权值加1。
如果当前取出的字符与链表中已经存在的字符都不相同,则将其加入到链表尾部,同时n++=n(tSize记录链表中字符总数,即哈夫曼树中叶子节点总数)5.创建哈夫曼树6.销毁链表源代码:void HuffmanTree::Init(string Input){Node *front=new Node; 建哈夫曼树(void HuffmanTree::CreateCodeTable(Node *p))算法伪代码:1.创建一个长度为2*tSize-1的三叉链表2.将存储字符及其权值的链表中的字符逐个写入三叉链表的前tSize个结点的data域,并将对应结点的孩子域和双亲域赋为空3.从三叉链表的第tSize个结点开始,i=tSize3.1从存储字符及其权值的链表中取出两个权值最小的结点x,y,记录其下标x,y。
3.2将下标为x和y的哈夫曼树的结点的双亲设置为第i个结点3.3将下标为x的结点设置为i结点的左孩子,将下标为y的结点设置为i结点的右孩子,i结点的权值为x结点的权值加上y结点的权值,i结点的双亲设置为空4. 根据哈夫曼树创建编码表源代码:void HuffmanTree::CreateHTree(Node *p,int n){root= new BiNode<int>[2*n-1]; ata=front->count;root[i].lchild=-1;root[i].rchild=-1;root[i].parent=-1;front=front->next;}front=p;int New1,New2;for(i=n;i<2*n-1;i++){SelectMin(New1,New2,0,i); arent=root[New2].parent=i; ata=root[New1].data+root[New2].data;child=New1;root[i].rchild=New2;root[i].parent=-1;}CreateCodeTable(p); 始化编码表2.初始化一个指针,从链表的头结点开始,遍历整个链表将链表中指针当前所指的结点包含的字符写入编码表中得到该结点对应的哈夫曼树的叶子结点及其双亲如果哈夫曼树只有一个叶子结点,将其字符对应编码设置为0如果不止一个叶子结点,从当前叶子结点开始判断如果当前叶子结点是其双亲的左孩子,则其对应的编码为0,否则为1child指针指向叶子结点的双亲,parent指针指向child指针的双亲,重复的操作将已完成的编码倒序取得链表中的下一个字符3.输出编码表源代码:void HuffmanTree::CreateCodeTable(Node *p){HCodeTable=new HCode[tSize]; ata=front->character; arent; ode[k]='0';k++;}while(parent!=-1) child) ode[k]='0';elseHCodeTable[i].code[k]='1';k++;child=parent;parent=root[child].parent;}HCodeTable[i].code[k]='\0';Reverse(HCodeTable[i].code); ata<<''<<HCodeTable[i].code<<endl;}}时间复杂度:需要遍历哈夫曼树获取编码,时间复杂度为O(n^2)4.选择两个最小权值的函数算法伪代码:1.从下标为begin的结点开始,寻找第一个没用过的结点2.遍历哈夫曼树中从下标为begin到下标为end的结点序列,寻找没用过的同时权值又是最小的结点。
3.暂时改变找到的权值最小结点的双亲域,防止第2次找到相同的结点。
4.将权值最小结点的下标记录下来。
5.重复步骤1~4,找到第2个权值最小的结点源代码:void HuffmanTree::SelectMin(int &New1,int &New2,int begin,int end){int min;for(int j=0;j<2;j++) arent==-1) ata;sign=i;break;}}for(i=begin;i<end;i++) arent==-1){if(min>root[i].data){min=root[i].data;sign=i;}}}root[sign].parent=0;将字符串倒序的函数(void HuffmanTree::Reverse(char*pch))算法伪代码:1.得到字符串的长度2.初始化两个记录下标的变量,一个为字符串开头字符所在的下标i,另一个为字符串结尾字符所在的下标j3.将下标为i和j的字符交换4.i++,j - -时间复杂度:时间复杂度为O(n)6.编码函数(void HuffmanTree::Encode(string &s,string &d))算法伪代码:1. 从s开头的字符开始,逐一对s中的字符进行编码2. 在编码表中查找与当前字符对应的字符3.如果找到了与当前字符对应的编码表中的字符,将其编码追加到解码串的末尾。
4. 重复以上步骤,直到所有待编码串中的字符都编码完毕5. 输出编码后的字符串源代码:void HuffmanTree::Encode(string &s,string &d){for(int j=0;j<();j++) ata){(HCodeTable[i].code); 码函数算法伪代码:1.得到指向哈夫曼树的根结点的指针和指向待解码串中的第1个字符的指针2.逐个读取待解码串中的字符,若为0,则指向哈夫曼树当前结点的指针指向当前结点的左孩子,若为1,则指向当前结点的右孩子3.指向待解码串的指针指向解码串中的下一个字符,直到指向哈夫曼树结点的指针的孩子结点为空4.如果哈夫曼树只有一个叶子结点,直接将待解码串中的编码转换为对应的字符5.如果指向哈夫曼树结点的指针的孩子结点已经为空,则将叶子结点下标对应的字符追加到解码串中。
6.输出解码串源代码:void HuffmanTree::Decode(string &s,string &d){for(int i=0;i<();){int parent=2*tSize-1-1; child!=-1) child;else child;i++;}if(tSize==1) ata);计算哈夫曼编码的压缩比(void HuffmanTree::Calculate(string s1,string s2))算法伪代码:1.获得编码前字符串的长度,即其占用的字节数2.获得编码后的字符串的长度,将其除以8然后向上取整,得到其占用的字节数3.压缩比将两个相除源代码:void HuffmanTree::Calculate(string s1,string s2){int cal1=();int cal2=();cal2=ceill((float)cal2/8); 打印哈夫曼树(voidHuffmanTree::PrintTree(int TreeNode,int layer) )算法伪代码:1.如果待打印结点为空,则返回2.递归调用函数打印当前结点的右子树3.根据当前结点所在的层次确定其前面要输出多少空格,先输出空格,在打印当前结点的权值4.递归调用函数打印当前结点的左子树源代码:void HuffmanTree::PrintTree(int TreeNode,int layer){if(TreeNode==-1) child,layer+1); ata<<endl; child,layer+1); 菜单函数(void HuffmanTree::Menu())算法伪代码:1. 逐一读取键盘缓存区中的字符,并将它们逐一追加到记录输入字符串的string变量中,直到读到回车输入符为止2. 删除string变量末尾的回车输入符3.利用string变量创建哈夫曼树,初始化编码表。
4. 直观打印哈夫曼树5. 对输入的字符串进行编码6. 对编码后的字符串进行解码7. 计算编码前后的压缩比并输出源代码:void HuffmanTree::Menu(){cout<<"请输入你要编码的文本,按回车键确定输入"<<endl;string Input;char letter;do 于题目要求能输入任意长的字符串,所以本程序采用了string变量来记录输入的字符串,并采用string类的类成员函数来完成各项任务2.打印哈夫曼树时采用了递归函数,且采用了凹凸表的形式打印哈夫曼树。
3.为了输入空格,输入时采取逐个字符输入的方式三.程序运行结果分析:主函数流程图:运行结果各函数运行正常,没有bug四. 总结:在实现整个算法设计中运用了二叉树结构及类创新,同时又复习了上学期C++的相应内容。
总结与流程分析过程虽然很辛苦但屡败屡战,获益匪浅,收获了很多。
也认识到自己的不足,希望自己继续努力。
