惠更斯菲涅尔原理基尔霍夫衍射理论
光的衍射理论

矩孔夫琅禾费衍射的积分形式:
衍射零点条件:
半角宽度为:
圆孔的夫琅禾费衍射
圆孔的衍射场存在一中心光斑,称为艾里斑。艾里斑的宽度d为 ,半角宽度 为:
8.瑞利判据
设相邻两个艾里斑中心间的角间距为 ,将 与艾里斑半角宽度 进行比较,二者相等时 ,为能分辨的最小角间距 ,即当第一个像的主极大和另一个像的第一极小重合时,这两个像刚好能分辨,称为瑞利判据。
光栅的色散范围: ,色散范围只与波长和衍射级有关。
12.闪耀光栅
两种照明方式:
入射光垂直光栅平面时的光栅方程:
入射光垂直沟槽面时的光栅方程:
13.菲涅耳波带
第m个波带边界半径为:
波带的面积为:
菲涅耳数: ,a为圆孔半径。
菲涅耳波带片:菲涅耳波带片等效透镜,其焦距为
分别表示入射光方向和场点相对曲面Q面元的法线方向的方位角; 为倾斜因子,表示次级波源发射的各向异性性。
3.亥姆霍兹-基尔霍夫积分定理
在满足定态波亥姆霍兹方程的无源空间取闭合曲面,通过格林公式,推导出曲面内任一点P的场满足: ,该场可由包围这点的任一闭合球面的场确定。
4.巴比涅原理
当两个屏透光部分加起来时,正好是整个平面,这时衍射场与没有衍射屏时的场 相等
第
本章从惠更斯-菲涅耳原理出发,一步步的阐述了光的衍射理论及相关应用,大概思路如下:
惠更斯-菲涅耳原理→亥姆霍兹-基尔霍夫积分定理
1.惠更斯原理
一个波阵面的每个面元,可各看做是一个产生球面子波的次级扰动中心,以后任何时刻的波阵面是所有这些子波的包络面。
2.惠更斯-菲涅耳原理
波阵面上每一个面元可看做次级波源,波场中任一点的光场,是所有次级波源发射的次级波在该场点的相干叠加。当波阵面 上面元dS足够小时,面元dS可认为是点光源,产生的次级波为球面波,那么惠更斯-菲涅耳原理可以将P点的总场表示为
第五章-光的衍射要点

5-2 二、菲涅尔-基尔霍夫衍射公式
目的:把亥姆霍兹-基尔霍夫积 分(5-13)转化为惠更斯-菲涅尔原 理的形式(5-4) 取’= 1+ 2+
(n, r)
r R P
上,E和∂E/∂n由入射光决定 基尔霍夫边界条件假定: 1上, E=∂E/∂n=0 2上,运用辐射条件:limR R(∂E/∂nikE)=0,可忽略2的影响
dE(P)=CK()EQexp(ikr)/r•d
C—常数,K()—倾斜因子
’
z’
图5-3
5-1
菲涅尔假设:K(),K(
只有面上的点对P有贡献 所有面上的点对P点的贡献和:
E(P)=∬dE(P)=C
>=90°)=0,故
E(Q) ∬exp(ikr)/r•K()d (5-2) —惠更斯-菲涅尔原理的数学表达 波前可以是任意曲面,此时 E(P)=∬dE(P)=C ∬ E(Q) exp(ikr)/r•K()d (5-4) —惠更斯-菲涅尔原理的推广
图5-18
5-5
I(P)=E(P)E*(P)=I0[2J1(Z)/Z]2
Z=ka =r/f I0=(a2)2|C’|2是观察屏轴上点的光强
(5-45)
衍射图样圆对称,随r振荡,中央亮斑(爱里斑)
集中了绝大部分能量。亮斑范围由Z=1.22决定, 此时
r0=1.22f/(2a),
基尔霍夫衍射公式形式
复杂,难以得到解析解 傍轴近似以简化衍射公 式:
(1)取cos1,K() 1 (2)球面波幅度因子1/r 1/z (3)相位因子须更高阶近似
y1 x1 z Q 图5-7 r
y x
P
5-3 二、菲涅尔近似
惠更斯-菲涅尔原理

ikr
基尔霍夫边界条件是不自洽严格的衍射理论--矢量衍 射理论光源Sຫໍສະໝຸດ Q r n
p
dS
对于点光源发出的球面波,初相位可取为零 1. P点位相: / 2 的相位差—不影响衍射图样(强度分布) 2. 解决倒退波问题 而原 0, F ( ) 1 菲设 , F ( ) 0 2
1 cos F ( ) 2
三.基尔霍夫衍射积分
数学上证明:光场中任一点P的扰动,可以通过曲面积分, 用包围该点任一闭和曲面上的场值及梯度值表出 基尔霍夫边界条件 1. 开口处光场及其梯度值与无屏时同 忽略屏对入射场的影响 2. 紧贴屏后(1)处无扰动—光场及光 场梯度值为零 忽略入射场在不透光屏后的扩展
...d ...d ...d ...d
叠加
概括为:波面上各点均是相干次波源
菲涅耳发展了惠更斯原理,从而深入认识了衍射现象。 惠-菲原理提供了用干涉解释衍射的基础。
◆ 惠更斯-菲涅耳原理
ikr e ( P) CE (Q) dE F ( )dS r ikr e ( P) C E (Q) E F ( )dS r
1 2
1
Q
R
P r
1
0
2
S
/ a 1
0 ( r )
0
基尔霍夫衍射公式
1 ~ e 1 ~ E ( P) E (Q) (cos 0 cos )d i r 2
标量衍射理论:衍射孔径远大于波长;观察点与孔径的 距离远大于波长——精确 注 意
CH5-2
惠更斯-菲涅耳原理
Huygens-Fresnel principle
§3—2惠更斯-菲涅耳原理
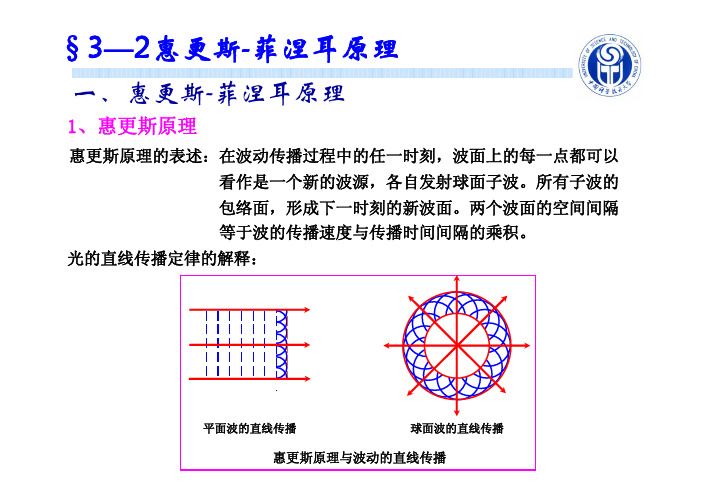
§3—2惠更斯-菲涅耳原理一、惠更斯-菲涅耳原理1、惠更斯原理惠更斯原理的表述:在波动传播过程中的任一时刻,波面上的每一点都可以 看作是一个新的波源,各自发射球面子波。
所有子波的 包络面,形成下一时刻的新波面。
两个波面的空间间隔 等于波的传播速度与传播时间间隔的乘积。
光的直线传播定律的解释:平面波的直线传播球面波的直线传播惠更斯原理与波动的直线传播衍射现象的定性解释:光波的衍射2、惠更斯-菲涅耳原理(1) 惠更斯原理的局限性没有涉及波动的时空周期特性,即波长、振幅、相位等。
虽然可以用 于确定光的传播方向,但无助于确定沿不同方向传播的光波的振幅和相位 大小。
(2) 惠更斯-菲涅耳原理菲涅耳对惠更斯原理的贡献:将不同子波的干涉叠加引入惠更斯原理,并赋予其以相应的相位和振幅表达式。
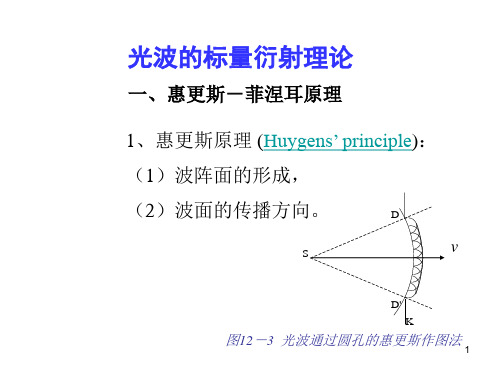
evΔS θ r P*S:t时刻波阵面 ΔS:波阵面上面元S(子波波源)ΣdΣθ0 nθSRQr惠更斯-菲涅耳原理S:光源Σ :光源S发出的光波的任一波面dΣ :波面Σ上位于Q点的面元Pn:面元d Σ 的法线方向单位矢量θ0:光源S到点Q连线与面元法线夹角θ:Q点到场点P的连线与面元法线夹角惠更斯-菲涅耳原理的表述:波面Σ 上的每个面元dΣ 都可以看作是新的波源,它们均发射球面子波,在与波面相距为r处的P点的光振动Ê0(P),等于所有球面子波在该点的 光振动Ê0(P)的相干叠加:E~(P) = ∫∫ d E~(P) Σ按照菲涅耳的假设,Q点处dΣ 面元发出的球面子波在P点的光振动复振幅:dE~(P) =KF (θ0,θ)E0(Q)eikr rdΣK:比例常数;Ê0(Q):光源S在Q点引起光振动复振幅;F(θ0, θ ):倾斜因子,随θ0和θ 的增大而减小。
P点总的光振动复振幅——菲涅耳衍射积分式:E~(P) =K ∫∫∑F(θ0,θ)E~0(Q)eikr rdΣ3、菲涅耳-基尔霍夫衍射积分基尔霍夫通过由电磁场理论严格地数学推导得到:K=−iλF(θ 0,θ)=1 2(cosθ 0+cosθ)基尔霍夫边界条件:设波面处放置一开孔的无限大不透明光屏,且开孔所对应的波面面积为Σ0,则透过光屏的光振动满足:E~0(Q)=⎨⎧E~0 ⎩0(Q)Q在Σ以内0Q在Σ以外0∫∫ 菲涅耳-基尔霍夫衍射积分:E~(P) =−iλΣ0(cosθ0 +2cosθ)E~0(Q)eikr rdΣ① 当波面为以S点为中心的球面时, θ 0=0,F(θ0, θ)=(1+cosθ )/2,只与场点P相对波面的方位有关。
光波的标量衍射理论
~
E
P=
A i
e
xpik
l
l
e
xpik
r
r
cosn,
r
2
cosn,
l
d
子波的复振幅与
K() cosn, r cosn,l
2 成正比,与波长成反比。
i 1 exp[i p]
i
2
表示子波的振动位相超前于入射波90。
6
当光线接近于正入射时 exp(ikl) exp(ikR)
l
R
cos(n, l) 1,
1 x x1 2 y y1 2
z12
z1
x
x1 2 y
2z1
y1 2
[x
x1 2 y
8z13
y1 2 ]2 ....
级数展开
r
z1
x
x1
2 y
2z1
y1 2
近似条件:
[x x1 2 y y1 2 ]2 p
z13
4
y1
Q C
K
x1 r
z1
y x
P
P0 E
11
r
z1
x
x1 2 y
2
光源S在波面ZZ '上
波阵面外任一点光振动应该是波面
上所有子波相干叠加的结果。
任意Q点产生的复振幅:
E~Q
A
exp ikR
R
Z
Q
R
Q点处d 大小的面元
r P
对P点的贡献为: S
dE~P
CK
E~Q
expik
r
r
d
Z'
子波向P点的球面波公式 子波法线方向的振幅 子波振幅随角的变化
基尔霍夫衍射理论
a
a
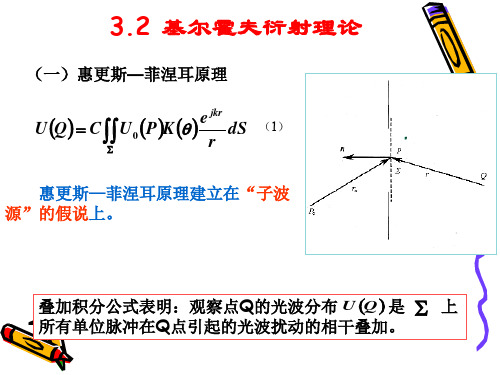
(3)双缝光栅,如图
y
aa
x
d
0
d
2
2
t
x,
y
rect
x
d a
/
2
rect
x
d a
/
2
1
常用衍射屏的透过率函数表示(2):
(4)圆孔衍射物,直径为d。
d
tx, y circ
x2 d
y2
circ
r d
1 0
r d/2 r d /2
说明:上面举例都是衍射屏的振幅变化分布,至于 相位变化型的衍射屏,最典型的是 透镜 。
对r进行二项式展开并化简,有
脉冲响应:
hx, x0; y, y0
1 jz
exp
jk
x
x0
2
y
y0
2
z2
hx x0 , y y0
显然,脉冲响应具有空间不变的函数形式。
无论孔径平面上子波源的位置如何,它所 产生的球面子波的形式是一样的。
hx x0 , y y0
1 jz
exp
jk
x
(2) 外, U 0 P 0
衍射公式的积分限可以被扩展到无穷,即:
UQ
U0
P
F
0
,
e jkr r
dS
衍射公式的适用范围:任意单色光波照明孔径的情况。
因为任意复杂的光波都可以看成是简单球面波的线性组
合。因此,上式中的 U0P 可以理解为在任意单色光照
明下对孔径平面产生的光场分布。
对教材80页一段话的理解。
与惠更斯—菲涅耳衍射积分公式比较:
UQ
1
j
惠更斯原理

1惠更斯-菲涅尔原理⏹ 惠更斯-菲涅耳原理可以表述如下:⏹ 波前上每一个面元都可看成是新的振动中心,它们发出次波(频率与入射波相同); ⏹ 在空间某一点P 的振动是所有这些次波在该点的相干迭加。
⏹ 是相干叠加→复振幅叠加 ⏹ 如图所示。
点光源S 在波面∑’ 上任一点Q 产生的复振幅为 ⏹ 式中,A 是离点光源单位距离处的振幅, ⏹ R 是波面∑’的半径。
⏹ 在Q 点处取面元d σ,面元发出的子波在P 点产生的复振幅与在面元上的复振幅 、面元大小和倾斜因子K(θ)成正比。
⏹ 面元d σ在P 点产生的复振幅可以表示为⏹ K(θ)表示子波的振幅随面元法线与QP 的夹角θ的变化。
( θ称为衍射角) ⏹ c 为一常数,r=QP 。
⏹ 菲涅耳假设:当时θ=0 ,倾斜因子K 有最大值,随着增加θ↑ ,K 减小, ⏹ 当θ≥π/2时,K=0。
(基尔霍夫理论证明不正确)⏹ 对P 点产生作用的将是波面∑’中界于z z’范围内的波面∑上的面元发出的子波。
⏹ 则:⏹ 此即为惠更斯-菲涅耳原理的菲涅耳表达式,此关系式还可推广为(5-4)式, ⏹ 即⏹ 若: ⏹ 有: 2基尔霍夫衍射理论⏹ 基尔霍夫理论,只适用于标量波的衍射,故又称标量衍射理论。
3巴俾涅(Babinet )原理 即两个互补屏单独产生的衍射场的复振幅之和等于没有屏时的复振幅。
在 的那些点,两个互补屏单独产生的强度相等。
菲涅耳衍射是普遍的,夫琅和费衍射是菲涅耳衍射的特例⏹ 基尔霍夫衍射公式的近似:⏹ 1.傍轴近似:入射光垂直孔径面 ⏹ 2.菲涅耳近似 :S ()ikR RA E Q exp ~→= ()()()()σθd r ikr R ikR A cK P E d exp exp ~→= ()()()()⎰⎰∑=σθd rikr K R ikR A c P E exp exp ~ ()ikR RA E Q exp ~ =()()()()⎰⎰∑=σθd K rikr Q E c P E exp ~~ ()0P ~=E ()111,1z r K ≈=θ()()⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡-+-+=2121211211z y y x x z r⏹ 3.夫琅和费近似:⏹ 4.菲涅耳衍射公式:⏹ 5.夫琅和费衍射公式: ⏹ 即只有在很远距离上才能观察到夫琅和费衍射条纹,在实验室中很难实现。
标量衍射理论-2
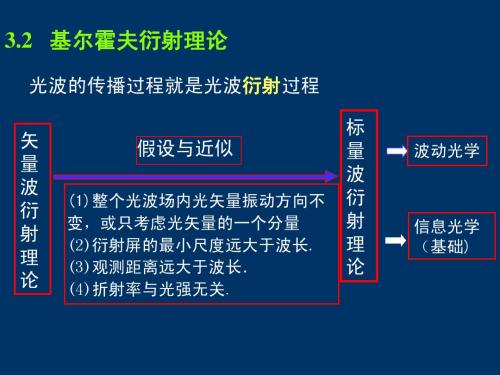
cosα cos β A0 , ,0 λ λ
xy
Uz ( x, y, z)
cosα cos β Az , , z λ λ
z
z=0
U 0 ( x0 , y0 ;0) = U z ( x, y; z ) =
∞ ∞
z=z
cos β cosα cos β cosα cos β cosα A0 , ;0 exp j 2π x0 + y0 d d ∫∞−∫∞ λ λ λ λ λ λ −
3.3 标量衍射的角谱理论
3.3-1单色平面波与线性平移不变系统的本征函数 单色平面波与线性平移不变系统的本征函数 在 z=0 平面上的复振幅分布为:
exp j 2π ( f x ⋅ x + f y ⋅ y ) = exp[ j 2π (ux + vy )]
[
]
cos β cosα = exp j 2π x+ y λ λ
3.2 基尔霍夫衍射理论
光波的传播过程就是光波衍射 衍射过程 衍射 矢 量 波 衍 射 理 论 假设与近似
(1)整个光波场内光矢量振动方向不 变,或只考虑光矢量的一个分量 (2)衍射屏的最小尺度远大于波长. (3)观测距离远大于波长. (4)折射率与光强无关.
标 量 波 衍 射 理 论
波动光学
信息光学 (基础)
∞ ∞
cos β cosα cos β cosα cos β cosα Az , ; z exp j 2π x+ y d d ∫∞−∫∞ λ λ λ λ λ λ −
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
若取 G~ 也满足亥姆霍兹方程,则
由
22GE~~
kk22GE~~
§5-1惠更斯-菲涅尔原理
波动具有两个基本性质,一方面,它是扰动 的传播,一点的扰动能够引起其它点的扰动, 各点相互之间是有联系的。另一方面,它具有 时空周期性,能够相干迭加。
惠更斯原理中的“次波概念反映了上述前一 基本性质,这是其成功的地方。但“时空周期 性”并没有反映。
利用惠更斯原理,可以说明衍射的存在,但 不能确定光波通过衍射屏后沿不同方向传播的 振幅,因而也就无法确定衍射图样中的光强分 布。
§5-1惠更斯-菲涅尔原理
二、惠更斯-菲涅耳原理 此是研究衍射现象的理论基础: 波动具有两个基本性质: 1、波动是扰动的传播,一点的扰动能够引 起其它点的扰动,各点的扰动相互之间是有 联系的; 2、波动具有时空周期性,能够相干叠加。
§5-1惠更斯-菲涅尔原理
在惠更斯原理中,由于缺少对时空周期性 的反映,从而对各次波如何叠加问题就不 能给出令人满意的回答。
1818年,在巴黎科学院举行的以解释衍射现 象为内容的有奖竞赛会上,年青的菲涅耳 出人意料地取得了优胜,他吸收了惠更斯 提出的次波概念,用“次波相干迭加”的 思想将所有衍射情况引到统一的原理中来, 这个原理就是惠更斯菲涅耳原理。
§5-1惠更斯-菲涅尔原理
惠更斯--菲涅耳原理
Z RQθ
其内容如下:
P
~ EQ
A expikR
R
Σ' Z'
§5-1惠更斯-Z菲涅尔原理
~ EQ
A expikR
R
RQθ
Σ
r
S
P
Σ' Z'
式中,A是离点光源单位距离处的振幅,
R是波面∑’的半径。
在Q点处取面元dσ,面元发出的子波~在P点 产生的复振幅与在面元上的复振幅 EQ、面 元大小和倾斜因子K成正比。
即
Z RQθ
若:
~ EQ
有:
A expikR
R
r
Σ S
P
Σ' Z'
E~P c
E~Q expikr K d
r
§5-2 基尔霍夫 标量衍射理论
§5-2基尔霍夫衍射理论
如前所述, 1818年菲涅耳提出了惠更斯-菲涅耳原理,
并给出了菲涅耳衍射积分公式。最初菲涅耳 作的各项假设时,只凭朴素的直觉。 六十余年后,基尔霍夫(1882年)建立了一 个严格的数学理论,证明菲涅耳的设想基本 上正确,只是菲涅耳给出的倾斜因子不对, 并对其进行了修正。
由惠更斯—菲涅耳原理知: 应该把∑面分割成无穷多的面元d ∑ ,把每
个面元d ∑看成发射次波的波源,从所有面 元发射的次波将在P点相遇。 一般说来,由各面元d ∑到P点的光程是不 同的,从而在P点引起的振动位相不同,P 点的总振动就是这些次波在这里相干叠加 的结果。 以上就是惠更斯-菲涅耳原理的基本思想
r Σ S
P
如图5-3所示:
Σ' Z'
“波前上任何一个未受阻挡的点都可以看作
是一个频率(或波长)与入射波相同的子波
源;在其后任何地点的光振动,就是这些子
波叠加的结果。”
s为点波源,∑为从S发出的球面波在某时刻 到达的波面,P为波场中的某个点。要问, 波在P点引起的振动如何?
§5-1惠更斯-菲涅尔原理
当≥π /2时,K=0。
对P点产生作用的将是波面∑’中界于z z’范 围内的波面∑上的面元发出的子波。
§5-1惠更斯-菲涅尔原理
则:
E~P
cA exp ik R
R
K expikr d
r
此即为惠更斯-菲涅耳原理的菲涅耳表达
式,此关系式还可推广为(5-4)式,
基尔霍夫理论,只适用于标量波的衍射,故 又称标量衍射理论。
E~
§5-2基尔霍夫衍射理论
一、亥姆霍兹-基尔霍夫积分定理
以简谐标量波的波动微分方程出发(此方程 在数学上称为“亥姆霍兹”方程)建立了一个 公式,使得空间任意一点的电磁场,可以用包 围该点的任意封闭曲面上的电磁场及其导数求 得”此即为:亥姆霍兹-基尔霍夫积分定理
§5-1 惠更斯-菲涅尔原理
§5-1惠更斯-菲涅尔原理
一、惠更斯原理: 1690年,惠更斯在其著作《论光》中提出假 设:“波前上的每一个面元都可以看作是一 个次级扰动中心,它们能产生球面子波”, 并且:“后一时刻的波前的位置是所有这些 子波前的包络面。”
这里,“波前”可以理解为:光源在某一时 刻发出的光波所形成的波面(等相面)。 “次级扰动中心可以看成是一个点光源”, 又称为“子波源”。
§5-1惠更斯-菲涅尔原理
惠更斯-菲涅耳原理可以表述如下:
波前上每一个面元都可看成是新的振动中心, 它们发出次波(频率与入射波相同);
在空间某一点P的振动是所有这些次波在该点
的相干迭加。
Z
是相干叠加→复振幅叠加
RQθ
如图所示。点光源S在波面∑’ Σ r 上任一点Q产生的复振幅为 S
面元dσ在P点产生的复振幅可以表示为
§5-1惠更斯-菲涅尔原理
dE~ P
cK
A
exp
ikR
exp
ikr
d
R
r
K表示子波的振幅随面元法线与QP的夹 角的变化。( 称为衍射角)
c为一常数,r=QP。
菲涅耳假设:当时0 ,倾斜因子K有最大 值,随着增加↑ ,K减小,
如图5-4所示:
Hale Waihona Puke 设有一单色光波通过Σ'
V
闭合曲面∑’传播。
则光波电磁场的 任一直角分量的复振幅
~ E
Σ' ε ε
P
n
n
§5-2基尔霍夫衍射理论
满足亥姆霍兹方程
即
2 E k2 E 0
若不考虑电磁场其它分量的影响,孤立地
把 表示E看面作内标任量一场点,的并E ,用这曲种面理上论的就E 和是标E n值量
衍射理论。
设
E
和一个位置坐标的任意复函数G在曲面
∑’上和∑’内部都有连续的一阶和二阶偏
导数
则由格林定理:
§5-2基尔霍夫衍射理论
G~2 E~ E~2G~ dv
G~ E~ E~ G~ d
V
'
n
n
(1)
V是闭合面∑’所包围的体积, 表示∑’ 上每一点沿向外法线的偏微商。n
