5基尔霍夫衍射理论
傅里叶光学课件 02_02基尔霍夫衍射理论
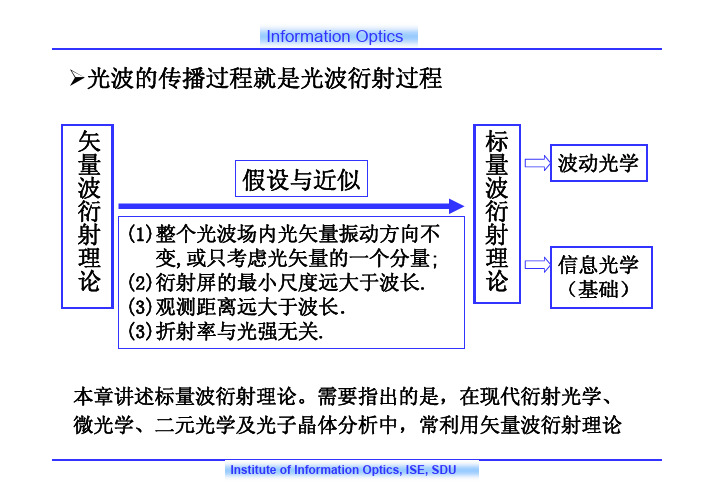
光波的传播过程就是光波衍射过程假设与近似(1)整个光波场内光矢量振动方向不变,或只考虑光矢量的一个分量;(2)衍射屏的最小尺度远大于波长.(3)观测距离远大于波长.光波衍射的线性系统分析基尔霍夫波衍射理论(书2.1惠更斯-菲涅耳原理与基尔霍夫衍射理论一、惠更斯-菲涅耳原理子波(次波)相干叠加0exp()(,)jkr K r θθdU (Q )0)jkr Σ••QrΣnθθS 1S 20exp()1(cos 2jkr r θi是在无限大不透光屏上有一开孔的情况下推导出的. 但可以推广到其它任何复杂的衍射屏。
只是此时,公式中:()()()i P U P t P =入射到衍射屏上的光场的复振幅分布,衍射屏的复振幅透过率。
光波衍射过程是线性系统变换基尔霍夫衍射积分公式为:1e (x )p j krjkr j r 1exp()1(cos 2λ=i 此式是一个叠加积分,满足线性系统的叠加性和均匀性。
因此衍射过程(光波从衍射平面到观察平面的传播过程)可以看作是一个线性系统。
是该线性系统的脉冲响应(点扩散函数可以看作是: 衍射屏上P 点的一个单位脉冲在场产生的复振幅分布。
它描述了衍射系统的特性。
相干光场在自由空间传播的平移不变性2z距z 足够大),且观察范围较0cos 1θ≈(U x 0r Si(x 0这表明,在满足一定条件下,衍射屏上各次波源在场点处所产生的复振幅分布具有相同的分布形式,只是发生了也就是说,具有平移不变性。
可写成卷积形式:21exp jk z zλ⎡+⎣0)(,)y h x x y y −−相干光场在自由空间传播的脉冲响应的近似表达式21exp jk z j zλ⎡⎣220)()1y y z ⎡+−=⎢⎣一、菲涅耳近似(傍轴近似) →菲涅耳衍射在衍射屏和观察范围确定后,当项以后的高次项,不会引起明显的相位误差。
高次项中,起主要作用的是第3项,即当由第20()(28x x zπλ⎡−+⎣201()(8x x λ⎡−+⎣exp()exp jkz jk j z λ⎡=⎢⎣系统的脉冲响应可表示为:菲涅耳衍射的脉冲响应,仍具有平移不变性0002(,)exp exp()exp 2U x y jk jkz x jk j z z λ∞−∞⎡⎢⎣⎡+⎢⎣∫二、夫琅禾费近似(远场近似)→在菲涅耳近似的基础上,如果z 进一步增大,且进一步限定衍射屏透光区域,以至于:2max 2π 可以忽略,忽略该项所引起的相位误差很小22)y y x ⎤−exp())exp jkz x jk j z λ⎛=⎜⎝22exp 2(2y x j x z z πλ⎞+⎡−⎟⎢⎣⎠000)(,;,)y h x y x y dx 则衍射的光场分布为:从上式可以看出:夫琅禾费衍射仍是线性系统,但不是平移不变系统,不再具有平移不变性。
菲涅尔基尔霍夫衍射积分公式

菲涅尔基尔霍夫衍射积分公式下载温馨提示:该文档是我店铺精心编制而成,希望大家下载以后,能够帮助大家解决实际的问题。
文档下载后可定制随意修改,请根据实际需要进行相应的调整和使用,谢谢!本店铺为大家提供各种各样类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,如想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by the editor. I hope that after you download them, they can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!In addition, our shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!是描述波前衍射的一种重要数学公式,它在光学领域有着广泛的应用。
基尔霍夫公式

(4)
3. 基尔霍夫衍射积分公式的证明 . ⑴ 应用基尔霍夫边界条件 为了简化亥姆霍兹-基尔霍夫公式,使其成为更便于计算衍射问题的形式,可按图 x 的方式选 取闭合面 S = Σ + Σ1 + Σ 2 ,其中
图3
Σ1 -位于 ( ξ ,η ) 平面上一个无穷大的不透明屏;
Σ -不透明屏上一个开孔(衍射孔径) ;
r
P
∂E 来表示(图 1) 。下面介 ∂n
r
n
ε
P1
Sε
S
V
图1
图2
3. 应用格林定理 . 格林定理表示为:
∫∫∫ ( G∇ E − E∇ G )dv = ∫∫ G ∂n − E ∂n dσ
2 2 v S
∂E
∂G
(5)
式中 E 为包围 P 点的任意封闭面 S 上的电场, 格林函数 G =
(17)
上式中, Ω 是 Σ 2 对 P 点所张的立体角, d ω 是立体角元。由于
GR = exp ( jkR ) 在 Σ 2 上一致有界,只要满足下述的索末菲辐射条件:
∂E lim R + jkE = 0 R →∞ ∂n
(18)
对 Σ 2 的积分就会随着 R → ∞ 而消失。
exp ( jkR ) R
∂G ( P ) 1 e jkR 1 = cos ( n , R ) jk − ≈ − jkG ∂n R R 因为:R → ∞, con ( n , R ) = −1
(16)
于是,对 Σ 2 的积分化简为:
1 4π ∂E ∂E + E ( jkG ) dσ = ∫∫ R + ( jkE ) ( GR ) dω G ∫∫ ∂n ∂n Σ1 Ω
惠更斯菲涅尔原理基尔霍夫衍射理论

若取 G~ 也满足亥姆霍兹方程,则
由
22GE~~
kk22GE~~
§5-1惠更斯-菲涅尔原理
波动具有两个基本性质,一方面,它是扰动 的传播,一点的扰动能够引起其它点的扰动, 各点相互之间是有联系的。另一方面,它具有 时空周期性,能够相干迭加。
惠更斯原理中的“次波概念反映了上述前一 基本性质,这是其成功的地方。但“时空周期 性”并没有反映。
利用惠更斯原理,可以说明衍射的存在,但 不能确定光波通过衍射屏后沿不同方向传播的 振幅,因而也就无法确定衍射图样中的光强分 布。
§5-1惠更斯-菲涅尔原理
二、惠更斯-菲涅耳原理 此是研究衍射现象的理论基础: 波动具有两个基本性质: 1、波动是扰动的传播,一点的扰动能够引 起其它点的扰动,各点的扰动相互之间是有 联系的; 2、波动具有时空周期性,能够相干叠加。
§5-1惠更斯-菲涅尔原理
在惠更斯原理中,由于缺少对时空周期性 的反映,从而对各次波如何叠加问题就不 能给出令人满意的回答。
1818年,在巴黎科学院举行的以解释衍射现 象为内容的有奖竞赛会上,年青的菲涅耳 出人意料地取得了优胜,他吸收了惠更斯 提出的次波概念,用“次波相干迭加”的 思想将所有衍射情况引到统一的原理中来, 这个原理就是惠更斯菲涅耳原理。
§5-1惠更斯-菲涅尔原理
惠更斯--菲涅耳原理
Z RQθ
其内容如下:
P
~ EQ
A expikR
R
Σ' Z'
§5-1惠更斯-Z菲涅尔原理
~ EQ
A expikR
R
RQθ
Σ
r
S
P
Σ' Z'
式中,A是离点光源单位距离处的振幅,
02-31.2 基尔霍夫衍射公式

(n, r)
并设 Σ 的线度δ 满足
n (n, l)
< <<Min(r, l)
l S
2 1
Q
R r
P
围绕 P 点作一闭合曲面。该闭合曲面由三部分组成:
①开孔 Σ; ②不透明屏的部分背照面 Σ1; ③以 P 点为中心、R 为半径的大球的部分球而 Σ2。
在这种情况下,P 点的光场复振幅为
2
1
(n, r) Q
(1)
r
E (P) i
eikr E (l)
cos(n,r)
cos(n, l) d (14)
r
2
① P 点的光场是Σ 上无穷多次波源产生的,次波源的复振幅与入射波在 该点的复振幅 成正比,与波长 成反比;
② 因子(- i) 表明,次波源的振动相位超前 于入射波 / 2;
E(Q) E(l) A eikl l
n (n, l)
R
E(P) 1 4π
E eikr 1 2n rd
eikr E
nr
(11)
S
r
l
P
下面确定这三个面上的 和 / 。
①在上Σ, 和 / 的值由入射波决
定,与不存在屏时的值完全相同。因此
E A eikl l
E cos(n, l) ik 1 A eikl (12)
n
ll
(n, r) n (n, l)
eik ik
4πnEe
n
0时
4π eik E
0
n
4π ikeik
0
eik
0
ik
ik E=4π e ik
4π ikeik
V
nn P
故有
惠更斯-菲涅尔原理§5-2基尔霍夫衍射理论

§5-1惠更斯-菲涅尔原理
波动具有两个基本性质,一方面,它是扰动 的传播,一点的扰动能够引起其它点的扰动, 各点相互之间是有联系的。另一方面,它具有 时空周期性,能够相干迭加。
惠更斯原理中的“次波概念反映了上述前一 基本性质,这是其成功的地方。但“时空周期 性”并没有反映。
利用惠更斯原理,可以说明衍射的存在,但 不能确定光波通过衍射屏后沿不同方向传播的 振幅,因而也就无法确定衍射图样中的光强分 布。
1818年,在巴黎科学院举行的以解释衍射现 象为内容的有奖竞赛会上,年青的菲涅耳 出人意料地取得了优胜,他吸收了惠更斯 提出的次波概念,用“次波相干迭加”的 思想将所有衍射情况引到统一的原理中来, 这个原理就是惠更斯菲涅耳原理。
§5-1惠更斯-菲涅尔原理
惠更斯--菲涅耳原理
Z RQθ
其内容如下:
V
闭合曲面∑’传播。
则光波电磁场的 任一直角分量的复振幅
~ E
Σ' ε ε P n
n
§5-2基尔霍夫衍射理论
满足亥姆霍兹方程
即
2 E k2 E 0
若不考虑电磁场其它分量的影响,孤立地
把 表示E看面作内标任量一场点,的并E ,用这曲种面理上论的就E 和是标E n值量
衍射理论。
设EΒιβλιοθήκη 和一个位置坐标的任意复函数G在曲面
§5-1惠更斯-菲涅尔原理
二、惠更斯-菲涅耳原理 此是研究衍射现象的理论基础: 波动具有两个基本性质: 1、波动是扰动的传播,一点的扰动能够引 起其它点的扰动,各点的扰动相互之间是有 联系的; 2、波动具有时空周期性,能够相干叠加。
§5-1惠更斯-菲涅尔原理
在惠更斯原理中,由于缺少对时空周期性 的反映,从而对各次波如何叠加问题就不 能给出令人满意的回答。
基尔霍夫公式

2 - 以考察点 P 为球心,半径 R 趋于无穷大的 球面。
于是公式(4)的亥姆霍兹-基尔霍夫积分可表示为:
E
7/26/2021
p
1 4
1 2
E
n
exp jkr
r
E
exp jkr
n学 习文r档
d
(14)
为了确定这三个面上的 E ,E 值,可以应用基尔霍夫边界条件(或基尔霍夫 n
(21)
7/26/2021
学习文档
⑶ 亥姆霍兹-基尔霍夫积分的进一步化简
如图 x 所示,对孔径平面上的任意点 Q ,设 E 是从 S0 点发出的单色球面波在 Q 点的分布,格林函数为 Q 点
发出的球面子波对考察点 P 的贡献量,于是有:
E Q A e jkr0 ,
r0
G Q e jkr
r
(22)
所示的闭合面传播时,光波复振幅 7/26/2021
E
r
可用学上习式文来档描述。
2.亥姆霍兹-基尔霍夫定理 1882 年,基尔霍夫从亥姆霍兹方程出发,利用数学上的格林定理,导出
了一个求解标量波衍射的基本公式,即亥姆霍兹-基尔霍夫定理:
E p
1 4
s
E n
exp
r
jkr
E
n
exp
r
2E K 2E 0
(6)
2E K 2E 0
并将上述方程代入格林定理,容易证明其左边:
G2E E2Gdv 0
v
于是,格林定理化简为:
S
G
E n
E
G n
d
S
G
E n
E
G n
d
(7) (8) (9)
基尔霍夫方程物理化学

基尔霍夫方程物理化学基尔霍夫方程是物理化学中非常重要的一个概念,它描述了电路中电流的分布规律。
本文将从人类的视角出发,用通俗易懂的语言,向读者介绍基尔霍夫方程的概念和应用。
第一段:引言基尔霍夫方程是物理化学中电路分析的基础,它能够帮助我们理解电流在电路中的流动规律。
无论是日常生活还是科学研究,电路都无处不在,因此了解基尔霍夫方程的原理和应用对我们来说是非常重要的。
第二段:基尔霍夫方程的概念基尔霍夫方程由德国物理学家基尔霍夫在19世纪提出,它是根据电流守恒和电荷守恒定律推导得出的。
基尔霍夫方程主要包括两个基本原理:电流守恒和电势守恒。
电流守恒原理表明,在一个节点处,进入和离开节点的电流之和为零;电势守恒原理则要求在一个回路中,电路中各个点的电势差之和为零。
第三段:基尔霍夫方程的应用基尔霍夫方程的应用非常广泛,几乎涵盖了电路中所有的分析问题。
通过运用基尔霍夫方程,我们可以计算电路中各个元件的电流和电势差,从而帮助我们理解电路的工作原理。
例如,在串联电路中,我们可以利用基尔霍夫方程计算电阻上的电流,从而了解电路中各个元件的能量分配情况。
在并联电路中,基尔霍夫方程可以帮助我们计算总电流和各个支路的电流。
第四段:基尔霍夫方程的意义和应用领域基尔霍夫方程的应用不仅限于电路分析,还可以在其他领域中发挥重要作用。
例如,在化学反应中,我们可以将反应过程看作一个电路,利用基尔霍夫方程来分析反应物和生成物之间的转化关系。
在光学领域,基尔霍夫方程可以帮助我们理解光的传播规律和干涉现象。
因此,掌握基尔霍夫方程不仅有助于我们在物理化学领域的学习和研究,也可以应用于其他科学领域。
结尾段:总结基尔霍夫方程作为物理化学中的重要概念,可以帮助我们理解电路中电流的分布规律。
通过应用基尔霍夫方程,我们可以计算电路中各个元件的电流和电势差,从而帮助我们分析电路的工作原理。
此外,基尔霍夫方程还可以在化学、光学等领域中发挥重要作用。
因此,学习和掌握基尔霍夫方程对我们来说是非常有益的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
上式表明:孔径平面上透射光场和观察平面上光场之间 存在一个卷积关系。
衍射屏的新定义
在波动光学中,一般认为衍射屏就是在不透明屏上开各种各样的孔。 如今,我们将“能引起衍射的障碍物”统称为衍射屏。
例如: 障碍物的振幅以一定的分布衰减;(以一定的形式限定波面的变化) 障碍物的相位延迟;(衍射屏的光学厚度发生变化) 或两者兼而有之。 表示衍射屏的光学性质的一个重要参数是:复振幅透过率,有些场合 里 tP t x, y, z 又称为孔函数或瞳函数,一般用 或 表示。 前 后
常用衍射屏的透过率函数表示:
(4)圆孔衍射物,直径为d。
d
r d /2 r d /2
x2 y2 r 1 circ t x , y circ d d 0
说明:上面举例都是衍射屏的振幅变化分布,至于相位变化型的衍射屏, 最典型的是透镜 。
通常的光学仪器都满足上述条件!
基尔霍夫衍射理论
惠更斯—菲涅耳原理
e jkr U Q C U 0 P K dS r
(1)
惠更斯—菲涅耳原理建立在“子波 源”的假说上。假定子波源振动相位比 实际光波在该点的振动超前 。 2
叠加积分公式表明:观察点Q的光波分布 U Q 是 所有单位脉冲在Q点引起的光波扰动的相干叠加。
(1)孔径平面上的光波分布是P0点发 射的单色球面波产生的; 因此有
U 0 P a0 jkr0 e r0
点光源P0照明平面屏幕
与惠更斯—菲涅耳衍射积分公式比较:
1 U Q j
a0 e r0
jkr0
jkr cosn, r cosn, r0 e dS 2 r
e jkr U Q c U 0 P F 0 , dS r
惠更斯—菲涅耳衍射积分公式
可以看出: 倾斜因子
常数 c
1 j
cosn, r cosn, r0 F 0 , 2
基尔霍夫假设:
(1)在上, U 0 P 与无屏时一样; (2) 外, U 0 P 0
满足以上条件,则有
2
1 e jkr hP , Q j r
2
r z 2 x x 0 y y0
对r进行二项式展开并化简,有 脉冲响应:
h x , x0 ; y, y0
2 2 2 e xp jk x x y y z 0 0 jz h x x0 , y y0
x y x t x , y rect , rect 1 a a
(3)双缝光栅,如图
a
d 2
a
0
d 2
x d /2 x d / 2 t x, y rect rect 1 a a
比如:通过孔径平面的场分布计 算孔径后面任意一点的复振幅。
解决的方法:利用格林定理,通过 假定衍射屏的边界条件,求解波动 方程,得到基尔霍夫衍射公式。
基尔霍夫衍射公式
1 U Q j
a0 e r0
jkr0
jkr cosn, r cosn, r0 e dS 2 r
光波传播的线性性质
基尔霍夫衍射公式
令
1 U Q j
e jkr U 0 P F 0 , dS r
( 1)
1 e jkr F 0 , hP , Q j r
则(1)式化简为 U Q
U P hP , Q dS
0
( 2)
说明:(2)式是叠加积分,它的物理意义是
P点有一个单位脉冲,它在观察点Q造成的光波 分布是 hP , Q ,它被称为脉冲响应。
叠加积分公式表明:观察点Q的光波分布 U Q 是 上所有单位脉冲在Q点引起的光波扰动的相干叠加。
Hale Waihona Puke 条件:(1)点光源P0足够远,且入射光在孔径平面上各点的 入射角都不大。 (2)观察平面与孔径平面的距离z远大于孔径,且在 观察面上仅仅考虑一个对孔径上各点张角不大的范围。
标量衍射理论
信息光学主要研究内容:光波作为载波,实现 信息的传递、变换、记录和再现问题。 标量衍射理论是研究上述问题的物理基础,我们 用它来研究光波传播规律。 光波是矢量波。当满足下列条件时,标量衍 射理论得到的结果与实际情况十分相符。 条件: 1)衍射孔径比波长大得多; 2)观察屏离衍射孔径相当远。
衍射公式的积分限可以被扩展到无穷,即:
e jkr U Q U 0 P F 0 , dS r
衍射公式的适用范围:任意单色光波照明孔径的情况。 因为任意复杂的光波都可以看成是简单球面波的线性组合。 U可以理解为在任意单色光照明下对 因此,上式中的 0 P 孔径平面产生的光场分布。
定义:
U t P t P U i P
U i P
衍射屏
U t P
常用衍射屏的透过率函数表示:
(1)一个矩形孔
0.2 2mm2
的衍射物 x
x y t x , y rect , 0.2 2
(2)平行y轴的单狭缝,x轴上宽度为a。
2
k 2 U Q 0
--------亥姆霍兹方程
k 2
2 c
说明: 1. 亥姆霍兹方程与时间变量无关,因此多用于解决单色光场的空间分布。 2. 我们今后假定,在自由空间传播的任何单色光波的光场分布必须满足亥姆 霍兹方程。
基尔霍夫衍射理论所要解决的问题 光场中任意一点Q的复振幅能否用光场中其他各点 的复振幅表示出来?
1
显然,脉冲响应具有空间不变的函数形式。
无论孔径平面上子波源的位置如何,它所产生的 球面子波的形式是一样的。
h x x0 , y y0 e xp jk jz 1
x x0 2 y y0 2 z 2
U x , y U 0 x0 , y0 h x x0 , y y0 dx0 y0 U 0 x0 , y0 h x , y
上
(二)亥姆霍兹方程
1. 波动方程(标量)
单色光场中任意一点Q的光振动u满足
2 2 2 2 2 2 2 x y z
1 u u 2 2 0 c t
2 2
其中
--------拉普拉斯算符
代入波动方程,得到
将单色光波分布
uQ, t U Qe j 2t
