环形电流在空间一点产生的磁场强度
第五章 稳恒磁场典型例题

第五章 稳恒磁场设0x <的半空间充满磁导率为μ的均匀介质,0x >的半空间为真空,今有线电流沿z 轴方向流动,求磁感应强度和磁化电流分布。
解:如图所示令 110A I H e r = 220A IH e r= 由稳恒磁场的边界条件知,12t t H H = 12n n B B = 又 B μ= 且 n H H =所以 1122H H μμ= (1) 再根据安培环路定律H dl I ⋅=⎰得 12IH H rπ+= (2) 联立(1),(2)两式便解得,21120I I H r rμμμμπμμπ=⋅=⋅++012120I I H r rμμμμπμμπ=⋅=⋅++ 故, 01110IB H e r θμμμμμπ==⋅+ 02220IB H e rθμμμμμπ==⋅+ 212()M a n M M n M =⨯-=⨯ 220()B n H μ=⨯-00()0In e rθμμμμπ-=⋅⋅⨯=+ 222()M M M J M H H χχ=∇⨯=∇⨯=∇⨯0000(0,0,)zJ Ie z μμμμδμμμμ--=⋅=⋅++ 半径为a 的无限长圆柱导体上有恒定电流J 均匀分布于截面上,试解矢势A 的微分方程,设导体的磁导率为0μ,导体外的磁导率为μ。
?解: 由电流分布的对称性可知,导体内矢势1A 和导体外矢势2A 均只有z e 分量,而与φ,z 无关。
由2A ∇的柱坐标系中的表达式可知,只有一个分量,即 210A J μ∇=- 220A ∇= 此即101()A r J r r r μ∂∂=-∂∂21()0A r r r r∂∂=∂∂ 通解为 21121ln 4A Jr b r b μ=-++212ln A c r c =+ 当0r =时,1A 有限,有10b =由于无限长圆柱导体上有恒定电流J 均匀分布于截面上,设r a =时, 120A A ==,得202121ln 04Ja b c a c μ-+=+=)又r a =时,12011e A e A ρρμμ⨯∇⨯=⨯∇⨯,得 112c Ja a μ-=所以 2221220111,,224c Ja c Ja b Ja μμμ=-=-=所以, 22101()4A J r a μ=--221ln 2a A Ja rμ=写成矢量形式为 22101()4A J r a μ=--221ln 2a A Ja rμ=设无限长圆柱体内电流分布,0()z J a rJ r a =-≤求矢量磁位A 和磁感应B 。
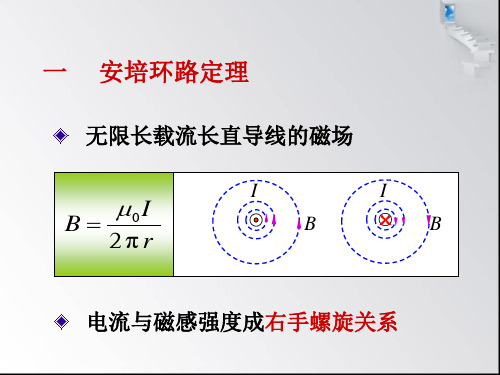
大学物理-磁场 安培环路定律
Φ BS cos BS
s
一般情况 Φ s BdS
dS2
B
S 2
dS1
1
B1
dΦ1 B1 dS1 0
dΦ2 B2 dS2 0
B2
SB cosdS 0
磁场高斯定理
S B d S 0
物理意义:通过任意闭合曲面的磁通
量必等于零(故磁场是无源的).
B B1 B2 B3
Bdl
l
0(I2 I3)
推广:
➢ 安培环路定理
n
B dl 0 Ii
i 1
n
安培环路定理
B dl 0 Ii
i 1
在真空的恒定磁场中,磁感强度 B沿任
一闭合路径的积分的值,等于 0乘以该闭合
路径所穿过的各电流的代数和.
注意
电流 I 正负的规定: I 与 L 成右螺旋
而与环路外电流无关。
3. B为环路上一点的磁感应强度,它与环路内外电流
都有关。
若
B
dl
0
并不一定说明环路上各点的 B 都为 0。
若 B dl 0 环路内并不一定无电流。
4.环路定理只适用于闭合电流或无限电流,
应用 安培环路定理的应用举例
例1
求载流螺绕环内的磁场
解 (1)对称性分析:环内B 线为同心
B dl B 2r 0 I
B 0 I 1 2r r
I
r LR
r L
分布曲线
B
0 I 2R B r
B 1 r
o
R
r
例4 无限大均匀带电(线密度为i)平面的磁场
解 如图,作安培环路
abcda,应用安培环路 定理
b
l B d l 2a B dl
磁场强度定律

三、磁感应强度
描述磁场性质的基本物理量。 描述磁场性质的基本物理量。 1.磁感应强度的定义 1.磁感应强度的定义
×
q
r v r
× ×
B
当把运动电荷放在磁场中后, 当把运动电荷放在磁场中后, × × × 它会受到一种与其速度有关的力, 它会受到一种与其速度有关的力, × r q 洛仑兹力。 这个力称为洛仑兹力 这个力称为洛仑兹力。 × r× ×v × 当电荷运动速度与磁场方向一 当电荷运动速度与磁场方向一 × B× × × 致时电荷受力为 0 。 当运动电荷速度ቤተ መጻሕፍቲ ባይዱ磁场方向垂直时受到洛伦兹力 fL 最大。 最大。 定义: 定义:磁感应强度
2
r θ Idl
∴ dl = a csc θdθ r = a csc θ
2
2
l o
r
θ1
r dB ⊗ P x
a
µ0 Ia csc θ sin θdθ µ0 I dB = = sin θdθ 2 2 4π a csc θ 4πa µ0 I θ 2 µ0 I (cosθ1 − cosθ 2 ) sin θdθ = B = ∫ dB = ∫θ1 4πa 4πa 10
2
一、磁的基本现象
1.磁铁及其特性 1.磁铁及其特性 人造磁铁: S 人造磁铁: 特性: 特性:
S
I
N
天然磁铁----磁铁矿(Fe3O4) 天然磁铁----磁铁矿( ----磁铁矿 N
N
I
v F
S N S 能吸引铁、 镍等物质--这种性质叫磁性。 --这种性质叫磁性 1)能吸引铁、钴、镍等物质--这种性质叫磁性。 具有两极且同性相斥,异性相吸。 2)具有两极且同性相斥,异性相吸。 3)目前还无法获得磁单极。 3)目前还无法获得磁单极。 目前还无法获得磁单极
环形电流产生的磁场强度计算公式

环形电流产生的磁场强度计算公式咱们先来说说环形电流产生的磁场强度计算公式哈。
这环形电流产生磁场强度的计算,那可是物理学中的一个重要知识点。
打个比方,就像你在一个游乐场里坐摩天轮,这个环形电流就像是摩天轮的轨道,而产生的磁场强度就像是你在不同位置感受到的刺激程度。
要计算环形电流产生的磁场强度,咱们得用到一个公式:B = μ₀I /2R 。
这里面的 B 就是磁场强度,μ₀是真空磁导率,是个常数,就像你的生日一样固定不变,I 是环形电流的强度,而 R 则是环形电流的半径。
咱们来具体讲讲这个公式的用法。
比如说,有一个环形电流,电流强度是 5 安培,半径是 2 米。
那咱们就把数字带进公式里算算。
先把真空磁导率μ₀的值带进去,它约等于4π×10⁻⁷特斯拉·米/安培。
然后I 是 5 安培,R 是 2 米,这么一算,就能得出这个环形电流产生的磁场强度啦。
还记得有一次,我给学生们讲这个知识点的时候,有个学生就问我:“老师,这环形电流产生的磁场在生活中有啥用啊?”我当时就想了想,给他举了个例子。
我说:“你看咱们的手机,里面的好多零件运行可都离不开电磁原理,这环形电流产生的磁场知识说不定就在其中发挥着作用呢。
就像手机里的扬声器,声音的产生就和电流以及磁场有关系。
”再说说这个公式的推导过程,那也是有点意思的。
它可不是凭空冒出来的,而是通过一系列的物理实验和理论推导得出的。
这就好比你要搭一座桥,得先准备好材料,设计好结构,然后一步步搭建起来。
学习这个公式的时候,大家可别死记硬背,得理解着来。
多做几道相关的练习题,感受一下不同情况下磁场强度的变化。
比如说,电流增大了,磁场强度怎么变;半径变小了,磁场强度又会怎么变。
其实啊,物理学中的很多知识都是相互关联的。
就像这个环形电流产生的磁场强度计算公式,它和电磁感应、安培力等知识都有着千丝万缕的联系。
当你把这些知识都融会贯通的时候,你就会发现物理学的世界就像一个大拼图,每一块都能完美地拼在一起。
磁感应强度与电流的关系

压力的变化也会对物质的磁性质产生影响。在某些情况下 ,压力的增加可能会增强物质的磁性,而在另一些情况下 则可能会减弱磁性。
化学成分对磁感应强度的影响
不同化学成分的物质具有不同的磁性质。例如,铁、钴、 镍等金属具有铁磁性,而铜、铝等金属则具有抗磁性。因 此,化学成分的差异也会对磁感应强度产生影响。
1. 将电源、导线、 磁感应强度计等器 材按照实验需求进 行搭建和连接。
3. 使用磁感应强度 计测量导线周围的 磁感应强度,并记 录测量数据。
5. 对实验数据进行 整理和分析,得出 磁感应强度与电流 的关系。
数据记录表格模板提供
| 序号 | 电流大小(A) | 磁感 应强度(T) |
| --- | --- | --- |
音响喇叭
音响喇叭中的音圈就是一个电磁 铁,通过音频信号控制电流大小 ,从而驱动音圈振动发出声音。
门锁
一些电子门锁中使用了电磁铁作 为锁舌的驱动机构。当门锁通电 时,电磁铁产生吸力将锁舌吸合
,实现门锁的锁定或解锁。
电磁炉
电磁炉利用电磁感应原理加热食 物。当电磁炉中的线圈通电时, 产生交变磁场,使放置在炉面上 的铁锅产生涡流而发热,从而煮
磁性材料的作用
电磁铁中的铁芯通常采用容易磁化且磁导率高的软磁材料 ,如纯铁、硅钢等。当线圈通电时,铁芯被磁化并大大增 强磁场强度,从而实现电磁铁的吸力作用。
控制电流以调节磁场强度
电磁铁的磁场强度可以通过改变线圈中的电流大小来进行 调节。电流越大,产生的磁场越强,电磁铁的吸力也越大 。
电磁铁在日常生活中的应用举例
熟食物。
工业领域中电磁铁的应用举例
电机与发电机
电机与发电机是电磁铁在工业领域中最广泛的应用之一。电机利用 电磁感应原理将电能转换为机械能,而发电机则将机械能转换为电 能。
高中物理磁感应强度的知识点归纳

高中物理磁感应强度的知识点归纳高中物理磁感应强度的知识点归纳物理学(physics)是研究物质最一般的运动规律和物质基本结构的学科。
作为自然科学的带头学科,物理学研究大至宇宙,小至基本粒子等一切物质最基本的运动形式和规律,因此成为其他各自然科学学科的研究基础。
以下是店铺收集整理的高中物理磁感应强度的知识点归纳,欢迎大家分享。
高中物理磁感应强度的知识点归纳1磁感应强度(magnetic flux density),描述磁场强弱和方向的物理量,是矢量,常用符号B表示,国际通用单位为特斯拉(符号为T)。
磁感应强度也被称为磁通量密度或磁通密度。
在物理学中磁场的强弱使用磁感应强度来表示,磁感应强度越大表示磁感应越强;磁感应强度越小,表示磁感应越弱。
磁感应强度的定义公式磁感应强度公式B=F/(IL)磁感应强度是由什么决定的?磁感应强度的大小并不是由F、I、L 来决定的,而是由磁极产生体本身的属性。
如果是一块磁铁,那么B的大小之和这块磁铁的大小和磁性强弱有关。
如果是电磁铁,那么B与I、匝数及有无铁芯有关。
很多文章都建议同学们采用类比的方法来理解各个物理量。
我们用电阻R来做个对比。
R的计算公式是R=U/I;可一个导体的电阻R大小并不是由U或者I来决定的。
而是由其导体自身属性决定的,包括电阻率、长度、横截面积。
同样,磁感应强度B也不是由F、I、L来决定的,而是由磁极产生体本身的属性。
如果同学们有时间,可以把静电场中电容的两个公式来对比着复习、巩固下。
B为矢量,方向与磁场方向相同,并不是在该处电流的受力方向,运算时遵循矢量运算法则(左手定则)。
描述磁感应强度的磁感线在磁场中画一些曲线,用(虚线或实线表示)使曲线上任何一点的切线方向都跟这一点的磁场方向相同(且磁感线互不交叉),这些曲线叫磁感线。
磁感线是闭合曲线。
规定小磁针的北极所指的方向为磁感线的方向。
磁铁周围的磁感线都是从N极出来进入S极,在磁体内部磁感线从S极到N极。
(完整word版)环形电流在空间一点产生的磁场强度

环形电流在空间一点产生的磁场强度摘要:利用毕奥——萨法尔定律通过计算磁场的情况,得到环电流在整个空间的磁场分布表达式,其中运用了数学软件matlab 辅助求解!关键词:环形电流 磁场 矢量叠加 毕奥——萨法尔定律引言:了解书本上环形电流中心轴线上的磁场分布情况后,为了更深入了解环形电流在空间的磁场分布情况,现运用毕奥——萨法尔定律对其求解,再根据矢量叠加原理,将其最终结果在直角坐标系中的三个坐标轴上的分量分离了出来,且验证了空间分布公式在特殊情况下也适用!计算过程;1. 建立坐标系:设环半径为R ,以环心0为原点,环形电流所在平面为x0y 平面,以环中心轴为z 轴建立如图坐标系,则圆环的表达式为:222x y R += 在空间内任意选取一点p(x,y,z),在环上任取一点11A(x ,y ,0),则在A 点处的电流元Idl 满足关系式:Idl IR(isin jcos )d βββ=-+ (1)而P,A 两点的矢径为:r (x R c o s )i (y R s i n ββ=-+-+ (2)xz y p(x,y,z)R β 11A(x ,y ,0)将(1)(2)式代入毕奥——萨法尔定律:03Idl rdB 4r μπ⨯= (3)得P 点的磁感应强度为:00332222IR Idl r zi cos z jsin (R x cos ysin )k B d 4r 4(R y z 2yR sin )μμβββββππβ⨯++--==++-⎰⎰(4) 则令:20x 302222IR zi cos B d 4(R y z 2yR sin )πμββπβ=++-⎰20y 302222IR z jsin B d 4(R y z 2yR sin )πμββπβ=++-⎰ (5) 20z 302222IR (R x cos ysin )k B d 4(R y z 2yR sin )πμβββπβ--=++-⎰这就是环形电流在空间产生的磁场在空间的分布分量情况!特别地当p(x,y,z)在环的中心轴线上即z 轴上时,其坐标为p(0,0,z),代入(5)组式,得到:20x 30222IR zi cos B d 4(R z )πμββπ=+⎰20y 30222IR z jsin B d 4(R z )πμββπ=+⎰20z 30222IR Rk B d 4(R z )πμβπ=+⎰利用matlab 分别输入以下程序并得相应结果:(其中0U 表示0μ,A 表示β)由求解结果显示得到:z 轴上的点磁通分量为:x y 20Z 223/2B 0B 0IR B k 2(R x )μ==-=+当p 在环中心时,其坐标为p(0,0,0),显然x y 0z B 0B 0I B 2Rμ===综上可知环形电流在空间形成的磁场表达式为:20x 302222IR zi cos B d 4(R y z 2yR sin )πμββπβ=++-⎰20y 302222IR z jsin B d 4(R y z 2yR sin )πμββπβ=++-⎰20z 302222IR (R x cos ysin )k B d 4(R y z 2yR sin )πμβββπβ--=++-⎰这组式子在特殊情况下也成立!。
高中物理竞赛《磁场》内容讲解

磁 场一、恒定电流的磁场1、直线电流的磁场通有电流强度为I 的无限长直导线,距导线为R 处的磁感应强度为:RIB πμ20=;如下图距通有电流强度为I 的有限长直导线为R 处的P 点的磁感应强度为:)cos (cos 40βαπμ+=RIB ----------------------------------①若P 点在通电直导线的延长线上,则R=0 α=0 β=π 无法直接应用上述式子计算,可进行如下变换lR d d 21)sin(2121=+βα 上式中1d 、2d 分别为P 点到A 、B 的距离,l 为直导线的长度所以:l d d R )sin(21βα+=代入①式得:)sin(cos cos 4210βαβαπμ++=d d Il B令2sin2cos2cos 2sin 22cos2cos2)sin(cos cos βαβαβαβαβαβαβαβα+-=++-+=++=y将α=0 β=π代入上式得0=y所以:在通电直导线的延长线上任意一点的磁感应强度为0=B2、微小电流元产生的磁场微小电流元的磁场,根据直线电流的磁场公式)cos (cos 40βαπμ+=rIB得:Ⅰ若α、β都是锐角,如左图,有:)cos (cos 40βαπμ+=r I B =)sin (sin 4210θθπμ∆+∆rI因1θ∆、2θ∆0→,所以≈∆+∆=)sin (sin 4210θθπμr I B )(4210θθπμ∆+∆rI所以:θπμ∆=rIB 40Ⅱ若α、β中有一个是钝角,如β(右图),则:]sin )[sin(cos 4)cos (cos 400000θθθθπμβαπμ-+∆=+=r Id I B -------------①00000sin sin cos cos sin sin )sin(θθθθθθθθ-∆+∆=-+∆因0→∆θ,所以:0000cos cos sin sin )sin(θθθθθθθ∆≈∆≈-+∆--------------------------------②②式代入①式得:θπμ∆=rIB40总上所述,电流元I 在空间某点产生的磁场为:θπμ∆=rIB 40,式中r 为电流元到该点的距离,θ∆为电流元端点与该点连线张开的角度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
环形电流在空间一点产生的磁场强度
摘要:利用毕奥——萨法尔定律通过计算磁场的情况,得到环电流在整个空间的磁场分布表达式,其中运用了数学软件matlab 辅助求解!
关键词:环形电流 磁场 矢量叠加 毕奥——萨法尔定律
引言:了解书本上环形电流中心轴线上的磁场分布情况后,为了更深入了解环形电流在空间的磁场分布情况,现运用毕奥——萨法尔定律对其求解,再根据矢量叠加原理,将其最终结果在直角坐标系中的三个坐标轴上的分量分离了出来,且验证了空间分布公式在特殊情况下也适用!
计算过程;
1. 建立坐标系:设环半径为R ,以环
心0为原点,环形电流所在平面为
x0y 平面,以环中心轴为z 轴建立如图坐标系,则圆环的表达式为:
222x y R += 在空间内任意选取一点p(x,y,z),在环
上任取一点11A(x ,y ,0),则在A 点处的电流元Idl 满足关系式:
Idl IR(isin jcos )d βββ=-+ (1)
而P,A 两点的矢径为:
r (x R cos )i (y R sin )j zk ββ=-+-+ (2)
将(1)(2)式代入毕奥——萨法尔定律:
03Idl r
dB 4r μπ⨯= (3)
得P 点的磁感应强度为:
00332222IR Idl r zi cos z jsin (R x cos ysin )k B d 4r 4(R y z 2yR sin )μμβββββππβ⨯++--==++-⎰⎰
(4) 则令:
20x 302222IR zi cos B d 4(R y z 2yR sin )πμββπβ=++-⎰
20y 302222IR z jsin B d 4(R y z 2yR sin )πμββπβ=++-⎰ (5) 20z 302222IR (R x cos ysin )k B d 4(R y z 2yR sin )πμβββπβ--=++-⎰
这就是环形电流在空间产生的磁场在空间的分布分量情况!
特别地
当p(x,y,z)在环的中心轴线上即z 轴上时,其坐标为p(0,0,z),代入
(5)组式,得到:
20x 30222IR zi cos B d 4(R z )πμββπ=+⎰
20y 30222IR z jsin B d 4(R z )πμββπ=+⎰
20z 30222IR Rk B d 4(R z )πμβπ=+⎰
利用matlab 分别输入以下程序并得相应结果:
(其中0U 表示0μ,A 表示β)
由求解结果显示得到:z 轴上的点磁通分量为:
x y 2
0Z 223/2B 0
B 0
IR B k 2(R x )μ==-=+
当p 在环中心时,其坐标为p(0,0,0),显然
x y 0z B 0
B 0
I B 2R
μ===
综上可知环形电流在空间形成的磁场表达式为:
20x 302222IR zi cos B d 4(R y z 2yR sin )πμββπβ=++-⎰
20y 302222IR z jsin B d 4(R y z 2yR sin )πμββπβ=++-⎰
20z 302222IR (R x cos ysin )k B d 4(R y z 2yR sin )πμβββπβ--=++-⎰
这组式子在特殊情况下也成立!。
