轨道计算
如何计算天体的轨道

如何计算天体的轨道
人类早就认识到天体的运动轨道是由很多不同因素确定的,而在这些因素的关系中,轨道计算便显得极为重要。
今天,让我们来探讨如何运用数学的方法来计算天体的轨道:
1、转动性原理及应用
转动性原理是指物体运动的合力扭矩为零,整体转动惯量为常数。
这一定律解释了天体受到多方力(如地心引力) 作用时,他们不可能坚持原始运动方向,只能向最稳定的运动轨道直至,并且任何运动的轨道变化都可以展示为轨道的内切圆的旋转。
2、离心率的计算
离心率是指物体在轨道上的偏离圆形的程度,它的数值决定了天体的运行方向,我们可以把它的计算表达为如下的式子:
e = $$
其中,e表示离心率,C为物体运动圆周的周长,a表示距离太阳的距离,v表示运动速度。
3、轨道定义
根据离心率的数值,可以得出给定天体运动的轨道,主要分两种:圆形轨道和椭圆形轨道。
当离心率e=0时,物体运动轨道即为圆形;当
离心率e不为0时,物体运动轨道即为椭圆形。
4、轨道计算
在计算天体运动轨道的过程中,通常需要求解轨道系数。
其具体运算为:将轨道方程式改写为标准星形的基本方程,然后解决系数a、b、c,即可求出天体的轨道。
5、轨道预测
在计算完天体的轨道后,我们可以对它未来的运动轨迹进行预测,这
一过程需要运用到推导法,利用轨道系数,先求出圆周运动的参数值,然后将它们进行累加比较,从而得出天体在一段时间内的运动轨迹。
总的来说,计算天体的轨道是很复杂的一项工作,科学家们需要利用
运用力学、数学和天文学知识,结合复杂的计算方法来完成。
不仅如此,良好的想象力和抽象思维能力也是完成这项工作必不可少的技能。
铁路轨道超高计算公式

铁路轨道超高计算公式铁路轨道超高计算公式,这可真是个有趣又重要的话题!咱们先来说说啥是铁路轨道超高。
简单来讲,就是为了让列车在弯道上能更平稳地行驶,轨道会故意做成一边高一边低的样子,这个高度差就叫超高。
那为啥要有这超高呢?想象一下,列车快速拐弯,如果轨道是平的,那离心力可就容易让列车“飘”出去,这得多危险呀!有了合适的超高,就能平衡离心力,让列车稳稳地转弯。
接下来就讲讲这计算公式。
常见的铁路轨道超高计算公式是:h = 11.8×V²÷R 。
这里的“h”就是超高值,单位是毫米;“V”是列车通过曲线的速度,单位是千米每小时;“R”是曲线半径,单位是米。
比如说,一列火车要以 120 千米每小时的速度通过一个半径为 800 米的弯道,那超高值就是:h = 11.8×120²÷800 = 212.4 毫米。
这公式看着简单,可实际运用起来得考虑好多因素呢。
就像我之前去一个铁路施工现场,工程师们正在为一段新的弯道计算超高。
他们拿着各种测量仪器,一丝不苟地测量着弯道的半径,还得考虑列车的实际运行速度,以及轨道的材质和条件等等。
我在旁边看着,心里都跟着紧张起来。
而且呀,这超高计算可不是一锤子买卖。
随着铁路线路的使用,轨道会有磨损,列车的速度也可能会调整,这都需要定期重新计算和调整超高值,以确保列车的安全和稳定运行。
还有啊,不同类型的列车,比如高速列车和普通列车,对超高的要求也不一样。
高速列车速度快,需要更大的超高来平衡离心力;而普通列车速度相对较慢,超高值就会小一些。
另外,地理环境也会影响超高的计算。
比如说在山区,弯道可能更急,半径更小,这就需要更精确的计算来保证列车安全通过。
总之,铁路轨道超高计算公式虽然看起来只是一个简单的数学式子,但背后涉及到的是铁路运输的安全和效率。
每一次准确的计算和调整,都是为了让我们的列车能更平稳、更安全地奔驰在铁轨上。
希望我这大白话能让您对铁路轨道超高计算公式有个大概的了解,这可真是铁路工程里一个不容小觑的环节呢!。
卫星轨道参数计算
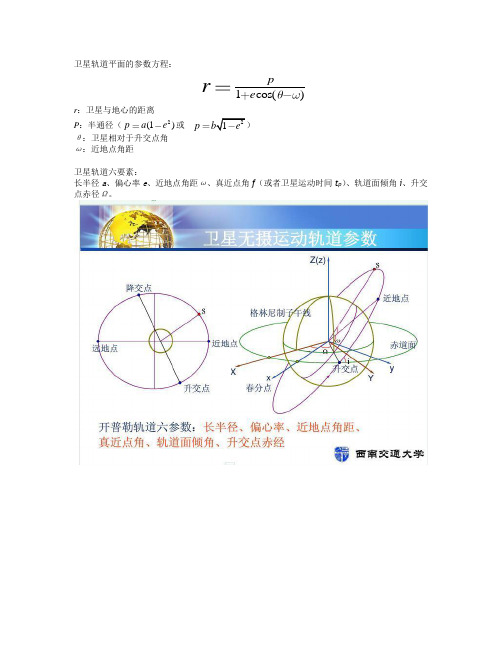
卫星轨道平面的参数方程:1cos()p e rr :卫星与地心的距离P :半通径(2(1)p a e 或21p b e ) θ:卫星相对于升交点角 ω:近地点角距卫星轨道六要素:长半径a 、偏心率e 、近地点角距ω、真近点角f (或者卫星运动时间t p )、轨道面倾角i 、升交点赤径Ω。
OXYZ─赤道惯性坐标系,X轴指向春分点T ;ON─卫星轨道的节线(即轨道平面与赤道平面的交线),N为升交点;S─卫星的位置;P─卫星轨道的近地点;f─真近点角,卫星位置相对于近地点的角距;ω─近地点幅角,近地点到升交点的角距;i─轨道倾角,卫星通过升交点时,相对于赤道平面的速度方向;Ω─升交点赤经,节线ON与X轴的夹角;e─偏心率矢量,从地心指向近地点,长度等于e;W─轨道平面法线的单位矢量,沿卫星运动方向按右旋定义,它与Z轴的夹角为i;a─半长轴;α,δ─卫星在赤道惯性坐标系的赤经、赤纬。
两个坐标系:地心轨道坐标系、赤道惯性坐标系。
地心轨道坐标系Ox0y0z0:以ee1为x0轴的单位矢量,以W为z0轴的单位矢量,y0轴的单位矢量可以由x0轴的单位矢量与z0轴的单位矢量确定,它位于轨道平面内。
赤道惯性坐标系:OXYZ,X轴指向春分点。
由地心轨道坐标系到赤道惯性坐标系的转换:1.先将地心轨道坐标绕W旋转角(-ω),旋转矩阵为R Z(-ω);2.绕节线ON旋转角(-i),旋转矩阵为R X(-i);3.最后绕Z轴旋转角(-Ω),旋转矩阵为R Z(-Ω);经过三次旋转后,地心轨道坐标系和赤道惯性坐标系重合。
在地心轨道坐标系中,卫星的位置坐标是:0 0 0cos sin 0x r f y r fz地心轨道坐标系到赤道惯性坐标系的转换关系是:000()()()cos cos sin cos sin sin cos cos cos sin sin sin cos =cos sincos cos sin sin sincos cos cos sin cos sin sin cos sin cos z x z x x y R R i R y z z i i i r f i i i i ii2sin 0cos sin()sin sin()cos(1)=sin cos()cos sin()cos 1cos sin()sin r f f f i a e f f ie ff i赤道惯性坐标系下的坐标确定后,可与r 、α、δ联系起来,关系式如下:1222()2arctan arctan(1)1cos 1cos y xz x y p a e re fe f若卫星六要素都已知,则可以解出α、δ。
卫星轨道计算范文

卫星轨道计算范文卫星轨道计算在航天领域中是非常重要的一个任务,它用来确定卫星在空间中的运动路径,以便能够精确地控制卫星的运动。
这种计算涉及到很多复杂的数学和物理理论,下面我将详细介绍卫星轨道计算的一些基本原理和方法。
卫星轨道计算主要涉及到三个关键的概念:卫星的位置、速度和加速度。
卫星的位置可以用三个坐标来表示,通常是在一个以地球为中心的坐标系中。
速度是指卫星在空间中的运动速率,而加速度则是指卫星受到的外力或加速度的大小和方向。
在卫星轨道计算中,采用的最常见的力学模型是开普勒模型。
开普勒模型是根据牛顿的引力定律和开普勒定律建立的,它假设卫星和地球之间只有引力相互作用,并忽略了其他影响因素。
根据开普勒模型,卫星在椭圆轨道上运动,地球位于椭圆的一个焦点上。
卫星轨道的计算可以使用一系列的数学公式来完成。
其中最重要的公式是开普勒运动定律,它可以用来计算卫星在椭圆轨道上的位置和速度。
这个公式可以使用卫星的初始位置、速度和时间来计算卫星的最终位置和速度。
具体的计算方法可以通过数值计算或解析计算来实现。
卫星轨道计算还涉及到一些其他的因素,例如大气阻力、太阳辐射压力、地球潮汐等。
这些因素可以对卫星的轨道产生影响,因此在计算卫星轨道时需要考虑进去。
这些影响因素可以通过建立更复杂的力学模型和数值模拟来进行计算。
最后,卫星轨道计算还需要考虑到卫星的控制和修正。
由于外界的因素或控制系统的误差,卫星的实际轨道可能会与计算的轨道有所偏差。
因此,卫星轨道计算需要进行实时监测和修正,以确保卫星能够按照预定的轨道进行运行。
总之,卫星轨道计算是航天领域中非常重要的一个任务,它涉及到许多复杂的数学和物理理论。
通过合理的轨道计算,可以确保卫星能够按照预定的轨道进行运行,从而实现各种航天任务的顺利进行。
轨道周期计算公式

轨道周期计算公式轨道周期计算公式是用来研究双星轨道运动的必要公式,它可以帮助我们准确预测双星系统的运动轨道。
它的发展起源于十六世纪法国数学家埃米尔古斯塔夫卢梭,他认为轨道运动是规律性的,并建立了轨道周期计算公式。
卢梭认为,轨道运动可以用椭圆函数来表示,这种函数的一个重要特点是它的实质性参数“周期”,即本征周期,也就是双星系统一次运行完毕的所需的时间。
按照卢梭的计算方法,如果想知道双星系统的周期,可以通过以下公式计算出来:T = 2π * SQRT(a^3/k)其中,a为双星轨道的半长轴,k是引力常数。
由于卢梭的计算方法只能用于简单的双星系统,他的计算结果有一定的偏差,不能用于更复杂的系统中。
直到1772年,苏格兰数学家麦克尔尼科尔利用平方根和超越函数,构建出了更加精确的轨道周期计算公式,从而建立了现代力学的理论基础:T = 2π * SQRT((1/4) * a^3/k)公式中a^3/k称为“系数”,是现代力学中重要的概念,可以用来描述双星系统的运动状态。
麦克尔尼科尔的轨道周期计算公式在它发表以后,逐渐成为双星系统研究中的重要工具,更重要的是,它提供了一种新的、精确的研究双星运动轨道的方法。
随着科学技术的发展,轨道周期计算公式也在不断改进,从而使双星系统的研究变得更加精确。
例如,普朗克改进了轨道参数的表达,将原来的两个参数a和k改写成了三个参数:a、e和M,其中e表示双星轨道的离心率,M表示每个双星的质量。
而另外的一个重要的参数p,则用于描述双星系统的运动轨道。
在20世纪,牛顿力学发展到了令人惊奇的今天,轨道周期计算公式也在不断改进,以更加精确和准确地描述双星系统的运动轨道。
例如,现代轨道周期计算公式结合了平方根、超越函数和牛顿力学,可以用来精确计算双星系统的轨道周期,也就是说,当一个双星轨道在太空中绕太阳转一周所需要的时间。
轨道周期计算公式的发展为科学的发展提供了重要的动力,使人们能够更加准确地研究双星系统,而这对航天探索以及研究太阳系结构和其他复杂运动系统都有着至关重要的意义。
轨道计算式

(
)
十一 、工字钢端部连接计算
单根钢筋上的剪力 V_2 := F 3_2 2 = 1.2 kN
单根钢ห้องสมุดไป่ตู้上的拉力 N_2 := F 3_3 2 = 2.07 kN
HPB235的抗拉强度设计值 fy_HPB235 := 210MPa
ϕ20钢丝绳的抗拉承载力 N_20 := fy_HPB235 3.14
SAP2000 建 模
荷载施加图 18号工字钢自重标准值 吊装的单元体的自重标准值
2、荷载组合
强度组合 荷载工况组 合
挠度组合
3、强度校核
根据导出 PM-Ratio图可知, 钢模型构件 PM-RATIO图 工20a工字钢:最大利用率为0.145 16mm钢丝绳:最大利用率为0225 均小于钢结构规范规定的0.95 限 值,故强度计算满足要求!
ϕ20钢丝绳的抗剪承载力
20mm 2
2
= 65.94 kN
V_20 :=
fy_HPB235 3
3.14
20mm 2
2
= 38.07 kN
因此 N _1 < N_20 = "OK!满足要求!"
(
)
因此 V _1 < V_20 = "OK!满足要求!"
-2
抗剪强度设计值 fv := 125N mm
-2
二 、荷载计算
荷载设计值 永久荷载分项系数 γg := 1.35 最大单元板块自重设计值 F d := F k1 γg F d = 13.5 KN
最大单元体自重标准值(考虑横梁立柱等其他构件自重取1.2 的放大系数) F k1 := 10kN
卫星轨道计算

④ 离
⑤ 卫星与地球质心的几何距离为:
3.卫星轨道计算
3.2 开普勒方程
① 开普勒第三定律可表示为:
② 假定为 点角:
卫星通过近地点A的时刻,对应t 时刻的平近
3.卫星轨道计算
3.2 开普勒方程
③ 对应任意t 时刻的开普勒方程可描述为:
④ 于是,可得到真近点角f 可表示为:
4.卫星坐标计算算法步骤
4.2 重要MATLAB函数说明
(三)计算卫星位置模块 (1)读观测值文件(*.o文件)函数 在求解卫星位置时,第一需要利用o文件中每个历元 的历元时刻t。在计算某时刻卫星位置时,这里的某时刻便 是o文件历元时刻t。第二需要利用读取的每个历元不同的
卫星PRN号。根据PRN号和历元时刻 t 在广播星历n文件中
单位为弧度,是由于摄动力而引起的改正项。
4.卫星坐标计算算法步骤
4.1 算法
① 计算卫星运行的平均角速度 n
② 计算归化时间
4.卫星坐标计算算法步骤
4.1 算法
③ 观测时刻卫星平近点角 的计算
④ 计算偏近点角
⑤ 真近点角
的计算
4.卫星坐标计算算法步骤
4.1 算法
⑥ 升交距角 的计算
⑦ 摄动改正项
计算卫星位置。
4.卫星坐标计算算法步骤
4.2 重要MATLAB函数说明
(3)dt = check_t(time) time—儒略日; 返回值—修复后的儒略日。 (4)X = satpos(tx_GPS, Eph(:,k)) tx_GPS—上节所述的归化时间,用儒略日表示的; Eph(:,k)—Eph星历矩阵中的某一列数据; 返回值—卫星在地心地固坐标系中坐标。
1.开普勒定律
第5章卫星轨道计算

第5章卫星轨道计算卫星轨道计算是卫星技术中非常重要的一部分,涉及到卫星的运行轨迹、轨道参数等内容。
在进行卫星轨道计算时,需要考虑多种因素,如地球引力、卫星自身推进力等,以保证卫星能够按照预定的轨道运行。
本文将介绍卫星轨道计算的基本原理和方法,并举例说明。
首先,需要明确卫星轨道计算的基本参数。
常用的卫星轨道参数有轨道高度、轨道倾角、轨道周期等。
轨道高度指的是卫星轨道与地球表面的最短距离,单位一般为千米。
轨道倾角则表示卫星轨道平面与地球赤道面之间的夹角,单位为度。
轨道周期是指卫星绕地球运行一周所需的时间,单位为分钟。
这些参数的计算是卫星轨道计算的基础。
其次,卫星轨道计算需要考虑地球引力的影响。
地球引力是卫星运行的主要力量之一,它会使卫星向地球中心方向做受力运动。
因此,在进行卫星轨道计算时,需要将地球引力的作用考虑进去。
具体来说,可以使用开普勒定律和牛顿第二定律来计算卫星的轨道。
开普勒定律是描述行星运动的基本定律之一,也适用于卫星的轨道运动。
根据开普勒第一定律,卫星绕地球的轨道是一个椭圆,地球位于椭圆焦点之一、根据开普勒第二定律,卫星在轨道上的相等时间内,扫过的面积是相等的。
根据开普勒第三定律,卫星绕地球的周期和轨道半长轴之间存在一个数学关系。
牛顿第二定律则是描述物体运动的基本定律之一,也适用于卫星的轨道运动。
牛顿第二定律指出,物体的受力与加速度成正比,与物体的质量成反比。
因此,在进行卫星轨道计算时,可以根据牛顿第二定律,计算卫星受力情况,从而推算出卫星的轨道运动。
卫星轨道计算的具体方法有多种,其中一种常用的方法是数值计算方法。
这种方法通过将轨道问题转换为数值求解的问题,使用计算机进行计算。
具体来说,可以使用微分方程数值解的方法,结合卫星的初始条件,通过迭代计算获得卫星的轨道。
这种方法可以较为准确地计算出卫星的轨道,适用于复杂的轨道计算问题。
综上所述,卫星轨道计算是卫星技术中非常重要的一部分,涉及到卫星的运行轨迹、轨道参数等内容。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一种粗略测定天体轨道的方法。
在轨道计算中,人们事先不必对天体轨道作任何初始估计,而是从若干观测资料出发,根据力学和几何条件定出天体的初始轨道,以便及时跟踪天体,或作为轨道改进的初值。
为了计算六个轨道要素(见二体问题),至少必须有三次光学观测,因为每次观测只能得到天体坐标的两个分量。
轨道计算是从研究彗星的运动开始的。
在牛顿以前,对天体运动的研究基本上带有几何描述的性质。
第谷首先试图计算彗星轨道,但未获成功。
困难在于只能观测彗星的方向,而不知道它同地球的距离,由于缺少力学规律的指引,无法根据这些定向资料求得天体的空间轨道。
在牛顿运动定律和万有引力定律发现后,开普勒定律有了力学解释,得到了椭圆运动的严格数学表达式,终于能利用少数几次时间相隔不长的观测来测定彗星的轨道。
拉普拉斯方法第一个正式的轨道计算方法是牛顿提出的。
他根据三次观测的资料,用图解法求出天体的轨道。
哈雷用这个方法分析了1337~1698年间出现的24颗彗星,发现1531年、1607年和1682年出现的彗星是同一颗彗星,它就是有名的哈雷彗星。
在这以后,欧拉、朗伯和拉格朗日等人也在轨道计算方面做了不少研究。
拉普拉斯于1780年发表第一个完整的轨道计算的分析方法。
这个方法不限制观测的次数,首先根据几次观测,定出某一时刻天体在天球上的视位置(例如赤经、赤纬)及其一次、二次导数,然后从这六个量严格而又简单地求出此时天体的空间坐标和速度,从而定出圆锥曲线轨道的六个要素。
这样,拉普拉斯就将轨道计算转化为一个微分方程的初值测定问题来处理。
从分析观点来看这是一个好方法,然而轨道计算是一个实际问题,要考虑结果的精确和计算的方便。
拉普拉斯方法在实用上不甚方便。
由于数值微分会放大误差,这就需要用十分精确的观测资料才能求出合理的导数。
尽管许多人曾设法降低这种过高的观测要求,并取得一定进展,但终究由于计算繁复,在解决实际问题时还是很少使用。
奥伯斯方法和高斯方法与拉普拉斯不同,奥伯斯和高斯则认为,如果能根据观测资料确定天体在两个不同时刻的空间位置,那么对应的轨道也就可以确定了。
也就是说,奥伯斯和高斯把轨道计算转化为一个边值测定问题来处理。
因此,问题的关键是如何根据三次定向观测来定出天体在空间的位置。
这既要考虑轨道的几何特性,又要应用天体运动的力学定律。
这些条件中最基本的一条是天体必须在通过太阳的平面上运动。
由于从观测掌握了天体在三个时刻的视方向,一旦确定了轨道平面的取向,除个别特殊情况外,天体在三个时刻的空间位置也就确定了。
轨道平面的正确取向的条件是所确定的三个空间位置能满足天体运动的力学定律,例如面积定律。
彗星轨道大都接近抛物线,所以在计算轨道时,常将它们作为抛物线处理。
完整的抛物线轨道计算方法是奥伯斯于1797年提出的。
他采用牛顿的假设,得到了彗星地心距的关系式;再结合表示天体在抛物线轨道上两个时刻的向径和弦关系的欧拉方程,求出彗星的地心距;从而求出彗星的抛物线轨道。
到现在为止,奥伯斯方法虽有不少改进,但基本原理并没有变,仍然是一个常用的计算抛物线轨道的方法。
1801年1月1日,皮亚齐发现了第一号小行星(谷神星),不久高斯就算出了它的椭圆轨道,他的方法发表于1809年。
高斯使用逐次近似法,先求出天体向径所围成的扇形面积与三角形面积之比,然后利用力学条件求得天体应有的空间位置,再从空间位置求得轨道。
高斯不仅从理论上、而且从实际上解决了轨道计算问题。
可以说,用三次观测决定轨道的实际问题是高斯首先解决的。
高斯以后,虽然有人提出一些新方法,但基本原理仍没有变。
人造卫星轨道计算计算小行星轨道的经典方法,原则上都能用来计算人造卫星的轨道。
在考虑到人造卫星的运动特点之后,又提出了一些新的方法。
人造卫星运动快,周期短,记时误差对轨道计算结果影响显著。
巴特拉科夫在高斯方法的基础上,用增加观测资料的办法,对记时有误差的轨道计算法作了改进。
近地卫星一天绕地球飞行十多圈,容易从观测定准它的周期,因而也就知道了轨道半长径,相应地提出了已知半长径的轨道计算法。
人造卫星离
地球近,视差现象明显,利用两站或多站同步观测容易求得卫星地心距,可以简化经典计算方法。
针对卫星摄动影响大的情况,又出现了考虑摄动的轨道计算法。
尽管这些方法多种多样,仍不外乎从观测资料求得两个点的向径,或一个点的向径和速度,从而得到轨道要素。
通过对人造卫星激光测距和多普勒测速,利用多站同步观测,或结合光学观测等方法,可以直接得到卫星的向径和速度,从而求得卫星的轨道。
应用高速电子计算机,可以进行复杂的迭代运算。
因此,目前更多的是综合各种类型的观测资料作轨道改进,而不把精力放在初始轨道的计算上。
现代技术条件已能使入轨后的卫星轨道同预定轨道相差不大。
这样,预定轨道就能作为初始轨道使用。
参考书目
P.R. Escobal,Methods of Orbit Determination,J.Wiley and Sons,New York,1965.
A. D. Dubyago, The Determination of Orbits,Macmillan Co.,New York,1961.
王昌彬。
