2020 中考数学压轴题破解策略专题训练 专题18《弦图模型》(02)
中考数学几何模型之弦图模型(解析版)

中考数学几何模型之弦图模型(解析版)中考数学几何模型:弦图模型名师点睛拨开云雾开门见山弦图模型,包含两种模型:内弦图模型和外弦图模型.(一)内弦图模型:如图,在正方形ABCD中,AE⊥BF于点E,BF⊥CG于点F,CG⊥DH于点G,DH ⊥AE于点H,则有结论:△ABE≌△BCF≌△CDG≌△DAH.注意局部弦图(二)外弦图模型:如图,在正方形ABCD中,E,F,G,H分别是正方形ABCD各边上的点,且四边形EFGH是正方形,则有结论:△AHE≌△BEF≌△CFG≌△DGH.包含“一线三垂直”典题探究启迪思维探究重点例题1. 如图,在△ABC中,∠ABC=90°,分别以AB,AC向外作正方形ABDE,ACFG,连接EG,若AB=12,BC=16,求△AEG的面积.变式练习>>>1.如图,四边形ABCD是边长为4的正方形,点E在边AD上,连接CE,以CE为边作正方形CEFG,点D,F在直线CE的同侧,连接BF,若AE=1,求BF的长.例题2. 如图,以Rt△ABC的斜边BC在△ABC同侧作正方形BCEF,该正方形的中心为点O,连接AO.若AB=4,AO=62,求AC的长.变式练习>>>2.如图,点A,B,C,D,E都在同一条直线上,四边形X,Y,Z都是正方形,若该图形总面积是m,正方形Y的面积是n,则图中阴影部分的面积是___________.例题3. 如图,在△ABC 中,∠BAC=45°,D 为△ABC 外一点,满足∠CBD=90°,BC=BD ,若=4.5ACD S △,求AC 的长.变式练习>>>3.点P 是正方形ABCD 外一点,PB=10cm ,△APB 的面积是60cm 2,△CPB 的面积是30cm 2.求正方形ABCD 的面积.例题4. 在边长为10的正方形ABCD 中,内接有6个大小相同的正方形,P 、Q 、M 、N 是落在大正方形边上的小正方形的顶点,如图所示,求这六个小正方形的面积.变式练习>>>4.如图,在平面直角坐标系中,经过点A的双曲线y=(x>0)同时经过点B,且点A在点B的左侧,点A的横坐标为,∠AOB=∠OBA=45°,则k的值为1+.【解答】解:在△AOM和△BAN中,,∴△AOM≌△BAN(AAS),∴AM=BN=,OM=AN=,∴OD=+,BD=﹣,∴B(+,﹣),∴双曲线y=(x>0)同时经过点A和B,∴(+)?(﹣)=k,整理得:k2﹣2k﹣4=0,解得:k=1±(负值舍去),∴k=1+;故答案为:1+.例题 5. 如图,在等腰Rt △ACB 和等腰Rt △DCE 中,∠AXB=∠DCE=90°,连接AD ,BE ,点I 在AD 上,(1)若IC ⊥BE ,求证:I 为AD 中点;(2)若I 为AD 中点,求证:IC ⊥BE例题6. 在平面直角坐标系中,直线l 的解析式为2y x b =+,其与x 轴交于点A,与y 轴交于点B ,在直线l 移动的过程中,直线y=4上是否存在点P ,使得△PAB 是等腰直角三角形,若存在,请求出满足条件的所有点P 的坐标,如不存在,请说明理由.。
2020年中考数学压轴题突破之动态问题(几何)(含详解)

2020年中考数学压轴题突破之动态问题(几何)1.如图,点O是等边ABC内一点,AOB 110 , BOC .以OC为一边作等边三角形OCD,连接AC、AD .(1)若120 ,判断OB OD BD (填“,或”)(2)当150 ,试判断AOD的形状,并说明理由;(3)探究:当时,AOD是等腰三角形.(请直接写出答案)【答案】(1) 二; (2) ADO是直角三角形,证明见详解;(3) 125、110、140 .【分析】(1)根据等边三角形性质得出COD 60 ,利用?BOC a = 120。
求出BOD 180 ,所以B, 0, D三点共线,即有OB+ OD = BD ;(2)首先根据已知条件可以证明BOC ADC ,然后利用全等三角形的性质可以求出ADO的度数,由此即可判定AOD的形状;(3)分三种情况讨论,利用已知条件及等腰三角形的性质即可求解.2 .如图,在平面直角坐标系中,矩形ABCO的顶点O与坐标原点重合,顶点A C在坐标轴上,B(18,6),将矩形沿EF折叠,使点A与点C重合.图3 G(1)求点E的坐标;(2)P O O A E2E时停止运动,设P的运动时间为t, VPCE的面积为S,求S与t的关系式,直接写出t 的取值范围;3(3)在(2)的条件下,当PA=]PE 时,在平面直角坐标系中是否存在点Q,使得以点P 、E 、G Q 为顶点的四边形为平行四边形?若不存在,请说明理由;若存在,请求出点Q 的坐标.【答案】(1) E (10, 6); (2) S= -8t+54 (0<t<3)或 S=-6t+48 (3vtW8); (3)存 在,Q (14.4 , -4.8 )或(18.4 , -4.8 ). 【详解】解:(1)如图 1,矩形 ABO, B (18, 6),• .AB=18 BC=6,设 AE=x,贝U EC=x BE=18-x,Rt^EBC 中,由勾股定理得: EB"+BC 2=EC 2,(18-x) 2+62=x 2, x=10,即 AE=10,①当P 在OA 上时,0WtW3,如图 2,=18X 6-1X10(62) — - X8X6 - 1X 18X2t , 2 2 2=-8t+54 ,②当P 在AE 上时,3<t<8,如图3,S = S 矩形 OABC S △ PAE -S △ BEC -S △OPCj• •E ( 10, 6);(2)分两种情况:S=1PE?BC=1 X 6X(16-2t)=3 (16-2t ) =-6t+48 ;2 2(3)存在,由PA=3PE可知:P在AE上,如图4,过G作GHLOC于H,2•.AP+PE=10.•.AP=6 PE=4,设OF=y,则FG=y, FC=18-y,由折叠得:/ CGFW AOF=90 ,由勾股定理得:FC2=FC+CG,•. ( 18-y) 2=y2+62,y=8,•.FG=8 FC=18-8=10,1FC?GH= 1FG?CG221X10XGH= 1 X6X8,22GH=4.8,由勾股定理得:FH=J82 4 82 =6.4 ,• .OH=8+6.4=14.4,.•.G ( 14.4 , -4.8 ),•・•点P、E G Q为顶点的四边形为平行四边形,且PE=4,.•.Q ( 14.4 , -4.8 )或(18.4 , -4.8 ). k ,3.如图1,平面直角坐标系xoy中,A(-4, 3),反比例函数y —(k 0)的图象分别x交矩形ABOC勺两边AC, BC于E, F (E, F不与A重合),沿着EF将矩形ABO所叠使A, D重合.②若折叠后点 D 落在矩形ABOCrt (不包括边界),求线段CE 长度的取值范围.(2)若折叠后,△ ABD 是等腰三角形,请直接写出此时点 D 的坐标.7 . 23 3. 11 3.【答案】(1)①EC= 2;②3 CE 4; (2)点D 的坐标为(一,一)或(一,一)88 2 5 5【详解】,k k解:(1)①由题意得E(k,3) , F( 4,-), 3 4k kk 0 ,则 EC — , FB 一, 3 4AF 3 一, 417(12 k) 4 3 1 3 4(12 k) 3..由 A(-4, 3)得:AC 4, AB 3,,AC 4一 --- 一,AB 3 AE AC AF AB '又A=Z A,・ .△AE% AACB ・ •/AEF4 ACB ・ •.EF// CB如图2,连接AD 交EF 于点H ,••• AE.AE (1)①如图2,当点D 恰好在矩形 ABOC 勺对角线BC 上时,求CE 的长;②由折叠得EF 垂直平分AD,••• /AHE 90 ,则 EAH AEF又• BAD EAH BAC 90 ,BAD AEF ,・ .△AE% ABAQAE AF 口"AB AE 4--- ----- ,则 ----- ------ -,AB BD BD AF 34 3 9 BDAB - 3 - 3 4 4设 AF=x,贝U FB=3— x, FD=AF=x 在Rt^BDF 中,由勾股定理得:FB 2 BD 2 FD 2,r i图2由折叠的性质得: •••D 在 BC 上, ,AE AHEC DH 1 EC AC 2AH=DH 1,则 AE EC 2;即(3 x)2x 2 ,解得:如图,当D 落在BO 上时,: EAF ABD 90 ,B力。
弦图与垂直模型-【压轴必刷】中考数学压轴大题之经典模型(全国通用)(解析版)
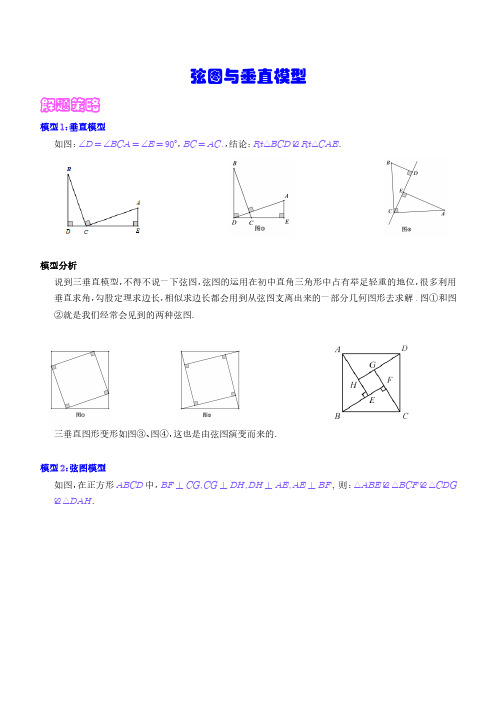
弦图与垂直模型解题策略模型1:垂直模型如图:∠D=∠BCA=∠E=90°,BC=AC.,结论:Rt△BCD≌Rt△CAE.模型分析说到三垂直模型,不得不说一下弦图,弦图的运用在初中直角三角形中占有举足轻重的地位,很多利用垂直求角,勾股定理求边长,相似求边长都会用到从弦图支离出来的一部分几何图形去求解.图①和图②就是我们经常会见到的两种弦图.三垂直图形变形如图③、图④,这也是由弦图演变而来的.模型2:弦图模型如图,在正方形ABCD中,BF⊥CG,CG⊥DH,DH⊥AE,AE⊥BF, 则:△ABE≌△BCF≌△CDG ≌△DAH.经典例题【例1】.(2021·全国·八年级专题练习)如图1,正方形ABCD中,点O是对角线AC的中点,点P是线段AO上(不与点A,O重合)的一个动点,过点P作PE⊥PB且PE交边CD于点E.(1)求证:PE=PB;(2)如图2,若正方形ABCD的边长为2,过点E作EF⊥AC于点F,在点P运动的过程中,PF的长度是否发生变化?若不变,试求出这个不变的值;若变化,请说明理由;(3)用等式表示线段PC,PA,CE之间的数量关系.【答案】(1)见解析;(2)在P点运动的过程中,PF的长度不发生变化.PF的长为定值2;(3)PC=PA+ 2EC.理由见解析.【分析】(1)做辅助线,构建全等三角形,根据ASA证明△BMP≅△PNE即可求解.(2)如图,连接OB,通过证明△OBP≅△FPE,得到PF=OB,则PF为定值是2.(3)根据△AMP和△PCN是等腰直角三角形,得PA=2PM,PC=2NC,整理可得结论.【详解】(1)证明:如图①,过点P作MN∥AD,交AB于点M,交CD于点N.∵PB⊥PE,∴∠BPE=90°,∴∠MPB+∠EPN=90°.∵四边形ABCD是正方形,∴∠BAD=∠D=90°.∵AD∥MN,∴∠BMP=∠BAD=∠PNE=∠D=90,∵∠MPB+∠MB P=90°,∴∠EPN=∠MB P.在Rt△PNC中,∠PCN=45°,∴△PNC是等腰直角三角形,∴PN=CN,∴BM=CN=PN,∴△BMP≌△PNE(ASA),∴PB=PE.(2)解:在P点运动的过程中,PF的长度不发生变化.理由:如图2,连接OB.∵点O是正方形ABCD对角线AC的中点,∴OB⊥AC,∴∠AOB=90°,∴∠AOB=∠EFP=90°,∴∠OBP+∠BPO=90°.∴∠BPE=90°,∴∠BPO+∠OPE=90°,∴∠OBP=∠OPE.由(1)得PB=PE,∴△OBP≌△FPE(AAS),∴PF=OB.=2.∵AB=2,△ABO是等腰直角三角形,∴OB=22∴PF的长为定值2.(3)解:PC=PA+2EC.理由:如图1,∵∠BAC=45°,∴△AMP是等腰直角三角形,∴PA=2PM.由(1)知PM=NE,∴PA=2NE.∵△PCN是等腰直角三角形,∴PC=2NC=2(NE+EC)=2NE+2EC=PA+2EC.【点睛】本题主要考查了四边形综合应用,通过对三角形全等的证明找出边之间的关系,准确分析代换求解是解题的关键.【例2】.(2021·黑龙江·哈尔滨市第四十九中学校九年级阶段练习)正方形ABCD中,点E、F在BC、CD 上,且BE=CF,AE与BF交于点G.(1)如图1,求证AE⊥BF;(2)如图2,在GF上截取GM=GB,∠MAD的平分线交CD于点H,交BF于点N,连接CN,求证:AN+CN=2BN;【答案】(1)见解析;(2)见解析;【分析】(1)根据正方形的性质得AB=BC,∠ABC=∠BCD=90°,用SAS证明△ABE≌△BCF,得∠BAE =∠CBF,根据三角形内角和定理和等量代换即可得;(2)过点B作BH⊥BN,交AN于点H,根据正方形的性质和平行线的性质,用SAS证明△A GB≌△AGM,得∠BAG=∠MAG,根据角平分线性质得∠BHA=∠GAN=45°,则△HBN是等腰直角三角形,用SAS证明△ABH≌△CBN,得AH=CN,在Rt△HBN中,根据勾股定理即可得;【详解】解:(1)∵四边形ABCD 是正方形,∴AB=BC,∠ABC=∠BCD=90°,在△ABE和△BCF中,AB=BC∠ABE=∠BCFBE=CF∴△ABE≌△BCF(SAS),∴∠BAE=∠CBF,∵∠AEB+∠BAE=180°-∠ABC=180°-90°=90°,∴∠AEB+∠CBF=90°,∴∠E GB=180°-(∠AEB+∠CBF)=180°-90°=90°,∴AE⊥BF;(2)如图所示,过点B作BH⊥BN,交AN于点H,∵四边形ABCD是正方形,∴AB=AC,∠ABC=∠HBN=90°,∵∠HBN=∠HBA+∠ABN=90°,∠ABC=∠CBN+∠ABN=90°,∴∠HBA=∠CBN,由(1)得,AE⊥BF,∴∠A GB=∠AGM=90°,∴∠HBG=∠AGM=90°,∴HB⎳AE,∴∠BHA=∠EAN,在△A GB和△AGM中,AG=AG∠A GB=∠AGMGB=GM∴△A GB≌△AGM(SAS),∴∠BAG=∠MAG,∵AN平分∠DAM,∴∠DAN=∠MAN,∴∠BAG+∠MAG+∠MAN+∠DAN=90°,2∠MAG+2∠MAN=90°,∠MAG+∠MAN=45°,∠GAN=45°,∴∠BHA=∠GAN=45°,∴∠BNH=180°-∠HBN-∠BHA=180°-90°-45°=45°,∴△HBN是等腰直角三角形,∴BH=BN,在△ABH和△CBN中,BH=BN∠HBA=∠CBNAB=CB∴△ABH≌△CBN(SAS),∴AH=CN,在Rt△HBN中,根据勾股定理HN=BH2+BN2=2BN,∴AN+CN=AN+AH=HN=2BN;【点睛】本题考查了正方形的性质,全等三角形的判定与性质,三角形内角和定理,角平分线,等腰直角三角形的判定与性质,勾股定理和锐角三角函数,解题的关键是掌握并灵活运用这些知识点.【例3】.(2021·云南曲靖·八年级期末)如图1,在正方形ABCD中,E为BC上一点,连接AE,过点B作BG⊥AE于点H,交CD于点G.(1)求证:AE=BG;(2)如图2,连接AG、GE,点M、N、P、Q分别是AB、AG、GE、EB的中点,试判断四边形MNPQ的形状,并说明理由;(3)如图3,点F、R分别在正方形ABCD的边AB、CD上,把正方形沿直线FR翻折,使得BC的对应边B'C'恰好经过点A,过点A作AO⊥FR于点O,若AB'=1,正方形的边长为3,求线段OF的长.【答案】(1)见解析;(2)四边形MNPQ为正方形,理由见解析;(3)10 6【分析】(1)由四边形ABCD为正方形,可得∠ABC=∠BCD=90°,推得∠ABG+∠CBG=90°,由BG⊥AE,可得∠BAE+∠ABG=90°,可证△ABE≅△BCG ASA即可;(2)M、N为AB、AG中点,可得MN为△ABG的中位线,可证MN⎳BG,MN=12BG,由点M、N、P、Q分别是AB、AG、GE、EB的中点,可得PQ是△BEG的中位线,MQ为△ABE的中位线,NP为△AEG的中位线,可证PQ⎳BG,PQ=12BG,MQ⎳AE,MQ=12AE,NP⎳AE,NP=12AE,可证四边形MNPQ为平行四边形.再证四边形MNPQ为菱形,最后证MN⊥MQ即可;(3)延长AO交BC于点S,由对称性可得BF=B'F,AB'=BS=1,AO=SO,由勾股定理可求AS=10,可得AO=12AS=102,设AF=x,在Rt△AB'F中,12+(3-x)2=x2,解得x=53,在Rt△AOF中,可求OF=106.【详解】(1)证明:∵四边形ABCD为正方形,∴∠ABC=∠BCD=90°,∴∠ABG+∠CBG=90°,∵BG⊥AE,∴∠AHB=90°,∴∠BAE+∠ABG=90°,∴∠BAE=∠CBG,在△ABE与△BCG中,∠BAE=∠CBGAB=BC∠ABC=∠BCD,∴△ABE≅△BCG ASA,∴AE=BG.(2)解:四边形MNPQ为正方形,理由如下:∵M、N为AB、AG中点,∴MN为△ABG的中位线,∴MN⎳BG,MN=12BG,∵点M、N、P、Q分别是AB、AG、GE、EB的中点,∴PQ是△BEG的中位线,MQ为△ABE的中位线,NP为△AEG的中位线,,∴PQ⎳BG,PQ=12BG,MQ⎳AE,MQ=12AE,NP⎳AE,NP=12AE,∴MN=PQ,MQ=NP,∴四边形MNPQ为平行四边形.∵AE=BG,∴MN=MQ,∴四边形MNPQ为菱形,∵BG⊥AE,MQ⎳AE,∴MQ⊥BG,∵MN⎳BG,∴MN⊥MQ,∴四边形MNPQ为正方形.(3)解:延长AO交BC于点S,由对称性可知BF=B'F,AB'=BS=1,AO=SO,在Rt△ABS中,AS=AB2+BS2=10,∴AO=12AS=102,设AF=x,则BF=B'F=3-x,在Rt△AB'F中,12+(3-x)2=x2,x=53,∴AF=53,在Rt△AOF中,2=106.OF=AF2-AO2=53 2-102【点睛】本题考查正方形性质与判定,等角的余角性质三角形全等判定与性质,三角形中位线判定与性质,勾股定理,根据勾股定理建构方程,解拓展一元一次方程等知识,掌握以上知识是解题关键.【例4】.(2021·河南商丘·八年级期中)在平面直角坐标系中,点A的坐标为4,0,点B为y轴正半轴上的一个动点,以B为直角顶点,AB为直角边在第一象限作等腰Rt△ABC.(1)如图1,若OB=3,则点C的坐标为______;(2)如图2,若OB=4,点D为OA延长线上一点,以D为直角顶点,BD为直角边在第一象限作等腰Rt△BDE,连接AE,求证:AE⊥AB;(3)如图3,以B为直角顶点,OB为直角边在第三象限作等腰Rt△OBF.连接CF,交y轴于点P,求线段BP的长度.【答案】(1)点C(3,7);(2)证明见详解过程;(3)2.【分析】(1)如图1,过点C作CH⊥y轴,由“AAS”可证△ABO≌△BCH,可得CH=OB=3,BH=AO=4,可求解;(2)过点E作EF⊥x轴于F,由“AAS”可证△ABO≌△BCH,可得BO=DF=4,OD=EF,由等腰直角三角形的性质可得∠BAO=45°,∠EAF=∠AEF=45°,可得结论;(3)由(1)可知△ABO≌△BCG,可得BO=GC,AO=BG=4,再由“AAS”可证△CPG≌△FPB,可得PB=PG=2.(1)如图1,过点C作CH⊥y轴于H,∴∠CHB=∠ABC=∠AOB=90°,∴∠BCH+∠HBC=90°=∠HBC+∠ABO,∴∠ABO=∠BCH,在△ABO和△BCH中,∠CHB=∠AOB∠BCH=∠ABOBC=AB,∴△ABO≌△BCH(AAS),∴CH=OB=3,BH=AO=4,∴OH=7,∴点C(3,7),故答案为:(3,7);(2)过点E作EF⊥x轴于F,∴∠EFD=∠BDE=∠BOD=90°,∴∠BDO+∠EDF=90°=∠BDO+∠DBO,∴∠DBO=∠EDF,在△BOD和△DFE中,∠BOD=∠EFD∠DBO=∠EDFBD=ED,∴△BOD≌△DFE(AAS),∴BO=DF=4,OD=EF,∵点A的坐标为(4,0),∴OA=OB=4,∴∠BAO=45°,∵OA=DF=4,∴OD=AF=EF,∴∠EAF=∠AEF=45°,∴∠BAE=90°,∴BA⊥AE;(3)过点C作CG⊥y轴G,由(1)可知:△ABO≌△BCG,∴BO=GC,AO=BG=4,∵BF=BO,∠OBF=90°,∴BF=GC,∠CGP=∠FBP=90°,又∵∠CPG=∠FPB,∴△CPG≌△FPB(AAS),∴BP=GP,∴BP=12BG=2.【点睛】本题是三角形综合题,考查了全等三角形的判定和性质,等腰直角三角形的性质等知识,添加恰当辅助线构造直角三角形是本题的关键.【例5】.(2021·黑龙江·哈尔滨市风华中学校九年级阶段练习)如图1,正方形ABCD中,点E是边BC延长线上一点,连接DE,过点B作BF⊥DE,垂足为点F,BF与CD相交于点G.(1)求证:△BCG≌△DCE;(2)如图2,连接BD,若BE=42,DG=22,求tan∠DBG的值.【答案】(1)见解析;(2)1 2【分析】(1)由正方形的性质结合已知条件,利用ASA判定三角形全等即可;(2)过点G作GH⊥BD垂足为H,由全等求得CG=CE,进一步结合图形求得BC和CG的长,然后在RT△BDC中求得GH和BH的长,最后在RT△BHG中,利用tan∠DBG=HGBH,即可求得答案.【详解】(1)证明:∵四边形ABCD是正方形,∴∠BCG=∠DCE=90°,BC=CD,∵BF⊥DE,∴∠DFG=∠BCG=90°,∵∠BGC=∠DGF,∴∠CBG=∠CDE.在△BCG和△DCE中,∠CBG=∠CDE BC=CD∠BCG=∠DCE,∴△BCG≌△DCE,(2)解:过点G作GH⊥BD垂足为H,∵△BCG≌△DCE,∴CG=CE,∵BE=BC+CE=42,DG=CD-CG=22,∴BC=CD=32,CG=CE=2,在RT△BDC中,∵∠BCD=90°,∴BD=CD2+BC2=322+322=6,∵∠DHG=45°,∠DHG=90°,DG=22,∴DHDG=sin45°=2 2,∴DH=2,∴GH=DH=2,∵BH=BD-DH,∴BH=6-2=4,在RT△BHG中,∵∠BHG=90°,∴tan∠DBG=HGBH,∴tan∠DBG=12【点睛】本题考查三角形全等的证明,直角三角形中锐角三角函数的定义等相关知识点,熟练掌握数形结合思想解题是重点.培优训练一、解答题1.(2022·江苏·八年级课时练习)如图1,在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.(1)由图1,证明:DE=AD+BE;(2)当直线MN绕点C旋转到图2的位置时,请猜想出DE,AD,BE的等量关系并说明理由;(3)当直线MN绕点C旋转到图3的位置时,试问DE,AD,BE又具有怎样的等量关系?请直接写出这个等量关系(不必说明理由).【答案】(1)证明见解析;(2)DE=AD-BE,证明过程见解析;(3)DE=BE-AD,证明过程见解析【分析】(1)先证明△ADC≌△CEB,得到AD=CE,DC=BE,进而得到DE=CE+DC=AD+BE即可;(2)同(1)中思路,证明△ADC≌△CEB,进而得到DE=CE-DC=AD-BE即可;(3)同(1)中思路,证明△ADC≌△CEB,进而得到DE=DC-CE=BE-AD即可.【详解】解:(1)证明:在△ABC中,∵∠ACB=90°,∴∠ACD+∠BCE=90°,∵AD⊥MN,∴∠ACD+∠CAD=90°,∴∠BCE=∠CAD,又∵AC=BC,∠ADC=∠CEB=90∘,∴△ADC≌△CEB(AAS),∴AD=CE,DC=BE,∵直线MN经过点C,∴DE=CE+DC=AD+BE;(2)DE,AD,BE的等量关系为:DE=AD-BE,理由如下:∵AD⊥MN于D,BE⊥MN于E∴∠ADC=∠BEC=∠ACB=90°,∴∠CAD+∠ACD=90°,∠ACD+∠BCE=90°,∴∠CAD=∠BCE,在△ADC和△CEB中∠CAD=∠BCE∠ADC=∠BEC=90∘AC=CB,∴△ADC≌△CEB AAS∴CE=AD,CD=BE,∴DE=CE-CD=AD-BE;(3)当MN旋转到图3的位置时,DE、AD、BE所满足的等量关系是DE=BE-AD,理由如下:∵AD⊥MN于D,BE⊥MN于E∴∠ADC=∠BEC=∠ACB=90°,∴∠CAD+∠ACD=90°,∠ACD+∠BCE=90°,∴∠CAD=∠BCE,在△ADC和△CEB中∠CAD=∠BCE∠ADC=∠BEC=90∘AC=CB,∴△ADC≌△CEB AAS∴CE=AD,CD=BE,∴DE=CD-CE=BE-AD.【点睛】本题考查了全等三角形的判定方法、等腰直角三角形的性质及等角的余角相等等知识点,熟练掌握三角形全等的判定方法是求解的关键.2.(2022·全国·八年级专题练习)如图所示,△ABC中,AB=AC,∠BAC=90°,点D为AB上一点,过点B作直线CD的垂线,垂足为E,连接AE,过点A作AE的垂线交CE于点F.(1)如图1,求∠AEC的度数;(2)如图2,连接BF,且∠ABF-∠EAB=15°,求证:BF=2CF;(3)如图3,在(2)的条件下,G为DF上一点,连接AG,若∠AGD=∠EBF,AG=2,求CF的长.【答案】(1)45°;(2)见解析;(3)2【分析】(1)先证明∠EAB=∠FAC, ∠AEB=∠AFC,再证明△ABE≅△ACF,再利用全等三角形的性质结合等腰直角三角形的性质可得答案;(2)利用全等三角形的性质先求解∠EBF=60°,证明BE=CF, 再求解∠EFB=30°,从而可得结论;(3)如图,过A作AM⊥EF于M, 交BF于N, 连接EN, 证明△BEN为等边三角形,再证明△AGM≅△ENM,再利用全等三角形的性质可得答案.【详解】解:(1)∵∠BAC=90°,AE⊥AF,∴∠EAB+∠DAF=∠DAF+∠FAC=90°,∠EAF=90°,∴∠EAB=∠FAC,∵BE⊥CE,∴∠BED=90°,∴∠AEB=∠BED+∠AEF=90°+∠AEF=∠AFC, 即∠AEB=∠AFC,∴△ABE≅△ACF,∴AE=AF,∠AEC=45°.(2)∵△ABE≅△ACF,∴∠ABE=∠ACF,BE=CF,∴∠AEB=∠AFC=90°+45°=135°,∴∠EBA+∠EAB=45°,∵∠ABF-∠EAB=15°,∴∠ABF=15°+∠EAB,∴∠EBF=∠EBA+∠ABF=∠EBA+∠EAB+15°=60°,∴∠BFE=90°-60°=30°,∴BF=2BE,∵BE=CF,∴BF=2CF.(3)如图,过A作AM⊥EF于M, 交BF于N, 连接EN,∵AE=AF,AM⊥EF,AE⊥AF,∴EM=MF=AM,NE=NF,∴∠NEF=∠NFE=30°,∴∠ENB=∠NEF+∠NFE=60°,∴∠EBN=∠ENB=60°,∴△BEN为等边三角形,∠ENF=120°,∴BE=BN=12BF=FN=EN,∵∠AGD=∠EBF=60°, AM⊥EF,∴∠ENM=12∠ENF=60°,∵AM=EM,∠AMG=∠EMN=90°,∠AGM=∠ENM=60°,∴△AGM≅△ENM,∴AG=EN=2,∴CF=BE=2.【点睛】本题考查的是全等三角形的判定与性质,等腰三角形的性质,直角三角形斜边上的中线等腰斜边的一半,等边三角形的判定与性质,含30°的直角三角形的性质,熟练的应用以上知识解题的关键.3.(2020·北京市第十三中学九年级期中)已知:Rt△ABC中,∠ACB=90°,AC=BC.(1)如图1,点D是BC边上一点(不与点B,C重合),连接AD,过点B作BE⊥AD,交AD的延长线于点E,连接CE.①若∠BAD=α,求∠DBE的大小(用含α的式子表示);②用等式表示线段EA,EB和EC之间的数量关系,并证明.(2)如图2,点D在线段BC的延长线上时,连接AD,过点B作BE⊥AD,垂足E在线段AD上,连接CE.①依题意补全图2;②直接写出线段EA,EB和EC之间的数量关系.【答案】(1)①∠DBE=45°-α;②AE-BE=2EC,证明见解析;(2)①补全图形见解析;②EB-EA= 2EC.【分析】(1)①根据等腰直角三角形的性质得到∠CAB=45°,即可求出∠CAD=45∘-α.根据三角形的内角和即可求出∠DBE=∠CAD=45∘-α;②过点C作CR⊥CE交AE于R,然后证明△ACR≌△BCE,得到AR=BE,CR=CE,即可得到△CER 是等腰直角三角形,ER=2CE,由此即可求解;(2)①根据题目要求作图即可;②过点C作CF⊥CE,交AD的延长线于点F.根据三角形的内角和定理得到∠CAF=∠CBE,证明△ACF ≌△BCE.根据全等三角形的性质有AF=BE,CF=CE.根据等腰直角三角形的性质有EF=2EC.则有 AF-EA=2EC,即可求出线段EA,EB和EC之间的数量关系.【详解】解:(1)①如图1中,∵∠ACB=90°,AC=BC,∴∠CAB=45°,∵∠BAD=α,∴∠CAD=45°-α.∵∠ACB=90°,BE⊥AD,∠ADC=∠BDE,∴∠DBE=∠CAD=45°-α;②结论:AE-BE=2EC.理由:如图,过点C作CR⊥CE交AE于R.∴∠ACB=∠RCE=90°,∴∠ACR=∠BCE,∵∠CAR+∠ADC=90°,∠CBE+∠BDE=90°,∠ADC=∠BDE,∴∠CAR=∠CBE,在△ACR和△BCE中,∠ACR=∠BCECA=CB∠CAR=∠CBE,∴△ACR≌△BCE(ASA),∴AR=BE,CR=CE,∴△CER是等腰直角三角形,∴ER=2CE,∴AE-BE=AE-AR=ER=2EC.(2)①补全图形,如图2所示:②猜想:当D 在BC 边的延长线上时,EB -EA =2EC ;理由如下:过点C 作CF ⊥CE ,交AD 的延长线于点F ,如图3所示:则∠ECF =90°,∵∠ACB =90°,∴∠ACD =90°,∴∠ECF +∠ACE =∠ACB +∠ACE ,即∠ACF =∠BCE ,∵∠CAF +∠ADB =90°,∠CBE +∠ADB =90°,∴∠CAF =∠CBE ,在△ACF 和△BCE 中,∠ACF =∠BCEAC =BC ∠CAF =∠CBE,∴△ACF ≌△BCE (ASA ),∴AF =BE ,CF =CE .∵∠ECF =90°,∴△CEF 是等腰直角三角形,∴EF =2EC ,即AF -EA =2EC .∴EB -EA =2EC .【点睛】考查等腰直角三角形的性质,三角形的内角和定理,全等三角形的判定与性质等,难度一般,掌握全等三角形的判定定理是解题的关键.4.(2021·四川省成都市七中育才学校七年级期中)已知:△ABC 中,∠ACB =90°,AC =CB ,D 为直线BC 上一动点,连接AD ,在直线AC 右侧作AE ⊥AD ,且AE =AD .(1)如图1,当点D 在线段BC 上时,过点E 作EH ⊥AC 于H ,连接DE .求证:EH =AC ;(2)如图2,当点D 在线段BC 的延长线上时,连接BE 交CA 的延长线于点M .求证:BM =EM ;(3)当点D在直线CB上时,连接BE交直线AC于M,若2AC=5CM,请求出S△ADBS△AEM的值.【答案】(1)见解析;(2)见解析;(3)43或47【分析】(1)由“AAS”可证△AHE≌△DCA,可得EH=AC,即可求证;(2)过点E作EN⊥AC,交CA延长线于N,由“AAS”可证△ANE≌△DCA,可得AC=EN=BC,由“AAS”可证△ENM≌△BCM,可得BM=EM;(3)AC=5a,CM=2a,分三种情况:当点D在线段BC上,点D在线段BC的延长线上,点D在线段CB的延长线上,由全等三角形的性质可求得相应线段的长,再由三角形的面积公式可求解.【详解】证明(1)∵AE⊥AD,∠ACB=90°,∴∠EAH=90°-∠CAD,∠ADC=90°-∠CAD,∴∠EAH=∠ADC,在△AHE与△DCA中∠AHE=∠ACB=90°∠EAH=∠ADCAE=AD,∴△AHE≌△DCA(AAS),∴EH=AC;(2)如图2,过点E作EN⊥AC,交CA延长线于N,∵AE⊥AD,∠ACB=90°,∴∠EAN=90°-∠CAD,∠ADC=90°-∠CAD,∴∠EAN=∠ADC,在△ANE与△DCA中,∠ANE=∠DCA=90°∠ENA=∠ACDAN=AD∴△ANE≌△DCA(AAS),∴EN=AC,又∵AC=BC,∴EN=BC,又在△ENM与△BCM中,∠EMN=∠BMC∠N=∠BCA=90°EN=BC∴△ENM≌△BCM(AAS),则BM=EM;(3)如图,当点D 在线段BC 上时,∵2AC =5CM ,∴可设AC =5a ,CM =2a ,由(1)得:△AHE ≌△DCA ,则AH =CD ,EH =AC =BC =5a ,由∵∠EHM =∠BCM =90° ,∠BMC =∠EMH ,∴△MHE ≌△MCB (AAS ),∴CM =HM ,即HM =CM =2a ,∴AH =AC -CM -HM =5a -2a -2a =a ,∴AM =AH +HM =3a ,CD =AH =a ,EH =AC =5a , BD =BC -CD =4a ,∴S △ADB S △AEM =12BD ×AC 12AM ×EH =12×4a ×5a 12×3a ×5a =43;如图,点D 在CB 延长线上时,过点E 作EN ⊥AC ,交AC 延长线于N ,∵2AC =5CM ,∴可设AC =5a ,CM =2a ,∵EN ⊥AC ,AE ⊥AD ,∴∠ANE =∠EAD =∠ACB =90° ,∴∠EAN =90°-∠CAD ,∠ADC =90°-∠CAD ,∴∠EAN =∠ADC ,在△ANE 与△DCA 中,∠ANE =∠DCA =90°∠ENA =∠ACDAN =AD∴△ANE ≌△DCA (AAS ),∴EN =AC ,AN =CD ,又∵AC =BC ,∴EN =BC ,又在△ENM 与△BCM 中,∠EMN =∠BMC∠N =∠BCA=90°EN =BC∴△ENM ≌△BCM (AAS ),∴CM =NM =2a ,NE =BC =AC =5a ,∴AN =AC +CM +MN =9a ,AM =AC +CM =7a ,AN =CD =9a ,∴BD =4a ,∴S △ADB S △AEM =12BD ×AC 12AM ×EN =12×4a ×5a 12×7a ×5a =47,点D 在BC 延长线上由图2得:AC <CM ,∴2AC =5CM 不可能,故舍去综上:S △ADB S △AEM的值为43 或47【点睛】本题是三角形综合题,考查了等腰直角三角形的性质,全等三角形的判定和性质,添加恰当辅助线构造全等三角形是本题的关键.5.(2022·江苏·八年级课时练习)在△ABC 中,AB =BC ,∠B =90°,点D 为直线BC 上的一个动点(不与B 、C 重合),连结AD ,将线段AD 绕点D 按顺时针方向旋转90°,使点A 旋转到点E ,连结EC .(1)如果点D 在线段BC 上运动,如图1:求证:∠BAD =∠EDC(2)如果点D 在线段BC 上运动,请写出AC 与CE 的位置关系.通过观察、交流,小明形成了以下的解题思路:过点E 作EF ⊥BC 交直线BC 于F ,如图2所示,通过证明△DEF ≌△ABD ,可推证△CEF 等腰直角三角形,从而得出AC 与CE 的位置关系,请你写出证明过程.(3)如果点D 在线段CB 的延长线上运动,利用图3画图分析,(2)中的结论是否仍然成若成立,请证明;若不成立,请说明理由.【答案】(1)见解析;(2)垂直,理由见解析;(3)成立,证明见解析【分析】(1)根据直角三角形的性质证明即可;(2)过点E 作EF ⊥BC 交直线BC 于F ,如图2所示,通过证明△DEF ≌△ABD ,可推证△CEF 等腰直角三角形,从而得出AC 与CE 的位置关系;(3)如图3所示,过点E 作EF ⊥DC 于F ,证明△ABD ≌△DFE ,进一步可证明AC ⊥EC【详解】解:(1)证明:∵∠B =90°∴∠BDA +∠BAD =90°∵∠ADE=90°∴∠BDA+∠EDC=90°∴∠BAD=∠EDC(2)垂直∵EF⊥BC∴∠EFD=90°∵∠B=90°∴∠EFD=∠B在△ABD和△DFE中∠BAD=∠FDE∠B=∠DFEAD=DE∴△ABD≌△DFE AAS∴AB=DF,BD=EF∵AB=BC∴BC=DF,∴BC-DC=DF-DC即BD=CF.∴EF=CF又∵∠EFC=90°∴∠ECF=45°,且∠ACB=45°∴∠ACE=180°-90°=90°即AC⊥CE.(3)(2)中的结论仍然成立如图3所示,过点E作EF⊥DC于F ∵∠ABD=90°∴∠EDF=∠DAB=90°-∠ADB在△ABD和△DFE中∠DAB=∠EDF∠ABD=∠DFEAD=DE∴△ABD≌△DFE AAS∴DB=EF,AB=DF=BC∴BC-BF=DF-BF即FC=DB∴FC=EF∴∠DCE=45°∴∠ACE=∠DCE+∠ACB=90°∴AC⊥EC.【点睛】此题是几何变换综合题,主要考查了旋转的性质,全等三角形的判定和性质,证明△ABD≌△DFE是解本题的关键.6.(2021·黑龙江·哈尔滨市第四十七中学八年级开学考试)如图,已知△ABC中,AB=AC,∠BAC= 90°,分别过B、C向过A的直线作垂线,垂足分别为E、F.(1)如图1,过A的直线与斜边BC不相交时,直接写出线段EF、BE、CF的数量关系是______;(2)如图2,过A的直线与斜边BC相交时,探究线段EF、BE、CF的数量关系并加以证明;(3)在(2)的条件下,如图3,直线FA交BC于点H,延长BE交AC于点G,连接BF、FG、HG,若∠AHB=∠GHC,EF=CF=6,EH=2FH,四边形ABFG的面积是90,求△GHC的面积.【答案】(1)数量关系为:EF=BE+CF;(2)数量关系为:EF=BE-CF.证明见详解;(3)S△GHC=15.【分析】(1)数量关系为:EF=BE+CF.利用一线三直角得到∠BEA=∠AFC=90°,∠EBA=∠FAC,再证△EBA≌△FEC(AAS)可得BE=AF,AE=CF即可;(2)数量关系为:EF=BE-CF.先证∠BEA=∠AFC=90°,∠EBA+∠EAB=90°,∠EAB+∠FAC= =90°,可得∠EBA=∠FAC,再证△EBA≌△FEC(AAS),可得BE=AF,AE=CF即可;(3)先由(2)结论EF=BE-CF;EF=CF=6,求出BE=AF=12,由EH=2FH,可求FH=2,EH=4,利用对角线垂直的四边形面积可求BG=2×90AF=18012=15,再求EG=3,AH=10,分别求出S△ACF=12AF⋅FC=36,S△HCF=12HF⋅FC=6,S△AGH=12AH⋅EG=15,利用面积差即可求出.【详解】解:(1)数量关系为:EF=BE+CF.∵BE⊥EF,CF⊥EF,∠BAC=90°,∴∠BEA=∠AFC=90°,∠EBA+∠EAB=90°,∠EAB+∠FAC=180°-∠BAC=90°,∴∠EBA=∠FAC,在△EBA和△FEC中,∵∠AEB=∠CFA ∠EBA=∠FAC AB=CA,∴△EBA≌△FAC(AAS),∴BE =AF ,AE =CF ,∴EF =AF +AE =BE +CF ;(2)数量关系为:EF =BE -CF .∵BE ⊥AF ,CF ⊥AF ,∠BAC =90°,∴∠BEA =∠AFC =90°,∠EBA +∠EAB =90°,∠EAB +∠FAC ==90°,∴∠EBA =∠FAC ,在△EBA 和△FEC 中,∵∠AEB =∠CFA∠EBA =∠FAC AB =CA,∴△EBA ≌△FAC (AAS ),∴BE =AF ,AE =CF ,∴EF =AF -AE =BE -CF ;(3)∵EF =BE -CF ;EF =CF =6,∴BE =AF =EF +CF =6+6=12,∵EH =2FH ,EH +FH =EF =6,∴2FH +FH =6,解得FH =2,∴EH =2FH =4,S 四边形ABFG =12AF ⋅BG =90,∴BG =2×90AF =18012=15,∴EG =BG -BE =15-12=3,AH =AE +EH =6+4=10,∵S △ACF =12AF ⋅FC =12×12×6=36,S △HCF =12HF ⋅FC =12×2×6=6,S △AGH =12AH ⋅EG =12×10×3=15,∴S △GHC =S △ACF -S △HCF -S △AGH =36-6-15=15.【点睛】本题考查图形变换探究线段和差问题,感知,探究以及应用,三角形全等判定与性质,三角形面积,四边形面积,与三角形高有关的计算,掌握图形变换探究线段和差问题,感知,探究以及应用,三角形全等判定与性质,三角形面积,四边形面积,与三角形高有关的计算是解题关键.7.(2021·江苏泰州·八年级期末)如图,正方形ABCD 边长为4,点G 在边AD 上(不与点A 、D 重合),BG 的垂直平分线分别交AB 、CD 于E 、F 两点,连接EG .(1)当AG =1时,求EG 的长;(2)当AG 的值等于时,BE =8-2DF ;(3)过G 点作GM ⊥EG 交CD 于M①求证:GB 平分∠AGM ;②设AG =x ,CM =y ,试说明16xy -4x -4y-1的值为定值.【答案】(1)178;(2)8-43(3)①见解析;②16xy -4x -4y-1=0,理由见解析【分析】(1)根据EF 是线段BG 的垂直平分线,BE =EG ,设EG =EB =x ,则AE =AB -BE =4-x ,再由勾股定理求解即可;(2)过点F 作FH ⊥AB 于H ,连接FB ,FG ,由BE =8-2DF ,CF =CD -DF =4-DF ,得到BE =2CF ,先证明四边形BCFH 是矩形,得到CF =HB ,则BH =EH =FC ,设AG =x ,BE =y ,则AE =4-y ,GD =4-x ,CF =12y ,DF =4-12y 由AE 2+AG 2=EG 2,GD 2+DF 2=GF 2,BC 2+FC 2=BF 2,可以得到4-y 2+x 2=y 2①,4-x 2+4-12y 2=42+12y 2②,联立①②求解即可得到答案;(3)①先证明∠EBG =∠E GB ,然后根据ABG +∠A GB =90°,∠E GB +∠BGM =90°,即可得到∠A GB =∠BGM ;②连接BM ,过点B 作BH ⊥GM ,由角平分线的性质得到BH =AB =4,由S 正方形ABCD =S △ABG +S △MB G +S △BCM +S △CDM =4×4=16,可以得到2x +2GM +2y +124-x 4-y =16,由勾股定理可以得到DM 2+GD 2=GM 即4-x 2+4-y 2=4-xy 4 ,最后解方程即可得到答案.【详解】解:(1)∵EF 是线段BG 的垂直平分线,∴BE =EG ,∵四边形ABCD 是正方形,且边长为4,∴AB =4,∠A =90°,设EG =EB =x ,则AE =AB -BE =4-x ,∵AE 2+AG 2=EG 2,∴4-x 2+12=x 2,解得x =178,∴EG =178;(2)如图所示,过点F 作FH ⊥AB 于H ,连接FB ,FG∵EF 是线段BG 的垂直平分线,∴BF =FG ,∵BE =8-2DF ,CF =CD -DF =4-DF ,∴BE =2CF ,∵四边形ABCD 是正方形,FH ⊥AB ,∴∠HBC =∠C =∠BHF =90°,∴四边形BCFH 是矩形,∴CF =HB ,∴BH =EH =FC ,设AG =x ,BE =y ,则AE =4-y ,GD =4-x ,CF =12y ,DF =4-12y ∵AE 2+AG 2=EG 2,GD 2+DF 2=GF 2,BC 2+FC 2=BF 2,∴4-y 2+x 2=y 2①,4-x 2+4-12y 2=42+12y 2②,联立①②解得x =8-43或x =8+43(舍去),∴当AG =8-43时,BE =8-2DF ,故答案为:8-43;(3)①∵EF 是线段BG 的垂直平分线,∴EG =BE ,∴∠EBG =∠E GB ,∵四边形ABCD 是正方形,EG ⊥GM ,∴∠A =∠EGM =90°,∴∠ABG +∠A GB =90°,∠E GB +∠BGM =90°,∴∠A GB =∠BGM ,∴BG 平分∠AGM ;②如图,连接BM ,过点B 作BH ⊥GM ,由(3)①得BG 平分∠AGM ,∴BH =AB =4,∵AG =x ,CM =y ,∴DG =4-x ,DM =4-y ,∵S 正方形ABCD =S △ABG +S △MB G +S △BCM +S △CDM =4×4=16,∴12AG ·AB +12GM ·BH +12CM ·BC +12DM ·GD =16,∴2x +2GM +2y +124-x 4-y =16,∴GM =4-xy 4,∵DM 2+GD 2=GM ,∴4-x 2+4-y 2=4-xy 4 ∴16-8x +x 2+16-8y +y 2=16-2xy +x 2y 216∴x +y 2-8x +y +16=x 2y 216,∴x +y -4 2=x 2y 216,∴x +y -4=±xy 4,当x +y -4=xy 4时,则4x +4y -16=xy ,∴y =16-4x 4-x =4(不符合题意),∴4x +4y -16=-xy∴16xy -4x -4y-1=0.【点睛】本题主要考查了正方形的性质,勾股定理,角平分线的性质,线段垂直平分线的性质,等腰三角形的性质与判定,三角形的面积等等,解题的关键在于能够熟练掌握相关知识进行求解.8.(2021·全国·八年级专题练习)已知,如图,在Rt △ABC 中,∠BAC =90°,∠ABC =45°,点D 为直线BC 上一动点(点D 不与点B ,C 重合).以AD 为边作正方形ADEF ,连接CF ,当点D 在线段BC 的反向延长线上,且点A ,F 分别在直线BC 的两侧时.(1)求证:△ABD ≌△ACF ;(2)若正方形ADEF 的边长为22,对角线AE ,DF 相交于点O ,连接OC ,求OC 的长度.【答案】(1)证明见解析; (2)OC =2【分析】(1)由题意易得AD =AF ,∠DAF =90°,则有∠DAB =∠FAC ,进而可证AB =AC ,然后问题可证;(2)由(1)可得△ABD ≌△ACF ,则有∠ABD =∠ACF ,进而可得∠ACF =135°,然后根据正方形的性质可求解.【详解】(1)证明:∵四边形ADEF 为正方形,∴AD =AF ,∠DAF =90°,又∵∠BAC =90°,∴∠DAB =∠FAC ,∵∠ABC =45°,∠BAC =90°,∴∠ACB =45°,∴∠ABC=∠ACB,∴AB=AC,∴△ABD≌△ACF(SAS);(2)解:由(1)知△ABD≌△ACF,∴∠ABD=∠ACF,∵∠ABC=45°,∴∠ABD=135°,∴∠ACF=135°,由(1)知∠ACB=45°,∴∠DCF=90°,∵正方形ADEF边长为22,∴DF=4,∴OC=12DF=12×4=2.【点睛】本题主要考查正方形的性质及等腰直角三角形的性质,熟练掌握正方形的性质及等腰直角三角形的性质是解题的关键.9.(2021·安徽安庆·八年级期末)如图1,点E为正方形ABCD内一点,∠AEB=90°,将Rt△ABE绕点B按顺时针方向旋转90°(即∠EBE'=90°),得到△CBE′(点A的对应点为点C)延长AE交CE于点F,连接DE.(1)试判断四边形BE′FE的形状,并说明理由.(2)如图2,若DA=DE,请猜想线段CF于FE'的数量关系并加以证明.(3)如图1,若AB=17,CF=3,请直接写出DE的长.【答案】(1)正方形,理由见解析;(2)CF=FE',证明见解析;(3)5【分析】(1)由旋转的特征可得到∠E′=∠AEB=90°、∠EBE′=90°、BE′=BE,再由∠BEF=180°-∠AEB =90°,可判定四边形BE′FE是正方形;(2)过点D作DG⊥AE于点G,由DA=DE得AG=12AE,再证明△ADG≌△BAE,且由四边形BE′FE是正方形,得到FE′=AG=12CE′,可证得结论;(3)过点D作DG⊥AE于点G,由旋转及四边形BE′FE是正方形可得如下关系:AE=CE′=FE′+CF= FE′+3=BE+3,在Rt△BAE中根据勾股定理求出BE、AE的长,由(1)可知,△ADG≌△BAE,得到DG=BE,AG=BE,再由勾股定理求出DE的长.【详解】解:(1)四边形BE′FE是正方形.理由如下:由旋转得,∠E′=∠AEB=90°,∠EBE′=90°,∵∠BEF=180°-∠AEB=90°,∴四边形BE′FE是矩形,由旋转得,BE′=BE,∴四边形BE′FE是正方形.(2)CF=FE',证明:如图2,过点D作DG⊥AE于点G,则∠DGA=∠AEB=90°,∵DA=DE,∴AG=12AE,∵四边形ABCD是正方形,∴DA=AB,∠DAB=90°,∴∠BAE+∠DAG=90°,∵∠ADG+∠DAG=90°,∴∠ADG=∠BAE,在△ADG和△BAE中∠ADG=∠BAE∠AGD=∠AEBAD=AB,∴△ADG≌△BAE(AAS),∴AG=BE;∵四边形BE′FE是正方形,∴BE=FE′,∴AG=FE′,由旋转得,AE=CE′,∴12AE=12CE′,∴FE′=12AE=12CE′,∴CF=FE'.(3)如图3,过点D作DG⊥AE于点G,∵BE=FE′,CF=3,∴AE=CE′=FE′+CF=FE′+3=BE+3,∵AE2+BE2=AB2,且AB=17,∴(BE+3)2+BE2=(17)2,解得,BE=1或BE=-4(不符合题意,舍去),∴AE=1+3=4,由(2)得,△ADG≌△BAE,∴DG=AE=4,AG=BE=1,∴GE=AE-AG=4-1=3,∵∠DGE=90°,∴DE=DG2+GE2=42+32=5.【点睛】此题考查了正方形的性质与判定、旋转的性质、等腰三角形的性质、全等三角形的判定与性质、勾股定理等知识点,解题的关键是正确地作出解题所需要的辅助线,构造全等三角形.10.(2021·湖北鄂州·八年级期末)如图,四边形ABCD是正方形,点P是线段AB的延长线上一点,点M是线段AB上一点,连接DM,以点M为直角顶点作MN⊥DM交∠CBP的角平分线于N,过点C作CE⎳MN交AD于E,连接EM,CN,DN.(1)求证:DM=MN.(2)求证:EM⎳CN.(3)若AE=1,BN=32,求DN的长.【答案】(1)见解析;(2)见解析;(3)52【分析】(1)在边DA上截取线段DF,使DF=MB连MF,证明△MDF≌△N MB即可求解;(2)由(1)△MDF≌△N MB,证明四边形EMNC为平行四边形即可求解;(3)过N作NQ⊥AP垂足为Q,由(2)知,△EDC≌△MAD;得到AD-DE=AB-AM,AE=MB,BN平分∠CBP所以∠NBQ=45°,可知三角形NBQ是等腰直角三角形,再用勾股定理即可求出和MN和DN.【详解】(1)证明:在边DA上截取线段DF,使DF=MB连MF.∵四边形ABCD是正方形∴AB=BC=CD=AD;∠DAB=∠ABC=∠BCD=∠CDA=90°∴∠CBP=180°-∠ABC=90°∵BN平分∠CBP∴∠CBP=45°∴∠NBM=∠ABC+∠CBN=90°+45°=135°∵DF=MB,AD=AB∴AD-DF=AB-MB∴AF =AM在Rt △FAM 中,AF =AM ,∴∠AFM =∠AMF =45°∴∠MFD =180°-∠AFM =135°∴∠MFD =∠NBM∵∠DMN =90°∴∠N MB +∠DMA =180°-90°=90°∵∠DMA +∠MDF =90°∴∠N MB =∠MDF在△MDF 和△N MB 中∠MFD =∠NBADF =MB∠MDF =∠NMB∴△MDF ≌△N MB (ASA )∴DM =MN .(2)如图,设DM 与CE 的交点为H ,∵四边形ABCD 是正方形∴AD =DC ,∠DAM =∠CDE =90°∵∠DMN =90°,CE ⎳MN∴∠DHC =90°,∴∠HDC +∠DCH =90°∴∠HDC +∠ADM =90°∴∠DCE =∠ADM ,在△EDC 和△MAD 中,∠CDE =∠DAMAD =DC∠DCE =∠ADM∴△EDC ≌△MAD (ASA ).∴EC =DM 又DM =MN ,∴EC =MN 又EC ⎳MN .∴四边形EMNC 为平行四边形.∴EM ⎳CN .(3)解:如图所示,过N 作NQ ⊥AP 垂足为Q .由(2)知,△EDC ≌△MAD∴DE =MA ,又AD =AB∴AD -DE =AB -AM 即AE =MB =1∵BN平分∠CBP所以∠NBQ=45°,∴三角形NBQ是等腰直角三角形,在Rt△NBQ中,设BQ=x,则NQ=BQ=x,即x2+x2=(32)2,∴x=3.∴NQ=3,MQ=1+3=4,在Rt△MQN中,MN=32+42=5,又∵在Rt△DMN中,MN=5,DM=5,∴DN=52+52=52.【点睛】此题考查的是全等三角形的性质、等腰三角形的性质和判定和判定以及勾股定理的应用,掌握它们的性质和判定是解题的关键.11.(2022·广东·塘厦初中八年级期中)四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.(1)如图,求证:矩形DEFG是正方形;(2)若AB=4,CE=22,求CG的长度;(3)当线段DE与正方形ABCD的某条边的夹角是40°时,直接写出∠EFC的度数.【答案】(1)见解析;(2)22;(3)∠EFC=130°或40°【分析】(1)作EP⊥CD于P,EQ⊥BC于Q,证明Rt△EQF≌Rt△EPD,得到EF=ED,根据正方形的判定定理证明即可;(2)通过计算发现E是AC中点,点F与C重合,△CDG是等腰直角三角形,由此即可解决问题;(3)分两种情形:①如图3,当DE与AD的夹角为40°时,求得∠DEC=45°+40°=85°,得到∠CEF=5°,根据角的和差得到∠EFC=130°,②如图4,当DE与DC的夹角为40°时,根据三角形的内角和定理即可得到结论.【详解】(1)证明:如图1,作EP⊥CD于P,EQ⊥BC于Q,∵∠DCA=∠BCA,∴EQ=EP,∵∠QEF+∠FEC=45°,∠PED+∠FEC=45°,∴∠QEF =∠PED ,在△EQF 和△EPD 中,∠QEF =∠PEDEQ =EP ∠EOF =∠EPD,∴△EQF ≌△EPD (ASA ),∴EF =ED ,∴矩形DEFG 是正方形;(2)如图2中,在Rt △ABC 中,AC =2AB =42,∵CE =22,∴AE =CE ,∴点F 与C 重合,此时△DCG 是等腰直角三角形,∴四边形DECG 是正方形,∴CG =CE =22;(3)①如图3,当DE 与AD 的夹角为40°时,∠DEC =45°+40°=85°,∵∠DEF =90°,∴∠CEF =5°,∵∠ECF =45°,∴∠EFC =130°,②如图4,当DE 与DC 的夹角为40°时,∵∠DEF =∠DCF =90°,∴∠EFC =∠EDC =40°,综上所述,∠EFC =130°或40°.【点睛】此题考查了正方形的判定以及性质,涉及了全等三角形的证明、等腰直角三角形等性质,熟练掌握相关基本性质是解题的关键.12.(2021·山西·八年级期末)综合与实践:如图1,在正方形ABCD 中,连接对角线AC ,点O 是AC 的中点,点E 是线段OA 上任意一点(不与点A ,O 重合),连接DE ,BE .过点E 作EF ⊥DE 交直线BC于点F.。
初中数学 动点最值类压轴题19大解题模型图解+典型例题解析!

初中数学| 动点最值类压轴题19大解题模型图解+典型例题解析!
1、将军饮马模型(对称点模型)
2、利用三角形两边差求最值
3、手拉手全等取最值
4、手拉手相似取最值
5、平移构造平行四边形求最小
6、两点对称勺子型连接两端求最小
7、两点对称折线连两端求最小
8、时钟模型,中点两定边求最小值
9、时钟模型,相似两定边求最小值
10、转化构造两定边求最值
11、面积转化法求最值
12、相似转化法求最值
13、相似系数化一法求最值
14、三角函数化一求最值
15、轨迹最值
16、三动点的垂直三角形
17、旋转最值
18、隐圆最值-定角动弦
19、隐圆最值-动角定弦
动点最值类典型题练习。
2020年(河南)中考数学压轴题全揭秘精品专题02 折叠与图形存在性(带答案解析)

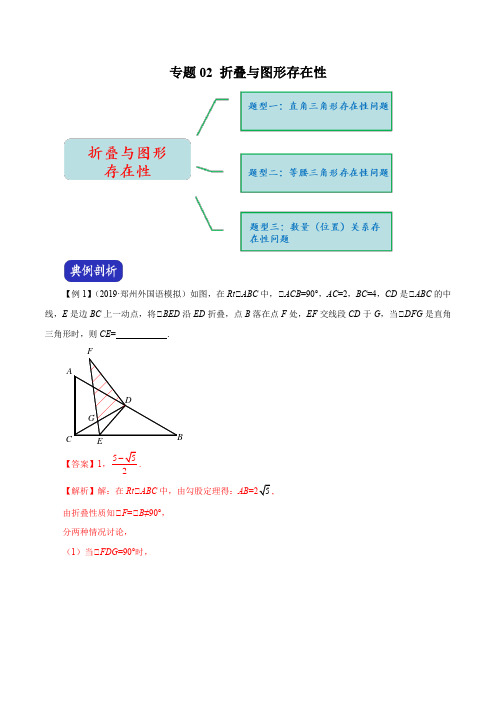
专题02 折叠与图形存在性【例1】(2019·郑州外国语模拟)如图,在Rt △ABC 中,△ACB =90°,AC =2,BC =4,CD 是△ABC 的中线,E 是边BC 上一动点,将△BED 沿ED 折叠,点B 落在点F 处,EF 交线段CD 于G ,当△DFG 是直角三角形时,则CE =.【答案】155. 【解析】解:在Rt △ABC 中,由勾股定理得:AB 5, 由折叠性质知△F =△B ≠90°, 分两种情况讨论, (1)当△FDG =90°时,CDG△D 是Rt △ABC 斜边AB 的中点,△CD =BD =AD 5, △△B =△DCE =△F ,△△DCE +△GEC =△F +△FDG , △△GEC =90°, 在Rt △DFG 中,tan △F =DGDF, △DG 5, △CG =CD -DG =52, 在Rt △CEG 中,CE =CG ·cos △GCE 525; (2)当△FGD =90°时,由(1)知△B =△F =△DCB ,BDG DG由BD=DF5△DG=DF·sin△F525,△CG=CD-DG51,△CE=CG÷cos△DCB=51)2555 -,故答案为:155 -.【变式1-1】(2018·洛阳三模)如图,在菱形ABCD中,∠DAB=45°,AB=8,点P为线段AB上一动点,过点P 作PE⊥AB交直线AD于E,沿PE将∠A折叠,点A的对称点为点F,连接EF、DF、CF,当△CDF是直角三角形时,AP=.【答案】22422+【解析】解:①如图,当DF⊥AB时,△CDF是直角三角形,∵在菱形ABCD中,AB=8,∴CD=AD=AB=8,在Rt△ADF中,AD=8,∠DAN=45°,DF=AF2,∴AP 2②如图,当CF ⊥AB 时,△DCF 是直角三角形,在Rt △CBF 中,∠CFB =90°,∠CBF =∠A =45°,BC =8,∴BF =CF 2∴AF =AB +BF 2∴AP =12AF 2 故答案为:4或2【例2】(2019·河南南阳一模)如图,矩形ABCD 中,AB =2,AD =4,点E 在边BC 上,将△DEC 沿DE 翻折后,点C 落在点C ’处. 若△ABC ’是等腰三角形,则CE 的长为.【分析】根据△ABC ’是等腰三角形,分△AB =AC ’=2;△AC ’=BC ’,即C ’落在AB 的垂直平分线上时;△AB =BC ’=2,三种情况讨论,逐一作出图形求解即可.【答案】223【解析】解:分三种情况讨论:CDEC'△AB =AC ’=2,如图所示,可得:四边形CDC ’E 是正方形,即CE =2;△AC ’=BC ’,即C ’落在AB 的垂直平分线MN 上时,如图所示,△DM =1,C ’D =2, △△C ’DM =30°,即得:△C ’DC =60°,△EDC =30°, △CE =CD ·tan △EDC3 =233; △AB =BC ’=2,此时作出C ’的运动轨迹,及以B 为圆心,2为半径的圆,发现二者不相交,如图所示,BC DABCDC'N即此种情况不存在;综上所述,答案为:223【变式2-1】(2019·郑州外外国语测试)如图所示,在△ABC 中,△C =90°,AC ≤BC ,将△ABC 沿EF 折叠,使点A 落在直角边BC 上的D 点,设EF 与AB 、AC 分别交于点E 、F ,如果折叠后△CDF 和△BDE 均为等腰三角形,那么△B =.【答案】45°或30°.【解析】解:若△CDF 是等腰三角形,△△C =90°, △△CDF =△CFD =45°,由折叠性质知,△A =△FDE ,△B =△EFD , 若△BDE 是等腰三角形,则:(1)若DE =BD ,设△B =△DEB =x °,则△A =△FDE =90-x , △△CDE =△B +△DEB , △45+90-x =x +x ,解得:x =45, 即△B =45°,ABCDEC'(2)若DE=BE,△CDE=180°-△BDE=180°-△B,△CDE =45°+△FDE=45°+△A=45°+90°-△B=135°-△B,△不符合题意,(3)若BD=BE,设△B=x,则△BDE=△BED=90°-12 x,△CDE =45°+△A=135°-x,△CDE =△B+△DEB=90°+12 x,△135°-x=90°+12x,解得:x=30,即△B=30°,综上所述,△B的度数为:45°或30°.【例3】(2019·商丘二模)如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,E为斜边AB的中点,点P 是射线BC上的一个动点,连接AP、PE,将△AEP沿着边PE折叠,折叠后得到△EP A′,当折叠后△EP A′与△BEP的重叠部分的面积恰好为△ABP面积的四分之一,则此时BP的长为.【答案】2或3【解析】解:∵∠ACB=90°,∠B=30°,AC=2,E为AB的中点,∴AB=4,AE=12AB=2,BC=3(1)若点A’落在BC上方时,连接A′B,由折叠可得S△A′EP=S△AEP,A′E=AE=2,.∵点E是AB的中点,∴S△BEP=S△AEP=12S△ABP.由题可得:S△EFP=14S△ABP,∴S△EFP=12S△BEP=12S△AEP=12S△A′EP,∴EF=BF,PF=A′F.∴四边形A′EPB是平行四边形,∴BP=A′E=2;②若点A’落在直线BC下方时,连接AA′,交EP与H,.可得:GP=BG,EG=1.∵BE=AE,∴EG=12AP=1,∴AP=2∴AP=AC,即此时点P与点C重合,∴BP=BC=3.故答案为:2或3【变式3-1】(2019·安阳二模)如图,在△ABC中,∠C=90°,AB=5,BC=4.点D是边AC的中点,点E在边AB上,将△ADE沿DE翻折,使点A落在点A′处,当线段AE的长为时,A′E∥BC.【答案】12或92.【解析】解:分两种情况:(1)当A'E∥BC时,∠A'EG=∠B,由折叠可得,∠A=∠A',∵∠B+∠A=90°,∴∠A'EG+∠A'=90°,∴∠A'GE=90°,∴△ABC∽△ADG,∴AG AD DG AC AB BC==,∵AD=12AC=32,∴AG=910,DG=65,A'G=310,设AE=A'E=x,则EG=910﹣x,则cos∠GEA’=4 '5 EGA E=,∴x=12,即AE=12;(2)当A'E∥BC时,∠AHE=∠C=90°,A'H⊥CD,设AE=y,由△AHE∽△ACB,得:AH AE EH AC AB BC==∴AH=35y,HE=45y,由折叠可得,A'E=AE=y,AD=A'D=32,∴A'H=15y,DH=35y﹣32,sin∠DA’H=4 '5 DHA D=,可得:y=92,即AE=92,故答案为:12或92.1.(2017·郑州一模)如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连结AD,将△ACD 沿AD折叠,点C落在点C′,连结C′D交AB于点E,连结BC′.当△BC′D是直角三角形时,DE的长为.【答案】32或34.【解析】解:(1)当点E与点C′重合时,△BC′D是直角三角形,在Rt△ABC中,由勾股定理得:BC=4.由翻折的性质可知;AE=AC=3,DC=DE,EB=2.设DC=ED=x,则BD=4﹣x.在Rt△DBE中,由勾股定理得:DE2+BE2=DB2,即x2+22=(4﹣x)2.解得:x=32.(2)当∠EDB=90时,由翻折的性质可知:AC=AC′,∠C=∠C′=90°.可得:四边形ACDC′为矩形.∵AC=AC′,∴四边形ACDC′为正方形.∴CD=AC=3.DB=BC﹣DC=1.∵DE∥AC,∴14DE BDAC BC==,134DE=.解得:DE=34.(3)∵点D在BC上运动,∴∠DBC′<90°,即∠DBC′不可能为直角.故答案为:32或34.2.(2019·洛阳三模)如图,已知Rt△ABC中,△B=90°,△A=60°,AB=3,点M,N分别在线段AC,AB上,将△ANM沿直线MN折叠,使点A的对应点D恰好落在线段BC上,若△DCM为直角三角形时,则AM的长为.【答案】2或333.【解析】解:△在△CDM 中,△C =30°,△分两种情况讨论△CDM 为直角三角形的情况,(1)当△CMD =90°时,如图所示,设AM =x ,则DM =x ,CM 3,△x 3=6,解得:x =333;(2)当△CDM =90°时,如图所示,A CDM A CDM N设AM =x ,则CM =2x ,DM =x ,△x +2x =6,解得x =2, 综上所述,答案为:333或2.3.(2019·周口二模)如图,在矩形纸片ABCD 中,已知AB =6,BC =8,E 是边AD 上的点,以CE 为折痕折叠纸片,使点D 落在点F 处,连接FC ,当△AEF 为直角三角形时,DE 的长为_________.【答案】3或6. 【解析】解:由题意知,△EAF ≠90°,(1)当△AEF =90°时,如下图所示,由折叠知,CD =CF =DE =EF =6,即DE =6;(2)当△AFE =90°时,如下图所示,E DC BA B C此时点F 落在对角线AC 上,AC =10,CF =6,AF =4,设DE =x ,则EF =x ,AE =8-x ,在Rt △AEF 中,由勾股定理得:x 2+42=(8-x )2,解得:x =3,故答案为:3或6.4.(2018·焦作一模)如图,在Rt △ABC 中,△A =90°,△B =30°,BC 3+1,点E 、F 分别是BC 、AC 边上的动点,沿E 、F 所在直线折叠△C ,使点C 的落对应点C '始终落在边AB 上,若△BEC '是直角三角形时,则BC '的长为 .33 或2. 【解析】解:△△B =30°,△分两种情况讨论:△当△BEC '=90°时,BC E FBE3'E,△CE=C'E,BC3+1,△BE3C'E=1,△Rt△BEC'中,由勾股定理得:BC'=2;△当△BC'E=90°时,BE=2C'E=2CE,BC3,△BE=23×(3+1),C'E=13(3+1),在Rt△BEC’中,由勾股定理得:BC 33+;综上所述,BC'33+或2.5.(2019·南阳毕业测试)如图,在Rt△ABC中,AC=8,BC=6,点D为斜边AB上一点,DE△AB交AC于点E,将△AED沿DE翻折,点A的对应点为点F.如果△EFC是直角三角形,那么AD的长为.【答案】75或5.【解析】解:在Rt△ABC中,AC=8,BC=6,由勾股定理得:AB=10,按直角顶点位置分类讨论,△若△CFE=90°,△在Rt△ABC中,△ACB=90°,△△CFB+△EFD=△B+△A=90°,由翻折知:△A=△EFD,AE=EF,△△CFB=△B,CF=BC=6,在Rt△CEF中,有CE2=EF2+CF2,即CE2=(8﹣CE)2+62,△CE=254,△AE=74,由△ADE=△ACB=90°,得△ADE△△ACB,△AE AD AB AC,得:AD=75;△当△ECF=90°时,点F与B重合,△AD=12AB=5;△当△CEF=90°时,则EF△BC,△AFE=△B,△△A=△AFE,△△A=△B,△AC=BC(与题设矛盾),这种情况不存在,综上所述:如果△EFC是直角三角形,AD的长为75或5.故答案为:75或5.6.(2019·开封二模)在Rt△ABC中,AC=3,AB=4,D为斜边BC中点,E为AB上一个动点,将△ABC沿直线DE折叠,A、C的对应点分别为A′、C′,EA′交BC于点F,若△BEF为直角三角形,则BE的长度为.【答案】12或54.【解析】解:△△B≠90°,△分两种情况讨论:△当△BEF=90°时,过D作DM△AB于M,则△EMD=90°,DM△AC,D为BC中点,可得:M为AB的中点,△BM=12AB=2,DM=12AC=32,由折叠可得,△MED=12△AEF=45°,△△DEM是等腰直角三角形,△EM=DM=32,△BE=2﹣32=12;△当△BFE=90°时,连接AD,A'D,根据对称性可得:△EAD=△EA'D,AD=A'D Rt△ABC中,AC=3,AB=4,由勾股定理得:BC =5,Rt △ABC 中,D 为BC 的中点,△AD =BD =A 'D =12BC =52, △△B =△EAD =△F A 'D ,设BE =x ,则BF =BE ·cosB =45x , △DF =BD ﹣BF =52﹣45x , 由sin △F A 'D =sinB ,得:54532525x -=⨯, 解得:x =54,即BE =54, 综上所述,BE 的长度为12或54. 7.(2019·安阳一模)如图,在Rt △ABC 中,△C =90°,AC =3BC =4,点D 是AC 的中点,点F 是边AB 上一动点,沿DF 所在直线把△ADF 翻折到△A ′DF 的位置,若线段A ′D 交AB 于点E ,且△BA ′E 为直角三角形,则BF 的长为_________.【答案】285或6. 【解析】解:由分析知△EBA ’≠90°,分两种情况讨论:(1)当△BA ’E =90°时,如图所示,A′A BC DE F连接BD ,过F 作FH △AC 于H ,可得:△BCD △△BA ’D ,△BDF =90°,设FH =x ,则AF =2x ,AH 3,DH 3x ,BF =8-2x ,由勾股定理得:BD 2+DF 2=BF 2,DF 2=DH 2+FH 2,即BD 2+ DH 2+FH 2= BF 2, △()()222282382x x x ++=-, 解得:x =125, 即BF =285; (2)当△BEA ’=90°时,如下图所示,B AC D EF A'A C D EF A'HADE F A'由折叠性质知,△A=△ADF=△EDF=30°,△AD3△DE3AE=3,△EF 3DE=1,△AF=2,即BF=6,综上所述,BF的值为285或6.8.(2019·省实验一模)如图,在Rt△ABC中,AB=3,BC=4,点P为AC上一点,过点P作PD△BC于点D,将△PCD沿PD折叠,得到△PED,连接AE.若△APE为直角三角形,则PC=.【答案】3532或12532.【解析】解:若△APE=90°,则△CPD=△EPD=45°,可得△C=45°,与题意不符,△△APE≠90°,在Rt△ABC中,AB=3,BC=4,由勾股定理得:AC=5,△当△AEP=90°时,设PC=x,在Rt△PDC中,sinC=35,cosC=45,所以PD=35x,CD=45x,由折叠知DE=CD=45x,△BE=BC﹣CE=4﹣85 x,△△B=△PDE,△BAE+△AEB=90°,△PED+△AEB=90°,△△BAE=△PED=△C,tan△BAE=tan△C,即843534x-=,解得:x=35 32,即PC=35 32;△当△EAP=90°时,如下图,设PC=x,则PE=x,PD=35x,CD=45x,CE=85x,BE=85x-4,可证:△AEB=△C,△tan△AEB= tan△C,△34BEAB=,ABPD即843534x -=, 解得:x =12532即PC =12532, 综上所述,答案为:3532或12532. 9.(2019·叶县一模)如图,矩形ABCD 中,AB =4,AD =6,点E 为AD 中点,点P 为线段AB 上一个动点,连接EP ,将△APE 沿PE 折叠得到△FPE ,连接CE ,CF ,当△ECF 为直角三角形时,AP 的长为 .【答案】1或94. 【解析】解:由图可知,△ECF ≠90°,所以分两种情况讨论:(1)当△CFE =90°时,由折叠可得,△PFE =△A =90°,AE =FE =DE ,△△CFP =180°,即点P ,F ,C 在一条直线上,△Rt △CDE △Rt △CFE ,△CF =CD =4,设AP=FP=x,则BP=4﹣x,CP=x+4,在Rt△BCP中,BP2+BC2=PC2,即(4﹣x)2+62=(x+4)2,解得x=94,即AP=94;(2)当△CEF=90°时,过F作FH△AB于H,作FQ△AD于Q,则△FQE=△D=90°,△△FEQ+△CED=△ECD+△CED,△△FEQ=△ECD,△△FEQ△△ECD,△FQ QE EF DE CD CE==,△3 345 FQ QE==,△FQ=95,QE=125,△AQ=HF=3-QE=35,AH=QE=95,设AP=FP=x,则HP=95﹣x,在Rt△PFH中,HP2+HF2=PF2,即(95﹣x)2+(35)2=x2,解得x=1,即AP=1.综上所述,AP的长为1或94.10.(2019·濮阳二模)如图,已知Rt△ABC中,△B=90°,△A=60°,AC=3+4,点M、N分别在线段AC、AB上,将△ANM沿直线MN折叠,使点A的对应点D恰好落在线段BC上,当△DCM为直角三角形时,折痕MN 的长为.【答案】234或6.【解析】解:△△C=30°,即C不可能是直角顶点,△分两种情况讨论:(1)当△CDM=90°时,在Rt△ABC中,△B=90°,△A=60°,AC=3+4,由折叠性质知,△MDN=△A=60°,△△BDN=30°,△BN=12DN=12AN,△BN=13AB=323,△AN=2BN 234+,由△DNB=60°,得:△ANM=△DNM=60°,△△AMN是等边三角形,△AN=MN=234+;(2)当△CMD=90°时,由题可得,△CDM=60°,△A=△MDN=60°,△△BDN=60°,△BND=30°,△BD=12DN=12AN,BN3BD,△CD=BC-BD3-BD3,△DM=AM=12CD3,△在Rt△ANH中,AH=12AN=1,NH3△HM=AM-AH3在Rt△HNM中,由勾股定理得:MN6234611.(2019·郑州联考)如图,正方形ABCD的边长是16,点E在边AB上,AE=3,点F是边BC上不与点B,C重合的一个动点,把△EBF沿EF折叠,点B落在B′处.若△CDB′恰为等腰三角形,则DB′的长为.【答案】16或5【解析】解:分三种情况讨论,(1)当B′D=B′C时,过B′作GH△AD交AB、CD于点G、H,则△B′GE=90°,可得:GH是CD、AB的垂直平分线,△AG=DH=12DC=8,由AE=3,AB=16,得BE=13.由翻折的性质,得B′E=BE=13.△EG=AG﹣AE=8﹣3=5,在Rt△B’EG中,由勾股定理得:B′G=12,△B′H=GH﹣B′G=16﹣12=4,在Rt△DB’H中,由勾股定理得:DB′=5(2)当DB′=CD时,则DB′=16.(3)当CB′=CD时,则CB=CB′,由翻折的性质,得EB=EB′,△EC垂直平分BB′,△EF是线段BB′的垂直平分线,△点F与点C重合,此种情况不存在;故答案为:16或5.12.(2019·西华县二模)如图,在Rt△ABC中,△C=90°,BC=3,AC=2,点D是BC的中点,点E是边AB上一动点,沿DE所在直线把△BDE翻折到△B′DE的位置,B′D交AB于点F.若△AB′F为直角三角形,则AE 的长为.【答案】3或14 5.【解析】解:△△C=90°,BC=3,AC=2,△△B=30°,AB=2AC=4,△点D是BC的中点,△DB=DC3EB′=EB,△DB′E=△B=30°,设AE=x,则BE=4﹣x,EB′=4﹣x,由题意知∠B’AF≠90°,分两种情况讨论:(1)当△AFB′=90°时,BF=32,EF=32﹣(4﹣x)=x﹣52,在Rt△B′EF中,△EB′F=30°,△EB′=2EF,即4﹣x=2(x﹣52),解得:x=3,即AE=3;(2)当∠AB’F=90°时,过E作EH⊥AB’于H,△DC=DB′,AD=AD,△Rt△ADB′△Rt△ADC,△AB′=AC=2,△△AB′E=△AB′F+△EB′F=90°+30°=120°,△△EB′H=60°,∠HEB’=30°,∴B′H=12B′E=12(4﹣x),EH3′H3(4﹣x),在Rt△AEH中,EH2+AH2=AE2,△34(4﹣x)2+[12(4﹣x)+2]2=x2,解得x=145,AE=145.故答案为3或145.。
【精编版】2020年(河南)中考数学压轴题全揭秘精品专题02 折叠与图形存在性
专题02 折叠与图形存在性【例1】(2019·郑州外国语模拟)如图,在Rt △ABC 中,△ACB =90°,AC =2,BC =4,CD 是△ABC 的中线,E 是边BC 上一动点,将△BED 沿ED 折叠,点B 落在点F 处,EF 交线段CD 于G ,当△DFG 是直角三角形时,则CE = .【答案】1. 【解析】解:在Rt △ABC 中,由勾股定理得:AB由折叠性质知△F =△B ≠90°,分两种情况讨论,(1)当△FDG =90°时,C△D是Rt△ABC斜边AB的中点,△CD=BD=AD△△B=△DCE=△F,△△DCE+△GEC=△F+△FDG,△△GEC=90°,在Rt△DFG中,tan△F=DG DF,△DG,△CG=CD-DG=2,在Rt△CEG中,CE=CG·cos△GCE;(2)当△FGD=90°时,由(1)知△B=△F=△DCB,由BD=DF△DG=DF·sin△F,△CG=CD-DG1,△CE=CG÷cos△DCB=1),故答案为:1【变式1-1】(2018·洛阳三模)如图,在菱形ABCD 中,∠DAB =45°,AB =8,点P 为线段AB 上一动点,过点P 作PE ⊥AB 交直线AD 于E ,沿PE 将∠A 折叠,点A 的对称点为点F ,连接EF 、DF 、CF ,当△CDF 是直角三角形时,AP = .【答案】4【解析】解:①如图,当DF ⊥AB 时,△CDF 是直角三角形,∵在菱形ABCD 中,AB =8,∴CD =AD =AB =8,在Rt △ADF 中,AD =8,∠DAN =45°,DF =AF ,∴AP ;②如图,当CF ⊥AB 时,△DCF 是直角三角形,在Rt △CBF 中,∠CFB =90°,∠CBF =∠A =45°,BC =8,∴BF =CF ,∴AF =AB +BF ,∴AP =12AF ,故答案为:4或.【例2】(2019·河南南阳一模)如图,矩形ABCD 中,AB =2,AD =4,点E 在边BC 上,将△DEC 沿DE 翻折后,点C 落在点C ’处. 若△ABC ’是等腰三角形,则CE 的长为.【分析】根据△ABC ’是等腰三角形,分△AB =AC ’=2;△AC ’=BC ’,即C ’落在AB 的垂直平分线上时;△AB =BC ’=2,三种情况讨论,逐一作出图形求解即可.【答案】2【解析】解:分三种情况讨论:△AB =AC ’=2,如图所示,可得:四边形CDC ’E 是正方形,即CE =2;△AC ’=BC ’,即C ’落在AB 的垂直平分线MN 上时,如图所示,△DM =1,C ’D =2,△△C ’DM =30°,即得:△C ’DC =60°,△EDC =30°,△CE =CD ·tan △EDC=2×3△AB =BC ’=2,DDD N此时作出C ’的运动轨迹,及以B 为圆心,2为半径的圆,发现二者不相交,如图所示,即此种情况不存在;综上所述,答案为:2或3. 【变式2-1】(2019·郑州外外国语测试)如图所示,在△ABC 中,△C =90°,AC ≤BC ,将△ABC 沿EF 折叠,使点A 落在直角边BC 上的D 点,设EF 与AB 、AC 分别交于点E 、F ,如果折叠后△CDF 和△BDE 均为等腰三角形,那么△B = .【答案】45°或30°.【解析】解:若△CDF 是等腰三角形,△△C =90°,△△CDF =△CFD =45°,由折叠性质知,△A =△FDE ,△B =△EFD ,若△BDE 是等腰三角形,则:(1)若DE =BD ,设△B =△DEB =x °,则△A =△FDE =90-x ,△△CDE =△B +△DEB ,△45+90-x =x +x ,解得:x =45,即△B =45°,(2)若DE =BE ,△CDE =180°-△BDE =180°-△B ,△CDE =45°+△FDE =45°+△A =45°+90°-△B =135°-△B ,△不符合题意,(3)若BD =BE ,设△B =x ,则△BDE =△BED =90°-12x , △CDE =45°+△A =135°-x ,△CDE =△B +△DEB =90°+12x , △135°-x =90°+12x ,解得:x =30, 即△B =30°,综上所述,△B 的度数为:45°或30°.【例3】(2019·商丘二模)如图,在Rt △ABC 中,∠ACB =90°,∠B =30°,AC =2,E 为斜边AB 的中点,点P 是射线BC 上的一个动点,连接AP 、PE ,将△AEP 沿着边PE 折叠,折叠后得到△EP A ′,当折叠后△EP A ′与△BEP 的重叠部分的面积恰好为△ABP 面积的四分之一,则此时BP 的长为 .【答案】2或【解析】解:∵∠ACB =90°,∠B =30°,AC =2,E 为AB 的中点,∴AB =4,AE =12AB =2,BC = (1)若点A ’落在BC 上方时,连接A ′B ,由折叠可得S △A ′EP =S △AEP ,A ′E =AE =2,.∵点E 是AB 的中点,∴S △BEP =S △AEP =12S △ABP . 由题可得:S △EFP =14S △ABP , ∴S △EFP =12S △BEP =12S △AEP =12S △A ′EP , ∴EF =BF ,PF =A ′F .∴四边形A′EPB是平行四边形,∴BP=A′E=2;②若点A’落在直线BC下方时,连接AA′,交EP与H,.可得:GP=BG,EG=1.∵BE=AE,∴EG=12AP=1,∴AP=2∴AP=AC,即此时点P与点C重合,∴BP=BC=.故答案为:2或【变式3-1】(2019·安阳二模)如图,在△ABC中,∠C=90°,AB=5,BC=4.点D是边AC的中点,点E在边AB上,将△ADE沿DE翻折,使点A落在点A′处,当线段AE的长为时,A′E∥BC.【答案】12或92.【解析】解:分两种情况:(1)当A'E∥BC时,∠A'EG=∠B,由折叠可得,∠A=∠A',∵∠B+∠A=90°,∴∠A'EG+∠A'=90°,∴∠A'GE=90°,∴△ABC∽△ADG,∴AG AD DG AC AB BC==,∵AD=12AC=32,∴AG=910,DG=65,A'G=310,设AE=A'E=x,则EG=910﹣x,则cos∠GEA’=4 '5 EGA E=,∴x=12,即AE=12;(2)当A'E∥BC时,∠AHE=∠C=90°,A'H⊥CD,设AE=y,由△AHE∽△ACB,得:AH AE EH AC AB BC==∴AH=35y,HE=45y,由折叠可得,A'E=AE=y,AD=A'D=32,∴A'H=15y,DH=35y﹣32,sin∠DA’H=4 '5 DHA D,可得:y=92,即AE=92,故答案为:12或92.1.(2017·郑州一模)如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连结AD,将△ACD沿AD折叠,点C落在点C′,连结C′D交AB于点E,连结BC′.当△BC′D是直角三角形时,DE的长为.【答案】32或34.【解析】解:(1)当点E与点C′重合时,△BC′D是直角三角形,在Rt△ABC中,由勾股定理得:BC=4.由翻折的性质可知;AE=AC=3,DC=DE,EB=2.设DC=ED=x,则BD=4﹣x.在Rt△DBE中,由勾股定理得:DE2+BE2=DB2,即x2+22=(4﹣x)2.解得:x=32.(2)当∠EDB=90时,由翻折的性质可知:AC=AC′,∠C=∠C′=90°.可得:四边形ACDC′为矩形.∵AC=AC′,∴四边形ACDC′为正方形.∴CD=AC=3.DB=BC﹣DC=1.∵DE∥AC,∴14DE BDAC BC==,134DE=.解得:DE=34.(3)∵点D在BC上运动,∴∠DBC′<90°,即∠DBC′不可能为直角.故答案为:32或34.2.(2019·洛阳三模)如图,已知Rt△ABC中,△B=90°,△A=60°,AB=3,点M,N分别在线段AC,AB上,将△ANM沿直线MN折叠,使点A的对应点D恰好落在线段BC上,若△DCM为直角三角形时,则AM的长为.【答案】2或3.【解析】解:△在△CDM中,△C=30°,△分两种情况讨论△CDM为直角三角形的情况,(1)当△CMD =90°时,如图所示,设AM =x ,则DM =x ,CM,△x=6,解得:x=3;(2)当△CDM =90°时,如图所示,设AM =x ,则CM =2x ,DM =x ,△x +2x =6,解得x =2,综上所述,答案为:3或2.3.(2019·周口二模)如图,在矩形纸片ABCD 中,已知AB =6,BC =8,E 是边AD 上的点,以CE 为折痕折叠纸片,使点D 落在点F 处,连接FC ,当△AEF 为直角三角形时,DE 的长为_________.【答案】3或6. 【解析】解:由题意知,△EAF ≠90°,(1)当△AEF =90°时,如下图所示,ACDA CDE DC BA由折叠知,CD =CF =DE =EF =6,即DE =6;(2)当△AFE =90°时,如下图所示,此时点F 落在对角线AC 上,AC =10,CF =6,AF =4,设DE =x ,则EF =x ,AE =8-x ,在Rt △AEF 中,由勾股定理得:x 2+42=(8-x )2,解得:x =3,故答案为:3或6.4.(2018·焦作一模)如图,在Rt △ABC 中,△A =90°,△B =30°,BC,点E 、F 分别是BC 、AC 边上的动点,沿E 、F 所在直线折叠△C ,使点C 的落对应点C '始终落在边AB 上,若△BEC '是直角三角形时,则BC '的长为 .或2. 【解析】解:△△B =30°,△分两种情况讨论:△当△BEC '=90°时,BBBE 'E ,△CE =C 'E ,BC ,△BE C 'E =1,△Rt △BEC '中,由勾股定理得:BC '=2;△当△BC 'E =90°时,BE =2C 'E =2CE ,BC +1,△BE =23×),C 'E =13+1),在Rt △BEC ’中,由勾股定理得:BC ;综上所述,BC '或2. 5.(2019·南阳毕业测试)如图,在Rt △ABC 中,AC =8,BC =6,点D 为斜边AB 上一点,DE △AB 交AC 于点E ,将△AED 沿DE 翻折,点A 的对应点为点F .如果△EFC 是直角三角形,那么AD 的长为 .【答案】75或5. 【解析】解:在Rt △ABC 中,AC =8,BC =6,由勾股定理得:AB=10,按直角顶点位置分类讨论,△若△CFE=90°,△在Rt△ABC中,△ACB=90°,△△CFB+△EFD=△B+△A=90°,由翻折知:△A=△EFD,AE=EF,△△CFB=△B,CF=BC=6,在Rt△CEF中,有CE2=EF2+CF2,即CE2=(8﹣CE)2+62,△CE=254,△AE=74,由△ADE=△ACB=90°,得△ADE△△ACB,△AE AD AB AC,得:AD=75;△当△ECF=90°时,点F与B重合,△AD=12AB=5;△当△CEF=90°时,则EF△BC,△AFE=△B,△△A=△AFE,△△A=△B,△AC=BC(与题设矛盾),这种情况不存在,综上所述:如果△EFC是直角三角形,AD的长为75或5.故答案为:75或5.6.(2019·开封二模)在Rt△ABC中,AC=3,AB=4,D为斜边BC中点,E为AB上一个动点,将△ABC 沿直线DE折叠,A、C的对应点分别为A′、C′,EA′交BC于点F,若△BEF为直角三角形,则BE的长度为.【答案】12或54.【解析】解:△△B≠90°,△分两种情况讨论:△当△BEF=90°时,过D作DM△AB于M,则△EMD=90°,DM△AC,D为BC中点,可得:M为AB的中点,△BM=12AB=2,DM=12AC=32,由折叠可得,△MED=12△AEF=45°,△△DEM是等腰直角三角形,△EM=DM=32,△BE =2﹣32=12; △当△BFE =90°时,连接AD ,A 'D ,根据对称性可得:△EAD =△EA 'D ,AD =A 'DRt △ABC 中,AC =3,AB =4,由勾股定理得:BC =5,Rt △ABC 中,D 为BC 的中点,△AD =BD =A 'D =12BC =52, △△B =△EAD =△F A 'D ,设BE =x ,则BF =BE ·cosB =45x , △DF =BD ﹣BF =52﹣45x , 由sin △F A 'D =sinB ,得:54532525x -=⨯, 解得:x =54,即BE =54, 综上所述,BE 的长度为12或54. 7.(2019·安阳一模)如图,在Rt △ABC 中,△C =90°,AC=BC =4,点D 是AC 的中点,点F 是边AB 上一动点,沿DF 所在直线把△ADF 翻折到△A ′DF 的位置,若线段A ′D 交AB 于点E ,且△BA ′E 为直角三角形,则BF 的长为_________.A′A B C DE F【答案】285或6. 【解析】解:由分析知△EBA ’≠90°,分两种情况讨论:(1)当△BA ’E =90°时,如图所示,连接BD ,过F 作FH △AC 于H ,可得:△BCD △△BA ’D ,△BDF =90°,设FH =x ,则AF =2x ,AHx ,DH-x ,BF =8-2x ,由勾股定理得:BD 2+DF 2=BF 2,DF 2=DH 2+FH 2,即BD 2+ DH 2+FH 2= BF 2,△()()2222882xx x ++=-, 解得:x =125, 即BF =285; (2)当△BEA ’=90°时,如下图所示,AC DA C DAC D由折叠性质知,△A=△ADF=△EDF=30°,△AD△DE AE=3,△EF=3DE=1,△AF=2,即BF=6,综上所述,BF的值为285或6.8.(2019·省实验一模)如图,在Rt△ABC中,AB=3,BC=4,点P为AC上一点,过点P作PD△BC 于点D,将△PCD沿PD折叠,得到△PED,连接AE.若△APE为直角三角形,则PC=.【答案】3532或12532.【解析】解:若△APE=90°,则△CPD=△EPD=45°,可得△C=45°,与题意不符,△△APE≠90°,在Rt△ABC中,AB=3,BC=4,由勾股定理得:AC=5,△当△AEP=90°时,设PC=x,在Rt△PDC中,sinC=35,cosC=45,所以PD=35x,CD=45x,由折叠知DE=CD=45x,△BE=BC﹣CE=4﹣85 x,△△B=△PDE,△BAE+△AEB=90°,△PED+△AEB=90°,△△BAE=△PED=△C,tan△BAE=tan△C,即843534x-=,解得:x=35 32,即PC=35 32;△当△EAP=90°时,如下图,设PC=x,则PE=x,PD=35x,CD=45x,CE=85x,BE=85x-4,可证:△AEB=△C,△tan△AEB= tan△C,△34 BEAB=,即843534x-=,解得:x=125 32即PC=125 32,综上所述,答案为:3532或12532.9.(2019·叶县一模)如图,矩形ABCD中,AB=4,AD=6,点E为AD中点,点P为线段AB上一个动点,连接EP,将△APE沿PE折叠得到△FPE,连接CE,CF,当△ECF为直角三角形时,AP的长为.【答案】1或94.ABD E【解析】解:由图可知,△ECF≠90°,所以分两种情况讨论:(1)当△CFE=90°时,由折叠可得,△PFE=△A=90°,AE=FE=DE,△△CFP=180°,即点P,F,C在一条直线上,△Rt△CDE△Rt△CFE,△CF=CD=4,设AP=FP=x,则BP=4﹣x,CP=x+4,在Rt△BCP中,BP2+BC2=PC2,即(4﹣x)2+62=(x+4)2,解得x=94,即AP=94;(2)当△CEF=90°时,过F作FH△AB于H,作FQ△AD于Q,则△FQE=△D=90°,△△FEQ+△CED=△ECD+△CED,△△FEQ=△ECD,△△FEQ△△ECD,△FQ QE EF DE CD CE==,△3 345 FQ QE==,△FQ=95,QE=125,△AQ=HF=3-QE=35,AH=QE=95,设AP=FP=x,则HP=95﹣x,在Rt△PFH中,HP2+HF2=PF2,即(95﹣x)2+(35)2=x2,解得x=1,即AP=1.综上所述,AP的长为1或94.10.(2019·濮阳二模)如图,已知Rt△ABC中,△B=90°,△A=60°,AC=,点M、N分别在线段AC、AB上,将△ANM沿直线MN折叠,使点A的对应点D恰好落在线段BC上,当△DCM为直角三角形时,折痕MN的长为.【解析】解:△△C=30°,即C不可能是直角顶点,△分两种情况讨论:(1)当△CDM=90°时,在Rt△ABC中,△B=90°,△A=60°,AC=,△△C=30°,AB+2,由折叠性质知,△MDN=△A=60°,△△BDN =30°,△BN =12DN =12AN ,△BN =13AB△AN =2BN =43, 由△DNB =60°,得:△ANM =△DNM =60°,△△AMN 是等边三角形,△AN =MN ; (2)当△CMD =90°时,由题可得,△CDM =60°,△A =△MDN =60°,△△BDN =60°,△BND =30°,△BD =12DN =12AN ,BN ,△AN =2,BN ,BD =1,△CD =BC -BD -BD ,△DM =AM =12CD ,△在Rt △ANH 中,AH =12AN =1,NH△HM =AM -AH ,在Rt △HNM 中,由勾股定理得:MN11.(2019·郑州联考)如图,正方形ABCD的边长是16,点E在边AB上,AE=3,点F是边BC上不与点B,C重合的一个动点,把△EBF沿EF折叠,点B落在B′处.若△CDB′恰为等腰三角形,则DB′的长为.【答案】16或【解析】解:分三种情况讨论,(1)当B′D=B′C时,过B′作GH△AD交AB、CD于点G、H,则△B′GE=90°,可得:GH是CD、AB的垂直平分线,△AG=DH=12DC=8,由AE=3,AB=16,得BE=13.由翻折的性质,得B′E=BE=13.△EG=AG﹣AE=8﹣3=5,在Rt△B’EG中,由勾股定理得:B′G=12,△B′H=GH﹣B′G=16﹣12=4,在Rt△DB’H中,由勾股定理得:DB′=(2)当DB′=CD时,则DB′=16.(3)当CB′=CD时,则CB=CB′,由翻折的性质,得EB=EB′,△EC垂直平分BB′,△EF是线段BB′的垂直平分线,△点F与点C重合,此种情况不存在;故答案为:16或12.(2019·西华县二模)如图,在Rt△ABC中,△C=90°,BC=AC=2,点D是BC的中点,点E是边AB上一动点,沿DE所在直线把△BDE翻折到△B′DE的位置,B′D交AB于点F.若△AB′F为直角三角形,则AE的长为.【答案】3或14 5.【解析】解:△△C=90°,BC=AC=2,△△B=30°,AB=2AC=4,△点D是BC的中点,△DB=DC,EB′=EB,△DB′E=△B=30°,设AE=x,则BE=4﹣x,EB′=4﹣x,由题意知∠B’AF≠90°,分两种情况讨论:(1)当△AFB′=90°时,BF=32,EF=32﹣(4﹣x)=x﹣52,在Rt△B′EF中,△EB′F=30°,△EB′=2EF,即4﹣x=2(x﹣52),解得:x=3,即AE=3;(2)当∠AB’F=90°时,过E作EH⊥AB’于H,△DC=DB′,AD=AD,△Rt △ADB ′△Rt △ADC ,△AB ′=AC =2,△△AB ′E =△AB ′F +△EB ′F =90°+30°=120°,△△EB ′H =60°,∠HEB ’=30°,∴B ′H =12B ′E =12(4﹣x ),EH ′H (4﹣x ), 在Rt △AEH 中,EH 2+AH 2=AE 2, △34(4﹣x )2+[12(4﹣x )+2]2=x 2,解得x =145, AE =145. 故答案为3或145.。
中考模型解题之弦图模型
5.(2011)如图,四边形ABCD,M为BC边的中点.若∠B=∠AMD=
∠C=45°,AB=8,CD=9,则AD的长为()
ﻩA.3B.4C.5D.6
6.(2011荆州)如图,P为线段AB上一点,AD与BC交干E,∠CPD=∠A=∠B,BC交PD于F,AD交PC于G,则图中相似三角形有()
中考模型解题-之-弦图模型
———————————————————————————————— 作者:
—————————————————————————————一、知识提要
1.弦图基本模型
模型一:
模型二:
2.弦图模型之变形
二、专项训练
【板块一】弦图基本模型
1.如图,Rt△ABC中,CD⊥AB,垂足为D,DE⊥AC,垂足为E,求证: .
A.1对B.2对C.3对ﻩD.4对
7.在△ABC中,AC=BC,∠ACB=90°,点M是AC上的一点,点N是BC上的一点,沿着直线MN折叠,使得点C恰好落在边AB上的P点,
求证:MC:NC=AP:PB.
2.如图,梯形ABCD中,AB//DC,∠B=90°,E为BC上一点,且AE⊥ED.若BC=12,DC=7,BE:EC=1:2,则AB的长为____________.
3.在△ABC中,AB= ,AC=4,BC=2,以AB为边向△ABC外作△ABD,使△ABD为等腰直角三角形,求线段CD的长.
【板块二】弦图模型之变形
2020届上海市各区初三数学二模试卷压轴题--第18题图文解析汇编
如图1,在△ABC 中,AB =AC =5,tan B =34,将△ABC 绕点B 逆时针旋转,得到 △A 1BC 1,当点C 1在线段CA 延长线上时△ABC 1的面积为 __________.图1答案 46825.思路如下:如图2,设BC 的中点为H . 在Rt △ABH 中,由AB =5,tan B =34,可得AH =3,BH =4. 所以BC =8,S △ABC =12.如图3,当点C 1落在线段CA 延长线上时,△ABC ∽△BC 1C .根据相似三角形的面积比等于对应边比的平方,得221525864ABC BC C S AB S BC ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭△△. 所以S △BC 1C =641225⨯. 所以S △ABC 1=64121225⨯-=391225⨯=46825.图2 图3如图1,在平面直角坐标系中,A (8, 0),B (8, 4),C (0, 4),反比例函数=ky x在第一象限内的图像分别与AB 、BC 交于点F 、E ,连结EF .如果点B 关于EF 的对称点恰好落在OA 边上,那么k 的值为__________.图1答案 12.思路如下:如图2,作EM ⊥x 轴于M .设E (m , 4),F (8, n ).由4m =8n =k ,得m =2n .所以882244BE m nBF n n--===--. 由△EMB ′∽△B ′AF ,得''2''EM MB B E BEB A AF FB FB====.所以4'2'MB B A n==.所以B ′A =2,MB ′=2n =m .再由EB =MA ,得8-m =m +2.解得m =3. 所以E (3, 4).所以k =12.如图1,在Rt△ABC中,∠ACB=90°,∠B=35°,CD是斜边AB上的中线,如果将△BCD沿CD所在直线翻折,点B落在点E处,连结AE,那么∠CAE的度数是__________.图1答案125°.思路如下:如图2,因为CD是Rt△ABC斜边上的中线,所以DA=DC=DB.所以∠DCB=∠B=35°,∠DCA=∠DAC=55°.所以∠ADC=70°,∠CDB=110°.因为△CDB与△CDE关于CD对称,所以∠CDE=∠CDB=110°.所以∠ADE=110°-70°=40°(如图3所示).所以在等腰三角形DAE中,∠DAE=70°.所以∠CAE=55°+70°=125°.图2 图3如图1,在Rt △ABC 中,∠C =90°,AC =6,BC =8,点D 、E 分别是边BC 、AB 上一点,DE //AC ,BD =BDE 绕着点B 旋转得到△BD ′E ′(点D 、E 分别与点D ′、E ′对应),如果A 、D ′、E ′在同一直线上,那么AE ′的长为 __________.图1答案如图2,在Rt △ABC 中,AC =6,BC =8,所以AB =10,tan ∠B =34.在Rt △EDB 中,DE =34BD =34⨯如图3,当点A 在E ′D ′的延长线上时.在Rt △ABD ′中,AB =10,BD ′=AD ′=此时AE ′=AD ′+D ′E ′=如图4,当点A 在D ′E ′的延长线上时,AE ′=AD ′-D ′E ′=图2 图3 图4定义:如果三角形的两个内角α与β满足α=2β,那么,我们将这样的三角形称为“倍角三角形”.如果一个等腰三角形是“倍角三角形”,那么这个等腰三角形的腰长与底边长的比值为 __________.答案如图1,如果α为等腰三角形的顶角,那么α+β+β=4β=180°.解得β=45°.如图2,如果α为等腰三角形的底角,那么α+α+β=5β=180°.解得β=36°.这个三角形是黄金三角形.如图3,设腰长AB =CB =x ,底边AC =1.作∠BAC 的平分线交BC 于D ,那么△BCA ∽△ACD .由BC AC AC DC =,得111x x =-.解得x =.图1 图2 图3如图1,在△ABC中,∠C=90°,AC=3,BC=4,把△ABC绕C点旋转得到△A′B′C,其中点A′在线段AB上,那么∠A′B′B的正切值等于__________.图1答案724.思路如下:如图2,在Rt△ABC中,AC=3,BC=4,所以AB=5,cos∠A=35.在等腰三角形ACA′和等腰三角形BCB′中,5''6 CA CBAA BB==.所以AA′=65CA=185,BB′=65CB=245.所以A′B=AB-AA′=1855-=75.由∠A+∠ABC=90°,∠A=∠1,得∠1+∠ABC=90°.如图3,在Rt△A′B′B中,tan∠A′B′B=''A BBB=724.图2 图3如果一条直线把一个四边形分成两部分,这两部分图形的周长相等,那么这条直线称为这个四边形的“等分周长线”.在直角梯形ABCD中,AB//CD,∠A=90°,DC=AD,∠B是锐角,cot B=512,AB=17.如果点E在梯形的边上,CE是梯形ABCD的“等分周长线”,那么△BCE的周长为__________.答案42.思路如下:如图1,作CH⊥AB于H,那么四边形AHCD是正方形.已知cot B=512,AB=17,设BH=5m,CH=12m,那么AB=17m=17.解得m=1.所以正方形的边长为12,BC=13.所以四边形ABCD的周长为54,周长的一半等于27.如图2,因为CD+DA=24,所以点E在AB上,AE=3.此时在Rt△CEH中,EH=12-3=9,CH=12,所以CE=15.所以△BCE的周长=15+(9+5)+13=42.图1 图2如图1,已知在△ABC 中,AB =AC =4,∠BAC =30°,将△ABC 绕点A 顺时针旋转,使点B 落在点B 1处,点C 落在点C 1处,且BB 1⊥AC .连结B 1C 和C 1C ,那么△B 1C 1C 的面积等于__________.图1答案 8-如图2,当BB 1⊥AC 时,AC 垂直平分BB 1,AB 1垂直平分CC 1. 此时△B 1C 1C 的面积等于△BCB 1的面积(如图3所示).如图2,在Rt △ABE 中,AB =4,∠BAE =30°,所以BE =2,AE =所以CE =AC -AE =4-所以S △BCB 1=112BB CE ⋅=14(42⨯-=8-图2 图3如图1,在Rt△ABC中,∠ACB=90°,∠BAC=60°,BC D是BC边上一点,沿直线AD翻折△ABD,点B落在点E处,如果∠ABE=45°,那么BD的长为__________.图1答案2.思路如下:如图1,在Rt△ABC中,∠BAC=60°,BC AB=2.如图2,当∠ABE=45°时,△ABE是等腰直角三角形.此时∠BAD=45°.如图3,作△ABD的高DH.设DH=AH=m,那么BH.由AB=1)m=2,得m1.所以BD=2DH=2m=2.图2 图3小明学习完《相似三角形》一章后,发现了一个有趣的结论:在两个不相似的直角三角形中,分别存在经过直角顶点的一条直线,把直角三角形分成两个小三角形后,如果第一个直角三角形分割出来的一个小三角形与第二个直角三角形分割出来的一个小三角形相似,那么分割出来的另外两个小三角形也相似.他把这样的两条直线称为这两个直角三角形的相似分割线.如图1、图2,直线CG、DH分别是两个不相似的Rt△ABC和Rt△DEF的相似分割线,CG、DH分别与斜边AB、EF交于点G、H,如果△BCG与△DFH相似,AC=3,AB=5,DE=4,DF=8,那么AG=__________.图1 图2答案3.思路如下:如图3,设∠A=α,∠B=β.已知AC=3,AB=5,所以BC=4.如图4,设∠E=γ,∠F=θ.如果△BCG与△DFH相似,因为钝角对应相等,所以∠BCG=∠F=θ,∠HDF=∠B =β.所以BC DFBG DH=.所以48BG DH=.设BG=m,那么DH=2m.根据等角的余角相等,∠ACG=∠E=γ,∠EDH=∠A=α.所以△ACG∽△DEH.所以AC DEAG DH=.所以3452m m=-.解得m=2.所以AG=5-m=3.图3 图4如图1,四边形ABCD 是⊙O 的内接矩形,将矩形ABCD 沿着直线BC 翻折,点A 、点D 的对应点分别为A ′、D ′,如果直线A ′D ′与⊙O 相切,那么ABBC的值为__________.图1答案 4.思路如下:如图2,设A ′D ′与⊙O 相切于点N ,连结ON 交BC 与点M ,那么ON ⊥A ′D ′.设OM =m ,那么AB =A ′B =MN =2m .在Rt △ABC 中,AB =2m ,AC =2ON =6m ,所以BC .所以4==AB BC .图2如图1,在平行四边形ABCD 中,AD =3,AB =5,sin A =45,将平行四边形ABCD 绕着点B 顺时针旋转θ(0°<θ<90°)后,点A 的对应点是点A ′,连结A ′C ,如果A ′C ⊥BC ,那么cos θ的值是__________.图1答案 725.思路如下:如图2,已知sin A =sin α=45. 如图3,在Rt △A ′BC 中,A ′B =5,BC =3,所以A ′C =4. 所以∠A ′BC =α.延长A ′C 交AB 的延长线于点E . 因为DA //CB ,所以∠CBE =∠A =α. 于是可得BC 垂直平分A ′E . 作A ′F ⊥AB 于F .由S △A ′BE =11''22A E BC BE A F ⋅=⋅,得'8324'55A E BC A F BE ⋅⨯===. 于是在Rt △A ′BF 中,sin θ=''A F A B =2425.所以cos θ=725.图2 图3例 2020年上海市杨浦区中考模拟第18题如图1,已知在平行四边形ABCD 中,AB =10,BC =15,tan ∠A =43,点P 是边AD 上一点,连结PB ,将线段PB 绕着点P 逆时针旋转90°得到线段PQ ,如果点Q 恰好落在平行四边形ABCD 的边上,那么AP 的值是__________.图1答案 6或10.思路如下:如图2,作BH ⊥AD 于H .在Rt △ABH 中,由AB =10,tan ∠A =43,可得AH =6,BH =8.所以DH =9. 如图3,当点Q 落在AD 上时,点P 与点H 重合,此时AP =6.图2 图3如图4,当点Q 落在CD 上时,作QG ⊥AD 交AD 的延长线于G ,那么△BHP ≌△PGQ . 设HP =GQ =4m ,那么DG =3m .由PG =BH =8,得PD +DG =8.所以(9-4m )+3m =8. 解得m =1.此时AP =AH +HP =6+4m =10.图4例 2020年上海市长宁区中考模拟第18题如图1,在△ABC 中,∠C =90°,BC =2,点D 是边BC 的中点,∠ABC =∠CAD ,将△ACD 沿直线AD 翻折,点C 落在点E 处,连结BE ,那么线段BE 的长为 __________.图1答案如图2,由∠ABC =∠CAD ,∠C 是公共角,得△CAD ∽△CBA .所以=CA CD CB CA .所以1=2CA CA.解得CA在Rt △ACD 中,CD =1,CA AD cos ∠ADC =CD AD 如图3,连结CE 交AD 于点F ,那么AD 垂直平分CE . 因为点D 是边BC 的中点,所以DF 是△CBE 的中位线.在Rt △FCD 中,DF =CD ∙cos ∠ADC =13 =3.所以BE =2DF图2 图3。
2020年(河南)中考数学压轴题全揭秘精品专题18 利用函数图象研究函数性质及新题型
中考数学 专题18 利用函数图象研究函数性质及新题型题型一、利用函数图象研究函数性质 第一步:确定函数自变量取值范围; 第二步:列表、描点、连线; 第三步:根据函数图象解答相关题目. 题型二、定义新题型提出一些新颖的概念,根据概念解答相关题型.【例1】(2019·开封模拟)参照学习函数的过程与方法,探究函数2x y x-=(x ≠0)的图象与性质. 因为221x y x x -==-,即21y x =-+,所以我们对比函数2y x=-来探究. 列表: x…-4-3-2-112- 121 2 3 4 …2y x =-…12 23 1 2 4-4-2 -123- 12- …2x y x-= (32)532 3 5 -3 -1 013 12…描点:在平面直角坐标系中,以自变量x 的取值为横坐标,以2x y x-=相应的函数值为纵坐标,描出相应的点,如图所示:(1)请把y 轴左边各点和右边各点,分别用一条光滑曲线顺次连接起来.(2)观察图象并分析表格,回答下列问题:①当x<0时,y随x的增大而__________;(填“增大”或“减小”)②2xyx-=的图象是由2yx=-的图象向_______平移______个单位而得到;③图象关于点__________中心对称.(填点的坐标)(3)函数2xyx-=与直线y=-2x+1交于点A,B,求△AOB的面积.【答案】(1)见解析;(2)增大;上,1;(0,1);(3)见解析.【解析】解:(1)如图所示;(2)①增大;②上,1;③(0,1);(3)联立:2xyx-=与直线y=-2x+1,解得:x=1,y=-1或x=-1,y=3,∴S△AOB=12×2×4-12×1×4-12×2×1=1.【变式1-1】(2019·郑州模拟)探究函数4y xx=+的图象与性质(1)函数4y xx=+的自变量x的取值范围是;(2)下列四个函数图象中可能是函数4y x x=+的图象的是(3)对于函数4y x x=+,当x >0时,求y 的取值范围. 解:∵x >0,∴4y xx=+=22+=2+,∵2≥0,∴y ≥.拓展运用(4)若函数259x x y x-+=,则y 的取值范围是.【答案】(1)x ≠0;(2)C ;(3)4,4;(4)y ≥1或y ≤-11. 【解析】解:(1)由分式的意义,知x ≠0; (2)∵x ≠0, ∴A 错误;当x >0时,y >0,故B 、D 错误, ∴选项C 正确; (3)4;4;(4)当x >0时,25995x x y xx x -+==+-=225+-=21+∵2≥0,∴y ≥1;当x <0时,25995x x y x x x-+==+-=225⎡⎤-+-⎢⎥⎢⎥⎣⎦=211--,∵2-≤0∴y ≤-11;综上所述,y ≥1或y ≤-11.【例2】(2018·洛阳三模)在平面直角坐标系中,我们定义直线y =ax -a 为抛物线y =ax 2+bx +c (a 、b 、c 为常数,a ≠0)的“梦想直线”. 有一个顶点在抛物线上,另有一个顶点在y 轴上的三角形为其“梦想三角形”.已知抛物线2y x =+A 、B 两点(点A 在点B 的左侧),与x 轴负半轴交于点C .(1)填空:该抛物线的“梦想直线”的解析式为,点A 的坐标为,点B的标为;(2)如图,点M 为线段CB 上一动点,将△ACM 以AM 所在直线为对称轴翻折,点C 的对称点为N ,若△AMN 为该抛物线的“梦想三角形”,求点N 的坐标;(3)当点E 在抛物线的对称轴上运动时,在该抛物线的“梦想直线”上,是否存在点F ,使得以点A 、C 、E 、F 为顶点的四边形为平行四边形?若存在,请直接写出点E 、F 的坐标;若不存在,请说明理由.【答案】(1)y =+,(-2,),(1,0);(2)(3)见解析.【解析】解:(1)抛物线2y =+,由定义知:其梦想直线的解析式为:y =+,联立y x =+,2y x =+ 2x y =-⎧⎪⎨=⎪⎩10x y =⎧⎨=⎩,故答案为:y x =,(-2,,(1,0). (2)由题意知C (-3,0),过A 作AG ⊥y 轴于G ,①当点N 在y 轴上时,△AMN 是梦想三角形,AC =AN由抛物线的对称轴x =-1,A (-2,,得:AG =2,G (0,), 在Rt △ANG 中,由勾股定理得: GN =3,∴N (0,或(0,3),当ON =时,则MN >OG >CM ,与MN =CM 矛盾,不合题意,∴N (0,3),②当点M 在y 轴上时,△AMN 为梦想三角形, 即M 点在坐标原点,M (0,0),在Rt △AGM 中, AG =2,GM =,tan ∠AMG ,∴∠AMG=30°,∴∠AMC=∠AMN=∠NMB=60°,过点N作NP⊥x轴,在Rt△NMP中,MN=CM=3,∴NP,OP=32,即N(32),综上所述,点N的坐标为(0,-3),(32).(3)设E(-1,m),F(n,33-+),∵A(-2,),C(-3,0),①当四边形ACEF是平行四边形时,有:213nm--=-+⎧⎪⎨+=⎪⎩解得:nm=⎧⎪⎨=⎪⎩,即E(-1,3-),F(0,3);②当四边形AECF是平行四边形时,有:231nm--=-+⎧⎪⎨=⎪⎩,解得:4nm=-⎧⎪⎨=⎪⎩,即E(-1,),F(-4);③当四边形AEFC是平行四边形时,有:213nm-+=--⎧⎪⎨+=⎪⎩,解得:2nm=-⎧⎪⎨=⎪⎩此时F与A重合,不符题意,舍去;综上所述,E(-1,),F(-4)或E(-1,),F(0).【变式2-1】(2019·安阳一模)如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”,[a,b,c]称为“抛物线系数”.(1)任意抛物线都有“抛物线三角形”是(填“真”或“假”)命题;(2)若一条抛物线系数为[1,0,﹣2],则其“抛物线三角形”的面积为;(3)若一条抛物线系数为[﹣1,2b,0],其“抛物线三角形”是个直角三角形,求该抛物线的解析式;(4)在(3)的前提下,该抛物线的顶点为A,与x轴交于O,B两点,在抛物线上是否存在一点P,过P作PQ⊥x轴于点Q,使得△BPQ∽△OAB?如果存在,求出P点坐标;如果不存在,请说明理由.【答案】(1)假;(2)(3)(4)见解析.【解析】解:(1)∵抛物线与x轴的交点个数有三种情况:没交点,一个交点,两个交点,∴任意抛物线都有“抛物线三角形”是假命题,故答案为:假;(2)∵一条抛物线系数为[1,0,﹣2],∴a=1,b=0,c=﹣2,∴抛物线解析式为y=x2﹣2,当x=0,y=﹣2,当y=0,解得,x=∴“抛物线三角形”的面积为12)×2=故答案为:.(3)由题意得:抛物线解析式为:y=﹣x2+2bx,与x轴交点为:(0,0),(2b,0);若“抛物线三角形”是个直角三角形,则是等腰直角三角形,∴顶点为(b,b)或(b,﹣b),①当顶点为(b,b)时,有:b=﹣b2+2b2,解得b=0(舍去)或b=1∴y=﹣x2+2x,②当顶点为(b,﹣b)时,有:﹣b=﹣b2+2b2,解得b=0(舍去)或b=﹣1∴y=﹣x2﹣2x,(4)∵△AOB为等腰直角三角形,且△BPQ∽△OAB,∴△BPQ为等腰直角三角形,①y=﹣x2+2x,设P(a,﹣a2+2a),则Q(a,0)则|﹣a2+2a|=|2﹣a|,解得:a=1(舍)或a=2(舍去)或a=-1,∴P(﹣1,﹣3);②y=﹣x2﹣2x,同理得:P(1,3);综上所述,点P(﹣1,﹣3)或(1,3).1.(2018·逆袭卷)有这样一个问题:探究函数222xyx=+的图象与性质.下面是小强的探究过程,请补充完整:(1)函数222xyx=+的自变量x的取值范围;(2)下表是y与x的几组对应值.如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点.①观察图中各点的位置发现:点A1和B1,点A2和B2,A3和B3,A4和B4均关于某点中心对称,则该点的坐标为;②小文分析函数222xyx=+的表达式发现:当x<-1时,函数的最大值为-2,则该函数图象在直线x=-1左侧的最高点的坐标为(3)画出该函数的图象,并写出该函数的一条性质【答案】(1)x≠-1;(2)①(-1,-1);②(-2,-2);(3)见解析.【解析】解:(1)由2x+2≠0得,x≠-1;(2)①由图象知,该点坐标为:(-1,-1);②当x=-2时,y=-2,∴图象在直线x=-1左侧的最高点的坐标为(-2,-2);③图象见下图.函数性质:函数图象不经过第四象限;当x<-2时,y随x的增大而增大;当-2<x<-1时,y随x的增大而减小;当x>0时,y随x的增大而增大;当-1<x<0时,y随x的增大而减小.答案不唯一.2.(2019·偃师一模)如图,抛物线y=ax2+bx+4(a≠0)交x轴于点A(4,0),B(-2,0),交y轴于点C.(1)求抛物线的解析式.(2)点Q 是x 轴上位于点A,B之间的一个动点,点E为线段BC上一个动点,若始终保持∠EQB=∠CAB,连接CQ,设△CQE 的面积为S,点Q的横坐标为m,求出S关于m的函数关系式,并求出当S 取最大值时点Q的坐标.(3)点P 为抛物线上位于AC 上方的一个动点,过点P 作PF⊥y 轴,交直线AC 于点F,点D 的坐标为(2,0),若O,D,F 三点中,当其中一点恰好位于另外两点的垂直平分线上时,我们把这个点叫做另外两点的“和谐点”,请判断这三点是否有“和谐点”的存在,若存在,请直接写出此时点P的坐标;若不存在,请说明理由.【答案】见解析.【解析】解:(1)∵y=ax2+bx+4交x轴于点A(4,0),B(-2,0),∴16440 4240a ba b++=⎧⎨-+=⎩,解得:a=12-,b=1,∴抛物线的解析式为:y=12-x2+x+4.(2)y=12-x2+x+4与y轴交于点C,∴C(0,4),∵A(4,0),B(-2,0),设直线AC的解析式为:y=kx+n,∴4k+n=0,n=4,解得:k=-1,n=4,即直线AC的解析式:y=-x+4,同理得:直线BC的解析式为:y=2x+4,∵∠EQB=∠CAB,∴EQ ∥AC ,∵点Q 的坐标为(m ,0), 设直线EQ 解析式为:y =-x +m , 联立:y =-x +m ,y =2x +4解得: x =43m -,y =243m +, 即E (43m -,243m +), 设直线EQ 交y 轴于点H , 如下图所示,∴S =12·CH ·|x E -x Q |=()21133m --+,其中:-2<m <4, ∵13-<0,∴当m =1时,S 取最大值,此时Q 点坐标为(1,0). (3)存在,理由如下,如下图所示,和谐点为O (0,0),D (2,0),设F (x ,-x +4), ①若O 是和谐点, 则OF =OD =2, 即:OF 2=OD 2=4,x 2+(-x +4)2=4,此方程无实数解,即O 不是和谐点; ②若D 是和谐点, 同理:OD =DF =2,即:(2-x )2+(-x +4)2=4, 解得:x =2或x =4(舍), 即F (2,2),令y =12-x 2+x +4=2,解得:x x =1,∴P 2); ③若F 为和谐点,同理有:OF =DF ,即F (1,3),令y =12-x 2+x +4=3,解得:x x =1,即P 3),综上所述,点P 的坐标为2),3).3.(2019·三门峡二模)定义:在平面直角坐标系xOy 中,把从点P 出发沿纵或横方向到达点Q (至多拐一次弯)的路径长称为P ,Q 的“实际距离”.如图,若P (﹣1,1),Q (2,3),则P ,Q 的“实际距离”为5,即PS +SQ =5或PT +TQ =5.环保低碳的共享单车,正式成为市民出行喜欢的交通工具.设A ,B ,C 三个小区的坐标分别为A (3,1),B (5,﹣3),C (﹣1,﹣5),若点M 表示单车停放点,且满足M 到A ,B ,C 的“实际距离”相等,则点M 的坐标为( )A .(1,﹣2)B .(2,﹣1)C .(12,﹣1)D .(3,0)【答案】A .【解析】解:设M (x ,y ),由“实际距离”的定义可知: 点M (x ,y )中,﹣1<x <5,﹣5<y <1, ∵M 到A ,B ,C 实际距离相等, ∴|x ﹣3|+|y ﹣1|=|x ﹣5|+|y +3|=|x +1|+|y +5|,A .(1,﹣2),将x =1,y =-2代入上式,满足要求,∴A 符合要求;验证B、C、D不符合要求,故答案为:A.4.(2019·开封模拟)【阅读理解】截长补短法,是初中数学几何题中一种辅助线的添加方法.截长就是在长边上截取一条线段与某一短边相等,补短是通过在一条短边上延长一条线段与另一短边相等,从而解决问题.(1)如图1,△ABC是等边三角形,点D是边BC下方一点,∠BDC=120°,探索线段DA、DB、DC之间的数量关系.解题思路:延长DC到点E,使CE=BD,连接AE,根据∠BAC+∠BDC=180°,可证∠ABD=∠ACE 易证得△ABD≌△ACE,得出△ADE是等边三角形,所以AD=DE,从而探寻线段DA、DB、DC之间的数量关系.根据上述解题思路,请直接写出DA、DB、DC之间的数量关系是;【拓展延伸】(2)如图2,在Rt△ABC中,∠BAC=90°,AB=AC.若点D是边BC下方一点,∠BDC=90°,探索线段DA、DB、DC之间的数量关系,并说明理由;【知识应用】(3)如图3,两块斜边长都为14cm的三角板,把斜边重叠摆放在一起,则两块三角板的直角顶点之间的距离PQ的长分别为cm.图1 图2 图3【答案】(1)DA=DC+DB;(2)见解析;(3【解析】解:(1)∵△ABC是等边三角形,∴AB=AC,∠BAC=60°,∵∠BDC=120°,∴∠ABD+∠ACD=180°,∵∠ACE+∠ACD=180°,∴∠ABD=∠ACE,∴△ABD≌△ACE,∴AD=AE,∠BAD=∠CAE,∵∠ABC=60°,即∠BAD+∠DAC=60°,∴∠DAC+∠CAE=60°,即∠DAE=60°,∴△ADE是等边三角形,∴DA=DE=DC+CE=DC+DB,即DA=DC+DB,(2DA=DB+DC,延长DC到点E,使CE=BD,连接AE,与(1)中证法知,△ABD≌△ACE,∴AD=AE,∠BAD=∠CAE,∴∠DAE=∠BAC=90°,∴DA2+AE2=DE2,即2DA2=(DB+DC)2,DA=DB+DC;(3)连接PQ,∵MN=14,∠QMN=30°,∴QN=12MN=7,在Rt△MQN中,由勾股定理得:MQ=由(2PQ=QN+QMPQ=∴PQ.5.(2019·郑州联考)如图1,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.(1)观察猜想:图1中,线段PM与PN的数量关系是,位置关系是;(2)探究证明:把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;(3)拓展延伸:把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN面积的最大值.图1 图2【答案】(1)PM=PN,PM⊥PN;(2)(3)见解析.【解析】解:(1)∵点P,N是BC,CD的中点,∴PN∥BD,PN=12 BD,同理:PM∥CE,PM=12 CE,∵AB=AC,AD=AE,∴BD=CE,∴PM=PN,∵PN∥BD,∴∠DPN=∠ADC,同理,∠DPM=∠DCA,∵∠BAC=90°,∴∠ADC+∠ACD=90°,∴∠MPN=∠DPM+∠DPN=∠DCA+∠ADC=90°,即PM⊥PN,(2)△PMN是等腰直角三角形,理由如下:由旋转性质得,∠BAD=∠CAE,∵AB=AC,AD=AE,∴△ABD≌△ACE,∴∠ABD=∠ACE,BD=CE,由三角形的中位线得,PM∥CE,PN∥BD,PN=12BD,PM=12CE,∴PM=PN,∠DPM=∠DCE,∠PNC=∠DBC,∴∠MPN=∠DPM+∠DPN=∠DCE+∠DCB+∠DBC=∠BCE+∠DBC=∠ACB+∠ACE+∠DBC=∠ACB+∠ABD+∠DBC=∠ACB+∠ABC,∵∠BAC=90°,∴∠ACB+∠ABC=90°,∴∠MPN=90°,即△PMN是等腰直角三角形;(3)由(2)知,△PMN是等腰直角三角形,PM=PN=12 BD,∴当PM最大时(即BD最大时),△PMN面积最大,当点D在BA延长线上时,BD最大,最大为:14,此时,PM=7,∴△PMN面积的最大值为:12PM2=492.6.(2019·平顶山三模)已知△ABC,AB=AC,D为直线BC上一点,E为直线AC上一点,AD=AE,设∠BAD=α,∠CDE=β,(1)如图1,若点D在线段BC上,点E在线段AC上.∠ABC=60°,∠ADE=70°,则α=°;β=°.(2)如图2,若点D在线段BC上,点E在线段AC上,则α,β之间有什么关系式?说明理由.(3)是否存在不同于(2)中的α,β之间的关系式?若存在,请写出这个关系式(写出一种即可),说明理由;若不存在,请说明理由.图1 图2【答案】(1)20,10;(2)(3)见解析.【解析】解:(1)∵AB=AC,∠ABC=60°,∴∠BAC=60°,∵AD=AE,∠ADE=70°,∴∠DAE=180°﹣2∠ADE=40°,∴α=∠BAD=20°,∴∠ADC=α+∠ABD=80°,∴β=∠ADC﹣∠ADE=10°,故答案为:20,10;(2)∠ADC=α+∠B,∠ADC=∠ADE+β=∠AED+β=β+∠C+β,∴α+∠B=β+∠C+β,∵∠B=∠C,∴α=2β;(3)存在;①当点E在CA的延长线上,点D在线段BC上,可得:α=2β﹣180°;②当点E在CA的延长线上,点D在CB的延长线上,可得α=180°﹣2β.7.(2019·郑州外国语模拟)如图,在平面直角坐标系xOy中,直线y=kx+k与双曲线4yx=(x>0)交于点A(1,a).(1)求a,k的值;(2)已知直线l过点D(2,0)且平行于直线y=kx+k,点P(m,n),(m>3)是直线l上一动点,过点P作坐标轴的平行线,交双曲线4yx=于点M、N,双曲线在点M、N之间的部分与线段PM、PN所围成的区域(不含边界)记为W. 横、纵坐标都是整数的点叫做整点.①当m=4时,直接写出区域W内的整点个数;②若区域W内的整点个数正好是8个,结合图象,求m的取值范围.【答案】见解析.【解析】解:(1)∵点A(1,a)在双曲线4yx上,∴a=4.∴点A的坐标为(1,4).将A(1,4)代入y=kx+k,得k=2;(2)①区域W内整点个数是3;∵直线l过点D(2,0)且平行于直线y=2x+2,∴直线l的解析式为y=2x-4.当m=4时,n=2m-4=4,点P的坐标为(4,4).画出图象,观察图形,可知区域W内的整点个数是3.②当2x-4=5时,x=4.5,此时区域W内有8个整点;结合函数图象,若区域W内的整点个数为8个,则m的取值范围为3<m≤4.5.8.(2019·郑州外国语模拟)如图,一段抛物线y=-x2+4(-2≤x≤2)为C1,与x轴交于A0、A1两点,顶点为D1;将C1绕点A1选择180°得到C2,顶点为D2;C1与C2组成一个新的图象,垂直于y轴的直线l 与新图象交于点P1(x1,y1),P2(x2,y2),与线段D1D2交于点P3(x3,y3),设x1,x2,x3均为正数,t= x1+x2+x3,则t的取值范围是()A. 6<t≤8B. 6≤t≤8C. 10<t≤12D. 10≤t≤12【答案】D.【解析】解:旋转后的抛物线的解析式为:y=(x﹣4)2﹣4,∵设x1,x2,x3均为正数,∴点P1(x1,y1),P2(x2,y2)在第四象限,由对称性可知:x1+x2=8,∵2≤x3≤4,∴10≤x1+x2+x3≤12,即10≤t≤12,故答案为:D.9.(2019·南阳二模)如图,在 8×8 的网格中,每个小方格都是边长为 1 的小正方形,每个小正方形的顶点称为格点.如果抛物线经过图中的三个格点,那么以这三个格点为顶点的三角形称为该抛物线的“内接格点三角形”.设对称轴平行于y轴的抛物线与网格对角线O M 的两个交点为A,B,其顶点为C,如果△ABC 是该抛物线的内接格点三角形,且A B=点A,B,C 的横坐标x A,x B,x C 满足x A<x C<x B,那么符合上述条件的抛物线的条数是.【答案】10.【解析】解:若抛物线开口朝下,当A(0,0)时,由AB=B(3,3),此时C(2,4),抛物线的解析式为:y=-x2+4x,该函数图象每向右平移1个单位,向上平移1个单位可得到一条抛物线,可平移4次,即有5条抛物线;同理,开口朝上的抛物线有5条,综上所述,共有10条抛物线符合要求.10.(2017•禹州市二模)有这样一个问题:探究函数y=12x2+1x的图象与性质,小东根据学习函数的经验,对函数y=12x2+1x的图象与性质进行了探究,下面是小东的探究过程,请补充完整:(1)下表是y与x的几组对应值.x…﹣3﹣2﹣112-13-1312123…y (25)63212-158-5318-55181783252m…函数y=12x2+1x的自变量x的取值范围是,m的值为;(2)在如图所示的平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点.并画出该函数的大致图象;(3)进一步探究函数图象发现:①函数图象与x轴有个交点,所以对应方程12x2+1x=0有个实数根;②方程12x2+1x=2有个实数根;③结合函数的图象,写出该函数的一条性质.【答案】(1)x≠0,296;(2)见解析.(3)1;1;3;函数没有最大值;这个函数没有最小值;函数图象不经过第四象限;当x<0时,y随x的增大而减小.【解析】解:(1)由题意:x≠0,m=296.(2)函数图象如图所示.(3)①由图象可知与x轴有一个交点,方程12x2+1x=0有一个实数根.故答案为:1,1.②观察图象可知,方程12x2+1x=2有3个实数根,故答案为:3.③函数性质:函数没有最大值;函数没有最小值;函数图象不经过第四象限等,答案不唯一.。
2020年九年级中考数学 几何压轴之几何探究题(含答案)
∴ △ABD≌△ CAF(AAS); 归 纳证明 :∵∠ 1=∠ 2=∠ BAC,∠1=∠BAE+ ∠ ABE, ∠ BAC=∠ BAE+∠ CAF,∠2=∠FCA+∠ CAF, ∴ ∠ABE=∠ CAF,∠BAE=∠FCA, 在 △ABE 和△CAF 中,
8 / 17
知识像烛光,能照亮一个人,也能照亮无数的人。--培根
2. 特 例探究 :如图 ①,已 知在△ABC 中,AB=BC,
∠ ABC=90°,D 为 AC 边 的中点 ,连接 BD,判断△ABD 是什 么三角 形,并 说明理 由;
归 纳证明 :如图 ②,已 知在△ABC 中,AB=BC,∠ ABC=90°,把 Rt△DEF 的 直角顶 点 D 放在 AC 的
中 点上,DE 交 AB 于 M,DF 交 BC 于 N,连接 BD. 证明:DM=DN;
拓 展应用 :在图 ②中,AC=4,其 他条件 都不发 生变化 ,请直接 写出 Rt△DEF 与△ABC 的重 叠部分
的面积.
2 / 17
知识像烛光,能照亮一个人,也能照亮无数的人。--培根
第 2 题图
特例探究 :解:△ABD 是等腰直角三角形.
知识像烛光,能照亮一个人,也能照亮无数的人。--培根
2020 中考数学 几何压轴之几何探究题(含答案)
1. 两个全等的直角三角形 ABC 和 DEF 重叠在一起,其中∠A=60°,AC=1,固定△ABC 不动,将△DEF 进行如下 操作:
(1)操作发现 如图①,△DEF 沿线段 AB 向右平移(即 D 点在线段 AB 内移动),连接 DC、CF、FB,四边形 CDBF 的形状在不断变化,但它的面积不变化,请求出其面积; (2)猜想论证 如图②,当 D 点移到 AB 的中点时,请你猜想四边形 CDBF 的形状,并说明理由; (3)拓展研究 如图③,将△DEF 的 D 点固定在 AB 的中点,然后绕 D 点按顺时针方向旋转△DEF,使 DF 落在 AB 的边上,此时 F 点恰好与 B 点重合,连接 AE,求 sinα 的值.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
GH AB
D
PF
C
G
Q
T
H
A
E
B
(2)因为 EF⊥GH,AM⊥BN.
所以由(1)中的结论可得 EF = AD , BN = AD . GH AB AM AB
所以 BN = EF = 11 . AM GH 15
(3)如图 5.过点 D 作平行于 AB 的直线,交过点 A 且平行于 BC 的直线于点 P,交 BC 的延长线于点 S.
x2 y2 25
联立方程组
(5
x)2
(10
y)2
102
,
得
x 5 y0
(舍),或
x y
3 4
.
所以 AR=5+x=8, 所以 DN = AR = 8 = 4 .
AM AB 10 5
R
D
S
C M
B
A
N
进阶训练 1.如图,在平面直角坐标系中,经过点 A 的双曲线,y= k (k>0)同时经过点 B.且 x
AE
F
D H G
B
CK
例 2 如图,△BCD 为等腰直角三角形,∠CBD=90°,∠BAC= 45°,若 S△ACD=4.5,求 AC 的长.
D B
A
C
解 如图,过点 B 作 BE⊥AC 于点 E,过点 D 作 DF⊥BF 交 EB 的延长线于点 F.
由“外弦图模型”可得△BFD≌△CEB,
所以 BF=CE.
AM
D
F
G
AE 图1
D
FN
C
C
G H
B
AE
图2
M H
B
A
D
M NB 图3
解 (1))如图 4.过点 A 作 AP∥EF.交 CD 于点 P,过点 B 作 BQ∥GH,交 AD 于点 Q. 因为四边形 ABCD 是矩形. 所以 AB∥DC,AD∥BC. 所以四边形 AEFP,四边形 BHGQ 都是平行四边形, 所以 AP=EF,GH=BQ. 又因为 CH⊥EF. 所以 AP⊥BQ. 所以∠QAT+∠AQT=90°. 因为四边形 ABCD 是矩形, 所以∠DAB=∠D=90°, 所以∠DAP+∠DPA=90°, 所以∠AQT=∠DPA. 所以△PDA∽△QAB. 所以 AP = AD ,
A
P
D
Q
N
BM
C
3.括展 (1)如图,在 Rt△ABH 中.∠ABH=90°,BE⊥AH 于点 E.所以
△A BE≌△BHE≌△AHB. (2)如图,在 Rt △QBM 和 Rt△BLK 中,QB=BL,QM⊥BK,所以 △QBM≌△BLK.
A
证明 因为∠BLK=90°,QM⊥BK, 所以∠KBL+∠QMB=∠KBI 十∠K= 90° 所以∠QMB=∠K, 又因为 QB= BL. 所以△QBM≌△BLK.
EF AD 于点 G.H 求证: =
GH AB
(2)如图 2,在满足(1)的条件下,又 AM⊥BN,点 M,N 分别在边 BC,CD 上,若
EF
11
=
GH 15
ቤተ መጻሕፍቲ ባይዱ
BN
,则 =
.
AM
(3)如图 3,在四边形 ABCD 中,∠ABC=90°,AB=AD=10,BC= CD-5,AM⊥DN,
DN 点 M,N 分别在边 BC,AB 上,求 的值.
E
B
H
Q
K E
B
ML
例题讲解 例 1 四边形 ABCD 是边长为 4 的正方形,点 E 在边 AD 所在的直线上,连结 CE,以 CE 为
边,作正方形 CEFG(点 D,F 在直线 CE 的同侧),连结 BF.当点 E 在线段 AD 上时,AE=1, 求 BF 的长.
F
AE D G
B
C
解 如图,过点 F 作 FH ⊥AD 交 AD 的延长线于点 H, 延长 FH 交 BC 的延长线于点 K.
易证 AE=BE,所以 AC=EF,
1
1
所以 S△ACD= AC·EF= AC2=4.5,
2
2
从而 AC=3.
F
B
D
A
EC
例 3 某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探
究,提出下列问题,请你给出证明.
(1)如图 1,在矩形 ABCD 中,EF⊥CH,EF 分别交 AB,CD 于点 F,F,GH 分别交 AD,BC
则四边形 ABSR 是平行四边形. 因为∠ABC=90°, 所以四边形 ABSR 是矩形. 所以∠R=∠S=90°,RS=AB=10,AR=BS. 因为 AM⊥DN. 所以由(1)中的结论可得 DN = AR .
AM AB 设 SC=x,DS=y,则 AR=BS=5+x.RD=10-y , 所以在 Rt△CSD 中,x2+y2=25. 在 Rt△ARD 中.(5+x)2+(10-y)2=100.
点 A 在点 B 的左侧,点 A 的横坐标为 2 .∠AOB=∠OBA=45°,则 k=__
__.
y
A
B
O
x
2.如图,巳知∠ABC=90°,D 是直线 AB 上的点,AD=BC.E 是直线 BC 上的一点,且 CE=BD.直线 AE,DC 相交于点 P,∠APD 的度数是一个固定的值吗?若是,请求出它的度数; 若不是,请说明理由.
专题 18《弦图模型》
破解策略 1.内弦图 如图,在正方形 ABCD 中,BF⊥CG,CG⊥DH,DH⊥AE,AE⊥BF,则△ABE≌△BCF≌△CDG≌△DAH. 证明 因为∠ABC=∠BFC=90° 所以∠ABE+∠FBC=∠FBC+∠FCB-90°. 所以∠ABE=∠FCB. 又因为 AB=BC.所以△ABE≌△BCF, 同理可得△ABE≌△BCF≌△CDG≌△DAH.
A D
G
H
F
E
B
C
2.外弦圈 如图,在正方形 ABCD 中,点 M,N,P,Q 在正方形 ABCD 边上,且 四边形 MUPQ 为正方形,则△QBM≌△MCN≌△NDP≌△PAQ. 证明 因为∠B=∠QMN=∠C=90°, 所以∠BQM+∠QMB=∠QMB+∠NMC=90°, 所以∠BQM=∠NMC. 又因为 QM =MN,所以△QBM≌△MCN. 同理可得△QHM≌△MCN≌△NDP≌△PAQ.
因为四边形 ABCD 和四边形 CEFG 是正方形, 根据“弦图模型”可得△ECD ≌△FEH,所以 FH =ED=AD-AE=3,EH= CD=4. 因为 CDHK 为矩形,所以 HK=CD=4,CK=DH=EH-ED=1. 所以 FK= FH 十 HK=7,BK=BC+CK=.5.
所以 BF= FK 2 BK 2 = 74
A
P
B
C
E
D
3.如图,在正方形 ABCD 中,点 P 在 AD 上,且不与 A,D 重合.BP 的垂直平分线分别 交 CD,AB 于 E,F 两点,垂足为 Q,过点 E 作 EH⊥AB 于点 H.EH 与 BP 交于点 M.求证:HF= AP.
