最新正比例函数知识点及练习题
正比例练习题及答案

正比例练习题及答案一、选择题1. 正比例函数的图象是一条直线,其斜率k表示:A. 正比例系数B. 反比例系数C. 常数项D. 截距答案:A2. 如果y与x成正比例,当x增加到原来的2倍时,y将:A. 减少到原来的一半B. 增加到原来的2倍C. 减少到原来的1/4D. 增加到原来的4倍答案:B3. 下列哪个函数不是正比例函数?A. y = 3xB. y = 2x^2C. y = -5xD. y = 7x + 1答案:B二、填空题4. 若y与x成正比例,且当x=2时,y=8,则正比例系数为______。
答案:45. 已知正比例函数的图象经过点(3,6),则该函数的解析式为y=______。
答案:2x三、解答题6. 已知函数y=kx,其中k>0,x>0。
若当x=5时,y=10,求k的值,并写出函数的解析式。
答案:将x=5,y=10代入y=kx得10=5k,解得k=2。
因此,函数的解析式为y=2x。
7. 某商品的单价与数量成正比例关系,若购买5个商品需支付25元,求购买10个商品需要支付多少元?答案:设单价为k元,根据题意有5k=25,解得k=5。
因此,购买10个商品需要支付10k=10×5=50元。
四、应用题8. 某工厂生产某种零件,每天的生产量与所需工时成正比例。
若生产100个零件需要4小时,求生产200个零件需要多少小时?答案:设生产x个零件需要y小时,根据题意有y=kx。
将x=100,y=4代入得4=100k,解得k=0.04。
因此,生产200个零件需要的时间为y=0.04×200=8小时。
9. 某公司销售产品,其销售额与销售量成正比例。
若销售100件产品的收入为2000元,求销售200件产品的收入是多少?答案:设销售x件产品的收入为y元,根据题意有y=kx。
将x=100,y=2000代入得2000=100k,解得k=20。
因此,销售200件产品的收入为y=20×200=4000元。
正比例函数训练题

正比例函数知识梳理:1、一般地,形如y=kx(k是常数,k ≠0)的函数,叫做正比例函数,其中k叫做比例系数。
2、正比例函数的性质:正比例函数y=kx(k是常数,k ≠0)的图像是一条经过原点的直线,我们称它为直线y=kx。
当k>0时,直线y=kx经过第三、第一象限,从左向右上升,即随着x的增大y也增大;当k<0时,直线y=kx经过第二、第四象限,从左向右下降,即随着x 的增大y反而减小。
3、一次函数的最简单的画法:因为两点确定一条直线,只需要确定原点和点(1,k)(k是常数,k ≠0),连接这两点就是正比例函数y=kx(k是常数,k ≠0)的图像。
上次课程检测:1.个体户小勤购进一批苹果,到集贸市场零售,已知卖出的苹果数是x(千克)与售价y(元)的关系如右表:(1)卖出的苹果数量x(千克)与售价y(元)的关系可以表示为;(2)当小勤卖出的苹果数量从5千克变到10千克时,苹果的售价从元变到元;(3)当小勤卖出苹果150千克时,得到苹果货款元;(4)当小勤卖出苹果千克时,得到苹果货款210元。
2、如图1,在正方形ABCD中,点E、F分别是BC、CD边上的点,且AE⊥EF,(1)延长EF交正方形∠BCD的外角平分线CP于点P(图2),试判断AE与EP大小关系,并说明理由;(2)在图2的AB边上是否存在一点M,使得四边形DMEP是平行四边形?若存在,请给予证明;若不存在,请说明理由.一、知识巩固:1、(1)形如 的函数,叫正比例函数,其中 叫比例系数.(2)下列式子中,哪此表示y 是x 的正比例函数?若是,请指出比例系数k .2、探究正比例函数的性质:试比较:(1)①y =2 x ; ② y =﹣2 x 的函数的图像(2)两个函数图象的共同点:形状都是 ,都经过 点.(3) 两个函数图象的不同点:①函数y =2 x 的图象经过第 象限,自变量x 从 到 (填“大”、“小”),函数y 的值 .这就是说,函数值y 随自变量x 的增大而__________.②函数y =-2x 的图象经过第 象限,y 从左到右 ,即y 随着x 的增大而 .二、典型例题;1、(1)若x k y )1(-=,y 是关于x 的正比例函数,则k ________.(2)若1-=k kx y ,y 是关于x 的正比例函数,则k =________.(3)若43-+=k x y ,y 是关于x 的正比例函数,则k =________.(4)若32)2(--=k x k y ,y 是关于x 的正比例函数,则k =________.(5)函数x k x k y )1()4(22++-=是正比例函数,且y 随x 的增大而减小,则k =________.2、(1)已知正比例函数kx y =,当x =3时,y=-15,求k 的值;(2)若y 关于x -1成正比例关系,当x =4时,y =9,则当x =6时,求出对应的函数值y .3.已知(x 1,y 1)和(x 2,y 2)是直线y =-3x 上的两点,且x 1>x 2,则y 1与y 2的大小关系是( )A .21y y >B .21y y <C .21y y =D .以上都有可能一、选择题1.下列函数是正比例函数的是( )A. 12+=x yB. )4(28-+=x yC. x y =D. xy 21-= 2.下列问题中的y 与x 成正比例函数关系的是( )A.圆的半径为x ,面积为yB.某地手机月租为10元,通话收费标准为0.1元/min ,若某月通话时间x (min ),月话费y (元)C.把10本书全部随意放入两个抽屉,第一个抽屉放x 本,第二个抽屉放y 本D.长方形的一边长为4,另一边长为x ,面积为y3.已知点P (1,m )在正比例函数y =- 4x 的图象上,则点P 的坐标为( )A. (1,4)B. (-1,-4)C.(1,-4)D.(-1,4)4.已知函数y=kx 的函数值y 随x 的增大而增大,则函数的图像经过( )A .第一、二象限B . 第一、三象限C .第二、三象限D .第二、四象限5.对于函数y =k 2x (k 是常数,k≠0)的图象,下列说法不正确的是( )A .是一条直线B .过点(1k ,k )C .经过一、三象限或二、四象限D .y 随着x 增大而增大6.若函数x m x m y )1()62(2-++=是正比例函数,则m 的值是( )A .m =-3B .m =1C .m =3D .3->m7.已知(x 1,y 1)和(x 2,y 2)是直线x y 23=上的两点,且x 1>x 2,则y 1与y 2的大小关系是( )A .21y y >B .21y y <C .21y y =D .以上都有可能8.下列说法中不正确的是( )A .在13-=x y 中y +1与x 成正比例;B .在2x y -=中y 与x 成正比例 C .在)1(2+=x y 中y 与x +1成正比例; D .在3+=x y 中y 与x 成正比例二、填空题1.当m =_______时,函数32)2(--=m x m y 是正比例函数.2.正比例函数y=kx 的图象经过点(2,﹣8),则该函数的解析式__________.3.已知函数y =kx 的函数值随x 值的增大而增大,则函数的图象经过_______象限.4.已知正比例函数x k y )13(-=,若y 随着x 的增大而减小,则k 的取值范围是_______.5.若正比例函数x k y )32(1-=及x k y )23(2-=的图象如图所示,则k 的取值范围是_______.6.已知y-1与x+1成正比例,且当x= -2时y= -1,则当x= -1时,y=_______.三、解答题1.某物体沿一斜坡下滑,它的速度v (m /s )与其下滑时间t (s )的关系如图(1)写出v 与t 之间的函数解析式.(2)下滑3s 时物体的速度是多少?xk y )23(2-=xk y )32(1-=2.已知y -3与2x -1成正比例,且x =1时y =6.(1)求y 与x 之间的函数关系式;(2)若y 的取值范围为50≤≤y ,求x 的取值范围;(3)若有A (x 1,y 1)、B (x 2,y 2)都在该函数的图象上,且y 1>y 2,试判断x 1、x 2的大小关系.3.如图,点B 、C 分别在两条直直线y =2x 和y =kx (0≠k )上,点A 、D 是x 轴上两点,已知四边形ABCD 是正方形,求k 的值.4.已知正比例函数y =kx (k 为常数,0≠k ),当13≤≤-x 时,对应的y 的取值范围是311≤≤-y , 且y 随x 的减小而减小,求k 的值.5.如图,长方形ABCD 的两组对边分别与x 轴、y 轴平行,点A 的坐标是(-2,2),△AOD 的面积是7,作射线OA 和OD .(1)确定折线AOD 对应的函数解析式;(2)如果x 轴是线段AB 的垂直平分线,计算长方形ABCD 的周长和面积.。
正比例函数知识点整理

正比例函数知识点整理一、正比例函数的定义。
1. 定义形式。
- 一般地,形如y = kx(k是常数,k≠0)的函数叫做正比例函数,其中k叫做比例系数。
例如y = 2x,y=(1)/(3)x都是正比例函数,这里k = 2和k=(1)/(3)分别是它们的比例系数。
2. 对定义的理解。
- 函数表达式必须是y = kx这种形式,x的次数为1,且不能有其他项。
比如y = 2x+1就不是正比例函数,因为它多了常数项1;y=x^2也不是,因为x的次数是2。
- k不能为0,如果k = 0,那么函数y = 0× x=0,它是一个常数函数,而不是正比例函数。
二、正比例函数的图象与性质。
1. 图象。
- 正比例函数y = kx(k≠0)的图象是一条经过原点(0,0)的直线。
- 当k>0时,例如y = 2x,图象经过一、三象限,从左向右上升;当k < 0时,比如y=-2x,图象经过二、四象限,从左向右下降。
2. 性质。
- 增减性。
- 当k>0时,y随x的增大而增大。
例如在y = 3x中,如果x_1 = 1,y_1 = 3×1 = 3;当x_2=2时,y_2 = 3×2 = 6,因为2>1且6 > 3,所以y随x增大而增大。
- 当k < 0时,y随x的增大而减小。
例如在y=-2x中,若x_1 = 1,y_1=-2×1=-2;当x_2 = 2时,y_2=-2×2=-4,因为2 > 1且-4<-2,所以y随x增大而减小。
- 倾斜程度。
- | k|越大,直线越靠近y轴,即直线越陡。
例如y = 5x比y = 2x的图象更陡,因为|5|>|2|;y=-5x比y=-2x的图象更陡,同样是因为| - 5|>|-2|。
三、正比例函数解析式的确定。
1. 方法。
- 因为正比例函数y = kx(k≠0),只需要知道一个点的坐标(除原点外)就可以确定k的值,从而确定函数解析式。
人教版八年级下册专项训练专题14 正比例函数图象和性质

专题14 正比例函数图象和性质一、知识点1、画正比例函数图象时,通常在坐标系中描出点________和________最为简单。
2、正比例函数y=kx(k是常数,k≠0)的图象是一条经过________的直线。
当k>0时,图象经过第________象限,y所x的增大而________。
当k<0时,图象经过第________象限,y所x的增大而________。
二、标准例题例1:若函数y=(2m+1)x2+(1﹣2m)x(m为常数)是正比例函数,则m的值为()A.m>12B.m=12C.m<12D.m=−12例2:若正比例函数y=(1+m)x 的图像经过点A(1,2m),则下列坐标对应的点也在该正比例函数的图像上的是()A.(2,1)B.(-1,2)C.(2,4)D.(-2,-1)例3:如图,在平面直角坐标系中,直线l:y=x+1与y轴交于点A1,如图所示依次作正方形A1B1C1O,正方形A2B2C2C1……正方形A n B n∁n C n﹣1(n为大于1的整数)使得点A1,A2,A3…A n在直线上,点C1,C2,C3,…∁n 在x轴正半轴上,请解决下列问题:(1)点A6的坐标是;点B6的坐标是;(2)点A n的坐标是,正方形A n B n∁n C n﹣1的面积是.例4:已知y与x﹣1成正比例,且当x=3时,y=4.(1)求y与x之间的函数表达式;(2)当x=﹣1时,求y的值;(3)当﹣3<y<5时,求x的取值范围.例5:已知正比例函数y=kx图象经过点(2,-4).(1)求这个函数的解析式;(2)图象上两点A(x1,y1)、B(x2,y2),如果x1<x2,比较y1,y2的大小.三、练习1.下列正比例函数中,y随x的值增大而增大的是()A.y=﹣2014x B.y=(√3﹣1)x C.y=(﹣π﹣3)x D.y=(1﹣π2)x2.已知点A(-5,y1)、B(-2,y2)都在直线y=-12x上,则y1与y2的关系是()A.y1≤y2B.y1=y2C.y1<y2D.y1>y23.若y关于x的函数y=(m–2)x+n是正比例函数,则m,n应满足的条件是()A.m≠2且n = 0B.m = 2且n ≠ 0C.m≠2D.n = 04.正比例函数y=2x的大致图象是()A.B.C.D.5.下列四组点中,可以在同一个正比例函数图象上的一组点是()A.(2 , −3),(−4 , 6)B.(−2 , 3),(4 , 6)C.(−2 , −3),(4 ,− 6)D.(2 , 3),(−4 , 6)6.直线y=kx过点A(m,n),B(m−3,n+4),则k的值是()A.43B.−43C.34D.−347.正比例函数y=kx(k>0)的图象大致是()A.B.C.D.8.已知正比例函数y=(2m﹣1)x的图象上两点A(x1,y1),B(x2,y2),当x1<x2时,有y1>y2,那么m 的取值范围是()A.m<12B.m>12C.m<0D.m>09.正比例函数y=kx的图像过点A(2,3),则此函数的图像还经过点()A.(-2,-3)B.(-2,3)C.(3,2)D.(-3,-2)10.已知y=(m+3)x m2−8是正比例函数,则m=______.11.点A(m,−3)向下平移3个单位后,恰好落在正比例函数y=−6x的图象上,则m的值为______.12.如图,直线y=√33x,点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按此做法进行下去,点A4的坐标为______,点A n______.13.函数y=(k-1)x2|k|-3是正比例函数,且y随x增大而减小,求(k+3)2019的值.14.如图,在边长为1个单位长度的小正方形组成的格点图中,点A、B、C都是格点.(1)点A坐标为;点B坐标为;点C坐标为;(2)画出△ABC关于原点对称的△A1B1C1;(3)已知M(1,4),在x轴上找一点P,使|PM﹣PB|的值最大(写出过程,保留作图痕迹),并写出点P 的坐标.15.一次函数y=kx+b.当x=-3时,y=0;当x=0时,y=-4(1)求k与b的值.(2)求该函数图象与x轴和y轴围成的图形面积.16.已知y与x+2成正比,当x=4时,y=4.(1)求y与x之间的函数关系式;(2)若点(a,3)在这个函数图象上,求a的值.17.请你用学习“一次函数”时积累的经验和方法研究函数y=|x|的图象和性质,并解决问题.(1)完成下列步骤,画出函数y=|x|的图象;①列表、填空;②描点:③连线(2)观察图象,当x______时,y随x的增大而增大;(3)结合图象,不等式|x|<x+2的解集为______.19.已知银行2006年9月的“半年期存款”年利率是2.25%,某人当年9月存入银行a元,经过半年到期时按规定缴纳20%利息税后,得到利息b元.问税后利息b(元)与本金a(元)成正比例吗?如果成正比例,那么求出这个比例系数.21.已知y与x成正比例,当x=4时,y=12.(1)写出y与x之间的函数解析式;(2)求当y=36时x的值;(3)判断点(-7,-10)是否是函数图象上的点.22.已知直线y=kx过点(−2,1),A是直线y=kx图像上的点,若过A向x轴作垂线,垂足为B,且SΔAB0=9,求点A的坐标.23.如图,点A(a,6)是第一象限内正比例函数y=3x的图象上的一点,AB⊥x轴,交直线OB于B点,三角形OAB的面积为5,求直线OB所对应的函数表达式.专题14 正比例函数图象和性质一、知识点1、画正比例函数图象时,通常在坐标系中描出点________和________最为简单。
北师大版八年级数学上册_最新精选《正比例函数的图象与性质》知识点训练(基础)
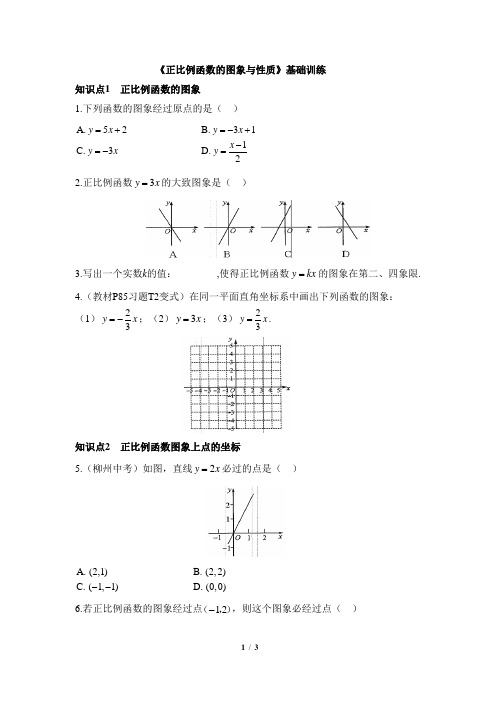
《正比例函数的图象与性质》基础训练知识点1 正比例函数的图象1.下列函数的图象经过原点的是( )A. 52B. 311C. 3 D. 2y x y x x y x y =+=-+-=-= 2.正比例函数3y x =的大致图象是( )3.写出一个实数k 的值:________,使得正比例函数y kx =的图象在第二、四象限.4.(教材P85习题T2变式)在同一平面直角坐标系中画出下列函数的图象:(1)23y x =-;(2)3y x =;(3)23y x =.知识点2 正比例函数图象上点的坐标5.(柳州中考)如图,直线2y x =必过的点是( )A. (2,1)B. (2,2)C. (1,1)D. (0,0)-- 6.若正比例函数的图象经过点12-(,),则这个图象必经过点( )A. (1,2)B. (1,2)C. (2,1)D. (1,2)---- 7.(西安期中)正比例函数y kx =的图象经过点12-(,),则k 的值是_______. 8.(教材P85习题T4变式)如图,正比例函数图象经过点A ,则该函数表达式是__________.9.函数6y x =是经过点(0,_______)和点(__________,6)的一条直线,点24A (,)__________(填“在”或“不在”)直线6y x =上.知识点3 正比例倒数的性质10.已知在正比例函数(2)y k x =-中,y 随x 的增大而减小,则k 的取值范围是( )A. 2B. 2C. 2D. 2k k k k >< 11.(西安期中)设正比例函数y mx =的图象经过点4A m (,),且y 的值随x 值的增大而减小,则m =( )A. 2B. 2C. 4D. 4-- 12.正比例函数1232y x y x y x ==-=-,,的共同特点是( ) A.图象经过同样的象限B.y 随x 的增大而减小C.y 随x 的增大而增大D.图象都过原点13.若点()()125,,2,A y B y --都在正比例函数12y x =-的图象上,则12_______y y (填“>”或“<”)参考答案1.C 2.B3.答案不唯一,如:2-4.解:图略.5.D6.A7.2-8.32 y x =9.0 1 不在10.B 11.B 12D 13.>。
第02讲 正比例函数(知识解读+题型精讲+随堂检测)(原卷版)

第02讲正比例函数1. 理解正比例函数的定义2. 学会观察正比例函数图像并分析,判断函数值随自变量的变化而变化3. 掌握正比例函数性质知识点1:正比例函数的定义一般地,形如y=kx(k≠0)函数,叫做正比例函数,其中k叫做比例系数.知识点2:正比例函数图像和性质正比例函数图象与性质用表格概括下:知识点三3:待定系数法求正比例函数解析式1.正比例函数的表达式为y=kx(k≠0),只有一个待定系数k,所以只要知道除(0,0)外的自变量与函数的一对对应值或图象上一个点的坐标(原点除外)即可求出k的值,从而确定表达式.2.确定正比例函数表达式的一般步骤:(1)设——设出函数表达式,如y=kx(k≠0);(2)代——把已知条件代入y=kx中;(3)求——解方程求未知数k;(4)写——写出正比例函数的表达式【题型1:正比例函数的定义】【典例1】(2023春•永定区期末)下列函数中,是正比例函数的是()A.B.C.y=x2D.y=2x﹣1【变式1-1】(2023春•赣州期末)下列式子中,表示y是x的正比例函数的是()A.y=3x2B.C.D.y2=3x【变式1-2】(2023春•洪江市期末)下列函数中,是正比例函数的是()A.y=2x﹣1B.C.D.y=2x2+1【变式1-3】(2023春•朝阳区校级期中)下列变量之间的关系,一个变量是另一个变量的正比例函数的是()A.正方形的面积S随边长x的变化而变化B.面积为20的三角形的一边上的高h随着这边长a的变化而变化C.正方形的周长C随着边长x的变化而变化D.水箱以0.5L/min的流量往外放水,水箱中的剩水量V(单位:L)随着放水时间t(单位:min)的变化而变化【典例2】(2023春•兴隆县期末)已知y=(m+1)x|m|,若y是x的正比例函数,则m的值为()A.1B.﹣1C.1或﹣1D.0【变式2-1】(2023春•南皮县月考)若函数y=(k+1)x+b﹣2是正比例函数,则()A.k≠﹣1,b=﹣2B.k≠1,b=﹣2C.k=1,b=﹣2D.k≠﹣1,b=2【变式2-2】(2023春•永春县期末)若y=x+b是正比例函数,则b的值是()A.0B.﹣1C.1D.任意实数【变式2-3】(2023春•孝感期末)若函数y=﹣2x m﹣2+n+1是正比例函数,则m+n()A.3B.2C.1D.﹣1【题型2:判断正比例函数图像所在象限】【典例3】(2023春•朔州期末)正比例函数的图象经过()A.第一、二象限B.第一、三象限C.第一、四象限D.第二、四象限【变式3-1】(2023春•凤庆县期末)正比例函数y=﹣3x的图象经过()象限.A.第一、三象限B.第二、四象限C.第一、四象限D.第二、三象限【变式3-2】(2023春•南岗区期末)在平面直角坐标系中,正比例函数y=﹣4x 的图象经过()A.第一、二象限B.第一、三象限C.第二、三象限D.第二、四象限【题型3:正比例函数的性质】【典例4】(2023春•乐陵市期末)关于函数y=2x,下列说法错误的是()A.它是正比例函数B.图象经过(1,2)C.图象经过一、三象限D.当x>0,y<0【变式4-1】(2022秋•东胜区期末)关于函数y=﹣3x,下列说法正确的是()A.该函数的图象经过点(﹣3,1)B.是一次函数,但不是正比例函数C.该函数的图象经过第一、三象限D.随着x的增大,y反而减小【变式4-2】(2023•金山区二模)已知函数y=kx(k≠0,k为常数)的函数值y 随x值的增大而减小,那么这个函数图象可能经过的点是()A.(0.5,1)B.(2,1)C.(﹣2,4)D.(﹣2,﹣2)【变式4-3】(2022•临渭区二模)已知正比例函数y=kx(k≠0),当自变量的值减小1时,函数y的值增大3,则k的值为()A.B.C.3D.﹣3【题型4:判断正比例函数的比例系数大小】【典例5】(2022春•南城县校级月考)如图,三个正比例函数的图象分别对应表达式:①y=ax,②y=bx,③y=cx.将a,b,c按从小到大排列并用“<”连接,正确的是()A.a<b<c B.c<b<a C.b<c<a D.a<c<b【变式5-1】(2022秋•渠县校级期中)三个正比例函数的表达式分别为①y=ax;②y=bx;③y=cx,其在平面直角坐标系中的图象如图所示,则a,b,c的大小关系为()A.a>b>c B.c>b>a C.b>a>c D.b>c>a【变式5-2】(2023秋•太仓市期末)如图,三个正比例函数的图象分别对应函数关系式:①y=ax,②y=bx,③y=cx,将a,b,c从小到大排列并用“<”连接为()A.a<b<c B.c<a<b C.c<b<a D.a<c<b【题型5:待定系数法求正比例函数解析式】【典例6】(2023春•鼓楼区校级期末)已知y与x成正比例,且当x=2时,y=4.(1)求y与x之间的函数关系式;(2)若点(a,3)在这个函数图象上,求a的值.【变式6-1】(2023春•荆门期末)已知y与x成正比例,且x=﹣2时y=4,(1)求y与x之间的函数关系式;(2)设点(a,﹣2)在这个函数的图象上,求a.【变式6-2】(2022秋•城关区期末)已知点(,1)在函数y=(3m﹣1)x的图象上,(1)求m的值,(2)求这个函数的解析式.【变式6-3】(2022秋•江宁区校级月考)已知y=y2﹣y1,其中y1与x成正比例,y2与x+2成正比例,当x=﹣1时,y=2,当x=2时,y=10.(1)求y与x的函数表达式;(2)当x取何值时,y的值为30?【题型6:正比例函数的图像性质综合】【典例7】(2022春•老城区校级期中)已知正比例函数y=kx的图象经过点A,点A在第四象限,过点A作AH⊥x轴,垂足为H,点A的横坐标为5,且△AOH的面积为10.(1)求正比例函数的解析式.(2)在坐标轴上能否找到一点P,使△AOP的面积为8?若存在,求点P的坐标;若不存在,请说明理由.【变式7】(2022春•德城区校级期中)如图,已知正比例函数y=kx的图象经过点A,点A在第四象限,过点A作AH⊥x轴,垂足为H,点A的横坐标为4,且△AOH的面积为8.(1)求正比例函数的解析式.(2)在x轴上能否找到一点P,使△AOP的面积为10?若存在,求点P的坐标;若不存在,请说明理由.1.(2019•梧州)下列函数中,正比例函数是()A.y=﹣8x B.y=C.y=8x2D.y=8x﹣4 2.(2023•陕西)在同一平面直角坐标系中,函数y=ax和y=x+a(a为常数,a<0)的图象可能是()A.B.C.D.3.(2020•上海)已知正比例函数y=kx(k是常数,k≠0)的图象经过第二、四象限,那么y的值随着x的值增大而.(填“增大”或“减小”)4.(2019•本溪)函数y=5x的图象经过的象限是.1.(2023秋•于洪区期中)以下y关于x的函数中,是正比例函数的为()A.y=x2B.C.D.2.(2022秋•烟台期末)若y关于x的函数y=(a﹣2)x+b是正比例函数,则a,b应满足的条件是()A.a≠2B.b=0C.a=2且b=0D.a≠2且b=0 3.(2023春•兴隆县期中)已知点P(m,0)在x轴负半轴上,则函数y=mx 的图象经过()A.二、四象限B.一、三象限C.一、二象限D.三、四象限4.(2023•玉环市校级开学)若函数y=kx的图象上有两点A(x1,y1)、B(x2,y2),当x1>x2时,y1<y2,则k的值可以是()A.﹣2B.0C.1D.2 5.(2022春•利川市期末)已知正比例函数y=﹣3x,则下列说法正确的是()A.函数值y随x的增大而增大B.函数值y随x的增大而减小C.函数图象经过一,三,四象限D.函数图象经过二,三,四象限6.(2023•金山区二模)已知函数y=kx(k≠0,k为常数)的函数值y随x值的增大而减小,那么这个函数图象可能经过的点是()A.(0.5,1)B.(2,1)C.(﹣2,4)D.(﹣2,﹣2)7.(2023秋•黄浦区期中)下列各图象中,表示函数y=x的大致图象是()A.B.C.D.8.(2023春•青龙县期末)函数y=kx(k≠0)的图象经过点(﹣2,1),则这个函数的解析式是()A.y=2x B.y=﹣2x C.y=x D.y=﹣x 9.(2023秋•法库县期中)一个正比例函数的图象经过点A(﹣2,3),B(a,﹣3),则a=.10.(2023秋•金山区期中)已知正比例函数y=(m﹣1)x,且y随着x的增大而减小.(1)求m的取值范围;(2)已知点P(m,6)在该函数图象上,求出这个正比例函数解析式.11.(2023春•青云谱区校级期末)已知y关于x的函数y=(2m+6)x+m﹣3,且该函数是正比例函数.(1)求m的值;(2)若点(a,y1),(a+1,y2)在该函数的图象上,请直接写出y1,y2的大小关系.12.(上城区一模)定义运算“※”为:a※b=(1)计算:3※4;(2)画出函数y=2※x的图象.。
正比例函数知识点及练习题

正比例函数1、正比例函数及性质一般地,形如y=kx(k是常数,k≠0)的函数叫做正比例函数,其中k叫做比例系数.注:正比例函数一般形式y=kx (k不为零) ①k不为零②x指数为1 当k>0时,直线y=kx经过三、一象限,从左向右上升,即随x的增大y也增大;当k<0时,•直线y=kx经过二、四象限,从左向右下降,即随x增大y 反而减小.(1)解析式:y=kx(k是常数,k≠0)(2)必过点:(0,0)、(1,k)(3)走向:k>0时,图像经过一、三象限;k<0时,•图像经过二、四象限(4)增减性:k>0,y随x的增大而增大;k<0,y随x增大而减小(5)倾斜度:|k|越大,越接近y轴;|k|越小,越接近x轴2、正比例函数专题练习知识点1.形如___________(k是常数,k≠0)的函数是正比例函数,其中k叫,正比例函数都是常数与自变量的乘积的形式.2.正比例函数y=kx(k是常数,k≠0)的图象是一条经过原点的直线,我们通常称之为直线y=kx.当k>0时,图像位于第象限,从左向右,y随x的增大而,也可以说成函数值随自变量的增大而_________;当k<0时,图像位于第象限,从左向右,y随x的增大而,也可以说成函数值随自变量的增大而_________.3.正比例函数的图像是经过坐标点和定点__ __两点的一条。
根据两点确定一条直线,可以确定两个点(两点法)画正比例函数的图象.例1、已知y=(k+1)x+k-1是正比例函数,求k的值.例2、根据下列条件求函数的解析式①y与x2成正比例,且x=-2时y=12.②函数y=(k2-4)x2+(k+1)x是正比例函数,且y随x的增大而减小.跟踪练习:一、根据正比例函数解析式的特点求值.1、若x、y是变量,且函数2=是正比例函数,则k的值为.y+k)1(k x2、如果y=x-2a+1是正比例函数,则a的值为.3、若1ny是正比例函数,则n的值为.=n x-(-)24、若函数y=(2m+6)x2+(1-m)x是正比例函数,则m的值是.5、已知函数y=(2m+1)x+m-3 若函数图象经过原点,则m的值.二、求正比例函数的解析式6、点A(2,4)在正比例函数图象上,则这个正比例函数的解析式?7、正比例函数图象过(-2,3),则这个正比例函数的解析式?8、已知y与x成正比例,且x=2时y=-6,则y=9时x的值是多少?9、已知y与x成正比例,且x=-3时y=-9,则y=-5时x的值是多少?10、已知y-3与x成正比例,且x=4时,y=7.(1)写出y与x之间的函数解析式.(2)计算x=9时,y的值.(3)计算y=2时,x的值.11、正比例函数y=(3m-1)x的图像经过点A(x1,x2)和B(y1,y2),且该图像经过第二、四象限.(1)求m的取值范围.(2)当x1>x2时,比较y1与y2的大小,并说明理由.12、在函数y=-3x的图象上取一点P,过P点作PA⊥x轴,已知P点的横坐标为-•2,求△POA的面积(O为坐标原点).。
第1课时 正比例函数的图象与性质(教材P152~154练习)

(2)当 t =4时,甲、乙两人的行程相差多少?
◉答案
解:(2)当 t =4时,甲走了5×4=20(km),乙走了 ×4=
(km),20-来自= (km).所以甲、乙两人的行程相差 km.
(
A. 2
AD )
B. 0
C. -4
D. 6
8. 对于正比例函数 y =-7 x ,下列说法正确的是( CC )
A. 图象必过点(-1,-7)
B. 图象经过第一、三象限
C. y 随 x 的增大而减小
D. 不论 x 取何值,总有 y <0
9. 若点 A (-5, y1)和点 B (-2, y2)都在函数 y =2 x 的图象上,则 y<
◉答案
(2) k >-3.
(3) k 为何值时, y 随 x 的增大而减小?
◉答案
(3) k <-3.
12. 若点 A (2,4)在函数 y = kx 的图象上,则下列各点在此函数图象上的是
(
A )
A. (1,2)
B. (-2,-1)
C. (-1,2)
D. (2,-1)
13. [一题多辨](1)已知( x1, y1),( x2, y2)是函数 y =- x 的图象上的两
D. b > c > a
15. 正比例函数 y =-2 x 的图象过 A ( x1, y1), B ( x2, y2)两点,若 x1- x2
D
=
3,则
A. 3 y1- y2的值为(
B. -3
D )
C. 6
D. -6
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正比例函数
1、正比例函数及性质
一般地,形如y=kx(k是常数,k≠0)的函数叫做正比例函数,其中k叫做比例系数.
注:正比例函数一般形式y=kx (k不为零) ①k不为零②x指数为1 当k>0时,直线y=kx经过三、一象限,从左向右上升,即随x的增大y也增大;当k<0时,•直线y=kx经过二、四象限,从左向右下降,即随x增大y 反而减小.
(1)解析式:y=kx(k是常数,k≠0)
(2)必过点:(0,0)、(1,k)
(3)走向:k>0时,图像经过一、三象限;k<0时,•图像经过二、四象限
(4)增减性:k>0,y随x的增大而增大;k<0,y随x增大而减小
(5)倾斜度:|k|越大,越接近y轴;|k|越小,越接近x轴
2、正比例函数专题练习
知识点
1.形如___________(k是常数,k≠0)的函数是正比例函数,其中k叫,正比例函数都是常数与自变量的乘积的形式.
2.正比例函数y=kx(k是常数,k≠0)的图象是一条经过原点的直线,我们通常称之为直线y=kx.
当k>0时,图像位于第象限,从左向右,y随x的增大而,也可以说成函数值随自变量的增大而_________;
当k<0时,图像位于第象限,从左向右,y随x的增大而,也可以说成函数值随自变量的增大而_________.
3.正比例函数的图像是经过坐标点和定点__ __两点的一条。
根据两点确定一条直线,可以确定两个点(两点法)画正比例函数的图象.
例1、已知y=(k+1)x+k-1是正比例函数,求k的值.
例2、根据下列条件求函数的解析式
①y与x2成正比例,且x=-2时y=12.
②函数y=(k2-4)x2+(k+1)x是正比例函数,且y随x的增大而减小.
跟踪练习:
一、根据正比例函数解析式的特点求值.
1、若x、y是变量,且函数2
=是正比例函数,则k的值为.
y+
k
)1
(k x
2、如果y=x-2a+1是正比例函数,则a的值为.
3、若1
n
y是正比例函数,则n的值为.
=n x
-
(-
)2
4、若函数y=(2m+6)x2+(1-m)x是正比例函数,则m的值是.
5、已知函数y=(2m+1)x+m-3 若函数图象经过原点,则m的值.
二、求正比例函数的解析式
6、点A(2,4)在正比例函数图象上,则这个正比例函数的解析式?
7、正比例函数图象过(-2,3),则这个正比例函数的解析式?
8、已知y与x成正比例,且x=2时y=-6,则y=9时x的值是多少?
9、已知y与x成正比例,且x=-3时y=-9,则y=-5时x的值是多少?
10、已知y-3与x成正比例,且x=4时,y=7.
(1)写出y与x之间的函数解析式.
(2)计算x=9时,y的值.
(3)计算y=2时,x的值.
11、正比例函数y=(3m-1)x的图像经过点A(x1,x2)和B(y1,y2),且该图像经过第二、四象限.
(1)求m的取值范围.
(2)当x1>x2时,比较y1与y2的大小,并说明理由.
12、在函数y=-3x的图象上取一点P,过P点作PA⊥x轴,已知P点的横坐标为-•2,求△POA的面积(O为坐标原点).。
