正比例函数及其性质练习题
正比例函数的图象与性质课件习题
在同一坐标系内画下列正比例函数的图像：
1 y 3x y x y x y 3
当k>0 时，它的图 像 经过第 一、三象 限
y 3x
3
yx
1 y x 3
1
3
1
o
x
在同一坐标系内画下列正比例函数的图像：
y 3x
y x
1 y x 3
y y 3x y x y 1 x
(1) 当k>0时，正比例函数的图像经过第一、三象 限，自变量x逐渐增大时，y的值也随着逐渐增大。 (2) 当k<0时，正比例函数的图像经过第二、四象限， 自变量x逐渐增大时，y的值则随着逐渐减小。
正 比 例 函 数
定义 图像
Y=kx(k≠0)
是经过原点和(1,k)点的一条直线 。
性 质
k>0
k<0
6.下列函数y=5x,y=-3x,y=1/2x,y=-1/3x中，y
随x的增大而减小的是———，y随x的增大而减小 且最先达到-10的是——。
能力提高：
想一想： 点燃蜡烛，蜡烛长度按照与时间成正比变短，长为21厘米 的蜡烛，已知点燃6分钟后，蜡烛变短3.6厘米，设蜡烛点 y 燃x分钟后变短y厘米，求 (1）用x表示函y数的解析式； （2）自变量x的取值范围； (3) 此蜡烛几分钟燃烧完？
能力提升！
m 2
1、已知函数 y (m 3) x ， = 3 时，函数是正比例函数，图 减小 在 二、四 象限，y随x增大而
x 2、已知函数 y= 3 A(3，y1)
, 点
和点B (6，y2)在函数图象上， < 则 y1 y2(填“>”或“<”)。
x 3、已知函数 y 6
人教版八年级下册专项训练专题14 正比例函数图象和性质
专题14 正比例函数图象和性质一、知识点1、画正比例函数图象时，通常在坐标系中描出点________和________最为简单。
2、正比例函数y=kx（k是常数，k≠0）的图象是一条经过________的直线。
当k>0时，图象经过第________象限，y所x的增大而________。
当k<0时，图象经过第________象限，y所x的增大而________。
二、标准例题例1：若函数y＝（2m+1）x2+（1﹣2m）x（m为常数）是正比例函数，则m的值为（）A．m＞12B．m＝12C．m＜12D．m＝−12例2：若正比例函数y=（1+m）x 的图像经过点A（1,2m），则下列坐标对应的点也在该正比例函数的图像上的是（）A．（2，1）B．（-1,2）C．（2,4）D．（-2，-1）例3：如图，在平面直角坐标系中，直线l：y＝x+1与y轴交于点A1，如图所示依次作正方形A1B1C1O，正方形A2B2C2C1……正方形A n B n∁n C n﹣1(n为大于1的整数)使得点A1，A2，A3…A n在直线上，点C1，C2，C3，…∁n 在x轴正半轴上，请解决下列问题：(1)点A6的坐标是；点B6的坐标是；(2)点A n的坐标是，正方形A n B n∁n C n﹣1的面积是．例4：已知y与x﹣1成正比例，且当x=3时，y=4．（1）求y与x之间的函数表达式；（2）当x=﹣1时，求y的值；（3）当﹣3＜y＜5时，求x的取值范围．例5：已知正比例函数y=kx图象经过点（2，－4）．（1）求这个函数的解析式；（2）图象上两点A（x1，y1）、B（x2，y2），如果x1<x2，比较y1，y2的大小．三、练习1．下列正比例函数中，y随x的值增大而增大的是（）A．y＝﹣2014x B．y＝（√3﹣1）x C．y＝（﹣π﹣3）x D．y＝（1﹣π2）x2．已知点A（-5，y1）、B（-2，y2）都在直线y=-12x上，则y1与y2的关系是（）A．y1≤y2B．y1=y2C．y1<y2D．y1>y23．若y关于x的函数y=（m–2）x+n是正比例函数，则m，n应满足的条件是（）A．m≠2且n = 0B．m = 2且n ≠ 0C．m≠2D．n = 04．正比例函数y=2x的大致图象是（）A．B．C．D．5．下列四组点中，可以在同一个正比例函数图象上的一组点是（）A．(2 ， −3)，(−4 ， 6)B．(−2 ， 3)，(4 ， 6)C．(−2 ， −3)，(4 ，− 6)D．(2 ， 3)，(−4 ， 6)6．直线y=kx过点A(m,n)，B(m−3,n+4)，则k的值是（）A．43B．−43C．34D．−347．正比例函数y＝kx（k＞0）的图象大致是（）A．B．C．D．8．已知正比例函数y＝（2m﹣1）x的图象上两点A（x1，y1），B（x2，y2），当x1＜x2时，有y1＞y2，那么m 的取值范围是（）A．m＜12B．m＞12C．m＜0D．m＞09．正比例函数y=kx的图像过点A（2，3），则此函数的图像还经过点（）A．（-2，-3）B．（-2，3）C．（3，2）D．（-3，-2）10．已知y=(m+3)x m2−8是正比例函数，则m=______．11．点A(m,−3)向下平移3个单位后，恰好落在正比例函数y=−6x的图象上，则m的值为______．12．如图，直线y=√33x，点A1坐标为(1，0)，过点A1作x轴的垂线交直线于点B1，以原点O为圆心，OB1长为半径画弧交x轴于点A2；再过点A2作x轴的垂线交直线于点B2，以原点O为圆心，OB2长为半径画弧交x轴于点A3，…，按此做法进行下去，点A4的坐标为______，点A n______．13．函数y=（k-1）x2|k|-3是正比例函数，且y随x增大而减小，求（k+3）2019的值．14．如图，在边长为1个单位长度的小正方形组成的格点图中，点A、B、C都是格点．（1）点A坐标为；点B坐标为；点C坐标为；（2）画出△ABC关于原点对称的△A1B1C1；（3）已知M（1，4），在x轴上找一点P，使|PM﹣PB|的值最大（写出过程，保留作图痕迹），并写出点P 的坐标．15．一次函数y=kx+b．当x=-3时，y=0；当x=0时，y=-4(1)求k与b的值．(2)求该函数图象与x轴和y轴围成的图形面积．16．已知y与x+2成正比，当x=4时，y=4．(1)求y与x之间的函数关系式；(2)若点(a,3)在这个函数图象上，求a的值．17．请你用学习“一次函数”时积累的经验和方法研究函数y=|x|的图象和性质，并解决问题．(1)完成下列步骤，画出函数y=|x|的图象；①列表、填空；②描点：③连线(2)观察图象，当x______时，y随x的增大而增大；(3)结合图象，不等式|x|<x+2的解集为______．19．已知银行2006年9月的“半年期存款”年利率是2.25%，某人当年9月存入银行a元，经过半年到期时按规定缴纳20%利息税后，得到利息b元．问税后利息b(元)与本金a(元)成正比例吗？如果成正比例，那么求出这个比例系数．21．已知y与x成正比例，当x＝4时，y＝12.(1)写出y与x之间的函数解析式；(2)求当y＝36时x的值；(3)判断点(－7，－10)是否是函数图象上的点．22．已知直线y=kx过点(−2，1)，A是直线y=kx图像上的点，若过A向x轴作垂线，垂足为B，且SΔAB0=9，求点A的坐标.23．如图，点A（a，6）是第一象限内正比例函数y=3x的图象上的一点，AB⊥x轴，交直线OB于B点，三角形OAB的面积为5，求直线OB所对应的函数表达式．专题14 正比例函数图象和性质一、知识点1、画正比例函数图象时，通常在坐标系中描出点________和________最为简单。
正比例函数练习题及答案
正比例函数习题姓名：家长签字:得分：选择题（每小题3分，共30分。
）一.1.下列函数表达式中，y是x的正比例函数的是（）A.y=-2x2B.y=xC.y=J^D.y=x-234x2.若y=x+2-b是正比例函数，则b的值是（）A.0B.-2C.2D.-0.53.若函数广（2-m）是关于x的正比例函数，则常数m的值等于（）A.±2B.-2C.±V3D.~V34.下列说法正确的是（）A.圆面积公式S=nr2中，S与r成正比例关系B・三角形面积公式S=lah中，当S是常量时，a与h成反比例关系2°y皂+i中，y与x成反比例关系XD・中，y与x成正比例关系25.下列各选项中的y与x的关系为正比例函数的是（）A.正方形周长y（厘米）和它的边长x（厘米）的关系B.圆的面积y（平方厘米）与半径x（厘米）的关系C.如果直角三角形中一个锐角的度数为x,那么另一个锐角的度数y与x间的关系D.一棵树的高度为60厘米，每个月长高3厘米，x月后这棵的树高度为y厘米6.若函数y=（m-3）x'®'*是正比例函数，则m值为（）A.3B.-3C.±37.已知正比例函数y=（k-2）x+k+2的k的取值正确的是（）A.k=2B.k^2C.k=-28.已知正比例函数）=1«（kOO）的图象如图所示，则在下列选项中k值可能是（）A.1B.2C.39.如图所示，在同一直角坐标系中，一次函数y=Mx、y=k2x>y=k3x>y=k」x的图象分别为£、12>13>1」，则下列关系中正确的是（）A.ki<k2<k3<k4B.k2<ki<k4<k3C.ki<k2<k4<k3D.k2<ki<k3<k410,在直角坐标系中，既是正比例函数尸=1«,又是y的值随X的增大而减小的图象是（）A. B.J,/ C.J'| D.二.填空题（每小题3分，共27分。
正比例函数性质
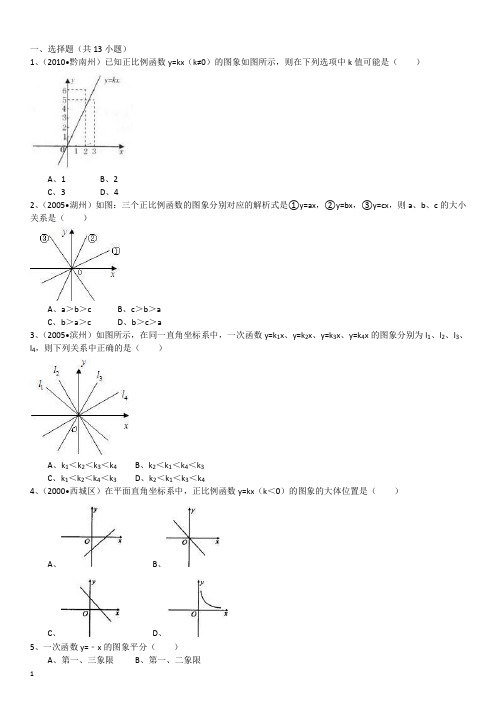
一、选择题（共13小题）1、（2010•黔南州）已知正比例函数y=kx（k≠0）的图象如图所示，则在下列选项中k值可能是（）A、1B、2C、3D、42、（2005•湖州）如图：三个正比例函数的图象分别对应的解析式是①y=ax，②y=bx，③y=cx，则a、b、c的大小关系是（）A、a＞b＞cB、c＞b＞aC、b＞a＞cD、b＞c＞a3、（2005•滨州）如图所示，在同一直角坐标系中，一次函数y=k1x、y=k2x、y=k3x、y=k4x的图象分别为l1、l2、l3、l4，则下列关系中正确的是（）A、k1＜k2＜k3＜k4B、k2＜k1＜k4＜k3C、k1＜k2＜k4＜k3D、k2＜k1＜k3＜k44、（2000•西城区）在平面直角坐标系中，正比例函数y=kx（k＜0）的图象的大体位置是（）A、B、C、D、5、一次函数y=﹣x的图象平分（）A、第一、三象限B、第一、二象限C、第二、三象限D、第二、四象限6、在平面直角坐标系中，一次函数y=2x+1的图象不经过（）A、第一象限B、第二象限C、第三象限D、第四象限7、在直角坐标系中，既是正比例函数y=kx，又是y的值随x的增大而减小的图象是（）A、B、C、D、8、（2011•湘西州）当k＞0时，正比例函数y=kx的图象大致是（）A、B、C、D、9、已知正比例函数y=kx+b的值随着x的增大而减小，则大致图象为（）A、B、C、D、10、已知正比例函数y=kx （k≠0），当x=﹣1时，y=﹣2，则它的图象大致是（）A、B、C、D、11、如图所示函数图象中，正比例函数的图象是（）A、B、C、D、12、正比例函数y=kx的图象是经过原点的一条（）A、射线B、双曲线C、线段D、直线13、结合函数y=﹣2x的图象回答，当x＜﹣1时，y的取值范围（）A、y＜2B、y＞2C、y≥D、y≤二、填空题（共1小题）14、正比例函数的图象是_________，当k＞0时，直线y=kx过第_________象限，y随x的增大而_________．答案与评分标准一、选择题（共13小题）1、（2010•黔南州）已知正比例函数y=kx（k≠0）的图象如图所示，则在下列选项中k值可能是（）A、1B、2C、3D、4考点：正比例函数的图象。
4.3 正比例函数的图像与性质 同步作业(含答案)
正比例函数的图像与性质1．[2018·陕西]如图，在矩形AOBC 中，A (－2，0)，B (0，1)．若正比例函数y ＝kx 的图象经过点C ，则k 的值为( )A ．－12 B.12 C ．－2 D ．22．关于正比例函数y ＝－2x ，下列说法正确的是( )A ．图象必经过点(－1，－2)B ．图象经过第一、三象限C ．y 随x 的增大而减小D ．不论x 取何值，总有y ＜03．已知正比例函数y ＝kx (k <0)的图象上两点A (x 1，y 1)，B (x 1，y 2)，且x 1<x 2，则下列不等式中恒成立的是( )A ．y 1＋y 2>0B ．y 1＋y 2<0C ．y 1－y 2>0D ．y 1－y 2<04．如图，三个正比例函数的图象分别对应表达式：①y ＝ax ；②y ＝bx ；③y ＝cx .将a ，b ，c 从小到大排列并用“＜”连接为_________．5．在正比例函数y ＝－3mx 中，函数y 的值随x 值的增大而增大，则P (m ，5)在第____象限． 6．已知正比例函数的图象经过点(－1，2)． (1)求此正比例函数的表达式； (2)点(2，－5)是否在此函数的图象上？7．在同一直角坐标系上画出函数y ＝2x ，y ＝－13x ，y ＝－0.6x 的图象．8．在如图所示的平面直角坐标系中，点P 是直线y ＝x 上的动点，A (1，0)，B (2，0)是x 轴上的两点，则P A ＋PB 的最小值为________．9．已知正比例函数y ＝(m ＋2)x 中，y 的值随x 的增大而增大，而正比例函数y ＝(2m －3)x 中，y 的值随x 的增大而减小，且m 为整数，你能求出m 的可能值吗？为什么？10．[2018·贵港]如图，直线l 为y ＝3x ，过点A 1(1，0)作A 1B 1⊥x 轴，与直线l 交于点B 1，以原点O 为圆心，OB 1长为半径画弧交x 轴于点A 2；再作A 2B 2⊥x 轴，交直线l 于点B 2，以原点O 为圆心，OB 2的长为半径画弧交x 轴于点A 3；…，按此作法进行下去，则点An 的坐标为__________．参考答案1．A2．C3．C4．a＜c＜b5．二6．解：(1)y＝－2x；(2)点(2，－5)不在此函数的图象上．7．解：列表如下：画出图象如下：答图8． 5答图【解析】如答图，作A点关于直线y＝x的对称点A′，连接A′B，交直线y＝x于点P，此时P A＋PB最小，由题意可得OA′＝1，BO＝2，P A′＝P A，此时，P A＋PB＝A′B＝12＋22＝ 5.9．解：m 的可能值为－1，0，1.理由如下：∵正比例函数y ＝(m ＋2)x 中，y 的值随x 的增大而增大， ∴m ＋2＞0，解得m ＞－2.∵正比例函数y ＝(2m －3)x 中，y 的值随x 的增大而减小， ∴2m －3＜0，解得m ＜32，∴－2<m <32.∵m 为整数，∴m 的可能值为－1，0，1. 10． (2n －1，0)【解析】 直线y ＝3x ，点A 1坐标为(1，0)，过点A 1作x 轴的垂线交直线l 于点B 1，可知B 1点的坐标为(1，3)，以原点O 为圆心，OB 1长为半径画弧交x 轴于点A 2，OA 2＝OB 1，所以OA 2＝12＋（3）2＝2，因此点A 2的坐标为(2，0)，同理，可求得点B 2的坐标为(2，23)，故点A 3的坐标为(4，0)，B 3(4，43)，…，所以An 的坐标为(2n －1，0)。
4.3.1 正比例函数的图象和性质 湘教版数学八年级下册同步练习(含答案)
4.3 一次函数的图象1 正比例函数的图象和性质要点感知1画函数图象的步骤：(1)__________；(2)__________：建立直角坐标系，以__________为横坐标，__________为纵坐标，确定点的坐标；(3)__________.预习练习1-1下面所给点的坐标满足y=-2x的是( )A.(2，-1)B.(-1，2)C.(1，2)D.(2，1)要点感知2 正比例函数y=kx(k为常数，k≠0)的图象是一条__________，因此画正比例函数图象时，只要描出图象上的__________，然后过两点作一条直线即可，这条直线叫作“直线__________”.预习练习2-1 如图，某正比例函数的图象过点M(-2，1)，则此正比例函数表达式为( )A.y=-xB.y=xC.y=-2xD.y=2x要点感知3 正比例函数图象的性质：直线y=kx(k≠0)是一条经过________的直线.当k>0时,直线y=kx经过第_______象限，从左到右，y随x的增大而________；当k<0时，直线y=kx经过第_____象限，从左到右，y随x的增大而________.知识点1 画正比例函数的图象1.正比例函数y=3x的大致图像是( )2.已知正比例函数y=x，请在平面直角坐标系中画出这个函数的图象.知识点2 正比例函数的图象与性质3.已知函数y=kx的函数值随x的增大而增大，则函数的图象经过( )A.第一、二象限B.第一、三象限C.第二、三象限D.第二、四象限4.对于函数y=-k2x(k是常数，k≠0)的图象，下列说法不正确的是( )A.其函数图象是一条直线B.其函数图象过点(，-k)C.其函数图象经过一、三象限D.y随着x增大而减小5.正比例函数y=-x的图象平分( )A.第一、三象限B.第一、二象限C.第二、三象限D.第二、四象限6.函数y=-5x的图象在第__________象限内，y随x的增大而__________.知识点3 实际问题中的正比例函数7.一根蜡烛长20 cm，点燃后每小时燃烧5 cm，则蜡烛燃烧的长度y(cm)与燃烧时间x(h)的函数关系用图象表示为下图中的( )8.小明用16元零花钱购买水果，已知水果单价是每千克4元，设买水果x千克用去的钱为y元，(1)求买水果用去的钱y(元)随买水果的数量x(千克)而变化的函数表达式；(2)画出这个函数的图象.9.已知正比例函数y=kx(k≠0)，当x=1时，y=-2，则它的图象大致是( )10.已知正比例函数y=(3k-1)x，若y随x的增大而增大，则k的取值范围是( )A.k＜0B.k＞0C.k＜D.k＞11.若点A(-2，m)在正比例函数y=-x的图象上，则m的值是( )A. B.- C.1 D.-112.已知正比例函数y=kx(k<0)的图象上两点A(x1，y1)、B(x2，y2)，且x1<x2，则下列不等式中恒成立的是( )A.y1+y2>0B.y1+y2<0C.y1-y2>0D.y1-y2<013.甲、乙两人在一次百米赛跑中，路程s(米)与赛跑时间t(秒)的关系如图所示，则下列说法正确的是( )A.甲、乙两人的速度相同B.甲先到达终点C.乙用的时间短D.乙比甲跑的路程多14.写出一个图像经过一、三象限的正比例函数y=kx(k≠0)的解析式(关系式)：_______________.15.当m=__________时，函数y=mx3m+4是正比例函数，此函数y随x的增大而__________.16.如图，正比例函数y=kx，y=mx，y=nx在同一平面直角坐标系中的图象如图所示.则系数k，m，n的大小关系是__________.17.已知正比例函数y=(k-2)x.(1)若函数图象经过第二、四象限，则k的范围是什么？(2)若函数图象经过第一、三象限，则k的范围是什么？18.已知正比例函数图象经过点(-1，2).(1)求此正比例函数的表达式;(2)画出这个函数图象;(3)点(2，-5)是否在此函数图象上？(4)若这个图象还经过点A(a，8)，求点A的坐标.19.已知正比例函数y=kx经过点A，点A在第四象限，过点A作AH⊥x轴，垂足为点H，点A的横坐标为3，且△AOH的面积为3.(1)求正比例函数的表达式；(2)在x轴上能否找到一点P，使△AOP的面积为5？若存在，求点P的坐标；若不存在，请说明理由.参考答案要点感知1（1）列表（2）描点自变量值相应的函数值（3）连线预习练习1-1B要点感知2 直线两点y=kx预习练习2-1A要点感知3 原点一、三上升增大二、四下降减少1.B2.图略.3.B4.C5.D6.二、四减小7.A8.(1)根据题意可得y=4x(0≤x≤4).(2)当x=0时，y=0；当x=4时，y=16.在平面直角坐标系中画出两点O(0，0)，A(4，16)，过这两点作线段OA，线段OA即函数y=4x(0≤x≤4)的图象，如图.9.A 10.D 11.C 12.C 13.B 14.y=3x(答案不唯一) 15.-1减小16.k＞m＞n 17.(1)k-2＜0，∴k＜2；(2)k-2>0，∴k>2.18.(1)设函数的表达式为：y=kx，则-k=2，即k=-2.故正比例函数的表达式为：y=-2x.(2)图象图略.(3)将点(2，-5)代入，左边=-5，右边=-4，左边≠右边，故点(2，-5)不在此函数图象上.(4)把(a，8)代入y=-2x，得8=-2a.解得a=-4.故点A的坐标是(-4，8).19.(1)∵点A的横坐标为3，且△AOH的面积为3，∴点A的纵坐标为-2，点A的坐标为(3，-2).∵正比例函数y=kx经过点A，∴3k=-2.解得k＝-.∴正比例函数的表达式是y＝-x.(2)∵△AOP的面积为5，点A的坐标为(3，-2)，∴OP=5.∴点P的坐标为(5，0)或(-5，0).。
中考数学《正比例函数图像和性质》专项练习题及答案
中考数学《正比例函数图像和性质》专项练习题及答案一、单选题1．若正比例函数的图象经过点（﹣1，2），则这个图象必经过点（ ）A ．（1，2）B ．（﹣1，﹣2）C ．（2，﹣1）D ．（1，﹣2）2．若正比例函数y=（1-2m ）x 的图象经过点A （x 1，y 1）和点B （x 2，y 2），当x 1＜x 2时，y 1＞y 2，则m的取值范围是（ ） A ．m ＞0B ．m ＜0C ．m ＜12D ．m ＞123．已知正比例函数 y =mx(m <0) 图象上有两点 P(x 1，y 1) ， Q(x 2，y 2) 且 x 1<x 2 ，则 y 1与 y 2 的大小关系是（ ） A ．y 1>y 2B ．y 1<y 2C ．y 1=y 2D ．不能确定4．正比例函数y ＝3x 的图象必经过点（ ）A ．（﹣1，﹣3）B ．（﹣1，3）C ．（1，﹣3）D ．（3，1）5．已知正比例函数y=(m-1)x ，若y 随x 增大而增大，则点（m ，1-m ）所在的象限是（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限6．正比例函数y=kx （k ≠0）的函数值y 随着x 增大而减小，则一次函数y=x+k 的图象大致是（ ）A ．B ．C ．D ．7．若函数y=kx 的图象经过点(1，-2)，那么该图象一定经过点( )A ．(2，-1)B ．（ −12，1）C ．(-2，1)D ．(1， 12)8．若正比例函数y ＝（m ﹣2）x 的图象经过点A(x 1，y 1)和点B(x 2，y 2)，当x 1＜x 2时，y 1＞y 2，则m 的取值范围是（ ） A ．m ＞0B ．m ＜0C ．m ＞2D ．m ＜29．正比例函数y＝2x与反比例函数y＝2x的图象或性质的共有特征之一是（）A．函数值y随x的增大而增大B．图象在第一、三象限都有分布C．图象与坐标轴有交点D．图象经过点（2，1）10．若一个正比例函数y=mx的图像经过P（4，-8），Q（m，n）两点，则n的值为（）A．1B．8C．-2D．411．对于正比例函数y＝kx，当自变量x的值增加3时，对应的函数值y减少6，则k的值为（）A．2B．﹣2C．﹣3D．﹣0.512．如图，在平面直角坐标系中，点A的坐标为(0，6)，沿x轴向右平移后得到A'，A点的对应点A'在直线y=35x上，则点B与其对应点B'之间的距离为（）A．4B．6C．8D．10二、填空题13．函数y= 1m−2 x中,如果y随x的增大而减小,那么m的取值范围是.（1）线段B1B2的长度为；（2）点A2022的坐标为；（3）线段B2021B2022的长度为．15．写出一个实数k的值，使得正比例函数y=kx的图象在二、四象限．16．正比例函数y=（m﹣2）x m的图象的经过第象限，y随着x的增大而．17．若正比例函数y=（m﹣2）x的图象经过一、三象限，则m的取值范围是．18．函数y=kx与y=6−x的图像如图所示，则k=．三、综合题19．已知正比例函数y=kx．（1）若函数图象经过第二、四象限，则k的范围是什么？（2）点（1，﹣2）在它的图象上，求它的表达式．20．已知正比例函数y=kx经过点A(−1,4) .（1）求正比例函数的表达式；（2）将（1）中正比例函数向下平移5个单位长度后得到的函数表达式是．21．已知正比例函数y=kx图象经过点（3，﹣6），求：（1）求这个函数解析式．（2）画出这个函数图象．（3）判断点A（4，﹣2）、点B（﹣1.5，3）是否在这个函数图象上（4）图象上的两点C（x1，y1）、D（x2，y2），如果x1＞x2，比较y1、y2的大小．22．如图，它表示甲乙两人从同一个地点出发后的情况．到十点时，甲大约走了13千米．根据图象回答：（1）甲是几点钟出发？（2）乙是几点钟出发，到十点时，他大约走了多少千米？ （3）到十点为止，哪个人的速度快？ （4）两人最终在几点钟相遇？23．已知函数y=（m+3）x m2+2m−2．（1）当m 为何值时，它是正比例函数？ （2）当m 为何值时，它是反比例函数？ （3）当m 为何值时，它是二次函数？24．一水果经销商购进了A ，B 两种水果各10箱，分配给他的甲、乙两个零售店（分别简称甲店、乙店）销售，预计每箱水果的盈利情况如下表：A 种水果/箱B 种水果/箱甲店11元 17元 乙店9元13元5箱，B 种水果两店各5箱，请你计算出经销商能盈利多少元？（2）在甲、乙两店各配货10箱（按整箱配送），且保证乙店盈利不小于100元的条件下，请你设计出使水果经销商盈利最大的配货方案，并求出最大盈利为多少？参考答案1．【答案】D2．【答案】D3．【答案】A4．【答案】A5．【答案】D6．【答案】A7．【答案】B8．【答案】D9．【答案】B10．【答案】D11．【答案】B12．【答案】D13．【答案】m＜214．【答案】（1）√3（2）A2021A2022=22020 （3）22020√315．【答案】-216．【答案】二、四；减小17．【答案】m＞218．【答案】219．【答案】（1）解：∵函数图象经过第二、四象限∴k＜0.（2）解：当x=1，y=﹣2时，则k=﹣2 即：y=﹣2x．20．【答案】（1）解：将点A(−1,4)代入y=kx，得4=−k，即k=−4．故函数解析式为：y=−4x（2）y=−4x−521．【答案】（1）解：将点（3，﹣6）代入y=kx得，﹣6=3k解得，k=﹣2函数解析式为y=﹣2x；（2）解：如图：函数过（0，0），（1，﹣2）．（3）解：将点A（4，﹣2）、点B（﹣1.5，3）分别代入解析式得，﹣2≠﹣2×4；3=﹣2×（﹣1.5）；故点A不在函数图象上，点B在函数图象上．（4）解：由于k=﹣2＜0，故y随x的增大而减小，可得y1＜y2．22．【答案】（1）解：甲8点出发（2）解：乙9点出发；到10时他大约走了13千米（3）解：到10时为止，乙的速度快（4）解：两人最终在12时相遇23．【答案】（1）解：当函数y=（m+3）x m2+2m−2是正比例函数∴m2+2m﹣2=1且m+3≠0解得：m1=﹣3（舍去），m2=1则m=1时，它是正比例函数；（2）解：当函数y=（m+3）x m2+2m−2是反比例函数∴m2+2m﹣2=﹣1且m+3≠0解得：m1=﹣1+√2，m2=﹣1﹣√2则m=﹣1±√2时，它是反比例函数；（3）解：当函数y=（m+3）x m 2+2m−2是二次函数 ∴m 2+2m ﹣2=2 且m+3≠0解得：m 1=﹣1+√5，m 2=﹣1﹣√5 则m=﹣1±√5时，它是二次函数．24．【答案】（1）解：经销商能盈利=5×11+5×17+5×9+5×13=5×50=250（2）解：设甲店配A 种水果x 箱，则甲店配B 种水果（10﹣x ）箱 乙店配A 种水果（10﹣x ）箱，乙店配B 种水果10﹣（10﹣x ）=x 箱． ∵9×（10﹣x ）+13x ≥100∴x ≥2 12经销商盈利为w=11x+17•（10﹣x ）+9•（10﹣x ）+13x=﹣2x+260． ∵﹣2＜0∴w 随x 增大而减小 ∴当x=3时，w 值最大．甲店配A 种水果3箱，B 种水果7箱．乙店配A 种水果7箱，B 种水果3箱．最大盈利：﹣2×3+260=254（元）．。
第1课时正比例函数的图象及性质练习试题(含答案解析)
WORD格式.整理版第1课时正比例函数的图象和性质一．选择题（共10小题）y=3．若函数是关于x的正比例函数，则常数m的值等于（）Dah中，中，8题图 9题图9．如图所示，在同一直角坐标系中，一次函数y=k1x、y=k2x、y=k3x、y=k4x的图象分别为l1、l2、l3、l4，则下列B C D11．若函数y﹦（m+1）x+m2﹣1是正比例函数，则m的值为_________ ．14．请写出直线y=6x 上的一个点的坐标： _________ ．15．已知正比例函数y=kx （k≠0），且y 随x 的增大而增大，请写出符合上述条件的k 的一个值： _________ ．16．已知正比例函数y=（m ﹣1）的图象在第二、第四象限，则m 的值为 _________ ．17．若p 1（x 1，y 1） p 2（x 2，y 2）是正比例函数y=﹣6x 的图象上的两点，且x 1＜x 2，则y 1，y 2的大小关系是：y 1 _________ y 2．点A （-5，y 1）和点B （-6，y 2）都在直线y= -9x 的图像上则y 1__________ y 218．正比例函数y=（m ﹣2）x m 的图象的经过第 _________ 象限，y 随着x 的增大而 _________ ．19．函数y=﹣7x 的图象在第 _________ 象限内，经过点（1， _________ ），y 随x 的增大而 _________ ．三．解答题（共3小题）20．已知：如图，正比例函数的图象经过点P 和点Q （﹣m ，m+3），求m 的值．21．已知y+2与x ﹣1成正比例，且x=3时y=4．（1）求y 与x 之间的函数关系式；（2）当y=1时，求x 的值．22．已知y=y 1+y 2，y 1与x 2成正比例，y 2与x ﹣2成正比例，当x=1时，y=5；当x=﹣1时，y=11，求y 与x 之间的函数表达式，并求当x=2时y 的值．23. 为缓解用电紧张矛盾，某电力公司特制定了新的用电收费标准，每月用电量()x kW h 与应付饱费y （元)的关系如图所示。
正比例函数图像及性质
WORD 格式整理版正比例函数的图像和性质知识精要1.正比例函数的图像一般地，正比例函数 y=kx（k 是常数， k 0）的图像是经过原点 O(0,0) 和点 M（1，k）的一条直线。
我们把正比例函数 y=kx 的图像叫做直线 y=kx。
2.正比例函数性质精讲名题x m 3例 1. 若函数 y=(m-1)是正比例函数，则m=,函数的图像经过象限。
解:m=4, 图像经过第一、三象限。
例 2. 已知 y-1 与 2x 成正比例，当 x=-1 时， y=5, 求 y 与 x 的函数解析式。
解：∵ y-1 与 2x 成正比例∴设y-1=k ·2x （k0 ）把x=-1,y=5代入，得k=-2,∴ y-1=-2·2x∴y=-4x+1例 3. 已知 y 与 x 的正比例函数，且当x=6 时 y=-2WORD 格式整理版(1)求出这个函数的解析式；(2)在直角坐标平面内画出这个函数的图像；(3)如果点 P（a， 4）在这个函数的图像上，求 a 的值；(4)试问，点 A（-6 ， 2）关于原点对称的点 B 是否也在这个图像上？解： (1)设 y=k·x （ k 0）当 x=6 时， y=-2 ∴-2=6k ∴k 1∴这个函数的解析式为 y1x 33(2)y 1x 的定义域是一切实数，图像如图所示：3(3)如果点 P（a， 4）在这个函数的图像上，∴41a ，∴a=-12 3(4)点 A（-6 ，2）关于原点对称的点 B 的坐标（ 6，-2 ），当 x=6 时， y=162因此，点 B 也在直线y 1x 上33例 4. 已知点 ( x1, y1 ) ，( x2, y2 ) 在正比例函数 y=(k-2)x的图像上，当x1x2时， y1y2，那么k 的取值范围是多少？解：由题意，得函数y 随 x 的值增大而减小，∴k-2<0, ∴k<2例 5. （1）已知 y=ax 是经过第二、四象限的直线，且 a 3 在实数范围内有意义，求 a 的取值范围。
中考数学-一次函数正比例函数的图像及性质(含答案)专题练习
中考数学-一次函数正比例函数的图像及性质（含答案）专题练习一、单选题1.已知正比例函数y=kx（k≠0），点（2，-3）在函数上，则y随x的增大而（）A. 增大B. 减小C. 不变D. 不能确定2.已知函数y=x+k+1是正比例函数，则k的值为（）A.1B.﹣1C.0D.±13.正比例函数y=（2k+1）x，若y随x增大而减小，则k的取值范围是（）A. k＞﹣B. k＜﹣C. k=D. k=04.若正比例函数y=kx的图象经过点A（k，9），且经过第一、三象限，则k的值是（）A. ﹣9B. ﹣3C. 3D. ﹣3或35.若正比例函数y＝(1－2m)x的图象经过点A(x1，y1)和点B(x2，y2)，当x1< x2时，y1>y2，则m的取值范围是（）A. m<0B. m>0C.D.6.在下列四组点中，可以在同一个正比例函数图象上的一组点是（）A. （2，﹣3），（﹣4，6）B. （﹣2，3），（4，6）C. （﹣2，﹣3），（4，﹣6）D. （2，3），（﹣4，6）7.正比例函数y=kx（k≠0）的图像在第二、四象限，则一次函数y=x+k的图像大致是（）A. B. C. D.8.下列点不在正比例函数y=﹣2x的图象上的是（）A. （5，﹣10）B. （0，0）C. （2，﹣1）D. （1，﹣2）9.正比例函数y=（2k+1）x，若y随x增大而减小，则k的取值范围是（）A. k＞﹣B. k＜﹣C. k=D. k=010.关于函数y=﹣x，下列结论正确的是（）A. 函数图象必过点（﹣2，﹣1）B. 函数图象经过第1、3象限C. y随x的增大而减小D. y随x的增大而增大11.下列式子中，表示y是x的正比例函数的是（）A.y=x﹣1B.y=2xC.y=2x2D.y2=2x12.下列变量之间关系中，一个变量是另一个变量的正比例函数的是（）A. 正方形的面积S随着边长x的变化而变化B. 正方形的周长C随着边长x的变化而变化C. 水箱有水10L，以0.5L/min的流量往外放水，水箱中的剩水量V（L）随着放水时间t（min）的变化而变化D. 面积为20的三角形的一边a随着这边上的高h的变化而变化13.P1（x1，y1），P2（x2，y2）是正比例函数图象上的两点，下列判断中，正确的是A. y1＞y2B. y1＜y2C. 当x1＜x2时，y1＜y2D. 当x1＜x2时，y1＞y214.下列四个点中，在正比例函数的图象上的点是（）A. （2，5）B. （5，2）C. （2，—5）D. （5，—2）15.若正比例函数的图象经过点（2，﹣3），则这个图象必经过点（）A. （﹣3，﹣2）B. （2，3）C. （3，﹣2）D. （﹣2，3）16.下列关系中，是正比例关系的是（）A. 当路程s一定时，速度v与时间tB. 圆的面积S与圆的半径RC. 正方体的体积V与棱长aD. 正方形的周长C与它的一边长a17.下列问题中，两个变量成正比例关系的是（）A. 等腰三角形的面积一定，它的底边和底边上的高B. 等边三角形的面积与它的边长C. 长方形的长确定，它的周长与宽D. 长方形的长确定，它的面积与宽18.下列各点中，在正比例函数y＝－2x图象上的是（）A. （－2，－1）B. （1，2）C. （2，－1）D. （1，－2）19.一次函数y=4x，y=﹣7x，y=的共同特点是（）A. 图象位于同样的象限B. y随x增大而减小C. y随x增大而增大D. 图象都过原点二、填空题20.已知正比例函数y=kx（k是常数，k≠0），y随x的增大而减小，写出一个符合条件的k的值为________．21.写出一个正比例函数，使其图象经过第二、四象限：________．22.若函数y=（2m+6）x+（1﹣m）是正比例函数，则m的值是________．23.写一个图象经过第二、四象限的正比例函数：________24.将正比例函数y＝2x的图象向上平移3个单位，所得的直线不经过第________象限．答案解析部分一、单选题1.已知正比例函数y=kx（k≠0），点（2，-3）在函数上，则y随x的增大而（）A. 增大B. 减小C. 不变D. 不能确定【答案】B【考点】正比例函数的图象和性质【解析】【解答】∵点（2，-3）在正比例函数y=kx（k≠0）上，∴函数图象经过二四象限，∴y随着x的增大而减小，故选B【分析】首先根据函数的图象经过的点的坐标确定函数的图象经过的象限，然后确定其增减性即可2.已知函数y=x+k+1是正比例函数，则k的值为（）A.1B.﹣1C.0D.±1【答案】B【考点】正比例函数的图象和性质【解析】【解答】解：由题意，得k+1=0，解得k=﹣1，故选：B．【分析】根据正比例函数的定义，可得答案．3.正比例函数y=（2k+1）x，若y随x增大而减小，则k的取值范围是（）A. k＞﹣B. k＜﹣C. k=D. k=0 【答案】B【考点】正比例函数的图象和性质【解析】【解答】解：∵正比例函数y=（2k+1）x中，y的值随自变量x的值增大而减小，∴2k+1＜0，解得，k＜﹣；故选B．【分析】根据正比例函数图象与系数的关系列出关于k的不等式2k+1＜0，然后解不等式即可．4.若正比例函数y=kx的图象经过点A（k，9），且经过第一、三象限，则k的值是（）A. ﹣9B. ﹣3C. 3D. ﹣3或3 【答案】C【考点】正比例函数的图象和性质【解析】【解答】解：∵正比例函数y=kx（k≠0）的图象经过第一、三象限∴k＞0，把（k，9）代入y=kx得k2=9，解得k1=﹣3，k2=3，∴k=3，故选C．【分析】根据正比例函数的性质得k＞0，再把（k，9）代入y=kx得到关于k的一元二次方程，解此方程确定满足条件的k的值．5.若正比例函数y＝(1－2m)x的图象经过点A(x1，y1)和点B(x2，y2)，当x1< x2时，y1>y2，则m的取值范围是（）A. m<0B. m>0C.D.【答案】D【考点】正比例函数的图象和性质【解析】【分析】由题目所给信息“当x1＜x2时，y1＞y2”可以知道，y随x的增大而减小，则由一次函数性质可以知道应有：1-2m＜0，进而可得出m的取值范围．【解答】由题目分析可知：在正比例函数y=（1-2m)x中，y随x的增大而减小由一次函数性质可知应有：1-2m＜0，即-2m＜-1，解得：m＞．【点评】此题主要考查了一次函数的图象性质，只有掌握它的性质才能灵活运用．6.在下列四组点中，可以在同一个正比例函数图象上的一组点是（）A. （2，﹣3），（﹣4，6）B. （﹣2，3），（4，6）C. （﹣2，﹣3），（4，﹣6）D. （2，3），（﹣4，6）【答案】A【考点】正比例函数的图象和性质【解析】【分析】根据正比例函数关系式y=kx，可得k=，再依次分析各选项即可判断。
正比例函数(六大类型)(题型专练)(原卷版)
专题12 正比例函数（六大类型）【题型一：正比例函数的定义】【题型二：判断正比例函数图像所在象限】【题型三：正比例函数的性质】【题型四：判断正比例函数的比例系数大小】【题型五：待定系数法求正比例函数解析式】【题型六：正比例函数的图像性质综合】【题型一：正比例函数的定义】1．下列函数中，是正比例函数的是（）A．B．y＝x2C．y＝2x D．y＝2x﹣1 2．下列函数中，表示y是x的正比例函数的是（）A．y＝﹣0.1x B．y＝2x2C．y2＝4x D．y＝2x+1 3．下列关系中，属于成正比例函数关系的是（）A．正方形的面积与边长B．三角形的周长与边长C．圆的面积与它的半径D．速度一定时，路程与时间4．若y＝（m﹣2）x+（m2﹣4）是正比例函数，则m的取值是（）A．2B．﹣2C．±2D．任意实数5．正比例函数的比例系数为（）A．﹣2B．C．D．26．函数y＝（m﹣n+1）x|n﹣1|+n﹣2是正比例函数，则m，n应满足的条件是（）A．m≠﹣1，且n＝0 B．m≠1，且n＝0C．m≠﹣1，且n＝2D．m≠1，且n＝27．已知函数y＝（m﹣1）x+m2﹣1是正比例函数，则m＝﹣1．8．若y＝2x+m2﹣1是正比例函数，则m＝±1．【题型二：判断正比例函数图像所在象限】9．正比例函数y＝的图象经过的象限是（）A．第一、三象限B．第二、四象限C．第三、四象限D．第一、二象限10．正比例函数的图象经过的象限是（）A．第一、三象限B．第一、二象限C．第二、四象限D．第三、四象限11．一次函数y＝8x的图象经过的象限是（）A．一、三B．二、四C．一、三、四D．二、三、四12．已知函数y＝（m﹣2）是关于x的正比例函数，且其图象经过第二、四象限，则m的值是．13．请写出一个图象经过第一、三象限的正比例函数的解析式．【题型三：正比例函数的性质】14．下列函数中，函数值y随x的增大而增大的有（）①y＝x②y＝﹣x③y＝﹣5x﹣2④y＝4x+1A．1个B．2个C．3个D．4个15．关于直线y＝﹣2x，下列结论正确的是（）A．图象必过点（1，2）B．图象经过第一、三象限C．与y＝﹣2x+1平行D．y随x的增大而增大16．对于函数y＝4x，下列说法正确的是（）A．当x＞0时，y随x的增大而减小B．当x＜0时，y随x的增大而减小C．y随x的增大而减小D．y随x的增大而增大17．P1（﹣2，y1），P2（7，y2）是正比例函数y＝kx（k＞0）的图象上的两个点，则y1，y2的大小关系是（）A．y1＞y2B．y1＜y2C．y1＝y2D．不能确定18．点A（1，m）在函数y＝2x的图象上，则m的值是（）A．1B．2C．D．019．已知：函数y1＝2x，y2＝﹣x+3，若x＜1，则y1y2（填“＞”或“＝”或“＜”）．【题型四：判断正比例函数的比例系数大小】20．如图，三个正比例函数的图象分别对应表达式：①y＝ax，②y＝bx，③y＝cx，将a，b，c从小到大排列为（）A．a＜b＜c B．a＜c＜b C．b＜a＜c D．c＜b＜a 21．如图，三个正比例函数的图象对应的解析式为①y＝ax，②y＝bx，③y＝cx，则a、b、c的大小关系是（）A．a＞b＞c B．c＞b＞a C．b＞a＞c D．b＞c＞a 22．如图，三个正比例函数的图象分别对应的解析式是：①y＝ax，②y＝bx，③y＝cx，请用“＞”表示a，b，c的不等关系．23．如图，正比例函数y＝kx，y＝mx，y＝nx在同一平面直角坐标系中的图象如图所示．则比例系数k，m，n的大小关系是．（按从大到小的顺序用“＞”连接）24．如图，三个正比例函数的图象分别对应表达式：①y＝ax，②y＝bx，③y＝cx，将a，b，c从小到大排列并用“＜”连接为．【题型五：待定系数法求正比例函数解析式】25．已知y＝（2m﹣1）x是正比例函数，且y随x的增大而减小，那么这个函数的解析式为（）A．y＝﹣5x B．y＝5x C．y＝3x D．y＝﹣3x26．已知y与x成正比例，当x＝4时，y＝3，则y与x之间的函数关系式为，将这个函数的图象向下平移3个单位长度，得到的新图象的函数关系式为．27．正比例函数的图象经过点（1，2），则函数的表达式为．28．已知y与x成正比例，且当x＝2时，y＝﹣3．则当x＝﹣时，y＝．29．已知y与x成正比例关系，当x＝2时，y＝4，求：当x＝﹣3时y的值．30．若y＝（m﹣2）x+m2﹣4是y关于x的正比例函数，求该正比例函数的解析式．31．已知y＝y1+y2，y1与x成正比例，y2与x﹣3成正比例，当x＝﹣1时，y＝4；当x＝1时，y＝8，求y与x之间的函数关系式．【题型六：正比例函数的图像性质综合】32．在物理学中，重力的表达关系式是G＝mg（G代表重力，g代表重力常数10，m代表物体的质量）（1）在这个正比例函数表达式中，是自变量，是因变量．（2）若一个物体的重力为100N，它的质量是kg（3）若甲乙两个物体总质量为9kg，乙的质量是甲的2倍，那么甲物体受到的重力是多少？33．分类讨论思想数学课上，老师要求同学们画函数y＝|x|的图象，小红联想绝对值的性质得y＝x（x≥0）或y＝﹣x（x≤0），于是她很快作出了该函数的图象（如图）．请回答：（1）小红所作的图对吗？如果不对，请你画出正确的函数图象．（2）根据上述的作图方法，请画出函数y＝﹣3|x|的图象．。
正比例函数图像及性质
正比例函数的图像和性质知识精要1.正比例函数的图像一般地，正比例函数y=kx（k是常数，k0≠）的图像是经过原点O(0,0)和点M（1，k）的一条直线。
我们把正比例函数y=kx的图像叫做直线y=kx。
2.正比例函数性质精讲名题例1.若函数y=(m-1)3-mx是正比例函数，则m= ,函数的图像经过象限。
解:m=4,图像经过第一、三象限。
例2.已知y-1与2x成正比例，当x=-1时，y=5,求y与x的函数解析式。
解：∵y-1与2x成正比例∴设y-1=k·2x （k0≠）把x=-1,y=5代入，得k=-2,∴y-1=-2·2x∴y=-4x+1例3.已知y与x的正比例函数，且当x=6时y=-2(1)求出这个函数的解析式；(2)在直角坐标平面内画出这个函数的图像；(3)如果点P （a ，4）在这个函数的图像上，求a 的值；(4)试问，点A （-6，2）关于原点对称的点B 是否也在这个图像上？解：(1) 设y=k ·x （k 0≠）当x=6时，y=-2∴-2=6k ∴31-=k ∴这个函数的解析式为x y 31-=(2) x y 31-=的定义域是一切实数，图像如图所示：(3)如果点P （a ，4）在这个函数的图像上，∴a 314-=，∴a=-12(4)点A （-6，2）关于原点对称的点B 的坐标（6，-2），当x=6时，y=2631-=⨯- 因此，点B 也在直线x y 31-=上例4.已知点(11,y x )，(22,y x )在正比例函数y=(k-2)x 的图像上，当21x x >时，21y y <，那么k 的取值范围是多少？解：由题意，得函数y 随x 的值增大而减小，∴k-2<0,∴k<2例5.（1）已知y=ax 是经过第二、四象限的直线，且3+a 在实数范围内有意义，求a 的取值范围。
（2）已知函数y=(2m+1)x 的值随自变量x 的值增大而增大，且函数y=(3m+1)x 的值随自变量x 的增大而减小，求m 的取值范围。
正比例函数的图象与性质
的图象从左向右下降．
（3）当m <2 时，正比例函数 y=(2小．
(4) 正比例函数 y (2m 1) x 的图象上 的两点 A( x1, y1 ), B( x2 , y2 ) ，当 x1 x2 时， 有 y1 y2 ，求 m 的取值范围．
1、巩固练习：
（1）正比例函数 y 2 x 是一条经
过原点的直线，位于第 一、三 象 限，从左向右上升 ，即随着x 的增 大y也增大 ．
（2）正比例函数y=-5x 是一条经 过 原点 直线，位于第 二、四 象
限，从左向右 下降 ，即随着x的
增大y 减小 ．
2、进阶练习： （1）正比例函数y=(m-4)x ， 当m >4 时，图象过第一、三象限．
比较 y1 、y2 、y3 的大小．
（2）当m
时，正比例函数 y=(2m-4)x
的图象从左向右下降．
（3）当m 时，正比例函数 y=(2m-4)x
中，y 的值随x 的增大而减小．
(4) 正比例函数
y (2m 1) x 的图象上的 两点 A( x1, y1 ), B( x2 , y2 ) ，当 x1 x2 时， 有 y1 y2 ，求 m 的取值范围．
3、拓展练习：
5 已知 A(11, y1 ), B ( , y2 ), C (5, y3 ) 2 在正比例函数 y 6 x 的图象上，试
比较
y3 的大小． y1 、y2 、
思考：
5 已知 A(11, y1 ), B ( , y2 ), C (5, y3 ) 2 在正比例函数 y mx 的图象上，试
4.3 正比例函数的图象及性质 练习题 2021——2022学年北师大版八年级数学上册
3 第1课时 正比例函数的图象及性质【基础练习】知识点 1 正比例函数的图象1.正比例函数y=3x 的大致图象是( )图12.(1)函数y=5x 的图象经过的象限是第 象限;(2)写出一个实数k 的值: ,使得正比例函数y=kx 的图象经过第二、四象限.3.在同一平面直角坐标系中画出下列函数的图象:(1)y=-23x ; (2)y=3x ; (3)y=23x.图2知识点 2 正比例函数图象上点的坐标4.已知正比例函数y=3x 的图象经过点(1,m ),则m 的值为( )A .13B .3C .-13D .-35.点(-2,6)在正比例函数y=kx 的图象上,下列各点在此函数图象上的为( )A .(3,1)B .(-3,1)C .(1,3)D .(-1,3)6.(1)函数y=6x 的图象是经过点(0, )和点( ,6)的一条直线;(2)若正比例函数的图象经过点(-1,4)和(m ,3),则m 的值为 .7.[教材习题4.3第4题变式]已知:如图3,正比例函数的图象经过点P(-1,2)和点Q(-m,m+3).(1)求该函数的表达式;(2)求m的值;(3)判定这个函数的图象必经过(1,-2),(-1,-2),(2,-1),(1,2)中的哪个点.图3知识点3正比例函数的性质8.关于正比例函数y=-3x,下列结论正确的是()A.图象不经过原点B.y随x的增大而增大C.图象经过第二、四象限D.当x=1时,y=139.已知函数y=(a-1)x,且y的值随着x值的增大而增大,那么a的取值范围是()A.a>1B.a<1C.a>0D.a<010.已知(x1,y1)和(x2,y2)是直线y=-3x上的两点,若x1>x2,则y1与y2的大小关系是()A.y1>y2B.y1<y2C.y1=y2D.以上都有可能11.设正比例函数y=mx的图象经过点A(m,4),且y的值随x值的增大而减小,则m的值为()A.2B.-2C.4D.-412.对于关于x的正比例函数y=mx|m|-1,若其图象经过第一、三象限,则m的值为,且y 的值随x值的增大而.13.已知关于x的正比例函数y=(m+2)x.(1)m为何值时,函数图象经过第一、三象限?(2)m 为何值时,y 随x 的增大而减小?(3)m 为何值时,点(1,3)在该函数的图象上?【能力提升】14.设点A (a ,b )是正比例函数y=-32x 图象上的任意一点,则下列等式一定成立的是( )A .2a+3b=0B .2a -3b=0C .3a -2b=0D .3a+2b=0 15.如果一个正比例函数的图象经过不同．．象限的两点A (2,m ),B (n ,3),那么一定有( ) A .m>0,n>0 B .m>0,n<0C .m<0,n>0D .m<0,n<016.若关于x 的正比例函数y=(1-m )x 的图象经过点A (x 1,y 1)和点B (x 2,y 2),当x 1<x 2时,y 1>y 2,则m 的取值范围是( )A .m<0B .m>0C .m<1D .m>117.正比例函数y=kx ,当x 每增加3时,y 就减小2,则k 的值为( )A .32B .-32C .23D .-23 18.如图4,在同一直角坐标系中,正比例函数y=k 1x ,y=k 2x ,y=k 3x ,y=k 4x 的图象分别是l 1,l 2,l 3,l 4,则下列关系正确的是( )图4A .k 1<k 2<k 3<k 4B .k 2<k 1<k 4<k 3C .k 1<k 2<k 4<k 3D .k 2<k 1<k 3<k 419.定义运算“※”为a ※b={ab (b ≥0),-ab (b <0),则函数y=2※x 的图象大致是( )图520.已知正比例函数图象上一点A 到x 轴的距离为4,点A 的横坐标为-2,则这个函数的表达式为 .21.已知正比例函数y=kx (k ≠0),当-3≤x ≤1时,对应的y 的取值范围是-1≤y ≤13,且y 随x 的增大而增大,则k 的值为 .22.已知y 与x 成正比例,当x=1时,y=2.(1)求y 与x 之间的函数关系式;(2)求当x=-1时的函数值;(3)若点(-1,m ),(5,n )在此函数的图象上,比较m ,n 的大小.23.(1)在同一坐标系内画出正比例函数y 1=-2x 与y 2=12x 的图象;(2)请你用量角器度量一下(1)中这两条直线的夹角,你发现这两条直线的位置关系是 ;(3)在平面直角坐标系中,直线y=23x 与直线y=-32x 的位置关系是 ;(4)若直线y=(m -1)x (m 为常数)与直线y=-3x 互相垂直,求m 的值.答案1.B [解析] 因为在y=3x 中,k=3>0,所以图象过原点且经过第一、三象限.故选B .2.(1)一、三 (2)答案不唯一,如-23.解:如图所示.4.B5.D6.(1)0 1 (2)-347.解:(1)设正比例函数的表达式为y=kx.因为它的图象经过点P (-1,2),所以2=-k ,即k=-2.所以正比例函数的表达式为y=-2x.(2)因为正比例函数的图象经过点Q (-m ,m+3),所以m+3=2m.所以m=3.(3)把点(1,-2),(-1,-2),(2,-1),(1,2)的坐标分别代入y=-2x 中,等号成立的点就在正比例函数y=-2x 的图象上,所以这个函数的图象必经过点(1,-2).8.C 9.A 10.B 11.B12.2 增大13.解:(1)因为函数图象经过第一、三象限,所以m+2>0,解得m>-2.(2)因为y 随x 的增大而减小,所以m+2<0,解得m<-2.(3)因为点(1,3)在该函数的图象上,所以m+2=3,解得m=1.14.D [解析] 把点A (a ,b )的坐标代入正比例函数y=-32x 中,可得-32a=b ,即3a+2b=0. 15.D 16.D17.D [解析] 根据题意得y -2=k (x+3),y -2=kx+3k ,而y=kx ,所以3k=-2,解得k=-23.18.B [解析] 对正比例函数的图象来说,当k>0时,k 的值越大,直线与x 轴正半轴所夹的锐角越大,所以k3>k4;当k<0时,k的值越大,直线与x轴负半轴所夹的锐角越小,所以k2<k1.因为正数大于一切负数,所以k2<k1<k4<k3.19.C20.y=2x或y=-2x21.1322.解:(1)设y与x之间的函数关系式为y=kx.将x=1,y=2代入,得k=2,故y与x之间的函数关系式为y=2x.(2)当x=-1时,y=2×(-1)=-2.(3)因为k=2>0,所以y的值随着x值的增大而增大.因为-1<5,所以m<n.23.解:(1)如图.(2)互相垂直(3)互相垂直.(4)由题意可得-3(m-1)=-1,解得m=43。
2020学年八年级数学下册 第十九章19.2.1 正比例函数 第2课时 正比例函数的图象与性质练习
第2课时 正比例函数的图象与性质知识点 1 正比例函数的图象1．正比例函数y ＝2x 的大致图象是( )图19－2－12．经过以下一组点可以画出函数y ＝－3x 的图象的是( ) A ．(0，0)和(3，－1) B ．(1，－3)和(－1，3) C ．(1，3)和(－3，1) D ．(－1，－3)和(1，3)3．若正比例函数y ＝kx 的图象在第二、四象限，则k 的取值可以是( ) A ．1 B ．0或1 C ．±1 D ．－14．[2018·常州]一个正比例函数的图象经过点(2，－1)，则它的解析式为( ) A ．y ＝－2x B ．y ＝2x C ．y ＝－12x D ．y ＝12x5．已知正比例函数y ＝(k ＋1)x 的图象经过第一、三象限，则k 的取值范围是________． 6．已知函数：①y ＝12x ，②y ＝x ，③y ＝2x ，④y ＝－2x .(1)在同一平面直角坐标系中画出各函数的图象；(2)观察这些函数的图象可以发现，随着|k |的增大，直线与y 轴的位置关系有何变化？(k 指比例系数) (3)猜想函数①和④的图象的位置关系．知识点 2 正比例函数的性质7．对于函数y ＝－2x ，下列说法不正确的是( ) A ．它的图象是一条直线 B ．y 随着x 的增大而增大 C ．它的图象过点(－1，2) D ．它的图象经过第二、四象限8．在关于x 的正比例函数y ＝(k －1)x 中，y 随x 的增大而减小，则k 的取值范围是( ) A ．k ＜1 B ．k ＞1 C ．k ≤1 D ．k ≥19．已知正比例函数y ＝kx (k <0)的图象上有两点A (x 1，y 1)，B (x 2，y 2)，且x 1<x 2，则下列不等式中恒成立的是( )A ．y 1＋y 2>0B ．y 1＋y 2<0C ．y 1－y 2>0D ．y 1－y 2<010．若正比例函数y ＝(1－4m )x 的图象经过点A (x 1，y 1)和点B (x 2，y 2)，当x 1<x 2时， y 1＞y 2，则m 的取值范围是( )A ．m ＜0B ．m ＞0C ．m ＜14D ．m ＞1411．[2018·陕西]如图19－2－2，在矩形AOBC 中，A (－2，0)，B (0，1)．若正比例函数y ＝kx 的图象经过点C ，则k 的值为( )图19－2－2A ．－12 B.12C ．－2D ．212．已知正比例函数y ＝3x 的图象经过点A (－1，y 1)，B (－2，y 2)，则y 1________y 2(填“＞”“＜”或“＝”)．13．写出一个图象经过第一、三象限的正比例函数y ＝kx (k ≠0)的解析式：________．14．如图19－2－3，三个正比例函数的图象对应的解析式为：①y ＝ax ，②y ＝bx ，③y ＝cx ，则a ，b ，c 的大小关系是( )A ．a ＞b ＞cB ．c ＞b ＞aC ．b ＞a ＞cD ．b ＞c ＞a图19－2－3 图19－2－415．放学后，小明骑车回家，他经过的路程s (千米)与所用时间t (分)的函数关系如图19－2－4所示，则小明的骑车速度是________千米/分．16．已知正比例函数y ＝kx (k 是常数，k ≠0)，当－3≤x ≤1时，对应的y 的取值范围是－1≤y ≤13，且y 随x 的增大而增大，则k 的值为________．17．已知正比例函数y ＝kx ，当x ＝1时，y ＝2.(1)求正比例函数的解析式； (2)求当x ＝－1时的函数值；(3)当y 的取值范围是0≤y ≤5时，求x 的取值范围．18．2[018·昆明改编]如图19－2－5，点A 的坐标为(4，2)，将点A 绕坐标原点O 旋转90°后，再向左平移1个单位长度得到点A ′，求过点A ′的正比例函数图象的解析式．图19－2－519．如图19－2－6，已知正比例函数y＝kx的图象经过点A，点A在第四象限，过点A作AH⊥x轴，垂足为H，点A的横坐标为3，且△AOH的面积为3.(1)求正比例函数的解析式．(2)在x轴上是否存在一点P，使△AOP的面积为5？若存在，求出点P的坐标；若不存在，请说明理由．图19－2－6拓广探究创新练冲刺满分20．[2018·贵港]如图19－2－7，直线l的解析式为y＝3x，过点A1(1，0)作A1B1⊥x轴，与直线l交于点B1，以原点O为圆心，OB1长为半径画弧交x轴于点A2；再作A2B2⊥x轴，交直线l于点B2，以原点O为圆心，OB2长为半径画弧交x轴于点A3；…；按此作法进行下去，则点A n的坐标为________．图19－2－7教师详解详析1．B 2.B3．D [解析] ∵正比例函数y ＝kx 的图象在第二、四象限，∴k ＜0.故选D. 4．C5．k ＞－1 [解析] ∵正比例函数y ＝(k ＋1)x 的图象经过第一、三象限，∴k ＋1＞0，∴k ＞－1. 6．解：(1)如图：(2)观察这些函数的图象可以发现，随着|k |的增大，直线与y 轴的夹角越来越小． (3)函数①和④的图象互相垂直． 7．B8．A [解析] 由正比例函数的性质可知：当y 随x 的增大而减小时，k －1＜0，即k ＜1.故选A. 9．C10．D [解析] 因为当x 增大时，y 减小，说明函数y 随着x 的增大而减小，则有1－4m ＜0，解得m ＞14.故选D.11．A [解析] 由A (－2，0)，B (0，1)可得C (－2，1)．把点C 的坐标代入y ＝kx ，得－2k ＝1，解得k ＝－12.故选A. 12．>13．y ＝2x (答案不唯一) [解析] ∵正比例函数y ＝kx 的图象经过第一、三象限， ∴k ＞0，当k 取2时可得函数解析式为y ＝2x .14．B [解析] ∵y ＝ax ，y ＝bx ，y ＝cx 的图象都在第一、三象限，∴a ＞0，b ＞0，c ＞0.∵直线越陡，则|k |越大，∴c ＞b ＞a .15．0.2 16.1317．解：(1)将x ＝1，y ＝2代入y ＝kx ，得k ＝2， 故正比例函数的解析式为y ＝2x .(2)当x ＝－1时，y ＝2×(－1)＝－2. (3)∵0≤y ≤5，∴0≤2x ≤5， 解得0≤x ≤52.18．解：当点A 绕坐标原点O 逆时针旋转90°后，再向左平移1个单位长度得到点A ′， 则A ′(－3，4)．设过点A ′的正比例函数图象的解析式为y ＝k 1x ， 则4＝－3k 1， 解得k 1＝－43，则过点A ′的正比例函数图象的解析式为y ＝－43x .同理可得：当点A 绕坐标原点O 顺时针旋转90°后，再向左平移1个单位长度得到点A ″，则A ″(1，－4)． 设过点A ″的正比例函数图象的解析式为y ＝k 2x ， 则k 2＝－4，则过点A ″的正比例函数图象的解析式为y ＝－4x .综上所述，过点A ′的正比例函数图象的解析式为y ＝－43x 或y ＝－4x .19．解：(1)∵点A 的横坐标为3，且△AOH 的面积为3， ∴点A 的纵坐标为－2，∴点A 的坐标为(3，－2)． ∵正比例函数y ＝kx 的图象经过点A ， ∴3k ＝－2，∴k ＝－23，∴正比例函数的解析式是y ＝－23x .(2)存在．∵△AOP 的面积为5，点A 的坐标为(3，－2)， ∴OP ＝5，∴点P 的坐标为(5，0)或(－5，0)．20．(2n －1，0) [解析] 直线l 的解析式为y ＝3x ，点A 1的坐标为(1，0)，过点A 1作x 轴的垂线交直线l 于点B 1，可知点B 1的坐标为(1，3)，以原点O 为圆心，OB 1长为半径画弧交x 轴于点A 2，则OA 2＝OB 1，所以OA 2＝12＋（3）2＝2，所以点A 2的坐标为(2，0)．同理，可求得点B 2的坐标为(2，2 3)，故OA 3＝22＋（2 3）2＝4，则点A 3的坐标为(4，0)，所以点B 3的坐标为(4，4 3)．…所以点A n 的坐标为(2n －1，0)．。
【初中数学】人教版八年级下册第2课时 正比例函数的图象与性质(练习题)
人教版八年级下册第2课时正比例函数的图象与性质(356)1.已知正比例函数y=(m−1)x的图象上有两点A(x1，y1)，B(x2，y2)，当x1<x2时，有y1>y2.(1)求m的取值范围；(2)当m取最大整数时，画出该函数图象2.已知正比例函数y=(1−2a)x．(1)若函数的图象经过第一、三象限，试求a的取值范围(2)若点A(x1，y1)和点B(x2，y2)为函数图象上的两点，且x1<x2，y1>y2，试求a的取值范围.(3)若函数的图象经过点(−1，2)．①求此函数的解析式并作出其图象；②如果x的取值范围是−1<x<5，求y的取值范围3.对于正比例函数y=kx(k≠0)，当自变量x的值减小2时，函数y的值减小−6，则k的值为（）A.13B.−13C.3D.−34.已知正比例函数y=(2m+4)x．求：(1)m为何值时，函数图象经过第一、三象限；(2)m为何值时，y随x的增大而减小？(3)m为何值时，点(1，3)在该函数图象上？5.已知正比例函数y=kx(k≠0)的图象如图所示，则k的值可能是（）A.1B.2C.3D.46.已知函数y=x，y=−2x，y=12x，y=3x．(1)在同一直角坐标系内画出它们的图象；(2)探索发现：观察这些函数的图象可以发现，随着|k|的增大，直线与y轴的位置关系有何变化？(3)灵活运用:已知正比例函数y1=k1x，y2=k2x在同一坐标系中的图象如图所示，则k1与k2的大小关系为．7.正比例函数y=kx的图象如图所示，则k的取值范围是（）A.k>0B.k<0C.k>1D.k<18.一次函数y=4x，y=−7x，y=−45x的共同特点是（）A.图象位于同样的象限B.y随x的增大而减小C.y随x的增大而增大D.图象都过原点9.已知正比例函数y=(2k+1)x，若y随x的增大而减小，则k的取值范围是（）.A.k>−12B.k<−12C.k=12D.k=010.已知一次函数y1=2x与y2=5x．(1)在同一直角坐标系中画出这两个函数的图象；(2)预测哪一个函数的函数值先达到10011.函数y=|2x|的图象是（）A. B. C. D.12.定义运算“∗”为：a∗b={ab(b>0)，−ab(b≤0)，如：1∗(−2)=−1×(−2)=2，则函数y=2∗x的图象大致是（）A. B. C. D.13.如图，三个正比例函数的图象分别对应的解析式是：①y=ax，②y=bx，③y=cx，则a，b，c的大小关系是（）A.a>b>cB.c>b>aC.b>a>cD.b>c>a14.下列关于正比例函数y=3x的说法中，正确的是（）A.当x=3时，y=1B.它的图象是一条过原点的直线C.y随x的增大而减小D.它的图象经过第二、四象限15.经过以下一组点可以画出函数y=2x的图象的是（）A.(0，0)和(2，1)B.(1，2)和(−1，−2)C.(1，2)和(2，1)D.(−1，2)和(1，2)16.正比例函数y=−2x的大致图象是（）A. B. C. D.参考答案1(1)【答案】解：依题意，得m−1<0，∴m<1，∴m的取值范围是m<1.(2)【答案】∵m<1，∴m取最大整数0，∴解析式为y=−x，图象如图所示：2(1)【答案】解:由正比例函数y=(1−2a)x的图象经过第一、三象限，可得1−2a>0，则a<12(2)【答案】∵正比例函数y=(1−2a)x的图象上两点A(x1，y1)和B(x2，y2)，且x1<x2时，y1>y2，∴y随x的增大而减小，∴1−2a<0，.解得a>12(3)【答案】①∵正比例函数y=(1−2a)x的图象经过点(−1，2)，∴2=−(1−2a)，，解得a=32∴正比例函数的解析式是y=−2x；画出函数图象如图：②把x=−1代入y=−2x得y=2，把x=5代入y=−2x得y=−10，∴y的取值范围为−10<y<2.3.【答案】:D【解析】:根据题意得y+6=k(x−2)，即y+6=kx−2k，而y=kx，所以−2k=6，解得k=−3.4(1)【答案】解：∵函数图象经过第一、三象限，∴2m+4>0，解得m>−2(2)【答案】∵y随x的增大而减小，∴2m+4<0，解得m<−2(3)【答案】∵点(1，3)在该函数图象上，∴2m+4=3，解得m=−125.【答案】:B<k<3【解析】:由图象知536(1)【答案】如图：(2)【答案】观察这些函数的图象可以发现，随着|k|的增大，直线与y轴的夹角越来越小(3)【答案】由(2)得到的规律可知，k1>k27.【答案】:A【解析】:∵函数y=kx的图象经过第一、三象限，∴k>0.8.【答案】:D9.【答案】:B【解析】:∵正比例函数y=(2k+1)x中，y随自变量x的增大而减小，∴2k+1<0，.解得k<−1210(1)【答案】解：在同一直角坐标系中画出这两个函数的图象如图：(2)【答案】预测函数y2=5x的函数值先达到10011.【答案】:C【解析】:函数y=|2x|，当x≥0时，y=2x；当x<0时，y=−2x.12.【答案】:C【解析】:y=2∗x={2x(x>0)−2x(x⩽0)，x＞0时，图象是y＝2x的正比例函数中y轴右侧的部分；x≤0时，图象是y＝﹣2x的正比例函数中y左侧的部分.故选：C.13.【答案】:C【解析】:首先根据图象经过的象限，得a>0，b>0，c<0，对于直线②①，过点(1，0)作垂直于x轴的直线，直线与②的交点高于直线与①的交点，即b>a.15.【答案】:B【解析】:A项，∵当x=2时，y=4≠1，∴点(2，1)不符合，故本选项错误；B项，∵当x=1时，y=2；当x=−1时，y=−2，∴两点均符合，故本选项正确；C项，∵当x=2时，y=4≠1，∴点(2，1)不符合，故本选项错误；D项，∵当x=−1时，y=−2≠2，∴点(−1，2)不符合，故本选项错误．16.【答案】:C。
上海初中数学八年级上---18.2(3)正比例函数的性质(含答案)
18.2（3）正比例函数的性质一、填空题1. 正比例函数y ＝2x 的图像经过第______象限，并且y 随x 的增大而__________．2. 正比例函数y ＝－2x 的图像经过第________象限，并且y 随x 的增大而________．3. 如果正比例函数y ＝kx (k ≠0)的图像经过第二、四象限，那么y 随x 的增大而________.4. 如果正比例函数y ＝kx (k ≠0)的图像经过第一、三象限，那么y 随x 的增大而________．5. 如果点P (a ，b )在第二象限，则函数y ＝b ax 的图像经过第________象限，那么y 随x 的增大而________．6. 已知正比例函数y ＝(1－k )x 的图像经过第一、三象限，则k 的取值范围为________．7. 已知正比例函数y ＝⎝ ⎛⎭⎪⎫1－23a x 中，y 随x 的增大而减小，则a 的取值范围为________． 8. 正比例函数y ＝kx (k ≠0)的图像与直线y ＝－2x 关于y 轴对称，则k ＝________.9.正比例函数y ＝kx 的图像经过第二、四象限，点A (a ，1)、B (－1，b )都在这个函数图像上，则a －b ________0.10. 已知点P 在直线y ＝－3x 上，若点P 的纵坐标大于3，则点P 的横坐标x 的取值范围为________．11．已知（x 1，y 1）和（x 2，y 2）是直线y = -3 x 上的两点，且x 1> x 2，则y 1与y 2•的大小关系是二、简答题12．正比例函数()x a y 15-=的图像经过点（1，4），求a 的值13．正比例函数1212-+⎪⎭⎫ ⎝⎛+=k x k y 的图像经过第一、第三象限，求函数的解析式14．在函数y = -3x 的图象上取一点P ，过P 点作PA ⊥x 轴，已知P 点的横坐标为-2，求△POA 的面积（O 为坐标原点）．15. 已知：正比例函数图像经过点(－2，4).(1)如果点(a，1)和(－1，b)在函数图像上，求：a、b的值；(2)过图像上一点P作y轴的垂线，垂足为Q(0，－8)，求：△OPQ的面积．16. 在正比例函数y＝kx(k≠0)的图像上有一点P(2，a)，过P作PA⊥x轴，PB⊥y轴，垂足分别为A、B，若S四边形OAPB＝6，求：此正比例函数的解析式．三、提高题17. 如图，长方形OABC边BC＝4，AB＝2.(1)直线y＝kx(k≠0)，交边AB于点P，求k的取值范围；(2)直线y＝kx(k≠0)，将长方形OABC的面积分成两部分，靠近y轴的一部分记作S，试写出S关于k的解析式；(3)直线y＝kx(k≠0)，是否可能将长方形OABC的面积分成两部分的面积比为2∶3？若能，求出k的值；若不能，说明理由．18.2（3）正比例函数的性质一．1.一、三 增大 2.二、四 减小 3.减小 4.增大 5.二、四 减小6.k ＜17.a ＞23 8.2 9. ＜ 10.x ＜-3 11. 12y y ＜ 二．12. a=1 13.y=23x 14.6 15.(1)a=-21 b=2 (2)16 16.y=23x 或y=-23x 三． 17.⑴(0＜k ≤21) ⑵ ①当点P 在BC 边上时21()2s k k =＞ ②当点P 在AB 边上时188(0)2s k k =-＜≤（3）①当点P 在BC 边上时58k = ② 当点P 在AB 边上时25k =。
人教版八年级下册知识点试题精选-正比例函数的性质
关于正比例函数的性质一．选择题（共20小题）1．正比例函数的图象经过第二、四象限，那么k为（）A．k=﹣1 B．k=2 C．k=﹣1或k=2 D．不能确定2．函数y=﹣3x中，y随x的变化正确的是（）A．增大而增大B．不变C．减小而减小D．增大而减小3．若正比例函数y=kx的图象经过点（1，3），则此正比例函数的图象经过（）A．第一、二象限B．第一、三象限C．第二、四象限D．第三、四象限4．已知正比例函数y=kx（k≠0），点（2，﹣3）在函数上，则y随x的增大而（）A．增大B．减小C．不变D．不能确定5．对于正比例函数y=mx，当x增大时，y随x增大而增大，则m的取值范围是（）A．m＜0 B．m≤0 C．m＞0 D．m≥06．若点A（﹣5，y1）和点B（﹣2，y2）都在y=﹣x上，则y1与y2的大小关系为（）A．y1＞y2B．y1=y2C．y1＜y2D．y1≤y27．正比例函数y=kx的y值随x的增大而减小，则此函数的图象经过（）A．一、二象限B．一、三象限C．二、三象限D．二、四象限8．关于函数y=﹣x，下列结论正确的是（）A．函数图象必过点（﹣2，﹣1）B．函数图象经过第1、3象限C．y随x的增大而减小 D．y随x的增大而增大9．对于正比例函数y=k2x（k是常数，k≠0）的图象，下列说法正确的是（）A．是一条抛物线B．过点（，k）C．经过一、二象限 D．y随着x增大而减小10．关于正比例函数y=﹣2x，下列结论正确的是（）A．图象必经过点（﹣1，﹣2）B．图象经过第一、三象限C．y随x的增大而减小 D．不论x取何值，总有y＜011．关于函数y=，下列结论正确的是（）A．函数图象必经过点（1，2）B．函数图象经过二、四象限C．y随x的增大而减小 D．y随x的增大而增大12．下面所给点的坐标满足y=﹣2x的是（）A．（2，﹣1）B．（﹣1，2）C．（1，2） D．（2，1）13．关于正比例函数y=﹣3x，下列结论正确的是（）A．图象经过点（﹣3，1）B．图象经过第一、三象限C．函数值y随x的增大而增大D．图象与直线y=1﹣3x的倾斜程度相同14．正比例函数y=2x的图象所过的象限是（）A．一、三象限B．二、四象限C．一、二象限D．三、四象限15．下列一次函数中，y的值随着x值的增大而减小的有（）①y=10x﹣9；②y=﹣0.3x+2；③y=x+4；④y=（﹣）x；⑤y=7﹣x；⑥y=8+（﹣2）x．A．①③⑥B．②⑤⑥C．④⑤⑥D．②④⑤16．若正比例函数的图象经过点（2，﹣3），则这个图象必经过点（）A．（﹣3，﹣2）B．（2，3） C．（3，﹣2）D．（﹣2，3）17．对于y=k2x（k≠0）的图象下列说法不正确的是（）A．是一条直线B．过点（，k）C．经过一、三象限或二、四象限D．y随x增大而增大18．已知函数y=（k﹣3）x，y随x的增大而减小，则常数k的取值范围是（）A．k＞3 B．k＜3 C．k＜﹣3 D．k＜019．已知正比例函数y=（m﹣3）x的图象过第二、四象限，则m的取值范围是（）A．m≥3 B．m＞3 C．m≤3 D．m＜320．下列函数中，y随x的增大而增大的函数是（）A．y=3﹣x B．y=﹣0.5x C．y=﹣2x+1 D．y=x二．填空题（共20小题）21．正比例函数y=x的图象与x轴所成的锐角的度数是．22．如果正比例函数y=（k﹣1）x的图象经过第二、四象限，那么k的取值范围是．23．若直线y=kx（k≠0）经过点（﹣2，6），则y随x的增大而．24．正比例函数y=kx的图象是经过点和的．25．已知正比例函数y=（k+3）x，若y随x的增大而减小，则k的取值范围是．26．正比例函数y=﹣x的图象经过第象限．27．正比例函数y=3x的图象经过第象限．28．函数y=5x的图象经过象限，函数图象从左往右呈趋势，y 随x的增大而；函数y=﹣5x的图象经过第象限，函数图象从左往右呈趋势，y 随x的增大而．29．正比例函数的图象一定经过的点的坐标为．30．正比例函数y=x的图象是经过点（0，）和点（1，）的一条直线．31．已知函数y=（2m﹣9）x|m|﹣5是正比例函数，且图象经过第二，四象限，则m的值为．32．在同一坐标系中，如图所示，一次函数y=k1x，y=k2x，y=k3x，y=k4x的图象分别为l1，l2，l3，l4，则k1，k2，k3，k4的大小关系是．33．正比例函数y=kx（k≠0）的图象是一条经过点的直线．34．已知点P1（x1，y1）和点P2（x2，y2）是正比例函数y=kx（k≠0）图象上的两点，且当x1＜x2时，y1＜y2，则k的取值范围是．35．A（﹣1，3）在正比例函数y=kx图象上，则y随着x的增大而．36．已知正比例函数y=kx（k≠0）的图象经过原点、第二象限与第四象限，请写出符合上述条件的k的一个值：．37．函数的图象经过第象限．38．正比例函数y=﹣5x中，y随着x的增大而．39．函数y=（m﹣3）是正比例函数，则m=，y随x的增大而．40．若函数y=（1﹣k）x2|k|﹣3是正比例函数，且y随x的增大而减小，则（k﹣3）2017=．三．解答题（共10小题）41．已知正比例函数图象上一个点A到x轴的距离为4，这个点A的横坐标为﹣2，请回答下列问题：（1）求这个正比例函数；（2）这个正比例函数经过哪几个象限？（3）这个正比例函数的函数值y是随着x增大而增大？还是随着x增大而减小？42．已知正比例函数y=（2m+4）x．求：（1）m为何值时，函数图象经过一、三象限；（2）m为何值时，y随x的增大而减小；（3）m为何值时，点（1，3）在该函数图象上．43．在物理学中，重力的表达关系式是G=mg（G代表重力，g代表重力常数10，m代表物体的质量）（1）在这个正比例函数表达式中，是自变量，是因变量．（2）若一个物体的重力为100N，它的质量是kg（3）若甲乙两个物体总质量为9kg，乙的质量是甲的2倍，那么甲物体受到的重力是多少？44．已知正比例函数y=（2﹣k）x的图象经过第二、四象限，求函数y=﹣kx的图象经过哪些象限？45．已知y﹣2与3x﹣4成正比例函数关系，且当x=2时，y=3．（1）写出y与x之间的函数解析式；（2）若点P（a，﹣3）在这个函数的图象上，求a的值；（3）若y的取值范围为﹣1≤y≤1，求x的取值范围．46．已知y与x成正比例函数，当x=1时，y=2．求：（1）求y与x之间的函数关系式；（2）求当x=﹣1时的函数值；（3）如果当y的取值范围是0≤y≤5，求x的取值范围．47．在学习一次函数时，通过描点画图，直观的得出正比例函数y=kx（k＞0）的图象是一条直线．现在你能对这个结论给出证明吗？48．当m为何值时，正比例函数y=（m﹣1）x的图象在哪几个象限y随x的增大而减小？49．已知正比例函数y=（3k﹣1）x，若y随x的增大而增大，求k的取值范围．50．已知正比例函数y1=﹣2x的图象如图．（1）在平面直角坐标系中，画出一次函数y2=2x﹣4的图象；（2）若y2＜y1，则x的取值范围是．关于正比例函数的性质参考答案与试题解析一．选择题（共20小题）1．正比例函数的图象经过第二、四象限，那么k为（）A．k=﹣1 B．k=2 C．k=﹣1或k=2 D．不能确定【分析】根据正比例函数所经过的象限确定（k﹣1）的符号，且k2﹣k﹣1=1．【解答】解：∵正比例函数的图象经过第二、四象限，∴k2﹣k﹣1=1，且k﹣1＜0，解得，k=2（不会题意，舍去），k=﹣1．故选A．【点评】本题考查了正比例函数的定义、正比例函数图象的性质．正比例函数y=﹣kx（k≠0）的图象是经过原点的一条直线．当k＞0时，图象经过一、三象限，y随x的增大而增大；当k＜0时，图象经过二、四象限，y随x的增大而减小．2．函数y=﹣3x中，y随x的变化正确的是（）A．增大而增大B．不变C．减小而减小D．增大而减小【分析】根据正比例函数的性质当k＜0时，图象经过二、四象限，y随x的增大而减小．可直接得到答案．【解答】解：∵k=﹣3＜0，∴y随x的增大而减小，故选：D．【点评】此题主要考查了正比例函数的性质，关键是掌握正比例函数图象的性质：它是经过原点的一条直线．当k＞0时，图象经过一、三象限，y随x的增大而增大；当k＜0时，图象经过二、四象限，y随x的增大而减小．3．若正比例函数y=kx的图象经过点（1，3），则此正比例函数的图象经过（）A．第一、二象限B．第一、三象限C．第二、四象限D．第三、四象限【分析】把点A（1，3）代入函数解析式求出k值即可得解，根据k的符号确定其图象所经过的象限．【解答】解：∵正比例函数y=kx的图象经过点（1，3），∴3=k，即k=3＞0，∴此正比例函数的图象经过第一、三象限．故选：B．【点评】考查了正比例函数图象的性质：它是经过原点的一条直线．当k＞0时，图象经过一、三象限；当k＜0时，图象经过二、四象限．4．已知正比例函数y=kx（k≠0），点（2，﹣3）在函数上，则y随x的增大而（）A．增大B．减小C．不变D．不能确定【分析】首先根据函数的图象经过的点的坐标确定函数的图象经过的象限，然后确定其增减性即可．【解答】解：∵点（2，﹣3）在正比例函数y=kx（k≠0）上，∴函数图象经过二四象限，∴y随着x的增大而减小，故选B．【点评】本题考查了正比例函数的性质，解题的关键是牢记正比例函数的比例系数对函数图象的影响．5．对于正比例函数y=mx，当x增大时，y随x增大而增大，则m的取值范围是（）A．m＜0 B．m≤0 C．m＞0 D．m≥0【分析】根据正比例函数的性质解答即可．【解答】解：∵对于正比例函数y=mx，当x增大时，y随x增大而增大，∴m＞0．故选C．【点评】此题利用的规律：在直线y=kx中，当k＞0时，y随x的增大而增大；当k＜0时，y随x的增大而减小．6．若点A（﹣5，y1）和点B（﹣2，y2）都在y=﹣x上，则y1与y2的大小关系为（）A．y1＞y2B．y1=y2C．y1＜y2D．y1≤y2【分析】把点A和点B的横坐标分别代入y=﹣x，分别求出y1与y2的值，然后比较即可．【解答】解：把点A（﹣5，y1）和点B（﹣2，y2）分别代入y=﹣x，得y1=﹣×（﹣5）=；y2=﹣×（﹣2）=1，∵＞1，∴y1＞y2．故选A．【点评】本题较简单，可把点A（﹣5，y1）和点B（﹣2，y2）分别代入函数解析式进行比较，也可直接根据正比例函数的增减性进行比较．7．正比例函数y=kx的y值随x的增大而减小，则此函数的图象经过（）A．一、二象限B．一、三象限C．二、三象限D．二、四象限【分析】直接根据正比例函数的性质求解．【解答】解：∵正比例函数y=kx的y值随x的增大而减小，∴图象经过第二、四象限．故选D．【点评】本题考查了正比例函数的性质：正比例函数y=kx（k≠0）的图象为直线，当k＞0，图象经过第一、三象限，y值随x的增大而增大；当k＜0，图象经过第二、四象限，y值随x的增大而减小．8．关于函数y=﹣x，下列结论正确的是（）A．函数图象必过点（﹣2，﹣1）B．函数图象经过第1、3象限C．y随x的增大而减小 D．y随x的增大而增大【分析】根据正比例函数图象的性质确定正确的选项即可．【解答】解：A、当x=﹣2时，y=1，错误；B、根据k＜0，得图象经过二、四象限，故错误；C、根据k＜0，得图象经过二、四象限，y随x的增大而减小，正确；D、不对；故选C．【点评】考查了正比例函数图象的性质：它是经过原点的一条直线．当k＞0时，图象经过一、三象限，y随x的增大而增大；当k＜0时，图象经过二、四象限，y随x的增大而减小．要判断一点是否在直线上，只需把点的坐标代入，看是否满足解析式．9．对于正比例函数y=k2x（k是常数，k≠0）的图象，下列说法正确的是（）A．是一条抛物线B．过点（，k）C．经过一、二象限 D．y随着x增大而减小【分析】先判断出函数y=k2x（k是常数，k≠0）图象的形状，再根据函数图象的性质进行逐一分析解答，解答．【解答】解：函数y=k2x（k是常数，k≠0）符合正比例函数的形式．A、错误，函数的图象是一条直线；B、正确，函数的图象过点（，k）；C、错误，∵k是常数，k≠0，∴k2＞0，∴函数的图象经过1，3象限；D、错误，是增函数，故y随着x的增大而增大．故选B．【点评】本题考查的是正比例函数的性质，在直线y=kx（k≠0）中：当k＞0时，函数图象过一、三象限，y随x的增大而增大；当k＜0时，函数图象过二、四象限，y随x的增大而减小．10．关于正比例函数y=﹣2x，下列结论正确的是（）A．图象必经过点（﹣1，﹣2）B．图象经过第一、三象限C．y随x的增大而减小 D．不论x取何值，总有y＜0【分析】根据正比例函数图象的性质可知．【解答】解：A、当x=﹣1时，y=2，错误；B、不对；C、根据k＜0，得图象经过二、四象限，y随x的增大而减小，正确；D、不对；故选C．【点评】了解正比例函数图象的性质：它是经过原点的一条直线．当k＞0时，图象经过一、三象限，y随x的增大而增大；当k＜0时，图象经过二、四象限，y随x的增大而减小．要判断一点是否在直线上，只需把点的坐标代入，看是否满足解析式．11．关于函数y=，下列结论正确的是（）A．函数图象必经过点（1，2）B．函数图象经过二、四象限C．y随x的增大而减小 D．y随x的增大而增大【分析】根据正比例函数图象的性质分析．【解答】解：A、当x=1时，y=，错误；B、因为k＞0，所以图象经过第一、三象限，错误；C、因为k＞0，所以y随x的增大而增大，C错误；D、正确．故选D．【点评】了解正比例函数图象的性质：它是经过原点的一条直线．当k＞0时，图象经过一、三象限，y随x的增大而增大．当k＜0时，图象经过二、四象限，y随x的增大而减小．12．下面所给点的坐标满足y=﹣2x的是（）A．（2，﹣1）B．（﹣1，2）C．（1，2） D．（2，1）【分析】用代入法即可．【解答】解：A、当x=2时，y=﹣4，错误；B、当x=﹣1时，y=2，正确；C、当x=1时，y=﹣2，错误；D、错误．故选B．【点评】能够正确把点的横坐标代入解析式，计算它的纵坐标的值，看是否一致，即可判断．13．关于正比例函数y=﹣3x，下列结论正确的是（）A．图象经过点（﹣3，1）B．图象经过第一、三象限C．函数值y随x的增大而增大D．图象与直线y=1﹣3x的倾斜程度相同【分析】根据正比例函数的性质直接解答即可．【解答】解：A、将（﹣3，1）代入解析式，得，1≠﹣9，故本选项错误；B、由于﹣3＜0，则函数图象过二、四象限，故本选项错误；C、由于函数图象过二、四象限，则函数值y随x的增大而减小，故本选项错误；D、由于两函数比例系数相同，则其倾斜程度相同，故本选项正确．故选D．【点评】本题考查了正比例函数的性质，熟悉函数的图象及系数与图象的关系是解题的关键．14．正比例函数y=2x的图象所过的象限是（）A．一、三象限B．二、四象限C．一、二象限D．三、四象限【分析】根据正比例函数的性质进行解答即可．【解答】解：∵正比例函数y=2x中，k=2＞0，∴此函数的图象经过一、三象限．故选A．【点评】本题考查的是正比例函数的性质，即正比例函数y=kx（k≠0）中，当k ＞0时，函数的图象经过一、三象限．15．下列一次函数中，y的值随着x值的增大而减小的有（）①y=10x﹣9；②y=﹣0.3x+2；③y=x+4；④y=（﹣）x；⑤y=7﹣x；⑥y=8+（﹣2）x．A．①③⑥B．②⑤⑥C．④⑤⑥D．②④⑤【分析】根据一次函数的性质对各题进行逐一分析即可．【解答】解：当k＜0时y随着x的增大而减小，①y=10x﹣9；②y=﹣0.3x+2；③y=x+4；④y=（﹣）x；⑤y=7﹣x；⑥y=8+（﹣2）x中，比例系数小于0的有②④⑤，故y的值随着x值的增大而减小的有②④⑤，故选：D．【点评】本题考查的是一次函数的性质，即一次函数y=kx+b（k≠0）中，k＞0，y随x的增大而增大；k＜0，y随x的增大而减小．16．若正比例函数的图象经过点（2，﹣3），则这个图象必经过点（）A．（﹣3，﹣2）B．（2，3） C．（3，﹣2）D．（﹣2，3）【分析】求出函数解析式，然后根据正比例函数的定义用代入法计算．【解答】解：设正比例函数的解析式为y=kx（k≠0），因为正比例函数y=kx的图象经过点（2，﹣3），所以﹣3=2k，解得：k=﹣，所以y=﹣x，把这四个选项中的点的坐标分别代入y=﹣x中，等号成立的点就在正比例函数y=﹣x的图象上，所以这个图象必经过点（﹣2，3）．故选D．【点评】本题考查正比例函数的知识．关键是先求出函数的解析式，然后代值验证答案．17．对于y=k2x（k≠0）的图象下列说法不正确的是（）A．是一条直线B．过点（，k）C．经过一、三象限或二、四象限D．y随x增大而增大【分析】根据y=k2x（k≠0），可知k2＞0，从而可知y=k2x（k≠0）的图象的情况，从而可以解答本题．【解答】解：∵y=k2x（k≠0），∴k2＞0．∴y=k2x（k≠0）的图象是正比例函数的图象，图象在第一、三象限，y随x的增大而增大，图象是一条直线．当x=时，y=k2x=．即y=k2x（k≠0）的图象过点（）．由上可得，选项A的说法正确，选项B的说法正确，选项C的说法不正确，选项D的说法正确．故选C．【点评】本题考查的是正比例函数的性质，解题的关键是明确在正比例函数y=kx （k≠0）中：当k＞0时，函数图象过一、三象限，y随x的增大而增大；当k＜0时，函数图象过二、四象限，y随x的增大而减小．18．已知函数y=（k﹣3）x，y随x的增大而减小，则常数k的取值范围是（）A．k＞3 B．k＜3 C．k＜﹣3 D．k＜0【分析】先根据正比例函数的性质列出关于k的不等式，求出k的取值范围即可．【解答】解：∵函数y=（k﹣3）x，y随x的增大而减小，∴k﹣3＜0，解得k＜3．故选B．【点评】本题考查的是正比例函数的性质，熟知正比例函数的增减性是解答此题的关键．19．已知正比例函数y=（m﹣3）x的图象过第二、四象限，则m的取值范围是（）A．m≥3 B．m＞3 C．m≤3 D．m＜3【分析】直接利用正比例函数的定义得出m的取值范围即可．【解答】解：∵正比例函数y=（m﹣3）x的图象过第二、四象限，∴m﹣3＜0，解得：m＜3．故选：D．【点评】此题主要考查了正比例函数的性质，正确把握正比例函数的性质是解题关键．20．下列函数中，y随x的增大而增大的函数是（）A．y=3﹣x B．y=﹣0.5x C．y=﹣2x+1 D．y=x【分析】根据一次函数的性质对各选项进行逐一分析即可．【解答】解：A、∵y=3﹣x中k=﹣1＜0，∴y随x的增大而减小，故本选项错误；B、∵y=﹣0.5x中k=﹣0.5＜0，∴y随x的增大而减小，故本选项错误；C、∵y=﹣2x+1中k=﹣2＜0，∴y随x的增大而减小，故本选项错误．D、∵y=x中k=＞0，∴y随x的增大而增大，故本选项正确；故选D．【点评】本题考查的是一次函数的性质，熟知一次函数y=kx+b（k≠0）中，当k ＞0时y随x的增大而增大是解答此题的关键．二．填空题（共20小题）21．正比例函数y=x的图象与x轴所成的锐角的度数是45．【分析】根据正比例函数y=x图象上的点到两坐标轴的距离相等可以得到答案．【解答】解：∵正比例函数y=x图象上的点到两坐标轴的距离相等，∴其图象是一、三象限的角平分线，∴与x轴所成的锐角的度数是45°，故答案为：45．【点评】本题考查了正比例函数的性质，牢记其性质是解决本题的关键．22．如果正比例函数y=（k﹣1）x的图象经过第二、四象限，那么k的取值范围是k＜1．【分析】根据正比例函数的性质（正比例函数y=kx（k≠0），当k＜0时，该函数的图象经过第二、四象限）解答．【解答】解：正比例函数y=（k﹣1）x的图象经过第二、四象限，∴k﹣1＜0，解得，k＜1．故答案是：k＜1．【点评】本题主要考查了正比例函数的性质．正比例函数y=kx（k≠0），当k＜0时，该函数的图象经过第二、四象限；当k＞0时，该函数的图象经过第一、三象限．23．若直线y=kx（k≠0）经过点（﹣2，6），则y随x的增大而减小．【分析】先把（﹣2，6）代入直线y=kx，求出k，然后根据正比例函数的性质即可得到y随x的增大而怎样变化．【解答】解：∵直线y=kx（k≠0）经过点（﹣2，6），∴6=﹣2•k，∴k=﹣3＜0，∴y随x的增大而减小．故答案为：减小．【点评】本题考查了正比例函数y=kx（k≠0）的性质：当k＞0，图象经过第一、三象限，y随x的增大而增大；当k＜0，图象经过第二、四象限，y随x的增大而减小．24．正比例函数y=kx的图象是经过点（0，0）和（1，k）的一条直线．【分析】正比例函数的图象是一条过原点的直线，当x=1时，y=k，由此可得出答案．【解答】解：由正比例函数图象的特点可得：正比例函数的图象是一条过原点的直线，当x=1时，y=k，∴图象还过（1，k）点，∴正比例函数y=kx的图象是经过点（0，0）和（1，k）的一条直线．故答案为：（0，0），（1，k），一条直线．【点评】此题主要考查了正比例函数的性质，同学们应熟练掌握根据函数式判断出函数图象的位置，这是考查重点内容之一．25．已知正比例函数y=（k+3）x，若y随x的增大而减小，则k的取值范围是k ＜﹣3．【分析】根据正比例函数图象与系数的关系列出关于k的不等式k+3＜0，然后解不等式即可．【解答】解：∵正比例函数y=（k+3）x中，y的值随自变量x的值增大而减小，∴k+3＜0，解得，k＜﹣3；故答案为：k＜﹣3．【点评】本题主要考查正比例函数图象在坐标平面内的位置与k的关系．解答本题注意理解：直线y=kx所在的位置与k的符号有直接的关系．k＞0时，直线必经过一、三象限，y随x的增大而增大；k＜0时，直线必经过二、四象限，y随x的增大而减小．26．正比例函数y=﹣x的图象经过第二、四象限．【分析】直接根据正比例函数的性质进行解答即可．【解答】解：∵正比例函数y=﹣x中，k=﹣＜0，∴此函数的图象经过第二、四象限．故答案为：二、四．【点评】本题考查的是正比例函数的性质，熟知正比例函数y=kx（k≠0）中，当k＜0时，函数图象经过第二、第四象限是解答此题的关键．27．正比例函数y=3x的图象经过第一、三象限．【分析】根据k=3＞0和正比例函数的性质即可得到答案．【解答】解：∵k=3＞0，∴正比例函数y=3x的图象经过一、三象限．故答案为：一、三．【点评】本题主要考查对正比例函数的性质的理解和掌握，能熟练地运用正比例函数的性质进行说理是解此题的关键．28．函数y=5x的图象经过一三象限，函数图象从左往右呈上升趋势，y 随x的增大而增大；函数y=﹣5x的图象经过第二四象限，函数图象从左往右呈下降趋势，y 随x的增大而减小．【分析】利用这个比例函数的性质结合比例系数的符号直接回答即可．【解答】解：函数y=5x的图象经过一三象限，函数图象从左往右呈上升趋势，y随x的增大而增大；函数y=﹣5x的图象经过第二四象限，函数图象从左往右呈下降趋势，y随x的增大而减小，故答案为：一三，上升，增大；二四，下降，减小．【点评】本题考查了正比例函数的性质，正比例函数y=kx（k≠0），k＞0时，图象在一三象限，呈上升趋势，当k＜0时，图象在二四象限，呈下降趋势．29．正比例函数的图象一定经过的点的坐标为（0，0）．【分析】由于正比例函数的一般形式为y=kx，所以当x=0时，y=0，由此即可确定正比例函数的图象一定经过什么点．【解答】解：∵正比例函数的一般形式为y=kx，∴当x=0时，y=0，∴正比例函数的图象一定经过原点．故答案为：（0，0）．【点评】此题比较简单，主要考查了正比例函数图象的性质：正比例函数的图象一定经过原点．30．正比例函数y=x的图象是经过点（0，0）和点（1，）的一条直线．【分析】分别将两点的横坐标代入正比例函数的解析式即可求得其纵坐标．【解答】解：当x=0时，y=×0=0，当x=1时，y=×1=，故答案为：0，．【点评】本题考查了正比例函数的性质，正比例函数的图象是过原点的一条直线，难度不大．31．已知函数y=（2m﹣9）x|m|﹣5是正比例函数，且图象经过第二，四象限，则m的值为﹣6．【分析】根据正比例函数的定义可得出关于m的方程，解出即可．【解答】解：由题意可得：2m﹣9＜0，|m|﹣5=1，∴m=﹣6．故填﹣6．【点评】解题关键是掌握正比例函数的定义条件以及题意：正比例函数y=kx的定义条件是：k为常数且k≠0，自变量次数为1．且图象经过第二，四象限，则k＜0．32．在同一坐标系中，如图所示，一次函数y=k1x，y=k2x，y=k3x，y=k4x的图象分别为l1，l2，l3，l4，则k1，k2，k3，k4的大小关系是k3＞k4＞k1＞k2．【分析】想知道k之间的大小关系，图中又无其他信息，对此我们可以自己找点来近似的估计k值，如可近似估计四条线上的各一个异于（0，0）的点，然后代入求出k1、k2、k3、k4．再比较即可．【解答】解：把x=1代入y=k1x，y=k2x，y=k3x，y=k4x中，可得：k3＞k4＞k1＞k2．故答案为：k3＞k4＞k1＞k2．【点评】本题考察学生对直线y=kx+b这个基本解析式的理解，尤其是对其中两个系数k，b的掌握和理解是关键．33．正比例函数y=kx（k≠0）的图象是一条经过点（0，0）的直线．【分析】正比例函数的图象是一条过原点的直线，由此可得出答案．【解答】解：由正比例函数图象的特点可得：正比例函数的图象是一条过原点的直线．故答案为（0，0）．【点评】本题考查正比例函数的图象的特点，属于基础题，注意掌握正比例函数的图象是一条过原点的直线．34．已知点P1（x1，y1）和点P2（x2，y2）是正比例函数y=kx（k≠0）图象上的两点，且当x1＜x2时，y1＜y2，则k的取值范围是k＞0．【分析】根据正比例函数的变化规律计算．【解答】解：由于x1＜x2，y1＜y2，说明y随x的减小而减小，∴k＞0；也可计算：y1=kx1，y2=kx2，y1＜y2，即kx1＜kx2k（x1﹣x2）＜0，∵x1＜x2，∴x1﹣x2＜0，∴k＞0．【点评】此题主要考查了正比例函数的变化规律：当k＞0时，图象经过一、三象限，y随x的增大而增大；当k＜0时，图象经过二、四象限，y随x的增大而减小．35．A（﹣1，3）在正比例函数y=kx图象上，则y随着x的增大而减小．【分析】把A（﹣1，3）代入y=kx求出k，根据议程函数的性质即可求出答案．【解答】解：把A（﹣1，3）代入y=kx得：3=﹣k，∴k=﹣3＜0，∴y随x的增大而减小．故答案为：减小．【点评】本题主要考查对解一元一次方程，一次函数的性质等知识点的理解和掌握，能根据一次函数的性质进行说理是解此题的关键．36．已知正比例函数y=kx（k≠0）的图象经过原点、第二象限与第四象限，请写出符合上述条件的k的一个值：﹣2（只要是负数即可，答案不唯一．）．【分析】根据正比例函数的性质：它是经过原点的一条直线，当k＜0时，图象经过二、四象限即可求解．【解答】解：根据题意，知k＜0．故填﹣2．（只要k＜0均可）【点评】考查了正比例函数图象的性质：它是经过原点的一条直线．当k＞0时，图象经过一、三象限，y随x的增大而增大；当k＜0时，图象经过二、四象限，y随x的增大而减小．37．函数的图象经过第二、四象限．【分析】根据正比例函数中k=﹣进行判断即可．【解答】解：∵函数中k=﹣＜0，∴此函数的图象经过二、四象限．故答案为：二、四．【点评】本题考查的是正比例函数的性质，即正比例函数y=kx中，当k＜0时，函数图象经过二、四象限．38．正比例函数y=﹣5x中，y随着x的增大而减小．【分析】直接根据正比例函数的图象与系数的关系进行解答即可．【解答】解：∵正比例函数y=﹣5x中k=﹣5＜0，∴y随着x的增大而减小．故答案为：减小．【点评】本题考查的是正比例函数的性质，熟知正比例函数y=kx中，当k＜0时，y随着x的增大而减小是解答此题的关键．39．函数y=（m﹣3）是正比例函数，则m=﹣3，y随x的增大而减小．【分析】根据正比例函数的定义可得出关于m的方程，继而可得出m的值．【解答】解：m﹣3≠0，m2﹣8=1，则m=﹣3，y=﹣6x，∴y随x的增大而减小．【点评】解题关键是掌握正比例函数的定义条件：正比例函数y=kx的定义条件是：k为常数且k≠0，自变量次数为1．40．若函数y=（1﹣k）x2|k|﹣3是正比例函数，且y随x的增大而减小，则（k﹣3）2017=﹣1．【分析】由正比例函数的定义可求得k的取值，再再利用其增减性进行取舍，代入代数式求值即可．【解答】解：∵y=（1﹣k）x2|k|﹣3是正比例函数，∴2|k|﹣3=1，解得k=2或k=﹣2，∵y随x的增大而减小，∴1﹣k＜0，即k＞1，∴k=2，∴（k﹣3）2017=（2﹣3）2017=﹣1，故答案为：﹣1．【点评】本题主要考查正比例函数性质，掌握正比例函数的增减性是解题的关键，即在y=kx中，当k＞0时，y随x的增大而增大，当k＜0时，y随x的增大而减小．三．解答题（共10小题）41．已知正比例函数图象上一个点A到x轴的距离为4，这个点A的横坐标为﹣2，请回答下列问题：（1）求这个正比例函数；（2）这个正比例函数经过哪几个象限？（3）这个正比例函数的函数值y是随着x增大而增大？还是随着x增大而减小？【分析】（1）根据题意得出A点坐标，进而求出函数解析式；（2）利用（1）中所求得出经过的象限；。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
正比例函数专题练习
知识点
1．形如___________（k是常数，k≠0）的函数是正比例函数，其中k 叫，正比例函数都是常数与自变量的乘积的形式
2．正比例函数y=kx（k是常数，k≠0）的图象是一条经过________的_______，我们通常称之为直线y=kx．当k>0时，图像位于第象限，从左向右，y随x的增大而，也可以说成函数值随自变量的增大而_________；当k<0时，图像位于第象限，从左向右，y随x的增大而，也可以说成函数值随自变量的增大而_________．
3．正比例函数的图像是经过坐标点和定点__ __两点的一条。
根据两点确定一条直线，可以确定两个点（两点法）画正比例函数的图象．
一、填空题(每小题3分，共30·分)
1、形如的函数是正比例函数。
2、大连市区与庄河两地之间的距离是160km，若汽车以每小时80 km 的速度匀速从庄河开往大连，则汽车距庄河的路程s (km)与行驶的时间t(h)之间的函数关系式为.
3、正比例函数y kx
=（k为常数，0
k<）的图像经过第象限，函数值随自变量的增大而。
4、已知一个正比例函数的图像经过点(-2，4)，则这个正比例函数的表达式是。
5、已知y与x成正比例，且2
x=时6
y=-，则9
y=时x=。
6如果函数23
y mx m
=+-是正比例函数，则m= 。
7.若x、y是变量，且函数2
)1
(k x
k
y+
=是正比例函数，则k的值为_____________。
8.已知y=（k+1）x+k-5是正比例函数求k的值是______________.
9.若函数y=（2m+6）x2+（1-m）x是正比例函数，则m的值是______________.
10.已知函数y=(2m+1)x+m－3若此函数图象经过原点,则m=____________. 8、已知正比例函数(12)
y a x
=-如果y的值随x的值增大而减小，那么a的取值范圆是
9、结合正比例函数4
y x
=的图像回答：当1
x>时，y的取值范围是。
10.函数y=－7x的图象在第象限内,经过点(0, )与点(1, ),y随x的增大而 .函数y=4x的图象在第
象限内,经过点(0, )与点(1, ),y随x的增而 .
11.正比例函数x
m
y)1
(-
=的图象经过一、三象限，则m的取值范围是
12.若正比例函数图像又x
k)6
3(
y-
=的图像经过点)
,
(
1
1
y
x
A和B)
,
(
2
2
y
x
B，当2
1
x
x<
时，
2
1
y
y>则k的取值范围是
13、已知正比例函数y=kx（k≠0）的图象如图所示，则在下列选项中k值可能是（）
A、1
B、2
C、3
D、4
14、（2000•西城区）在平面直角坐标系中，正比例函数y=kx（k＜0）的图象
的大体位置是（）
15、一次函数y=﹣x的图象平分（）
A、第一、三象限
B、第一、二象限
C、第二、三象限
D、第二、四象限
16、在直角坐标系中，既是正比例函数y=kx，又是y的值随x的增大而减小的图象是（）
17、当k＞0时，正比例函数y=kx的图象大致是（）
18、已知正比例函数y=kx （k≠0），当x=﹣1时，y=﹣2，则它的图象大致是（）
19、如图所示函数图象中，正比例函数的图象是（）20、正比例函数y=kx的图象是经过原点的一条（）
A、射线
B、双曲线
C、线段
D、直线
21、结合函数y=﹣2x的图象回答，当x＜﹣1时，y的取值范围（）
A、y＜2
B、y＞2
C、y≥错误!未找到引用源。
D、y≤错误!未找到引用源。
22.正比例函数x
m
y)1
3(-
=的图像经过点)
,
(
)
,
(
2
2
1
1
y
x
B
y
x
A和且该图像经过第二、四象限.
(1)求m的取值范围
(2)当x1>x2时，比较y1与y2的大小,并说明理由.。