材料力学(金忠谋)第六版完整编辑版规范标准答案
材料力学(金忠谋)第六版课后习题及答案

解
(1) ∆l1
=
1 3
Ρxl1
Ε 1Α1
∆l1 = ∆l2 x = 0.6m
∆l 2
=
1 3
Ρ (3 − x)l2
Ε 2Α2
(2) Ρ ≤ 3Ε1Α1 = 3× 200 × 2 ×10−1 = 200ΚΝ
xl1
0.6× 2
2-11 铰接的正方形结构如图所示,各杆材料皆为铸铁,许用拉应力[σ +]=400kg/cm2, 许用压应力[σ − ]=600kg/cm2,各杆的截面积均等于25cm2。试求结构的许用载荷P。
习题
2-1 一木柱受力如图示,柱的横截面为边长20cm的正方形,材料服从虎克定律,其
弹性模量 E = 0.10 ×105 MPa.如不计柱自重,试求:
(1) (2) (3) (4)
作轴力图; 各段柱横截面上的应力; 各段柱的纵向线应变; 柱的总变形.
解:
(1) 轴力图
(2) AC 段应力
σ
=
−100 ×103 0.2 2
= −2.5×106 Ρa = −2.5ΜΡa
CB 段应力
σ
=
− 260 ×103 0.2 2
= −6.5×106 Ρa = −6.5ΜΡa
(3) AC 段线应变
ε = σ = −2.5 = −2.5×10−4 Ε 0.1×105 CB 段线应变
ε
=σ Ε
=
−6.5 0.1×10 5
解:
AC、CB、BD、DA 杆受拉力,大小为 Τ1 =
Ρ 2
DC 杆受压力,大小为 Τ2 = Ρ
[σ
+
]≥
Τ1 Α
得 Ρ1 ≤ 2 × 400 × 25 = 14142kg
材料力学(金忠谋)第六版答案第03章
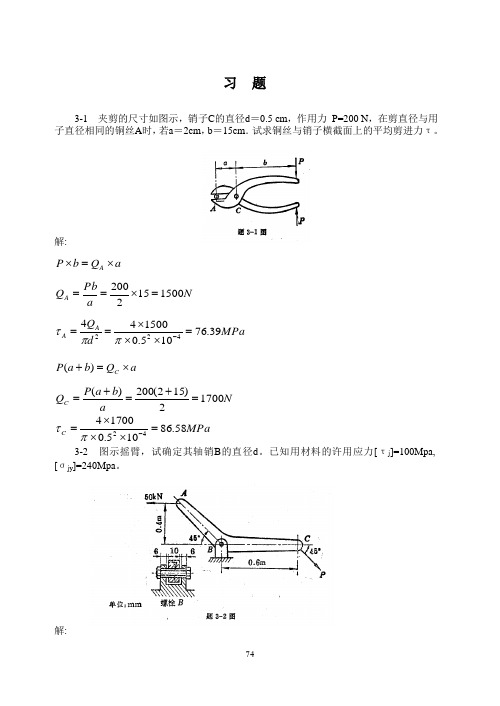
3-7图示轴的直径d=80mm,键的尺寸b=24mm,h=14mm,键的许用剪应力[τj]=40Mpa,许用挤压应力[σjy]=90Mpa。若通过键所传递的扭矩为3200N.m。试确定键的长度 。
解:
取
3-8销钉式安全联轴器如图所示.允许传递扭矩Mn=300N.m。销钉材料的剪切强度极限τb=360 MPa,轴的直径D=30mm。试确定销订的直径d。
解:
3-9冲床的最大冲击力为400 kN,冲头材料的许用应力[σ]=440MPa,被冲钢板的剪切强度极限 =360 MPa.求在最大冲力作用下所能冲剪的圆孔的最小直径d和的最大厚度t。
解:
3-10以楔C把钩杆AB固定联接于平板D的孔中。试求楔的尺寸:宽度δ,高度 以及钩杆的尾长 。设挤压许用应力[σjy]=320MPa,剪切许用应力[τj]=100MPa,P力可由钩杆中的抗拉许用应力[σ]=160MPa来求得。
=15.4mm
验算挤压应力
3-3图示直径为d的拉杆,其端头的直径为D,高度为h,试建立D、h与d的合理比值(从强度考虑)。
已知:[σ]=120 MPa,[τj]=90 MPa,[σjy]=240 MPa.
解:
3-4两根矩形截面木杆,用两块钢板连接在一起,受轴向载荷P=45kN作用。已知截面宽度b=25 cm,沿材的顺纹方向,许用拉应力[σ]=6MPa,许用挤压应力[σjy]=10 MPa,许用剪应力[τj]=1MPa,试确定接头的尺寸δ、 和h。
解:
解
3-5货轮的传动轴和艉轴系利用轴端凸缘法兰上的12只螺栓相联接,螺栓直径d=75 mm,螺栓中心圆的直径D=650 mm,已知传递的扭矩Mn=600 kN·m,螺栓和轴的材料均为35号钢,其许用应力[ ]=80Mpa,[σjy]=120MPa、试校核螺栓的剪切和挤压强度。
材料力学(金忠谋)第六版完整版问题详解

第一章 绪论1-1 求图示杆在各截面(I )、(II )、(III )上的力,并说明它的性质.解:(a )I-I 截面: N = 20KN (拉)II-II 截面: N = -10KN (压)III-III 截面: N = -50KN (压)(b )I-I 截面: N = 40KN (拉)II-II 截面: N = 10KN (拉)III-III 截面: N = 20KN (拉)1-2 已知P 、M 0、l 、a ,分别求山下列图示各杆指定截面(I )、(II)上的力解:(a ):(I )截面:力为零。
(II )截面:M = Pa (弯矩)Q = -P (剪力)(b ):(I )截面:θsin 31P Q =θsin 61PL M = (II )截面:θsin 32P Q = θsin 92PL M =(c ):(I )截面:L M Q 0-= 021M M = (II )截面:L M Q 0-= 031M M =1-3 图示AB 梁之左端固定在墙,试求(1)支座反力,(2)1-1、2-2、3-3各横截面上的力(1-1,2-2是无限接近集中力偶作用点.)解:10110=⨯=A Y (KN )1055.110-=+⨯-=A M (KN-M )(1-1) 截面:10110=⨯=Q (KN )521110-=⨯⨯-=M (KN-M ) (2-2)截面:10=Q (KN )055=-=M (KN-M )(2-3)截面:10=Q (KN )551110-=+⨯⨯-=M (KN-M )1-4 求图示挂钩AB 在截面 1-1、2-2上的力.解:(1-1)截面:P N 32=a P M ⋅=43 (2-2)截面:P Q 32=a P M ⋅=321-5 水平横梁AB 在A 端为固定铰支座,B 端用拉杆约束住,求拉杆的力和在梁1-1截面上的力.解:(1)拉杆力T :1230sin 0⨯=⨯⋅=∑P T M A ο 10030sin 2100=⨯=οT (KN )(拉) (2)(1-1)截面力:Q 、N 、M :5030sin -=-=οT Q (KN )6.8630cos -=-=οT N (KN )(压)()2550.030sin =⨯=οT M (KN-M )1-6 一重物 P =10 kN 由均质杆 AB 及绳索 CD 支持如图示,杆的自重不计。
材料力学(金忠谋)第六版答案第14章

材料力学(金忠谋)第六版答案第14章第十三章 动载荷13-1 铸铁杆AB 长m l 8.1=,以等角速度绕垂直轴O -O 旋转如图示。
已知铸铁的比重3/74m kN =γ,许用拉应力[]MPa 40=σ,材料的弹性模量E =160 Gpa 。
试求此杆的极限转速,并计算此杆在转速m r n /100=时的绝对伸长。
解: (1) 极限转速m rn s s l g l g A A Ndl gA dr r qd r Nd x r gAdr ma r qd x r a jx dl n n 1092260137.114175.130799.010*******.92)2(][2][)2(21][)2(21)()()()()(235222222222====⨯⨯⨯⨯⨯=≤≤≤======⎰πωωγσωσωγσσωγωγω(2) 当n =1000m rcm m Eg l r EA r Nd l s n l 0252.01052.28.91016039.072.104107423)2(2)(2172.1046010002602492233220=⨯=⨯⨯⨯⨯⨯⨯⨯===∆=⨯==-⎰ωππω(2)吊索: MPa A P d d 55.2105276.14max=⨯==-σ13-3 轴上装一钢质圆盘,盘上有一圆孔。
若轴与盘以s140=ω的匀角速度旋转,论求轴内由这一圆孔引起的最大正应力。
解:23max max 22225.1212.021*********.01060041411060064003.03.047800640404.0mMN W M mN L P N Na gA ma P s m r a z d d d d n n d n =⨯⨯==⋅=⨯⋅===⨯⨯⨯⨯=⋅⋅⋅===⨯==πσπδγω13-4 飞轮轮缘的平均直径D =1.2m ,材料比重3/72m kN =γ,弹性模量GPa E 200=,轮缘与轮幅装配时的过盈量mmD2.0=∆,若不计轮相的影响,求飞轮允许的最大转速。
材料力学(金忠谋)第六版答案第02章

习题2-1一木柱受力如图示,柱的横截面为边长20cm 的正方形,材料服从虎克定律,其弹性模量E0.10 10 5MPa.如不计柱自重,试求:(1)作轴力图;(2)各段柱横截面上的应力;(3)各段柱的纵向线应变;(4)柱的总变形.解:(1)轴力图(2) AC 段应力100 10 3 2.5 10 6 a 2.5 a0.2 2CB 段应力260 10 3 6.5 10 6 a 6.5a0.2 2( 3)AC 段线应变0.12.5 2.510 4N- 图105CB 段线应变0.16.5 6.510 4 105( 4)总变形 2.510 4 1.5 6.5 10 4 1.5 1.35 103 m2-2图 (a) 所示铆接件,板件的受力情况如图(b)所示.已知:P= 7 kN , t= 0.15cm, b1= 0.4cm,b2 =0.5cm, b3=0.6cml 。
试绘板件的轴力图,并计算板内的最大拉应力。
解:(1)轴力图1 7(2) 1310 710 6194.4a0.40.15 22 7310 7 10 20.50.15 230.15 7107 100.6 266311.1a388.9 a 最大拉应力 max3388.9 a2-3 直径为1 cm 的圆杆, 在拉力 P = 10 kN 的作用下, 试求杆内最大剪应力, 以及与横截面夹角为= 30o 的斜截面上的正应力与剪应力。
解 :( 1) 最大剪应力max122 ( 2)30 界面上的应力2 10 10 710663.66a41 d 2121 cos 263.66395.49 a22sin 263.66 sin 3055.13 a22-4 图示结构中 ABC 与 CD 均为刚性梁, C 与D 均为铰接,铅垂力 P = 20kN 作用在 C 铰,若( 1)杆的直径 d 1=1cm ,( 2)杆的直径 d 2=2cm ,两杆的材料相同, E = 200Gpa ,其他尺寸如图示,试求( 1)两杆的应力;( 2) C 点的位移。
材料力学(金忠谋)第六版答案第05章

解:
(a) (b)
(M图)(M图)
5-14已知梁的弯矩图,试求此梁的载荷及剪力图。
解:
(Q图)(Q图)
5-15图示梁上作用有集度为m=m(x)的分布力偶矩,试建立m、 、M之间的微分关系。
解:
5-16悬臂梁上表面受切向分布力t作用,t为单位长度上的力N/m,已知t、h、L。试分别作此梁的轴力、剪力和弯矩图。
解:
8m
4m 0.5a
(a)Q图(b)Q图(c)Q图
(a)M图(b)M图(c)M图
5-5求作下列各饺接梁的剪力图和弯矩图。
解:
(a)Q图(b)Q图(c)Q图
(a)M图(b)M图(c)M图
(d)Q图(e)Q图(f)Q图
(d)M图(e)M图(f)M图
5-6根据q、 、M的微分关系,检查并改正下列各梁的 图和M图的错误。
(c)
(M图) (Q图) (N图)
(d)
(M图) (Q图) (N图)
(e)
(M图) (Q图) (N图)
(f)
N图)
(h)
(M图) (Q图) (N图)
5-12简支梁上的分布载荷按抛物线规律变化,其方程为 试作剪力图和弯矩图。
解:
(Q图) (M图)
若
解:
a
x
P P
L
5-9作图示梁ABC的剪力图和弯矩图。
解:
D B C E D B C E
A D B C A D B C
(Q图)(M图)
5-10用叠加法作下列各梁的弯矩图
(a)(b)(c)
(d)(e)(f)
5-11求作下列图示平面刚架的内力图。
材料力学(金忠谋)第六版答案第02章

习 题2-1 一木柱受力如图示,柱的横截面为边长20cm 的正方形,材料服从虎克定律,其弹性模量51010.0⨯=E MPa .如不计柱自重,试求:(1)作轴力图; (2)各段柱横截面上的应力; (3)各段柱的纵向线应变; (4) 柱的总变形.解:(1) 轴力图(2) AC 段应力a a MP P σ5.2105.22.010100623-=⨯-=⨯-= CB 段应力 a a MP P σ5.6105.62.010260623-=⨯-=⨯-=(3) AC 段线应变 45105.2101.05.2-⨯-=⨯-==E σε N-图CB 段线应变45105.6101.05.6-⨯-=⨯-==E σε (4) 总变形 m 3441035.15.1105.65.1105.2---⨯=⨯⨯-⨯⨯-=AB ∆2-2 图(a)所示铆接件,板件的受力情况如图(b)所示.已知:P =7 kN ,t =0.15cm ,b 1=0.4cm ,b 2=0.5cm ,b 3=0.6cml 。
试绘板件的轴力图,并计算板内的最大拉应力。
解:(1)轴力图(2)a MP σ4.194101024.015.0767311=⨯⨯⨯⨯⨯=-a MP σ1.311101025.015.0767322=⨯⨯⨯⨯⨯=- a MP σ9.388101026.015.07673=⨯⨯⨯⨯=- 最大拉应力a MP σσ9.3883max == 2-3 直径为1cm 的圆杆,在拉力P =10 kN 的作用下,试求杆内最大剪应力,以及与横截面夹角为α=30o 的斜截面上的正应力与剪应力。
解:(1) 最大剪应力a d MP ππP στ66.6310101102212672241max =⨯⨯⨯⨯===- (2) ︒=30α界面上的应力()a MP ασσα49.952366.632cos 12=⨯=+= a MP αστα13.5530sin 66.632sin 2=⨯=⨯=︒2-4 图示结构中ABC 与CD 均为刚性梁,C 与D 均为铰接,铅垂力P =20kN 作用在C 铰,若(1)杆的直径d 1=1cm ,(2)杆的直径d 2=2cm ,两杆的材料相同,E =200Gpa ,其他尺寸如图示,试求(1)两杆的应力;(2)C 点的位移。
材料力学第六版答案第07章

材料力学(金忠谋)第六版答案第07章(总23页)-CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面,使用请直接删除244习 题7-1 用积分法求图示各悬臂梁自由端的挠度和转角,梁的抗弯刚度EI 为常量。
7-1(a ) 0M()M x = ''0EJ M y ∴='0EJ M y x C =+ 201EJ M 2y x Cx D =++ 边界条件: 0x =时 0y = ;'0y =代入上面方程可求得:C=D=0201M 2EJ y x ∴= '01=M EJy x θ= 01=M EJ B l θ 201=M 2EJB y l (b )222()1M()222q l x qx x ql qlx -==-+- 2''21EJ 22qx y ql qlx ∴=-+- 3'2211EJ 226qx y ql x qlx C =-+-+ 422311EJ 4624qx y ql x qlx Cx D =-+-++ 边界条件:0x = 时 0y = ;'0y =代入上面方程可求得:C=D=02454223111()EJ 4624qx y ql x qlx ∴=-+- '2231111=(-)EJ 226y ql x qlx qx θ=+- 3-1=6EJ B ql θ 4-1=8EJB y ql (c )()()()()()0303''04'050()1()()286EJ 6EJ 24EJ 120l x q x q lq l x M x q x l x l x l q y l x lq y l x C lq y l x Cx D l-=-⎛⎫=--=-- ⎪⎝⎭∴=-=--+=-++ 边界条件:0x = 时 0y = ;'0y = 代入上面方程可求得:4024q l C l -= 50120q l D l= ()455000232230120EJ 24EJ 120EJ (10105)120EJq q l q l y l x x l l l q x l l lx x l ∴=---+-=-+- 3024EJ B q l θ=- 4030EJB q l y =- (d)'''223()EJ 1EJ 211EJ 26M x Pa Pxy Pa Pxy Pax Px C y Pax Px Cx D =-=-=-+=-++ 边界条件:0x = 时 0y = ;'0y =代入上面方程可求得:C=D=024623'232321112611253262B C C B y Pax Px EJ y Pax Px EJ Pa Pa Pa y y a a EJ EJ EJ Pa EJθθθ⎛⎫∴=- ⎪⎝⎭⎛⎫==- ⎪⎝⎭=+=+==(e)()()()21222''1'211231113()02()2223EJ 231EJ ()2231EJ ()46a M x q qax x a q M x a x a x a a y q qax a y qa x x C a y qa x x C x D =-+≤≤=--≤≤=-+=-++=--+++ 边界条件:0x = 时 0y = ;'0y =代入上面方程可求得:C=D=0()()()22118492024EJ 12EJqax qax y a x a x x a ∴=--=--≤≤ ''2223'222242232221EJ ((2)4)21EJ (42)2312EJ (2)2312y q a ax x x y q a x ax C x y q a x ax C x D =--+=--++=---+++ 边界条件:x a = 时 12y y = ;12θθ=代入上面方程可求得:2296a C = 4224qa D =- ()()43223421612838464162384q y x ax a x a a a x a EJ-=-+-+≤≤247 43412476B B qa y EJ qa EJθ=-=- (f)()()221222''212'231122341115()20225()2225251EJ 22251EJ 26511EJ 4324qa qx M x qax x a qa qa a M x qax x a x a a y q ax x a y q x ax x C a y q x ax x C x D =-+-≤≤⎛⎫=-+--≤≤ ⎪⎝⎭⎛⎫=--+ ⎪⎝⎭⎛⎫=--++ ⎪⎝⎭⎛⎫=--+++ ⎪⎝⎭边界条件:0x = 时 0y = ;'0y =代入上面方程可求得:C 1=D 1=0''22'2222223222EJ (2)1EJ (2)21EJ ()6y q a ax y q a x ax C y q a x ax C x D =--=--+=---++ 边界条件:x a = 时 12y y = ; ''''12y y =3296a C =- 4224a D =- 437124136B B qa y EJ qa EJθ=-=-7-2 用积分法求图示各梁的挠曲线方程,端截面转角θA 和θB ,跨度中点的挠度和最大挠度,梁的抗弯刚度EI 为常量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解:(a):(I)截面:内力为零。
(II)截面:M = Pa(弯矩)
Q = -P(剪力)
(b):(I)截面:
(II)截面:
(c):(I)截面:
(II)截面:
1-3图示AB梁之左端固定在墙内,试求(1)支座反力,(2)1-1、2-2、3-3各横截面上的内力(1-1,2-2是无限接近集中力偶作用点.)
解:
(1)
(2)
即
解得
各杆的长度为
2-37图示三杆结构中,杆(1)是铸铁的,E1=120Gpa, =80MPa;杆(2)是铜的,EA=100GPa, =60Gpa;杆(3)是钢的,EA=200GPa, =120Mpa。载荷P=160kN,设A1:A2:A3=2:2:1,试确定各杆的截面积。
解:
各杆的应力关系为
解
(1)
(2)
2-11铰接的正方形结构如图所示,各杆材料皆为铸铁,许用拉应力[ +]=400kg/cm2,许用压应力[ ]=600kg/cm2,各杆的截面积均等于25cm2。试求结构的许用载荷P。
解:
AC、CB、BD、DA杆受拉力,大小为
DC杆受压力,大小为
得
得
故
2-12图示拉杆沿斜截面m-n由两部分胶合而成,设在胶合面上许用拉应力[ ]=100MPa,许用剪应力 =50MPa,胶合面的强度控制杆件的拉力,试求:为使杆件承受最大拉力P, 角的值应为多少?若横截面面积为4cm2,并规定 ,试确定许可载荷P。
解:
只计P时,有
只计2P时,有
且有
联立,解得
(方向水平向左) (方向水平向右)
(b)
解得 (方向水平向左) (方向水平向右)
2-31图示钢杆,其横截面面积A1=25cm2,弹性模量E=210Gpa。加载前,杆与右壁的间隙 =0.33mm,当P=200kN时,试求杆在左、右端的支反力。
解:
解得 (方向情况如图示。水平梁AB为变形可忽略的粗刚梁,CA是钢杆,长 =2 m,横截面面积A1=2 cm2,弹性模量E1=200Gpa;DB是钢杆,长 =1m,横截面面积A2=8cm2,弹性模量E2=100Gpa,试求:
(1)使刚性梁AB仍保持水平时,载荷P离DB杆的距离x;
(2)如使水平梁的竖向位移不超过0.2cm,则最大的P力应为多少?
第一章
1-1求图示杆在各截面(I)、(II)、(III)上的内力,并说明它的性质.
解:(a)I-I截面:N = 20KN (拉)
II-II截面:N = -10KN(压)
III-III截面:N = -50KN (压)
(b)I-I截面:N = 40KN(拉)
II-II截面:N = 10KN (拉)
III-III截面:N = 20KN(拉)
N-图
CB段线应变
(4)总变形
2-2图(a)所示铆接件,板件的受力情况如图(b)所示.已知:P=7 kN,t=0.15cm,b1=0.4cm,b2=0.5cm,b3=0.6cml。试绘板件的轴力图,并计算板内的最大拉应力。
解:
(2)
最大拉应力
2-3直径为1cm的圆杆,在拉力P=10 kN的作用下,试求杆内最大剪应力,以及与横截面夹角为 =30o的斜截面上的正应力与剪应力。
(2)y截面上的应力; ;
(3)最大轴力 ,最大应力
解:
(1)截面 的直径为
截面以下体积为
轴力
(2) 截面上的应力
(3)最大轴力、应力都在 处
2-23支架由AB和BC两杆组成,承受铅直载荷如图示。这两杆由同一材料制成,若水平杆BC的长度保持常数L, 角随A点沿竖直方向移动而变化,AB杆的长度随A点的位置而定。设材料的拉伸许用应力与压缩许用应力相等,当这两杆受力均完全达到许用应力时,该结构具有最小重量,试求此时的 角。
解(1): ( )
( )
( )
(2):
习
2-1一木柱受力如图示,柱的横截面为边长20cm的正方形,材料服从虎克定律,其弹性模量 MPa.如不计柱自重,试求:
(1)作轴力图;
(2)各段柱横截面上的应力;
(3)各段柱的纵向线应变;
(4)柱的总变形.
解:
(1)轴力图
(2)AC段应力
CB段应力
(3)AC段线应变
解
钢丝绳的拉力为T,则
钢丝绳的伸长
C点铅垂直位移为
2-20图示空间简单桁架,三杆均由钢制成,杆A1C1与杆B1C1的截面积A=10cm2,C1D1杆的截面积 =20GPa,弹性模量E=200cm2,承受载荷P=150kN,试求各杆内的应力及节点C的位移。
解:
此结构为空间垂直结构
各杆的应力为
各杆的伸长为
解:(I-I)截面:
(II-II)截面:
(压)
(压)
1-8图示为一端固定的圆弧形杆,在自由端承受P力如图示.试求各横截面1-1,2-2,3-3
上的内力.
解:1-1截面: , ,
2-2截面: , ,
3-3截面: , ,
1-9铰接梁的尺寸及载荷如图示,D为中间铰.试求:(1)支座反力,(2)中间铰
两侧截面上的内力.
解:
(a)
(b)
2-35图示(1)杆与(2)杆的刚度EA相同,水平刚梁AB的变形略去不计,试求两杆的内力。
解:
即
得
2-36两刚性铸件,用螺栓1与2联接,相距20cm如图示。现欲移开两铸件,以便将长度为20.02cm、截面积A=6cm2的铜杆3自由地安装在图示位置。已知E1=E2=200Gpa,试求(1)所需的拉力P;(2)力P去掉后,各杆的应力及长度。
解: (KN)
(KN-M)
(1-1)截面: (KN)
(KN-M)
(2-2)截面: (KN)
(KN-M)
(2-3)截面: (KN)
(KN-M)
1-4求图示挂钩AB在截面1-1、2-2上的内力.
解:(1-1)截面:
(2-2)截面:
1-5水平横梁AB在A端为固定铰支座,B端用拉杆约束住,求拉杆的内力和在梁1-1截面上的内力.
解:(1)拉杆内力T:
(KN)(拉)
(2)(1-1)截面内力:Q、N、M:
(KN)
(KN)(压)
(KN-M)
1-6一重物P=10 kN由均质杆AB及绳索CD支持如图示,杆的自重不计。求绳索CD的拉力及AB杆在截面1-1上的内力.
解:(1)绳索CD拉力T:
(2)1-1截面内力:
1-7杆AC及BD铰接于A、B、D三处如图示.在C端作用一铅直载荷P,AB=BC=BD=a。试求截面1-1和II-II上的内力.
将变形
2-32两根材料不同但截面尺寸相同的杆件,同时固定联接于两端的刚性板上,且E1>E2,若使两杆都为均匀拉伸,试求拉力P的偏心距e。
解:
解得
2-33图示(1)与(2)两杆为同材料、等截面、等长度的钢杆,若取许用应力[ ]=150MPa,略去水平粗刚梁AB的变形, ,试求两杆的截面积。
解:
2-34两杆结构其支承如图示,各杆的刚度EA相同,试求各杆的轴力。
解:
(1)
时杆件承受最大拉力。
(2)
故许可载荷 为46.1
2-13油缸盖与缸体采用6个螺栓连接.已知油缸内径D=350 mrn,油压p=1Mpa。若螺栓材料的许用应力[ ]=40 MPa,求螺栓的内径d.
解
2-14试确定轧钢机承压装置安全螺栓的直径d,当P=6000kN时,螺径即行断裂,其材料的强度极限 =600 Mpa。各接触面间的摩擦力可不计。
解:
(1)
(2)被压试件的缩短量
2-16设水平刚性杆AB不变形,拉杆CD的直径d=2cm,许用应力[ ]=160MPa,材料的弹性模量E=200GPa,在B端作用载荷P=12kN.试校核CD杆的强度并计算B点的位移.
解:
故安全
B点的位移 ,方向向下。
2-17设压入机体中的钢销子所受的连结力是沿着它的长度 平均分布的,为了拔出这个销子,在它的一端施加P=20kN的力。已知销子截面积A=2cm2,长度 =40cm,a=15 cm,E=200GPa,试绘出杆的应力图和计算杆的伸长。
解: 部分应力沿 分布:
当 时,
应力图为
2-18试求下列各简单结构中节点A的位移,设各杆的抗拉压刚度均为EA。
解:
(a)AC杆受力为零,BA杆伸长为
A点沿BA方向移动
(b)AB杆受拉力为P,BC杆受拉力为P,BD杆受压力为 P
由几何关系,得B点位移
水平位移
垂直位移
故A点位移
水平位移
垂直位移
2-19水平刚性梁ABCD在B、D两点用钢丝绳悬挂,尺寸及悬挂方式如图示,E、F两处均为无摩阻力的小滑轮。若已知钢丝绳的横截面面积A=1.0cm2,弹性模量E=200GPa,铅垂载荷P=20kN作用于C点,试求C点的铅垂向位移。
解:
两杆同时达到许用应力时的截面积为
结构重量W为
得
2-24图示铰接正方形结构,各杆的横截面面积均为A1,材料的弹性模量均为E,试计算当载荷P作用时节点B、D间的相对位移。
解:
B、D相对位移为
2-25钢制受拉杆件如图所示.横截面面积A=2cm2, =5m,单位体积的重量为76.5kN/m3。如不计自重,试计算杆件的变形能U和比能u;如考虑自重影响,试计算杆件的变形能,并求比能的最大值。设E=200Gpa。
解:
2-8常用仓库搁架前后面用两根圆钢杆AB支持,其平面投影图如图示,估计搁架上的最大载重量为P=10kN,假定合力P作用在搁板BC的中线上。已知 ,杆材料的许用应力[ ]=160 Mpa,试求所需圆钢杆的直径。
解
杆轴力
