2016松江区初三数学二模试卷
2016.4.5松江二模
• 解:(1)比较图(a)和(b)可以看出是水的质量和蒸发面积 相同,水面上方空气流速相同,温度不同,故可得出:质量和面 积相同的水,当水面上方空气流动速度相同时,温度越高,水蒸 发越快. • (2)比较图(a)和(c)及相关条件可以看出,水的质量和蒸 发面积相同,水的温度相同,只是水面上方空气流速不同,故可 得出结论:质量和面积相同的水,当温度相同时,水面上方空气 流动速度越快,水蒸发越快. • 故答案为:(1)当水面上方空气流动速度相同时,温度越高, 水蒸发越快; • (2)质量和面积相同的水,当温度相同时,水面上方空气流动 速度越快,水蒸发越快
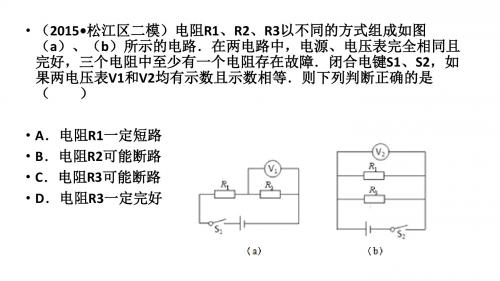
• (2015•松江区二模)细心的小明发现:“瓢泼大雨”以很大的速度 落到地面,“毛毛细雨”则缓慢地飘落到地面.这是怎么回事呢? 老师告诉他,从高空下落的物体,速度会越来越大,而所受空气阻 力也会随速度的增大而增大,因此物体下落一段距离后将以某一速 度做匀速直线运动,通常把这个速度称为收尾速度.小明研究发现, 在相同环境下,球形物体下落的收尾速度v与球的半径r和质量m有 关.下表为小明某次研究的实验数据 • (1)通过比较1号和2号小球可以得出结论:在相同环境下, • 小球半径相同时,小球质量越大,小球的收尾速度越大 • (2)根据二力平衡知识,可以确定编号为4号的小球,受到的最大 阻力为0.392牛. • (3)小明想探究小球的收尾速度与小球的半径是否有关.与4号小 球做对比,请给5号小球的质量设置合适的数据填在表中,以便完成 探究.
(2015•松江区二模)两个底面积不等的圆柱形容器,分别盛有甲 乙两种不同的液体,将两个完全相同的小球分别浸入这两种液体 中,小球静止时的位置如图所示,此时两液面刚好齐平.若将这 两小球从液体中取出,则液体对容器底部的压强的变化量△p甲、 △p乙的大小关系是( ) A.△p甲一定小于△p乙 B.△p甲一定等于△p乙 C.△p甲一定大于△p乙 D.△p甲可能小于△p乙
2016年上海中考二模数学24题图文解析

因此对应的点 P 有两个(如图 6 所示).
那么求点 D(点 P)的坐标还有更简便的方法:由勾股定理,得 AB2=AD2+BD2.
由 A(-1, 0)、B(0, 3)、D(1, 2m),得 12+32=22+(2m)2+12+(3-2m)2.
解得 m=1,或 m= 1 . 2
例
2016 年上海市虹口区中考模拟第 24 题
例
2015 年上海市奉贤区中考模拟第 24 题
如图 1,在平面直角坐标系中,抛物线 y=-x2+bx+c 与 x 轴交于 A(-1, 0)、C(3, 0)两 点,与 y 轴交于点 B,点 P 为 OB 上一点,过点 B 作射线 AP 的垂线,垂足为点 D,射线 BD 交 x 轴于点 E.
(1)求该抛物线的解析式; (2)联结 BC,当点 P 的坐标为 (0, 2) 时,求△EBC 的面积;
如图 1,在平面直角坐标系中,直线 AB 过点 A(3,0)、B(0,m)(m>0),tan∠BAO=2. (1)求直线 AB 的表达式; (2)反比例函数 y k1 的图像与直线 AB 交于第一象限内的 C、D 两点(BD<BC),
x 当 AD=2DB 时,求 k1 的值;
例
2016 年上海市崇明县中考模拟第 24 题
如图 1,一条抛物线的顶点为 E(-1,4),且过点 A(-3,0),与 y 轴交于点 C.点 D 是这 条抛物线上一点,它的横坐标为 m,且-3<m<-1,过点 D 作 DK⊥x 轴,垂足为 K,DK 分别交线段 AE、AC 于点 G、H.
(1)求这条抛物线的解析式; (2)求证:GH=HK; (3)当△CGH 是等腰三角形时,求 m 的值.
如图 5,一方面,当点 D 落在抛物线的对称轴上时,D(1, 2m).
松江区初三数学二模试卷及参考答案

.CBA〔第6题图〕2021年松江区初三数学二模试卷〔总分值150分,完卷时间100分钟〕 2021.4考生注意:1.本试卷含三个大题,共25题;2.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效;3.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.一、选择题:〔本大题共6题,每题4分,总分值24分〕【以下各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上】1〔A〔B〔C〔D 2.以下运算正确的选项是〔▲〕 〔A 〕532x x x =+;〔B 〕532x x x =⋅; 〔C 〕235()x x =;〔D 〕623x x x ÷=.3.以下图形中,既是中心对称又是轴对称图形的为〔▲〕 〔A 〕正三角形;〔B 〕等腰梯形;〔C 〕平行四边形;〔D 〕菱形.4.关于反比例函数2y x=,以下说法中错误的选项是〔▲〕 〔A 〕它的图像是双曲线; 〔B 〕它的图像在第一、三象限; 〔C 〕y 的值随x 的值增大而减小;〔D 〕假设点〔a ,b 〕在它的图像上,则点〔b ,a 〕也在它的图像上.5.将一组数据中的每一个数都加上1得到一组新的数据,那么以下四个统计量中,值保持不变的是〔▲〕 〔A 〕方差;〔B 〕平均数;〔C 〕中位数;〔D 〕众数.6.如图,在△ABC 中,∠C =90°,AC =3,BC =4,⊙B 的半径为1,⊙A 与直线BC 相交,且与⊙B 没有公共点,那么⊙A 的半径可以是〔▲〕 〔A 〕4; 〔B 〕5; 〔C 〕6;〔D 〕7.二、填空题:〔本大题共12题,每题4分,总分值48分〕 【请将结果直接填入答题纸的相应位置上】7.因式分解:34a a - = ▲ ..8x =的根是 ▲ . 9.函数32x y x-=的定义域是 ▲ . 10.方程240x x m -+=有两个不相等的实数根,则m 的取值范围是 ▲ . 11.把抛物线22y x =-向左平移1个单位,则平移后抛物线的表达式为 ▲ . 12.函数y kx b =+的图像如下图,则当0y <时,x 的取值范围是 ▲ .13.一枚质地均匀的正方体骰子的六个面上分别刻有1到6的点数,随机投掷这枚骰子,那么向上一面的点数为合数的概率是 ▲ .14.某区有4000名学生参加学业水平测试,从中随机抽取500名,对测试成绩进行了统计,统计结果见下表:那么根据上述数据可以估量该区这次参加学业水平测试成绩小于60分的有 ▲ 人. 15. 如图,在△ABC 中,D 是AB 的中点,E 是AC 上一点,且AE =2EC ,如果AB a =,AC b =,那么DE =▲ .〔用a 、b 表示〕.16边形的一个内角等于它的中心角的2倍,则n17假设抛物线2y ax =上的两点A ,通径.那么抛物线212y x =18.如图,平行四边形ABCD 中,AC =BC ,∠ACB =45°,将三角形ABC 沿着AC 翻折,点B 落在点E 处,联结DE ,那么DEAC的值为 ▲ . 三、解答题:〔本大题共7题,总分值78分〕 19.〔此题总分值10分〕 计算:031-.20.〔此题总分值10分〕解不等式组:2312136x x x x -<⎧⎪+⎨-≤⎪⎩ 并把解集在数轴上表示出来.A C DE (第15题图) B (第12题图) (第18题图).21.〔此题总分值10分, 每题各5分〕如图,△ABC 中,∠B =45°,1tan 2C =,BC =6.〔1〕求△ABC 面积;〔2〕AC 的垂直平分线交AC 于点D ,交BC 于 点E. 求DE 的长. 22.〔此题总分值10分〕某条高速铁路全长540公里,高铁列车与动车组列车在该高速铁路上运行时,高铁列车的平均速度比动车组列车每小时快90公里,因此全程少用1小时,求高铁列车全程的运行时间.23.〔此题总分值12分,第〔1〕小题总分值7分,第〔2〕小题总分值5分〕如图,梯形ABCD 中,AB ∥CD ,∠D =90°,BE 平分∠ABC ,交CD 于点E , F 是AB 的中点,联结AE 、EF ,且AE ⊥BE .求证:〔1〕四边形BCEF 是菱形;〔2〕2BE AE AD BC ⋅=⋅.24.〔此题总分值12分,每题各4分〕如图,抛物线y=ax 2+bx 的顶点为C 〔1,1-〕,P 是抛物线上位于第一象限内的一点,直线OP 交该抛物线对称轴于点B ,直线CP 交x 轴于点A . 〔1〕求该抛物线的表达式;〔2〕如果点P 的横坐标为m ,试用m 的代数式表示线段BC 的长; 〔3〕如果△ABP 的面积等于△ABC 的面积,求点P 坐标.25.〔此题总分值14分,第〔1〕小题4分,第〔2 如图,Rt △ABC 中,∠ACB =90°,BC =2,AC =3,以点C 于点D ,过点A 作AE ∥CD ,交BC 延长线于点E. 〔1〕求CE 的长;〔2〕P 是 CE 延长线上一点,直线AP 、CD 交于点Q.① 如果△ACQ ∽△CPQ ,求CP 的长;② 如果以点A 为圆心,AQ 为半径的圆与⊙C 相切,求2021年松江区初三数学二模试卷0 1 2 3 4 5–––––(第24题图)(第23题图)FA CDE(第25题图)CBADE CBADE.参考答案2021.4一、选择题:〔本大题共6题,每题4分,总分值24分〕 1.B; 2.B; 3. D; 4. C; 5. A; 6. D; 二、填空题:〔本大题共12题,每题4分,总分值48分〕7. (2)(2)a a a +-; 8. 2x =; 9. 0x ≠; 10. 4m <; 11.22(1)y x =-+;12. 1x <-; 13.13; 14. 120; 15. 1223a b -+;16. 6;17. 2; 18. 1 .三、解答题:〔本大题共7题,总分值78分〕 19.〔此题总分值10分〕计算:031-+.解:原式=11)-2分〕 =22分 20.〔此题总分值10分〕解不等式组:2312136x xx x -<⎧⎪+⎨-≤⎪⎩ 并把解集在数轴上表示出来.解:由① 得 3x <.………………………………………………………………〔2分〕 由② 得 6212x x -≤+…………………………………………………………〔2分〕 36x -≤…………………………………………………………〔1分〕 解得 2x ≥-.………………………………………………………………〔2分〕 所以,原不等式组的解集是23x -≤<.…………………………………………〔1分〕 在数轴上表示不等式组的解集,正确得2分〔端点有一处错误,扣1分〕. 21.〔此题总分值10分, 每题各5分〕解:〔1〕过点A 作AH ⊥BC 于点H …………1分 在Rt ABC ∆中,∠B =45°设AH =x ,则BH =x ………………………………1分 在Rt AHC ∆中,1tan 2AH C HC == ∴HC=2x ………………………………………………………1分 ∵BC =6∴x+2x =6 得x =20 1 2 3 4 5–––––(第21题图)DAC.∴AH =2…………………………………………………………1分 ∴162ABC S BC AH ∆=⋅⋅=……………………………………1分(2)由〔1〕得AH =2,CH =4在Rt AHC ∆中,AC =2分 ∵DE 垂直平分AC∴12CD AC =ED ⊥AC …………………………………………………1分 在Rt EDC ∆中,1tan 2ED C CD ==……………………………1分∴DE =………………………………………………1分 22.〔此题总分值10分〕解:设高铁列车全程的运行时间为x 小时,…〔1分〕 则动车组列车全程的运行时间为(x +1)小时,…〔1分〕∴540540901x x -=+,……………………………………………〔3分〕 6611x x -=+.………………………………………………〔1分〕 260x x +-=…………………………………………………〔1分〕 122,3x x ==-………………………………………………〔1分〕经检验:它们都是原方程的根,但3x =-不符合题意.……〔1分〕 答:高铁列车全程的运行时间为2小时.…………………〔1分〕 23.〔此题总分值12分,第〔1〕小题总分值7分,第〔2〕小题总分值5分〕 证明:(1) ∵BE 平分∠ABC ,∴∠ABE =∠CBE …………………………………………………1分 ∵AE ⊥BE ∴∠AEB =90° ∵F 是AB 的中点 ∴12EF BF AB ==………………………………………………1分 ∴∠FEB =∠FBE …………………………………………………1分 ∴∠FEB =∠CBE …………………………………………………1分 ∴EF ∥BC …………………………………………………1分 ∵AB ∥CD∴四边形BCEF 是平行四边形…………………………1分(第23题图)FACDE B∵EF BF=∴四边形BCEF是菱形……………………………………1分(2)∵四边形BCEF是菱形,∴BC=BF∵12 BF AB=∴AB=2BC………………………………………………1分∵AB∥CD∴∠DEA=∠EAB∵∠D=∠AEB∴△EDA∽△AEB………………………………………2分∴AD AEBE AB=…………………………………………1分∴BE·AE=AD·AB∴2BE AE AD BC⋅=⋅…………………………………1分24.〔此题总分值12分,每题各4分〕解:〔1〕∵抛物线y=ax2+bx的顶点为C〔1,1-〕∴112a bba+=-⎧⎪⎨-=⎪⎩…………………………………2分解得:12ab=⎧⎨=-⎩…………………………………1分∴抛物线的表达式为:y=x2-2x;…………………………1分〔2〕∵点P的横坐标为m,∴P的纵坐标为:m2-2m……………………………1分令BC与x轴交点为M,过点P作PN⊥x轴,垂足为点N∵P是抛物线上位于第一象限内的一点,∴PN= m2-2m,ON=m,O M=1由PN BMON OM=得221m m BMm-=………………………1分∴BM=m-2…………………………………………………1分∵点C的坐标为〔1,1-〕,∴BC=m-2+1=m-1………………………………………1分(第24题图)..〔3〕令P (t ,t 2-2t ) ………………………………………………1分 △ABP 的面积等于△ABC 的面积 ∴AC =AP过点P 作PQ ⊥BC 交BC 于点Q ∴CM =MQ =1∴t 2-2t =1 …………………………………………………1分∴1t =1t =………………………………1分 ∴ P的坐标为〔1〕……………………………………1分25.〔此题总分值14分,第〔1〕小题4分,第〔2〕小题每个小题各5分〕 解:〔1〕∵AE ∥CD ∴BC DCBE AE=…………………………………1分 ∵BC=DC∴BE=AE …………………………………1分 设CE =x则AE =BE =x +2 ∵ ∠ACB =90°, ∴222AC CE AE +=即229(2)x x +=+………………………1分∴54x =即54CE =…………………………………1分〔2〕①∵△ACQ ∽△CPQ ,∠QAC>∠P∴∠ACQ=∠P …………………………………1分 又∵AE ∥CD ∴∠ACQ=∠CAE∴∠CAE=∠P ………………………………1分 ∴△ACE ∽△PCA ,…………………………1分 ∴2AC CE CP =⋅…………………………1分即2534CP =⋅ ∴365CP = ……………………………1分CBA DEPQ(第25题图)CBADE.②设CP =t ,则54PE t =- ∵∠ACB =90°,∴AP ∵AE ∥CD∴AQ ECAP EP=……………………………1分5545454t t ==--∴AQ =……………………………1分假设两圆外切,那么145AQ t ==-此时方程无实数解……………………………1分假设两圆内切切,那么5AQ ==∴21540160t t -+=解之得t =1分又∵54t >∴t =1分。
【精品】2015年上海松江区初三数学二模试卷及答案word

2
三、解答题: (本大题共 7 题,满分 78 分)
19.(本题满分 10 分) 计算:(1
1 ) x2 x 2
x3
x3
x 3y 8 20.(本题满分 10 分) 解方程组: x2 4xy 5 y 2 0
21. (本题满分 10 分) 某品牌电动车经销商一月份销售该品牌电动车
100 辆,二月份的销售量比一月份增加
1分
∴△EFC ∽△AGB ……………………………………………………………………………… ∴∠EFC =∠AGB=90° …………………………………………………………………………
1分 1分
∴BG⊥AF ………………………………………………………………………………………
1分
24. 解:( 1)∵抛物线 y x2 bx 经过点 A( 4, 0)
是(
)
(A) k 4;
( B) k 4 ;
(C) k 0;
( D) k 0 .
3.已知一次函数 y=kx﹣ 1,若 y 随 x 的增大而增大,则它的图像经过(
)
( A )第一、二、三象限;
( B )第一、三、四象限;
( C)第一、二、四象限;
( D )第二、三、四象限.
4.一组数据: -1, 1, 3, 4, a,若它们的平均数为 2,则这组数据的众数为(
∵ ∠AGD =∠GDF +∠ DFG =90°+∠ DFG
∴ ∠AGD =∠CFD ………………………………………………………………………………
1分
∴ △ADG ≌△CDF ………………………………………………………………………………
1分
( 2)∵∠ ADE =∠ EFC ,∠ DEA =∠ FEC,∴△ ADE ∽△ CFE ,∴ DE AD
2016上海中考数学二模试卷含闵行,普陀,杨浦,虹口,黄浦,松江,浦东,长宁8个区包括答案

闵行区2015-2016学年第二学期九年级质量调研考试2016.4数学试卷(考试时间100分钟,满分150分)考生注意:1.本试卷含三个大题,共25题.2.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效.3.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.一、选择题:(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个选项是正确的,请选择正确选项的代号并填涂在答题纸的相应位置上】1.如果单项式22n a b c是六次单项式,那么n的值取(A)6;(B)5;(C)4;(D)3.2(A;(B(C1;(D1.3.下列函数中,y随着x的增大而减小的是(A)3y x=;(B)3y x=-;(C)3yx=;(D)3yx=-.4.一鞋店销售一种新鞋,试销期间卖出情况如下表,对于鞋店经理来说最关心哪种尺码的鞋畅销,那么下列统计量对该经理来说最有意义的是(A)平均数;(B)中位数;(C)众数;(D)方差.5.下列图形中,既是轴对称又是中心对称图形的是(A)正五边形;(B)等腰梯形;(C)平行四边形;(D)圆.6.下列四个命题,其中真命题有(1)有理数乘以无理数一定是无理数;(2)顺次联结等腰梯形各边中点所得的四边形是菱形;(3)在同圆中,相等的弦所对的弧也相等;(4)如果正九边形的半径为a,那么边心距为sin20a⋅o.(A)1个;(B)2个;(C)3个;(D)4个.二、填空题:(本大题共12题,每题4分,满分48分) 7.计算:22-= ▲ .8.在实数范围内分解因式:32a a -= ▲ . 92=的解是 ▲ . 10.不等式组30,43x x x -≥⎧⎨+>-⎩的解集是 ▲ .11.已知关于x 的方程20x x m --=没有实数根,那么m 的取值范围是 ▲ .12.将直线213y x =-+向下平移3个单位,那么所得到的直线在y 轴上的截距为 ▲ .13.如果一个四边形的两条对角线相等,那么称这个四边 形为“等对角线四边形”.写出一个你所学过的特殊 的等对角线四边形的名称 ▲ .14.如图,已知在梯形ABCD 中,AD // BC ,且BC = 3AD ,点E 是边DC 的中点.设AB a =uu u r r ,AD b =uuu r r ,那么 AE =uu u r ▲ (用a r 、b r的式子表示).15.布袋中有大小、质地完全相同的4个小球,每个小球上分别标有数字1、2、3、4,如果从布袋中随机抽取两个小球,那么这两个小球上的数字之和为偶数的概率是 ▲ .16.9月22日世界无车日,某校开展了“倡导绿色出行”为主题的调查,随机抽查了部分师生,将收集的数据绘制成下列不完整的两种统计图.已知随机抽查的教师人数为学生人数的一半,根据图中信息,乘私家车出行的教师人数是 ▲ .17.点P 为⊙O 内一点,过点P 的最长的弦长为10cm ,最短的弦长为8cm ,那么OP的长等于 ▲ cm .18.如图,已知在△ABC 中,AB = AC ,1tan 3B ∠=,将△ABC 翻折,使点C 与点A 重合,折痕DE 交边BC 于点D ,交边AC 于点E ,那么BDDC的值为 ▲ . ABD C(第14题图)EABC(第18题图)(第16题图) 乘公车 y % 步行 x %骑车 25%私家车 15%学生出行方式扇形统计图师生出行方式条形统计图三、解答题:(本大题共7题,满分78分)19.(本题满分10分)110212(cos60)32--++-o.20.(本题满分10分)解方程:222421242xx x x x x-+=+--.21.(本题满分10分,其中每小题各5分)如图,已知在△ABC中,∠ABC = 30º,BC = 8,sin A∠=,BD是AC边上的中线.求:(1)△ABC的面积;(2)∠ABD的余切值.22.(本题满分10分,其中每小题各5分)如图,山区某教学楼后面紧邻着一个土坡,坡面BC平行于地面AD,斜坡AB的坡比为i =1∶512,且AB = 26米.为了防止山体滑坡,保障安全,学校决定对该土坡进行改造.经地质人员勘测,当坡角不超过53º时,可确保山体不滑坡.(1)求改造前坡顶与地面的距离BE的长.(2)为了消除安全隐患,学校计划将斜坡AB改造成AF(如图所示),那么BF至少是多少米?(结果精确到1米)(参考数据:sin530.8≈o,cos530.6≈o,tan53 1.33≈o,cot530.75≈o).BCD(第21题图)BDC(第22题图)F23.(本题满分12分,其中每小题各6分)如图,已知在矩形ABCD 中,过对角线AC 的中点O 作 AC 的垂线,分别交射线AD 和CB 于点E 、F ,交边DC 于 点G ,交边AB 于点H .联结AF ,CE . (1)求证:四边形AFCE 是菱形; (2)如果OF = 2GO ,求证:2GO DG GC =⋅. 24.(本题满分12分,其中每小题各4分)如图,已知在平面直角坐标系xOy 中,抛物线22y ax x c =++与x 轴交于 点A (-1,0)和点B ,与y 轴相交于点C (0,3),抛物线的对称轴为直线l . (1)求这条抛物线的关系式,并写出其对称轴和顶点M 的坐标;(2)如果直线y kx b =+经过C 、M 两点,且与x 轴交于点D ,点C 关于直 线l 的对称点为N ,试证明四边形CDAN(3)点P 在直线l 上,且以点P 为圆心的圆经过A 、B 两点,并且与直线CD 相切, 求点P 的坐标.(第24题图)(第23题图)AB CDE FGOH25.(本题满分14分,其中第(1)小题各4分,第(2)、(3)小题各5分)如图,已知在△ABC中,AB = AC = 6,AH⊥BC,垂足为点H.点D在边AB上,且AD = 2,联结CD交AH于点E.(1)如图1,如果AE = AD,求AH的长;(2)如图2,⊙A是以点A为圆心,AD为半径的圆,交AH于点F.设点P为边BC上一点,如果以点P为圆心,BP为半径的圆与⊙A外切,以点P为圆心,CP为半径的圆与⊙A内切,求边BC的长;(3)如图3,联结DF.设DF = x,△ABC的面积为y,求y关于x的函数解析式,并写出自变量x的取值范围.(第25题图3)普陀区2015-2016学年度第二学期初三质量调研数学试卷 2016年4月13日(时间:100分钟,满分析150分)一、选择题:(本大题共6题,每题4分,满分24分)1、据统计,2015年上海市全年接待国际旅游入境者共80016000人次,80016000用科学记数法表示是( )(A )8.0016⨯610; (B )8.0016710⨯; (C )8100016.8⨯; (D )9100016.8⨯2、下列计算结果正确的是( )(A )824a a a =⋅; (B )()624a a =; (C )()222b a ab =; (D )()222b a b a -=-.3、下列统计图中,可以直观地反映出数据变化的趋势的统计图是( )(A )折线图; (B )扇形图; (C )统形图; (D )频数分布直方图。
上海市松江区2016届九年级上学期期末考试数学试题(含详细答案)

上海市松江区2016届九年级上学期期末考试数学试题一. 选择题1. 如果两个相似三角形的面积比是1:4,那么它们的周长比是( ) A. 1:16; B. 1:4; C. 1:6; D. 1:2;2. 下列函数中,属于二次函数的是( )A. 21y x =+;B. 22(1)y x x =--;C. 227y x =-;D. 21y x =-; 3. 在Rt △ABC 中,90ACB ∠=︒,1BC =,2AB =,则下列结论正确的是( )A. sin A =; B. cos A = C. 1tan 2A =; D. cot A = 4. 若四边形ABCD 的对角线交于点O ,且有2AB DC =u u u r u u u r,则以下结论正确的是( )A. 2AO OC =u u u r u u u r ;B. ||||AC BD =u u u r u u u r ;C. AC BD =u u u r u u u r ;D. 2DO OB =u u u r u u u r;5. 如果二次函数2y ax bx c =++(0a ≠)的图像 如图所示,那么( )A. 0a <,0b >,0c >;B. 0a >,0b <,0c >;C. 0a >,0b >,0c <;D. 0a <,0b <,0c <;6. P 是△ABC 一边上的一点(P 不与A 、B 、C 重合),过点P 的一条直线截△ABC , 如果截得的三角形与△ABC 相似,我们称这条直线为过点P 的△ABC 的“相似线” Rt △ABC 中,90C ∠=︒,30A ∠=︒,当点P 为AC 的中点时,过点P 的△ABC 的 “相似线最多有几条?( )A. 1条;B. 2条;C. 3条;D. 4条;二. 填空题7. 若::1:3:2a b c =,且24a b c ++=,则a b c +-= ;8. 已知线段2a cm =,8b cm =,那么线段a 、b 的比例中项等于 cm ; 9. 二次函数223y x x =--+的图像与y 轴的交点坐标为 ;10. 在Rt △ABC 中,90C ∠=︒,如果4AC =,2sin 3B =,那么AB = ; 11. 一位运动员投掷铅球,如果铅球运行时离地面的高度为y (米)关于水平距离x (米)的函数解析式为21251233y x x =-++,那么铅球运动过程中最高点离地面的距离为 米;12. 如图,直线AD ∥BE ∥CF ,23BC AB =,6DE =,那么EF 的值是 ;13. 在一个斜坡上前进5米,水平高度升高了1米,则该斜坡坡度i = ;14. 若点1(3,)A y -、2(0,)B y 是二次函数22(1)3y x =--+图像上的两点,那么1y 与2y 的大小关系是 (填12y y >、12y y =或12y y <);15. 将抛物线2y x =沿x 轴向右平移2个单位后所得抛物线的解析式是 ; 16. 如图,已知DE ∥BC ,且DE 经过△ABC 的重心G ,若6BC cm =,那么DE 等于 cm ;17. 已知二次函数的图像经过(0,3)、(4,3)两点,则该二次函数的图像对称轴为直线 ;18. 已知在△ABC 中,90C ∠=︒,3BC =,4AC =,点D 是AB 边上一点,将△ABC沿着直线CD 翻折,点A 落在直线AB 上的点'A 处,则sin 'A CD ∠= ;三. 解答题19. 已知抛物线23y x bx =++经过点(1,8)A -,顶点为M ; (1)求抛物线的表达式;(2)设抛物线对称轴与x 轴交于点B ,连接AB 、AM ,求△ABM 的面积;20. 如图,已知平行四边形ABCD ,点M 、N 是边DC 、BC 的中点,设AB a =u u u r r ,AD b =u u u r r;(1)求向量MN u u u u r (用向量a r 、b r表示);(2)在图中求作向量MN u u u u r 在AB u u u r 、AD u u u r方向上的分向量; (不要求写作法,但要指出所作图中表示结论的向量)21. 如图,小明所在教学楼的每层高度为3.5米,为了测量旗杆MN 的高度,他在教学楼一 楼的窗台A 处测得旗杆顶部M 的仰角为45°,他在二楼窗台B 处测得M 的仰角为31°, 已知每层楼的窗台离该层的地面高度均为1米,求旗杆MN 的高度;(结果保留两位小数) (参考数据:sin 310.52︒≈,cos310.86︒≈,tan 310.60︒≈)22. 如图,已知△ABC 中,90C ∠=︒,1tan 2A =,点D 在边AB 上,:3:1AD DB =,求cot DCB ∠的值;23. 已知如图,在△ABC 中,BD 平分ABC ∠交AC 于点D ,点E 在AB 上,且2BD =BE BC ⋅;(1)求证:BDE C ∠=∠; (2)求证:2AD AE AB =⋅;24. 如图,已知抛物线23y ax bx =+-与x 轴交于A 、B 两点,与y 轴交于点C ,O 是坐 标原点,已知点B 的坐标是(3,0),tan 3OAC ∠=; (1)求该抛物线的函数表达式;(2)点P 在x 轴上方的抛物线上,且PAB CAB ∠=∠,求点P 的坐标;(3)点D 是y 轴上一动点,若以D 、C 、B 为顶点的三角形与△ABC 相似,求出符合条件的点D 的坐标;25. 已知,等腰梯形ABCD 中,AD ∥BC ,45B BCD ∠=∠=︒,3AD =,9BC =, 点P 是对角线AC 上的一个动点,且APE B ∠=∠,PE 分别交射线AD 和射线CD 于点E 和点G ;(1)如图1,当点E 、D 重合时,求AP 的长;(1)如图2,当点E 在AD 的延长线上时,设AP x =,DE y =,求y 关于x 的函数解 析式,并写出它的定义域;(3)当线段DG =AE 的值;2016年松江区中考数学一模卷一、选择题1.D2.C3.B4.A5.A6.C二、填空题 7.8 8.4 9.(0,3) 10.6 11.3 12.413. 6214.21y y < 15.()22-=x y16.4 17.x =2 18.54三、解答题19.【解】(1)∵抛物线32++=bx x y 经过点(1,8)A -,∴28(1)3b =--+,……………………………………………………(2分) 解得4b =-,……………………………………………………………(2分) ∴所求抛物线的表达式为342+-=x x y ;…………………………(1分) (2)作AH ⊥BM 于点H ,∵由抛物线243y x x =-+解析式可得,点M 的坐标为(2,1)-,点B 的坐标为(2,0),………………………(2分) ∴BM =1,…………………………………………………………………(1分) ∵对称轴为直线2=x ,∴AH =3,……………………………………(1分) ∴△ABM 的面积1132S =⨯⨯=23.……………………………………(1分)第19题图20.【解】(1)方法一:∵四边形ABCD 是平行四边形,∴AB P DC ,AD P BC ,AB =DC ,AD =BC ,……………………………(1分) ∵=,=,∴=,=,…………………………(1分)∵点M 、N 分别为DC 、BC 的中点,∴a MC 21=,b NC 21=,…………(2分) ∴b a CN MC MN 2121-=+=,……………………………………(1分)方法二: ∵a AB =,b AD =,∴b a AD AB DB -=-=,……………………………………………………(2分)∵点M 、N 分别为DC 、BC 的中点,b a DB MN 212121-==,………………………………………………………(3分) (2)作图.………………………………………………………………(4分)结论:AP 、AQ 是向量MN 分别在AB 、AD 方向上的分向量.………(1分)第20题图21.【解】过点M 的水平线交直线AB 于点H ,由题意,得∠AMH =∠MAH =45°,31BMH ∠=︒,AB =3.5,………………(3分) 设MH =x ,则AH =x , tan310.60BH x x =︒=, ……………………………(2分) ∴0.600.4 3.5AB AH BH x x x =-=-==,…………………………………(3分) ∴x =8.75,…………………………………………………………………………(1分) 则旗杆高度19.75MN x =+=(米)答:旗杆MN 的高度度约为9.75米.…………………………………………(1分) 22.【解】过D 点作DH ⊥BC 于点H ,…………………………………………(1分)∵90,ACB ∠=︒∴DH P AC , ∵:3:1,AD DB =∴::1:4,DH AC BH BC == ……(2分)∵设DH =x ,则AC =4 x , ……………………………………………………(2分) ∵90C ∠=︒,1tan ,2A =∴2BC x = , …………………………………………………………………(2分)∵:1:4,BH BC =∵CH =x 23, ……………………………………………………………………(2分) ∴23cot =∠DCB .…………………………………(1分)第22题图23.【证明】(1)∵BD 平分∠ABC ,∴∠ABD =∠CBD ,……………………………………………………………(1分)∵BC BE BD ⋅=2,∴BDBCBE BD =,…………………………………………………………………(2分) ∴△EBD ∽△DBC ,……………………………………………………………(2分) ∴∠BDE =∠C ;…………………………………………………………………(1分) (2) ∵∠BDE =∠C ,∠DBC +∠C=∠BDE +∠ADE ,………………………………………………(1分) ∴∠DBC =∠ADE ,……………………………………………………………(1分) ∵∠ABD =∠CBD ,∴∠ABD =∠ADE ,………………………………………………………………(1分) ∴ADE ABD △∽△,…………………………………………………………(1分) ∴ADAEAB AD =, 即AB AE AD ⋅=2.……………………………………………………………(2分)第23题图24.【解】(1)∵抛物线23y ax bx =+-与y 轴交于点C ,∴点C 的坐标为(0,3)-,∴3OC =,∵tan 3OAC ∠=,∴OA =1,即点A 的坐标为(1,0)-,…(1分)又点(3,0)B ,∴ ⎩⎨⎧=-+=--.0339,03b a b a ∴a =1,b =-2, ………………………………(2分)∴抛物线的函数表达式是223y x x =--;……………………………(1分)(2)∵∠P AB =∠CAB ,∴tan tan 3PAB CAB ∠=∠=,……………………………………………(1分) ∵点P 在x 轴上方,设点P 的横坐标为x ,则点P 的纵坐标为3(1)x +,∴23(1)23x x x +=--,得x =-1(舍去)或x =6,……………………(2分)当x =6时,y =21,∴点P 的坐标为(6,21); …………………………………………………(1分) (3)设点D 的坐标为(0,)y ,易得ABC △为∠ABC =45°的锐角三角形,所以△DCB 也是锐角三角形,∴点D 在点C 的上方, …………………………………………………………(1分) ∴∠DCB =45°, ∴∠ABC =∠DCB ,Q AB =4,BC =23,DC =y +3, ………………………………………………(1分)①如果BC AB BC DC =则234233=+y , ∴y =1,即点D (0,1), ………………………………………………………(1分) ②如果AB BCBC DC =则423233=+y , ∴y =23,即点D (0,23). ……………………………………………………(1分)第24题图25.【解】(1)作AH ⊥BC 于点H , ∵∠B =∠BCD =45°,AD =3,BC =9, ∴BH =AH =3,AB =23,CH =6,∴AC =53,………………………………(1分) ∵AD P BC ,∴∠DAP =∠ACB ,又∠APE =∠B ,∴ADP CAB △∽△,……………………………………………………………(2分) ∴BC APAC AD =,即9533AP =, ∴559=AP ;…………………………………………………………………(1分)第25题图1(2)∵∠DAP =∠ACB ,∠APE =∠B ,∴APE CBA △∽△,……………………(1分) ∴BCAPAC AE =, ∴9533xy =+,………………………………………………………………(1分) ∴335-=x y , ……………………………………………………………(1分) 95355x <… ……………………………………………(1分) (3)方法一:①当点G 在线段CD 上时, 作DM P EP 交AC 于点M , 由(1)得AM =559,∴CM =556,……………………………………(1分) Q DG =2,CD =AB =23,∴CG =22,QMPCPDG CG =, ∴PM =552,……………………………………………………………………(1分)由MP AM DE AD =得DE =32,………………………………………………………(1分) ∴AE =311323=+,………………………………………………………………(1分)第25题图2②当点G 在CD 的延长线上时,同①可得DE =32, ………………………………………………………………(1分) ∴AE =27333-=;………………………………………………………………(1分)第25题图3方法二:当点G 在线段CD 上时,Q AD P BC ,∴∠EAC =∠ACB , ∴∠EDC =∠BCD ,Q ∠B =∠BCD=45°,∴∠EDC =∠B , Q ∠APE =∠B , ∴∠APE=∠ EDC , ∴∠EGD =∠EAP , ∴∠EGD =∠ACB ,∴△ACB ∽△EGD ,……………………………………………………………(1分) ∴BA BCDE DG =, ∴2392=DE ,∴得DE =32,……………………………………………………………………(1分) ∴AE =311323=+,………………………………………………………………(1分) ②当点G 在CD 的延长线上时,ACB EGD △∽△, ……………………………………………………………(1分)同①可得DE =32,…………………………………………………………………(1分) ∴AE =37323=-.…………………………………………………………………(1分)第25题图4。
松江区二模考试数学试卷题(印刷稿)

高三数学 第1页 共4页松江区2016学年度第二学期期中质量监控试卷高三数学(满分150分,完卷时间120分钟) 2017.4一.填空题(本大题满分54分)本大题共有12题,考生必须在答题纸相应编号的空格内直接填写结果,第1~6题每个空格填对得4分,第7~12题每个空格填对得5分,否则一律得零分.1.已知()21x f x =-,则1(3)f -= ▲ .2.已知集合{}{}11,1,0,1,M x x N =+≤=-则M N = ▲ .3.若复数122,2z a i z i =+=+(i 是虚数单位),且12z z 为纯虚数,则实数a = ▲ .4.直线23x y ⎧=--⎪⎨=+⎪⎩(t 为参数)对应的普通方程是 ▲ .5.若()1(2),3nnn x x axbx c n n -*+=++++∈≥N ,且4b c =,则a 的值为 ▲ .6.某空间几何体的三视图如图所示,则该几何体的侧面积是 ▲ .7.若函数()2()1xf x x a =+-在区间[]0,1上有零点,则实数a 的取值范围是 ▲ .8.在约束条件123x y ++-≤下,目标函数2z x y =+的最大值为 ▲ .9.某学生在上学的路上要经过2个路口,假设在各路口是否遇到红灯是相互独立的,遇到红灯的概率都是13,则这名学生在上学路上到第二个路口时第一次遇到红灯的概率是 ▲ .10.已知椭圆()222101y x b b+=<<的左、右焦点分别为12F F 、,记122F F c =.若此椭圆上存在点P ,使P 到直线1x c=的距离是1PF 与PF b 的最大值为 ▲ .11.如图同心圆中,大、小圆的半径分别为2和1,点P 在大圆上,PA 与小圆相切于点A ,Q 为小圆上的点,则PA PQ ⋅的取值范围是▲ .高三数学 第2页 共4页12.已知递增数列{}n a 共有2017项,且各项均不为零,20171a =,如果从{}n a 中任取两项,i j a a ,当i j <时,j i a a -仍是数列{}n a 中的项,则数列{}n a 的各项和2017S = ▲ .二、选择题(本大题满分20分)本大题共有4题,每题有且只有一个正确答案,考生必须在答题纸相应编号上,将代表答案的小方格涂黑,选对得5分,否则一律得零分.13.设a b 、分别是两条异面直线12l l 、的方向向量,向量a b、夹角的取值范围为A ,12l l 、所成角的取值范围为B ,则“A α∈”是“B α∈”的 (A) 充要条件 (B) 充分不必要条件 (C) 必要不充分条件 (D) 既不充分也不必要条件 14. 将函数sin 12y x π⎛⎫=-⎪⎝⎭图像上的点,4P t π⎛⎫⎪⎝⎭向左平移(0)s s >个单位,得到点P ',若P '位于函数sin 2y x=的图像上,则(A) 12t =,s 的最小值为6π(B) t =,s 的最小值为6π(C) 12t =,s 的最小值为12π(D) 2t =,s 的最小值为12π15.某条公共汽车线路收支差额y 与乘客量x 的函数关系如图所示(收支差额=车票收入-支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(Ⅰ)不改变车票价格,减少支出费用;建议(Ⅱ)不改变支出费用,提高车票价格,下面给出的四个图形中,实线和虚线分别表示目前和建议后的函数关系,则 (A) ①反映了建议(Ⅱ),③反映了建议(Ⅰ) (B) ①反映了建议(Ⅰ),③反映了建议(Ⅱ) (C) ②反映了建议(Ⅰ),④反映了建议(Ⅱ) (D) ④反映了建议(Ⅰ),②反映了建议(Ⅱ)高三数学 第3页 共4页16.设函数()y f x =的定义域是R ,对于以下四个命题:(1) 若()y f x =是奇函数,则(())y f f x =也是奇函数; (2) 若()y f x =是周期函数,则(())y f f x =也是周期函数; (3) 若()y f x =是单调递减函数,则(())y f f x =也是单调递减函数;(4) 若函数()y f x =存在反函数1()y f x -=,且函数1()()y f x f x -=-有零点,则函数()y f x x =-也有零点.其中正确的命题共有 (A) 1个 (B) 2个 (C) 3个 (D) 4个三.解答题(本大题满分76分)本大题共有5题,解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤.17.(本题满分14分;第1小题6分,第2小题8分)直三棱柱111C B A ABC -中,底面ABC 为等腰直角三角形,AC AB ⊥,2==AC AB ,41=AA ,M 是侧棱1CC 上一点,设h MC =.(1) 若C A BM 1⊥,求h 的值;(2) 若2h =,求直线1BA 与平面ABM 所成的角.18.(本题满分14分;第1小题6分,第2小题8分)设函数()2xf x =,函数()g x 的图像与函数()f x 的图像关于y 轴对称.(1)若()4()3f x g x =+,求x 的值;(2)若存在[]0,4x ∈,使不等式3)2()(≥--+x g x a f 成立,求实数a 的取值范围.B高三数学 第4页 共4页19.(本题满分14分;第1小题6分,第2小题8分)如图所示,PAQ ∠是某海湾旅游区的一角,其中 120=∠PAQ ,为了营造更加优美的旅游环境,旅游区管委会决定在直线海岸AP 和AQ 上分别修建观光长廊AB 和AC ,其中AB 是宽长廊,造价是800元/米,AC 是窄长廊,造价是400元/米,两段长廊的总造价为120万元,同时在线段BC 上靠近点B 的三等分点D 处建一个观光平台,并建水上直线通道AD (平台大小忽略不计),水上通道的造价是1000元/米.(1) 若规划在三角形ABC 区域内开发水上游乐项目,要求ABC △的面积最大,那么AB 和AC 的长度分别为多少米?(2) 在(1)的条件下,建直线通道AD 还需要多少钱?20.(本题满分16分;第1小题4分,第2小题6分,第3小题6分)设直线l 与抛物线24y x =相交于不同两点A 、B ,与圆)0()5(222>=+-r r y x相切于点M ,且M 为线段AB 中点.(1) 若AOB △是正三角形(O 是坐标原点),求此三角形的边长; (2) 若4r =,求直线l 的方程;(3) 试对()0,r ∈+∞进行讨论,请你写出符合条件的直线l 的条数(直接写出结论).21.(本题满分18分;第1小题4分,第2小题6分,第3小题8分)对于数列{}n a ,定义12231n n n T a a a a a a +=+++ ,*n N ∈. (1) 若n a n =,是否存在*k N ∈,使得2017k T =?请说明理由; (2) 若13a =,61nn T =-,求数列{}n a 的通项公式;(3) 令21*112122,n n n nT T n b T T T n n N+--=⎧=⎨+-≥∈⎩,求证:“{}n a 为等差数列”的充要条件是“{}n a 的前4项为等差数列,且{}n b 为等差数列”.AB CPQ D。
2016上海各区初中数学二模试题及解答

十分遗憾最低的同学仍然只得了 56 了。这说明本次考试分数的众数是(
)
A、82;
B、91;
C、11;
D、56;
5、如果点 K、L、M、N 分别是四边形 ABCD 的四条边 AB、BC、CD、DA 的中点,且四边形 KLMN
是菱形,那么下列选项正确的是(
)
A、AB⊥BC;
B、AC⊥BD;
C、AB=BC;
6、如图 1,梯形 ABCD 中,AD∥BC,AB=DC,∠DBC=45°,
D、AC=BD;
AD
点 E 在 BC 上,点 F 在 AB 上,将梯形 ABCD 沿直线 EF 翻折,
F
使得点 B 与点 D 重合。如果 AD 1 ,那么 AF 的值是(
)
BC 4
BF
A、 1 ; 2
B、 3 ; 5
C、 2 ; 3
三、解答题(本大题共 7 题,满分 78 分)
19.(本题满分 10 分)
1
计算: 273 (
3
1)2
1 2
1
2 3 1
M C
N
B
A
(第 18 题图)
20.(本题满分 10 分)
解方程组:
x 2y 1
x2
3xy
2y2
0
21.(本题满分 10 分,其中每小题各 5 分)
如图,在平面直角坐标系 xOy 中,一次函数 y kx b (k 0) 的图像经过 A(0, 2) , B(1, 0)
BF 相交于 H,BF 与 AD 的延长线相交于 G.求证:
(1)CD=BH; (2)AB 是 AG 和 HE 的比例中项.
A
D
G
HF
B
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B
2016松江区初三数学二模试卷
一、 选择题
1. 下列各数是无理数的是( ) A.
22
7
;
D.16.
2. 下列式子中,属于最简二次根式的是( )
3. 在平面直角坐标系中,直线y=x -1经过( ) A.第一、二、三象限; B.第一、二、四象限; C.第一、三、四象限;
D.第二、三、四象限.
4. 某班一个小组7名同学的体育测试成绩(满分30分)依次为:27,29,27,25,27,30,25,这组数据的中位数和众数分别是( ) A.27,25;
B.25,27;
C.27,27;
D.27,30.
5. 如图,已知四边形ABCD 是平行四边形, 要使它成为菱形,那么需要添加的条件 可以是( ) A.AC ⊥BD ;
B.AB=AC ;
C.∠ABC=90°;
D.AC=BD.
6. 已知
的半径16r =,的半径为2r ,圆心距12O O =3,如果
与
有交点,那么2
r 的取值范围是( ) A.23r ≥;
B. 23r ≤
C.239r <<
D.239r ≤≤
二、 填空题
7. 因式分解:223a a -=____________;
8. 函数2
1y x =
-的定义域是____________; 9. 计算:()
23a b b -+
=____________;
10. 关于x 的一元二次方程220x x m -+=有两个实数根,则m 的取值范围是____________;
11. 不等式组1
2240
x x ⎧-≤⎪⎨⎪->⎩的解集为__________;
第5题图
12. 将抛物线22y x =-向左平移3个单位长度,再向上平移2个单位长度,所得抛物线的解析式为__________;
13. 反比例函数k
y x
=的图象经过点(1,2-),A (1x ,1y )、B (2x ,2y )是图象上另两点,其中120x x <<,则1y 、2y 的大小关系是__________________; 14. 用换元法解分式方程
13101x x x x --+=-时,如果设1
x y x
-=,将原方程化为关于y 的整式方程,那么这个整式方程是__________________________;
15. 某服装厂从20万件同类产品中随机抽取了100件进行质检,发现其中有2件不合格,那么你估计该厂这20万件产品中合格品约为________万件;
16. 从1到10的十个自然数中,随意取出一个数,该数为3的倍数的概率是________; 17. 某商品原价289元,经连续两次降价后售价为256元,设平时每次降价的百分率为x ,那么根据题意可列关于x 的方程是_______________________________; 18. 如图,梯形ABCD 中,AD ∥BC ,∠B=90°,AD =2,BC =5, E 是AB 上一点,将△BCE 沿着直线CE 翻折, 点B 恰好与D 点重合,则BE =_____________. 三、 解答题
19.
计算:(
)2
011 3.143π-⎛⎫-+-+ ⎪
⎝⎭
20. 解方程组:2
2
212...........32......x y x xy y +=⎧⎪⎨
-+⎪⎩①②
第18题图
A
F
E D
C
B
A
21. 已知气温的华氏度数y 是摄氏度数x 的一次函数,如图所示是一个家用 温度表的表盘。
其左边为摄氏温度的刻度和读数(单位℃).,右边为华氏 温度的刻度和读数(单位℉).观察发现表示与
的刻度线恰好
对齐(在一条水平线上),而表示
与
的刻度线恰好对齐。
(1) 求y 关于x 的函数关系式(不需要写出函数的定义域); (2) 当华氏温度为104时,温度表上摄氏温度为多少?
22. 如图,在△ABC 中,AB=AC=10,BC =12,AD ⊥BC 于点D ,O 为AD 上一点,以O 为圆心,OA 为半径的圆交AB 于G ,交BC 于E 、F ,且AG=AD . (1) 求EF 的长; (2) 求tan ∠BDG 的值。
23. 如图,已知等腰△ABC 中,AB=AC ,AD ⊥BC ,CE ⊥AB ,垂足分别为D 、E . (1) 求证:∠CAD=∠ECB ;
(2) 点F 是AC 的中点,联结DF ,求证:2BD FC BE =⋅.
第22题图
第23题图
N
24. 如图,平面直角坐标系xOy 中,已知()1,0B -,一次函数y=5x -+的图像与x 轴、y 轴分别交于A 、C 两点,二次函数2y x bx c =-++的图像经过点A 、点B . (1) 求这个二次函数的解析式;
(2) 点P 是该二次函数图像的顶点,求△APC 的面积;
(3) 如果点Q 在线段AC 上,且△ABC 与△AOQ 相似,求点Q 的坐标。
25. 已知,如图1,在梯形ABCD 中,AD ∥BC ,∠BCD =90°,BC=11,CD =6,tan ∠ABC =2,点E 在AD 边上,且AE=3ED ,EF ∥AB 交BC 于点F ,点M 、N 分别在射线FE 和线段CD 上。
(1) 求线段CF 的长;
(2) 如图2,当点M 在线段FE 上,且AM ⊥MN ,设FM ·cot ∠EFC=x ,CN=y ,求y 关于x 的函数解析式,并写出它的定义域;
(3) 如果△AMN 为等腰直角三角形,求线段
FM 的长。
第25题图1
第25题图2。
