类比探究题
类比探究(习题及答案)
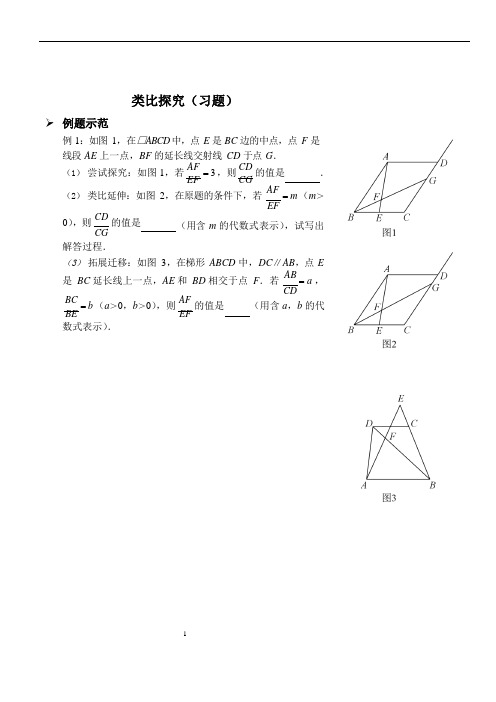
➢例题示范类比探究(习题)例1:如图1,在□ABCD 中,点E 是BC 边的中点,点F 是线段AE 上一点,BF 的延长线交射线CD 于点G.(1)尝试探究:如图1,若AF= 3 ,则CD的值是.EF CG(2)类比延伸:如图2,在原题的条件下,若AF=m (m>EF0),则CD的值是CG解答过程.(用含m 的代数式表示),试写出(3)拓展迁移:如图3,在梯形ABCD 中,DC∥AB,点E是BC 延长线上一点,AE 和BD 相交于点F.若AB=a ,CDBC=b(a>0,b>0),则AF的值是(用含a,b 的代BE EF 数式表示).1【思路分析】根据特征确定问题结构,设计方案解决第一问.问题背景是平行四边形,且已知线段比例关系,考虑通过相似传递比例关系,进而求 CD的值.CG构造相似利用作平行线的方法,即过中点 E 作 EH ∥AB 交 BG于点 H ,可得“A ”字型相似△BEH ∽△BCG ,“X ”型相似△EFH ∽△AFB ,结合 AF= 3 ,可得 CG =2EH ,AB =3EH ,故EFCD = 3 .CG 2类比第一问思路,解决第二问.分析不变特征,此时平行四边形、中点特征均不变,变化的是 AF ,EF 的比例,照搬第一问思路,过点 E 作 EH ∥AB 交BG 于点 H ,同样可得△BEH ∽△BCG ,△EFH ∽△AFB ,此时 CG =2EH ,AB =mEH ,故 CD = m.CG 2照搬思路解决第三问.虽然此问中图形、中点 E 、比例关系均发生变化,但 DC ∥AB 不变,依然可利用相似来整合条件,可照搬前面思路处理, 依然构造平行.过点 E 作 EH ∥AB 交 BD 的延长线于点 H ,可得△BCD ∽△BEH ,△AFB ∽△EFH ,可得 BC = CD,BE EHAF = AB ,结合 AB = a , BC = b ,可知 EF EH CD BE AF = AB = a ⋅CD = ab . EF EH EH212 3➢巩固练习1.如图1,一副直角三角板满足AB=BC,AC=DE,∠ABC=∠DEF=90°,∠EDF=30°.【操作】将三角板DEF 的直角顶点E 放置于三角板ABC 的斜边AC 上,再将三角板DEF 绕点E 旋转,并使边DE 与边AB 交于点P,边EF 与边BC 交于点Q.【探究】在旋转过程中,(1)如图2,当CE=1时,EP 与EQ 满足怎样的数量关系?EA并给出证明.(2)如图3,当CE= 2 时,EP 与EQ 满足怎样的数量关系?EA并给出证明.(3)根据你对(1),(2)的探究结果,试写出当CE=m时,EAEP 与EQ 满足的数量关系式为.3,=2.如图1,在等边三角形ABC 中,线段AD 为其内角角平分线,过点D 的直线B1C1⊥AC 于C1,交AB 的延长线于B1.(1)请你探究:AC =CD AC1 C1D 是否都成立?AB BD AB1DB1(2)请你继续探究:如图2,若△ABC 为任意三角形,线段AD 为其内角角平分线,请问AC=CD一定成立吗?并证明AB BD你的判断.(3)如图3,在Rt△ABC 中,∠ACB=90°,AC=8,AB=40,3E 为AB 上一点且AE=5,CE 交其内角角平分线AD 于F.试求DF的值.FA43.如图1,将两个完全相同的三角形纸片ABC 和DEC 重合放置,其中∠C =90°,∠B =∠E =30°.(1) 操作发现如图 2,固定△ABC ,使△DEC 绕点 C 旋转,当点 D 恰好落在 AB 边上时,填空:①线段 DE 与 AC 的位置关系是 ;②设△BDC 的面积为 S 1,△AEC 的面积为 S 2,则 S 1 与 S 2 的数量关系是.图 1图 2(2) 猜想论证当△DEC 绕点 C 旋转到图 3 所示的位置时,小明猜想(1) 中 S 1 与 S 2 的数量关系仍然成立,并尝试分别作出了△BDC 和△AEC 中 BC ,CE 边上的高,请你证明小明的猜想.(3) 拓展探究如图 4 , 已知∠ ABC =60°, 点 D 是其角平分线上一点, BD =CD =4,DE ∥AB 交 BC 于点 E .若在射线 BA 上存在点 F , 使 S △DCF =S △BDE ,请直.接.写.出.相应的 BF 的长.5➢思考小结总结类比探究问题中的常见结构①旋转结构始终含有等腰结构(正方形、等腰直角三角形等),并且经过旋转后,能将各条件重新组合应用.②中点结构平行夹中点(类)倍长中线中位线始终含有中点,常考虑利用中点结构补全图形,然后将所证目标放在一个较大的背景下(等腰三角形、直角三角形、等腰直角三角形等)研究.③直角结构始终含有直角,常构造直角与斜直角配合,得到同角的余角相等;再配合构造的其他直角证明相似,所求目标往往和比例关系相关.6④平行结构所求目标为线段间的比例关系,题目中没有相似三角形,往往考虑利用平行线构造相似求解.78 3 3 【参考答案】 ➢ 巩固练习1. (1)EP =EQ ,证明略;(2) EP = 1EQ ,证明略;2 (3) EP = 1EQ .m2. (1)都成立,证明略; (2)一定成立,证明略;(3) DF = 5 .FA 83. (1)①DE ∥AC ;②S 1=S 2.(2) 证明略; (3) BF 的长为4 3或 .38。
类比探究专题(一)——平行结构(含答案).docx

学生做题前请先回答以下问题问题1:类比探究问题的处理思路是什么?类比探究专题(一)一一平行结构一、单选题(共6道,每道16分)1.如图1, D是厶ABC的边BC上一点,过点D的一条直线交AC于点F,交BA的延长线于点E.AE(1)若BD二CD, CF=2AF,则巧童的值为()£A.2B. 21羽C. WD. 3答案:B 解题思路:如图,过点川作?tG" EC,交DE于点G,易得ZUFaAC肋,A A EG^ABED,.AG_AF _\ AG _ AE** ~CD~CF = 29 ~BD~~BE f设BD=CD=a,^\AG = -f2a.AE _ AG _ 2^ _ 1BE BD a 2即空的值为二BE 2难度:三颗星知识点:平行结构AE2.(上接第1题)(2)如图2,若BD=CD, CF=mAF,则巧应的值为((用含m的代数式表示)A.叨B.血丄C.2/D•加图2答案:D解题思路:如图,过点川作?1G" EG交DE于点G,易得△MGSACFZ), /\AEG^/\BED f.AG _,4F _ 1 AG _ AE** ~CD~CF = m9丽一旋’ 设BD=CD=a,则AG = -,ma.AE _AG _ 1即空的值为丄.BE m试题难度:三颗星知识点:平行结构3.(上接第1, 2题)(3)如图3,将原题改为“过点D的一条直线交AC的延长线于点F,交AEAB 于点E",若BD=nCD, CF=mAF,则的值为()(用含m, n的代数式表示)答案:c解题思路:如图,过点M 作AGllBC,交DE 的延长线于点G,易得厶0妙厶677), AAEG^ABED,.AG_AF _ 1 AG _ AE"~CD = CF~m 9 ~BD~1E 9设 BD= nCD=na f 则AG =—,ma・血 ■ ■ 卫G…BE BD na即竺 的值为 1---- ■BE mn 试题难度:三颗星知识点:平行结构4. 已知AD 是△ ABC 的中线,将BC 边所在直线绕点D 顺时针旋转°角,交AB 边于点M’交射线AC 于点N,设观二如'泗=陀(存0,尸0)1+1=2丄+丄显C.X 尹D.x 尹 °答案:c解题思路: (1)如图1, X 歹满足的函数关系式为(1+1 = 42B .X歹 图11如图,过点C作CEllAB,交胚V于点£,则厶NCES△也4胚・CN _ CE…AN = AM'・・・血)是厶ABC的中线,・\BD=CD・'/CEll BM,易得△3D遊△(?%,/. CE=BM,・CN _ BM"AN = AM'*.* AAf = xAB f AN = JL4C (x h 0, y h 0),BAI = AB—AAI = AB—x^4B , CN — AN— AC — \-AC- AC,•r.vAC — AC AB一xABvAC xAB整理得丄+丄=2,x y即丄与丄满足的函数关系式为2+丄=2・X V X V试题难度:三颗星知识点:平行结构5.(上接第4题)(2)如图2,当G是AD上任意一点时(点G不与点A重合),过点G的直线交AB 边于点皿' ,交AC 边于点“,设丄与丄AG=mAD,AM i = x i AB f百旷*^0(x70,”工0),则卍"满足的函数关系式为()丄+丄=2丄+丄工A.卅才 B .X ,X 21 12 —+ —=—— D 卅 y' m答案:D解题思路:如图,过点D 作MM"交43的延长线于点交47于点N,AM AD AN•' AG = utiD , AXf — x f AB , AV = X'r AC (x r h 0, y r h 0), JAf = AN = y^AC (x^O, y 0)由(1)可知,-+- = 2, x y.1 1 1 12 ..—+ — = ----- + ---- =—. x r v r wx mv m即丄与丄满足的函数关系式为1+1=- x v x v m6. (上接第4, 5题)(3)如图3,当G 是AD 上任意一点时(点G 不与点A 重合),过点G 的直线交 AB 边于点加,交 AC的延长线于点“,设CT难度:三颗星知识点:平行结构图2丄+丄乜 丄+丄/C.0 0D.* 歹" 答案:D解题思路:如图,过点。
类比探究题

类比探究题五年动态几何类比探究题动态几何类比探究题是一类综合性题目,常以三角形、四边形为背景,结合几何变换、几何模型、似结构、三线合一、面积等进行考查。
这类题目由特殊情形到一般情形,由简单情形到复杂情形逐步深入,问与问之间属递进关系,往往一题三问,第一问猜结论,第二问证结论,第一问用结论。
解决类比探究问题的一般方法是根据题干条件,结合分支条件先解决第一问,然后用解决上一问的方法类比解决下一问,如果不能,两问结合起来分析,找出不能类比的原因和不变特征,依据不变的特征,探索新的方法,也就是知识的迁移。
题型特征动态几何类比探究题中常见的题型特征有:1.动点问题:需要分析起点、终点、状态转折点,确定分段,常以速度已知的几何问题为主。
2.几何综合问题:常以三角形、四边形为背景,结合几何变换、几何模型、似结构、三线合一、面积等进行考查。
解题方法解决动态几何类比探究题的方法包括研究基本图形,找特征(中点、特殊角、折叠等)、找模型(相似、图形结构类似、问法类似等),常见不变结构及方法有直角,作横平竖直的线,找全等或相似;中点,作倍长,通过全等转移边和角;平行,找相似,转比例;旋转,找等边等角,证全等、相似或特殊图形等。
例题如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.填空:①AEB的度数为;②线段AD,BE之间的数量关系为.拓展探究如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.解决问题如图3,在正方形ABCD中,CD=,若点P满足PD=1,且∠BPD=90°,请直接写出点A到BP的距离。
2、如图1,在Rt△ABC中,∠B=90°,BC=2AB=8,点D和E分别是边BC和AC的中点,连接DE。
类比探究问题(习题及答案)

类比探究问题(习题)>例题示范例1:如图1,在正方形ABCD中,E, F分别是BC, CD上的点, 且ZE4F=45。
,则有结论EF=BE+DF成立.(1)如图2,在四边形ABCD中,AB=AD. ZB=ZD=90。
, E, F分别是BC, CD上的点,且ZEAF是ZB4D的一半,那么结论EF二BE+DF 是否仍然成立?若成立,请证明;若不成立,请说明理山.⑵ 如图3,若恪(1)中的条件改为:在四边形ABCD 4^,AB=AD.ZB+上ADC=180。
,延长SC到点E,延长CD到点F,使得ZEAF 仍然是ZBAD的一半,则结论EF二BE+DF是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.图1D图2F思路分析:1.题目中有旋转结构,可以类比.题U结论思路:如图1,延长CB到G,使BG二DF,根据已知条件容易证明^ ABG幻△ADF,由此可以推出ZBAG=ZD4F, AG=AF.而Z EAF』ABAD.2 所以得到ZDAF+ZBAE二ZEAF,进一步得到ZEAF二上EAG, 所以故EF=EG=BE+BG=BE+DF ・2.类比上面思路,解决笫一问•如图2,延长CB到G,使BG=DF, 根据已知条件容易证明^ABG^^ADF.山此可以推出ZBAG=ZD4F, AG=AF.而Z EAF=_ ZBAD,2 所以得到ZDAF+ZBAE二ZEAF,进一步得到ZEAF二上EAG, 所以△故EF=EG=BE+BG=BE+DF ・3.照搬思路解决第二问•结论EF=BE+DF不成立,应为EF=BE-DF.如图3,在BC上截取BG=DF, 山于ZB+ZAQC=180。
,Z/1DF+Z/IDC=18O^ 可以得到ZB=ZADF,所以△ABG幻△ADF,山此可以推出ZBAG=ZD4F, AG=AF.而Z EAF』ZBAD.2 所以得到ZEAF=ZEAG,所以△AEF竺△AEG,A)90。
△ADF空△ABG (SAS)I AAEF^AAEG (SAS)I故EF=EG=BE-BG=BE-DF ・D>巩固练习1.如图1,在正方形ABCD和正方形CGEF (CG>BC)中,点C, G在同一直线上,M是AE的中点.(1)探究线段MD, MF的位置关系及数量关系,并证明.(2)若将图1中的正方形CGEF绕点C顺时针旋转,使D, C, G三点在同一直线上,如图2,其他条件不变,则(1)中得到的两个结论是否发生变化?请写出你的猜想并加以证明.(3)若将图1中的正方形CGEF绕点C顺时针旋转,使正方形CGEF的对角线CE恰好与正方形ABCD的边在同一直线上,如图3,其他条件不变,则(1)中得到的两个结论是否发生变化?请写出你的猜想并加以证明.图2E2.在△ABC中,已知BC >AC.动点D绕△ABC'的顶点A逆时针旋转,丄LAD=BC,连接CD. E, F分别为AB, CD的中点,直线EF与直线AD眈分别交于点M, N.如图1,当点D旋转到BQ 的延长线上时,点N恰好与点Fifi合,取AC的中点H,连接HE, HF.根据三角形中位线定理和平行线的性质,可得结论ZAMF二ZBNE (无需证明).(1)当点D旋转到图2中的位置时,ZAMFLj ZBNE有何数量关系?请写出猜想,并给出证明.(2)当点Q旋转到图3中的位置时,ZAMF与ZBNE有何数量关系?请直接写出结论.3.已知AABC,以△ABC的边4C为直角边向外作等腰直角三角形ABE和等腰直角三角形ACD AB=AE. AC=AD. ZBAE= ZCAD=90\ M 是BC中点,连接AM, DE.(1)如图1,在△ABC中,当ZB4C二90。
专题:动点引起的类比探究综合题

专题四十二:动点引起的类比探究综合题方法点睛解决动点引起的类比探究题的一般思路通常需要先分析点在线段上运动的情况,运用相关知识,得到相关结论,再将问题进行升华,探究点在线段延长线上或反向延长线上的情况,抓住运动过程中不变的量和探究对象之间的关系,通过研究基本图形,分析运动过程,从特殊再到一般来解决问题.典例分析例.(2022鄂尔多斯中考)(12分)在△ABC中,AB=AC,∠BAC=90°,AD是△ABC的角平分线.(1)如图1,点E、F分别是线段BD、AD上的点,且DE=DF,AE与CF的延长线交于点M,则AE与CF的数量关系是,位置关系是;(2)如图2,点E、F分别在DB和DA的延长线上,且DE=DF,EA的延长线交CF于点M.①(1)中的结论还成立吗?如果成立,请给出证明;如果不成立,请说明理由;②连接DM,求∠EMD的度数;③若DM=6,ED=12,求EM的长.(1)如图1,在△ABC 中,AB =AC .①BD ,CE 是△ABC 的角平分线.求证:BD =CE .②点D ,E 分别是边AC ,AB 的中点,连接BD ,CE .求证:BD =CE .(从①②两题中选择一题加以证明)(2)猜想:用数学的眼光观察经过做题反思,小明同学认为:在△ABC 中,AB =AC ,D 为边AC 上一动点(不与点A ,C 重合).对于点D 在边AC 上的任意位置,在另一边AB 上总能找到一个与其对应的点E ,使得BD =CE .进而提出问题:若点D ,E 分别运动到边AC ,AB 的延长线上,BD 与CE 还相等吗?请解决下面的问题:如图2,在△ABC 中,AB =AC ,点D ,E 分别在边AC ,AB 的延长线上,请添加一个条件(不再添加新的字母),使得BD =CE ,并证明.(3)探究:用数学的语言表达如图3,在△ABC 中,AB =AC =2,∠A =36°,E 为边AB 上任意一点(不与点A ,B 重合),F 为边AC 延长线上一点.判断BF 与CE 能否相等.若能,求CF 的取值范围;若不能,说明理由.专题过关1.(2022威海中考)回顾:用数学的思维思考(1)如图1,当点G 在BC 边上时,写出PG 与PC 的数量关系.(不必证明)(2)如图2,当点F 在AB 的延长线上时,线段PC 、PG 有怎样的数量关系,写出你的猜想,并给予证明;(3)如图3,当点F 在CB 的延长线上时,线段PC 、PG 又有怎样的数量关系,写出你的猜想(不必证明).2.(2022牡丹江中考)在菱形ABCD 和正三角形BGF 中,60ABC ∠=︒,P 是DF 的中点,连接PG 、PC .点B C 、重合),过点D 作DE AD ⊥,交射线AB 于点E.(1)分别探索以下两种特殊情形时线段AE 与BE 的数量关系,并说明理由;①点E 在线段AB 的延长线上且BE BD =;②点E 在线段AB 上且EB ED =.(2)若6AB =.①当2DE AD =时,求AE 的长;②直接写出运动过程中线段AE 长度的最小值.3.(2022扬州中考)如图1,在ABC ∆中,90,60BAC C ∠=︒∠=︒,点D 在BC 边上由点C 向点B 运动(不与D 从O 点出发,沿OM 方向运动.当点D 不与点A 重合时,将线段CD 绕点C 逆时针方向旋转60°得到CE .连接BE ,DE.(1)如图1,当点D 在线段OA 上运动时,线段BD 、BE 、BC 之间的数量关系是______,直线AD 和直线BE 所夹锐角的度数是______;(2)如图2,当点D 运动到线段AB (不与A 点重合)上时,(1)中的结论是否仍然成立,若成立,请说明理由;若不成立,请写出正确的结论并说明理由;(3)如图3,将ABC 改为等腰直角三角形,其中斜边6AB =,其它条件不变,以CD 为斜边在其右侧作等腰直角三角形CDE ,连接BE ,请问BE 是否存在最小值,若存在,直接写出答案;若不存在,说明理由.4.(2022河南西平一模)如图1,ABC 是边长为6cm 的等边三角形,边AB 在射线OM 上,且9OA =cm .点BE 与CD 交于点P .试判断:①∠BPD 的度数为______;②线段PB ,PD ,PE 之间的数量关系:PB______PD+PE .(填写“>”或“<”或“=”)(2)若点E 是边AC 所在射线AC 上一动点(102CE AC <<).按下列步骤画图:(ⅰ)连接BE ,作点A 关于BE 所在直线的对称点D ,连接BD ;(ⅱ)作射线DC ,交BE 所在直线于点P .小明所做的图形如图2所示,他猜想:PB PD PC =+.下面是小明的思考过程:如图2,延长PD 到F ,使得DF PC =,连接BF .发现BPC BFD △△≌,从而得到BP BF =,又因为60ABC ∠=︒所以可得60PBF ∠=︒,进而得到PBF △为等边三角形,从而得到线段PB ,PC ,PD 之间关系是PB PD PC =+.小华同学画图时,把点E 标在了边AC 的延长线上,请就图3按要求画出图形,猜想线段PB ,PC ,PD 之间的数量关系,并说明理由.(3)如图4,在ABC 中,若90ABC ∠=︒,AB BC =,点E 是射线AC 上一动点(102CE AC <<),连接BE ,作点A 关于直线BE 的对称点D ,连接DC ,射线DC 与射线BE 交于点P ,若PC m =,PB n =,请直接用m ,n 表示PD的长.5.(2022平顶山二模)(1)如图1,已知△ABC 是等边三角形,D ,E 分别为边AB ,AC 的中点,连接BE ,CD ,直线MN 上一点,连接AP ,将线段PA 绕点P 顺时针旋转90得到线段PQ ,连接AQ ,CQ.(1)【问题发现】如图1,当点P 与点M 重合时,线段CQ 与PN 的数量关系是,∠ACQ=°.(2)【探究证明】当点P 在射线MN 上运动时(不与点N 重合),(1)中结论是否一定成立?请利用图2中的情形给出证明.(3)连接PC ,当△PCQ 是等边三角形时,请直接写出AB PN的值.6.(2022郑州外国语三模)在△ABC 中,AB AC =,90BAC ∠=,点M ,N 分别是AC ,BC 的中点,点P 是一点,连接AP ,将线段PA 绕点P 顺时针旋转90°得到线段PM ,连接AM ,CM.(1)问题发现如图(1),当点P 与点D 重合时,线段CM 与PE 的数量关系是,∠ACM =°.(2)探究证明当点P 在射线ED 上运动时(不与点E 重合),(1)中结论是否一定成立?请仅就图(2)中的情形给出证明.(3)问题解决连接PC ,当△PCM 是等边三角形时,请直接写出AC PE 的值.7.(2022信阳三模)在△ABC 中,AB =AC ,∠BAC =90°,点D ,E 分别是AC ,BC 的中点,点P 是直线DE 上不与点A ,B 重合),以CD 为边作正方形CDEF ,连接AE ,AF.(1)观察猜想当点D 在线段AB 上时,线段BD 与AF 的数量关系是______,∠CAE 的度数是______.(2)探究证明当点D 不在线段AB 上时,(1)中的两个结论是否仍然成立?如果成立,请仅就图2的情形进行证明;如果不成立,请说明理由.(3)解决问题当BD AE 的长.8.(2022河南天一大联考)如图1,在△ABC 中,∠ACB =90°,AC =BC =3,点D 是直线AB 上一动点(点D连接AD,把AD绕点A逆时针旋转90°得到AE,连接DE,F,G分别是DE,CD的中点,连接FG.【特例感知】(1)如图1,当点D是BC的中点时,FG与BD的数量关系是,FG与直线BC的位置关系是;【猜想论证】(2)当点D在线段BC上且不是BC的中点时,(1)中的结论是否仍然成立?①请在图2中补全图形;②若成立,请给出证明;若不成立,请说明理由.【拓展应用】(3)若AB=AC=,其他条件不变,连接BF、CF.当△ACF是等边三角形时,请直接写出△BDF 的面积.9.(2022河南社旗一模)在Rt△ABC中,∠BAC=90°,AB=AC,动点D在直线BC上(不与点B,C重合),10.(2022三门峡一模)问题情境:如图1,M是线段AB上任意一点(不与点A,B重合),分别以AM和BM为斜边在AB同侧构造等腰直角三角形.AMC和等腰直角三角形BMD,连接CD,取AB中点E,CD中点F,连接EF(1)观察猜想:如图2,当点M与点E重合时,EF与CD之间的数量关系为______;(2)延伸探究:如图3,当点M与点E不重合时,问题(1)中的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;AB ,线段EF是否存在最小值?若存在,请直接写出最小值;若不存在,请说(3)应用提升:如图3,若2cm明理由.线AD、EC上的动点,且AP,连结BP,PQ,过点B,Q分别作PQ,BP的平行线交于点F.(1)当点P在线段AE上(不包含端点)时,①求证:四边形BFQP是正方形;②若BC将四边形BFQP的面积分为1:3两部分,求AP的长;(2)如图2,连结PF,若点C在对角线PF上,求△BFC的面积(直接写出答案)11.(2022苏州中学三模)如图,在矩形ABCD中,AD=2AB=8,点E是边AD的中点.连结EC,P、Q分别是射点,连接BE ,过点C 作BE 的垂线交AD 于点F ,试猜想BE 与CF 的数量关系.【类比探究】(2)如图2,在矩形ABCD 中,4AB =,6BC =,G 为边AB 上的一个点,E 为边CD 延长线上的一个点,连接GE 交AD 于点H ,过点C 作GE 的垂线交AD 于点F ,试猜想GE 与CF 的数量关系并说明理由.【拓展延伸】(3)如图3,在正方形ABCD 中,点E 从点B 出发沿射线BC 运动,连接AE ,过点B 作AE 的垂线交射线CD 于点F ,过点E 作BF 的平行线,过点F 作BC 的平行线,两平行线交于点H .当点E 运动的路程为8时,请直接写出点H运动的路径长度.12.(2022南阳淅川一模)【问题发现】(1)如图1,在矩形ABCD 中,4AB =,6BC =,E 为边DC 上的一个其中∠ECF =90°,过点F 作FG ⊥BC 交BC 的延长线于点G ,连接DF 交CG 于点H.(1)发现如图1,若AB =AD ,CE =CF ,猜想线段DH 与HF 的数量关系是______(2)探究如图2,若AB =nAD ,CF =nCE ,(1)中的猜想是否仍然成立?若成立,请给予证明;若不成立,请说明理由.(3)拓展在(2)的基础上,若FC 的延长线经过AD 的三等分点,且AD =3,AB =4,请直接写出线段EF 的值13.(2022平顶山一模)点E 是矩形ABCD 边AB 延长线上一动点(不与点B 重合),在矩形ABCD 外作Rt △ECF(1)如图1,当点E在边AB上时,DE⊥DF,且B,C,F三点共线.求证:AE=CF;(2)如图2,当点E在正方形ABCD外部时,DE⊥DF,AE⊥EF,且E,C,F三点共线.猜想并证明线段AE,CE,DE之间的数量关系;(3)如图3,当点E在正方形ABCD外部时,AE⊥EC,AE⊥AF,DE⊥BE,且D,F,E三点共线,DE与AB交于G点.若DF=3,AE,求CE的长.14.(2022驻马店六校联考二模)已知正方形ABCD,E,F为平面内两点.不与点B 、点C 重合),以AD 为边在AD 右侧作正方形ADEF ,连接CF.(1)观察发现:如图1,当点D 在线段BC 上时,①BC 、CF 的位置关系为___________;②BC 、CD 、CF 之间的数量关系为___________.(2)探究证明:如图2,当点D 在线段CB 的延长线上时,(1)中的两个结论是否仍然成立?请说明理由.(3)问题解决:如图3,当点D 在线段BC 的延长线上时,延长BA 交CF 于点G ,连接GE.若AB =,4BC CD =时,直接写出GE 的长.15.(2022河南新野一模)在ABC 中,22BAC ABC ACB ∠=∠=∠,D 是BC 所在直线上的一个动点(点D(1)△ABC 是边长为3的等边三角形,E 是边AC 上的一点,且AE=1,小亮以BE 为边作等边三角形BEF ,如图(1)所示.则CF 的长为.(直接写出结果,不说明理由)(2)△ABC 是边长为3的等边三角形,E 是边AC 上的一个动点,小亮以BE 为边作等边三角形BEF ,如图(2)所示.在点E 从点C 到点A 的运动过程中,求点F所经过的路径长.思路梳理并填空:当点E 不与点A 重合时,如图,连结CF ,∵△ABC 、△BEF 都是等边三角形∴BA=BC ,BE=BF ,∠ABC=∠EBF=60°∴①∠ABE+=∠CBF+;∴∠ABE=∠CBF∴△ABE ≌△CBF∴∠BAE=∠BCF=60°又∠ABC=60°∴∠BCF=∠ABC∴②______∥______;当点E 在点A 处时,点F 与点C 重合.当点E 在点C 处时,CF=CA .∴③点F 所经过的路径长为.(3)△ABC 是边长为3的等边三角形,M 是高CD 上的一个动点,小亮以BM 为边作等边三角形BMN ,如图(3)所示.在点M 从点C 到点D 的运动过程中,求点N所经过的路径长.16.(2022河南方城一模)在数学兴趣小组活动中,小亮进行数学探究活动.作正方形BFGH ,其中点F ,G 都在直线AE 上,如图(4).当点E 到达点B 时,点F ,G ,H 与点B 重合.则点H 所经过的路径长为.(直接写出结果,不说明理由)(4)正方形ABCD 的边长为3,E 是边CB 上的一个动点,在点E 从点C 到点B 的运动过程中,小亮以B 为顶点。
四边形之类比探究(一)(习题及答案)

四边形之类比探究(一)(习题)例题示范例1:已知等腰三角形ABC 中,∠ACB =90°,点E 在AC 的延长线上,且∠DEC =45°,M ,N 分别是DE ,AE 的中点,连接MN ,交直线BE 于点F .当点D 在CB 的延长线上时,如图1所示,易证MF +FN =1BE .2(1)如图2,当点D 在CB 边上时,上述结论是否成立?若成立,请给出证明;若不成立,请写出你的猜想,并说明理由.(2)当点D 在BC 的延长线上时,如图3所示,请直接写出线段MF ,FN ,BE 之间的数量关系(不需要证明).1【思路分析】1.里面有多个中点,考虑中位线,先证明易证的思路.连接AD ,由中位线定理可知MN =1AD ,2由题意可证△ACD ≌△BCE ,得到AD =BE ,即MN =1BE ,2所以MF +FN =1BE .22.照搬易证的思路解决第一问.连接AD ,由中位线定理可知MN =1AD ,2由题意可证△ACD ≌△BCE ,得到AD =BE ,即MN =1BE ,2所以NF -MF =1BE .23.照搬易证的思路解决第二问.连接AD ,由中位线定理可知MN =1AD ,2由题意可证△ACD ≌△BCE ,得到AD =BE ,即MN =1BE ,2所以MF -NF =1BE .2【过程书写】证明:(1)不成立,理由如下:连接AD ,在△AED 中,M 是DE 的中点,N 是AE 的中点,∴MN 是中位线∴MN =1AD2在等腰三角形ABC 中,∠ACB =90°∴AC =CB ,∵∠ACB =90°,∠DEC =45°∴CD =CE∴△ACD ≌△BCE (SAS )∴AD =BE∴MN=1BE 2∴FN-MF=1BE 2(2)MF-FN=1BE 2巩固练习1.已知△ABC是等边三角形,D是直线BC上一动点(不与点B,C重合),以AD为边作菱形ADEF(A,D,E,F按逆时针排列),使∠DAF=60°,连接CF.(1)如图1,当点D在BC边上时,求证:①BD=CF;②AC=CD+CF.(2)如图2,当点D在BC的延长线上时,其他条件不变,结论AC=CD+CF是否仍成立?若成立,请证明;若不成立,请写出AC,CD,CF之间的数量关系,并说明理由.(3)如图3,当点D在CB的延长线上时,其他条件不变,探究AC,CD,CF之间的数量关系.图1图2图32.如图1,C是线段BG上一点,分别以BC,CG为边,向外作正方形BCDA和正方形CGEF,使点D落在线段CF上,M是AE的中点,连接DM,FM.(1)求证:DM=FM,DM⊥FM.(2)如图2,将正方形CGEF绕点C顺时针旋转45°,其他条件不变,探究线段DM,FM之间的关系,并加以证明.(3)如图3,将正方形CGEF绕点C旋转任意角度,其他条件不变,探究线段DM,FM之间的关系,并加以证明.图1图2图33.(1)如图1,△ABC和△BDE都是等腰直角三角形,AB⊥AC,BD⊥DE,点D在AB边上.取CE的中点F,连接AF,DF,猜想AF,DF之间的数量关系和位置关系,并加以证明.(2)将△BDE旋转至如图2所示的位置,使点E在AB的延长线上,点D在CB的延长线上,其他条件不变,判断(1)中AF,DF之间的数量关系和位置关系是否发生变化,并加以证明.图1图2【参考答案】巩固练习1.(1)证明略.提示:证明△ABD≌△ACF,得到BD=CF,进而得到AC=CD+CF.(2)AC=CF-CD,理由略.(3)AC=CD-CF.2.(1)证明略.提示:延长DM,交EF于点H.证明△ADM≌△EHM(ASA),得到AD=EH,DM=HM,进而得到△DFH是等腰直角三角形,所以DM=FM,DM⊥FM.(2)DM=FM,DM⊥FM,证明略.提示:延长DM,交CE于点H,连接DF,HF.证明△ADM≌△EHM(ASA),得到AD=EH,DM=HM,再证明△CDF≌△EHF(SAS),得到DF=HF,∠CFD=∠EFH,进而得到△DFH是等腰直角三角形,则可得证.(3)DM=FM,DM⊥FM,证明略.提示:过点E作EH∥AD,交DM的延长线于点H,连接DF,HF.3.(1)AF=DF,AF⊥DF,证明略.提示:延长DF,交AC于点H.证明△DEF≌△HCF,得到DE=HC,DF=HF,进而得到△ADH是等腰直角三角形,所以AF=DF,AF⊥DF.(2)(1)中AF,DF之间的数量关系和位置关系不发生变化,证明略.提示:过点C作CH∥DE,交DF的延长线于点H,连接AD,AH.。
类比探究问题(含答案)

类比探究问题(讲义)➢ 课前预习1. 类比探究是一类共性条件与特殊条件相结合,由特殊情形到一般情形(或由简单情形到复杂情形)逐步深入,解决思想方法一脉相承的综合性题目,常以几何综合题为主.2. 解决类比探究问题的一般方法:(1)根据题干条件,结合_______________先解决第一问; (2)用解决_______的方法类比解决下一问,整体框架照搬. 整体框架照搬包括_________________,________________, _________________.3. 用铅笔做讲义第1,2题,并将计算、演草保留在讲义上,先看知识点睛,再做题,思路受阻时(某个点做了2~3分钟)重复上述动作,若仍无法解决,课堂重点听.➢ 知识点睛1. 类比探究属于几何综合题,类比(__________,___________,___________)是解决此问题的主要方法,做好类比需要把握变化过程中的____________. 2. 类比探究问题中常见结构举例①旋转结构AB=AC DCD'A②中点结构ABCE MDA BMCNM A(类)倍长中线 平行夹中点 中位线➢ 精讲精练1. 原题:如图1,点E ,F 分别在正方形ABCD 的边BC ,CD 上,∠EAF =45°,连接EF ,易证EF =BE +DF .图1B C DEF A(1)类比引申:如图2,在四边形ABCD 中,AB =AD ,∠BAD =90°,∠B +∠D =180°,点E ,F 分别在边BC ,CD 上,∠EAF =45°,连接EF ,则原题中的结论是否仍然成立?请说明理由.AF E DCB 图2(2)联想拓展:如图3,在△ABD 中,∠BAD =90°,AB =AD ,点E ,F 均在边BD 上,且∠EAF =45°.猜想EF ,BE ,DF 之间满足的数量关系,并写出推理过程.图3B DEF A2. 在△ABC 中,∠ACB =90°,∠A < 45°,O 为AB 的中点,一个足够大的三角板的直角顶点与点O 重合,一边OE 经过点C ,另一边OD 与AC 交于点M .(1)如图1,当∠A =30°时,求证:222MC AM BC =+. (2)如图2,当∠A ≠30°时,(1)中的结论是否仍然成立?如果成立,请说明理由;如果不成立,请写出你认为正确的结论,并说明理由.(3)如图3,将三角板ODE 绕点O 旋转,若直线OD 与线段AC 的延长线相交于点M ,直线OE 与线段CB 的延长线相交于点N ,连接MN ,则MN 2=AM 2+BN 2成立吗?请说明理由.N图3E BC O MD A图1EBCOMD AADM OCBE图23.已知P是Rt△ABC的斜边AB上一动点(不与点A,B重合),分别过点A,B向直线C P作垂线,垂足分别为点E,F,Q为斜边AB的中点.(1)如图1,当点P与点Q重合时,AE与BF的位置关系是___________,QE与QF的数量关系是______________.图1B CQ(P)EFA(2)如图2,当点P不与点Q重合时,试判断QE与QF的数量关系,并给予证明.A FEPQCB 图2(3)如图3,当点P在线段BA(或AB)的延长线上时,(2)中的结论是否仍然成立?请画出图形并给予证明.4.某校活动小组在作三角形的拓展图形,研究其性质时,经历了如下过程.(1)操作发现:在等腰△ABC中,AB=AC,分别以AB和AC为斜边,向△ABC 的外侧作等腰直角三角形,如图1所示,其中DF⊥AB于点F,EG⊥AC于点G,M是BC的中点,连接MD和ME,则下列结论正确的是___________.(填写序号)①12AF BA AG==;②MD=ME;③MD⊥ME.(2)数学思考:在任意△ABC中,分别以AB和AC为斜边,向△ABC的外侧作等腰直角三角形,如图2所示,M是BC的中点,连接MD和ME,则MD与ME具有怎样的数量关系和位置关系?请给出证明.(3)类比探究:在任意△ABC中,仍分别以AB和AC为斜边,向△ABC的内侧作等腰直角三角形,如图3所示,M是BC的中点,连接MD和ME,则△MED是_____________三角形.图1CD EF GMBA图2C DEMA图3AB CMDE【参考答案】➢课前预习2.(1)分支条件(2)第一问;照搬字母,照搬辅助线,照搬思路➢知识点睛1.类比字母,类比辅助线,类比思路,不变特征➢精讲精练1.(1)原题中的结论仍成立,理由略提示:延长CD到点G,使DG=BE,证明△ABE≌△ADG(SAS);再证明△AEF ≌△AGF(SAS),得EF=FG=BE+DG。
类比探究(人教版)(含答案)

类比探究(人教版)一、单选题(共9道,每道11分)1.如图1,△ABC的边BC在直线l上,AC⊥BC,且AC=BC;△EFP的边FP也在直线l上,边EF与边AC重合,且EF=FP.如图1,易证AB=AP,且AB⊥AP.(1)将△EFP沿直线l向左平移到图2的位置时,EP交AC于点O,连接AP,BO.则BO与AP所满足的数量及位置关系是( )A.相等但不垂直B.不相等但垂直C.相等且垂直D.不相等也不垂直答案:C解题思路:试题难度:三颗星知识点:类比探究2.(上接第1题)(2)将△EFP沿直线l继续向左平移到图3的位置时,EP的延长线交AC 的延长线于点O,连接AP,BO.此时,BO与AP的数量关系和位置关系是( )A.相等但不垂直B.不相等但垂直C.相等且垂直D.不相等也不垂直答案:C解题思路:试题难度:三颗星知识点:类比探究3.已知:如图,在Rt△ABC中,AB=BC,∠ABC=90°.一块等腰直角三角板的直角顶点放在斜边AC的中点O处,将三角板绕点O旋转,三角板的两直角边分别交AB,BC或其延长线于点E,F,图1,图2是旋转三角板所得图形的两种情况.(1)如图1,当点E和点F分别在AB和BC边上时,OE和OF的大小关系是( )A.OE>OFB.OE=OFC.OE<OFD.无法确定答案:B解题思路:试题难度:三颗星知识点:类比探究4.(上接第3题)(2)如图2,当点E和点F分别在AB和BC边的延长线上时,OE和OF的大小关系是( )A.OE>OFB.OE=OFC.OE<OFD.无法确定答案:B解题思路:试题难度:三颗星知识点:类比探究5.如图1,在正方形ABCD和正方形CGEF(CG>BC)中,点B,C,G在同一直线上,点M是AE的中点。
(1)探究线段MD,MF的位置关系,并证明。
解题思路:(1)小明猜测MD⊥MF,看到图1中M是AE的中点,并且AD∥EF,考虑延长DM交EF于点H,如下图,先利用全等三角形的判定定理_____,证明_____,由全等的性质可以得到_____,所以CD=EH,进而可以得到FD=FH,在等腰△DFH中,由等腰三角形三线合一可以得到_____,从而证明结论。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
五年动态几何、类比探究题
动态几何类比探究题;类比探究10年8考,动态几何考查年(09年、16年),类比探究性问题是一类共性条件与特殊条件相结合,由特殊情形到一般情形,由简单情形到复杂情形逐步深入,是利用类比的思想方法解决问题的一脉相承的综合性题目,问与问之间属递进关系,往往一题三问,第一问猜结论,第二问证结论,第一问用结论。
解决类比探究问题的一般方法:1、根据题干条件,结合分支条件先解决第一问;2、用解决上一问的方法类比解决下一问,如果不能,两问结合起来分析,找出不能类比的原因和不变特征,依据不变的特征,
1、(2014年)(1)问题发现
如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.
填空:
①AEB的度数为;
②线段AD,BE之间的数量关系为.
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.
(3)解决问题
如图3,在正方形ABCD中,CD=,若点P满足PD=1,且∠BPD=90°,请直接写出点A 到BP的距离.
2、(2015年)如图1,在Rt△ABC中,∠B=90°,BC=2AB=8,点D,E分别是边BC,AC的中点,连接DE.将△EDC绕点C按顺时针方向旋转,记旋转角为α
(1)问题发现
①当α=0°时,;②当α=180°时,.
(2)拓展探究
试判断:当0°≤α<360°时,的大小有无变化?请仅就图2的情形给出证明.(3)问题解决
当△EDC旋转至A,D,E三点共线时,直接写出线段BD的长.
3、(2016年)(10分)(1)问题如图1,点A为线段BC外一动点,且BC=a,AB=b。
填空:当点A位于时线段AC的长取得最大值,且最大值为
(用含a,b的式子表示)
(2)应用
点A为线段B除外一动点,且BC=3,AB=1.如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE.
①请找出图中与BE相等的线段,并说明理由
②直接写出线段BE长的最大值.
(3)拓展
如图3,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=900.请直接写出线段AM长的最大值及此时点P的坐标。
4、(2017年)如图1,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)观察猜想
图1中,线段PM与PN的数量关系是,位置关系是;
(2)探究证明
把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN 的形状,并说明理由;
(3)拓展延伸
把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN面积的最大值.
5、(2018年)(1)问题发现
如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.填空:
①的值为_____________;
②∠AMB的度数为_____________.
(2)类比探究
如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC
交BD的延长线于点M.请判断的值及∠AMB的度数,并说明理由.
(3)拓展延伸
在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M.若OD=1,OB=,请直接写出当点C与点M重合时AC的长.
图1 图2 备用图。
