声学PML方法理论1
pml边界条件表达式

pml边界条件表达式标题:PML边界条件表达式的应用实例引言:在计算物理领域中,PML(Perfectly Matched Layer)边界条件表达式是一种用于模拟波动现象的重要工具。
它能够有效地吸收入射波并减少反射,从而更准确地模拟真实环境中的物理现象。
本文将通过一个实例来详细介绍PML边界条件表达式的应用。
1. 实例背景假设我们需要研究声波在水中的传播过程,并对其进行数值模拟。
为了尽可能准确地模拟真实的水中声波传播,我们需要考虑水体边界的影响。
这时,PML边界条件表达式就能派上用场了。
2. PML边界条件表达式的原理PML边界条件表达式是一种人工引入的吸收层,通过改变模拟区域的边界条件来模拟波的衰减。
其核心思想是在边界处引入一个复杂的阻尼层,使入射波能够被吸收而不产生反射。
3. PML边界条件表达式的数学形式PML边界条件表达式的具体形式较为复杂,但我们可以简要介绍一下其基本形式。
在二维情况下,PML边界条件表达式可以写为:Ex = Ex * exp(-σm*dt)Ey = Ey * exp(-σm*dt)其中,Ex和Ey分别表示电场在x和y方向的分量,σm为阻尼因子,dt为时间步长。
4. PML边界条件在声波传播模拟中的应用在声波传播模拟中,我们可以通过将PML边界条件表达式应用于模拟区域的边界来减少声波的反射。
通过调整阻尼因子和时间步长,我们可以控制声波在边界处的衰减程度,使其更贴近真实情况。
5. 结论PML边界条件表达式是一种有效的数值模拟工具,能够减少波动现象模拟中的反射,并提高模拟结果的准确性。
在声波传播模拟等领域中,PML边界条件表达式的应用具有重要的意义。
通过合理调整参数,我们能够更好地模拟真实环境中的物理现象。
总结:通过以上实例,我们详细介绍了PML边界条件表达式在声波传播模拟中的应用。
通过引入复杂的阻尼层,PML边界条件能够有效地吸收入射波并减少反射,提高模拟结果的准确性。
一类带PML声波导中的共轭特征函数构造及其应用

关 键
词 : l o z 程 ;完 美 匹配层 ; 轭 特 征 函数 ;坐标 计 算 He mh h 方 共
文献标识码 : A 文 分 类 号 : 7 . Ol 5 9
Z HU in xn,QI Ja — i AN e— iDe a t n / M ah ma is W i we( p rme t0 t e tc ,Zh Ja g Un v riy,Ha g h u3 0 2 ,Ch n ) e i n ie st n z o 1 0 7 ia Co sr cino O j g t ie f n to sa d i p l a in f racaso c u t a vg ie t M L. o r a f n tu t fCn u aeeg n u cin n t a p i t o ls fa o si lwa e ud swih P o s c o c J u n lo Z ein iest ( ce c io ) 0 7 3 ( ) 6 5 6 8 h j gUnv r i S in eEdt n ,2 0 , 4 6 : 0 ~ 0 a y i
a d tec nu a ef n to s n h o j g t u cin .Ont eo h rh n ,asmpea d c n e in o muai ie Oc lu aet ec o dn ts h t e a d i l n o v ne tfr l sgv nt ac lt h o r iae
telc lb s swh n t ee u t ni ov d b o u rc l r hn to s h o a a e e h q ai ss le ys men meia ma c ig meh d .Th q ain o h o jg t i o ee u to ft ec nu aee—
TTI介质声波方程分裂式PML吸收边界条件研究

TTI介质声波方程分裂式PML吸收边界条件研究张衡;刘洪;李博;丁仁伟;李丽青;李福元【摘要】We study split perfectly matched layer (SPML) absorbing boundary conditions for TTI media based on the characteristics of TTI media acoustic wave equation.We firstly summarize several common TTI media acoustic wave equations and compare these wave equations in detail from the perspective of wavefield propagation stability for TTI media.We conclude that the TTI acoustic approximation equation introduced SV-wave component is applicable for TTI media.Then we derive the TTI media first-order acoustic wave equation based on the SPML boundary condition from the TTI P-wave and SV-wave coupled second-order wave equation.Afterwards we give the concrete implementation method for high-order staggered-grid finite-difference algorithm.The numerical modeling examples show that the SPML boundary condition can absorb the artificial boundary reflection very well.The boundary reflection absorbing effect of the proposed SPML algorithm is much better compared with the optimal sponge boundary condition.%针对倾斜横向各向同性(TTI)介质声波波动方程的特点,研究了TTI介质分裂式完全匹配层(Split perfectly matched layer,SPML)吸收边界条件.首先对常见的几种TTI介质声波波动方程进行了归纳,并从TTI介质波场传播稳定性的角度进行对比分析,结果表明,引入横波分量的TTI介质纵横波耦合方程适用于TTI介质.然后从TTI介质纵横波耦合二阶波动方程出发,推导得到其一阶波动方程的形式,进而推导出一阶波动方程形式的SPML波动方程,并给出了高阶交错网格有限差分算法的具体实现过程.数值模拟结果表明,SPML吸收边界条件能达到很好的人工边界反射吸收效果,相比优化海绵吸收边界条件,其人工边界反射吸收效果更好.【期刊名称】《石油物探》【年(卷),期】2017(056)003【总页数】13页(P349-361)【关键词】TTI介质;分裂式完全匹配层;纵横波耦合方程;一阶波动方程;高阶交错网格有限差分【作者】张衡;刘洪;李博;丁仁伟;李丽青;李福元【作者单位】国土资源部海底矿产资源重点实验室,中国地质调查局广州海洋地质调查局,广东广州510075;中国科学院地质与地球物理研究所,中国科学院油气资源研究重点实验室,北京100029;中国石油化工股份有限公司石油物探技术研究院,江苏南京211103;山东科技大学地球科学与工程学院,山东青岛266590;国土资源部海底矿产资源重点实验室,中国地质调查局广州海洋地质调查局,广东广州510075;国土资源部海底矿产资源重点实验室,中国地质调查局广州海洋地质调查局,广东广州510075【正文语种】中文【中图分类】P631Keywords:TTI media,split perfectly matched layer,P-wave and SV-wave coupled equation,first-order wave equation,high-order staggered-grid finite-difference各向异性正演数值模拟是各向异性逆时偏移和各向异性全波形反演的基础[1]。
声波方程逆时偏移中的无分裂PML吸收边界条件

声波方程逆时偏移中的无分裂PML吸收边界条件王鹏飞;何兵寿【摘要】逆时偏移是当前地震资料处理的前沿技术,吸收边界条件是逆时偏移技术的重要组成部分.目前,业界常用的基于波场分裂思路的完全匹配层PML(Perfectly Matched Layer)吸收边界条件在改善边界吸收效果和改进偏移成像质量方面发挥了巨大作用,但这种方法需要在边界处为分裂后的各个分量开辟额外的内存空间,且需要分边角处理,增加了逆时偏移技术的内存负担和计算开销.为了减少内存负担和提高计算效率,首先从双程声波方程出发,推导了声波方程的无分裂PML吸收边界条件,然后给出该边界条件下波动方程逆时延拓的数值实现过程.理论分析和模型实验结果得到:无分裂PML边界条件具有与分裂算法相同的边界吸收效果,并且基于无分裂PML的逆时偏移算法效率更高,更便于程序代码的编写和GPU (GraphicProcessing Unit)的并行实现.【期刊名称】《工程地球物理学报》【年(卷),期】2015(012)005【总页数】8页(P583-590)【关键词】逆时偏移;吸收边界条件;无分裂完全匹配层;计算效率【作者】王鹏飞;何兵寿【作者单位】中国海洋大学海底科学与探测技术教育部重点实验室,山东青岛266100;中国海洋大学海底科学与探测技术教育部重点实验室,山东青岛266100【正文语种】中文【中图分类】P631.5逆时偏移是当前地震资料成像处理领域的热点技术。
目前,国内外在逆时偏移领域的研究工作主要集中在以下几个方面:①波动方程逆时延拓算法[1,2]研究,包括差分格式推导、边界伪反射压制和数值频散压制等;②成像准则和成像方法[3-8]研究;③逆时偏移噪声压制方法[9-14]研究,主要研究波场延拓过程中由层间反射导致的低频噪音的压制方法;④逆时偏移存储策略[15-17]研究,主要用于降低逆时偏移的临时文件存储量和硬盘访问量,拓展逆时偏移处理的并行性并提高处理效率;⑤偏移处理的并行算法[18-20]研究,包括CPU(Central Processing Unit)并行、GPU并行以及CPU+GPU协同并行。
声波加pml边界条件
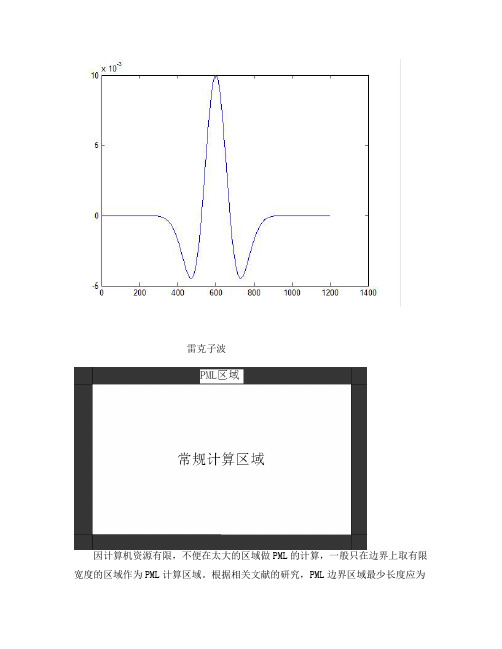
雷克子波因计算机资源有限,不便在太大的区域做PML的计算,一般只在边界上取有限宽度的区域作为PML计算区域。
根据相关文献的研究,PML边界区域最少长度应为半个波长[6]。
本文综合考虑了效果与开销等因素,选取了边界上50层作为PML 的计算区域。
常规计算区域与PML 边界区域的如图2-4所示。
x x x x x P v a P K t xω∂∂+=∂∂ z z zz z P v a P K t z ω∂∂+=∂∂ x z x x v v P a P K t x z ω∂∂∂⎛⎫+=+ ⎪∂∂∂⎝⎭衰减系数2331log 2x z P v R L ηωωη⎛⎫== ⎪∆⎝⎭式中L 为PML 层的厚度,η为层内的点距PML 与非PML 的边界的距离,P v 为纵波速度,R 那么在PML 边界区域内,对于式(2-13)1x x x v Pv t xωρ∂∂+=∂∂即为理论反射系数,一般取0.001较为合适,η∆为η方向的空间步长。
1x x x v Pv t xωρ∂∂=-∂∂,可看作为在常规的计算方程基础上,减去一项进行PML 的阻尼修正项。
因本文中只考虑各项同性介质中的地震波传播规律,故可做x z ηωωω==假设。
在此利用一下三个假设:⎪⎪⎭⎫ ⎝⎛+=-++++2121,2121,21,21k j i xk j i x kj i x v v v ⎪⎪⎭⎫ ⎝⎛+=-++++21,2121,21,2121k j i zk j i zkj i zvv v ()1,1,21,21-+++=k j i k j i k j i P P P 因为以上三个近似精度均为时间方向上的近似,且时间精度均为二阶精度,因交错网格技术的时间精度为二阶,故以上近似不影响本式的计算精度。
故可得:()()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-∆∆+∆-∆+=∑=-+++-+++N m k m j i k m j i m kj i k j i x k j i xP P a x t v t t v 11,,21,2121,2121,15.015.011ρωωηη(2-18a ) 同理:()()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-∆∆+∆-∆+=∑=-+++-+++N m kj m i k j m i m kj i k j i zk j i z P P a z t v t t v1,1,21,21,2121,2115.015.011ρωωηη(2-18b )()⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-∆∆+⎪⎪⎭⎫ ⎝⎛-∆∆+∆-∆+=∑∑=++-+-+=++-+-+++N m k m j i z k m j i x m N m k j m i z k j m i z m k j i k j i k j i v v a x t v v a z t K P t t P 12121,2121,121,2121,2121,,1,5.015.011ηηωω(2-18c )此为在PML 边界区域内的弹性声波应力-速度方程组。
基于COMSOL的空腔声学覆盖层的斜入射吸声性能分析

基于COMSOL的空腔声学覆盖层的斜入射吸声性能分析YE Hanfeng;TAO Meng;LI Junjie【摘要】基于平面波斜入射理论,利用有限元软件COMSOL建立了双层平板空腔声学覆盖层单元的斜入射仿真模型,并研究了斜入射条件下覆盖层结构和材料参数对其吸声性能的影响.通过与理论解的对比,验证了该仿真模型的准确性;讨论了入射角度,空腔结构,穿孔率和覆盖层厚度等参数变化对于覆盖层吸声性能的影响.结果表明:当入射角度变化时,吸声系数的峰值谷值间的频率间隔会随着入射角度的增加而增大,而且峰值和谷值也会随着入射角度的增加而增大;当穿孔率较大或者覆盖层厚度较厚时,吸声系数的峰值和谷值频率值会向低频移动,且数值也会更大.【期刊名称】《振动与冲击》【年(卷),期】2019(038)012【总页数】6页(P213-218)【关键词】斜入射;声学覆盖层;吸声性能【作者】YE Hanfeng;TAO Meng;LI Junjie【作者单位】;;【正文语种】中文【中图分类】TB56声学覆盖层是敷设在水下航行器外表壳,介于航行器壳体与海水之间的一种重要的声学结构[1]。
目前对于空腔声学覆盖层的研究主要有解析法、数值方法等,但是这些研究大多是聚焦于平面波垂直入射条件下覆盖层的吸声特性,并没有考虑平面波斜入射的情况。
而覆盖层所需要吸收的探测声呐信号往往并不会全部垂直入射到覆盖层表面,斜入射的情况也较为普遍,因而研究平面波斜入射条件下的覆盖层吸声特性是有其实际应用价值的。
国内外对于空腔声学覆盖层有诸多研究,有的研究分析了圆柱和椭圆柱形状的管栅结构峰谐振空腔声学覆盖层的声学特性[2]。
有的研究基于波导理论分析了在水介质中含多重细长管栅的黏弹性介质的声学特性[3-4]。
Lakhtakia等[5]通过 Fourier-Bessel 展开式和 T 矩阵理论,对于圆柱空腔弹性介质的声学性能展开了研究。
陶猛等推导出了声学覆盖层吸声性能的简化计算方法,并且计算了在不同静压下声学覆盖层的声学性能[6]。
理论声学 Theoretical Acoustics
音频声学实验室
• 主体建筑建成 于1964、1985 年,国内外少有 • 大量的声场实 验和标准测量 •仪器设备改造 投资逾400万元
2018/10/10
理论声学(1) 绪论
30
Pneumatic loudspeaker
2018/10/10
理论声学(1) 绪论
31
Equipment Made in China
2018/10/10 理论声学(1) 绪论 1
主要参考书
马大猷,现代声学理论基础,科学出版社 (2004)。 杜功焕、朱哲民、龚秀芬著,声学基础(第2版), 南京大学出版社(2001年)。 Allan D. Pierce, Acoustics, McGraw-Hill Book Company P.M.莫尔斯、K.U.英格特著,理论声学(上、下 两册),科学出版社(1984、1986年)。 Dan Russell /~drussell/Demos.html,
2018/10/10
理论声学(1) 绪论
11
振动
• 频率 单位时间里波动的次数 单位 Hz次/秒 赫兹 • 周期 波动一次的时间 • 波长 波动一次传播的距离 • 声速 声速等于波长乘以频率 • 振幅
2018/10/10 理论声学(1) 绪论 12
声音的频谱
A4=440Hz
2018/10/10 理论声学(1) 绪论 13
2018/10/10
理论声学(1) 绪论
8
声波的定性描述
2018/10/10
理论声学(1) 绪论
9
声是弹性介质中传播的机械波
• 弹性介质: 空气 • 真空中没有声波 水 (流体) 固体
2018/10/10
第七章声学基本理论及分析方法及分析
法是:找到声压级最大的噪声源(即主噪声源),并设法使之
降低。
第七章声学基本理论及分析方法及 分析
2、声压级的分解
若要从n个声源中将任一声源的声压级 p i 分解出来,将
式 p 2p 1 2p 2 2p 3 2 p n 2进行改写得: pi2 p2 pb2
式中:p i ——第 i 个声源的声压,N/m2 ;
Lpi (1010 1010分)析
[例题2] 测得n个声源总的声压级 Lp 90dB,移去一个主 要声源后,重新对其它各声源合成的声压级进行测量,其结
果为Lpb 80dB,求移去的那个声源的声压级 L pi 。
解:将已知量Lp 90dB、Lpb 80dB代入上式得:
Lp
Lp b
Lpi 10lg1( 010 1010 )
第七章声学基本理论及分析方法及 分析
等响曲线
第七章声学基本理论及分析方法及 分析
响度的单位是宋(Sone),1宋的响度相当于1000Hz
的纯音、声压级为40dB(响度级为40仿)的听觉反
应。50仿为2宋,60仿为4宋。实验证明,响度级每增
加10仿,响度增加一倍。若用 L N 代表响度级,N表
示响度,二者的关系为:
第七章声学基本理论及分析方法及 分析
第二节 声压级的合成与分解
有n各声源,各单一声源的声压分别为
p1,p2,p3, ,pn,对应的声压级分别为
Lp1,Lp2,Lp3, ,Lpn。下面分别介绍声压的
合成与分解。
第七章声学基本理论及分析方法及 分析
1、声压的合成
由式 p
1 T
T
0
p2
tdt知,声压是一定时间间隔内瞬时声压的
第七章声学基本理论及分析方法及 分析
波动方程pml matlab
波动方程PML(Perfectly Matched Layer)是一种用于模拟波传播的有效方法,特别适用于处理波在介质边界处的反射和折射现象。
而Matlab作为一种强大的数学建模和仿真软件,被广泛应用于波动方程的数值求解和仿真研究中。
在本文中,我将深入探讨波动方程PML在Matlab中的应用,旨在帮助您更全面地理解这一主题。
1. 波动方程的基本概念波动方程是描述波动现象的数学模型,广泛应用于声波、电磁波和地震波等领域。
其一般形式为:\[ \nabla^2 p - \dfrac{1}{c^2} \dfrac{\partial^2 p}{\partial t^2} = S \]其中,\(p\)表示波场的物理量,\(c\)为介质中的波速,\(S\)表示波源的项。
波动方程的数值求解需要考虑介质边界的影响,而PML方法正是为了处理波在边界处的吸收和反射而被提出。
2. PML方法的原理与应用PML方法是通过在模拟区域周围引入特殊的吸收层,使得波在边界处能够被有效吸收,从而减小边界效应对波场的影响。
PML方法在波动方程的数值模拟中起着至关重要的作用,能够更真实地模拟波在复杂介质中的传播过程。
在Matlab中,可以通过编写PML吸收边界条件的自定义函数,结合有限差分或有限元等数值方法,实现对波动方程PML的数值求解。
Matlab提供了丰富的数学函数和绘图工具,能够方便地实现PML方法的仿真研究。
3. Matlab中波动方程PML的实现在Matlab中,首先需要定义模拟区域的网格和介质参数,设置好波源的位置和波形类型。
通过调用自定义的PML吸收边界条件函数,将吸收层的参数和边界条件添加到波动方程的数值求解过程中。
利用Matlab的绘图功能,可以直观地展示波场在介质中的传播和反射情况。
4. 我对波动方程PML在Matlab中的理解在实际工程和科研中,波动方程PML在Matlab中的应用具有重要意义。
通过对复杂介质中波的传播行为进行数值模拟,可以更深入地理解波与介质之间的相互作用,为声波成像、地震勘探和无损检测等领域的研究提供有力支持。
PML快速入门
REAL 数值变量
变量的声明(可省略) !r=real() 变量的查询: q var !r 变量的赋值: !r= 10 变量的运算: + - * / () 等
例: !r1= 2 !r2= 3 !sum=!r1 + !r2 注:直接赋值时加空格 Q var !sum 查询结果为: <REAL>5STຫໍສະໝຸດ ING 字符串变量
变量的声明(可省略) !t=string() 变量的查询: q var !t 变量的赋值: !t= ‘abc’ 变量的运算: 1.连接运算:+ 或 & 2.字符串函数或方法
例: !t1=‘abc’ !t2=‘ABC’ !T=!t1 + ‘/’ + !t2 注:运算符前后有空格 Q var !T 查询结果: <STRING>’abc/ABC’
变量的相互转换
Real至String 如: !num= 100 !string=string(!num)
String至Real 如: !string= ‘100’ !num=real(!string)
或!string=!num.string()
或!num=!string.real()
Q var !string
常用符号(2)
!A=值 !A=object x() !A.b !A.c() d(!A) !!fun(!A) !a.delete()
A赋值 声明A为对象x A的成员b A执行c方法 对A执行d方法 fun函数带参数A运算 删除变量a
宏文件举例
1. 2.
在D盘创建记事本macro.txt 在记事本中写入:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
article info
Article history: Received 1 February 2012 Received in revised form 11 October 2012 Accepted 12 October 2012 Available online 2 November 2012
Ó 2012 Elsevier Inc. All rights reserved.
1. Introduction
One of the great challenges for wave propagation is the efficient and stable computation of waves in unbounded domains. The crucial point for these computations is that the numerical scheme avoids any reflections at the boundaries, even in case the diameter of the computational domain is just a fraction of a wavelength. Since the eighties of the last century, several numerical techniques have been developed to deal with this topic: infinite elements, Dirichlet-to-Neumann operators based on truncated Fourier expansions, absorbing boundary conditions, etc. The advantages and drawbacks of these different approaches have been widely discussed in literature, see e.g. [19,33,4]. Especially higher order absorbing boundary conditions (ABCs) have gained increasing interest, since new methods do not involve high order derivatives [6,21–24,26,27,25,28,8].
Journal of Computational Physics 235 (2013) 407–422
Contents lists available at SciVerse ScienceDirect
Journal of Computational Physics
journal homepage: /locate/jcp
A modified and stable version of a perfectly matched layer technique for the 3-d second order wave equation in time domain with an application to aeroacoustics
Keywords: Finite element method Perfectly matched layer Time-domain analysis
abstract
We consider the second order wave equation in an unbounded domain and propose an advanced perfectly matched layer (PML) technique for its efficient and reliable simulation. In doing so, we concentrate on the time domain case and use the finite-element (FE) method for the space discretization. Our un-split-PML formulation requires four auxiliary variables within the PML region in three space dimensions. For a reduced version (rPML), we present a long time stability proof based on an energy analysis. The numerical case studies and an application example demonstrate the good performance and long time stability of our formulation for treating open domain problems.
Once a PML formulation has been obtained, the question of stability arises, which is a topic of strong ongoing research. A stability analysis is not trivial and in general it has to be performed for each new formulation. Several works have analyzed the properties of the PML technique, such as [1,7,2,16,30,17] among others. E.g., in [16] a time-domain analysis of PML methods for wave equations in 2D by using the Cagniard-de Hoop method has been presented. The main result is to validate the modxtended to the absorbing layers. This method is easily applicable to the wave equation with any time-dependent point source. However, the evaluation is not easy for general initial value problems of the wave equation, because those in general include not only propagating but also evanescent waves [29]. Our stability analysis investigates the evolution of the energy over time and we are able to show decay of an upper bound on the energy for our formulation, thus achieving long term stability.
Barbara Kaltenbacher a, Manfred Kaltenbacher b,⇑, Imbo Sim c
a Institute of Applied Analysis, Alpen-Adria-Universität Klagenfurt, Austria b Institute of Mechanics and Mechatronics, Technische Universität Wien, Austria c Institute of Applied Mechatronics, Alpen-Adria-Universität Klagenfurt, Austria
⇑ Corresponding author.
E-mail address: manfred.kaltenbacher@tuwien.ac.at (M. Kaltenbacher).
0021-9991/$ - see front matter Ó 2012 Elsevier Inc. All rights reserved. /10.1016/j.jcp.2012.10.016
An alternative approach to approximate free radiation is to surround the computational domain by an additional damping layer and guarantee within the formulation, that no reflections occur at its interface with the computational domain. This socalled perfectly matched layer (PML) technique was first introduced by Berenger [11] using a splitting of the physical variables and considering a system of first order partial differential equations (PDEs) for electromagnetics. Since then, there has been much research work on this technique which subsequently was applied to different PDEs [2,5,15,31,37,3,38,41,43]. In the framework of time-harmonic wave propagation, the PML can be interpreted as a complex-valued coordinate stretching [42]. Therewith, a PML formulation for a linear PDE in frequency domain can be considered as a straightforward approach. However, in time domain most PML formulations require a first order hyperbolic system, e.g., [44,31,13,37]. The difficulty arising for the second order wave equation in time domain is, that an inverse Fourier transform of its frequency representation will lead to convolution integrals, see e.g. [39]. A method to avoid convolution integrals is the use of auxiliary variables
