风险价值度
财务风险度量方法

财务风险度量方法在企业的经营过程中,财务风险是无法避免的一个重要风险。
为了更有效地管理和控制风险,企业需要对财务风险进行度量和评估。
本文将介绍一些常见的财务风险度量方法,帮助企业更好地了解和管理财务风险。
一、价值风险度量方法价值风险度量方法是通过对企业价值进行度量,评估财务风险的方法。
其中,市场价值风险度量方法是最常见的一种方法。
它通过对企业市场价值的波动进行分析,评估财务风险的变化情况。
市场价值风险度量方法的核心是通过计算企业股票价格的波动性来度量财务风险。
股票价格波动率越高,意味着企业财务风险越高。
企业可以通过定期计算股票价格的历史波动率,来评估财务风险的变化趋势,并及时采取相应的风险管理措施。
二、信用风险度量方法信用风险是企业面临的另一个重要的财务风险。
为了度量和评估信用风险,企业可以使用信用评级模型。
常见的信用评级模型包括Moody's、标准普尔等评级体系。
企业可以将自身的财务指标与信用评级体系进行对比,评估自身信用风险的等级。
通过了解自身信用等级,企业可以更准确地估计未来的偿付能力,制定相应的财务风险管理策略。
三、流动性风险度量方法流动性风险是企业面临的另一个重要财务风险。
为了度量和评估流动性风险,企业可以使用现金流量度量方法。
现金流量度量方法是通过对企业现金流量的变化情况进行分析,评估流动性风险的变化趋势。
企业可以通过计算现金流量的净值、净现值等指标,评估自身的流动性状况,并制定相应的流动性管理策略。
四、汇率风险度量方法对于存在国际业务的企业来说,汇率风险是一个不可忽视的财务风险。
为了度量和评估汇率风险,企业可以使用价值变动度量方法。
价值变动度量方法是通过对企业资产和负债的价值变动进行分析,评估汇率风险的变化情况。
企业可以通过计算资产和负债的价值变动率,了解自身的汇率风险敏感性,并制定相应的汇率风险管理策略。
五、市场风险度量方法市场风险是企业面临的另一个重要的财务风险。
为了度量和评估市场风险,企业可以使用风险价值度量方法。
信用风险价值度

WCDR(T, X) EAD LGD
Gordy (2003) 能够将上式扩展。假定有一个由n笔贷款组成的
贷款组合,其中每笔贷款相比整个组合来说都很小,损失分布
的第X个分位数大致为
VaR WCDRi (T, X) EADi LGDi
i1
n
Credit Risk Plus 1997年,由瑞士信贷金融产品小组开发的一个计算VaR的模型, 这一模型基于保险行业中一种较为成熟的想法
Baa 0.89 4.71 18.88 60.98 18.20 3.27 0.93 0.31 0.00
Ba 0.21 0.73 3.24 12.93 44.69 13.28 3.52 1.39 0.00
B 0.05 0.25 1.06 4.64 20.07 43.05 16.80 5.89 0.00
由1年期计算出的一个月期的信用评级迁移矩阵(%)
初始 评级
1月末的信用等级
Aaa 99.16 0.09 0.00 0.00 0.00 0.00 0.00 0.00 0.00
Aa 0.82 99.12 0.26 0.01 0.00 0.00 0.00 0.00 0.00
A 0.02 0.77 99.18 0.44 0.02 0.01 0.00 0.00 0.00
初始 评级
5年末的信用等级
Aaa 61.12 3.45 0.44 0.22 0.07 0.04 0.01 0.00 0.00
Aa 29.99 61.89 9.72 1.69 0.44 0.20 0.08 0.02 0.00
A 7.70 28.70 65.78 16.38 3.40 0.83 0.23 0.06 0.00
4第四讲风险价值度

满足一致性条件的风险度量(续)
同质性:假定一个交易组合内含资产品种和相对比例不变, 但内含资产的数量增至原数量的λ倍,此时新交易组合的风 险应是原风险的λ倍
次可加性:两个交易组合相加所组成的一个新交易组合的风 险度量小于或等于最初两个交易组合的风险度量的和
VaR满足前3个条件,但不一定永远满足第4个条件 预期损失满足所有4个条件
VaR 和资本金(续)
对应于99.9%置信度和1年展望期,某交易组合的VaR为5 000 万美元,这意味着在极端条件下(理论上讲,每1 000年出现 一次),金融机构在1年时损失会超过5 000万美元
这同时也说明,如果金融机构持有5 000万美元的资本金,我 们会有99.9%的把握,金融机构不会在1年内完全损失自身持 有的资本金
失的期望值 两个具有同样VaR的投资组合,其预期亏损却可能差距非常大
相同 VaR 不同预期亏损
VaR VaR
预期亏损
从风险分散的意义上来讲,预期亏损要比VaR有更好的性态 但是,预期亏损的不利之处在于比VaR更为复杂,因此,这一
风险度量比VaR更难以理解 另外,预期亏损的准确性很难得到回顾测试(用历史数据来检
独立性假设
对于独立同分布的投资组合,T天展望期的方差是1天展望期方 差的T倍
如果存在自相关性的影响,其乘数就从T倍增加到
T 2(T 1) 2(T 2) 2 2(T 3)3 2T 1
自相关性的影响
当存在一阶自相关性时T天的VaR和一天的VaR的比率
VaR xi
xi
某一大交易组合的第 i 个成分VaR与这一成分的递增VaR近似
相等
欧拉定理
令V是一个交易组合的风险度量,而xi是第i个子组合的大小, 假设对所有的xi,当xi变为λxi时(即整个交易组合变为原来的λ 倍),V变为λV,即线性同质性
风险价值评估概述

风险价值评估概述
风险价值评估是指对各种潜在危害和可能发生的损失进行系统的综合评估和分析的过程。
通过对风险进行评估,可以帮助组织或个人更好地了解潜在风险对其目标和利益的威胁程度,为决策和管理提供基础。
风险价值评估通常包括以下几个步骤:
1. 风险识别:这是评估的第一步,通过分析和评估当前和潜在的风险源,识别出可能对组织或个人产生不利影响的各种潜在风险。
2. 风险分析:在识别出潜在风险后,需要对其进行分析,包括确定风险事件的可能性和严重程度,评估其对组织或个人的影响程度。
通过风险分析可以帮助确定风险的优先级和重要程度。
3. 风险评估:在风险分析的基础上,进行综合评估,确定风险的价值和意义。
这可以包括对各种风险的成本和收益进行衡量和量化,从而为决策提供参考依据。
4. 风险应对:根据风险的评估结果,制定相应的风险应对策略和计划。
这包括采取预防和控制措施,减轻风险带来的损失和影响,同时也需要制定应急预案和恢复计划,以应对潜在的风险事件。
风险价值评估的重要性在于帮助组织或个人更好地识别和理解潜在风险的价值和意义,从而更有针对性地进行风险管理和决
策。
通过合理的风险价值评估,可以帮助组织或个人避免或减少潜在风险带来的损失,提高风险管理的效果和决策的科学性。
最后需要指出的是,风险价值评估是一个动态的过程,需要不断地进行监测和更新。
随着环境和条件的变化,风险的价值和意义可能会发生变化,因此需要定期进行评估和调整。
只有持续地关注和评估风险,才能更好地保护组织或个人的利益并做出明智的决策。
VaR估计与检验
一、引言VaR(风险价值度)是用来估计给定金融产品或组合在未来价格波动下可能的或潜在的最大损失, 其最大的优点是以一个简单的数字来揭示金融风险情况,使投资者快速了解到某金融产品的风险特征。
VaR在风险控制和业绩评估方面有突出的应用价值,因此,关于VaR的估计方法备受关注,目前已有多种模型方法能够估计出金融产品或组合的风险价值度。
本文采用GARCH(1,1)模型、历史模拟法和波动率加权模拟法,基于沪深300ETF历史收盘价数据进行VaR的估计与检验,并将结果进行对比分析,从而更好地理解VaR。
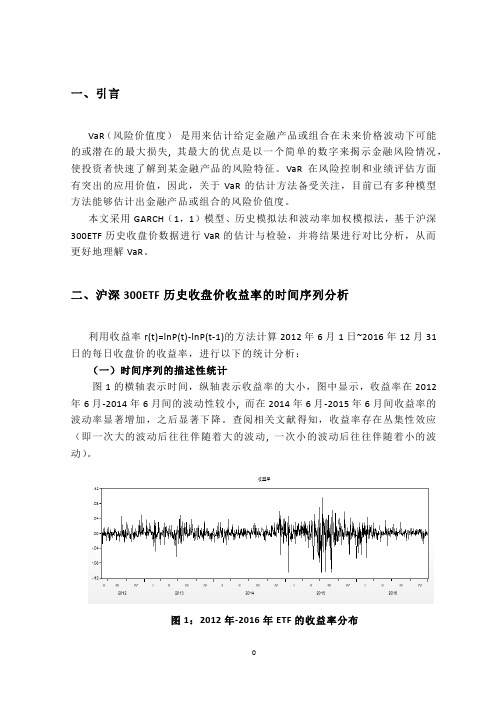
二、沪深300ETF历史收盘价收益率的时间序列分析利用收益率r(t)=lnP(t)-lnP(t-1)的方法计算2012年6月1日~2016年12月31日的每日收盘价的收益率,进行以下的统计分析:(一)时间序列的描述性统计图1的横轴表示时间,纵轴表示收益率的大小,图中显示,收益率在2012年6月-2014年6月间的波动性较小, 而在2014年6月-2015年6月间收益率的波动率显著增加,之后显著下降。
查阅相关文献得知,收益率存在丛集性效应(即一次大的波动后往往伴随着大的波动, 一次小的波动后往往伴随着小的波动)。
图1:2012年-2016年ETF的收益率分布图2是利用Eviews软件得出的相关统计数据,数据显示收益率的最小值为-10.55%,最大值为9.52%,图形显示分布比较对称, 但峰度为11.06, 偏度为-0.77,呈现出“尖峰肥尾、左偏”的特征。
Jarque-Bera统计量非常大(P值=0.00),因此JB 统计位于拒绝域内,可以认为收益率不是来源于正态分布。
图2:收益率的描述性统计(二)时间序列的自相关性检验对收益率的十阶滞后量求自相关函数值与偏自相关函数值,结果如表1所示。
可以看出自相关性在一阶时并不显著,但在高阶后十分显著,存在自相关性。
表1:收益率的自相关性(三)时间序列的平稳性检验对收益率进行ADF平稳性检验,结果见表2。
8风险价值度

损失(以100万美元为计) -2 2 4 6 8 10 图8-3 例8-3和例8-4中的累计损失分布
例:8-4 考虑8-3中的情况,假定我们想求得对在 99.5%置信度下 的VaR,这时,图8-3显示,损失介于400万美元和1000万美 元之间的任何一点的损失,均为99.5%的把握不会被超出, 对于这一区间的任意数值V,损失超出V的概率均为0.5%. VaR 在这一情形不具有唯一性,一个合理的选择是将VaR 设定为这一区间的中间值,这意味着,在99.5%置信度下的 VaR 为700美元.
VaR计算例子 例8-1:假定一个交易组合在6个月时的收益服从正态分布, 分布均值为200万美元,标准差为1000万美元,计算在6 个月展望,在99%置信度下交易组合的VaR。
解:设X表示交易组合在6个月的收益,依题意知: X N(200,10002 ) Q P( X ≤ −V ) = 1 − 0.99 X − 200 −V − 200 QP ≤ = 0.01 1000 1000 −V − 200 Q = −2.33 1000 ∴V = 2130 (万美元)
例8-2假定一个1年的项目的最终结果介于5000万美元损 失和5000万美元收益之间,5000万美元损失和5000万美 元收益之间的任意结果具有均等的可能,这时,项目的最 终结果服从由-5000万美元到5000万美元的均匀分布,求 对于1年展望期,在99%置信度下的VaR为多少?
解 : 设 X表 示 项 目 在1 年 的 收 益 , 依 题 意 知 : X U ( − 5000, 5000) 1 , − 5000 ≤ x ≤ 5000 ∴ f ( x ) = 10000 0, 其 他 Q P ( X ≤ −V ) = 1 − 0.99 −V 1 ∴∫ dx = 0.01 − 5000 10000 − v + 5000 ∴ = 0.01 10000 ∴ V = 4900( 万 美 元 )
第18章信用风险价值度

Risk Management and Financial Institutions 3e, Chapter 18, Copyright © John C. Hull 2012
10
Copula 模型: xA 和 xB服从标准正态分布
Risk Management and Financial Institutions 3e, Chapter 18, Copyright © John C. Hull 2012
Risk Management and Financial Institutions 3e, Chapter 18, Copyright © John C. Hull 2012
9
CreditMetrics
通过考虑可能的信用评级迁移来计算信用 VaR
高斯 Copula模型可以用来构造信用变化的 联合概率分布
7
VaR 模型
假定我们有一个有 n 笔贷款组成的贷款组合 ,其中每笔贷款相比整个组合来说都很小。 损失的第X个分位数大致为
VaR WCDRi (T , X ) EADi LGDi
i
其中,我们假定存在单一的r 。
Risk Management and Financial Institutions 3e, Chapter 18, Copyright © John C.用风险: 新增风险 资本金
银行必须计算1年展望期 99.9% VaR 这是为了保证交易账户上信用敏感产品的
资本金不会低于银行账户上的相应产品的 资本金 银行可以假设风险水平是恒定的。 (最小流 动区间是3个月)
Risk Management and Financial Institutions 3e, Chapter 18, Copyright © John C. Hull 2012
风险价值名词解释

风险价值是金融领域中常用的风险度量指标,用于衡量在一定的置信水平下,投资组合或资产可能遭受的最大预期损失。
VaR可以帮助投资者、金融机构和风险管理团队评估风险暴露,并制定相应的风险管理策略。
具体而言,风险价值指标将风险量化为一个特定的数值,表示在给定的时间段内,特定置信水平下可能出现的最大损失金额。
例如,一个10%的一日95% VaR为100万美元,意味着在未来一天内,有95%的置信水平使得投资组合的损失不会超过100万美元。
风险价值的计算通常基于历史数据或统计模型,并结合置信水平和时间段的选择来确定风险度量的精度。
常见的计算方法包括历史模拟法、蒙特卡洛模拟法和参数法等。
这些方法考虑了投资组合或资产的收益分布、相关性和波动性等因素,以评估可能的损失范围。
需要注意的是,风险价值是一种度量风险的方法,但它并不能完全预测未来的损失。
它基于历史数据和假设,无法考虑到突发事件和极端市场情况。
因此,在使用风险价值进行风险管理时,还需要结合其他风险指标和方法进行综合评估和决策。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
预期亏损为:0.8×10 + 0.2×1,即820万美元 将两个贷款结合到一起,在2.5%的尾部分布中,有0.04%的概
率损失为2 000万美元,有2.46%的概率损失为1 100万美元
预期亏损为:0.16×20 + 0.84×11,即1114.4万美元 820 + 820>1 114.4,因此,预期亏损满足次可加性
例 9.6 考虑两笔期限均为1年的1 000万美元贷款。违约的概率见下表 结果 两笔贷款均不违约 第一笔贷款违约,第二笔贷款不违约 第二笔贷款违约,第一笔贷款不违约 两笔贷款均违约
概率 97.5% 1.25% 1.25% 0.00%
如果贷款违约,回收率介于0~100%的可能性均等。当贷款没 有违约时,贷款盈利均为20万美元
另外,预期亏损的准确性很难得到回顾测试(用历史数据来检
验VaR度量可靠性的一种方式)
VaR 和资本金 VaR被监管当局以及金融机构用来确定资本金的持有量 对于市场风险,监管人员所要求的资本金等于在10天展望期的 99% VaR的一定倍数(至少3倍)
对于信用风险和操作风险,《巴塞尔协议Ⅱ》中,监管人员要
预期亏损是指在T时间段的损失超出了第X分位数的条件下,损
失的期望值
两个具有同样VaR的投资组合,其预期亏损却可能差距非常大
相同 VaR 不同期亏损
VaR
VaR
预期亏损
从风险分散的意义上来讲,预期亏损要比VaR有更好的性态 但是,预期亏损的不利之处在于比VaR更为复杂,因此,这一 风险度量比VaR更难以理解
例 9.6(续) 首先考虑第一笔贷款,违约可能为1.25%,在违约发生的条件 下,损失均匀介于0到1 000万美元,这意味着有1.25%的概率 损失大于零,有0.625%的概率损失大于500万美元,损失超过 1 000万美元的事件不会发生
损失超过200万美元的概率为1%(损失发生前提下,有80%的 概率损失会超过200万美元,因为损失的概率为1.25%,损失 大于200万美元的无条件概率为80%×1.25%=1%),因此,1
满足一致性条件的风险度量
假定想设计某种风险度量来确定金融机构应持有的资本金数量, VaR是最好的选择吗(在合适的展望期和臵信水平下)?
Artzner etc. (1999)指出,度量应满足一定性态:
单调性:如果在所有的不同情形下,第1个交易组合的回报
均低于另一个交易组合,那么这里的第1个交易组合的风险
求在资本金计算中采用1年展望期及99.9%的臵信区间
VaR 和资本金(续) 对应于99.9%臵信度和1年展望期,某交易组合的VaR为5 000 万美元,这意味着在极端条件下(理论上讲,每1 000年出现 一次),金融机构在1年时损失会超过5 000万美元
这同时也说明,如果金融机构持有5 000万美元的资本金,我 们会有99.9%的把握,金融机构不会在1年内完全损失自身持 有的资本金
风险价值度
VaR的定义 当使用VaR来度量风险时,我们是在陈述以下事实:“我们有 X%的把握,在T时间段,我们的损失不会大于V。”
这里的变量V就是交易组合的VaR VaR是两个变量的函数:事件展望期(T时间段)、臵信度
(X%)
VaR对应于在今后T时间段及在X%把握下,交易损失的最大值
VaR 的优点 仅用一个数字就抓住了风险的要点 容易理解 提出一个简单问题:“最坏情况会是怎样?”
VaR满足前3个条件,但不一定永远满足第4个条件 预期损失满足所有4个条件
例 9.5 假定两个独立贷款项目在1年内均有0.02的概率损失1 000万美元, 同时均有0.98的概率损失100万美元,任意一个单笔贷款在展望 期为1年,97.5%的臵信度下的VaR为100万美元
将两个贷款叠加产生一个资产组合,组合有0.02×0.02=0.000 4 的概率损失2 000万美元,并且有2×0.02×0.98=0.039 2的概率 损失1 100美元,有0.98×0.98=0.960 4的概率损失200万美元
项目的最终结果服从由-5 000万美元到+5 000万美元的均匀分 布,损失大于4 900万美元的可能性为1%
对于1年的展望期,在99%臵信度下的VaR为4 900万美元
例 9.3 和 9.4 假定一个1年的项目有98%的概率收益为200万美元,1.5%的 概率损失为400万美元,0.5%的概率损失为1 000万美元
在这一累计分布下,对应于99%累计概率的点为400万美元, 因此,对于1年展望期,在99%臵信度下的VaR为400万美元
99.9%的臵信度下的VaR为多少呢? 99.5%的臵信度下的VaR为多少呢?
例 9.3 和 9.4(续)
VaR与预期亏损 VaR是为了展示损失会糟成什么样 预期亏损给出当市场条件变糟而触发损失时,损失的期望值为 多大(有时被称为条件风险价值度;条件尾部期望;尾部损失)
在展望期为1年,97.5%臵信度下,组合的VaR为1100万美元,
单笔贷款所对应VaR的和为200万美元,贷款组合的VaR比贷款
VaR的总和高900美元,这违反了次可加性
例 9.7 考虑例9.5,单笔贷款,在2.5%的尾部分布中,有2%的概率损 失为1 000万美元,有0.5%的概率损失为100万美元
度量一定要比另一个大
平移不变性:如果我们在交易组合中加入K数量的现金,交 易组合所对应的风险度量要减少K数量
满足一致性条件的风险度量(续)
同质性:假定一个交易组合内含资产品种和相对比例不变, 但内含资产的数量增至原数量的λ倍,此时新交易组合的风 险应是原风险的λ倍
次可加性:两个交易组合相加所组成的一个新交易组合的风 险度量小于或等于最初两个交易组合的风险度量的和
例 9.1 假定一个交易组合在6个月时的收益服从正态分布,分布均值为 200万美元,标准差为1 000万美元
根据正态分布的性质得出,分布的第一个分位数为2-2.33×10, 即-2 130万美元
对于6个月展望期,在99%臵信度下的VaR为2 130万美元
例 9.2 假定一个1年的项目的最终结果介于5 000万美元损失和5 000 万美元收益之间,5 000万美元损失和5 000万美元收益之间的 任意结果具有均等的可能
