数轴穿根法
专题8数轴穿根法

专题:数轴穿根法“数轴穿根法”又称“数轴标根法”第一步:通过不等式得诸多性质对不等式进行移项,使得右侧为0、(注意:一定要保证x 前得系数为正数)例如: (x -2)(x—1)(x+1)>0第二步:将不等号换成等号解出所有根。
例如:(x-2)(x-1)(x+1)=0得根为:x =2,x =1,x=—1第三步:在数轴上从左到右依次标出各根、例如:-1 1 2第三步:画穿根线:以数轴为标准,从“最右根"得右上方穿过根,往左下画线,然后又穿过“次右跟”上去,一上一下依次穿过各根、第四步:观察不等号,如果不等号为“>”,则取数轴上方,穿根线以内得范围;如果不等号为“<”则取数轴下方,穿根线以内得范围。
例如:若求(x -2)(x-1)(x+1)>0得解。
因为不等号威“〉”则取数轴上方,穿根线以内得范围。
即:-1<x<1或x>2、 穿根法得奇过偶不过定律: “奇穿过,偶弹回”。
还有关于分式得问题:当不等式移项后,可能就是分式,同样就是可以用穿根法得,但就是注意,解不能让原来分式下面得式子等于0专项训练:1、解不等式ﻩ解析:1)一边就是因式乘积、另一边就是零得形式,其中各因式未知数得系数为正。
2)因式、、得根分别就是、、。
在数轴上把它们标出(如图1)。
3)从最大根3得右上方开始,穿线(图象,)。
4)数轴上方曲线对应得得取值区间,为得解集,数轴下方曲线对应得得取值区间,为得解集。
不等式得解集为。
在上述解题过程中,学生存在得疑问往往有:为什么各因式中未知数得系数为正;为什么从最大根得右上方开始穿线;为什么数轴上方曲线对应得得集合就是大于零不等式得解集,数轴下方曲线对应得集合就是小于零不等式得解集。
2、解不等式解析:1)一边就是因式乘积、另一边就是零得形式,其中各因式未知数得系数为正。
2)因式、、得根分别为、、,在数轴上把它们标出(如图2)。
3)从最大根3得右上方开始向左依次穿线,次数为奇数得因式得根一次性穿过,次数为偶数得因式得根穿而不过。
数轴穿根法

数轴穿根法1“数轴穿根法”又称“数轴标根法”第一步:通过不等式的诸多性质对不等式进行移项,使得右侧为0。
(注意:保证X最高次项系数为正)例如:将x^3-2x^2-x+2>0化为(x-2)(x-1)(x+1)>0第二步:将不等号换成等号解出所有根。
例如:(x-2)(x-1)(x+1)=0的根为:x1=2,x2=1,x3=-1第三步:在数轴上从左到右依次标出各根。
例如:-1 1 2第四步:画穿根线:以数轴为标准,从“最右根”的右上方穿过根,往左下画线,然后又穿过“次右根“上去,一上一下依次穿过各根。
第五步:观察不等号,如果不等号为“>”,则取数轴上方,穿跟线以内的范围;如果不等号为“<”则取数轴下方,穿跟线以内的范围。
例如:若求(x-2)(x-1)(x+1)>0的根。
在数轴上标根得:-1 1 2 画穿根线:由右上方开始穿根。
因为不等号威“>”则取数轴上方,穿跟线以内的范围。
即:-1<x2。
</x编辑本段穿根法的奇过偶不过定律:就是当不等式中含有有单独的x偶幂项时,如(x^2)或(x^4)时,穿根线是不穿过0点的。
但是对于X奇数幂项,就要穿过0点了。
还有一种情况就是例如:(X-1)^2.当不等式里出现这种部分时,线是不穿过1点的。
但是对于如(X-1)^3的式子,穿根线要过1点。
也是奇过偶不过。
可以简单记为“奇穿过,偶弹回”。
编辑本段还有关于分式的问题:当不等式移项后,可能是分式,同样是可以用穿根法的,直接把分号下面的乘上来,变成乘法式子。
继续用穿根法,但是注意,解不能让原来分式下面的式子等于0 数轴的作用(观察通道)规定了原点,正方向,单位长度的直线,叫做数轴。
在某一事物上通过某一维度的评估,可以将事物分成很多不同的层次加以认识。
这样,能够更加准确,详细地描述事物的本质。
2数轴穿根法什么时候会有连续穿?就是在数轴下方向上穿时,碰到根后不上去,继续反弹回来,此时在下面而不是在上面希望有哪位知道的老师能为晚辈解答,谢谢了.最佳答案穿针引线法,标根分区法.或者叫穿根法,呵呵,是解高次不等式的一个好技巧, 第一:最高次项系数化为正数.保证因式分解后各因式中x的系数为正.第二:将这若干个根按从小到大的顺序标在数轴上,注意是空心点(不能取到)还是实心点(可以取到).第三:按照从右至左,从上至下的顺序画一条曲线,穿过这些点,注意"奇过偶不过"(奇次方的点过,偶次方的点不过).第四:根据第一步整理的不等式的不等号的方向来写出解集,大于号取在数轴上方的区间,小于号取在数轴下方的区间.。
穿针引线的画法

穿针引线法
穿针引线法,又称“数轴穿根法”或“数轴标根法”
第一步:通过不等式的诸多性质对不等式进行移项,使得右侧为0。
(注意:一定要保证x前的系数为正数)
例如:将x^3-2x^2-x+2>0化为(x-2)(x-1)(x+1)>0
第二步:将不等号换成等号解出所有根。
例如:(x-2)(x-1)(x+1)=0的根为:x1=2,x2=1,x3=-1
第三步:在数轴上从左到右依次标出各根。
第四步:画穿根线:以数轴为标准,从“最右根”的右上方穿过根,往左下画线,然后又穿过“次右根”
上去,一上一下依次穿过各根。
第五步:观察不等号,如果不等号为“>”,则取数轴上方,穿根线以内的范围;如果不等号为“<”则取数轴下方,穿根线以内的范围。
例如:若求(x-2)(x-1)(x+1)>0的根。
在数轴上标根得:-1 1 2
画穿根线:由右上方开始穿根。
因为不等号为“>”则取数轴上方,穿根线以内的范围。
即:-1<x<1或x>2
奇透偶不透即假如有两个解都是同一个数字。
这个数字要按照两个数字穿。
如(x-1)^2=0 两个解都是1 ,那么穿的时候不要透过1
可以简单记为,秘籍口诀:或“自上而下,从右到左,奇次根一穿而过,偶次根一穿不过”。
1。
数轴标根法又称数轴穿根法或穿针引线法

“数轴标根法”又称“数轴穿根法”或“穿针引线法”是高次不等式的简单解法当高次不等式f(x)>0(或<0)的左边整式、分式不等式φ(x)/h(x)>0(或<0)的左边分子、分母能分解成若干个一次因式的积(x-a1)(x-a2)…(x -an)的形式,可把各因式的根标在数轴上,形成若干个区间,最右端的区间f (x)、φ(x)/h(x)的值必为正值,从右往左通常为正值、负值依次相间,这种解不等式的方法称为序轴标根法。
为了形象地体现正负值的变化规律,可以画一条浪线从右上方依次穿过每一根所对应的点,穿过最后一个点后就不再变方向,这种画法俗称“穿针引线法”,如图1(图片自上而下依次为图一,二,三,四)。
步骤第一步:通过不等式的诸多性质对不等式进行移项,使得右侧为0。
(注意:一定要保证x前的系数为正数)例如:将x^3-2x^2-x+2>0化为(x-2)(x-1)(x+1)>0第二步:将不等号换成等号解出所有根。
例如:(x-2)(x-1)(x+1)=0的根为:x1=2,x2=1,x3=-1第三步:在数轴上从左到右依次标出各根。
例如:-1 1 2第四步:画穿根线:以数轴为标准,从“最右根”的右上方穿过根,往左下画线,然后又穿过“次右根”上去,一上一下依次穿过各根。
第五步:观察不等号,如果不等号为“>”,则取数轴上方,穿根线以内的范围;如果不等号为“<”则取数轴下方,穿根线以内的范围。
x的次数若为偶数则不穿过,即奇过偶不过。
例如:若求(x-2)(x-1)(x+1)>0的根。
在数轴上标根得:-1 1 2画穿根线:由右上方开始穿根。
因为不等号为“>”则取数轴上方,穿跟线以内的范围。
即:-1<x<1或x>2。
(如图四)奇过偶不过就是当不等式中含有有单独的x偶幂项时,如(x^2)或(x^4)时,穿根线是不穿过(X-1)^2. 0点的。
但是对于X奇数幂项,就要穿过0点了。
数轴穿根法的口诀

数轴穿根法的口诀
以下是五个符合要求的口诀:
《数轴穿根法口诀一》
奇穿偶不穿,这话要记全。
从右往左看,数轴铺眼前。
遇到一个根,奇数就穿线。
若是偶数个,轻轻放旁边。
不等式求解,此法最灵验。
就像走迷宫,路线清晰见。
小朋友们呀,快来记心间。
《数轴穿根法口诀二》
数轴穿根并不难,记住步骤很简单。
先把方程变一边,零点全部找出来。
从大到小排排队,一奇一穿像钻洞。
二偶不穿像站岗,求解范围快快看。
如同游戏玩通关,轻松愉快掌握它。
《数轴穿根法口诀三》
要想用穿根法,顺序不能差。
先把因式分解啦,数轴上面来安家。
奇数根呀用力穿,像箭一样飞向前。
偶数根呀别着急,在那旁边歇一歇。
不等式里用一用,答案马上就出现。
《数轴穿根法口诀四》
数轴穿根有妙招,听我慢慢说诀窍。
因式分解是基础,各个零点要清楚。
沿着数轴向前走,奇数穿根别回头。
偶数如同小云朵,飘在旁边不捣乱。
范围一看就知晓,数学世界真奇妙。
《数轴穿根法口诀五》
小朋友们听我说,数轴穿根有法则。
一找零点排排站,二看奇偶定规则。
奇数就像勇敢者,直接穿过去探索。
偶数好似小乖乖,安静待着不瞎穿。
这样就能解难题,快乐学习笑嘻嘻。
数轴标根法
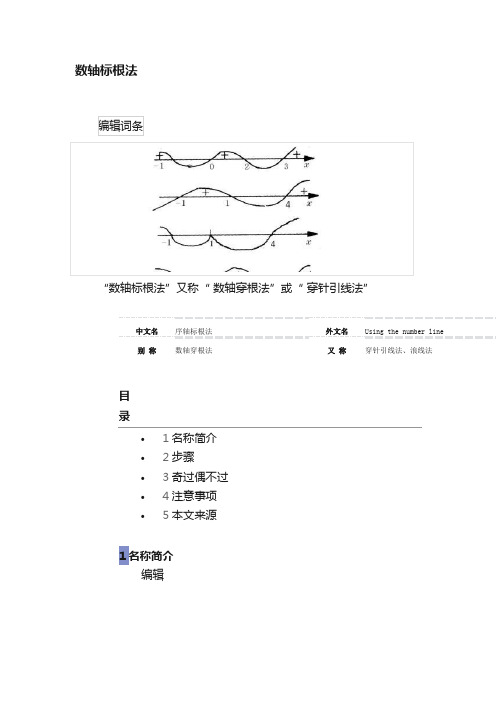
数轴标根法“数轴标根法”又称“数轴穿根法”或“穿针引线法”中文名序轴标根法别称数轴穿根法外文名Using the number line 又称穿针引线法、浪线法目录•1名称简介•2步骤•3奇过偶不过•4注意事项•5本文来源1名称简介编辑或“ 穿针引线法”或“浪线法”准确的说,应该叫做“序轴标根法”。
序轴:省去原点和单位,只表示数的大小的数轴。
序轴上标出的两点中,左边的点表示的数比右边的点表示的数小。
是高次不等式的简单解法当高次不等式f(x)>0(或<0)的左边整式、分式不等式φ(x)/h(x)>0(或<0)的左边分子、分母能分解成若干个一次因式的积(x-a1)(x-a2)…(x-an)的形式,可把各因式的根标在数轴上,形成若干个区间,最右端的区间f(x)、φ(x)/h(x)的值必为正值,从右往左通常为正值、负值依次相间,这种解不等式的方法称为序轴标根法。
为了形象地体现正负值的变化规律,可以画一条浪线从右上方依次穿过每一根所对应的点,穿过最后一个点后就不再变方向,这种画法俗称“ 穿针引线法”,如图1(图片自上而下依次为图一,二,三,四)。
2步骤编辑第一步:通过不等式的诸多性质对不等式进行移项,使得右侧为0。
(注意:一定要保证x前的系数为正数)例如:将x³-2x²-x+2>0化为(x-2)(x-1)(x+1)>0第二步:将不等号换成等号解出所有根。
例如:(x-2)(x-1)(x+1)=0的根为:x1=2,x2=1,x3=-1第三步:在数轴上从左到右依次标出各根。
例如:-1 1 2第四步:画穿根线:以数轴为标准,从“最右根”的右上方穿过根,往左下画线,然后又穿过“次右根”上去,一上一下依次穿过各根。
第五步:观察不等号,如果不等号为“>”,则取数轴上方,穿根线以内的范围;如果不等号为“<”则取数轴下方,穿根线以内的范围。
x的次数若为偶数则不穿过,即奇过偶不过。
专题8-数轴穿根法之欧阳与创编

专题:数轴穿根法“数轴穿根法”又称“数轴标根法”第一步:通过不等式的诸多性质对不等式进行移项,使得右侧为0。
(注意:一定要保证x前的系数为正数)例如:(x-2)(x-1)(x+1)>0第二步:将不等号换成等号解出所有根。
例如:(x-2)(x-1)(x+1)=0的根为:x1=2,x2=1,x3=-1第三步:在数轴上从左到右依次标出各根。
例如:-1 1 2第三步:画穿根线:以数轴为标准,从“最右根”的右上方穿过根,往左下画线,然后又穿过“次右跟”上去,一上一下依次穿过各根。
第四步:观察不等号,如果不等号为“>”,则取数轴上方,穿根线以内的范围;如果不等号为“<”则取数轴下方,穿根线以内的范围。
例如:若求(x-2)(x-1)(x+1)>0的解。
因为不等号威“>”则取数轴上方,穿根线以内的范围。
即:-1<x<1或x>2。
穿根法的奇过偶不过定律:“奇穿过,偶弹回”。
还有关于分式的问题:当不等式移项后,可能是分式,同样是可以用穿根法的,但是注意,解不能让原来分式下面的式子等于0专项训练:1、解不等式0)3)(1)(12(>--+x x x解析:1)一边是因式乘积、另一边是零的形式,其中各因式未知数的系数为正。
2)因式)12(+x)1(-x )3(-x 21-、1、31)。
3)从最大根3的右上方开始,向左依次穿线(数轴上方有线表示数轴上方有函数图象,数轴下方有线表示数轴下方有函数图象,此线并不表示函数的真实图象)。
4)数轴上方曲线对应的x 的取值区间,为0)3)(1)(12(>--+x x x 的解集,数轴下方曲线对应的x 的取值区间,为0)3)(1)(12(<--+x x x 的解集。
∴不等式0)3)(1)(12(>--+x x x 的解集为),3()1,21(+∞- 。
在上述解题过程中,学生存在的疑问往往有:为什么各因式中未知数的系数为正;为什么从最大根的右上方开始穿线;为什么数轴上方曲线对应的x 的集合是大于零不等式的解集,数轴下方曲线对应x 的集合是小于零不等式的解集。
3.2.2数轴穿根法及分式不等式

4、解不等式 ( x 1)( x 2) 0 ( x 1)( x 3)
解:原不等式等价于(x+1)(x-1)(x-2)(x-3)<0,将方程 (x+1)(x-1)(x-2)(x-3)=0的根-1,1,2,3标在数轴上,从右到左 画出示意图,
∴原不等式的解集是{x|-1<x<1或2<x<3}
解 : 因 为 关 于x的 不 等 式a x 1的 解 集 是{ x | x 0},
a 1, 又∵ loga ( x 2 4x 4) 0,
x2 4x 4 0
x2
4x
ቤተ መጻሕፍቲ ባይዱ
4
1
解 得1 x 2或2 x 3
原 不 等 式 的 解 集 是{ x | 1 x 2或2 x 3}
数轴标根法
复习:解一元二次不等式的一般步骤 (1)对不等式变形,使一端为零且二次项系数大 于零; (2)计算相应的判别式; (3)当△>0时,求出相应的一元二次方程的两个 根; (4)画出相应二次函数的草图; (5)根据函数图像写出一元二次不等式的解集。
记忆口诀: (前提a>0). 大于取两边,小于取中间
① 当a 1时
a f (x) a g(x) f ( x) g( x);
f (x) 0
loga
f ( x) loga
g(
x)
g(x) 0
f ( x) g( x)
② 当0 a 1时
a f (x) a g(x) f ( x) g( x);
f (x) 0
loga
f ( x) loga
g(
x)
g(x) 0
f ( x) g( x)
1、求y log 1 (2x 2 x)的定义域 __________
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1“数轴穿根法”又称“数轴标根法”
第一步:通过不等式的诸多性质对不等式进行移项,使得右侧为0。
(注意:保证X最高次项系数为正)例如:将x^3-2x^2-x+2>0化为(x-2)(x-1)(x+1)>0
第二步:将不等号换成等号解出所有根。
例如:(x-2)(x-1)(x+1)=0的根为:x1=2,x2=1,x3=-1
第三步:在数轴上从左到右依次标出各根。
例如:-1 1 2
第四步:画穿根线:以数轴为标准,从“最右根”的右上方穿过根,往左下画线,然后又穿过“次右根“上去,一上一下依次穿过各根。
第五步:观察不等号,如果不等号为“>”,则取数轴上方,穿跟线以内的范围;如果不等号为“<”则取数轴下方,穿跟线以内的范围。
例如:若求(x-2)(x-1)(x+1)>0的根。
在数轴上标根得:-1 1 2 画穿根线:由右上方开始穿根。
因为不等号威“>”则取数轴上方,穿跟线以内的范围。
即:-1<x<1或x>2。
编辑本段穿根法的奇过偶不过定律:
就是当不等式中含有有单独的x偶幂项时,如(x^2)或(x^4)时,穿根线是不穿过0点的。
但是对于X奇数幂项,就要穿过0点了。
还有一种情况就是例如:(X-1)^2.当不等式里出现这种部分时,线是不穿过1点的。
但是对于如(X-1)^3的式子,穿根线要过1点。
也是奇过偶不过。
可以简单记为“奇穿过,偶弹回”。
编辑本段还有关于分式的问题:
当不等式移项后,可能是分式,同样是可以用穿根法的,直接把分号下面的乘上来,变成乘法式子。
继续用穿根法,但是注意,解不能让原来分式下面的式子等于0 数轴的作用(观察通道)规定了原点,正方向,单位长度的直线,叫做数轴。
在某一事物上通过某一维度的评估,可以将事物分成很多不同的层次加以认识。
这样,能够更加准确,详
细地描述事物的本质。
2数轴穿根法什么时候会有连续穿?
就是在数轴下方向上穿时,碰到根后不上去,继续反弹回来,此时在下面而不是在上面
希望有哪位知道的老师能为晚辈解答,谢谢了.
最佳答案穿针引线法,标根分区法.或者叫穿根法,呵呵,是解高次不等式的一个好技巧, 第一:最高次项系数化为正数.保证因式分解后各因式中x的系数为正.
第二:将这若干个根按从小到大的顺序标在数轴上,注意是空心点(不能取到)还是实心点(可以取到).
第三:按照从右至左,从上至下的顺序画一条曲线,穿过这些点,注意"奇过偶不过"(奇次方的点过,偶次方的点不过).
第四:根据第一步整理的不等式的不等号的方向来写出解集,大于号取在数轴上方的区间,小于号取在数轴下方的区间.。
