高中数学教案——等比数列 第二课时
高三数学等比数列2

3.如果 a n bn 是项数相同的等比数列,那 么 a n bn 也是等比数列.
结论:如果 a b 是项数相同的等 比数列,那么 a n bn 也是等比数列.
n n
bn 的公比为 证明:设数列a n 的公比为p, q,那么数列 a n bn 的第n项与第n+1项分 n 1 n n 别为 a1p n 1 b1q n 1 与 a1p b1q ,即 a1b1 (pq) n 与 a1b1 (pq) .
因为 它是一个与n无关的常数,所以是一个以pq 为公比的等比数列.
a n 1 b n 1 a1b1 (pq) n pq, n 1 a n bn a1b1 (pq)
特别地,如果是a 等比数列ቤተ መጻሕፍቲ ባይዱc是不等 于0的常数,那么数列 c a 也是等比数列.
n
n
探究
对于例4中的等比数列 a n 与 bn ,数
1.定义法:
an1 q(是与n无关的数或式子 , 且q 0 ) an
2.中项法:
an1 an1 an ( 0)
2
三个数a,b,c成等比数列
2 ac b
五、等比数列的性质
1、若m, n, p, q N , 且m n p q,
则a m a n a p a q
an , 若a1 a2 a3 7, 4.已知等比数列
a1 a2 a3 8, 求an.
a1 1, q 2或a1 4, q
1 2
课后作业
P60 习题 2.4 A 组 第 3、 7、 8题
选做: P59 探究 选做: P75 第1,2,4题
高中数学:2.4《等比数列》(第二课时)教案(新人教A版必修5)

2.4《等比数列》(第二课时)一、能力要求:1、理解并掌握等比数列的性质;2、利用等比数列的定义推导等比数列的性质。
二、教学重点、难点:重点:等比数列的性质及推导。
难点:等比数列的性质及应用。
三、新课讲解:等比数列的常见性质:若数列{}n a 为等比数列,且公比为q ,则此数列具有以下性质: ①m n m n q a a -⋅=;②对任意正整数s r q p ,,,,满足s r q p +=+,则s r q p a a a a +=+; ③)(*2N m a a a m n m n n ∈=+-证明:①右边==⋅=⋅⋅=---n n m n m a q a q q a 1111左边②2211111-+--=⋅=+q p q p q p q a q a q a a a因为s r q p +=+,所以s r q p a a a a +=+。
③右边()==⋅=⋅=⋅⋅⋅=---+--221122211111n n n m n m n a q a q a q a q a 左边。
三、例题讲解:例1、已知数列{}n a 为等比数列(1)若6,475==a a ,求12a ; (2)若125,6,243224==+=-n a a a a a ,求n 。
例2、已知数列{}n a 为等比数列,320,2423=+=a a a ,求{}n a 的通项公式。
例3、在各项均为正数的等比数列{}n a 中,若965=a a ,则1032313log log log a a a ++等于( )A12 B10 C8 D 5log 23+注:若{}n a 为正项等比数列,则数列{}n m a log 为等差数列。
五、小结:等比数列的性质众多,最常用的是能够列出恒等式的性质,也就是本课主讲的三条。
还有一些特殊性质需在平时积累、总结、记忆。
课本上没有等比数列性质这一节内容,但作为解决等比数列问题的常用工具,对性质的熟练掌握对解题有很大的帮助。
【高中数学】第4章 4.3.1 等比数列的概念(第2课时)

4.3.1 等比数列的概念(第2课时)素养目标学科素养1.能够根据等比数列的定义和通项公式推出等比数列的常用性质.2.能够运用等比数列的性质解决有关问题.(重点)3.能够运用等比数列的知识解决简单的实际问题.1.数学运算; 2.逻辑推理情境导学一组有趣的对话,折了38次的纸,最后一次的厚度可是一个庞大的数字哦!1.等比数列的性质(1)若m +n =p +q (m ,n ,p ,q ∈N *),则a m ·a n =a p ·a q ; 若m +n =2k (m ,n ,k ∈N *),则a 2k =a m ·a n . (2)若数列{a n }是等比数列,则{|a n |},{a 2n},⎩⎨⎧⎭⎬⎫1an 仍为等比数列.判断(正确的打“√”,错误的打“×”).(1)在等比数列{a n }中,若a m a n =a p a q ,则m +n =p +q .(×)(2)若数列{a n },{b n }都是等比数列,则数列{a n +b n }也一定是等比数列.(×) (3)若数列{a n }是等比数列,则{λa n }也是等比数列.(×)2.等比数列性质的应用一般来说,当三个数成等比数列时,可设这三个数分别为a ,aq ,aq 2或aq ,a ,aq ,此时公比为q ;当四个数成等比数列时,可设这四个数分别为a ,aq ,aq 2,aq 3(公比为q ),当四个数均为正(负)数时,可设为a q 3,aq,aq ,aq 3(公比为q 2).(1)在等比数列{a n }中,若a 1=19,a 4=3,则该数列前五项的积为__1__.(2)已知三个数成等比数列,它们的积为27,它们的平方和为91,则这三个数是1,3,9或-1,3,-9或9,3,1或-9,3,-1.1.对任意等比数列{a n },下列说法一定正确的是( ) A .a 1,a 3,a 9成等比数列 B .a 2,a 3,a 6成等比数列 C .a 2,a 4,a 8成等比数列 D .a 3,a 6,a 9成等比数列D 解析:当下标成等差数列时,对应的项成等比数列. 2.在等比数列{a n }中,若a 2a 8=9,则a 3a 7=( ) A .3 B .±3 C .9D .±9C 解析:∵2+8=3+7,∴a 3a 7=a 2a 8=9.3.在等比数列{a n }中,若a 3a 4a 5=3,a 6a 7a 8=24,则a 9a 10a 11=( ) A .48 B .72 C .144D .192D 解析:∵a 6a 7a 8a 3a 4a 5=q 9=8(q 为公比),∴a 9a 10a 11=a 6a 7a 8q 9=24×8=192.4.在由正数组成的等比数列{a n }中,若a 4a 5a 6=3,则log 3a 1+log 3a 2+log 3a 8+log 3a 9的值为________.43 解析:因为a 4a 6=a 25,所以a 4a 5a 6=a 35=3,解得a 5=313.因为a 1a 9=a 2a 8=a 25,所以log 3a 1+log 3a 2+log 3a 8+log 3a 9=log 3(a 1a 2a 8a 9)=log 3a 45=log 3343=43. 5.在等比数列{a n }中,a 9+a 10=a (a ≠0),a 19+a 20=b ,则a 99+a 100=________.b 9a 8 解析:因为a 19+a 20=a 9q 10+a 10q 10=(a 9+a 10)q 10=aq 10=b ,所以q 10=b a ,a 99+a 100=q 90(a 9+a 10)=a ⎝⎛⎭⎫b a 9=b 9a 8.【例1】(1)在等比数列{a n }中,若a 3=12,a 9=2,则a 15=________.(2)已知公比为q 的等比数列{a n },a 5+a 9=q ,则a 6(a 2+2a 6+a 10)的值为________. (3)在等比数列{a n }中,a 7a 11=6,a 4+a 14=5,则a 20a 10等于________.(1)8 (2)1 (3)32或23解析:(1)∵a 3a 15=a 29,∴a 15=a 29a 3=2212=8.(2)∵a 5+a 9=q ,∴a 4+a 8=1,∴a 6(a 2+2a 6+a 10)=a 6a 2+2a 26+a 6a 10=a 24+2a 4a 8+a 28=(a 4+a 8)2=1.(3)设公比为q .∵a 7a 11=a 4a 14=6,又a 4+a 14=5,∴⎩⎪⎨⎪⎧ a 4=2,a 14=3或⎩⎪⎨⎪⎧a 4=3,a 14=2,∴q 10=a 14a 4=32或23,∴a 20a 10=q 10=32或23.等比数列的常用性质:(1)设{a n }为等比数列,m ,n ,p ,q ∈N *,若m +n =p +q ,则a m ·a n =a p ·a q .若m +n =2p ,则a m a n =a 2p .(2)若{a n }为等比数列,m ,n ∈N *,则a m a n =q m -n .(3)若{a n }为等比数列,则数列{a 2n }为等比数列.(4)若数列{a n }是公比为q 的等比数列,则数列⎩⎨⎧⎭⎬⎫1a n 是公比为1q 的等比数列.(5)等比数列{a n }中,每隔k 项取出一项,按原来的顺序排列,所得数列仍为等比数列,且公比为q k +1.在等比数列{a n }中,a 2+a 5=18,a 3·a 4=45,求a n .解:设等比数列{a n }的公比为q .根据题意,得⎩⎪⎨⎪⎧a 2a 5=a 3a 4=45,a 2+a 5=18,解得⎩⎪⎨⎪⎧ a 2=3,a 5=15或⎩⎪⎨⎪⎧a 2=15,a 5=3.∴q =513或q =5-13.∴a n =3×5n -23或a n =3×55-n 3.【例2】2017年,某县甲、乙两个林场森林木材的存量分别为16a 和25a ,甲林场木材存量每年比上一年递增25%,而乙林场木材存量每年比上一年递减20%. (1)哪一年两林场木材的总存量相等? (2)两林场木材的总量到2021年能否翻一番? 解:(1)由题意可得16a (1+25%)n -1=25a (1-20%)n -1, 解得n =2,故到2019年两林场木材的总存量相等.(2)令n =5,则a 5=16a ⎝⎛⎭⎫544+25a ⎝⎛⎭⎫454<2(16a +25a ), 故到2021年不能翻一番.一般地,涉及产值增长率、银行利息、细胞繁殖等实际问题时,往往与等比数列有关,可建立等比数列模型进行求解.一种专门占据内存的计算机病毒开始时占据内存2 KB ,然后每3分钟自身复制一次,复制后所占内存是原来的2倍,那么开机后________分钟,该病毒占据内存64 MB(1 MB =210 KB).45 解析:3分钟后占据内存22 KB ,两个3分钟后占据内存23 KB ,三个3分钟后占据内存24 KB ,……,n 个3分钟后占据内存为2n +1 KB .令2n +1=64×210=216,得n =15.所以15×3=45(分钟),故开机后45分钟,该病毒占据内存64 MB .探究题1 已知数列{a n }是公差为2的等差数列,且a 1,a 2,a 5成等比数列,则a 2的值为( ) A .3 B .-3 C .2D .-2A 解析:∵a 1,a 2,a 5成等比数列, ∴a 22=a 1a 5=(a 2-2)(a 2+6),解得a 2=3.探究题2 已知等比数列{a n },各项都是正数,且a 1,12a 3,2a 2成等差数列,则a 9+a 10a 7+a 8=( )A .3+2 2B .1- 2C .1+ 2D .3-2 2 A 解析:∵a 1,12a 3,2a 2成等差数列,∴a 3=a 1+2a 2.∴a 1q 2=a 1+2a 1q ,即q 2-2q -1=0, ∴q =1±2.∵a n >0,∴q =1+ 2.∴a 9+a 10a 7+a 8=(a 7+a 8)q 2a 7+a 8=q 2=(1+2)2=3+2 2. 探究题3 有四个实数,前三个数成等比数列,后三个数成等差数列,前三个数之积为27,中间两个数之和为9,求这四个数.解:(方法一)设前三个数分别为aq ,a ,aq (a ≠0),则第四个数为2aq -a .由题意得⎩⎪⎨⎪⎧a q ·a ·qa =27,a +aq =9,解得⎩⎪⎨⎪⎧a =3,q =2,∴这四个数分别为32,3,6,9.(方法二)设后三个数分别为a -d ,a ,a +d (a ≠0),则第一个数为(a -d )2a.由题意得⎩⎪⎨⎪⎧(a -d )2a (a -d )a =27,a -d +a =9,化简得⎩⎪⎨⎪⎧ a -d =3,2a -d =9,解得⎩⎪⎨⎪⎧a =6,d =3,∴这四个数分别为32,3,6,9.(方法三)设前三个数分别为a ,aq ,aq 2(a ≠0),则第四个数应为2aq 2-aq .由题意得⎩⎪⎨⎪⎧a ·aq ·aq 2=27,aq +aq 2=9,化简得⎩⎪⎨⎪⎧aq =3,aq (1+q )=9,解得⎩⎪⎨⎪⎧a =32,q =2,∴这四个数分别为32,3,6,9.探究题4 三个互不相等的实数成等差数列,如果适当安排这三个数,又可以成等比数列,且这三个数的和为6,求这三个数.解:由题意,这三个数成等差数列,可设这三个数分别为a -d ,a ,a +d .∵a -d +a +a +d =6,∴a =2,即三个数分别为2-d,2,2+d .①若2-d 为等比中项,则有(2-d )2=2(2+d ), 解得d =6或d =0(舍去),此时三个数为-4,2,8. ②若2+d 是等比中项,则有(2+d )2=2(2-d ), 解得d =-6或d =0(舍去),此时三个数为8,2,-4. ③若2为等比中项,则有22=(2+d )(2-d ), 解得d =0(舍去).综上可知,这三个数是-4,2,8或8,2,-4.探究题5 数列{a n }的前n 项和记为S n ,a 1=1,a n +1=2S n +1(n ≥1). (1)求{a n }的通项公式;(2)等差数列{b n }的各项为正,其前n 项和为T n ,且T 3=15,又a 1+b 1,a 2+b 2,a 3+b 3成等比数列,求T n .解:(1)由a n +1=2S n +1, 可得a n =2S n -1+1(n ≥2),两式相减,得a n +1-a n =2a n ,a n +1=3a n (n ≥2). 又∵a 2=2S 1+1=3,∴a 2=3a 1,故{a n }是首项为1,公比为3的等比数列, ∴a n =3n -1.(2)设{b n }的公差为d ,由T 3=15,得b 1+b 2+b 3=15,可得b 2=5, 故b 1=5-d ,b 3=5+d . 又a 1=1,a 2=3,a 3=9,由题意可得(5-d +1)(5+d +9)=(5+3)2, 解得d 1=2,d 2=-10. ∵等差数列{b n }的各项为正, ∴d >0, ∴d =2,∴b 1=3.∴T n =3n +n (n -1)2×2=n 2+2n .巧设等差数列、等比数列的方法:(1)若三个数成等差数列,常设成a -d ,a ,a +d ;若三个数成等比数列,常设成aq ,a ,aq或a ,aq ,aq 2(a ≠0,q ≠0).(2)若四个数成等比数列,可设为aq,a ,aq ,aq 2(a ≠0,q ≠0).等差数列{a n }中,a 4=10且a 3,a 6,a 10成等比数列,求数列{a n }前20项的和S 20. 解:设等差数列{a n }的公差为d ,则 a 3=a 4-d =10-d ,a 6=a 4+2d =10+2d , a 10=a 4+6d =10+6d .由a 3,a 6,a 10成等比数列得,a 3a 10=a 26, 即(10-d )(10+6d )=(10+2d )2, 整理得10d 2-10d =0, 解得d =0或d =1.当d =0时,S 20=20a 4=200;当d =1时,a 1=a 4-3d =10-3×1=7, S 20=20a 1+20×192d =20×7+190=330.因此,S 20=200或S 20=330.1.在等比数列{a n }中,a 3=-9,a 7=-1,则a 5的值为( ) A .3或-3 B .3 C .-3D .不存在C 解析:a 25=a 3·a 7=9,所以a 5=-3或a 5=3(舍去). 2.已知等比数列{a n }满足a 1+a 2=3,a 2+a 3=6,则a 8=( ) A .243 B .128 C .81D .64B 解析:设等比数列{a n }的公比为q ,∴q =a 2+a 3a 1+a 2=63=2,∴a 1+a 2=3a 1=3,即a 1=1,∴a 8=a 1q 7=128.3.等比数列{a n }不具有单调性,且a 5是a 4和3a 3的等差中项,则数列{a n }的公比q =( ) A .-1 B .1 C .-2D .-3 A 解析:∵a 5是a 4和3a 3的等差中项,∴2a 5=a 4+3a 3,得2a 1q 4=a 1q 3+3a 1q 2,解得q =32或q =-1.又等比数列{a n }不具有单调性,故q =-1.故选A .4.等比数列{a n }的各项均为正数,公比q ≠1,设P =12(log 0.5a 5+log 0.5a 7),Q =log 0.5a 3+a 92,则P 与Q 的大小关系是( ) A .P ≥Q B .P <Q C .P ≤QD .P >QD 解析: P =12(log 0.5a 5+log 0.5a 7)=log 0.5a 5a 7=log 0.5a 6,Q =log 0.5a 3+a 92≤log 0.5a 3a 9=log 0.5a 6 (当且仅当a 3=a 9时取等号). ∵{a n }各项均为正数且q ≠1,∴a 3≠a 9, ∴Q <log 0.5a 6.∴P >Q .故选D .5.设{a n }是等比数列,a 1=1,a 3=34a 2.求{a n }的通项公式.解:设等比数列{a n }的公比为q ,则q =a 3a 2=34.因为a 1=1,所以a n =⎝⎛⎭⎫34n -1.1.等比数列的性质及其应用一方面,等比数列的性质要与等差数列的性质对比记忆,加深理解并作区分;另一方面,等比数列一般运算量大,巧用等比数列的性质,减少计算量这一点很重要.2.等比数列各项之间可由公比建立关系,在三个(四个)数成等比数列问题中,应注意灵活设项.课时分层作业(八) 等比数列的概念(第2课时)(60分钟 110分) 基础对点练基础考点 分组训练知识点1 等比数列的性质1.(5分)公比不为1的等比数列{a n }满足a 5a 6+a 4a 7=8,若a 2a m =4,则m 的值为( ) A .8 B .9 C .10D .11B 解析:∵公比不为1的等比数列{a n }满足a 5a 6+a 4a 7=8,∴a 5a 6=a 4a 7=4. ∵a 2·a m =4,∴2+m =5+6=11,解得m =9.故选B .2.(5分)已知等比数列{a n }的公比q 为正数,且a 3a 9=2a 25,a 2=1,则a 1=( ) A .12B .22C . 2D .2B 解析:∵a 3a 9=a 26,∴a 6=2a 5,∴q = 2. ∵a 2=a 1q =1,∴a 1=22. 3.(5分)在等比数列{a n }中,若a 7=-2,则该数列的前13项的乘积等于( ) A .-213 B .213 C .26D .-26A 解析:a 1·a 2·…·a 13=(a 7)13=(-2)13=-213. 知识点2 等比数列的实际应用4.(5分)一张报纸的厚度为a ,面积为b ,现将此报纸对折(沿对边中点连线折叠)7次,这时报纸的厚度和面积分别为( ) A .8a ,18bB .64a ,164bC .128a ,1128bD .256a ,1256bC 解析:对折后,报纸的厚度和面积也依次成等比数列,公比分别为2和12, ∴对折7次后的厚度为27·a =128a ,面积为⎝⎛⎭⎫127·b =b 128. 5.(5分)某工厂去年产值为a ,计划10年内每年比上一年产值增长10%,那么从今年起第几年这个工厂的产值将超过2a ?( )A .6B .7C .8D .9C 解析:由题意知每年的产值构成以1.1a 为首项,公比为1.1的等比数列,则a n =a ·1.1n . ∴a ·1.1n >2a .∵1.17<2,1.18>2,∴n =8.知识点3 等比数列的综合应用6.(5分)已知等差数列{a n }的首项a 1和公差d 均不为零,且a 2,a 4,a 8成等比数列,则a 1+a 5+a 9a 2+a 3=( )A .6B .5C .4D .3D 解析:∵a 2,a 4,a 8成等比数列,∴a 24=a 2a 8,∴(a 1+3d )2=(a 1+d )(a 1+7d ),∴d 2=a 1d .又d ≠0,a 1≠0,∴d =a 1,∴a n =a 1+(n -1)d =na 1≠0,∴a 1+a 5+a 9a 2+a 3=a 1+5a 1+9a 12a 1+3a 1=3.故选D . 7.(5分)已知等差数列{a n }的公差为2,若a 1,a 3,a 4成等比数列,则数列{a n }前6项的和为( )A .-20B .-18C .-16D .-14B 解析:∵a 1,a 3,a 4成等比数列,∴a 23=a 1·a 4.∴(a 1+4)2=a 1·(a 1+6).∴a 1=-8.∴S 6=6×(-8)+6×5×22=-18. 8.(5分)已知数列{a n }满足log 3a n +1=log 3a n +1(n ∈N *),且a 2+a 4+a 6=9,则log 13(a 5+a 7+a 9)的值为( )A .-5B .-15C .5D .15A 解析:∵log 3a n +1=log 3a n +1,∴log 3a n +1-log 3a n =1,∴log 3a n +1a n =1, ∴a n +1a n=3,∴{a n }是等比数列,公比为3. ∴log 13(a 5+a 7+a 9)=log 13[(a 2+a 4+a 6)·q 3]=log 13(9×27)=-5. 9.(5分)已知数列{a n }是公比为2的等比数列,满足a 6=a 2a 10.设等差数列{b n }的前n 项和为S n ,若b 9=2a 7,则S 17=( )A .34B .39C .51D .68D 解析:∵a 6=a 2a 10=a 26, ∴a 6=1.∴a 7=2a 6=2.∴b 9=4.∴S 17=17(b 1+b 17)2=17b 9=17×4=68. 能力提升练能力考点 拓展提升10.(5分)在等比数列{a n }中,a 1=1,公比q ≠±1.若a m =a 1a 2a 3a 4a 5,则m 等于( )A .9B .10C .11D .12C 解析:∵a m =a 1a 2a 3a 4a 5=a 53=q 10=a 11,∴m =11.11.(5分)已知等比数列{a n }满足a 1=3,且4a 1,2a 2,a 3成等差数列,则a 3+a 4+a 5等于( )A .33B .84C .72D .189B 解析:设等比数列{a n }的公比为q ,由4a 1,2a 2,a 3成等差数列,得4a 1+a 3=4a 2,即12+3q 2=4×3q ,解得q =2,∴a 3+a 4+a 5=a 1q 2+a 1q 3+a 1q 4=3×(22+23+24)=84.12.(5分)(多选)在正项等比数列{a n }中,已知a 1a 2a 3=4,a 4a 5a 6=12,a n -1a n a n +1=324,则( )A .q 2=3B .a 32=4C .a 4a 6=2 3D .n =14BD 解析:设数列{a n }的公比为q ,由a 1a 2a 3=4=a 31q 3与a 4a 5a 6=12=a 31q 12可得q 9=3,a 32=4,a 35=12,AC 不正确.又a n -1a n a n +1=a 31q 3n -3=324,因此q 3n -6=81=34=q 36,所以n =14.故选BD .13.(5分)已知数列{a n }是等比数列,且a 3+a 5=18,a 9+a 11=144,则a 6+a 8=________.±362 解析:设等比数列{a n }的公比为q , ∵a 9+a 11a 3+a 5=q 6=14418=8, ∴q 3=±2 2.∴a 6+a 8=(a 3+a 5)·q 3=18×(±22)=±36 2.14.(5分)公差不为零的等差数列{a n }中,2a 3-a 27+2a 11=0,数列{b n }是等比数列,且b 7=a 7,则b 6b 8=________.16 解析:∵2a 3-a 27+2a 11=2(a 3+a 11)-a 27=4a 7-a 27=0,b 7=a 7≠0,∴b 7=a 7=4.∴b 6b 8=b 27=16.15.(10分)设公比不为1的等比数列{a n }满足a 1a 2a 3=-18,且a 2,a 4,a 3成等差数列,求a 1.解:设{a n }的公比为q (q ≠1),∵a 1a 2a 3=a 32=-18,∴a 2=-12. ∵a 2,a 4,a 3成等差数列,∴2a 4=a 2+a 3.∴2×⎝⎛⎭⎫-12·q 2=-12+⎝⎛⎭⎫-12·q , 解得q =-12或q =1(舍). ∴a 1=a 2q=1. 16.(10分)已知四个数成等比数列,其乘积为1,第2项与第3项之和为-32,求这四个数.解:设四个数依次为a ,aq ,aq 2,aq 3,则⎩⎪⎨⎪⎧ a 4q 6=1,aq (1+q )=-32,解得⎩⎪⎨⎪⎧ a =-18,q =-4或⎩⎪⎨⎪⎧a =8,q =-14.故所求四个数依次为-18,12,-2,8或8,-2,12,-18. 17.(10分)已知数列{a n }是首项为1,公比为q 的等比数列.(1)求证:当0<q <1时,{a n }是递减数列.(2)若对任意k ∈N *,都有a k ,a k +2,a k +1成等差数列,求q 的值.(1)证明:∵a n =q n -1,∴a n +1-a n =q n -q n -1=q n -1(q -1).当0<q <1时有q n -1>0,q -1<0,∴a n +1-a n <0,∴{a n }为递减数列.(2)解:∵a k ,a k +2,a k +1成等差数列, ∴2a k +2=a k +a k +1.∴2q k +1-(q k -1+q k )=0,即q k -1·(2q 2-q -1)=0.∵q ≠0,∴2q 2-q -1=0,解得q =1或q =-12. 18.(10分)设数列{a n }的前n 项和为S n ,已知a 1=1,S n +1=4a n +2,且b n =a n +1-2a n .(1)求证:数列{b n }是等比数列.(2)求数列{a n }的通项公式.(1)证明:由S n +1=4a n +2,S n +2=4a n +1+2,两式相减,得 S n +2-S n +1=4(a n +1-a n ),即a n +2=4a n +1-4a n , ∴b n +1b n =a n +2-2a n +1a n +1-2a n =4a n +1-4a n -2a n +1a n +1-2a n=2. 当n =1时,由S 2=4a 1+2得a 2=5, ∴b 1=a 2-2a 1=3,∴{b n }是首项为3,公比为2的等比数列.(2)解:由(1)知等比数列{b n }中,首项b 1=3,公比q =2,∴a n +1-2a n =3×2n -1,则a n +12n +1-a n 2n =34, ∴因此数列⎩⎨⎧⎭⎬⎫a n 2n 是首项为12,公差为34的等差数列, ∴a n 2n =12+(n -1)×34=34n -14, ∴a n =(3n -1)·2n -2.。
高中数学选择性必修二 4 3 1(第2课时)等比数列的性质及应用 教案
重点
等比数列的性质、等比数列的应用
难点
等比数列的运算、等比数列的性质及应用
教学过程
教学环节
教师活动
学生活动
设计意图
导入新课
温故知新
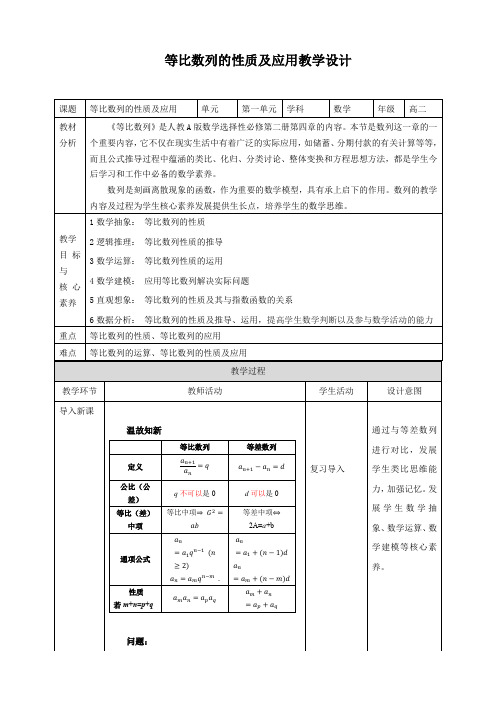
等比数列
等差数列
定义
公比(公差)
q不可以是0
d可以是0
等比(差)中项
等比中项
等差中项 2A=a+b
等比数列的性质及应用教学设计
课题
等比数列的性质及应用
单元
第一单元
学科
数学
年级
高二
教材分析
《等比数列》是人教A版数学选择性必修第二册第四章的内容。本节是数列这一章的一个重要内容,它不仅在现实生活中有着广泛的实际应用,如储蓄、分期付款的有关计算等等,而且公式推导过程中蕴涵的类比、化归、分类讨论、整体变换和方程思想方法,都是学生今后学习和工作中必备的数学素养。
分析:复利是把前一期的利息与本金之和算作本金,再计算下一期的利息,所以若原始本金为a元,每期的利率为r,则从第一期开始,各期的本利和 构成等比数列.
解:(1)设这笔钱存n个月以后的本利和组成一个数列 ,则 是等比数列,
首项 ,
公比q=1+0.400%,所以
所以,
12个月后的利息为 (元)
(2)设季度利率为r,这笔钱存n个季度以后的本金和组成一个数列 ,则 也是一个等比数列,首项 ,公比为1+r,于是
因此,以季度复利计息,存4个季度后的利息为 元.
解不等式 ,得
所以,当季度利率不小于1.206%时,按季结算的利息不少于按月结算的利息.
例5已知数列Байду номын сангаас的首项 .
高中数学 第1章 数列 3.1 等比数列 第2课时 等比数列的性质教案 高二数学教案

第2课时 等比数列的性质阅读教材P 23思考交流以下P 24例3以上部分,完成下列问题.对于等比数列{a n },通项公式a n =a 1·q n -1=a 1q·q n.根据指数函数的单调性,可分析当q >0时的单调性如下表:思考:(1)若等比数列{a n }中,a 1=2,q =2,则数列{a n }的单调性如何?[提示] 递减数列.(2)等比数列{a n }中,若公比q <0,则数列{a n }的单调性如何? [提示] 数列{a n }不具有单调性,是摆动数列. 2.等比中项阅读教材P 25练习2以上最后两段部分,完成下列问题. (1)前提:在a 与b 中间插入一个数G ,使得a ,G ,b 成等比数列.(2)结论:G 叫作a ,b 的等比中项. (3)满足关系式:G 2=ab .思考:(1)任意两个数都有等差中项,任意两个数都有等比中项吗?[提示] 不是,两个同号的实数必有等比中项,它们互为相反数,两个异号的实数无等比中项.(2)两个数的等差中项是唯一的,若两个数a ,b 存在等比中项,唯一吗?[提示] 不唯一,如2和8的等比中项是4或-4.1.已知{a n }是等比数列,a 2=2,a 5=14,则公比q 等于( )A .-12B .-2C .2D .12D [由a 5=a 2q 3,得q 3=a 5a 2=142=18,所以q =12,故选D .]2.将公比为q 的等比数列{a n }依次取相邻两项的乘积组成新的数列a 1a 2,a 2a 3,a 3a 4,…,则此数列是( )A .公比为q 的等比数列B .公比为q 2的等比数列 C .公比为q 3的等比数列 D .不一定是等比数列B [由于a n a n +1a n -1a n =a n a n -1×a n +1a n=q ·q =q 2,n ≥2且n ∈N +,所以{a n a n +1}是以q 2为公比的等比数列,故选B .]3.等比数列{a n }中,若a 1=2,且{a n }是递增数列,则数列{a n }的公比q 的取值范围是________.(1,+∞) [因为a 1=2>0,要使{a n }是递增数列,则需公比q >1.]4.4-23与4+23的等比中项是________. 2或-2 [由题意知4-23与4+23的等比中项为 ±4-234+23=±16-12=±2.]等比中项及应用x =_____________.(2)设a ,b ,c 是实数,若a ,b ,c 成等比数列,且1a ,1b ,1c成等差数列,则c a +ac的值为________.(1)-4 (2)2 [(1)由题意得(2x +2)2=x (3x +3),x 2+5x +4=0,解得x =-1或x =-4,当x =-1时,2x +2=0,不符合题意,舍去, 所以x =-4.(2)由a ,b ,c 成等比数列,1a ,1b ,1c成等差数列,得⎩⎪⎨⎪⎧b 2=ac ,2b =1a +1c,即4ac =⎝ ⎛⎭⎪⎫1a +1c 2,故(a -c )2=0, 则a =c ,所以c a +ac=1+1=2.]应用等比中项解题的两个注意点(1)要证三数a ,G ,b 成等比数列,只需证明G 2=ab ,其中a ,b ,G 均不为零.(2)已知等比数列中的相邻三项a n -1,a n ,a n +1,则a n 是a n -1与a n +1的等比中项,即a 2n =a n -1·a n +1,运用等比中项解决问题,会大大减少运算过程.1.(1)已知1既是a 2与b 2的等比中项,又是1a 与1b的等差中项,则a +ba 2+b2的值是( ) A .1或12B .1或-12C .1或13D .1或-13(2)已知等比数列{a n }的前三项依次为a -1,a +1,a +4,则a n =________.(1)D(2)4×⎝ ⎛⎭⎪⎫32n -1[(1)由题意得,a 2b 2=(ab )2=1,1a +1b=2,所以⎩⎪⎨⎪⎧ab =1,a +b =2或⎩⎪⎨⎪⎧ab =-1,a +b =-2.因此a +b a 2+b 2的值为1或-13.(2)由已知可得(a +1)2=(a -1)(a +4), 解得a =5,所以a 1=4,a 2=6,所以q =a 2a 1=64=32,所以a n =4×⎝ ⎛⎭⎪⎫32n -1.]等比数列的设法与求解【例2】 已知四个实数,前三个数依次成等比数列,它们的积是-8,后三个数依次成等差数列,它们的积是-80,则这四个数为________.1,-2,4,10或-45,-2,-5,-8 [由题意设此四个数分别为b q,b ,bq ,a ,则b 3=-8,解得b =-2,q 与a 可通过解方程组⎩⎪⎨⎪⎧2bq =a +b ,ab 2q =-80求出,即为⎩⎪⎨⎪⎧a =10,b =-2,q =-2或⎩⎪⎨⎪⎧a =-8,b =-2,q =52,所以此四个数为1,-2,4,10或-45,-2,-5,-8.]灵活设项求解等比数列的技巧(1)三个数成等比数列设为aq,a ,aq .(2)四个符号相同的数成等比数列设为a q 3,a q,aq ,aq 3.(3)四个数成等比数列,不能确定它们的符号相同时,可设为:a ,aq ,aq 2,aq 3.2.已知三个数成等比数列,其积为1,第2项与第3项之和为-32,则这三个数依次为________.-25,1,-52 [设这三个数分别为aq,a ,aq ,则⎩⎪⎨⎪⎧a 3=1,a +aq =-32,解得a =1,q =-52,所以这三个数依次为-25,1,-52.]等比数列的性质及应用[探究问题]1.在等差数列{a n }中,a n =a m +(n -m )d ,类比等差数列中通项公式的推广,你能得出等比数列通项公式推广的结论吗?[提示] a n =a m ·qn -m.2.在等差数列{a n }中,由2a 2=a 1+a 3,2a 3=a 2+a 4,…我们推广得到若2p =m +n ,则2a p =a m +a n ,若{a n }是等比数列,我们能得到什么类似的结论.[提示] 若2p =m +n ,则a 2p =a m ·a n .3.在等差数列{a n }中,若m +n =p +q ,则a m +a n =a p +a q ,类比这个性质,若{a n }是等比数列,有哪个结论成立?[提示] 若m +n =p +q ,则a m ·a n =a p ·a q .【例3】 (1)在等比数列{a n }中,a n >0,若a 3·a 5=4,则a 1a 2a 3a 4a 5a 6a 7=________.(2)设{a n }为公比q >1的等比数列,若a 2 018和a 2 019是方程4x 2-8x +3=0的两根,则a 2 030+a 2 031=________.(3)在等比数列{a n }中,已知a 4a 7=-512,a 3+a 8=124,且公比q 为整数,则a n =________.思路探究:利用等比数列的性质求解.(1)128 (2)2·312 (3)-(-2)n -1[(1)a 3a 5=a 24=4,又a n>0,所以a 4=2,a 1a 2a 3a 4a 5a 6a 7=(a 1·a 7)·(a 2·a 6)·(a 3·a 5)·a 4=a 24·a 24·a 24·a 4=a 74=27=128.(2)解方程4x 2-8x +3=0得x 1=12,x 2=32,因为q >1,故a 2 019=32,a 2 018=12,故q =3, ∴a 2 030+a 2 031=a 2 018q 12+a 2 019·q 12=(a 2 018+a 2 019)q 12=2·312.(3)在等比数列{a n }中,由a 4a 7=-512得a 3a 8=-512, 又a 3+a 8=124,解得a 3=-4,a 8=128或a 3=128,a 8=-4,因为公比q 为整数,所以q =5a 8a 3=-51284=-2, 故a n =-4×(-2)n -3=-(-2)n -1.]1.(变条件)将例3(3)中等比数列满足的条件改为“a 4+a 7=2,a 5a 6=-8”,求a 1+a 10.[解] 因为{a n }是等比数列,所以a 5a 6=a 4a 7=-8, 又a 4+a 7=2,解得a 4=4,a 7=-2或a 4=-2,a 7=4, 当a 4=4,a 7=-2时,q 3=-12,a 1+a 10=a 4q3+a 7q 3=-7,当a 4=-2,a 7=4时,q 3=-2,a 1+a 10=a 4q3+a 7q 3=-7.故a 1+a 10=-7.2.(变结论)例3(3)题的条件不变,求log 4|a 2|+log 4|a 3|+log 4|a 8|+log 4|a 9|.[解] 因为a 4a 7=-512,所以a 2a 9=a 3a 8=-512, 故log 4|a 2|+log 4|a 3|+log 4|a 8|+log 4|a 9| =log 4(|a 2a 9|·|a 3a 8|)=log 45122=log 229=9.等比数列的常用性质性质1:通项公式的推广:a n =a m ·qn -m(m ,n ∈N +).性质2:若{a n }为等比数列,且k +l =m +n (k ,l ,m ,n ∈N +),则a k ·a l =a m ·a n .特别的,若k +φ=2m (m ,k ,φ∈N +),则a k ·a φ=a 2m .性质3:若{a n },{b n }(项数相同)是等比数列,则{λb n },⎩⎨⎧⎭⎬⎫1a n ,{a 2n },{a n ·b n },⎩⎨⎧⎭⎬⎫a nb n 仍是等比数列.性质4:在等比数列{a n }中,序号成等差数列的项仍成等比数列.性质5:⎩⎪⎨⎪⎧a 1>0,q >1或⎩⎪⎨⎪⎧a 1<0,0<q <1⇔{a n }递增;⎩⎪⎨⎪⎧a 1>0,0<q <1或⎩⎪⎨⎪⎧a 1<0,q >1⇔{a n }递减;q =1⇔{a n }为常数列;q<0⇔{a n }为摆动数列.1.解题时,应该首先考虑通式通法,而不是花费大量时间找简便方法.2.所谓通式通法,指应用通项公式,前n 项和公式,等差中项,等比中项等列出方程(组),求出基本量.3.巧用等比数列的性质,减少计算量,这一点在解题中也非常重要.1.判断正误(正确的打“√”,错误的打“×”)(1)数列-1,-2,-4,-8,-16是递减数列.( ) (2)等比数列{a n }中,a 1>1,q <0,则数列|a 1|,|a 2|,|a 3|,…,|a n |,…是递增数列.( )(3)若G 是a ,b 的等比中项,则G 2=ab ,反之也成立.( ) [答案] (1)√ (2)× (3)× [提示] (1)正确;(2)不正确,如a 1=2,q =⎝ ⎛⎭⎪⎫-12,则|a n |=2×12n -1=12n -2是递减数列;(3)不正确,当G 是a ,b 的等比中项时,G 2=ab 成立,但当G 2=ab 时,G 不一定是a ,b 的等比中项,如G=a =b =0.2.在等比数列{a n }中,a 4=6,则a 2a 6的值为( ) A .4 B .8 C .36D .32C [因为{a n }是等比数列,所以a 2a 6=a 24=36.]3.在等比数列{a n }中,a 888=3,a 891=81,则公比q =_____________.3 [因为a 891=a 888q891-888=a 888q 3,所以q 3=a 891a 888=813=27.所以q =3.]4.在等比数列{a n }中,a 3a 4a 5=8,求a 2a 3a 4a 5a 6的值.[解] 在等比数列{a n }中,由a 3a 4a 5=a 34=8,得a 4=2,又因为a2a6=a3a5=a24,所以a2a3a4a5a6=a54=25=32.。
等比数列(第二课时)课件PPT

放射性衰变过程中,原子核的数目按 照等比数列的方式减少。
透镜的焦距按照等比数列的方式排列, 可以用于制造不同焦距的透镜。
声音传播
在声波传播过程中,振动的次数按照 等比数列的方式增加,形成不同的音 高。
等比数列在计算机科学中的应用
数据压缩
在数据压缩算法中,等比数列可 以用于高效地存储和传输数据。
网络传输
在等比数列 { a_n } 中, 已知 a_2 = 4,a_6 = 32,求首项 a_1 和公比 q。
基础练习题3
已知等比数列 { a_n } 的 前 n 项和 S_n = 3^n + r,求 a_3 和 r 的值。
提升练习题
1 2
提升练习题1
在等比数列 { a_n } 中,已知 a_1 = 1,a_4 = 8, 求数列的前 4 项和 S_4。
推导求和公式
通过等比数列的性质,我们可以将等比数列的各项进行分组 求和,再利用等比数列的性质化简,最终得到等比数列的求 和公式:S_n=a_1*(1-r^n)/(1-r)。
等比数列求和公式的应用
解决实际问题
等比数列求和公式可以应用于解决一 些实际问题,例如计算复利、评估投 资回报等。
简化计算
对于一些特殊的等比数列,如几何级 数,等比数列求和公式可以大大简化 计算过程。
复利计算
等比数列可以用于计算复利,帮 助投资者了解投资收益的增长情
况计算未来价值 和赔偿金额。
股票分析
股票价格的增长往往呈现出等比数 列的特点,投资者可以通过分析等 比数列来预测股票价格的走势。
等比数列在物理领域的应用
放射性衰变
光学透镜
提升练习题2
已知等比数列 { a_n } 的公比 q = 2,前 n 项和 S_n = 63,求首项 a_1。
高一数学 等比数列(二)教案

芯衣州星海市涌泉学校师范大学附属中学高一数学教案:等比数列〔二〕教材:等比数列〔二〕目的:在熟悉等比数列有关概念的根底上,要求学生进一步熟悉等比数列的有关性质,并系统理解判断一个数列是否成等比数列的方法。
过程:一、复习:1、等比数列的定义,通项公式,中项。
2、处理课本P128练习,重点是第三题。
二、等比数列的有关性质:1、与首末两项等间隔的两项积等于首末两项的积。
与某一项间隔相等的两项之积等于这一项的平方。
2、假设q p n m +=+,那么q p n m a a a a =。
例一:1、在等比数列{}n a ,51=a ,100109=a a ,求18a 。
解:∵109181a a a a =,∴205100110918===a a a a 2、在等比数列{}nb 中,34=b ,求该数列前七项之积。
解:()()()45362717654321b b b b b b b b b b b b b b =∵53627124b b b b b b b ===,∴前七项之积()2187333732==⨯3、在等比数列{}n a 中,22-=a ,545=a ,求8a ,解:145825454255358-=-⨯=⋅==a a a q a a 另解:∵5a 是2a 与8a 的等比中项,∴25482-⨯=a∴14588-=a三、判断一个数列是否成GP 的方法:1、定义法,2、中项法,3、通项公式法 例二:无穷数列 ,10,10,10,1051525150-n ,求证:〔1〕这个数列成GP〔2〕这个数列中的任一项是哪一项哪一项它后面第五项的101, 〔3〕这个数列的任意两项的积仍在这个数列中。
证:〔1〕5152511101010==---n n n n a a 〔常数〕∴该数列成GP 。
〔2〕101101010154515===-+-+n n n n a a ,即:5101+=n n a a 。
〔3〕525151101010-+--==q p q p q p a a ,∵N q p ∈,,∴2≥+q p 。
高中数学 第三章 3.4 等比数列(2)教案.doc

3.4 等比数列(二)教学目的:1.灵活应用等比数列的定义及通项公式.2.深刻理解等比中项概念.3.熟悉等比数列的有关性质,并系统了解判断数列是否成等比数列的方法 教学重点:等比中项的理解与应用教学难点:灵活应用等比数列定义、通项公式、性质解决一些相关问题 授课类型:新授课 课时安排:1课时教 具:多媒体、实物投影仪 教学过程:一、复习引入:首先回忆一下上一节课所学主要内容:1.等比数列:如果一个数列从第二项起,每一项与它的前一项的比等于同一个常数,那么这个数列就叫做等比数列.这个常数叫做等比数列的公比;公比通常用字母q 表示(q ≠0),即:1-n na a =q (q ≠0) 2.等比数列的通项公式:)0(111≠⋅⋅=-q a q a a n n , )0(≠⋅⋅=-q a q a a m m n m n3.{n a }成等比数列⇔nn a a 1+=q (+∈N n ,q ≠0) “n a ≠0”是数列{n a }成等比数列的必要非充分条件 4.既是等差又是等比数列的数列:非零常数列.二、讲解新课:1.等比中项:如果在a 与b 中间插入一个数G ,使a ,G ,b 成等比数列,那么称这个数G 为a 与b 的等比中项. 即G =±ab (a ,b 同号)如果在a 与b 中间插入一个数G ,使a ,G ,b 成等比数列,则ab G ab G Gba G ±=⇒=⇒=2, 反之,若G 2=ab ,则Gba G =,即a ,G ,b 成等比数列∴a ,G ,b 成等比数列⇔G 2=ab (a ·b ≠0) 2.等比数列的性质:若m+n=p+k ,则k p n m a a a a = 在等比数列中,m+n=p+q ,k p n m a a a a ,,,有什么关系呢?由定义得:11n 11 --==n m m q a a q a a 11k 11 --⋅==k p p q a a q a a221-+=⋅n m n m q a a a ,221-+=⋅k p k p q a a a则k p n m a a a a =3.判断等比数列的方法:定义法,中项法,通项公式法4.等比数列的增减性:当q>1, 1a >0或0<q<1, 1a <0时, {n a }是递增数列;当q>1, 1a <0,或0<q<1, 1a >0时, {n a }是递减数列;当q=1时, {n a }是常数列;当q<0时, {n a }是摆动数列;三、例题讲解例1 已知:b 是a 与c 的等比中项,且a 、b 、c 同号,求证:3,3,3abc ca bc ab c b a ++++ 也成等比数列 证明:由题设:b 2=ac 得:22333)3(333ca bc ab bc b ab b c b a abc c b a ++=++=⨯++=⨯++ ∴3,3,3abc ca bc ab c b a ++++ 也成等比数列 例2 已知{}{}n n b a ,是项数相同的等比数列,求证{}n n b a ⋅是等比数列. 证明:设数列{}n a 的首项是1a ,公比为1q ;{}n b 的首项为1b ,公比为2q ,那么数列{}n n b a ⋅的第n 项与第n+1项分别为:n n nn n n q q b a q q b a q b q a q b q a )()(2111121112111121111与即为与---⋅⋅⋅⋅⋅⋅.)()(2112111211111q q q q b a q q b a b a b a n n n n n n ==⋅⋅-++Θ 它是一个与n 无关的常数,所以{}n n b a ⋅是一个以q 1q 2为公比的等比数列.例3(1)已知{na }是等比数列,且252,0645342=++>a a a a a a a n , 求53a a +(2) a ≠c,三数a, 1, c 成等差数列,22,1,c a 成等比数列,求22ca ca ++ 解:(1) ∵{n a }是等比数列,∴ 2a 4a +23a 5a +4a 6a =(3a +5a )2=25,又n a >0, ∴3a +5a =5;(2) ∵a, 1, c 成等差数列, ∴ a +c =2,又a 2, 1, c 2成等比数列, ∴a 2 c 2=1, 有ac =1或ac =-1, 当ac =1时, 由a +c =2得a =1, c =1,与a ≠c 矛盾,∴ ac =-1, 62)(222=-+=+ac c a c a ∴3122=++ca c a . 例4 已知无穷数列ΛΛΛΛ,10,10,10,105152515-n ,求证:(1)这个数列成等比数列(2)这个数列中的任一项是它后面第五项的101, (3)这个数列的任意两项的积仍在这个数列中证:(1)5152511101010==---n n n n a a (常数)∴该数列成等比数列(2)101101010154515===-+-+n n n n a a ,即:5101+=n n a a (3)525151101010-+--==q p q p q p a a ,∵N q p ∈,,∴2≥+q p∴11≥-+q p 且()N q p ∈-+1,∴⎭⎬⎫⎩⎨⎧∈--+51n 521010q p ,(第1-+q p 项) 例5 设d c b a ,,,均为非零实数,()()0222222=+++-+c b d c a b d b a ,求证:c b a ,,成等比数列且公比为d证一:关于d 的二次方程()()0222222=+++-+c b d c a b d b a 有实根,∴()()0442222≥+-+=∆b a c a b ,∴()022≥--acb则必有:02=-ac b ,即ac b =2,∴c b a ,,成等比数列 设公比为q ,则aq b =,2aq c =代入()()02422222222=+++-+q a q a d aq a aq d q a a ∵()0122≠+a q ,即0222=+-q qd d ,即0≠=q d 证二:∵()()0222222=+++-+c b d c a b d b a∴()()022222222=+-++-c bcd db babd d a∴()()022=-+-c bd b ad ,∴b ad =,且c bd = ∵d c b a ,,,非零,∴d bca b == 四、练习: 1.求2323-+与2323+-的等差中项;解:21(2323-++2323+-)=5; 2.求a 4+a 2b 2与b 4+a 2b 2的等比中项解:±))((224224b a b b a a ++=±ab(a 2+b 2). 五、小结 本节课学习了以下内容:1.若a ,G ,b 成等比数列,则G ab G ,2=叫做a 与b 的等经中项. 2.若m+n=p+q ,q p n m a a a a ⋅=⋅3.判断一个数列是否成等比数列的方法:定义法,中项法,通项公式法六、课后作业:1、在等比数列{}n a ,已知51=a ,100109=a a ,求18a 解:∵109181a a a a =,∴205100110918===∴a a a a 2、在等比数列{}n b 中,34=b ,求该数列前七项之积 解:()()()45362717654321b b b b b b b b b b b b b b =∵53627124b b b b b b b ===Θ,∴前七项之积()2187333732==⨯3、在等比数列{}n a 中,22-=a ,545=a ,求8a ,解:145825454255358-=-⨯=⋅==a a a q a a 另解:∵5a 是2a 与8a 的等比中项,∴)2(5482-⨯=a∴14588-=a 七、板书设计(略) 八、课后记:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课题:3.4 等比数列(二)
教学目的:
1.灵活应用等比数列的定义及通项公式.
2.深刻理解等比中项概念.
3.熟悉等比数列的有关性质,并系统了解判断数列是否成等比数列的方法教学重点:等比中项的理解与应用
教学难点:灵活应用等比数列定义、通项公式、性质解决一些相关问题
授课类型:新授课
课时安排:1课时
教具:多媒体、实物投影仪
教学过程:
一、复习引入:
首先回忆一下上一节课所学主要内容:
1.等比数列:如果一个数列从第二项起,每一项与它的前一项的比等于同
一个常数,那么这个数列就叫做等比数列.这个常数叫做等比数列的公比;公比通常用字母q 表示(q ≠0),即:1
-n n
a a =q (q ≠0) 2.等比数列的通项公式:
)0(111≠⋅⋅=-q a q a a n n , )0(≠⋅⋅=-q a q a a m m n m n
3.{n a }成等比数列⇔
n
n a a 1+=q (+
∈N n ,q ≠0) “n a ≠0”是数列{n a }成等比数列的必要非充分条件
4.既是等差又是等比数列的数列:非零常数列.
二、讲解新课:
1.等比中项:如果在a 与b 中间插入一个数G ,使a ,G ,b 成等比数列,那么称这个数G 为a 与b 的等比中项. 即G =±ab (a ,b 同号)
如果在a 与b 中间插入一个数G ,使a ,G ,b 成等比数列,则
ab G ab G G
b
a G ±=⇒=⇒=2, 反之,若G 2
=ab ,则
G
b
a G =,即a ,G ,
b 成等比数列∴a ,G ,b 成等比数列⇔G 2
=ab (a ·b ≠0)
2.等比数列的性质:若m+n=p+k ,则k p n m a a a a = 在等比数列中,m+n=p+q ,k p n m a a a a ,,,有什么关系呢?
由定义得:11n 11 --==n m m q a a q a a 11k 1
1 --⋅==k p p q a a q a a
221-+=⋅n m n m q a a a ,22
1-+=⋅k p k p q a a a
则k p n m a a a a =
3.判断等比数列的方法:定义法,中项法,通项公式法
4.等比数列的增减性:当q>1, 1a >0或0<q<1, 1a <0时, {n a }是递增数
列;当q>1, 1a <0,或0<q<1, 1a >0时, {n a }是递减数列;当q=1时, {n a }是常数列;当q<0时, {n a }是摆动数列;
三、例题讲解
例1 已知:b 是a 与c 的等比中项,且a 、b 、c 同号,
求证:
3
,3
,3abc ca bc ab c b a ++++ 也成等比数列 证明:由题设:b 2=ac 得:
2
2333)3
(333ca bc ab bc b ab b c b a abc c b a ++=++=⨯++=⨯++ ∴
3
,3
,3abc ca bc ab c b a ++++ 也成等比数列 例2 已知{}{}n n b a ,是项数相同的等比数列,求证{}n n b a ⋅是等比数列. 证明:设数列{}n a 的首项是1a ,公比为1q ;{}n b 的首项为1b ,公比为2q ,那么数列{}n n b a ⋅的第n 项与第n+1项分别为:
n n n
n n n q q b a q q b a q b q a q b q a )()(21111211121111
2
11
1
1与即为与---⋅⋅⋅⋅⋅⋅
.)()(211
2111211111q q q q b a q q b a b a b a n n
n n n n ==⋅⋅-++
它是一个与n 无关的常数,所以{}n n b a ⋅是一个以q 1q 2为公比的等比数列.
例3 (1) 已知{n a }是等比数列,且252,0645342=++>a a a a a a a n ,
求3a a +
(2) a ≠c,三数a, 1, c 成等差数列,2
2,1,c a 成等比数列,求
2
2c
a c
a ++ 解:(1) ∵{n a }是等比数列,
∴ 2a 4a +23a 5a +4a 6a =(3a +5a )2=25, 又n a >0, ∴3a +5a =5;
(2) ∵a, 1, c 成等差数列, ∴ a +c =2,
又a 2, 1, c 2成等比数列, ∴a 2 c 2=1, 有ac =1或ac =-1, 当ac =1时, 由a +c =2得a =1, c =1,与a ≠c 矛盾,
∴ ac =-1, 62)(2
2
2
=-+=+ac c a c a ∴
31
2
2=++c
a c a . 例4 已知无穷数列 ,10,10,10,105
15
25
15
-n ,
求证:(1)这个数列成等比数列
(2)这个数列中的任一项是它后面第五项的
10
1
, (3)这个数列的任意两项的积仍在这个数列中
证:(1)51
5
2
5
11
101010
==---n n n n a a (常数)∴该数列成等比数列 (2)
10110101015
45
15===-+-+n n n n a a ,即:10
1
+=n n a a (3)5
25
15
110
10
10
-+--==q p q p q p a a ,∵N q p ∈,,∴≥+q p
∴11≥-+q p 且()N q p ∈-+1,
∴⎭
⎬⎫⎩⎨⎧∈--+51
n 5
21010
q p ,(第1-+q p 项) 例5 设d c b a ,,,均为非零实数,()
()022
2
2
2
2
=+++-+c b d c a b d b a ,
求证:c b a ,,成等比数列且公比为d
证一:关于d 的二次方程()
()022
2
2
2
2
=+++-+c b d c a b d b a 有实根,
∴()()0442
22
2≥+-+=∆b a c a b ,∴()
02
2≥--ac
b
则必有:02=-ac b ,即ac b =2
,∴c b a ,,成等比数列 设公比为q ,则aq b =,2
aq c =代入
(
)
(
)
024
2222
2
2
22=+++-+q a q a d aq a aq d q a a ∵(
)
012
2
≠+a q ,即022
2=+-q qd d ,即≠=q d 证二:∵()
()022
2
2
2
2
=+++-+c b d c a b d b a
∴(
)()
02222
22
22=+-++-c bcd d
b b
abd d a
∴()()02
2
=-+-c bd b ad ,∴b ad =,且c bd = ∵d c b a ,,,非零,∴d b
c
a b == 四、练习: 1.求
2
323-+与
2
323+-的等差中项;
解:
21(2323-++2
323+-)=5; 2.求a 4
+a 2
b 2
与b 4
+a 2
b 2
的等比中项 解:±))((224224b a b b a a ++=±ab(a 2+b 2
). 五、小结 本节课学习了以下内容:
1.若a ,G ,b 成等比数列,则G ab G ,2
=叫做a 与b 的等经中项. 2.若m+n=p+q ,q p n m a a a a ⋅=⋅
3.判断一个数列是否成等比数列的方法:定义法,中项法,通项公式法
六、课后作业:
1、在等比数列{}n a ,已知51=a ,100109=a a ,求18a
解:∵109181a a a a =,∴205
100
110918===
∴a a a a 2、在等比数列{}n b 中,34=b ,求该数列前七项之积 解:()()()45362717654321b b b b b b b b b b b b b b =
∵5362712
4b b b b b b b === ,
∴前七项之积()21873
337
3
2
==⨯
3、在等比数列{}n a 中,22-=a ,545=a ,求8a ,
解:14582
54
542553
58-=-⨯=⋅
==a a a q a a 另解:∵5a 是2a 与8a 的等比中项,∴)2(5482
-⨯=a
∴14588-=a 七、板书设计(略) 八、课后记:。
