第五届全国中学生数理化学科能力展示活动九年级数学解题技能展示试题选择题解答
九年级数学物理竞赛试卷【含答案】

九年级数学物理竞赛试卷【含答案】专业课原理概述部分一、选择题(每题1分,共5分)1. 下列哪个选项是勾股定理的表达式?A. a² + b² = c²B. a² b² = c²C. a² + b² + c² = 0D. a² b² c² = 02. 下列哪个选项是牛顿第一定律的表达式?A. F = maB. F = mvC. F = mgD. F = m²3. 下列哪个选项是欧姆定律的表达式?A. V = IRB. V = VRC. V = IR²D. V = I/R4. 下列哪个选项是光的反射定律的表达式?A.入射角 = 反射角B.入射角 + 反射角= 180°C.入射角反射角= 180°D.入射角= 0°5. 下列哪个选项是阿基米德原理的表达式?A. F = mgB. F = maC. F = GD. F = Buoyancy二、判断题(每题1分,共5分)1. 勾股定理只适用于直角三角形。
()2. 牛顿第一定律也被称为惯性定律。
()3. 欧姆定律描述的是电压、电流和电阻之间的关系。
()4. 光的反射定律说明反射光线、入射光线和法线在同一平面内。
()5. 阿基米德原理描述的是物体在液体中受到的浮力等于其排开的液体重量。
()三、填空题(每题1分,共5分)1. 勾股定理的表达式是:______ = c²。
2. 牛顿第一定律的表达式是:______ = 0。
3. 欧姆定律的表达式是:______ = IR。
4. 光的反射定律的表达式是:______ = 反射角。
5. 阿基米德原理的表达式是:______ = Buoyancy。
四、简答题(每题2分,共10分)1. 请简要说明勾股定理的应用场景。
2. 请简要说明牛顿第一定律的意义。
第九届中学生数理化学科能力展示活动初赛试题A卷初三数学试卷答案

第九届全国中学生数理化学科能力展示活动九年级数学解题技能展示试题(A 卷)答案一、选择题(每题6分,共48分)1.D .解析从01至10的3个连号的情况有8种;从11至20的2个连号的情况有9种;从21至30的单选号的情况有10种,从31至36的单选号的情况有6种,故总的选法有8×9×10×6=4320种,可得需要8640元.故选D.2.A .解析竖木料总长=3x +4x =7x,三根横木料总长=6-7x ∴窗框的高为3x ,宽为376x -.即窗框的面积y =3x ·376x -=-7x 2+6x (0<x <76)配方y =79)73(72+--x (0<x <76),∴当x =73米时,即上框架高为73米、下框架为76米、宽为1米时,光线通过窗框面积最大.3.D .解析∵水桶底面半径:铁柱底面半径=2:1,∴水桶底面积:铁柱底面积=22:12=4:1,设铁柱底面积为a ,水桶底面积为4a ,则水桶底面扣除铁柱部分的环形区域面积为4a ﹣a =3a ,∵原有的水量为3a ×12=36a ,∴水桶内的水面高度变为9436=aa (公分).4.C .解析因为项数为99的数列a 1,a 2,a 3,…,a 99的“凯森和”为1000,所以S 1+S 2+…+S 9999=1000,故100,a 1,a 2,a 3,…,a 99的“凯森和”为100+100+S 1+100+S 2+…+100+S 99100=100+S 1+S 2+…+S 99100=100+990=1090.5.B .解析由推理可得a =6,t =62-1=35,故a +t =41.6.D .(译)在一份20道题目的考试中,若答对每题可得5分,未作答者每题得1分,答错每题得0分,试问下面哪个成绩是不可能的?解析满分为100分,其次对19题,1题未答,得96分,故97分不可能。
第五届全国中学生数理化学科能力展示活动七年级数学解题技能展示试题详解(A)

第五届全国中学生数理化学科能力展示活动七年级数学解题技能展示试题(A )试卷说明:1、本试卷共计15题,满分为120分 2、考试时间为120分钟一、选择题(共6小题,每题6分,共36分)1、在“桑迪”飓风中,一家美国商店的某种商品被歹徒偷走了1/5,被水损坏了1/6.剩下的全部售出,结果这种商品还盈利14%。
那么这种商品的售价与进价之比为 . A. 9:5 B. 2:1 C. 3:2 D. 5:32、一种叫“快乐”的微生物由快乐细胞组成。
1个快乐细胞每次裂变为5个快乐细胞,这5个快乐细胞中的每一个又可依次裂变为5个快乐细胞,依次类推。
那么在一定时间内,1个快乐细胞可以裂变为( )个快乐细胞。
A. 2012 B. 2013 C. 2014 D. 20153、机器猫跑7步与机器狗跑5步的路程相同;机器狗跑11步与机器人跑7步路程相同。
机器猫跑5步的时间与机器狗跑3步的时间;机器狗跑7步的时间与机器人跑5步的时间相同。
那么机器猫、机器人的速度之比为( ) A. 33:35 B. 25:21 C. 35:33 D. 49:554、1233+78被111除的商和余数分别是( )。
A.商16765,余28 B. 商16765,余30 C.商16775,余28 D. 商16775,余305、|a-b|=2,|b-c|=3,|c-d|=4.那么|a-d|的结果有几种不同的值,这些不同值的和为( )A. 16B. 18C. 20D. 226、The figures F 1,F 2,F 3,and F 4 shown are the first in a sequence of figures.For n ≧3,F n is constructed from F n-1 by surrounding it with a square and placingonemore diamond on each side of the new square than F n-1 had on each side of its outside square. For example,figure F 3 has 13 diamonds.How many diamonds are there in figure F 20?( )A. 401B. 485C. 585D. 761二、填空题:(共6小题,每题8分,共48分)7、已知a+4=b-4=-c/2=2013,且a+b+c=2013k,那么k 的值为 .8、2012年《北京社会发展报告》编委会选取了101位市民进行问卷调查,结果显示32.6%的市民感到生活压力加重,而这些人的压力来源是医疗费用(73.3%)、房价居高不下(65.3%)、养老保障(64.4%)、物价上涨(61.4%).那么在感觉生活压力加重的人群中,同时选择医疗费用和物价上涨作为压力来源的人最多有 人. 9、某银行设立大学生助学贷款,6年期的年利率为6%,贷款利率的50%由国家财政补贴.某大学生预计6年后能一次性偿还2万元,则他现在可以向银行贷款 万元(精确到0.1万元,不计复利. 10、在边长均为整数的三角形PQR 中,QR=16,QR 边的中线PT=9,PQ 的最大值为 .F4F3F2F1积相等,那么AE的长度为.12、如果A﹤B﹤C﹤D,且均为自然数,有1/2=1/A+1/B+1/C+1/D,则D的最大值为 .三、解答题(每小题12分,共36分)13、夏季的某一天,恰好有2012名中国人在巴黎游玩,参观巴黎圣母院、埃菲尔铁塔、卢浮宫或者在塞纳河游船.在上述的4个景点中,他们至少去了1个,至多去了4个,那么他们之中至少有多少人去的景点完全相同?14、E是长方形ABCD的边BC上一点,EC=3BE,对角线BD与AE交与F,求三角形BFC与长方形ABCD的面积之比。
第五届“睿达杯”初中生数学能力竞赛答案卷(A卷)九年级

3 a 2 3 b 2 a 6 ( ) 6 ( ) , 得 24a 2 36b 2 , 所以 . 4 3 4 6 b 2
9. 延长 AE 交 BC 于 F , 易得等腰 ABF 和□ AFCD , 则 AD = CF = BC BF = BC AB =
3 . 2
10.如图,作 GP ⊥ DC .可得, AFE ≌ PHG ,从而 GP = AE =3, 当 CH 最小时, GHC 面积最小,此时要求 DH 最大, 又 DE 长度固定,则要求 EH 最大,又 EF = EH , 即要求 EF 最大,又 AE 长度固定,则要求 AF 最大, 显然,当点 F 与点 B 重合时, GHC 面积最小.
2 x, 3
(2 分)
CF=
6 1 2 x ,由 DF:AD=AD:AB,得 x: 1 1:x ,则 x . 3 3 2
1 1 ,从而 CF= x , x x
④ 如图 5,DF:AD=AD:AB,易得,DF= 由 CH:CF=AD:AB,易得,CH=1
2
1 , பைடு நூலகம்2
由 GH:BH=AD:AB,易得,CH= x 1 , 由 CH+BH=AD,得1
2
2 2
(4 分)
x 2
2
(2 分)
图1
图2 第 3 页 共 4 页
图3
图4
(2) ① 如图 2,由 DF:AD=AD:AB,得 : 1 1:x ,则 x
x 3
3;
(4 分)
② 如图 3,在图 1 的基础上把矩形 BCFE 自相似 2 分割,此时 x
2;
(4 分)
③ 如图 4,由 AD:CH=DF:CF,得 DF:CF=1:2,又 DF+CF=x,得 DF=
第五届“学用杯”全国数学知识应用竞赛九年级初赛试题(含答案)
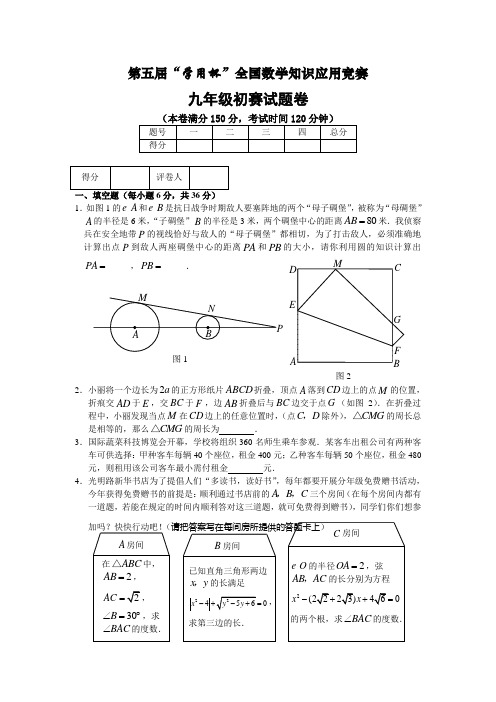
第五届“学用杯”全国数学知识应用竞赛九年级初赛试题卷1.如图1的A 和B 是抗日战争时期敌人要塞阵地的两个“母子碉堡”,被称为“母碉堡”A 的半径是6米,“子碉堡”B 的半径是3米,两个碉堡中心的距离80AB =米.我侦察兵在安全地带P 的视线恰好与敌人的“母子碉堡”都相切,为了打击敌人,必须准确地计算出点P 到敌人两座碉堡中心的距离PA 和PB 的大小,请你利用圆的知识计算出____PA =,____PB =.2.小丽将一个边长为2a 的正方形纸片ABCD 折叠,顶点A 落到CD 边上的点M 的位置,折痕交AD 于E ,交BC 于F ,边AB 折叠后与BC 边交于点G (如图2).在折叠过程中,小丽发现当点M 在CD 边上的任意位置时,(点C D ,除外),CMG △的周长总是相等的,那么CMG △的周长为 .3.国际蔬菜科技博览会开幕,学校将组织360名师生乘车参观.某客车出租公司有两种客车可供选择:甲种客车每辆40个座位,租金400元;乙种客车每辆50个座位,租金480元,则租用该公司客车最小需付租金 元. 4.光明路新华书店为了提倡人们“多读书,读好书”,每年都要开展分年级免费赠书活动,今年获得免费赠书的前提是:顺利通过书店前的A B C ,,三个房间(在每个房间内都有一道题,若能在规定的时间内顺利答对这三道题,就可免费得到赠书),同学们你们想参图1 A B CDEF GM图2 O 的半径AB AC ,的长分别为方程2(22x -+题目并不难哟,把答案写在下面吧! A 房间答题卡: ; B 房间答题卡: ; C 房间答题卡: .5.某校数学课外活动探究小组,在教师的引导下,对“函数(00)ky x x k x=+>>,的性质”作了如下探究:因为222(kk k y x x x x =+=-++=+ 所以当0x >,0k >时,函数kyx x=+有最小值=x =借助上述性质:我们可以解决下面的问题:某工厂要建造一个长方体无盖污水处理池,其容积为34800m ,深为3m ,如果池底每平方米的造价为150元,池壁每平方米的造价为120元,问怎样设计水池能使总造价最低,最低总造价为 元. 6.某公司员工分别住在A B C ,,三个住宅区,A 区有30人,B 区有15人,C 区有10人,三个区在一条直线上,位置如图3所示.公司的接送车打算在A 区,B 区,C 区中只设一个停靠点,要使所有员工步行到停靠点的路程总和最小,那么停靠点的位置应在 .二、选择题(每小题6分,共36分)7.如图是一个圆形的街心花园,AB C ,,是圆周上的三个娱乐点,且A B C ,,三等分圆周,街心花园内除了沿圆周的一条主要道路外还有经过圆心的沿AOB ,BOC ,AOC 三条道路,一天早晨,有甲、乙两位晨练者同时从A 点出发,其中甲沿着圆走回原处A ,乙沿着AOB ,BOC ,COA 也走回原处,假设他们行走的速度相同,则下列结论正确的是( ) A.甲先回到A B.乙先回到A C.同时回到A D.无法确定8.小明很喜欢打篮球,他是班里篮球队的主力队员,恰好这个星期他所在的九年级十个班要进行篮球比赛,比赛是每五个队进行单循环比赛,得分规则如下表,小组赛后总积分最高A 区 区区图3ABCOm图4现在小明若想直接进入半决赛,问小明所在的队至少要积( ) A.9分 B.10分 C.11分 D.12分 9.如图5,A B C ,,是固定在桌子上的三根立柱,其中A 柱上穿有三个大小不同的圆片,下面的直径总比上面的大,现想将这三个圆片移动到B 柱上,要求每次只能移动一片(叫移动一次),被移动的圆片只能放入A B C ,,三个柱之一,且较大的圆片不能叠在小圆片的上面,那么完成这件事至少要移动圆片的次数是( ) A.6B.7C.8 D.910.有红、黄、绿三块面积均为220cm 的正方形纸片,放在一个底面是正方形的盒子内,它们之间互相叠合(如图6),已知露在外面的部分中,红色纸片面积是220cm ,黄色纸片面积是214cm ,绿色纸片面积是210cm ,那么正方形盒子的底面积是( ) A.2256cm 5B.254cmC.248cmD.2246cm 511.小明玩套圈游戏,套中小鸡一次得9分,套中小猴一次得5分,套中小狗一次得2分,小明共套10次,每次都套中了,每个小玩具都至少套中一次,小明套10次得61分,则小鸡被套中( ) A.2次 B.3次 C.4次 D.5次 12.如图7,在边长是20m 的正方形池塘周围是草地,池塘边A B C D ,,,处各有一棵树,且4AB BC CD ===m ,现用长5m 的绳子将一头牛拴在一棵树上,为了使牛在草地上活动区域的面积最大,应将绳子拴在( ) A.A 处或C 处 B.B 处C.B 处或D 处分)13.(本题12分)阳光中学全体学生都办理了一种“学生团体住院医疗保险”,保险公司按下表中的级距分段计算付给被保险人的“住院医疗险金”.A B图5图6图7(注:在被保险期间,被保险人按上述标准累计自付金额超过6 000元的部分,保险公司按100%的标准给付)现在,该中学的学生李明因病住院,除去保险公司给付的“住院医疗保险金”外,李明的家人又支付了医疗费用3 000元.请问保险公司为李明支付了多少保险金?14.(本题12分)轻纺城服装批发市场经营季节性服装,当季节即将来临时,服装价格呈上升趋势.设某种服装开始时预定价为每件10元,从第一周上市开始每周(7天)涨价2元,从第5周开始保持20元的价格平稳销售;在季节即将过去时,从第11周开始,服装批发市场开始削价,平均每周削价2元,直到16周周末后,该服装已不再销售.(1)试建立价格y与周次x之间的函数关系;(2)若此服装每件进价Q与周次x之间的关系为:2≤≤,,试问该服装第几周每件销售利润=--+且是整数0.125(8)12(016)Q x x xM最大?15.(本题14分)如图8,某房地产开发公司购得一块三角形地块,在靠近B ∠的内部有一千年的古樟树要加以保护,市政府规定要过P 点划一三角形的保护区,你怎样划这条线才能使被划去的BDE △的面积最小?为什么?四、开放题(本大题满分40分)16.(本题20分)在生活中不难发现这样的例子:三个量a b ,和c 之间存在着数量关系a bc =.例如:长方形面积=长×宽,匀速运动的路程=速度×时间. (1)如果三个量ab ,和c 之间有着数量关系a bc =,那么: ①当0a =时,必须且只须 ;②当b (或c )为非零定值时,a 与c (或b )之间成 函数关系;③当(0)a a ≠为定值时,b 与c 之间成 函数关系.(2)请你编一道有实际意义的应用性问题,解题所列的方程符合数量关系:a bx x c=-,(其中x 为未知数,a b c ,,为已知数,不必解方程).C图817.(本题20分)金字塔是古代世界著名的奇迹之一,矗立在尼罗河西岸的70多座金字塔,每年都吸引着来自世界各地的游客,流连在金字塔下,抬眼望去,几十层楼高的塔像柄巨剑直刺云天,显得气势非凡.此刻,游人心里很自然地会想:金字塔究竟有多高呢?假设你是一位游人,如何测量金字塔的高度呢?写出你的测量方案,并说明理由(注意:至少提供两种测量方案,并且,你的方案一定要切实可行).参考答案一、填空题(每小题6分,共36分)1.160米,80米 2.4a 3.3 520元 4.A :105︒或15︒;B:C :15︒或75︒ 5.297 600 6.A 区二、选择题(每小题6分,共36分) 7~12.CBBAD B三、解答题(13题12分,14题12分,15题14分,满分38分) 13.解:当住院医疗费为7 000元时,被保险人应支付:1000(155)3000(160)3000(170)2550⨯-+⨯-+⨯-= % % % (元). 由于李明家支付费用30002550>元元 ,所以李明住院的医疗费用在7 000元至10 000元之间(即第4级别). ················ 5分 所以超过7 000元部分的医疗费为:(30002550)(180)2250-÷-= % 元. 所以保险公司为李明给付的保险费应为:7000225030006250+-= 元. ··· 11分答:保险公司要再为李明给付保险金6 250元(付给医院). ···························· 12分 14.解:(1)根据价格的“上升”、“平稳”、“削价”,建立分段函数.102(05)120(510)3402(1016)5x x x y x x x x x +⎧⎪=⎨⎪-⎩且是整数且是整数且是整数分分分≤≤,…………≤≤,………≤≤,………(2)每件利润=每件售价-每件进价,即M y Q =-,所以当05x ≤≤时,221020.125(8)120.1256M x x x ⎡⎤=+---+=+⎣⎦. 所以当5x =时,M 取最大值9.125元.······················································ 7分 当510x ≤≤时,20.125216M x x =-+.所以当5x =时,M 取最大值9.125元.······················································ 9分 当1016x ≤≤时,20.125436M x x =-+.所以当10x =时,M 取最大值8.5元. ······················································· 11分以上x 的取值均为整数,因此,该服装第5周每件销售利润M 最大. ················ 12分15.过P 作直线DE AB ∥,交BC 于D ,交AC 于E ,在BC 上取点F ,使DF BD =,延长FP 交AB 于点G ,则BFG △的面积最小. ·········································· 6分 证明:若过P 任作一直线,交BC 于M ,交AB 于N , 过G 作GK BC ∥,交MN 于K . ····························································· 8分 由DP AB ∥,BD DF =知:DP 是BFG △的中位线,得PG PF =. 进而可得MPF KPG △△≌. ··································································· 12分 NPG MPF S S >△△,所以BMN BFG S S >△△. ····················································· 14分四、开放题(每小题20分,共40分) 16.(1)①b 或c 中有一个为零;②正比例;③反比例.(每空2分,共6分) (2)答案不惟一. 评分标准:(满分共计14分) ①编写题目符合实际(5分);②解题所列方程符合所要求的数量关系(7分); ③题目新颖、有创新意义(2分). 17.方案一:应用相似三角形知识如图1所示:在距离金字塔一定距离的D F ,两点,分别竖立两个竿CD 和EF (长度都为h ),当人分别站在M N ,两点时能保证A C A E ,,,分别在一条直线上测出M N F N M D ,,的距离,则塔高即可得到(其中人的高度忽略不计). 理由如下: ····························································································· 6分从图中易知:MCD MAB △△Rt ∽Rt ,NEF NAB △△Rt ∽Rt . ················· 7分 可得AB MBCD MD =,即AB MD MB CD =.① ··············································· 8分 AB NBEF FN=,即AB FN NB EF =.② ······················································· 9分 ②-①得()()AB FN MD NB MB CD -=-. 又知MN NB MB =-,可得MN CDAB FN MD=-.因为CD 已知,MN FN MD ,,均可测出,所以AB 的高度可以计算得出. ························································· 10分C方案二:应用解直角三角形知识如图2所示,在平面内取C D ,两点,使B C D ,,三点在同一条直线上,用测角器在C D ,两点分别测得塔顶A 的仰角为αβ,,再测量出CD 间的距离,则塔高可求得(测角器的高度忽略不计). ························································································ 6分 理由如下:在ACB △Rt 和ADB △Rt 中,cot CB AB α=,cot DB AB β=. ·························································· 7分 因为CB DB CD -=,所以cot cot AB AB CD αβ-=. ····························································· 8分 所以cot cot CDAB αβ=-.因为CD ,αβ,都可以测出,所以塔高AB 可求得. ···································· 10分 (方案设计合理,正确可酌情给分)ABC D E图1ACD 图2αβ。
初三数学竞赛试题(含答案)-

初三数学竞赛试题班级 姓名一、选择题(共8小题,每小题5分,共40分)1.要使方程组⎩⎨⎧=+=+23223y x a y x 的解是一对异号的数,则a 的取值范围是( )(A )334<<a (B )34<a (C )3>a (D )343<>a a 或 2.一块含有︒30AB =8cm, 里面空 心DEF ∆的各边与ABC ∆的对应边平行,且各对应边的距离都是1cm,那么DEF ∆的周长是( )(A)5cm (B)6cm (C) cm )(36- (D) cm )(33+3.将长为15cm 的木棒截成长度为整数的三段,使它们构成一个三角形的三边,则不同的截法有( )(A)5种 (B) 6种 (C)7种 (D)8种4.作抛物线A 关于x 轴对称的抛物线B ,再将抛物线B 向左平移2个单位,向上平移1个单位,得到的抛物线C 的函数解析式是1122-+=)x (y ,则抛物线A 所对应的函数表达式是 ( )(A)2322-+-=)x (y (B) 2322++-=)x (y(C) 2122---=)x (y (D) 2322++-=)x (y5.书架上有两套同样的教材,每套分上、下两册,在这四册教材中随机抽取两册,恰好组成一套教材的概率是( ) (A)32 (B) 31 (C) 21 (D) 61 6.如图,一枚棋子放在七边形ABCDEFG 的顶点处,现顺时针方向移动这枚棋子10次,移动规则是:第k 次依次移动k 个顶点。
如第一次移动1个顶点,棋子停在顶点B 处,第二次移动2个顶点,棋子停在顶点D 。
依这样的规则,在这10次移动的过程中,棋子不可能分为两停到的顶点是( )(A)C,E,F (B)C,E,G (C)C,E (D)E,F.7.一元二次方程)a (c bx ax 002≠=++中,若b ,a 都是偶数,C 是奇数,则这个方程( )(A)有整数根 (B)没有整数根 (C)没有有理数根 (D)没有实数根8.如图所示的阴影部分由方格纸上3个小方格组成,我们称这样的图案为L 形,那么在由54⨯ 个小方格组成的方格纸上可以画出不同位置的L 形图案个数是( )(A)16 (B) 32 (C) 48 (D) 64二、填空题:(共有6个小题,每小题5分,满分30分)9.已知直角三角形的两直角边长分别为3cm,4cm ,那么以两直角边为直径的两圆公共弦的长为 cm.10.将一组数据按由小到大(或由大到小)的顺序排列,处于最中间位置的数(当数据的个数是奇数时),或最中间两个数据的平均数(当数据的个数是偶数时)叫做这组数据的中位数,现有一组数据共100个数,其中有15个数在中位数和平均数之间,如果这组数据的中位数和平均数都不在这100个数中,那么这组数据中小于平均数的数据占这100个数据的百分比是11.ABC ∆中,c ,b ,a 分别是C ,B ,A ∠∠∠的对边,已知232310-=+==C ,b ,a ,则C s i n c B s i n b +的值是等于 。
全国初三初中数学竞赛测试带答案解析

全国初三初中数学竞赛测试班级:___________ 姓名:___________ 分数:___________一、选择题1.如图,已知在Rt△ABC中,AB=35,一个边长为12的正方形CDEF内接于△ABC.则△ABC的周长为( ).(A)35 (B)40 (C)81 (D)842.设n=9+99+…+99…9(99个9).则n的十进制表示中,数码1有( )个.A.50B.90C.99D.1003.已知f(x)=x2+6ax-a,y=f(x)的图像与x轴有两个不同的交点(x1,0),(x2,0),且=8a-3.则a的值是( ).A.1B.2C.0或D.4.若不等式ax2+7x-1>2x+5对-1≤a≤1恒成立,则x的取值范围是( ).A.2≤x≤3B.2<x<3C.-1≤x≤1D.-1<x<15.在Rt△ABC中,∠B=60°,∠C=90°,AB=1,分别以AB、BC、CA为边长向△ABC外作等边△ABR、等边△BCP、等边△CAQ,联结QR交AB于点T.则△PRT的面积等于( ).(A) (B) (C) (D)6.在3×5的棋盘上,一枚棋子每次可以沿水平或者垂直方向移动一小格,但不可以沿任何斜对角线移动.从某些待定的格子开始,要求棋子经过全部的小正方格恰好一次,但不必回到原来出发的小方格上.在这15个小方格中,有( )个可以是这枚棋子出发的小方格.A.6B.8C.9D.10二、填空题1.正方形ABCD的边长为5,E为边BC上一点,使得BE=3,P是对角线BD上的一点,使得PE+PC的值最小.则PB= .2.设a、b、c为整数,且对一切实数x,(x-a)(x-8)+1="(x-b)(x-c)" 恒成立.则a+b+c的值为 .3.如图,在以O为圆心的两个同心圆图2中,MN为大圆的直径,交小圆于点P、Q,大圆的弦MC交小圆于点A、B.若OM=2,OP= 1,MA=AB=BC,则△MBQ的面积为 .4.从1, 2,…, 2 006中,至少要取出个奇数,才能保证其中必定存在两个数,它们的和为2 008.三、解答题1.(20分)实数x、y、z、w满足x≥y≥z≥w≥0,且5x+4y+3z+6w=100.求x+y+z+w的最大值和最小值.2.(25分)如图,在Rt△ABC中,∠B=90°,它的内切圆分别与边BC、CA、AB相切于点D、E、F,联结AD与内切圆相交于另一点P,联结PC、PE、PF.已知PC⊥PF.求证:(1)EP/DE=PD/DC;(2)△EPD是等腰三角形.3.(25分)在中,有多少个不同的整数(其中,[x]表示不大于x的最大整数)?全国初三初中数学竞赛测试答案及解析一、选择题1.如图,已知在Rt△ABC中,AB=35,一个边长为12的正方形CDEF内接于△ABC.则△ABC的周长为( ).(A)35 (B)40 (C)81 (D)84【答案】D【解析】分析:首先设BC=a,AC=b,由勾股定理与正方形的性质,可得:a2+b2=352,Rt△AFE∽Rt△ACB,再由相似三角形的对应边成比例,可得12(a+b)=ab,解方程组即可求得.解答:解:如图,设BC=a,AC=b,则a2+b2=352=1225.①又Rt△AFE∽Rt△ACB,所以=,即=,故12(a+b)=ab.②由①②得(a+b)2=a2+b2+2ab=1225+24(a+b),解得a+b=49(另一个解-25舍去),所以a+b+c=49+35=84.故答案为D.2.设n=9+99+…+99…9(99个9).则n的十进制表示中,数码1有( )个.A.50B.90C.99D.100【答案】C【解析】由于9=10-1,99=100-1,…,所以n="9+99+999+…+" =10+102+103+…1099-99×1.然后据此等式求出n的值后,即能得出n的十进制表示中,数码1有多少个.解:n=9+99+999+…+=10+102+103+…1099-99×1,=1111111…10(99个1)-99,=11111…1011(99个1).所以在十进制表示中,数码1有99个.故答案为:99.根据式中数据的特点将式中的数据变为10的n次方相加的形式是完成本题的关键.3.已知f(x)=x2+6ax-a,y=f(x)的图像与x轴有两个不同的交点(x1,0),(x2,0),且=8a-3.则a的值是( ).A.1B.2C.0或D.【答案】D【解析】本题考查二次函数与一元二次方程关系的综合应用问题。
最新2022九年级五月调考数学试卷 解析版

一.选择题(共10小题)1.实数﹣的相反数是()A.B.﹣C.2D.﹣22.式子在实数范围内有意义,则x的取值范围是()A.x>﹣2B.x≥﹣2C.x<﹣2D.x≤﹣23.有五张背面完全相同的卡片,正面分别标有数字1、2、3、4、5,从中同时抽取两张,则下列事件为随机事件的是()A.两张卡片的数字之和等于1B.两张卡片的数字之和大于1C.两张卡片的数字之和等于9D.两张卡片的数字之和大于94.下列手机手势解锁图案中,是中心对称图形的是()A.B.C.D.5.如图所示的几何体的主视图是()A.B.C.D.6.在反比例函数图象的每一支曲线上,y都随x的增大而减小,则k的取值范围是()A.k<0B.k>0C.k<1D.k>17.在学校举行的运动会上,帅童和胖何报名参加百米赛跑,预赛分A、B、C、D四组进行,运动员通过抽签来确定要参加的预赛小组,帅童和胖何恰好抽到同一组的概率是()A.B.C.D.8.小明从家去上学,先步行一段路,因时间紧,他改骑共享单车,结果到学校时迟到了7min,其行驶的路程y(单位:m)的图象关系如图.若他出门时直接骑共享单车(两次骑车速度相同),则下列说法正确的是()A.小明会迟到2 min到校B.小明刚好按时到校C.小明可以提前1 min到校D.小明可以提前2 min到校9.如图,在扇形OAB中,∠AOB=90°,C是上一点,连接OC 交AB于点D,过点C作CE∥OA交AB于点E.若∠BOC=30°,OB=2,则CE的长是()A.2﹣B.C.D.﹣110.古希腊数学家把1、3、6、10、15、21、…叫做三角形数,它有一定的规律性.若把第一个三角形记为a1,第二个三角形记为a2,…第n个三角形记为an,则的值是()A.B.C.D.二.填空题(共6小题)11.=.12.为了参加中学生篮球联赛,某校篮球队准备购买10双运动鞋收集尺码,并整理如下统计表:尺码/cm 25 25.5 26 26.5 27购买量/双 1 2 3 2 2则这组数据的中位数是.13.计算:=.14.如图,将△ABC绕点A逆时针旋转60°得到△ADE,连接CD.若∠CDE=78°,则∠BCD=°.15.二次函数y=ax2+bx+c(a、b、c为常数,a≠0)中的x与y 的部分对应值如表:x ﹣1 0 3y n ﹣3 ﹣3当n>0时,下列结论中一定正确的是.(填序号即可)①bc>0;②当x>2时,y的值随x值的增大而增大;③n>4a;④当n=1时,关于x的一元二次方程ax2+(b+1)x+c=0的解是x1=﹣1,x2=3.16.如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,D是AC的中点,点E在BC上,分别连接BD、AE交于点F.若∠BFE=45°,则CE=.三.解答题(共8小题)17.计算:[6a2•a4﹣(2a3)2]÷a3.18.如图,在四边形ABCD中,AD∥BC,∠ABC=∠CDA,BE平分∠ABC交AD于点E,DF平分∠CDA交BC于点F,求证:BE∥DF.19.为提高学生身体素质,某校决定开展足球、篮球、排球、兵乓球等四项课外体育活动,要求全员参与,并且每名学生只能选择其中一项.为了解选择各种体育活动项目的学生人数,该校随机抽取了部分学生进行调查,并绘制出如下两幅不完整的统计图,请根据统计图回答下列问题:(1)直接写出这次抽样调查的学生人数;(2)补全条形统计图;(3)若该学校总人数是1500人,请估计选择篮球项目的学生约有多少人?20.如图是由边长为1的小正方形构成的网格,每个小正方形的顶点叫做格点.△ABC的顶点在格点上,仅用无刻度尺的直尺在给定网格中画图,画图过程用虚线表示,画图结果用实线表示,按步骤完成下列问题:(1)将边BC绕点C顺时针旋转90°得到线段CD;(2)画边AC的中点E;(3)连接DE并延长交BC于点F,直接写出的值;(4)在AB上画点G,连接FG,使FG∥CD.21.如图,⊙O过正方形ABCD的顶点A、D,且与BC相切于点M,⊙O分别交AB、CD于E、F两点,连接MO并延长交AD于点N.(1)求证:AN=DN;(2)连接BF交⊙O于点G,连接EG.若AD=8,求EG的长.22.A城有肥料200t,B城有肥料300t.现要把这些肥料全部运往C、D两乡,C乡需要肥料240t,D乡需要肥料260t,其运往C、D两乡的运费如表:两城/两乡C/(元/t)D/(元/t)A 20 24B 15 17设从A城运往C乡的肥料为xt,从A城运往两乡的总运费为y1元,从B城运往两乡的总运费为y2元.(1)分别写出y1、y2与x之间的函数关系式(不要求写自变量的取值范围);(2)试比较A、B两城总运费的大小;(3)若B城的总运费不得超过4800元,怎样调运使两城总费用的和最少?并求出最小值.23.如图,四边形ABCD是矩形.(1)如图1,E、F分别是AD、CD上的点,BF⊥CE,垂足为G,连接AG.①求证:;②若G为CE的中点,求证:sin∠AGB=;(2)如图2,将矩形ABCD沿MN折叠,点A落在点R处,点B 落在CD边的点S处,连接BS交MN于点P,Q是RS的中点.若AB=2,BC=3,直接写出PS+PQ的最小值为.24.如图,经过(1,0)和(2,3)两点的抛物线y=ax2+c交x 轴于A、B两点,P是抛物线上一动点,平行于x轴的直线l经过点(0,﹣2).(1)求抛物线的解析式;(2)如图1,y轴上有点C(0,),连接PC,设点P到直线l 的距离为d,PC=t.童威在探究d﹣t的值的过程中,是这样思考的:当P是抛物线的顶点时,计算d﹣t的值;当P不是抛物线的顶点时,猜想d﹣t是一个定值.请你直接写出这个定值,并证明;(3)如图2,点P在第二象限,分别连接PA、PB,并延长交直线l于M、N两点.若M、N两点的横坐标分别为m、n,试探究m、n之间的数量关系.参考答案与试题解析一.选择题(共10小题)1.实数﹣的相反数是()A.B.﹣C.2D.﹣2【分析】根据只有符号不同的两数叫做互为相反数解答.【解答】解:实数﹣的相反数是,故选:A.2.式子在实数范围内有意义,则x的取值范围是()A.x>﹣2B.x≥﹣2C.x<﹣2D.x≤﹣2【分析】根据被开方数大于等于0列式计算即可得解.【解答】解:由题意得,x+2≥0,解得x≥﹣2.故选:B.3.有五张背面完全相同的卡片,正面分别标有数字1、2、3、4、5,从中同时抽取两张,则下列事件为随机事件的是()A.两张卡片的数字之和等于1B.两张卡片的数字之和大于1C.两张卡片的数字之和等于9D.两张卡片的数字之和大于9【分析】根据事件发生的可能性大小判断.【解答】解:A、两张卡片的数字之和等于1,是不可能事件;B、两张卡片的数字之和大于1,是必然事件;C、两张卡片的数字之和等于9,是随机事件;D、两张卡片的数字之和大于9,是不可能事件;故选:C.4.下列手机手势解锁图案中,是中心对称图形的是()A.B.C.D.【分析】根据中心对称图形的概念判断.【解答】解:A、不是中心对称图形;B、是中心对称图形;C、不是中心对称图形;D、不是中心对称图形.故选:B.5.如图所示的几何体的主视图是()A.B.C.D.【分析】根据从正面看得到的图形是主视图,可得答案.【解答】解:从正面看第一层是两个小正方形,第二层左边一个小正方形,第三层左边一个小正方形,故选:B.6.在反比例函数图象的每一支曲线上,y都随x的增大而减小,则k的取值范围是()A.k<0B.k>0C.k<1D.k>1【分析】根据反比例函数的性质,当反比例函数的系数大于0时,在每一支曲线上,y都随x的增大而减小,可得k﹣1>0,解可得k的取值范围.【解答】解:根据题意,在反比例函数图象的每一支曲线上,y都随x的增大而减小,即可得k﹣1>0,解得k>1.故选:D.7.在学校举行的运动会上,帅童和胖何报名参加百米赛跑,预赛分A、B、C、D四组进行,运动员通过抽签来确定要参加的预赛小组,帅童和胖何恰好抽到同一组的概率是()A.B.C.D.【分析】根据题意可以画出相应的树状图,从而可以求得两人恰好分在同一组的概率.【解答】解:如下图所示,帅童和胖何两人恰好分在同一组的情况有4种,共有16种等可能的结果,∴帅童和胖何两人恰好分在同一组的概率是=,故选:B.8.小明从家去上学,先步行一段路,因时间紧,他改骑共享单车,结果到学校时迟到了7min,其行驶的路程y(单位:m)的图象关系如图.若他出门时直接骑共享单车(两次骑车速度相同),则下列说法正确的是()A.小明会迟到2 min到校B.小明刚好按时到校C.小明可以提前1 min到校D.小明可以提前2 min到校【分析】根据题意和函数图象中的数据,可以计算出小明从开始到到学校全程骑共享单车用的时间,然后再根据题意,可以得到小明正常到校用的时间,然后即可解答本题.【解答】解:由题意可得,小明到学校正常时间为20﹣7=13(min),如果小明从开始到到学校全程骑共享单车,用的时间为:=13(min),故如果小明从开始到到学校全程骑共享单车,小明刚好按时到校,故选:B.9.如图,在扇形OAB中,∠AOB=90°,C是上一点,连接OC 交AB于点D,过点C作CE∥OA交AB于点E.若∠BOC=30°,OB=2,则CE的长是()A.2﹣B.C.D.﹣1【分析】作DF⊥OA于F,证△ADF是等腰直角三角形,∠ODF=30°,得出DF=AF,DF=OF,OD=2OF,求出OF=﹣1,OD=2﹣2,CD=OC﹣OD=4﹣2,由平行线得出△CDE∽△ODA,进而得出答案.【解答】解:作DF⊥OA于F,如图所示:∵OA=OB=2,∠AOB=90°,∴∠OAB=45°,∠AOD=90°﹣∠BOC=60°,∵DF⊥OA,∴△ADF是等腰直角三角形,∠ODF=30°,∴DF=AF,DF=OF,OD=2OF,∵AF+OF=OA=2,∴OF+OF=2,∴OF=﹣1,∴OD=2﹣2,∴CD=OC﹣OD=4﹣2,∵CE∥OA,∴△CDE∽△ODA,∴=,即=,解得:CE=﹣1,故选:D.10.古希腊数学家把1、3、6、10、15、21、…叫做三角形数,它有一定的规律性.若把第一个三角形记为a1,第二个三角形记为a2,…第n个三角形记为an,则的值是()A.B.C.D.【分析】先观察得出规律,再按规律进行计算.【解答】解:,,,,,,……由上可知,,∴===,故选:D.二.填空题(共6小题)11.= 5 .【分析】根据二次根式的基本性质进行解答即可.【解答】解:原式==5.故答案为:5.12.为了参加中学生篮球联赛,某校篮球队准备购买10双运动鞋收集尺码,并整理如下统计表:尺码/cm 25 25.5 26 26.5 27购买量/双 1 2 3 2 2则这组数据的中位数是26 .【分析】找中位数要把数据按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数.【解答】解:处于这组数据中间位置的数是26、26,那么由中位数的定义可知,这组数据的中位数是26;故答案为:26.13.计算:=.【分析】原式第一项约分后,两项通分并利用同分母分式的加法法则计算即可求出值.【解答】解:原式=+=+==.故答案为:.14.如图,将△ABC绕点A逆时针旋转60°得到△ADE,连接CD.若∠CDE=78°,则∠BCD=138 °.【分析】根据旋转的性质和四边形的内角和定理以及周角的定义即可得到结论.【解答】解:∵将△ABC绕点A逆时针旋转60°得到△ADE,∴∠CAE=60°,∠E=∠ACB,∴∠CAE+∠CDE=360°﹣(∠ACD+∠E),∵∠BCD=360°﹣∠ACB﹣∠ACD=360°﹣(∠ACD+∠E),∴∠BCD=∠CDE+∠CAE=60°+78°=138°,故答案为:138.15.二次函数y=ax2+bx+c(a、b、c为常数,a≠0)中的x与y 的部分对应值如表:x ﹣1 0 3y n ﹣3 ﹣3当n>0时,下列结论中一定正确的是①②④.(填序号即可)①bc>0;②当x>2时,y的值随x值的增大而增大;③n>4a;④当n=1时,关于x的一元二次方程ax2+(b+1)x+c=0的解是x1=﹣1,x2=3.【分析】①确定对称轴的位置和对称轴左侧函数y随x的变化情况,即可求解;②x=2在函数对称轴的右侧,故y的值随x值的增大而增大,即可求解;③当x=﹣1时,n=y=a﹣b+c=4a﹣3<4a,即可求解;④ax2+(b+1)x+c=0可以变形为ax2+bx+c=﹣x,即探讨一次函数y=﹣x与二次函数为y=ax2+bx+c图象情况,即可求解.【解答】解:①函数的对称轴为直线x=(0+3)=,即=﹣,则b=﹣3a,∵n>0,故在对称轴的左侧,y随x的增大而减小,故抛物线开口向上,则a>0,对称轴在y轴的右侧,故b<0,而c=﹣3,故bc>0正确,符合题意;②x=2在函数对称轴的右侧,故y的值随x值的增大而增大,故②正确,符合题意;③当x=﹣1时,n=y=a﹣b+c=4a﹣3<4a,故③错误,不符合题意;④当n=1时,即:x=﹣1时,y=1,ax2+(b+1)x+c=0可以变形为ax2+bx+c=﹣x,即探讨一次函数y=﹣x与二次函数为y=ax2+bx+c图象情况,当x=1,y=﹣1,即(1,﹣1)是上述两个图象的交点,根据函数的对称性,另外一个交点的横坐标为:×2=3,则该交点为(3,﹣3),故两个函数交点的横坐标为﹣1、3,即关于x的一元二次方程ax2+(b+1)x+c=0的解是x1=﹣1,x2=3,正确,符合题意,故答案为:①②④.16.如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,D是AC的中点,点E在BC上,分别连接BD、AE交于点F.若∠BFE=45°,则CE=.【分析】过点A,B分别作BC,AC的平行线交于点K,则四边形ACBK为矩形,过点A作AM∥DB交KB于点M,过点M作MN ⊥AM交AE的延长线于点N,过点N作BC的平行线分别交AC,KB的延长线于点H,Q,则四边形CHBQ为矩形,证明△AKM≌△MQN(AAS),得出KM=NQ,MQ=AK=8,证明△ACE∽△AHN,可求出CE的长.【解答】解:过点A,B分别作BC,AC的平行线交于点K,则四边形ACBK为矩形,过点A作AM∥DB交KB于点M,过点M作MN⊥AM交AE的延长线于点N,过点N作BC的平行线分别交AC,KB的延长线于点H,Q,则四边形CHBQ为矩形,∵∠BFE=45°,AM∥BD,∴∠BFE=∠MAN=45°,∴△AMN为等腰直角三角形,∴AM=MN,∵∠AMK+∠NMQ=∠AMK+∠MAK=90°,∴∠NMQ=∠MAK,又∵∠AKM=∠MQN=90°,∴△AKM≌△MQN(AAS),∴KM=NQ,MQ=AK=8,∵D为AC的中点,AC=6,∴AD=DC=BM=3,∴MK=NQ=3,∴BQ=CH=5,∴HN=HQ﹣NQ=8﹣3=5,∵CE∥HN,∴△ACE∽△AHN,∴,即,∴CE=,故答案为:.三.解答题(共8小题)17.计算:[6a2•a4﹣(2a3)2]÷a3.【分析】原式利用同底数幂的乘法,积的乘方与幂的乘方运算法则计算,再利用单项式除以单项式法则计算即可求出值.【解答】解:原式=(6a6﹣4a6)÷a3=2a6÷a3=2a3.18.如图,在四边形ABCD中,AD∥BC,∠ABC=∠CDA,BE平分∠ABC交AD于点E,DF平分∠CDA交BC于点F,求证:BE∥DF.【分析】由角平分线的定义结合∠ABC=∠CDA,可得出∠EBC=∠ADF,由AD∥BC,利用“两直线平行,内错角相等”可得出∠EBC =∠AEB,进而可得出∠AEB=∠ADF,再利用“同位角相等,两直线平行”可证出BE∥DF.【解答】证明:∵BE平分ABC交AD于点E,DF平分∠CDA交BC于点F,∴∠EBC=∠ABC,∠ADF=∠ADC.∵∠ABC=∠CDA,∴∠EBC=∠ADF.∵AD∥BC,∴∠EBC=∠AEB,∴∠AEB=∠ADF,∴BE∥DF.19.为提高学生身体素质,某校决定开展足球、篮球、排球、兵乓球等四项课外体育活动,要求全员参与,并且每名学生只能选择其中一项.为了解选择各种体育活动项目的学生人数,该校随机抽取了部分学生进行调查,并绘制出如下两幅不完整的统计图,请根据统计图回答下列问题:(1)直接写出这次抽样调查的学生人数;(2)补全条形统计图;(3)若该学校总人数是1500人,请估计选择篮球项目的学生约有多少人?【分析】(1)由“足球”人数及其百分比可得总人数;(2)根据各项目人数之和等于总人数求出“篮球”的人数,补全图形即可;(3)用总人数乘以样本中篮球所占百分比即可得出答案.【解答】解:(1)这次活动一共调查的学生人数是:140÷35%=400(人);(2)选择“篮球”的人数为:400﹣140﹣20﹣80=160(人),补全统计图如下:(3)估计该学校选择篮球项目的学生人数约是:1500×=600(人).20.如图是由边长为1的小正方形构成的网格,每个小正方形的顶点叫做格点.△ABC的顶点在格点上,仅用无刻度尺的直尺在给定网格中画图,画图过程用虚线表示,画图结果用实线表示,按步骤完成下列问题:(1)将边BC绕点C顺时针旋转90°得到线段CD;(2)画边AC的中点E;(3)连接DE并延长交BC于点F,直接写出的值;(4)在AB上画点G,连接FG,使FG∥CD.【分析】(1)根据旋转的性质即可将边BC绕点C顺时针旋转90°得到线段CD;(2)根据网格即可画边AC的中点E;(3)根据网格,连接DE并延长交BC于点F,即可写出的值;(4)根据网格即可在AB上画点G,连接FG,使FG∥CD.【解答】解:(1)如图,线段CD即为所求;(2)点E即为所求;(3)==3,所以的值为3;(4)点G即为所求.21.如图,⊙O过正方形ABCD的顶点A、D,且与BC相切于点M,⊙O分别交AB、CD于E、F两点,连接MO并延长交AD于点N.(1)求证:AN=DN;(2)连接BF交⊙O于点G,连接EG.若AD=8,求EG的长.【分析】(1)根据⊙O与BC相切于点M,可得∠BMN=90°,得四边形ABCD是正方形,再根据垂径定理即可证明AN=DN;(2)接DE,EF,DG,可得DE是⊙O的直径,且四边形AEFD 是矩形,由(1)知四边形ABMN是矩形,设OD=r,则ON=8﹣r,DN=4,在Rt△ODN中,根据勾股定理可得r的值,然后由∠BFE=∠EDG,得sin∠BFE=sin∠EDG,进而可得EG的长.【解答】解:(1)证明:∵⊙O与BC相切于点M,∴∠BMN=90°,∵四边形ABCD是正方形,∴AD∥BC,∴∠ONA=90°,由垂径定理得,AN=DN;(2)如图,连接DE,EF,DG,∵∠DAE=90°,∴∠DFE=90°,∴DE是⊙O的直径,且四边形AEFD是矩形,由(1)知四边形ABMN是矩形,∴MN=AB=8,设OD=r,则ON=8﹣r,DN=4,在Rt△ODN中,根据勾股定理,得42+(8﹣r)2=r2,解得r=5,∴DE=10,∵AD=8,∴AE=6,∴BE=2,∵EF=AD=8,∴BF==2,∵∠BFE=∠EDG,∴sin∠BFE=sin∠EDG,∴=,即=,解得EG=.22.A城有肥料200t,B城有肥料300t.现要把这些肥料全部运往C、D两乡,C乡需要肥料240t,D乡需要肥料260t,其运往C、D两乡的运费如表:两城/两乡C/(元/t)D/(元/t)A 20 24B 15 17设从A城运往C乡的肥料为xt,从A城运往两乡的总运费为y1元,从B城运往两乡的总运费为y2元.(1)分别写出y1、y2与x之间的函数关系式(不要求写自变量的取值范围);(2)试比较A、B两城总运费的大小;(3)若B城的总运费不得超过4800元,怎样调运使两城总费用的和最少?并求出最小值.【分析】(1)根据题意即可得出y1、y2与x之间的函数关系式;(2)根据(1)的结论列方程或列不等式解答即可;(3)设两城总费用为y,根据(1)的结论得出y与x之间的函数关系式,根据题意得出x的取值范围,再根据一次函数的性质解答即可.【解答】解:(1)根据题意得:y1=20x+24(200﹣x)=4800﹣4x,y2=15(240﹣x)+17(300﹣240+x)=2x+4620.(2)由4800﹣4x<2x+4620,解得x>30,当0≤x<30时,y1>y2,B城的总运费较少;当x=30时,y1=y2,两城的总运费相等;当30<x≤200时,y1<y2,A城的总运费较少.(3)由y2≤4800得2x+4620≤4800,解得x≤90,设两城总费用为y,则y=y1+y2=﹣2x+9420,∵k=﹣2<0,∴y随x的增大而减小,∴当x=90时,y有最小值9240.答:当从A城调往C乡肥料90t,调往D乡肥料110t,从B城调往C乡肥料150t,调往D乡肥料150t,两城总费用的和最少,最小值为9240元.23.如图,四边形ABCD是矩形.(1)如图1,E、F分别是AD、CD上的点,BF⊥CE,垂足为G,连接AG.①求证:;②若G为CE的中点,求证:sin∠AGB=;(2)如图2,将矩形ABCD沿MN折叠,点A落在点R处,点B 落在CD边的点S处,连接BS交MN于点P,Q是RS的中点.若AB=2,BC=3,直接写出PS+PQ的最小值为.【分析】(1)①证明△FBC∽△ECD可得结论.②想办法证明∠AEB=∠AGB,可得sin∠AGB=sin∠AEB====.(2)如图2中,取AB的中点T,连接PT,CP.因为四边形MNSR 与四边形MNBA关于MN对称,T是AB中点,Q是SR中点,所以PT=PQ,MN垂直平分线段BS,推出BP=PS,由∠BCS=90°,推出PC=PS=PB,推出PQ+PS=PT+PC,当T,P,C共线时,PQ+PS的值最小.【解答】(1)①证明:如图1中,∵四边形ABCD是矩形,∴∠CDE=∥BCF=90°,∵BF⊥CE,∴∠BGC=90°,∴∠BCG+∠FBC=∠BCG+∠ECD=90°,∴∠FBC=∠ECD,∴△FBC∽△ECD,∴=.②证明:如图1中,连接BE,GD.∵BF⊥CE,EG=CG,∴BF垂直平分线段EC,∴BE=CB,∠EBG=∠CBG,∵DG=CG,∴∠CDG=∠GCD,∵∠ADG+∠CDG=90°,∠BCG+∠ECD=90°,∴∠ADG=∠BCG,∵AD=BC,∴△ADG≌△BCG(SAS),∴∠DAG=∠CBG,∴∠DAG=∠EBG,∴∠AEB=∠AGB,∴sin∠AGB=sin∠AEB====.(2)如图2中,取AB的中点T,连接PT,CP.∵四边形MNSR与四边形MNBA关于MN对称,T是AB中点,Q是SR中点,∴PT=PQ,MN垂直平分线段BS,∴BP=PS,∵∠BCS=90°,∴PC=PS=PB,∴PQ+PS=PT+PC,当T,P,C共线时,PQ+PS的值最小,最小值===,∴PQ+PS的最小值为.故答案为.24.如图,经过(1,0)和(2,3)两点的抛物线y=ax2+c交x 轴于A、B两点,P是抛物线上一动点,平行于x轴的直线l经过点(0,﹣2).(1)求抛物线的解析式;(2)如图1,y轴上有点C(0,),连接PC,设点P到直线l 的距离为d,PC=t.童威在探究d﹣t的值的过程中,是这样思考的:当P是抛物线的顶点时,计算d﹣t的值;当P不是抛物线的顶点时,猜想d﹣t是一个定值.请你直接写出这个定值,并证明;(3)如图2,点P在第二象限,分别连接PA、PB,并延长交直线l于M、N两点.若M、N两点的横坐标分别为m、n,试探究m、n之间的数量关系.【分析】(1)将(1,0)、(2,3)代入y=ax2+c,求出a、c的值即可得;(2)过点P作PD⊥y轴于点D,设P(p,p2﹣1),在Rt△CDP 中,由勾股定理得PC2=PD2+CD2,据此知PC2=p2+(p2﹣1+)2=(p2+)2,继而知t=PC=p2+,结合d=PH=p2﹣1﹣(﹣2)=p2+1可得d﹣t的值;(3)过点P作PH⊥l于点H,交x轴于点G,证△PAG∽△PMN 得=,设P(p,p2﹣1),知==,据此可得m=,同理用含p的式子表示n,从而得出答案.【解答】解:(1)根据题意,得:,解得,∴抛物线解析式为y=x2﹣1;(2)d﹣t=,证明:如图1,过点P作PD⊥y轴于点D,设P(p,p2﹣1),p≠0,在Rt△CDP中,由勾股定理得PC2=PD2+CD2,∴PC2=p2+(p2﹣1+)2=p2+(p2﹣)2=(p2+)2,∴t=PC=p2+,∵d=PH=p2﹣1﹣(﹣2)=p2+1,∴d﹣t=;(3)如图2,过点P作PH⊥l于点H,交x轴于点G,∵抛物线y=x2﹣1与x轴交于点A,B,∴A(﹣1,0)、B(1,0),∵直线l∥x轴,∴△PAG∽△PMN,∴=,设P(p,p2﹣1),∴==,∴m=,同理可得n=,∴mn=﹣1.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
本题得分 评卷人 第五届全国中学生数理化学科能力展示活动 九年级数学解题技能展示试题选择题解答 试卷说明:1、本试卷共计15题,满分为120分 2、考试时间为120分钟 一、选择题(共6小题,每题6分,共36分) 1、初三毕业时必做的一件事是照毕业照, 某校初三两个班的学生和教师共100人一起在台阶上拍毕业照留念,摄影师要将其排列成前多后少得梯形队阵(排数n ≥3),且要求各行的人数必须是连续的自然数,这样才能使后一排的人均站在前一排两人间的空挡,那么满足上述要求的方案有( B )种. A. 1; B. 2; C. 4; D. 0 解:设第一排有m 人,则第n 排有(m-n+1) 人,所以 21[m +(m-n+1)]×n=100, n(2m-n+1)=200, 因m-n+1≥1,所以m ≥n, (2m-n+1)-n=2(m-n)+1≥1 又200=4×50=5×40=8×25=10×20 所以:n=4, 2m-n+1=50; n=5, 2m-n+1=40; n=8, 2m-n+1=25; n=10, 2m-n+1=20. 经验证:符合要求的为:n=5,m=22;n=8,m=16. 2、 化简:22312523+++得( D ) A.1; B. 2+2; C. 2+1; D. 22+1.
解: 22312523+++=)12(12523+++ =2121723++ =)223(23++ =249+
=22+1.
3、在某海防观测站的正东方向12海里处有A 、B 两艘船相会之后,A船以
每小时12海里的速度往南航行,B船则以每小时3海里的速度向北漂
流.则观测站及A、B两船恰成一个直角三角形需要的时间是( C ).
A. 1h;
B. 1.5h;
C.2h;
D. 4h.
解: 设观测站及A、B两船恰成一个直角三角形需要的时间为xh.
则 122=12x ·3x ,x=2
总分
4、在3×5的棋盘上,一枚棋子每次可以沿水平或者垂直方向移动一个小格,但不可以沿任何斜对角线移动.从某些待定的格子出发,要求棋子经过全部的小正方格恰好一次,但不必回到原来出发的小方格上.在这15个小方格中,则可作为这枚棋子出发的小方格个数为(B)个.
A. 6;
B. 8;
C. 9;
D. 10.
解:(1)从四个顶点所在的格子中的任意一个出发,都可以,如从A
格出发:
同理从E、K、O都可以作为起点,一共有4个起点;
(2)C作为起点,如下图:
同理M也可以作为起点,一共有2个起点;
(3)I格出发,可以不重复走完全程:
同理从G出发也可以走完全程不重复,有2个起点.
4+2+2=8(个);
答:有8个小方格可以作为这个棋子的起点.
故答案为:8.
5、工地上竖立着两根电线杆AB、CD规定,它们相距15米,分别自两杆上高出地面4米、6米的A、C处,向两侧地面上的E、D,B、F点处,用钢丝绳拉紧,以固定电线杆.以下说法
正确的是()
A. 钢丝绳AD与BC的交点离地面的高度是3.6米;
B. △AED的面积是△CBF的面积的一半;
C. P点离地面的高度与AB、CD之间的相距无关;
D. EF长度的2倍与△CBF的周长相等.
解:作PQ⊥BD于Q,设BQ=x米,QD=y米,PQ=h米,
∴AB∥PQ∥CD,
∴ PQ:AB=QD:BD,PQ:CD=BQ:BD
即h:4=y:(x+y) ,h:6=x:(x+y)
∴两式相加得5h/12=1
由此得h=2.4米.
即点P离地面的高度为2.4米.
故答案为:2.4.
(注:由上述解法知,AB、CD之间相距多远,与题目结论无关.)
6、定义符号y x表示与自变量x所对应的函数值.例如对于函数y=x2-2x+4,当x=2时,对应的函数值y=4,则可以写为:y2=4.在二次函数y=ax2+bx+c中,若y t+1=y-t+1,对任意实数t都成立,那么下列结论错误的是( B ).
A. y0=y2
B. y-1﹥y1
C. y4﹤y3
D. y2﹥y1
解:∵y t+1=y-t+1,
∴抛物线对称轴为x=[(t+1)+(-t+1)]÷2=1,
∵a>0,∴抛物线开口向上,
∴横坐标为1的点为顶点,最低,
∴y-1>y1,
故选B.
由y t+1=y-t+1,根据抛物线对称性得出抛物线对称轴,根据横坐标为-1,1两点离对称轴的距离,判断y-1,y1的大小.
济宁市任城区济东中学zxl。
