基于图论的奖金分配问题
welsh-powell定理 概述及解释说明

welsh-powell定理概述及解释说明1. 引言1.1 概述Welsh-Powell定理,也被称为排序染色算法,是一种用于对图进行着色的算法。
该定理基于图边缘染色问题,并提供了一种有效的方法来解决这个问题。
1.2 文章结构本篇文章将首先介绍Welsh-Powell定理的基本概念和原理,然后探讨其在实际中的应用领域。
接下来,我们将深入研究该定理的证明方法,通过特殊情况的例子分析加深理解,并展示具体的实际应用示例。
最后,在引申讨论部分,我们将探讨Welsh-Powell定理的拓展与改进可能性,并与相关研究和其他定理及算法进行比较和评价。
1.3 目的本文旨在全面介绍和解释Welsh-Powell定理,并通过详细说明其原理、证明方法和实际应用示例,使读者能够充分理解和应用该定理。
同时,通过引申讨论部分,希望能够激发读者思考并进一步研究图着色问题以及相关领域的算法和定理。
请注意:- 请根据实际内容完整撰写上述文章内容,文章中的标题不能作答。
- 以上文本为英文回答,请根据需要翻译成中文。
2. Welsh-Powell定理:2.1 定理解释:Welsh-Powell定理是一种图论中的颜色分配算法,用于对无向图进行顶点着色。
根据该定理,可以将相邻的顶点着不同的颜色,从而使得相邻顶点之间不会有相同的颜色。
在具体的定义中,若给定一个无向图G=(V, E),其中V表示顶点集合,E表示边集合。
则Welsh-Powell定理指出,在某个特定的顺序下,可以按照以下方式对图中的每个顶点进行标记/着色:首先,将所有顶点按照度数(即与之相连的边数)递减的顺序进行排序。
如果有多个度数相同的顶点,则任意选择其中一个进行排序。
然后,按照排序后的次序对每个未标记的顶点执行以下操作:为该顶点选择一个未使用过的最小自然数作为其标记/着色值,并且保证其与已经标记/着色过的相邻节点没有相同的标记/着色值。
这样处理完所有未标记/未着色过的顶点后,就能够得到一个有效且最少使用颜色数量的着色方案。
对三种典型分布式任务分配算法的分析_何炎祥

第18卷 第11期小型微型计算机系统Vo l.18N o.11 1997年11月M IN I-M I CR O SY ST EM S No v.1997对三种典型分布式任务分配算法的分析*何炎祥 罗先林 吴 思 彭堂玉 祝向幸(武汉大学计算机科学与技术学院 武汉430072)摘 要 本文先分析了基于图论的分配算法,整数规划方法和试探法等几种典型的分布式任务分配算法的基本思想、特点,不足和算法复杂度,以及可进一步改进之处,然后给出了一种试探法的改进算法,并简单讨论了其特点和性能,最后指出了分布式任务分配的发展方向。
关键词 通信开销,执行开销,负载平衡,合一,试探法在分布式系统中非同居模块间的数据传递产生处理机间的通信,这种机间通信可能使得增加处理机数目反而会引起系统吞吐量的降低,即产生“饱和效应”。
为降低饱和效应,人们倾向于把模块分配到尽可能少的处理机上,但这又导致系统负载不平衡,从而降低了系统的吞吐量。
显然,这是任务分配中相互冲突的两个方面,不同的任务分配算法试图用不同的策略来平衡这两个方面。
传统的分布式任务分配算法大致可分为三类:基于图论的分配算法,整数规划方法和试探法。
这三类算法并非互斥的,一类算法中往往可以借鉴其它方法中的某些技术。
下面,我们先对这三类典型算法进行分析和比较,然后给出一种试探法的改进算法。
在讨论中,我们假定提交的任务已分解成一组模块并使模块间的通信量尽可能小。
还假定分配模式为:一任务被分解成m个模块T={t1,t2,…,t m},系统中有n个可利用的处理机P={p1,p2,…,p n}。
任务分配的目的就是将这m个模块分配到n个处理机上,使预期的性能目标函数值最小。
1 对三种典型算法的分析1.1 基于图论的分配算法基本思想是给定矩阵C mxm表示模块间的通信开销:C={c i,j 1≤i≤m&1≤j≤m&c i,j为t i与t j间的通信量}给定矩阵Q mxn表示模块的执行开销:Q={q i,j 1≤i≤m&1≤j≤n&q i,j为t i在p j上的执行开销}将模块t1,t2,…,t m作为图中结点,若两模块间有数据传递,则相应结点间有一条无向边,1996-04-26收稿 *软件工程国家重点实验室开放基金部分资助。
运筹学上机试题5-图论
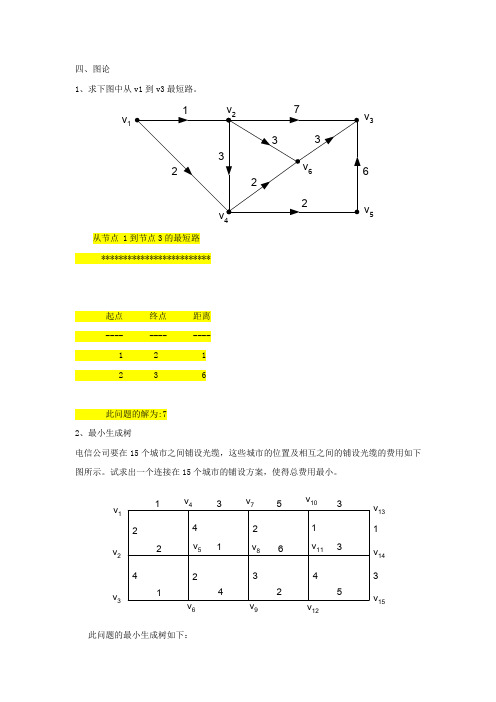
四、图论1、求下图中从v1到v3最短路。
v 1v 3v 546从节点 1到节点3的最短路 *************************起点 终点 距离 ---- ---- ---- 1 2 1 2 3 6此问题的解为:7 2、最小生成树电信公司要在15个城市之间铺设光缆,这些城市的位置及相互之间的铺设光缆的费用如下图所示。
试求出一个连接在15个城市的铺设方案,使得总费用最小。
v 1v 2v 3v 4v 5v 6v 7v 8v 9v 10v 11v 12v 13v 14v 152241131456422323135134此问题的最小生成树如下:*************************起点终点距离---- ---- ----1 4 11 2 22 5 25 8 15 6 26 3 18 7 28 9 39 12 212 11 411 10 110 13 313 14 114 15 3此问题的解为:283、最短路问题例. 求下图中从v1到各点的最短路,并指出有哪些点是不可达到的。
vv7v8v4从节点 1到节点2的最短路*************************起点终点距离---- ---- ---- 1 2 4此问题的解为:41到3没有路1到4没有路从节点 1到节点5的最短路*************************起点终点距离 ---- ---- ---- 1 5 1此问题的解为:1从节点 1到节点6的最短路*************************起点终点距离 ---- ---- ---- 1 5 1 5 6 6此问题的解为:7从节点 1到节点7的最短路*************************起点终点距离 ---- ---- ---- 1 7 3此问题的解为:3从节点 1到节点8的最短路*************************起点终点距离 ---- ---- ---- 1 5 1 5 6 66 8 3此问题的解为:104、最短路问题有6个村庄,各村庄的距离如下图所示。
图论在统计中的应用

图论在统计中的应用①图论算法研究图论算法在计算机科学中扮演着很重要的角色,它提供了对很多问题都有效的一种简单而系统的建模方式。
很多问题都可以转化为图论问题,然后用图论的基本算法加以解决。
本方向研究内容涉及图的最优划分问题,图的遍历与活动网络问题,谱聚类算法等。
②结构图论研究研究给定条件的图结构,比如,匹配覆盖图、有Pfaffian定向的图结构。
应用结构图论、组合计数、矩阵代数来研究化学分子的各种结构性质和化学物理性质。
本方向研究内容还涉及分子图的极图结构、稳定性估计、热力学性质等各种拓扑指标、完美匹配计数问题等。
概述图可用于在物理、生物、社会和信息系统中建模许多类型的关系和过程,许多实际问题可以用图来表示。
因此,图论成为运筹学、控制论、信息论、网络理论、博弈论、物理学、化学、生物学、社会科学、语言学、计算机科学等众多学科强有力的数学工具。
在强调其应用于现实世界的系统时,网络有时被定义为一个图,其中属性(例如名称)之间的关系以节点和或边的形式关联起来。
对现实生活中的场景抽象建模,再结合图论相关算法与知识解决实际问题分述计算机科学图被用来表示通信网络、数据组织、计算设备、程序执行流程、芯片设计等网站的链接结构可以用一个有向图表示,其中顶点表示网页,有向边表示从一个页面到另一个页面的链接语言学各种形式的图论方法已证明在语言学中特别有用,因为自然语言常常适合于离散结构。
传统上,语法和组合语义遵循基于树的结构,其表达能力取决于组合原则,在层次图中建模。
更现代的方法,如头驱短语结构语法,使用类型化特征结构对自然语言的语法建模,这些特征结构是有向无环图。
在词汇语义学中,特别是在计算机上,当一个给定的单词被相关的单词理解时,建模单词的意义就更加容易了。
因此,语义网络在计算语言学中非常重要。
音系学中的其他方法(例如,使用格点图的最优性理论)和形态学(例如,使用有限状态形态学,使用有限状态传感器)在语言作为图的分析中也很常见。
彩票方案模型

用效用函数与均衡的观点分析彩票的设奖问题摘要:本文引入经济学中的效用理论与市场均衡的思想,借助概率统计与随机过程等数学工具,对于问题一给出了两个模型,从不同的角度,逐层深入的分析了彩票设奖方案的合理性。
对于问题二,首先分析各奖项概率之间联系,得出了29种方案均不宜将奖项设计为8个及8个以上的结论;然后考虑第i 等奖单注金额期望m i 与其风险1/p i 的关系,按心理曲线的对数规则,将问题一中求得的最合理方案的奖金额进行重新分配;最后提出了中末等奖彩民可以在2元钱奖金与价值2元彩票之间选择的想法,给出了一种更好的方案。
问题一包括以下两个方面:① 合理性的评价标准如何提炼?我们的准则是要提高设奖方案对彩民的吸引力以实现彩票销售额的最大化。
大吸引力主要体现在;最高奖金额(x 1)、中奖面(x 2)、高等奖占总奖金额的比例(x 3)、单注期望回报(x 4)这4个标准上。
文中我们分别给出了提炼出这4个标准的根据以及相应的量化算法,以便处理。
② 多个评价标准如何综合处理?模型Ⅰ:基于经济学中效用理论的思想,我们知道,作为综合指标的一个工具的效用函数与人们通常的直觉是相符合的,这里的效用可以解释为综合指标对彩民的吸引力。
通过对效用函数应有基本性质的考虑,并结合本问题的具体情况,我们先从彩民的偏好倾向(前3个标准)给出一个效用函数:321321321),,(αααx x Ax x x x f =..t s 1,1,,0,0321321=++<<>ααααααA 然后采用“无差异曲线法”确定系数。
效用函数确定后就可以对29种方案进行量化评价,除去奇点(最不合常理的方案23)后,得到方案的合理性排序为(26 22 4 18 3 20 24 2 16 21 25 28 9 19 17 8 15 27 11 14 29 13 12 7 5 1 6 10)。
不同彩民的不同博采心理会使他们对各个标准的偏好会不同,此时采用“序结构分析法”,分别对其中一个指标进行控制,考虑另外两个指标综合所形成的效用,在二维平面种画出了3张无差异曲线簇与方案点所取位置的关系图(见附录三),适合具有不同心理的彩民偏好取向。
基于图论技术的FPGA资源管理算法

2 齐 齐哈尔大学 计算机 与控制 工程学 院 , . 黑龙江 齐齐哈尔 1 10 ) 6 0 6
摘
要 : 对可 重 构硬件 上 的 空 闲资 源进 行 管理 时 , 用 平 面划 分 算法 寻找 最 大 空 闲矩 在 采
形 存在 冗余计 算和 重复计 算 的 问题 . 此 , 中提 出了一种基 于虚拟 无 向 图的计 算 最大 空 为 文 闲矩形 的算 法. 算法基 于 F G 二 维区域模 型 , 用 无向 图与 F G 该 PA 利 P A模 型之 间的相 互映 射关系, 通过在 虚 拟无 向 图 中寻找 有效 回路 和通路 间接 完成 寻找 最大 空 闲矩形 的任 务 , 使 空 闲区域 划分过 程 大 大简化. 最后 , 中通过仿 真 实验 对 比 了该 方 法 与 已有 的 S 文 L算 法的 性 能 , 果表 明 , AME — u算 法有 效 降低 了 系统硬 件 布 局 时 间 , 高 了为任 务 分 配硬 结 K RV 提
进, 该方 法在 大多 数情 况 下 不 能标 识 出可 重 构硬 件 中的最 大空 闲 区域 , 因此 为任 务 分配 资源 时 的成 功 率 会受 到较 大影 响. 与 不重 叠 空 闲矩 形 列 表相 比 , 使用 最 大 空 闲矩 形 列表 管理空 闲区域 , 源 利 用 率 较 高 , 是 寻 找 资 但
收 稿 日期 : 0 00 —5 2 1 —10
闲资 源. 由于任 务 的动 态添 加和删 除 , 得顶 点链表 使 的管 理和查 找 比较复 杂. 针对 现 有算 法 存 在 的一 些 问题 , 中将 无 向 图 文 与 FG P A区域模 型有 机 结 合 , 出基 于 虚拟 无 向 图 提
华 南 理 工 大 学 学 报 (自 然 科 学 版 )
离散数学中常用的图论算法简介

离散数学中常用的图论算法简介图论是高等数学中的一个分支,主要涉及在图中寻找什么样的路径,以及什么样的点之间有什么样的关系。
在计算机科学中,图论的应用越来越广泛。
因为所有的计算机程序都是基于数据结构的,而图是一种最基本的数据结构之一。
离散数学中的图论算法大致可以分为两类:一类是针对稠密图的算法,另一类是针对稀疏图的算法。
稠密图指的是一种图,其中每对顶点都有一条边相连,而稀疏图则是指只有一部分顶点之间相连的图。
以下是一些常见的图论算法的简介。
1. Dijkstra算法Dijkstra算法是一种用于求图中最短路径的算法,也是最常用的图论算法之一。
Dijkstra算法的主要思想是通过贪心策略,从起点出发,逐步扩展最短路径的范围,直到找到终点。
Dijkstra算法可以用来解决单源最短路径问题。
如果图中有n个顶点,算法的时间复杂度为O(n²)。
2. Kruskal算法Kruskal算法是一种用于求最小生成树的算法。
最小生成树指的是,通过连接图中一些顶点形成一棵树,使得这些顶点之间的总权重最小。
Kruskal算法的主要思想是将图中的所有边按照权重进行排序,然后依次加入到生成树中,如果新加入的边会形成环,则不将其加入到生成树中。
如果图中有n个顶点,那么算法的时间复杂度为O(nlogn)。
3. Floyd算法Floyd算法用于求图中任意两个点之间的最短路径。
如果图中所有的权重都是正的,那么Floyd算法的时间复杂度为O(n的三次方),但是如果存在负权重,那么该算法不适用。
关于负权环的处理,可以通过Bellman-Ford算法进行解决。
4. Prim算法Prim算法是一种用于求最小生成树的算法。
与Kruskal算法不同的是,Prim算法是基于顶点集来实现,而不是基于边集。
Prim 算法首先找到一个起点,将其加入到生成树中,然后找到与其相连的边中权重最小的那一条,将其相连的顶点加入到生成树中,重复这一步骤直至所有顶点都被加入到生成树中。
基于VNS算法的图论相关问题求解

基于VNS算法的图论相关问题求解摘要:TSP作为典型的NPC问题,在各个领域都有着不可替代的应用价值。
本文针对传统的TSP问题,首先设置一个随机的初始解,然后结合常用的VNS算法进行MATLAB编程对解进行迭代优化,最后得到优化度为17.62%的新的最优解。
关键词:变邻域搜索算法;TSP;MATLAB0.引言作为典型的NPC问题,TSP在各个领域都有着不可替代的实际应用价值,而关于TSP问题的描述也是非常的简单,假设可以用点与点之间的距离来衡量现实生活中两座城市之间的距离,然后需要遍历每一座城市,并且,一座城市只能经过一次,满足该条件的最短路径的路线便是TSP问题的最优解。
TSP问题一直都是研究的热点问题,对该问题的求解分为两大类,一种是传统的确定性算法,另一种是智能算法。
第一种算法包括动态规划等传统数学模型的算法,智能算法主要包括神经网络算法、蚁群算法、遗传算法等比较热门的算法。
相比于第一种算法,智能算法的优势是比较精确,对最优解的求取也比较精准。
而传统算法的优势便是比较简易可行,但缺点便是对最优解的求取比较粗糙,因此在本文中,我们提出了VNS算法来解决TSP问题,相比于传统算法和智能算法,VNS有着独特的优势。
1 VNS算法VNS也称为变邻域搜索算法(Varisble Neighborhood Search),它属于一种局部搜索算法。
VNS工作过程便是通过改变邻域结构来达到搜索得到近似最优解的过程。
他的优化过程主要基于以下两个定理:一个邻居的局部最优解不一定是另一个邻居的局部最优解。
全局最优解是所有可能邻域的最优解。
1.1 改变邻域结构我们改变邻域结构的方法便是通过对算子的变换操作来得到新的解的集合。
通常使用的方法为交换算子、插入算子。
假设初始解为1、2、3、4,1)交换算子交换算子便是把上一个解的两个元素的位置进行交换,得到新的一组解:比如对解(1、2、3、4)进行交换,可得:(2、1、3、4)、(3、2、1、4)、(4、2、3、1)、(1、3、2、4)、(1、4、3、2)、(1、2、4、3)六种新解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
五、详细设计
#include <iostream>
#include <vector>
using namespace std;
//图结点
typedef struct Node
{
int to;
Node* next;
Node(int to_ = 0, Node* next_ = NULL)
{
to = to_;
next = next_;
}
}Node;
//判断图是否有环
bool isCircle(const vector<Node> &edges) {
int i;
//记录各个结点的入度
vector<int> indegree(edges.size(), 0);
for (i = 1; i < edges.size(); ++i)
{
Node* node = edges[i].next;
while (node)
{
indegree[node->to] ++;
node = node->next;
}
}
//记录入度为0的结点
vector<int> indegree0;
for (i = 1; i < edges.size(); ++i)
{
if (indegree[i] == 0)
{
indegree0.push_back(i);
}
}
//利用队列实现是否存在环的判断
for (i = 0; i < indegree0.size(); ++i)
{
Node *node = edges[indegree0[i]].next;
while (node)
{
indegree[node->to] --;
if (indegree[node->to] == 0)
{
indegree0.push_back(node->to);
}
node = node->next;
}
}
return indegree0.size() < edges.size() - 1; }
//利用bfs计算各个员工的奖金
int solve(const vector<Node> &edges)
{
int i;
//记录各个结点的入度
vector<int> indegree(edges.size(), 0);
for (i = 1; i < edges.size(); ++i)
{
Node* node = edges[i].next;
while (node)
{
indegree[node->to] ++;
node = node->next;
}
}
//记录入度为0的结点
vector<int> tmp;
for (i = 1; i < edges.size(); ++i)
{
if (indegree[i] == 0)
{
tmp.push_back(i);
}
}
vector<bool> isVisited(edges.size(), false);
vector<int> bnous(edges.size(), 100);
//利用队列实现bfs,利用bfs计算各个员工的奖金for (i = 0; i < tmp.size(); ++i )
{
Node* node = edges[tmp[i]].next;
while (node)
{
if (bnous[node->to] < bnous[tmp[i]] + 1)
{
bnous[node->to] = bnous[tmp[i]] + 1;
}
tmp.push_back(node->to);
node = node->next;
}
}
int ret = 0;
//输出奖金
for (i = 1; i < bnous.size(); ++i)
{
ret += bnous[i];
}
return ret;
}
//主函数
int main()
{
vector<Node> edges;
int n, m;
cin>>n>>m;
edges.resize(n + 1);
//输入边
while (m--)
{
int from, to;
cin>>to>>from;
//构造图
Node *newNode = new Node(to, edges[from].next);
edges[from].next = newNode;
}
//判断是否存在环
if (isCircle(edges))
{
cout<<"Poor Xed"<<endl;
}
else
{
cout<<solve(edges)<<endl;
}
return 0;
}。
