湖南大学课程考试试卷
湖南大学课程考试试卷5
一、选择题（每题2 分，共10分）1．以下叙述中正确的是( )A) 构成C程序的基本单位是函数B) 可以在一个函数中定义另一个函数C) main()函数必须放在其它函数之前D) 所有被调用的函数一定要在调用之前进行定义2．设a和b均为double型变量，且a=5.5、b=2.5，则表达式（int）a+b/b的值是( ) A）6.500000 B）6 C) 5.500000 D) 6.0000003．已知i、j、k为int型变量，若从键盘输入：1，2，3<回车>，使i的值为1、j的值为 2、k的值为3，以下选项中正确的输入语句是( )A) scanf(“%2d%2d%2d”,&i,&j,&k);B) scanf(“%d %d %d”,&i,&j,&k);C) scanf(“%d,%d,%d”,&i,&j,&k);D) scanf(“i=%d,j=%d,k=%d”,&i,&j,&k);4.若x 为unsigned int 型变量，则执行下列语句后x值为（）x = 65535；printf(“%d\n”,x);A）65535 B）1 C）无定值 D）-15.定义全局变量时，若变量的的存储类别缺省，则默认的存储类型是（）。
A）auto B） registerC）extern D） static二、判断题（每题 1 分，共10分）1、C程序中的函数不能嵌套调用，但可嵌套定义。
（）。
2、当形式参数为指针变量名时，实际参数可为指针变量名、数组名或其它类型变量的首地址（）。
3、若有说明：static int a[3][4];，则数组a中各数组元素可在程序的编译阶段得到初值0（）。
4、若用数组名作为函数调用时的实参，则实际上传递给形参数组的是数组的第一个元素的值（）。
5、共用体变量的地址和它的各成员的地址都是同一起始地址。
湖南大学课程考试试卷(开卷)答案
湖南大学课程考试试卷(开卷)答案一、填空题〔每题3分，共15分〕一、通过数据文件共享方式开发；通过对通用CAD系统的用户化开发；通过通用CAD系统提供的嵌入式语言开发。
二、交、并、差3、256 10 1 804、用N+1维来表示N维空间的一种表示方式。
五、陈述格式；GPA符号格式；EDA符号格式。
二、选择题〔每题2分，共10分〕一、C二、B3、D4、C五、B六、C三、简答题〔每题6分，共18分〕〔略〕四、计算题〔14分〕T=总1000010000101l m n⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦.cos sin00sin cos0000100001αααα-⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦.cos0sin00100sin0cos00001ββββ⎡⎤⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦.cos sin00sin cos0000100001θθθθ⎡⎤⎢⎥-⎢⎥⎢⎥⎢⎥⎣⎦.cos0sin00100sin0cos00001ββββ-⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦.cos sin00sin cos0000100001αααα⎡⎤⎢⎥-⎢⎥⎢⎥⎢⎥⎣⎦.1000010000101l m n⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦五、程序分析题〔每题12分，共24分〕一、二、ENTITY/ln(4),pt(4),txt1,suf1 ……………………………………pt1点未概念NUMBER/x,y,zpt(1)=POINT/0,0pt(2)=POINT/3,0pt(3)=POINT/3,2pt(4)=POINT/0,2ln(1)=LINE/pt(1),pt(2)ln(2)=LINE/pt(2),pt(3)ln(3)=LINE/pt(3),pt(4)ln(4)=LINE/pt(4),pt(1)suf1=RLDSRF/ln(2),pt(2),ln(4),pt(1)l10 …………………………………………………………格式错误，未加“：〞PARAM/ 'X',x,'Y',y,'Z',z,rsp $$在屏幕上指定一点JUMP/l10,hal:,,,,rsp ………………………………………“l10”应改成“l10:〞pt1=POINT/x,y,zCRTWRT/'Congratulations!',x,y,z, TXT1=NOTE/2,-2,'VIEW A'MASK/26 $$只有尺寸实体可选DELETE/pt1,pt(1..4)………………………………………………………语句缺失，缺“hal：〞HALT六、编程题〔15分〕ENTITY/ln(4),obj(3)NUMBER/mat1(12),mat2(12),mat3(12)ln(1)=line/0,0,0,10ln(2)=line/0,10,-20,10ln(3)=line/-20,10,-20,0ln(4)=line/0,0,-20,0mat1=matrix/xyrot,-135mat2=matrix/transl,20,20,0 mat3=matrix/mat1,mat2obj(1)=transf/mat3,ln(1..4) halt七、附加题〔略〕。
湖南大学课程考试试卷.doc
（A ）0.1 mol·kg -1CuSO 4 （B ）0.1 mol·kg -1Na 2SO 4 （C ）0.1 mol·kg -1Na 2S （D ）0.1 mol·kg -1氨水5. 298K 时，电池Zn|ZnCl 2(m = 0.5 mol·kg -1)|AgCl(s) |Ag 的电动势E = 1.015 V ，其温度系数为- 4.92×10-3 V·K -1，若电池以可逆方式输出2法拉第的电量，则电池反应的Δr H m (单位：kJ·mol -1)应为 ( D )（A ）– 198 （B ）198 （C ）239 （D ）–2396. 298K 时，溶液中有Ag +(a = 1)，Ni 2+(a = 1)和H +(a = 0.001)离子，已知氢在Ag 、Ni 的超电势分别为0.20V 和0.24V ，φ (Ag/Ag +) = 0.799 V ，φ (Ni/Ni 2+) = -0.250 V ，电解时外加电压从零开始逐步增加，则在阴极上析出物质的顺序是( A ) （A ）Ag 、Ni 、H 2 （B ） Ni 、Ag 、H 2 （C ）Ag 、H 2、Ni （D ）Ni 、H 2、Ag7. 在海上航行的轮船，常将锌块镶嵌于船底四周，这样船身可减轻腐蚀，此种方称为( A )（A ）阴极保护牺牲阳极法 （B ）阳极保护法（C ）金属保护层法 （D ）电化学保护法8. LiCl 的无限稀释摩尔电导率为 115.03×10-4 S·m 2·mol -1，在 298 K 时，测得 LiCl 稀溶液中 Li + 的迁移数为 0.3364，则 Cl - 离子的摩尔电导率为：（ A ） （A ）76.33×10-4 S·m 2·mol -1 （B ）113.03×10-4 S·m 2·mol -1 （C ）38.70×10-4 S·m 2·mol -1 （D ）76.33×102 S·m 2·mol -19. 在温度 T 时，实验测得某化合物在溶液中分解的数据如下：考试中心填写装订钱（答案不得超过此线）湖南大学课程考试试卷湖南大学教务处考试中 半衰期 4280 885 174则该化合物分解反应的级数为： ( D ) （A ）零级（B ）一级反应 （C ）二级反应 （D ）三级反应10. 2M → P 为二级反应，若 M 的起始浓度为1 mol·dm -3，反应1 h 后 ，M 的浓 度减少 1/2，则反应 2 h 后 ，M 的浓度是： ( B ) （A ）1/4 mol·dm -3 （B ）1/3 mol·dm -3（C ）1/6 mol·dm -3 （D ）缺少k 值无法求 二． 简答题（32分，每题8分） 1. Zn 和Ag 插在HCl 溶液中所构成的原电池是否是可逆电池？为什么？ 答：不是可逆电池。
自动控制原理试卷C湖南大学课程考试试卷7套
(答题请做在答卷纸上，并写清题号。
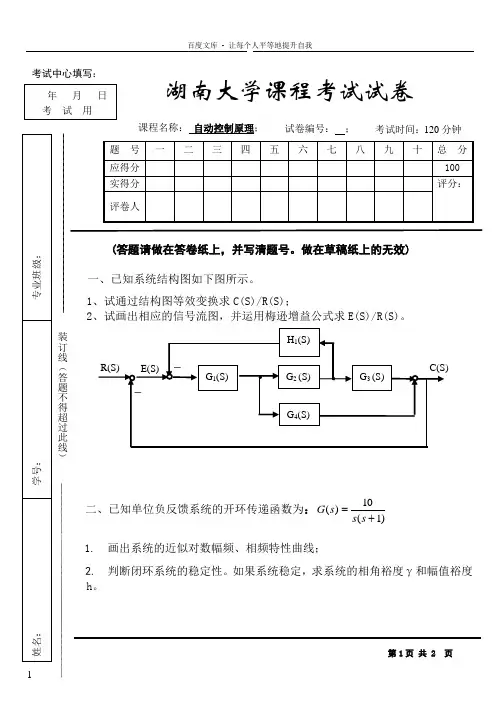
做在草稿纸上的无效)一、已知系统结构图如下图所示。
1、试通过结构图等效变换求C(S)/R(S)；2、试画出相应的信号流图，并运用梅逊增益公式求E(S)/R(S)。
二、已知单位负反馈系统的开环传递函数为：)1(10)(+=s s s G1. 画出系统的近似对数幅频、相频特性曲线；2. 判断闭环系统的稳定性。
如果系统稳定，求系统的相角裕度γ和幅值裕度h 。
第1页 共 2 页考试中心填写： ___年___月___日 考 试 用湖南大学课程考试试卷课程名称： 自动控制原理； 试卷编号： ； 考试时间：120分钟题 号 一 二 三 四 五 六 七 八 九 十 总 分应得分 100实得分 评分：评卷人姓名： 学号： 专业班级：装订线（答题不得超过此线）G 1(S) G 2 (S) G 3 (S) H 1(S)G 4(S)R(S) C(S) _ ·· E(S)_三、一线性连续控制系统如下图所示。
1、用劳斯判据判断K 为何值时，系统稳定；2、当K为何值时，系统发生持续等幅振荡，求其振荡角频率ωn 。
一四、已知控制系统开环传递函数为G(S)H(S)= )3)(6(++s s k1、绘制当K 从0→∞变化时系统的根轨迹；2、求闭环系统稳定的K 值范围。
五、离散系统如下图所示。
1、设G 1(S)=s e Ts --1，G 2(S)= )1(10+s s ，样周期T=1s ，试写出闭环脉冲传递函数Φ（Z ）；2、在z 域中分析系统的稳定性；3、求 r(t)=1(t)+t 时系统的稳态误差。
六、最小相角系统的近似对数幅频特性曲线如图所示，试确定系统的开环传递函数。
R(S) C(S) 2)10(++s s k 220ss + G 1 (S) G 2 (S)考试中心填写年月日第2页共 2 页湖南大学课程考试试卷考试用课程名称：自动控制原理；试卷编号：C；考试时间：120分钟题号 一 二 三 四 五 六 七 八 九 十 总分 应得分 15 10 20 15 24 16 100 实得分 评分评卷人一．绘制如图1所示无源网络的结构图，并求系统的传递函数U c (S)/U r (s)。
湖南大学课程考试试卷(开卷)
湖南大学课程考试试卷(开卷)课程编号： ；课程名称： 机械CAD 技术 ；试卷编号: B ；考试时间：120分钟2、以下说法不．正确的是……………………………………………( ) A 、模型是信息的载体，信息完备的设计模型是现代CAD 技术的核心B 、组合变换由多个基本变换复合而成，复合变换矩阵为各个基本变换矩阵的乘积，且与相乘的顺序无关。
C 、特征类是对特征的所有相同性质或属性的抽象概括，特征对象是特征类的一个实例。
D 、B-rep 模型是基于图的，所有的几何拓扑信息显示地表达在面－边－顶点图中。
3、 如果要把图（a ）所示坐标系通过旋转变为图（b ）所示坐标系，应采取的操作是（是右手坐标系吗？）………………………………………………（ ）A 、+ZC 轴：XC →YC 角度90度B 、-ZC 轴：XC →YC 角度90度 C 、+YC 轴：XC →ZC 角度90度D 、-YC 轴：XC →ZC 角度90度4、下列不是．．GRIP 语言中主词的是…………………………( ) A 、LINE B 、MATRIX C 、TRANSL D 、SOLSPH5、在语句NUMBER/B （2，2，2），DATA/B ，1，2，3，4，5，6，7，8中，数组B 中列2行1深1的值为……………………………………( )A 、3B 、5C 、6D 、76.下面哪种装配方法不是．．UG 中创建装配体的方法？…………………（ ） A 、自上向下装配 B 、自底向上装配C 、自前向后装配D 、混合装配题号 一 二 三 四 五 六 附加题 总分应得分 15 18 18 10 24 15 20 100+20实得分评分：评卷人第1页（共8页）第2页（共8页）考试中心填写： 年 月 日 考 试 用湖南大学课程考试卷 湖南大学教务处考试中心专业班级：学号 姓名：装订线（答案不得超过此线） 一、填空题（每题3分，共15分）1、通过CAD 软件系统的二次开发工作，主要可以分为三种方式，分别为：2、布尔运算操作用于UG 建模时确定多个体（片体或实体）之间的组合关系分别是 共3种。
湖南大学课程考试试卷
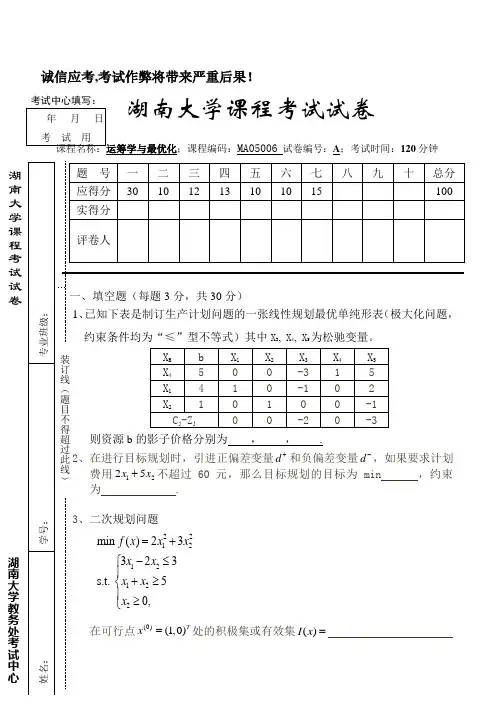
诚信应考,考试作弊将带来严重后果！湖南大学课程考试试卷课程名称：运筹学与最优化；课程编码：MA05006试卷编号：A；考试时间：120分钟4、双人博弈即矩阵对策中，局中人采用的是什么决策准则？5、动态规划是具有 性质的多阶段决策问题.6、已知()f x 是n R 中的连续可微的凸函数，则在满足 条件下，*x 是无约束问题min ()f x 的全局最优解。
7、在求解无约束优化问题的牛顿法中，若牛顿方向)()(12k k N k x f x f d ∇-∇=-不是下降方向，你可以采取的策略主要有(至少2个) 8、若在x D ∈处 成立,则(,)(,)SFD x D LFD x D =.9、采用精确线性搜索的共轭梯度算法求解n R 空间中凸二次函数极小化问题1min ()2T T f x x Qx q x =+，则算法最多经过 次迭代达到问题的最优解。
10、下列约束优化问题221213123min ()s.t. 1f x x x x x x x x =-+-+=的增广拉格朗日函数是 . 二、(10分)设:n f R R →是连续可微的凸函数,证明:n d R ∈是f 在x 处的下降方向的充要条件是()0T f x d ∇<.三、(12分）已知 ,,n m n m n x R A R b R c R ⨯∈∈∈∈，，考虑下面的线性规划问题（P ）：mins.t. 0T z c x Ax b x ==⎧⎨≥⎩（1）写出该线性规划的KKT 条件；（5分） （2）写出该线性规划的对偶问题（D ）；（5分）（3）说明线性规划问题（P ）的解和它的对偶问题（D ）的解有何关系？（2分）四、(13分)已知二次函数c x b Qx x x f T T++=21)(，其中Q 为n 阶对称正定矩阵，n R b ∈.现在从任意初始点0x 出发，使用精确搜索的Newton 法求解极小化问题)(min x f nRx ∈， （1）证明： 最多经一次迭代即可达到f 的最小值点.（8分）（2）该问题如果采用最速下降法或共轭梯度法，计算速度如何？请根据你的数值计算经验和相关理论加以分析比较。
湖南大学课程考试试卷(闭卷) 课程名称：弹性力学; 试卷编号：A ;考试
湖南大学课程考试试卷(闭卷)一、填空题（每空2分，共40分）1、弹性力学边值问题中第一类边值问题又称为( )。
对于该类边值问题，作用在其边界上的集中力应转换为( )，集中力偶应转换为( )。
第二类边值问题又称为( )。
第三类边值问题又称为( )。
对于该类边值问题，如果物体的表面S 的一部分S σ上作用面力，在另一部分S u 上给定位移，则S 、S σ、S u 之间的关系应该满足( )。
2、已知平面应力状态下，板的应力函数为ϕ =x 3+2x 2y +y 3，如果不计体积力，则应力分量为σx =( )、σy =( )、τxy =( )。
对应的应变分量为(已知弹性常数E 和)εx =( )、εz =( )、γxy =()。
3、在直角坐标系下，平面应力问题的基本未知量包括应力分量( )、应变分量( )和位移分量()。
此外有非零不独立量()。
平面应变问题的基本未知量与平面应力问题( )( 填相同或不同 )。
其非零不独立量有( )。
、如图所示曲梁受集中力P 和弯矩M 的作用，则在r=a , b 处应该满足的边界条件为( )；在θ =0处，由圣维南原理，应满足的边界条件为( )。
考试中心填写 姓名：学号：专业班级：二、计算题（共60分）1、一闭口薄壁杆如图所示，承受扭矩T作用，若杆件的壁厚均为 ，试求管壁中的最大剪应力及单位长度扭转角。
（10分）ϕ=+，试求对如图所示正方形板的面力（以表面的法向和切向2、已知应力函数为32A x xy()力表示），并画出面力分布图。
（10分）3、将一弹性立方体放在同样大小的刚性盒内，如图所示。
在弹性体的上表面受均布压力q作用，弹性体的E、 为已知。
试求刚体盒内侧面所受的压力、弹性体的体积应变和弹性体中的最大剪应力。
（10分）4、如图所示为一在集中力P、力偶M和均布载荷q共同作用下的矩形截面悬臂梁。
(1) 试根据材料力学写出σx和τxy公式；(2) 然后验证该公式是否满足平衡方程和边界条件，并导出σy的表达式；(3) 所得到的应力解是不是弹性力学的精确解？为什么？（15分）q5、如图所示矩形截面悬臂梁受均匀分布载荷作用。
湖南大学物理试题及答案
湖南大学物理试题及答案work Information Technology Company.2020YEAR湖南大学课程考试试卷课程名称：大学物理2；试卷编号： 1 ；考试时间：120分钟题号一二三四五六七八九十总分应得分100 实得分评分：评卷人一、选择题（单选题，每小题3分，共30分）1. 一点电荷，放在球形高斯面的中心处．下列哪一种情况，通过高斯面的电场强度通量发生变化：(A) 将另一点电荷放在高斯面外．(B) 将另一点电荷放进高斯面内．(C) 将球心处的点电荷移开，但仍在高斯面内．(D) 将高斯面半径缩小．［］2. 充了电的平行板电容器两极板(看作很大的平板)间的静电作用力F与两极板间的电压U的关系是：(A) F∝U． (B) F∝1/U．(C) F∝1/U 2． (D) F∝U 2．［］3. 一导体球外充满相对介电常量为εr的均匀电介质，若测得导体表面附近场强为E，则导体球面上的自由电荷面密度σ为(A) ε 0 E． (B) ε 0ε r E．(C) ε r E． (D) (ε 0ε r- ε 0)E．［］4. 如图，在一圆形电流I所在的平面内，选取一个同心圆形闭合回路L，则由安培环路定理可知(A)d=⎰⋅LlB，且环路上任意一点B = 0．(B)d=⎰⋅LlB，且环路上任意一点B≠0．B≠0．B =常量．［］5. 一载有电流I 的细导线分别均匀密绕在半径为R 和r 的长直圆筒上形成两个螺线管，两螺线管单位长度上的匝数相等．设R = 2r ，则两螺线管中 的磁感强度大小B R 和B r 应满足： (A) B R = 2 B r ． (B) B R = B r ．(C) 2B R = B r ． (D) B R = 4 B r ． ［ ］6. 在圆柱形空间内有一磁感强度为 B 的均匀磁场，如图所示． B的大小以速率d B /d t 变化．在磁场中有A 、B 两点，其间可放直导线AB 和弯曲的导线AB ，则 (A) 电动势只在AB 导线中产生． (B) 电动势只在AB 导线中产生．(C) 电动势在AB 和AB 中都产生，且两者大小相等．(D) AB 导线中的电动势小于AB 导线中的电动势． ［ ］7. 用频率为ν1的单色光照射某种金属时，测得饱和电流为I 1，以频率 为ν2的单色光照射该金属时，测得饱和电流为I 2，若I 1> I 2，则 (A) ν1 >ν2． (B) ν1 <ν2．(C) ν1 =ν2． (D) ν1与ν2的关系还不能确定． ［ ］8. 关于不确定关系 ≥∆∆x p x ( )2/(π=h ，有以下几种理解：(1) 粒子的动量不可能确定． (2) 粒子的坐标不可能确定．(3) 粒子的动量和坐标不可能同时准确地确定． (4) 不确定关系不仅适用于电子和光子，也适用于其它粒子． 其中正确的是： (A) (1)，(2). (B) (2)，(4).(C) (3)，(4). (D) (4)，(1). ［ ］9. 直接证实了电子自旋存在的最早的实验之一是 (A) 康普顿实验． (B) 卢瑟福实验．(C) 戴维孙－革末实验． (D) 斯特恩－革拉赫实验． ［ ］10. 有下列四组量子数： (1) n = 3，l = 2，m l = 021=s m ． (2) n = 3，l = 3，m l = 121=s m ． (3) n = 3，l = 1，m l = -121-=s m ． (4) n = 3，l = 0，m l = 021-=s m ． 其中可以描述原子中电子状态的(A) 只有(1)和(3)． (B) 只有(2)和(4)． (C) 只有(1)、(3)和(4)．(D) 只有(2)、(3)和(4)． ［ ］二、 填空题（共30分）1.（本题3分）一半径为R 的均匀带电圆环，电荷线密度为λ． 设无穷远处为电势零点，则圆环中心O 点的电势U ＝______________________．2.（本题4分）一个带电的金属球，当其周围是真空时，储存的静电能量为W e 0，使其电荷保持不变，把它浸没在相对介电常量为εr 的无限大各向同性均匀电介质中，这时它的静电能量W e =__________________________．3.（本题3分）有一半径为a ，流过稳恒电流为I 的1/4圆弧形载流导线bc ，按图示方式置于均匀外磁场 B中，则该载流导线所受的安培力大小为_______________________．4.（本题3分）在相对介电常量为εr 的各向同性的电介质中，电位移矢量与场强之间的关系 是___________________ ．5.（本题3分）一平行板空气电容器的两极板都是半径为R 的圆形导体片，在充电时，板间电场强度的变化率为d E /d t ．若略去边缘效应，则两板间的位移电流为_________________________．6.（本题3分）某一波长的X 光经物质散射后，其散射光中包含波长________和波长__________ 的两种成分，其中___________的散射成分称为康普顿散射．7.（本题4分）图示被激发的氢原子跃迁到低能级时(图中E 1不是基态能级)，可发出波长为λ1、λ2、λ3的辐射， 其频率ν1、ν2和ν3满足关系式______________________；三个波长满足关系式__________________．8.（本题3分）1921年斯特恩和革拉赫在实验中发现：一束处于s态的原子射线在非均匀磁场中分裂为两束．对于这种分裂用电子轨道运动的角动量空间取向量子化难于解释，只能用___________________________来解释．9.（本题4分）多电子原子中，电子的排列遵循__________________________原理和______________________原理．三、计算题（每小题10分，共40分）1. 半径为R的带电细圆环，其电荷线密度为λ=λ0sinφ，式中λ0为一常数，φ为半径R与x轴所成的夹角，如图所示．试求环心O处的电场强度．2. 一半径为R 的带电球体，其电荷体密度分布为4πRqr=ρ(r≤R) (q为一正的常量)ρ = 0 (r>R)试求：(1) 带电球体的总电荷；(2) 球内、外各点的电场强度；(3) 球内、外各点的电势．3. 有一闭合回路由半径为a和b的两个同心共面半圆连接而成，如图．其上均匀分布线密度为λ 的电荷，当回路以匀角速度ω 绕过O点垂直于回路平面的轴转动时，求圆心O点处的磁感强度的大小．4. 由质量为m、电阻为R的均匀导线做成的矩形线框，宽为b，在t =0 时由静止下落，这时线框的下底边在y =0平面上方高度为h处(如图所示)．y =0平面以上没有磁场；y =0平面以下则有匀强磁场B，其方向在图中垂直纸面向里．现已知在时刻t = t1和t = t2，线框位置如图所示，求线框速度v与时间t的函数关系(不计空气阻力，且忽略线框自感)．大学物理试卷（二）答案与评分标准一 选择题（每小题3分，共30分）1（B ）2（D ）3（B ）4（B ）5（B ）6（D ）7（D ）8（C ）9（D ）10（C ）二 填空题（共 30分）1． λ / (2ε0) 3分 2． W e 0 / εr 4分3． aIB 3分4．E D r εε0= 3分5．t E R d /d 20πε 3分 6． 不变 1分 变长 1分 波长变长 1分7． 123ννν+= 2分 123111λλλ+=2分 8． 电子自旋的角动量的空间取向量子化 3分9． 泡利不相容原理 2分 能量最低原理 2分三．计算题（每小题10分，共40分）1．解：在任意角φ 处取微小电量d q =λd l ，它在O 点产生的场强为：R R l E 00204d s co 4d d εφφλελπ=π=3分它沿x 、y 轴上的二个分量为：d E x =－d E cos φ 1分 d E y =－d E sin φ 1分对各分量分别求和⎰ππ=20200d s co 4φφελRE x ＝R 004ελ 2分 0)d(sin sin 42000=π=⎰πφφελR E y2分故O 点的场强为： iR i E E x 004ελ-== 1分2．解：(1) 在球内取半径为r 、厚为d r 的薄球壳，该壳内所包含的电荷为d q = ρd V = qr 4πr 2d r /(πR 4) = 4qr 3d r/R 4 则球体所带的总电荷为()qr rR q V Q r V===⎰⎰034d /4d ρ 2分(2) 在球内作一半径为r 1的高斯球面，按高斯定理有404102401211d 414R qr r r R qr E r r εε=π⋅π=π⎰得402114R qr E επ= (r 1≤R)， 1E方向沿半径向外． 2分在球体外作半径为r 2的高斯球面，按高斯定理有0222/4εq E r =π得 22024r qE επ=(r 2 >R )， 2E 方向沿半径向外． 2分(3) 球内电势⎰⎰∞⋅+⋅=RRr r E r E U d d 2111⎰⎰∞π+π=R R r rr q r R qr d 4d 4204021εε40310123R qr R qεεπ-π=⎪⎪⎭⎫ ⎝⎛-π=3310412R r R q ε ()R r ≤1 2分 球外电势2020224d 4d 22r q r r q r E U r Rr εεπ=π=⋅=⎰⎰∞()R r >2 2分3．解：321B B B B ++=B 1、B 2分别为带电的大半圆线圈和小半圆线圈转动产生的磁感强度，B 3为沿直径的带电线段转动产生的磁感强度．ππ=21bI λω，422200101λωμλωμμ=π⋅π==b b b I B 3分ππ=22aI λω，422200202λωμλωμμ=π⋅π==a a a I B 3分)2/(d 2d 3π=r I λω 1分r rB bad 203⋅π=⎰λωμab ln 20π=λωμ=B )ln (20a b+ππλωμ 3分 4．解：(1) 在线框进入磁场之前( 0 ≤t ≤ t 1 )线框作自由落体运动：v =gt当 g h t t /21==时 hg 21==v v2分 (2) 线框底边进入磁场后，产生感应电流，因而受到一磁力bBt R IbB F d d 1Φ== (方向向上)t y R b B d d 22=vR b B 22= 2分线框运动的微分方程为：v R b B mg 22-t md d v = 1分令mR b B K 22=，求解上式，注意到 t = t 1 时 v = v 1，得]e )([1)(11t t K K g g K ----=v v (t 1 ≤t ≤ t 2 ) 2分当 2t t =， ]e )([1)(1212t t k K g g K ----==v v v(3) 当线框全部进入磁场后( t > t 2 )，通过线框的磁通量不随时间变化，线框回路不存在感生电流，磁力为零．故线框在重力作用下作匀加速下落，)(22t t g -+=v v即 )(]e )([12)(112t t g K g g K t t K -+--=--v v ( t ≥ t 2 ) 3分[试卷]。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
诚信应考,考试作弊将带来严重后果！
湖南大学课程考试试卷
课程名称： 概率统计A ；课程编码：GE03004 试卷编号： B ；考试时间：120分钟
一、 填空题（每小题3分，共21分）
1. 设两两相互独立的三事件A ，B 和C 满足条件：
1
,()()(),2ØABC P A P B P C ===<
9
(),16
P A B C =
且已知 则()P A =________________。
2. 设随机变量X 服从正态分布2
(,)(0),N μσσ>且二次方程2
40y y X ++=无实根的
概率为
1
2
，则μ=_____________。
3. 设随机变量X 服从二项分布(4,0.8)B ，Y 服从泊松分布(4)P ，已知() 3.6D X Y +=，则X 和Y 的相关系数XY ρ=________。
4. 设随机变量X 和Y 的数学期望分别是-2和2，方差分别是1和4，而相关系数为-0.5，
根据切比雪夫不等式估计{6}P X Y +≥≤_____________。
5. 设总体X 服从正态分布2
(0,2)N ，而1215,,
,X X X 是来自总体X 的简单随机样本，
则随机变量22
110
22
11152()
X X Y X X ++=++所服从的分布为______________。
6. 设12,,
,n X X X 为取自总体),(~2σμN X 的样本，则22μσ+的矩估计量为
______________。
7. 设12(,,,)n X X X 为来自正态总体2(,)N μσ的样本，2σ未知，现要检验假设
00:H μμ=，则应选取的检验统计量是____________________，当0H 成立时，该统计量
服从______________分布。
二、 计算题（共51分）
1. （8分）设随机变量X 的密度函数为3(1),01,
()0,
Ax x x f x ⎧-≤≤=⎨⎩其他，
求：（1）系数A ；（2）X 的分布函数；（3）1{}2
P X >。
2. （8分）设随机变量X 服从标准正态分布，求Y X =的概率密度函数。
3. （8分）2. 设二维随机变量（X ，Y ）的联合密度函数为
3
,01,,
(,)2
0,
x x y x f x y ⎧≤≤≤⎪=⎨⎪⎩其他， 求：（1）X 与Y 的边缘密度函数(),()X Y f x f y ；（2）X 与Y 是否相互独立？
4.（9分）设相互独立的两个随机变量X ，Y 具有同一分布律，且X 的分布律为
111
{0},{1},{2}326
P X P X P X ======，求（1）Z X Y =+的分布律；
（2）max{,}U X Y =的分布律；
（3）min{,}W X Y =的分布律。
湖南大学课程考试试卷
湖南大学教务处考试中心
5.（8分）已知随机变量X 和Y 分别服从正态分布2
2
(0,2)(1,3)N N 和，且X 与Y 的相关系数为13XY ρ=
，设23
X Y Z =+，求（1）Z 的数学期望E (Z )与方差D (Z )；（2）X 与Z 的相关系数XZ ρ。
6. （10分）设总体X 的概率分布为2
{1},{2}2(1),P X P X θθθ====-
2{3}(1)P X θ==-，其中1
(0)2
θθ<<是未知参数，利用总体X 的如下样本值:
3，1，3，2，3，1，2，3，求θ的矩估计值和最大似然估计值。
三、 应用题（共28分） 1.（10分）1. 甲盒装有1个红球2个黑球，乙盒装有3个红球2个黑球，丙盒装有4个红球1个黑球。
现采取掷一骰子决定选盒，出现1、2或3点选甲盒，出现4或5点选乙盒，出现6点选丙盒，在选出的盒里随机摸一球，经过秘密选盒摸球后，宣
布摸得一红球，问此球最有可能来自那个盒子？
湖南大学课程考试试卷
湖南大学教务处考试中心
2. （8分）某种清漆的5个样本，其干燥时间（单位：小时）分别为：6.0，5.8，5.5，6.3，6.4，设干燥时间总体服从正态分布2
(,)N μσ，求μ的置信度为0.95的置信区间。
3. （10分）食品厂用自动装罐机装罐头食品，每罐标准重量为500克，每隔一定时间需要检验机器的工作情况。
现抽25罐，测得其平均值为502克，根据以往的经验，标准差不变。
假设重量X 服从正态分布2
(,6.5)N μ，试问该机器工作是否正常？（显著性水平0.02α=）。