矢量控制技术基础
永磁同步电机的矢量控制系统

永磁同步电机的矢量控制系统一、本文概述随着科技的不断进步和工业的快速发展,电机作为核心动力设备,在各种机械设备和工业自动化系统中扮演着至关重要的角色。
其中,永磁同步电机(Permanent Magnet Synchronous Motor,简称PMSM)因其高效率、高功率密度和优良的控制性能等优点,被广泛应用于电动汽车、风力发电、机床设备等领域。
为了实现永磁同步电机的精确控制,提高其运行效率和稳定性,矢量控制(Vector Control)技术被引入到永磁同步电机的控制系统中。
本文将对永磁同步电机的矢量控制系统进行深入探讨。
文章将简要介绍永磁同步电机的基本结构和运行原理,为后续的矢量控制理论奠定基础。
接着,文章将重点阐述矢量控制的基本原理和实现方法,包括坐标变换、空间矢量脉宽调制(SVPWM)等关键技术。
文章还将分析矢量控制系统中的传感器选择、参数辨识以及控制策略优化等问题,以提高系统的控制精度和鲁棒性。
通过本文的研究,读者可以对永磁同步电机的矢量控制系统有一个全面而深入的了解,为实际应用中提高永磁同步电机的控制性能提供理论支持和指导。
本文还将探讨未来永磁同步电机矢量控制系统的发展趋势和挑战,为相关领域的研究者和工程师提供有价值的参考信息。
二、永磁同步电机的基本原理永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)是一种高效、高性能的电机类型,其工作原理基于电磁感应和磁场相互作用。
PMSM的核心组成部分包括定子、转子和永磁体。
定子通常由三相绕组构成,负责产生旋转磁场;转子则装有永磁体,这些永磁体在定子产生的旋转磁场作用下,产生转矩从而驱动电机旋转。
PMSM的工作原理可以简要概括为:当定子三相绕组通入三相交流电时,会在定子内部形成旋转磁场。
由于转子上的永磁体具有固定的磁极,它们在旋转磁场的作用下会受到力矩的作用,从而使转子跟随定子磁场的旋转而旋转。
通过控制定子电流的相位和幅值,可以精确控制旋转磁场的转速和转向,从而实现对PMSM的精确控制。
简述矢量控制的基本原理

简述矢量控制的基本原理矢量控制是一种常见的控制技术,用于控制电机或其他旋转机械系统。
它的基本原理是通过将矢量的瞬时变化与预期的控制信号进行比较,从而产生与期望行为相符合的控制指令。
这种控制方法可以实现高效、精确的位置和速度控制,并能够处理一些特殊情况,如低速启动、高速转折等。
矢量控制基于电机的数学模型,通常采用电机转子的瞬时位置、速度和电流等作为输入量,通过控制电机的电流及频率,实现对电机的精确控制。
一般来说,矢量控制可以分为速度矢量控制和位置矢量控制两种方式,下面将分别介绍它们的基本原理。
在速度矢量控制中,首先需要将输入信号转换为矢量形式。
这一过程通常通过将输入信号与旋转矢量进行矢量仿真,得到矢量表达式。
然后,根据控制目标以及电机当前状态,计算出需要施加到电机上的电流指令。
这些指令会经过电流变流器,最终驱动电机。
同时,反馈回路会不断监测电机的状态,并将其传递给控制器,以便根据实际输出进行调整和纠正。
位置矢量控制是在速度矢量控制的基础上进一步发展而来的控制方法。
它引入了额外的转子位置信息,并根据位置误差来调整速度指令。
具体而言,控制器会根据预定的位置轨迹和电机当前位置之间的差异计算出位置误差,然后将其传递给速度控制器。
速度控制器根据位置误差以及电机当前的速度,来计算电机所需的速度指令。
最后,电机根据速度指令和电流指令进行调整,从而实现对位置的精确控制。
除了基本的速度和位置调节外,矢量控制还可以通过调整矢量模型的参数来实现更高级的功能。
例如,可以通过增加反馈环路的增益来提高系统的稳定性和鲁棒性。
此外,还可以根据系统的动态响应特性,调整控制器的参数,以提高其响应速度和准确性。
然而,矢量控制也存在一些问题和挑战。
首先,矢量控制的实现需要对电机系统进行精确的参数测量和模型建立,这需要一定的技术和时间成本。
其次,矢量控制的复杂性限制了其在某些特殊应用中的广泛应用。
例如,在一些高速转折和急停情况下,矢量控制的实时性和响应速度可能无法满足要求。
矢量控制技术的原理和方法

矢量控制技术的原理和方法矢量控制技术是一种重要的控制方法,广泛应用于工程、自动化、电子等领域。
本文将介绍矢量控制技术的原理和方法,包括矢量控制的基本概念、矢量控制的原理和实现方法等。
一、矢量控制的基本概念矢量控制是一种基于矢量分析的控制方法,它通过对矢量参数的控制实现对系统的控制。
矢量控制可以综合考虑系统的多个参数,并通过对参数的优化控制来实现系统的稳定性和优化性能。
二、矢量控制的原理矢量控制的原理是将系统的输入和输出表示为矢量形式,通过对输入和输出之间的关系进行矢量分析,建立控制模型,并通过对模型中的矢量参数进行控制来实现对系统的控制。
矢量控制的原理主要基于以下几个基本概念:1. 矢量变换:通过对输入和输出信号进行矢量变换,将其表示为矢量形式。
常用的矢量变换方法有坐标变换、矩阵变换等。
2. 矢量分析:通过对输入和输出之间的关系进行矢量分析,建立系统的数学模型。
矢量分析可以将系统的复杂关系简化为矢量之间的相互作用。
3. 矢量控制器:根据系统的模型和控制要求,设计合适的矢量控制器。
矢量控制器可以对系统的输入矢量进行优化控制,以达到系统的稳定性和性能要求。
三、矢量控制的方法矢量控制的方法主要包括直接矢量控制和间接矢量控制两种。
1. 直接矢量控制:直接矢量控制是指将系统的输入矢量直接控制到期望值,并通过对输出矢量的反馈控制来校正误差。
直接矢量控制简单直观,但对信号的响应要求较高,容易受到系统参数波动的影响。
2. 间接矢量控制:间接矢量控制是通过对系统的输入和输出进行变换,将系统的输入控制为期望矢量,通过调整系统的参数来实现对输出的控制。
间接矢量控制相对复杂,但对系统的鲁棒性和稳定性较强。
根据系统的特点和要求,可以选择合适的矢量控制方法。
一般来说,对于要求较高的系统,可以采用间接矢量控制方法,以提高系统的稳定性和控制性能。
四、矢量控制技术的应用矢量控制技术在工程、自动化、电子等领域有广泛的应用。
例如,在电机控制中,可以采用矢量控制技术实现电机的精确控制;在工业自动化中,可以采用矢量控制技术实现系统的优化控制;在电子通信中,可以采用矢量控制技术实现信号的高效传输等。
开环矢量控制

开环矢量控制开环矢量控制是电机驱动技术中的一种高级数字控制技术,它可以实现对交流电机的磁通和转速进行精确控制。
本文将从开环矢量控制的基础概念、原理、应用等方面进行详细介绍。
一、基础概念矢量控制是指在电机运行中,控制电机的磁场方向和大小,从而控制电机的运动。
在传统的直接转矩控制(DTC)中,只能控制电机的电流和相位,而无法准确控制电机的磁场。
而通过矢量控制,可以实时掌控电机的磁场方向和大小,达到更加精确的控制效果。
开环控制是一种简单的控制方式,它通过外部给定的控制信号来直接控制被控对象。
开环控制不会通过反馈进行修正,因此具有简单、便捷等优点。
但是,由于无法感知被控对象的实际状态,存在很大的误差和鲁棒性问题,因此在应用中较为有限。
二、原理开环矢量控制通过开环控制方式,直接控制电机的磁场方向和大小,从而实现对电机的转速和转矩进行精确控制。
其控制原理如下:1. 测量电机参数首先需要测量电机的一些基本参数,包括电阻、电感、磁极对数等。
这些参数对于控制电机的电流、电压和磁场都有重要影响,需要在控制中进行精确计算。
2. 计算反电动势反电动势是指电机在运行中产生的电动势,其大小和方向与电机的速度和磁场有关。
在控制中,需要实时计算反电动势,以便准确掌控电机的状态。
3. 确定控制策略开环矢量控制的控制策略包括磁通控制和转速控制两个部分。
在磁通控制中,需要控制电机的磁场大小和方向,从而控制其输出的转矩;在转速控制中,需要控制电机的转速,从而实现对电机的速度精确控制。
4. 计算控制信号通过上述步骤得到电机的基本参数、反电动势和控制策略等信息后,就可以计算出控制信号,即实际输出给电机的电流和电压。
这里的电流和电压需要经过一系列的处理,包括磁场定向、空间矢量调制等,以达到理想控制效果。
计算出控制信号后,就可以将其输出到电机的输入端,从而实现对电机的精确控制。
在控制中,需要实时监测电机的状态,根据测量结果对控制信号进行修正,并更新反电动势等参数。
矢量控制_精讲

矢量控制——深入讲解矢量控制实现的基本原理是通过测量和控制异步电动机定子电流矢量,根据磁场定向原理分别对异步电动机的励磁电流和转矩电流进行控制,从而达到控制异步电动机转矩的目的。
具体是将异步电动机的定子电流矢量分解为产生磁场的电流分量(励磁电流) 和产生转矩的电流分量(转矩电流) 分别加以控制,并同时控制两分量间的幅值和相位,即控制定子电流矢量,所以称这种控制方式称为矢量控制方式。
矢量控制方式又有基于转差频率控制的矢量控制方式、无速度传感器矢量控制方式和有速度传感器的矢量控制方式等。
基于转差频率控制的矢量控制方式同样是在进行U / f =恒定控制的基础上,通过检测异步电动机的实际速度n,并得到对应的控制频率f,然后根据希望得到的转矩,分别控制定子电流矢量及两个分量间的相位,对通用变频器的输出频率f进行控制的。
基于转差频率控制的矢量控制方式的最大特点是,可以消除动态过程中转矩电流的波动,从而提高了通用变频器的动态性能。
早期的矢量控制通用变频器基本上都是采用的基于转差频率控制的矢量控制方式。
无速度传感器的矢量控制方式是基于磁场定向控制理论发展而来的。
实现精确的磁场定向矢量控制需要在异步电动机内安装磁通检测装置,要在异步电动机内安装磁通检测装置是很困难的,但人们发现,即使不在异步电动机中直接安装磁通检测装置,也可以在通用变频器内部得到与磁通相应的量,并由此得到了所谓的无速度传感器的矢量控制方式。
它的基本控制思想是根据输入的电动机的铭牌参数,按照转矩计算公式分别对作为基本控制量的励磁电流(或者磁通)和转矩电流进行检测,并通过控制电动机定子绕组上的电压的频率使励磁电流(或者磁通)和转矩电流的指令值和检测值达到一致,并输出转矩,从而实现矢量控制。
采用矢量控制方式的通用变频器不仅可在调速范围上与直流电动机相匹配,而且可以控制异步电动机产生的转矩。
由于矢量控制方式所依据的是准确的被控异步电动机的参数,有的通用变频器在使用时需要准确地输入异步电动机的参数,有的通用变频器需要使用速度传感器和编码器,并需使用厂商指定的变频器专用电动机进行控制,否则难以达到理想的控制效果。
矢量控制的原理和应用

矢量控制的原理和应用1. 矢量控制的概念矢量控制是一种基于矢量图形的控制方式,通过对图形的坐标、方向和大小进行数学计算,实现对图形的控制和变形。
与传统的位图控制方式不同,矢量控制具有无损放大、编辑方便和图形质量高等优点,被广泛应用于计算机图形学、机器人控制、工业设计等领域。
2. 矢量控制的原理矢量控制的原理包括图像表示、坐标计算和变换操作三个方面。
2.1 图像表示矢量控制中的图像使用数学表达形式表示,常用的表示方法有点集表示和向量表示。
点集表示将图像分解为一系列离散的点,通过连接这些点形成线段、多边形等图形。
向量表示则使用向量表达图像的形状、方向和大小。
2.2 坐标计算矢量控制需要对图像的坐标进行计算,常见的坐标计算方法有直角坐标系和极坐标系。
直角坐标系使用横纵坐标定义点的位置,极坐标系使用极径和极角表示点的位置。
2.3 变换操作矢量控制通过对图像的坐标、方向和大小进行变换操作,实现对图像的控制和变形。
常见的变换操作有平移、旋转、缩放和翻转等。
3. 矢量控制的应用矢量控制广泛应用于计算机图形学、机器人控制、工业设计等领域。
以下是一些常见的矢量控制应用:3.1 计算机图形学在计算机图形学中,矢量控制用于图像的创建、编辑和显示。
矢量图形可以无损放大和编辑,保证图形质量的同时提高了用户的操作体验。
常见的计算机图形学应用包括图像绘制、GUI设计和动画制作等。
3.2 机器人控制矢量控制在机器人控制中起着重要作用。
通过对机器人的坐标、方向和大小进行矢量计算,可以实现机器人运动的控制和路径规划。
矢量控制使机器人可以准确执行各种复杂的任务,提高了机器人的灵活性和智能性。
3.3 工业设计在工业设计中,矢量控制用于设计产品的外形和标志。
通过对矢量图形的编辑和变换操作,可以快速绘制出复杂的产品形状,并进行设计修改和效果预览。
矢量控制在工业设计中提高了设计效率和设计质量。
3.4 制造业矢量控制在制造业中也有广泛应用。
通过对机械设备的坐标、方向和大小进行矢量计算,可以实现对机械设备的控制和调整。
变频器基本知识
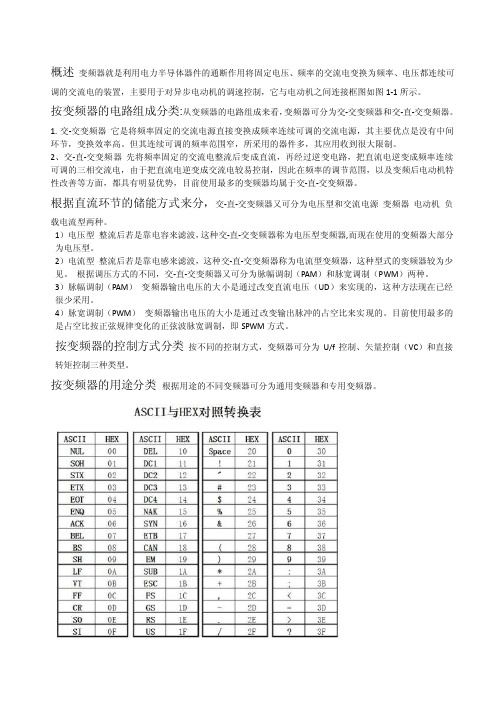
概述变频器就是利用电力半导体器件的通断作用将固定电压、频率的交流电变换为频率、电压都连续可调的交流电的装置,主要用于对异步电动机的调速控制,它与电动机之间连接框图如图1-1所示。
按变频器的电路组成分类:从变频器的电路组成来看,变频器可分为交-交变频器和交-直-交变频器。
1.交-交变频器它是将频率固定的交流电源直接变换成频率连续可调的交流电源,其主要优点是没有中间环节,变换效率高。
但其连续可调的频率范围窄,所采用的器件多,其应用收到很大限制。
2、交-直-交变频器先将频率固定的交流电整流后变成直流,再经过逆变电路,把直流电逆变成频率连续可调的三相交流电,由于把直流电逆变成交流电较易控制,因此在频率的调节范围,以及变频后电动机特性改善等方面,都具有明显优势,目前使用最多的变频器均属于交-直-交变频器。
根据直流环节的储能方式来分,交-直-交变频器又可分为电压型和交流电源变频器电动机负载电流型两种。
1)电压型整流后若是靠电容来滤波,这种交-直-交变频器称为电压型变频器,而现在使用的变频器大部分为电压型。
2)电流型整流后若是靠电感来滤波,这种交-直-交变频器称为电流型变频器,这种型式的变频器较为少见。
根据调压方式的不同,交-直-交变频器又可分为脉幅调制(PAM)和脉宽调制(PWM)两种。
3)脉幅调制(PAM)变频器输出电压的大小是通过改变直流电压(UD)来实现的,这种方法现在已经很少采用。
4)脉宽调制(PWM)变频器输出电压的大小是通过改变输出脉冲的占空比来实现的。
目前使用最多的是占空比按正弦规律变化的正弦波脉宽调制,即SPWM方式。
按变频器的控制方式分类按不同的控制方式,变频器可分为U/f控制、矢量控制(VC)和直接转矩控制三种类型。
按变频器的用途分类根据用途的不同变频器可分为通用变频器和专用变频器。
目前变频器技术主要发展方向为:1、高水平的控制2、网络智能化3、结构小型化4、高集成化5、专门化6、开发清洁电能的变频器图2-2 交-直-交电压型变频器典型主电路整流器由VD1~VD6组成三相整流桥,它们将三相380V工频交流电整流成直流,设电源的线电压有效值为UL,那么三相全波整流后的平均直流电压UD大小是:UD=1.35UL=513V整流管VD1~VD6通常采用可以承受高电压大电流具有较大耗散功率的电力二极管,中间电路中间电路包括滤波电路、限流电路和制动电路三部分。
永磁同步电机基础知识

(一) PMSM 的数学模型交流电机是一个非线性、强耦合的多变量系统。
永磁同步电机的三相绕组分布在定子上,永磁体安装在转子上。
在永磁同步电机运行过程中,定子与转子始终处于相对运动状态,永磁体与绕组,绕组与绕组之间相互影响,电磁关系十分复杂,再加上磁路饱和等非线性因素,要建立永磁同步电机精确的数学模型是很困难的。
为了简化永磁同步电机的数学模型,我们通常做如下假设:1) 忽略电机的磁路饱和,认为磁路是线性的;2) 不考虑涡流和磁滞损耗;3) 当定子绕组加上三相对称正弦电流时,气隙中只产生正弦分布的磁势,忽略气隙中的高次谐波;4) 驱动开关管和续流二极管为理想元件;5) 忽略齿槽、换向过程和电枢反应等影响。
永磁同步电机的数学模型由电压方程、磁链方程、转矩方程和机械运动方程组成,在两相旋转坐标系下的数学模型如下:(l)电机在两相旋转坐标系中的电压方程如下式所示:d d s d d c q q q s q q c d di u R i L dt di u R i L dt ωψωψ⎧=+-⎪⎪⎨⎪=++⎪⎩其中,Rs 为定子电阻;ud 、uq 分别为d 、q 轴上的两相电压;id 、iq 分别为d 、q 轴上对应的两相电流;Ld 、Lq 分别为直轴电感和交轴电感;ωc 为电角速度;ψd 、ψq 分别为直轴磁链和交轴磁链。
若要获得三相静止坐标系下的电压方程,则需做两相同步旋转坐标系到三相静止坐标系的变换,如下式所示。
cos sin 22cos()sin()3322cos()sin()33a d b q c u u u u u θθθπθπθπθπ⎛⎫ ⎪-⎛⎫⎪⎛⎫ ⎪⎪=--- ⎪ ⎪⎪⎝⎭ ⎪⎪⎝⎭ ⎪+-+⎝⎭(2)d/q 轴磁链方程: d d d f q q qL i L i ψψψ=+⎧⎪⎨=⎪⎩ 其中,ψf 为永磁体产生的磁链,为常数,0f r e ωψ=,而c r p ωω=是机械角速度,p 为同步电机的极对数,ωc 为电角速度,e0为空载反电动势,其值为每项倍。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ABC坐标系
坐标系
C2s/2r
dq坐标系
描述(坐标)空间变换原理
三、异步电动机的动态数学模型变换
4. 基于坐标系变换的异步电动机模型变换 坐标系变换的最终目的是进行电机的模型变换。电机的 模型变换就是利用坐标变换矩阵来进行的。一般步骤是:
1. 将异步电动机的全部电压量、电流量以及磁通量均变换到二相旋 转坐标系; 2. 建立异步电动机的电压、电流以及磁通平衡方程式; 3. 建立异步电动机基于原三相坐标系的数学模型; 4. 再利用变换矩阵将其变换到二相旋转坐标系; 5. 进一步将两相坐标系两轴分别按励磁电流和转矩电流定位,二相 同步旋转坐标系(M,T)便转换成了磁场定向(D轴为磁场轴、 Q轴为转矩轴)的同步旋转坐标系,再对上面模型实施相应变换 得到最终的数学模型。
交流异步电动机原始模型
二、异步电动机原始数学模型
B uB ub uc
uC
1
ua a
b
uA A
C
图6-44
c
交流异步电动机原始模型
三相异步电动机的物理模型
二、异步电动机原始数学模型
三相定子绕组的电压平衡方程为
d A uA iA Rs dt
d B uB iB Rs dt
d C uC iC Rs dt
Te C m m I a C m K m I m I a
1. 直流电动机中,励磁电流和电枢电流原理上是“自然 解耦”的; 2. 主磁通仅由电机励磁电流决定,与电枢电流无关 3. 当励磁电流一定时,电枢电流唯一线性决定电磁转矩
一、概述
电枢绕组q励磁绕组 NhomakorabeaA
i
a
F if
d
补偿绕组
ic
C
图6-46 直流电机的物理模型
一、概述
交流电动机电磁转矩与转子电流、电机主磁通的关系:
Te C m I cos 2 C m I
' m 2
' I 2t 是转子电流的有功分量 公式中:
' m 2t
1. 电磁转矩由主磁通和转子电流的有功分量决定; 2. 交流电机的主磁通由定子电流和转子电流共同决定,是 一种合成磁通。而电机电流中即含有产生磁场的电流又 包含产生转矩的电流。 3. 转子功率因数与转速(转差率)有关,这就进一步增加 了交流电机控制的复杂性。
运动控制系统
交流电动机矢量控制技术基础
书中6.6以后的内容编辑
一、概述
交流电机矢量控制技术是一种将交流电动机按 直流电动机方式进行调速控制的技术。目前,矢量 控制的变频调速是交流电动机最好的一种调频调速 控制模式。
一、概述
直流电动机和交流电动机特性上的区别比较
直流电动机电磁转矩与转子(电枢)电流、电机主磁 通的关系:
一、概述
B uB ub uc
uC
1
ua a
b
uA A
C
图6-44
c
三相异步电动机的物理模型
一、概述
结论:
直流电动机电磁转矩与电枢电流、电机磁场是一种简
单的比例关系,使得电机特性呈现一种明显的线性关系。
交流电动机的电磁转矩与电机电流、磁场、转速等呈 现一种非常复杂的紧耦合关系,使其特性具有明显的非线 性特征。
交流异步电动机原始模型
二、异步电动机原始数学模型
三相转子绕组折算到定子侧后的电压方程为
d a ua ia Rr dt d b ub ib Rr dt
d c uc ic Rr dt
交流异步电动机原始模型
二、异步电动机原始数学模型
将电压方程写成矩阵形式,并以微分算子 p 代替微分符 号 d /dt
im cos i sin t
sin iα cos i sin cos β
1
sin iα i cos β
C2s / 2r
描述(坐标)空间变换原理
三、异步电动机的动态数学模型变换
描述(坐标)空间变换原理
三、异步电动机的动态数学模型变换
哈哈,看得好清楚!
描述(坐标)空间变换原理
三、异步电动机的动态数学模型变换
因此,要针对交流异步电动机采用类似于直流电动 机的控制方式和获得直流调速系统的效果(线性控制特 性),就必需针对交流异步电动机的数学模型进行一定 规律的坐标变换,实现定(转)子电流的解耦,以得到 类似于直流电动机的控制模型。 这些坐标变换包括: 三相静止坐标系变换为二相静止坐标系: 3/2变换 二相静止坐标系变换为二相旋转坐标系: 2s/2r变换
导致关系复杂的原因:基于静止三相坐标系的电机行为描述。
交流异步电动机原始模型
三、异步电动机的动态数学模型变换
模型的变换,首先是描述空间(坐标系统)的变换。 找出坐标变换准则之后,再进行电机模型的变换。
描述(坐标)空间变换原理
1.变换的目的及原则 变换目的: 将三相坐标体系变换为两相坐标体系—简化坐标系; 将基于三相电流的旋转磁场变换为静止磁场—参量解耦。 变换原则: 变换前后功率关系和基本电磁关系不变
由于折算后定、转子绕组匝数相等,且各绕组间互感 磁通都通过气隙,磁阻相同,故可认为
Lms = Lmr
交流异步电动机原始模型
二、异步电动机原始数学模型
将上面的方程组,结合转矩方程、电流方程进行整理 和归纳得到描述异步电动机运行行为的数学模型如下,显 然是一种多变量非线性且参量间存在紧密耦合的数学模型。
1
Fs
im
itcos
M
imsin
it sin
i
imcos
描述(坐标)空间变换原理
三、异步电动机的动态数学模型变换
变换结果:变换矩阵及变换关系见公式(6-98)式( 式中 1t )。所有原二相静止坐标系的电量到二相旋 转坐标系变换均可通过这个变换矩阵求得。 (6-98)
(6-67a)
或写成:
u Ri pΨ
(6-67b)
交流异步电动机原始模型
二、异步电动机原始数学模型
每个绕组的磁链是它本身的自感磁链和其它绕组对它的 互感磁链之和,因此,六个绕组的磁链可表达为
A LAA L B BA C LCA a LaA b LbA c LcA LAB LBB LCB LaB LbB LcB LAC LBC LCC LaC LbC LcC LAa LBa LCa Laa Lba Lca LAb LBb LCb Lab Lbb Lcb LAc iA LBc iB LCc iC Lac ia Lbc ib LcC ic
描述(坐标)空间变换原理
三、异步电动机的动态数学模型变换
变换原理:
① 将两坐标系原点重叠; ② 将原二相坐标系的二相电流分别向目标坐标系进行投影; ③ 求出(α,β)到(M,T)的变换矩阵 C 2 s / 2 r
描述(坐标)空间变换原理
三、异步电动机的动态数学模型变换
T iβ it
图6-48 静止坐标系到旋转坐标系设置方案
二、异步电动机原始数学模型
异步电动机是一种基于旋转磁场(旋转速度为同步转 速)工作的能量变换机构。其旋转磁场是基于静止三相坐
标系的三相交流电流产生。在这种情况下,可以建立表达
定、转子电流、电压及磁场关系的异步电动机数学模型。
二、异步电动机原始数学模型
建立原始模型的假设条件: (1)忽略空间谐波,设三相绕组对称,在空间互差 120°电角度,所产生的磁动势沿气隙周围按正 弦规律分布; (2)忽略磁路饱和,各绕组的自感和互感都是恒定的; (3)忽略铁心损耗; (4)不考虑频率变化和温度变化对绕组电阻的影响。
三、异步电动机的动态数学模型变换
2. 变换的基本思路
交流电动机分析的复杂性的原因是工作磁场的“运动
性”。而所谓运动(旋转)是站在静止空间来看。 那么假如站在和旋转磁场同步旋转的空间情况又怎样 呢?结论就是:如果站在和磁场同步旋转的空间里,磁场 除幅值变化外,位置是绝对静止的,这就和直流电动机情
况类似。
(6-68a)
或写成:
Ψ Li
(6-68b)
交流异步电动机原始模型
二、异步电动机原始数学模型
式中,L 是6×6电感矩阵,其中对角线元素 LAA, LBB, LCC,Laa,Lbb,Lcc 是各有关绕组的自感,其余各项则是 绕组间的互感。 实际上,与电机绕组交链的磁通主要只有两类:一类 是穿过气隙的相间互感磁通,另一类是只与一相绕组交链 而不穿过气隙的漏磁通,前者是主要的。
(3)三相静止坐标系到二相旋转坐标系的变换 (3/2r变换) 综合上述两步变换可直接获得由三相静止坐标系到二 相旋转坐标系的变换:
[二相旋转坐标系电参量] = C 3 / 2 r [三相静止坐标系电参量]
这里: C 3 / 2 r = [ C 2 s / 2 r × C 3 / 2 ]
三相静止坐标系到二相旋转坐标系的变换矩阵 3/2变换
描述(坐标)空间变换原理
。
三、异步电动机的动态数学模型变换
3. 坐标变换原理简述 (1)三相静止坐标系到二相静止坐标系的变换(3/2变换) 参见图6-48。 原坐标系: 三相静止坐标系(A,B,C) 目标坐标系: 二相静止坐标系(α,β) 变换原理: ① 将原坐标系的A轴与目标坐标系的α轴重叠 ② 将原坐标系的三相电流分别向目标坐标系进行投影; ③ 求出(A,B,C)到(α,β)的变换矩阵 C 3 / 2
描述(坐标)空间变换原理
三、异步电动机的动态数学模型变换
B F
A
iB
B
ω1
