组合数学习题4(共5章)

合集下载

组合数学习题解答

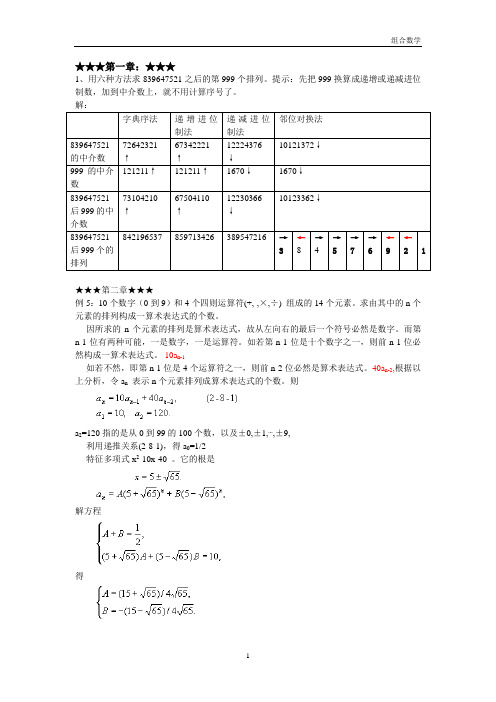
★★★第一章：★★★1、用六种方法求839647521之后的第999个排列。

提示：先把999换算成递增或递减进位制数，加到中介数上，就不用计算序号了。

解：字典序法递增进位制法递减进位制法邻位对换法839647521的中介数72642321↑67342221↑12224376↓10121372↓999的中介数121211↑121211↑1670↓1670↓839647521后999的中介数73104210↑67504110↑12230366↓10123362↓839647521后999个的排列842196537 859713426 389547216 →3←8→4→5→7→6←9←21★★★第二章★★★例5：10个数字（0到9）和4个四则运算符(+,-,×,÷) 组成的14个元素。

求由其中的n个元素的排列构成一算术表达式的个数。

因所求的n个元素的排列是算术表达式，故从左向右的最后一个符号必然是数字。

而第n-1位有两种可能，一是数字，一是运算符。

如若第n-1位是十个数字之一，则前n-1位必然构成一算术表达式。

10a n-1如若不然，即第n-1位是4个运算符之一，则前n-2位必然是算术表达式。

40a n-2,根据以上分析，令a n表示n个元素排列成算术表达式的个数。

则a2=120指的是从0到99的100个数，以及±0,±1,...,±9,利用递推关系(2-8-1)，得a0=1/2特征多项式x2-10x-40 。

它的根是解方程得例7：平面上有一点P，它是n个域D1,D2,...,D n的共同交界点，见图2-8-4现取k种颜色对这n个域进行着色，要求相邻两个域着的颜色不同。

试求着色的方案数。

令a n表示这n个域的着色方案数。

无非有两种情况（1）D1和D n-1有相同的颜色；（2）D1和D n-1所着颜色不同。

第一种情形，域有k-1种颜色可用，即D1D n-1域所用颜色除外；而且从D1到D n-2的着色方案，和n-2个域的着色方案一一对应。

组合数学课后习题答案

第一章答案1．(a) 45 ( {1,6},{2,7},{3,8},…,{45,50} )(b) 45⨯5+(4+3+2+1) = 235( 1→2~6, 2→3~7, 3→4~8, …,45→46~50, 46→47~50, 47→48~50, 49→50 ) 2．(a) 5!8!(b) 7! P(8,5) (c) 2 P(5,3) 8! 3. (a) n!P(n+1, m) (b) n!(m+1)!(c) 2!((m+n-2)+1)! 4. 2 P(24,5) 20!5. 2⨯5⨯P(8,2)+3⨯4⨯P(8,2)6. (n+1)!-17. 用数学归纳法易证。

8. 41⨯319. 设 n=p 1n 1p 2n 2…p kn k , 则n 2的除数个数为 ( 2p 1+1) (2p 2+1) …(2p k+1).10．1）用数学归纳法可证n 能表示成题中表达式的形式；2）如果某n 可以表示成题中表达式的形式，则等式两端除以2取余数，可以确定a 1；再对等式两端的商除以3取余数，又可得a 2；对等式两端的商除以4取余数，又可得a 3；…；这说明表达式是唯一的。

11．易用C(m,n)=m!/(n!(m-n)!)验证等式成立。

组合意义：右：从n 个不同元素中任取r+1个出来，再从这r+1个中取一个的全体组合的个数；左：上述组合中，先从n 个不同元素中任取1个出来，每一个相同的组合要生复 C(n-1,r) 次。

12．考虑,)1(,)1(101-=-=+=+=∑∑n nk k k n nnk kknx n x kC x x C 求导数后有令x=1, 即知.210-==∑n nk kn n kC13. 设此n 个不同的数由小到大排列后为a 1, a 2, …, a n 。

当第二组最大数为a k 时，第二组共有2k-1种不同的可能，第一组有2n-k -1种不同的可能。

故符合要求的不同分组共有12)2()12(21111+-=-----=∑n k n k n k n 种。

组合数学（卢开澄）第4章课后习题答案

组合数学（卢开澄）版第四章答案4.1，若群G 的元素a 均可表示为某一个元素x 的幂，即a=x m，则称这个群为循环群，若群的元素交换律成立。

即a ，b ∈G 满足，a ·b=b ·a证明：令a= x m ，b= x n ，则a ·b= x m ·x n = x n ·x m=b ·a ，因此是阿贝尔群4.2若x 是群G 的一个元素，存在一最小的正整数m ，使x m=e ，则称m 为x 的阶，试证： C={e,x,x 2,…x m-1}是G 的一个子群。

证明：一个群G 的不空集合H 作成G 的一个子群的充分必要条件是：1,a b H ab H a H a H-∈⇒∈∈⇒∈,a b 是H 的任意元素。

由题意知C 中的任意两个元素如,a b C ∈则ab C ∈；a C ∈则1a C -∈。

所以21{,,,,}m C e x x x -= 是G 的一个子群。

4.3设G 是阶为n 的有限群，则G 的所有元素的阶都不超过n 。

证明；因为G 中每有元素都能生成一个与元素等阶的子群，子群的阶当然不能超过群G 的阶；所以则G 的所有元素的阶都不超过n 。

4.4若G 是阶为n 的循环群，求群G 的母元素的数目，即G 的元素可表示a 的幂： a 1 ，a 2 。

a n 的元素a 的数目。

证明：若一个群G 的每一个元都是G 的某一固定元a 的乘方，我们就把G 叫做循环群；我们也说，G 是由元a 所生成的，并且用符号()G a =来表示。

所以就有一个这样的a ，即就有一个母元素。

4.5 试证循环群G 的子集也是循环群根据子群的定义，循环群G 的子群应满足循环群G 所满足的所有运算。

所以其子群页应该是循环群。

4.6若H 是G 的子群，x 和y 是G 的元素，试证xH ∩yH 或为空，或为xH=yHx,y ∉G若 xH ⋂yH ≠Φ可知：存在g ∈xH,g ∈yH 由g ∈xH,知存在h 1∈H,有g=xh 1;由g ∈yH,知存在h 2∈H,有g=yh 2; 从而有 xh1=yh2 ⇒x=y(h 2h 11-)------------式1任取z ∈xH,则存在h ∈H,有z=xh-------------------式2将-式1代入-式2： z=y(h 2h 11-)h=y(h 2h 11-h)--------- -式3H 是子群，有h 1，h 2，h ∈H 可推知，h 2h 11-h ∈H从而 y(h 2h 11-h) ∈yH.再由式3知 z ∈yH,这样我们就可推知xH ⊆yH 同理可推得 yH ⊆xH综上知道 yH=xH4.7若H 是G 的子群，H =k ，试证：xH =k ，其中x ∈GH =k设 H={n h h h h 32,1,} 同时对于i,j ∈{k ,3,2,1} 当i ≠j 时，有ah i≠ah j(否则，若有ah i =ah j ，由消去律得h i =h j ，矛盾) 表明{}n h h h h 32,1, 为n 个不同元而aH 恰有这些元组成，故 aH =k, ∴aH =H4．8有限群G 的阶为n ，H 是G 的子群，则H 的阶必除尽G 的阶。

组合数学第四版答案

组合数学第四版答案组合数学第四版答案【篇一：组合数学参考答案(卢开澄第四版)60页】>1.1 题从{1，2，……50}中找两个数{a，b}，使其满足（1）|a- b|=5；（2）|a-b|?5；解：（1）：由|a-b|=5?a-b=5或者a-b=-5，由列举法得出，当a-b=5时，两数的序列为（6，1）（7，2）……（50，45），共有45对。

当a-b=-5时，两数的序列为（1，6），（2，7）……（45，50）也有45对。

所以这样的序列有90对。

（2）：由题意知，|a-b|?5?|a-b|=1或|a-b|=2或|a-b|=3或|a-b|=4 或|a-b|=5或|a-b|=0；由上题知当|a-b|=5时有90对序列。

当|a- b|=1时两数的序列有（1，2），（3，4），（2，1）（1，2）…（49，50），（50，49）这样的序列有49*2=98对。

当此类推当|a-b|=2，序列有48*2=96对，当|a-b|=3时，序列有47*2=94对，当|a-b|=4时，序列有46*2=92对，当|a-b|=0时有50对所以总的序列数=90+98+96+94+92+50=5201.2题5个女生，7个男生进行排列，(a) 若女生在一起有多少种不同的排列？(b) 女生两两不相邻有多少种不同的排列？(c) 两男生a 和b之间正好有3个女生的排列是多少？所以总的排列数为上述6种情况之和。

1.3题m个男生，n个女生，排成一行，其中m,n都是正整数，若(a)男生不相邻(m?n?1); (b)n个女生形成一个整体；(c)男生a和女生b排在一起；分别讨论有多少种方案。

解：(a) 可以考虑插空的方法。

n个女生先排成一排，形成n+1个空。

因为m?n?1正好m个男生可以插在n+1个空中，形成不相邻的关系。

则男生不相邻的排列个数为ppnnn?1m(b) n个女生形成一个整体有n！种可能，把它看作一个整体和m个男生排在一起，则排列数有(m+1)!种可能。

组合数学习题

r r −2 cn − c − r +1 ( n − 4 ) − ( r − 2 ) +1
4
20．任一正整数 n 可唯一地表成如下形式：
n =
∑
i≥ 1
a i ⋅ i! ,
其中 0 ≤ a i ≤ i ,
i ≥ 1
证：（1）存在性
（对 n 用归纳法）
当 n=1 时，1＝1· 1！命题成立。假设对 n＝k 时，命题成立，即
结论成立
由归纳法知，结论成立。（2）唯一性（反证法）设 n = ∑ ai ⋅ p i = ∑ bi ⋅ p i , 0 ≤ a i , bi ≤ p − 1, i ≥ 0
i≥ 0 i≥ 0
若
∃i , 使得 a i ≠ bi ，则
i i
{i ai ≠ bi } 令 j = min i ≥0
i i≥ 相当于从 1,,2,…,n 取 r 个作不相邻组合。于是，从 1,2,…,n－r＋1 这 n－ r＋1 个中任取 r 个作不允许重复组合，总可以从 1,,2,…,n 这 n 个中取 r 个作不相邻组合与之对应。因此，在 1～n 这 n 个不同元素中取出 r 个作不相邻的组合与在 1～n－ r＋1 这 n－ r＋1 个不同元素中取出 r 个进行不允许重复的组合之间一一对应，故有结论。『注』若将 1 和 n 看成是两个相邻的数，结果又如何？
k=
∑a
i= 1
t
i
⋅ i!,
其中 0 ≤ a i ≤ i,
i = 1, 2 , L t ,
则 n＝k＋1 时，有
k +1 =
∑a
i =1
t
i
⋅ i! + 1 ,
t i =1

组合数学第四版卢开澄标准答案-第四章.docx

习题四4.1.若郡G的元素。

均可表示为某一元素X的幕，即« = r,则称这个群为循环郡。

若群的元索交换律成立，W a ,b wG满足ab = b-a则称这个群为阿贝尔(Abel)群，试证明所有的循环群都是阿贝尔群。

［证］•设循环群(G,・)的生成元是兀owG o于是,对任何元素a,bwG, 3m, nwN,使得*席, b= xo，从而a b = x()n• X Q=xo/z，+W(指数衛=xo?，+W(数的加法交换律)=鼎・霸”(指数律)=ba故•运算满足交换律；即(G,・)是交换群。

4.2.若x是群G的一个元素，存在一个最小的正整数加，使x m=e f则称加为x的阶，试证: C={e^c,x2, ...y N 1}是G的一个子群。

［证］.⑴非空性CH0:因为BeeG；(2)包含性CUG：因为x G G,根据群G的封闭性，可知G,故CgG；(3)封闭性X/d , b G C=>a • b eC： P ci, b G C,3k> IwN (0< k<m, 0< Is),使o =』,b =』, 从而a •b = x k• x1 = x{k+l) nK)d m eC (因为0 S (k+l) mod m < m)；(4)有逆元X/a G C=> a 'wC： V a G C,3k E N(0< k<m)f使a = x k ,从而a -i =丄”-k w c (|对为0 5 n?乂 < tn)。

综合⑴⑵⑶⑷，可知(C,・)是9, •)的一个子群。

4.3.若G是阶为n的有限群，则G的所有元素的阶都不超过no［证］.对任一元素xwG,设其阶为加，并令C={e^^c2,则|tl习题4.2.HT知(C,"是匸,•)的一个子群，故具有包含性CyG。

因此有m = \C\<\G\ = n所以群G的所有元索的阶都不超过77。

4.4.若G是阶为n的循环群，求群G的母元素的数目，即G的元素可以表示成a的幕：的元素a的数th［证］•设(G,・)是循环群，。

《组合数学》第二版(姜建国著)-课后习题答案全

习题一（排列与组合）1．在1到9999之间，有多少个每位上数字全不相同而且由奇数构成的整数？解：该题相当于从“1，3，5，7，9”五个数字中分别选出1，2，3，4作排列的方案数；（1）选1个，即构成1位数，共有15P 个；（2）选2个，即构成两位数，共有25P 个；（3）选3个，即构成3位数，共有35P 个；（4）选4个，即构成4位数，共有45P 个；由加法法则可知，所求的整数共有：12345555205P P P P +++=个。

2．比5400小并具有下列性质的正整数有多少个？（1）每位的数字全不同；（2）每位数字不同且不出现数字2与7；解：（1）比5400小且每位数字全不同的正整数；按正整数的位数可分为以下几种情况：① 一位数，可从1～9中任取一个，共有9个；② 两位数。

十位上的数可从1～9中选取，个位数上的数可从其余9个数字中选取，根据乘法法则，共有9981⨯=个；③ 三位数。

百位上的数可从1～9中选取，剩下的两位数可从其余9个数中选2个进行排列，根据乘法法则，共有299648P ⨯=个；④ 四位数。

又可分三种情况：⏹ 千位上的数从1～4中选取，剩下的三位数从剩下的9个数字中选3个进行排列，根据乘法法则，共有3942016P ⨯=个；⏹ 千位上的数取5，百位上的数从1～3中选取，剩下的两位数从剩下的8个数字中选2个进行排列，共有283168P ⨯=个；⏹ 千位上的数取5，百位上的数取0，剩下的两位数从剩下的8个数字中选2个进行排列，共有2856P =个；根据加法法则，满足条件的正整数共有：9816482016168562978+++++=个；（2）比5400小且每位数字不同且不出现数字2与7的正整数；按正整数的位数可分为以下几种情况：设{0,1,3,4,5,6,8,9}A =① 一位数，可从{0}A -中任取一个，共有7个；② 两位数。

十位上的数可从{0}A -中选取，个位数上的数可从A 中其余7个数字中选取，根据乘法法则，共有7749⨯=个；③ 三位数。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第四章生成函数1. 求下列数列的生成函数：（1）{0,1,16,81,…,n 4,…} 解：G{k 4}=235(11111)1x x x x x +++-（）（2）343,,,333n +⎧⎫⎛⎫⎛⎫⎛⎫⎨⎬ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎩⎭ 解：3n G n +⎧⎫⎛⎫⎨⎬ ⎪⎝⎭⎩⎭=41(1)x - （3）{1,0,2,0,3,0,4,0,……} 解：A(x)=1+2x 2+3x 4+4x 6+…=211x-. （4）{1,k ,k 2,k 3,…}解：A(x)=1+kx+k 2x 2+k 3x 3+…=11kx -. 2. 求下列和式：（1）14+24+…+n 4解：由上面第一题可知，{n 4}生成函数为A(x)=235(11111)1x x x x x +++-（）=0kk k a x ∞=∑，此处a k =k 4.令b n =14+24+…+n 4，则b n =0nk k a =∑，由性质3即得数列{b n }的生成函数为 B(x)= 0nn n b x ∞=∑=()1A x x -=34125(1111)ii i x x x x x i ∞=++++⎛⎫ ⎪⎝⎭∑. 比较等式两边x n 的系数，便得14+24+…+n 4=b n =1525354511111234n n n n n n n n -+-+-+-++++----⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭321(1)(691)30n n n n n =+++-（2）1·2+2·3+…+n (n +1)解：{ n (n +1)}的生成函数为A(x)=32(1)x x -=0k k k a x ∞=∑，此处a k = n (n +1).令b n =1·2+2·3+…+n (n +1)，则b n =0nk k a =∑.由性质3即得数列{b n }的生成函数为B(x)=nn n b x ∞=∑=()1A x x -=42(1)xx -=032nk kk x x k =+⎛⎫⎪⎝⎭∑. 比较等式两边x n 的系数，便得1·2+2·3+…+n (n +1)= b n =2(1)(2)213n n n n n +++=-⎛⎫ ⎪⎝⎭. 3. 利用生成函数求解下列递推关系：（1）()7(1)12(2)(0)2,(1)7f n f n f n f f =---==⎧⎨⎩;解：令A(x)=0()n n f n x ∞=∑则有A(x)-f(0)-f(1)x=2()nn f n x ∞=∑=2(7(1)12(2))n nf n f n x∞=---∑=217()12()nnn n x f n x xf n x∞∞==-∑∑=7x(A(x)-f(0))-12x 2A(x).将f(0)=2，f(1)=7代入上式并整理，得22711()(34)17121314n nn x A x x x x x ∞=-==+=+-+--∑. （2）()3(1)53(0)0nf n f n f =-+⋅=⎧⎨⎩;解：令A(x)=0()n n f n x ∞=∑，则有A(x)-f(0)= 1(3(1)53)n nnf n x∞=-+⋅∑=03()153nn n n n x f n x x x ∞∞==+∑∑=3xA(x)+15x ·113x-.A(x)= 215(13)xx -（3）()2(1)(2)(0)0,(1)1f n f n f n f f =-+-==⎧⎨⎩;解：令A(x)=0()n n f n x ∞=∑，则有A(x)-f(0)-f(1)x=2(2(1)(2))n nf n f n x ∞=-+-∑=212()()nnn n x f n x xf n x∞∞==+∑∑=2x(A(x)-f(0))+x 2A(x).将f(0)=0，f(1)=1代入上式并整理，得2()12x A x x x=--.4. 设序列{n a }的生成函数为：343(1)(1)xx x x --+-,但00b a =,110b a a =-, ……,1n n n b a a -=-,……,求序列{n b }的生成函数.解：由00b a =,110b a a =-,……,1n n n b a a -=-,得0nk n k b a ==∑，所以A(x)=()1B x x-.由此得B(x)=(1-x)A(x)= 3431xx x -+-，亦即序列{n b }的生成函数。

5. 已知生成函数239156xx x---,求对应的序列{n a }. 解：239156xx x ---=528171x x --+=11521817x x --⋅-+⋅所以a n =-5·8n -2·(-7)n.6. 有红,黄,蓝,白球各两个,绿,紫,黑球各3个,从中取出10个球,试问有多少种不同的取法？解：M r =M y =M b =M w ={0,1,2}，M g =M p =M h ={0,1,2,3}，所以该取法的个数为(1+x+x 2)4(1+x+x 2+x 3)3中x 10的系数，为678.7. 口袋中有白球5个,红球3个,黑球2个,每次从中取5个,问有多少种取法？解：M w ={0,1,2,3,4,5}，M r ={0,1,2,3}，M b ={0,1,2}，所以从中取5个的取法个数为(1+x+x 2)(1+x+x 2+x 3) (1+x+x 2+x 3+x 4+x 5)中x 5的系数，为12。

8. 求1,3,5,7,9这5个数字组成的n 位数个数,要求其中3和7出现的次数位偶数,其它数字出现的次数无限制.解：M 1=M 5 =M 9={0,1,2,3,…}，M 3 =M 7={0,2,4,…}该排列的生成函数为24232(1...)(1...)2!4!2!x x x x ++++++=14(e x +e -x )2e 3x =14(e 5x +e 3x +e x )=140(5231)!n n nn x n ∞=+⋅+∑ 所以a n =14(5231)n n +⋅+.9. 用3个1,2个2,5个3这十个数字能构成多少个偶的四位数？解：因要组成偶的四位数，所以个位必为2，然后确定其它三位的排列即可.M 1={0,1,2,3}，M 2 ={0,1}，M 3={0,1,2,3,4,5}，故生成函数为2325(1)(1)(1)2!3!2!5!x x x x x x x ++++++++ .其中33!x 的系数为20，即可以组成20个偶的四位数。

10. 求由A,B,C,D 组成的允许重复的排列中AB 至少出现一次的排列数目. 解：可把AB 看作一个整体，用E 表示，则M A =M B =M C =M D ={0,1,2,…}，M E ={1,2,…}故有224(1)()2!2!x x x x +++++ =e(4x)(e(x)-1)=e(5x)-e(4x)=5n -4n .11. 从⋅⋅⋅{,,}n a n b n c 中取出n 个字母,要求a 的个数为3的倍数,b 的个数是偶数,问有多少种取法?解：由题意可知，M a ={0,3,6,…}，M b =M c ={0,1,2,…}，该取法的生成函数为(1+x 3+x 6+…)(1+x+x 2+x 3)2=311x -·421()1x x-- 12. 把正整数8写成三个非负整数之和，要求n 1≤3,n 2≤3,n 3≤6.问有多少种不同的方案？解：由题意可知，M 1=M 2 ={0,1,2,3}，M 3={0,1,2,3,…,6}，则生成函数为 (1+x+x 2+x 3)2(1+x+x 2+x 3+…+x 6)= 421()1x x --·711x x --=(1-2x 4-x 7+x 8+2x 11-x 15) ·31(1)x -符合题意的方案数为x 8的系数，为82421221222+++--+⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭=13. 13. 在一个程序设计课程里,每个学生的每个任务最多可以运行10次.教员发现某个任务共运行了38次.设有15名学生,每个学生对这一任务至少做一次.求观察到的总次数的组合数.解：M 1=M 2 =…=M 15={1,2,3,…,10}，生成函数为(x+x 2+x 3+…+x 10)15=1015151()1x x x--，其中x 38的系数为371527151714114214-+⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭。

14. 用1角、2角、3角的邮票可贴出多少种不同数值的邮资？解：生成函数为G(x)=(1+x+x 2+…)(1+x 2+x 4+…)(1+x 3+x 6+…)=11x -·211x -· 311x-=1+x+2x 2+3x 3+4x 4+… 15. 设多重集合=∞⋅∞⋅∞⋅∞⋅1234{,,,}S e e e e ,n a 表示集合S 满足下列条件的n 组合数,分别求数列{n a }生成函数. （1）每个i e 出现奇数次（i ＝1,2,3,4）；（2）每个i e 出现4的倍数次i ＝1,2,3,4）；（3）1e 出现3或7次,3e 出现2,6或8次；（4）每个i e 至少出现6次（i ＝1,2,3,4）；解：（1）由题意知，M 1=M 2=M 3=M 4={1,3,5,…}，故该组合数序列的生成函数为(x+x 2+x 3+…)4=x 4·41(1)x -= x 4·03n n n n x ∞=+⎛⎫ ⎪⎝⎭∑=403n n n n x ∞+=+⎛⎫ ⎪⎝⎭∑. X n 的系数为13n -⎛⎫⎪⎝⎭. （2）由题意知，M 1=M 2=M 3=M 4={0,4,8,…}，故该组合数序列的生成函数为(1+x 4+x 8+…)4= 441(1)x -. （3）由题意知，M 1={3,7}，M 2= M 4={0,1,2,…}，M 3={2,6,8} 故该组合数序列的生成函数为(x 3+x 7)(x 2+x 6+x 8)(1+x+x 2+…)2=(x 5+2x 9+x 11+x 13+x 15) ·011n n n x ∞=+⎛⎫ ⎪⎝⎭∑. X n 的系数为5191111131151111112n n n n n -+-+-+-+-+⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫++++ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭＝6n-56.（4）由题意知，M 1=M 2=M 3=M 4={6,7,8,…}，故该组合数序列的生成函数为(x 6+x 7+x 8+…)4=x 24·41(1)x -= x 24·03n n n n x ∞=+⎛⎫ ⎪⎝⎭∑=2403n n n n x ∞+=+⎛⎫ ⎪⎝⎭∑. X n的系数为213n -⎛⎫⎪⎝⎭. 16. 设多重集合=∞⋅∞⋅∞⋅∞⋅ 123{,,,,}k S e e e e ,n a 表示集合S 满足下列条件的n 排列（1）S 的每个元素出现偶数次；（2）S 的每个元素至少出现4次；（3）S 的每个元素至多出现i 次（i =1,2,…,k ）；（4）S 的每个元素至少出现i 次（i =1,2,…,k ）；解：（1）由题意知，M 1=M 2=M 3=…=M k ={0,2,4,…}，故该组合数序列的生成函数为24(1...)2!4!k x x +++=()()2ke x e x +-⎛⎫⎪⎝⎭.（2）由题意知，M 1=M 2=M 3=…=M k ={4,5,6,…}，故该组合数序列的生成函数为54(...)4!5!kx x ++=3212!3!(())k x x e x --- =(-1)i 0(())[(1)(2)(3)]k i i k e k i x e e e i =-++⎛⎫ ⎪⎝⎭∑ =00((1)[1(2)(3)])/!ki i n i nk n e e i x n ∞==-++⎛⎫ ⎪⎝⎭∑∑ 0(1)[1(2)(3)]()knn i n i e e k a k i i =-++⎛⎫=- ⎪⎝⎭∑（3）由题意知，M 1=M 2=M 3=…=M k ={0,1,2,…,i}，故该组合数序列的生成函数为2(1...)2!!i kx x x i ++++.（4）由题意知，M 1=M 2=M 3=…=M k ={i,i+1,i+2,…}，故该组合数序列的生成函数为 1(...)!(1)!i i k x x i i ++++.17. 用生成函数法证明下列等式：（1）2122n n n n r r r r ++⎛⎫⎛⎫⎛⎫⎛⎫-+= ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭⎝⎭证明：(1+x)n+2=(1+x)n ·(1+x)2=(1+2x+x 2) (1+x)n =x 2(1+x)n +2(1+x)n+1-(1+x)n对比左右两边x r 的系数，左边=2n r +⎛⎫⎪⎝⎭，右边=122n n n r r r +⎛⎫⎛⎫⎛⎫+- ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭，整理得：2122n n n n r r r r ++⎛⎫⎛⎫⎛⎫⎛⎫-+= ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭⎝⎭.等式得证.（2）0(1)qj j q n q j n j r r q =+-⎛⎫⎛⎫⎛⎫-= ⎪⎪ ⎪-⎝⎭⎝⎭⎝⎭∑证明：(1+x)n [(1+x)-1]q =x q (1+x)n ，对比左右两边x r 的系数，左边=00(1)(1)(1)q qnq j q j j q q x x j r n q j j -==++-+-=⎛⎫⎛⎫⎛⎫ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭∑∑，右边=n r q -⎛⎫ ⎪⎝⎭，因此等式得证.18. 设有砝码重为1g 的3个,重为2g 的4个,重为4g 的2个,问能称出多少种重量？各有多少种方案？解：由题意知，M 1={0,1,2,3}，M 2={0,1,2,3,4}，M 4={0,1,2}，故生成函数为 (1+x+x 2+x 3)(1 +x 2+x 4+x 6+x 8)(1+x 4+x 8)=1+x+2x 2+2x 3+3x 4+3x 5+4x 6+4x 7+5x 8+5x 9+5x 10+5x 11+4x 12+4x 13+3x 14+3x 15+2x 16+2x 17+x 18+x 19故共能称出20种重量，指数即为重量类型，系数为方案数. 19. 求方程x 1+2x 2+4x 3=21的正整数解的个数. 解：由题目可以看出，x 1为奇数，故生成函数为(x+x 3+x 5+…)(x 2+x 4+x 6+…)(x 4+x 8+x 12+…)=(x 7+2x 9+x 11)4022k k k x ∞=+⎛⎫ ⎪⎝⎭∑，展开式中x 21的系数为20，亦即该方程正整数解的个数。