由三视图到立体图形-
4.2.2由视图到立体图形
下面是一些立体图形的三视图，请根据视图说 出立体图形的名称:
主视图
左视图 主视图 左视图 俯视图
俯视图
四棱 柱
圆锥
一个几何体的三视图如下,你能说出它是什么 立体图形吗?
主视图
左视图
俯视图
四棱锥
你能根据下面的三视图找出它的原立体图形吗?
主视图
俯视图
左视图
原图形
下面是一个组合图形的三视图，请描述物体形状
主视图
左视图
俯视图
物体形状
由四个小长方形搭成的物体，它的俯视图如图所示。 问这个物体有几种搭法？试分别画出来。
用小方块搭成一个几何体，使它的主视图和俯视 图如图所示，它最少需要多少个小立方块，最多 需要多少个小立方块?
主视图俯视图ຫໍສະໝຸດ 最少十个符合条件 的几何体 有几种？
最多十三个
用小方块搭成的一个几何体，它的俯视图如图所 示，小方块中的数字表示的是在该位置小方块堆 的层数。试用手头的模型搭出它的原形并画出它 的三视图。
2 3 1
1
作业：
1、p129 习题4.2 第4题； 2、课时训练； 3、一课三练。
第2课时由三视图想象出立体图形
[解析]由三视图想象立体图形时，要先分别依照主视图、俯视图和左视图想象立体图形的前面、上面和左侧面，然后再综合起来考虑整体图形.
解：(1)由主视图是矩形，能够想象到立体图形可能是棱柱；由俯视图是矩形，能够想象到立体图形是四棱柱，再由左视图是矩形，能够想象到立体图形是直四棱柱，由三个矩形的长和宽不相等，可知该立体图形是长方体.
(2)由主视图是等腰三角形，能够想象到立体图形可能是棱锥，也可能是圆锥，也可能是三棱柱，由俯视图是带圆心的圆，可确定立体图形是圆锥，同时圆锥的左视图也是等腰三角形.
师生活动：用课件展现一些三视图，请学生观看、想象、描述、讨论这些三视图所对应的实物.
在前面的学习中，差不多探究了由立体图形画出三视图，本活动探讨由三视图想象出立体图形，与上节课形成逆向思维。
本课例题部分补充中考常考的一类题目(给出一个由多个相同小正方体堆积而成的几何体的俯视图，依照视图，数出组成该几何体的小正方体的个数)，这类题目一样难度较大，在课堂操作时事先预备了一些骰子，让学生通过自由组合并画出立方体体会和明白得三视图与几何体之间的联系，从而解决难点.
③[师生互动反思]
______________________________________________________
【知识网络】
提纲挈领，重点突出.
活动
四：
课堂
总结
反思
【教学反思】
①[授课流程反思]
______________________________________________________
______________________________________________________
②[讲授成效反思]
由三视图还原立体图形-PPT课件
例1：根据三视图中主视图、俯视图和左视图， 说出立体图形的名称。
隐藏主视图 隐藏俯视图
隐藏左视图
隐藏圆柱
隐藏三棱柱
隐藏长方体
三视图
隐藏主视图 隐藏点
隐藏左视图
隐藏俯视图
隐藏圆锥
隐藏三棱锥
三视图
圆柱无中轴
三视图
隐藏几何体
三视图
隐藏几何体
三视图
隐藏几何体 显示对象
H
例2：根据物体的三视图，描述物体的形状.
移动点 移动点 还原系列2个动作
三视图
移动点 移动点 线段系列2个动作
隐藏对象
移动隐藏几何体
三视图
隐藏对象
A
B
C
三视图
A
B
C
隐藏几何体
显示对象
三视图
隐藏几何体
根据下面的三视图，说出这个几何体是由几个正方体怎么组合而成的.
建筑物的形状
某建筑物模型的三视图如图所示，请你描述建造的建筑物是什么样 子的？共有几层？模型一共需要多少个小正方体？
反馈练习
隐藏对象
显示点 移动点 移动点 系列2个动作
由三视图到立体图形
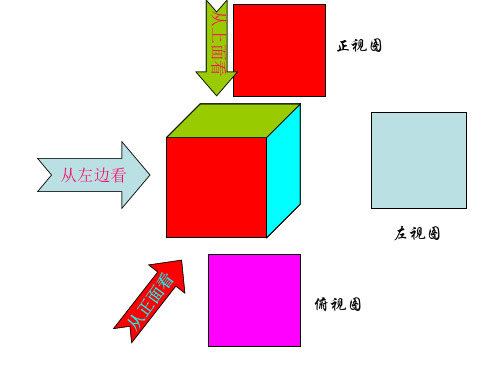
探究 根据三视图摆出它旳立体图形
主视图 左视图
俯视图
俯视图
21
不用摆出这个几何体，你能画出 这个几何体旳正视图与左视图吗？
12
思索措施
先根据俯视图拟定正视图有 列，
正视图：
再根据数字拟定每列旳方块有 个，
正视图有 3 列，第一列旳方块有 1 个， 第二列旳方块有 2 个，第三列旳方块有 1 个， 左视图有 2 行， 第一行旳方块有 2 个，
至少8个
最多10个
至少十个
正视图 俯视图
最多十三个
俯视图 正视图
6cm 9cm
4.5cm
6cm 9cm
4.5cm 3cm
3cm
由主视图、左视图懂得，这个几何体是直棱 柱, 但不能拟定棱旳条数. 再由俯视图能够拟定它 是直四棱柱，且底面是梯形.
合作交流，分类学习
已知几何体旳视图，能够拟定几何体旳形状 吗？
例2、如图是一种物体旳三视图，试说出物 体旳形状。
左视图 正视图 俯视图
试一试： （1）如图是一种物体旳三视图，试
说出物体旳形状。
左视图
正视图
俯视图
（2）下列是一种物体旳三视图，请描述出它旳形状
正视图
左视图
俯视图
3、 下面是一种物体旳三视图，试说出物体旳形状. 想一想
物体形状
和你想出旳物体形状一样吗？
下列是一种物体旳三视图，请描述出它旳形状
主视图 左视图
俯视图
下列是一种由正方体构成旳几何体旳三视图， 你能描述出它旳形状吗？
一定要注意百分比 啊
右视图
b h
正视图
a h
ab h
俯视图
a b
下面所给旳三视图表达什么几何体?
由三视图想象出立体图形课件
解：物体是正五棱柱形状的，如图所示.
例3 一个几何体由大小相同的小立方块搭成，从上面看 到的几何体的形状如图所示，其中小正方形中的数字表 示在该位置的小立方块的个数，则从正面看到几何体的 形状是图中的( D )
解析：俯视图中，第一列最高有3个小立方块，第 二列最高有2个小立方块，第三列最高有3个小立方 块，因此，主视图从左到右可看到的小立方块个数 依次为3、2、3，故选D.
由三视图想象出立体图形
知识回顾 下面是哪个几何体的三视图？
主视图
左视图
俯视图
A
B
C
D
例题讲解 例1 如图，分别根据三视图(1) (2)说出立体图形的名称.
(先分别根据主视图、 俯视图和左视图想象立体图形的前面、上面和左侧面， 然后再综合起来考虑整体图形.
解：(1) 从三个方向看立体图形，视图都是矩形，可以想象出： 整体是 长方体 ，如图①所示；
②
①
(2) 从正面、侧面看立体图形，视图都是等腰三角形； 从上面看，视图是圆；可以想象出：整体是 圆锥 ， 如图②所示.
例2 根据物体的三视图描述物体的形状.
分析：由主视图可知，物体的正面是正五边形； 由俯视图可知，由上向下看到物体有两个面的 视图是矩形，它们的交线是一条棱 (中间的实线 表示)，可见到，另有两条棱 (虚线表示) 被遮挡； 由左视图可知，物体左侧有两个面是矩形， 它们的交线是一条棱 (中间的实线表示)，可见 到；综合各视图可知，物体的形状是正五棱柱.
获取新知
归纳： 由三视图想象立体图形时，先分别根据主视图、
俯视图和左视图想象立体图形的前面、主面和左侧面 的局部形状，然后再综合起来考虑整体图形．
4、2、2由视图到立体图形
海南省洋浦中学教师教案 1
上面图圆柱和长方体只有给出的几种可能的图形，其实物图为长方形的立体图形有很多。
二、新授
上节课我们学习了从立体图形的三个不同
⑴⑵⑶
解：⑴长方体；⑵圆锥；⑶四棱锥
例2：下面是一个物体的三视图，
的形状.
例3：如图是几个小立方体所搭成的立体图形的俯视图，小正方形中的数字表示在该位置上小立方体的个数，请画出这个立体图形的正视
四、课堂小结
本节学习了由视图到立体图形，
想象能力，要充分认识到角度的转化。
五、作业。
怎样将几何的三视图还原为立体几何图形
怎样将几何的三视图还原为立体几何图形
三视图还原立体几何简单与否因人而异，空间想象力强的人，一眼便能看出是什么样的图形。
我就觉得这种题目还是挺简单的，哈哈。
首先我给你几个最常见的例子。
1.三面都是长方，就是长方体；2.上面看圆，两个侧面看长方，就是圆柱；3.上面看圆，两侧面看三角，就是圆锥；4.上面看多边形，两侧面看三角，就是棱锥；5.上面看多边形，两侧看长方，就是棱柱；6.上面看圆，两侧看梯形，就是圆台；7.三面都是圆，就是球。
其次要注意的是，三视图显示了图形的长宽高，从上方看的图显示了长宽或者直径之类的东西，从侧面看的图显示了长和高，或者宽和高，或者直径和高之类的。
第三要是你空间想象力不强，那么就得多练习。
至于方法，我觉得多锻炼逆向思维能力是最好的。
你可以随便想象出一个立体图形，然后自己给那个图形画三视图，然后再只看你的三视图想象你刚才想的图形，反复练习，多总结，我想你会有启发、收获的。
最后说说三视图的作用。
要是你单看三视图，这个东西高考也不会考，看似没有用，实际上它是很有用的。
它为你以后的立体几何题的分析打下了一定的基础，是一个融入于解题思路中的方法。
综上所述，建议你好好练习三视图。
由三视图想象立体图形3
课堂练习： 由三视图想象实物的形状：
由物知图——利用正方体组合提升空间想象力 如图都是由7个小立方体搭成的几何体，从不 同方向看几何体，分别画出它们的主视图、左视 图与俯视图，并在小正方形内填上表示该位置的 小正方体的个数.
（1）
（2）
（3）
（4）
做一做：由几个相同的小立方块搭成的几何体的 俯视图如图所示。方格中的数字表示该位置的小 方块的个数.请画出这个几何体的三视图。
2.锥体——有两个视图是三角形. 3.台体
圆台——有两个视图是等腰梯形
棱台——有两个视图是梯形 4.球——三个视图都是圆
上节课我们讨论了由立体图形(实物)画出三视图， 下面我们讨论由三视图想象出立体图形(实物)。
分析：由三视图想象立体图形时，要分别根据主视图、俯视图 和左视图想象立体图形的前面、上面和左侧面，然后再综合起 来考虑整体图形。
5.一个几何体的主视图和左视图如图所示,它是什么 几何体?请补画这个几何体的俯视图.
(第5题)
直三棱柱
(第6题)
6.一个直棱柱的主视图和俯视图如图所示.描述这 个直棱柱的形状,并补画它的左视图.
直五棱柱,底面是五边形
7、右图是由一些相同的小正方体构成的几何 体的 三视图，则构成这个几何体的小正方体 的个数是【 】 A.5 B.6 C.7 D.8
由三视图想象几何体 下面是一些立体图形的三视图，请根据视 图说出立体图形的名称:
正视图
侧视图
俯视图
四棱柱
由三视图想象几何体 下面是一些立体图形的三视图，请根据视 图说出立体图形的名称:
正视图
左视图
圆锥 俯视图
由三视图想象几何体 一个几何体的三视图如下,你能说出它是 什么立体图形吗?
从三视图到立体图形课件
在建筑设计中，三视图主要用于表现建筑物的外观、内部空间和结构，通过不同角度的视图展示建筑物的立体效果和设计细节。
建筑表现
三视图还可以作为施工指点，帮助施工人员理解建筑物的构造和尺寸，确保施工过程中的准确性和规范性。
施工指点
三视图是一种国际通用的工程设计表达方式，能够方便地与不同国家和地区的工程师、设计师进行交流和合作。
建筑设计
在建筑设计中，设计师通常会使用三视图来表达建筑物的外观、结构和空间布局，通过三视图可以直观地展示建筑物的立体效果。
机械制图
THANKS
感谢您的观看。
左视图是从物体的左侧方视察得到的视图，通常用来表示物体的左侧面和背面的形状。
左视图可以提供物体的宽度和深度信息。
俯视图是从物体的上方视察得到的视图，通常用来表示物体的顶面和底面的形状。
俯视图可以提供物体的长度和深度信息。
三视图之间是相互关联的，通过三个视图可以完整地表示物体的形状和尺寸。
在绘制立体图形时，需要将三个视图结合起来，通过投影和转换得到物体的立体形状。
02
CHAPTER
如何从三视图构建立体图形
总结词
通过将立体图形投影到三个互相垂直的平面上，得到三个视图。
详细描述
投影法是利用光线将立体图形投射到三个互相垂直的平面上，分别得到主视图、俯视图和左视图。这三个视图可以完整地表达出立体图形的形状和尺寸。
通过截取立体图形的部分，得到三视图。
截面法是通过截取立体图形的一部分，得到三视图的方法。这种方法适用于一些不规则的立体图形，可以通过截取部分来简化视图。
利用CAD软件进行电路板的三维建模和布线。
电子设计
06
CHAPTER
三视图与立体几何的关系
由视图到立体图形
1、如图是一个物体的三视图，试想象 该物体的形状。
主 视 图
左 视 图
俯 视 图
2、如图是一个物体的三视图，试说出物体 的形状。
主 视 图
左 视 图
俯 视 图
3、一个物体由几块相同的正方体叠成， 它的三个视图如图所示，试 回答下 列问题：
（1）该物体共有多少层？ 3层 （2）最高部分位于哪里？ 左侧最后一排 （3）至少需要几个小正方体？9个
华师大版义务教育课程标准实验教科书《数学》七年级（上）
挑战 记忆
1、立体图形的三视图是指
_主__视__图___、_俯__视___图__、_左__（__或__右__）__视__图____。 主视图：从__正_面____看到物体的形状，并绘制成 的图叫做主视图。
俯视图：从__上_面____看到的物体形状，并绘制成 的图叫做俯视图。 左视图：从__左_面____看到的物体形状，并绘制成 的图叫做左视图。
2、画物体的三视图时,要符合如下原则:
长对正,高平齐,宽相等.
挑战 记忆
3、回忆以下立体图形的三视图，并回答问题：
解： 主视图 左视图 俯视图
问题： 左视图是长方形的有圆柱、长方体、三棱柱； 主视图、左视图都是长方形的有 圆柱、长方体 ； 主视图、左视图、俯视图都是长方形的有 长方体 。
如图所示的是一些立体图形的三视图，
请根据视图说出立体图形的名称。
（1） 主 视
左 视
图
图
俯 视 图 解：该立体图形是长方体，如图所示。
（2）
主 视
左 视
图
图
俯 视 图 解：该立体图形是正方体，如图所示。
（3）
正视图
左视图
俯视图 解：该立体图形是球体，如图所示。
《由三视图到立体图形》学情分析方案
《由三视图到立体图形》学情分析方案几何学习调查问卷1、做题时，你能认真读题审题吗？A 认真B 不太认真C 不认真2、做几何题时，你一般读题A 1~2遍B 2~3遍C 3~4遍3、在几何知识学习过程中，就你个人而言，你认为有效的学习方式是A.记忆解题法B.公式法则套用C.自主合作探究D.“说”、“讲”的方式4、在最初学习几何知识时，你最希望在哪方面得到帮助A.思路分析B.关键知识点的提示C.关键步骤的讲解D.完整详细的解题步骤5、在初步学习几何知识过程中，“说”、“讲”方式对于你对知识点的掌握理解程度如何？A.完全理解掌握B.基本理解掌握C.理解掌握一部分D.多数无法理解掌握6、在你理解和巩固掌握一道几何题时，你是否有通过“说”、“讲”的方式检验自己对于知识的理解程度？A.经常B.偶尔C.很少D.从来没有7、在通过“说”、“讲”的过程中分析和巩固几何知识时，你认为反向推理的方法分析和巩固几何知识学习的帮助有多大？A.帮助很多B.有一些帮助C.帮助不大D.完全没有帮助8、从整体而言，你认为“说”、“讲”方式在几何知识学习中，对你哪方面的帮助最多？A.记忆知识方面B.分析知识方面C.理解知识方面9、通过“说”、“讲”方式对于你上课集中记忆力是否有帮助？A.帮助很多B.有一些帮助C.帮助不大D.完全没有帮助10、你是否希望在几何知识学习的过程中，将“说”、“讲”方式持续下去？A.非常希望B.有一些希望C.对我完全没有影响D.不希望11、你认为通过“说”、“讲”的方式对你理解和巩固几何知识的帮助有多大？A.帮助很多B.有一些帮助C.帮助不大D.完全没有帮助12、请给老师关于几何的“说”、“讲”方式提个建议：。
数学华东师大版4.2.2由视图到立体图形-说课稿
4.2.2 由视图到立体图形（说课稿）一、教材结构与地位分析本节课是华师大版七年级上册第四章第二节第二课时的内容，本节课内容是在学生学习了由立体图形到视图的基础上进行的。
人们在日常生活中接触到的是立体图形，而要研究它，往往把它转化成平面图形来研究。
“由视图到立体图形”的主要作用是初步培养学生的空间观念．本节由物体的三视图辨认出该物体的形状，是一个充满丰富想象力和创造性的探索过程．根据三视图描述基本几何体或实物原型，因此是学生学习平面图形到立体图形的一个重要的纽带。
教材结构分析，本节教材中分为两部分，第一部分是根据熟悉的立体图形的三视图说出简单的立体图形，第二部分是根据一个物体的三视图想象该物体的形状。
二、目标设置【课标要求】会根据视图描述简单的几何体。
【学习目标】1、能根据物体的三视图说出物体的形状2、能根据几个小立方块所搭几何体的俯视图及小正方形中的数字画出相应几何体的主视图、左视图。
3、能根据几个小方块搭成的几何体及它的主视图和俯视图，说出它最少需要多少个小立方块，最多需要多少个小立方块三、学情分析从已有的认知水平：七年级学生对身边有趣的事物充满好奇，对一些有规律性的问题充满探求的欲望，他们非常乐意动手操作，有很强的好胜心和表现欲，有一定的归纳能力。
但是他们开始接触几何知识，空间想象力太弱，缺乏从多角度观察事物的经验。
从已有的活动经验：已有根据立体图形画三视图的方法经验。
四、四基三点：基础知识：物体的三视图基本技能：能根据物体的三视图说出物体的形状基本思想：空间观念重点：由物体的三视图辨认出物体形状难点：能根据几个小立方块所搭几何体的俯视图及小正方形中的数字画出相应几何体的主视图、左视图。
五、重难点处理方法重点的处理方法：先用实物将同一个物体的三视图拼出来，将有关视图联系起来，找出各视图间的关系，引导学生综合考虑三个视图之间的联系，从而培养学生的空间想象能力，并将物体的形状画出来。
难点的处理方法：先用小立方块将几何体的俯视图及小正方形中的数字拼出来，这样立体图形就出来了，再根据立体图形将左视图和主视图画出来，观察俯视图中的小正方形中的数字与左视图，主视图每一列，行的个数的关系，从中总结方法规律。
由三视图确定立体图形
主视图 俯视图
左视图
思考>回答
下面三视图对应的几何体是（ D ）
主视图
左视图
俯视图
检测
检测
B
检测
这节课你有什么收获？
作业： 习题5.5 第1,2,3题
最美的风景，一直在路上
下面所给的三视图表示什么几何体?
主视图
左视图
俯视图
直五棱柱
思考>回答
下面是一种几何体的三种视图，说出该几何体。
主视图
左视图
俯视图
思考>回答
下列是一个由若干正方体组成的立体图形的三 种视图，它由几个正方体组成？
主视图
左视图
俯视图
思考>回答
下列三种视图对应的几何体是什么？
主视图
左视图
俯视图
思考>回答
北师大版 九年级上册
第五章
投影与视图
5.2 视图 第3课时 由三视图确定立体图形
兰州市第三十四中学 黎笋
学习目标
1.会辨别复杂的几何体的三视图，能由三视图想 象出几何体的形状，判断实物原型。（重点） 2.理解三视图与几何体之间的联系。（难点）
002号航母三种视图
思考？?
右图是某种零件，你知道工人师傅是怎样制造这 个零件的吗？画出该几何体的三视图。
主视图
左视图
俯视图
思考>回答
某商品的外包装盒的三视图如图所示，则这个包
装盒是什么几何体？其体积是( B )
10cm
A．200 cm3
20cm
主视图
左视图
B．500 cm3Fra bibliotekC．1000 cm3
D．2000 cm3
三视图还原实物图“五步走”
三视图还原直观图“五步走”石门县第一中学415300陈锦鑫三视图是高中立体几何中的一个重要知识点，也是今后进一步学习机械制图、建筑制图等的必修课，三视图也是近几年高考必考的知识点。
主要题型就是给出几何体的三视图，计算几何体的面积和体积等相关量。
学生丢分的主要原因是不能由三视图还原为几何体，画出相应的直观图。
本文通过一道例题介绍一种将三视图还原成实物图的方法。
如图，网格纸上小正方形的边长为1，粗线画出的是某多面体的三视图，将该三视图还原成实物图第一步：根据三视图中三种视图的长与宽，作一个与正视图等长等高，与俯视图等宽的长方体。
例如本例中需要作一个边长为2的正方体ABCD-A’B’C’D’，如图。
第二步:根据三视图中的正视图对长方体切割。
例如本例中由正视图知道，原几何体只能在三棱柱ADD’-BCC’范围内，因此将三棱柱AA’D’-BB’C’部分截掉，如图。
第三步：根据三视图中的侧视图对剩余几何体切割。
例如本例中由侧视图知道，原几何体只能在四棱锥C’-ABCD范围内，因此将三棱锥D’-ADC’部分截掉，如图。
第四步：根据三视图中的俯视图对剩余几何体切割。
，同时结合三种视图需要将例如本例中由俯视图知道，原几何体在底面上的投影为BCD三棱锥C’-ABDC部分截掉，得到三棱锥C’-BCD，如图。
第五步：根据三种视图多边形内部的实线或虚线对剩余几何体切割。
例如本例中正视图、俯视图中均有一条虚线，三视图的虚线表示虚线所在的位置有立体图形的轮廓线,只是在观察者所在的位置看不到。
根据正视图、俯视图中知点E为三棱锥C’-BCD 中BC边的中点，连接ED、EC’，ED、EC’是立体图形的轮廓线，因此我们需要将截掉三棱锥C’-ECD,得到三棱锥C’-BDE即为三视图所对应的实物图。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
主视图
左视图
俯视图
用小立方块搭出符合下列三视图的几何体：
主视图
左视图
俯视图
下列是一个物体的三视图，请描述出它的形状
主视图
俯视图
左视图
主视图
俯视图
左视图
下面图(1)与图(2)是几个小方块所搭几何体俯视图, 小正方形中的数字表示在该位置的小立方块的个数. 请画出这两个几何体的主视图、左视图. 2 4 1 2 3
图3-25
作业:
1.作业本 2.教与学
； / 票选第一资讯平台
suc52rvt
爹听了哈哈大笑，高兴地把小尚武搂在怀里，在他的额头上亲了一口，说：“谁说爹不相信了？爹相信！我的小直子是最聪明的娃儿！”于是乎， 尚文兄妹三人除了干活儿之外，就跟着这个“爹爹”认字、写字。兄妹三人你追我赶比着学，进步很快。至于吹笛子、拉二胡、唱曲儿什么的， 他们也都多多少少地学会了一些。哪天如果有兴致了，这“父子们”就吹奏、吹拉、哼唱一会儿，逗得李长善夫妇乐呵一番，也引来了邻里不少 娃娃们无比羡慕的目光。86第五十六回 李家人感恩助恩人|（李长善家仨儿女，如今都成耿家人；“慈父”真情倍感人，李家感恩助恩人。）耿 老爹救的这个和耿直年龄相仿，长得也颇有几分相似的男娃儿的家，就在耿老爹误认为长高了的“三六九镇”的这个山镇上。这里离鄱阳湖不是 太远，地势较高，加之距离碧山溃坝的地方已经很远了，所以盛夏期间发生的溃坝之灾，对这里的影响不是很大。这个男娃儿的父亲姓李名长善， 家有妻子和三个孩子。耿老爹救起的这个男娃儿正是他的小儿子李尚武。一听回去报信的那个男娃儿说尚武落到水塘里了，他夫妻二人和大儿子 李尚文、女儿李尚英就拼着命跑来了。在李家的三个孩子中，尚文最大，是年十九岁；他老实憨厚，已经能帮着父亲种田干活儿了。爱女尚英十 五岁了，聪明懂事，夫妻俩爱若珍宝。小儿子尚武还不满十岁，虽然也相当聪明伶俐挺惹人喜爱，但却很是贪玩儿，也免不了淘气惹事儿。总之， 这老疙瘩非常让父母操心。这不，一个不留神，差点儿就酿成大祸。不过话又说回来，尽管淘气包李尚武这一出着实把他的爹娘和兄姐吓了个半 死，但却也恰恰地成就了他与耿老爹之间一场感人的父子缘分。这是后话且不多述，只说眼下发生的事情。李长善夫妻俩把耿老爹搀扶到自己家 里后，全家人一起动手，很快就收拾出一个向阳的大屋子来。然后，李长善和大儿子又忙着照顾耿老爹在家里的洗浴房间里洗澡，李妻则找出丈 夫日常穿的干净衣服来，让小儿子送去给耿老爹换上。然后大家围坐在一起吃了晚饭。晚饭后，夫妇俩把耿老爹领到给他收拾出来的屋子里来。 耿老爹回头看看，发现尚文兄妹三人没有跟来，就说：“我的娃儿们呢？”李妻赶快出来招呼兄妹三人：“文儿，你们也都过来吧！”耿老爹赶 快纠正：“大嫂你叫错了，是正儿！”尚文兄妹三人也过来了。李长善说：“大哥，你以后就住这屋吧！这屋子向阳，又宽敞又明亮，挺好住 的！”耿老爹四下看看，发现这个屋子收拾得很干净，大大的窗户两侧垂着墨绿色的窗帘。在屋里的一角放了一个不大的衣柜，旁边还有一张简 洁实用的方桌子。靠近窗户的一侧，沿墙摆放了好大的一张通铺大木床，但床上只放了一床被褥。耿老爹奇怪地问：“怎么只有一床被褥？我还 有
5.一个几何体的主视图和左视图如图所示,它是什么 几何体?请补画这个几何体的俯视图.
(第5题)
直三棱柱
(第6题)
6.一个直棱柱的主视图和俯视图如图所示.描述这 个直棱柱的形状,并补画它的左视图.
直五棱柱,底面是五边形
探究活动
用6个相同的小方块搭成一 个几何体,它的俯视图如图3-25所 示.则一共有几种不同形状的搭救 法(你可以用实物模型动手试一 试)?你能用三视图表示你探究的 结果吗?
课内练习
1.某两个物体的三视图如图所示.请分别说出它们的形状.
直三棱柱
正四棱锥
2.由几个相同的小立方块搭 成的几何体的俯视图如图所 示.方格中的数字表示该位置 的小方块的个数.请画出这个 几何体的三视图.
1
3 2
3.一个几何体的三个视图都是全等的正方形, 则这 立方体 个几何体是______. 4.一个几何体的三视图都是半径相等的圆,则这个几 球 何体是_______.
已知一个几何体的三视图如图3-23所示,描述该 几何体的形状,量出三视图的有关尺寸,并根据已知的 比例求出它的侧面积(精确到0.1cm2)
6cm 4.5cm 9cm
图3-23
3cm
图3-24
由主视图、左视图知道，这个几何体是直棱 从图上看出有五个面的面积可以直接求出 ,关 柱 , 但不能确定棱的条数. 再由俯视图可以确定它是 键只要求出另个侧面的面积就行了 ,怎样求呢? 直四棱柱，且底面是梯形.
俯视图
俯视图
长方体
圆锥
这是一个立体图形的三视图，你能说出 主视图 左视图 它的名称
主视图
左视图
俯视图
俯视图
圆柱
四棱锥
下列是一个物体的三视图，请描述出它的形状
主视图
左视图
俯视图
三棱锥
下面是一个物体的三视图，试说出它的形状
主视图
下列是一个物体的三视图，请描述出它的形状
主视图
左视图
俯视图
下列是一个物体的三视图，请描述出它的形状
主视图
左视图
下面图(1)与图(2)是几个小方块所搭几何体俯视图, 小正方形中的数字表示在该位置的小立方块的个数. 请画出这两个几何体的主视图、左视图.
3 4 2
2 1
主视图
左视图
由三视图描述几何体(或实物原型), 一般先根据各视图想像从各个方向看到 的几何体形状, 然后综合起来确定几何 体(或实物原型)的形状, 再根据三视图 “长对正、高平齐、宽相等”的关系, 确定轮廓线的位置,以及各个方向的尺 寸.
下面所给的三视图表示什么几何体?
主视图
左视图
直四棱柱
俯视图
下面所给的三视图表示什么几何体?
主视图
左视图
俯视图
直五棱柱
下面所给的三视图表示什么几何体?
主视图
左视图
俯视图
下面所给的三视图表示什么几何体?
主视图 左Байду номын сангаас图
俯视图
这是一个立体图形的三视图，你能说出 它的名称 左视图
主视图
主视图
·
左视图
复习：
请说出下列几何体的主视图、左视图和 俯视图：
复习：由5个相同的小立方块搭成的几何体如图
所示,请画出它的三视图:
空间想象力3
画出三视图：
主视图
左视图
主视图
左视图
俯视图(3)
俯视图(4)
3.4 由三视图描述几何体
根据如图 右边的椅子的 视图,工人就能 制造出符合设 计要求的椅子.
由于三视图不仅反映了物体的形状,而且反映了 各个方向的尺寸大小,设计人员可以把自己构思的创 造物用三视图表示出来,再由工人制造出符合各种要 求的机器、工具、生活用品等,因此三视图在许多行 业有着广泛的应用.