等量同种电荷中垂线上的电场强度最大值怎么求.
等量同种电荷中垂线上最大场强位置的推导
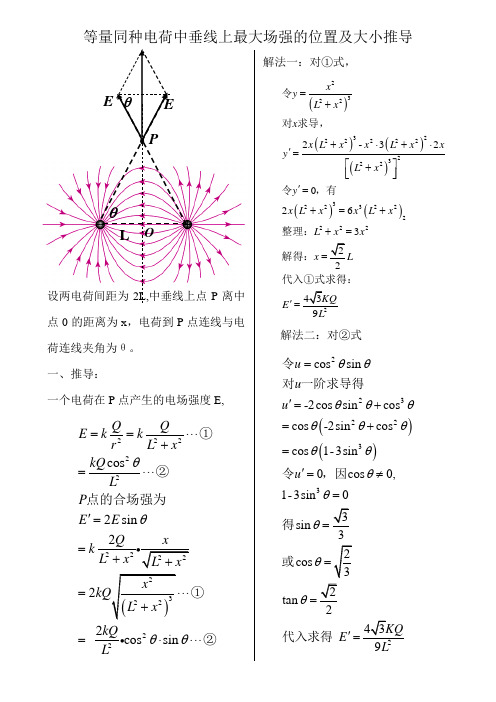
等量同种电荷中垂线上最大场强的位置及大小推导设两电荷间距为2L,中垂线上点P 离中点0的距离为x ,电荷到P 点连线与电荷连线夹角为θ。
一、推导:一个电荷在P 点产生的电场强度E,()222222222232222cos 2sin 222 cos sin Q Q E k k r L x kQ LP E E Q x kL x L x x kQL x kQLθθθθ==⋅⋅⋅+=⋅⋅⋅'==++=⋅⋅⋅+=⋅⋅⋅⋅①②点的合场强为①②解法一:对①式,()()()()()()232232222222322322322222222-32026322439x y L x x x L x x L x xy L x y x L x x L x L x x x L KQ E L =++⋅+⋅'=⎡⎤+⎢⎥⎣⎦'=+=++=='=令对求导,令,有整理:解得:代入①式求得:解法二:对②式()()22322332cos sin -2cos sin cos cos -2sin cos cos 1-3sin 0cos 0,1-3sin 03sin 32cos 32tan 2439u u u u KQ E L θθθθθθθθθθθθθθθ='=+=+='=≠===='=令对一阶求导得令,因得或代入求得OPθθEE L解法三:对②式, ()()()222222222223222233223cos sin 0.cos cos sin 1cos cos 2sin 2cos cos 2sin 22cos cos 2sin 3cos 2sin 3a b c abc a b c a b c a b u c ab u u c u θθθθθθθθθθθθθθθθθ=≥=⋅⋅=⋅⋅⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭++=⎛⎫⋅⋅≤ ⎪⎝⎭==++≥++≥++==由不等式性质即若一定,时令,,最为锐角,变式 因为定值当,大时31242327⎛⎫⋅= ⎪⎝⎭则场强最大值222 9kQ E uL L '===二、问题的结论及意义1.对相距为2L 等量同种电荷Q 连线的中垂线上,离连线中点距离为2L 的点场强最大.且最大值为E=2.对相距为L 的等量同种电荷Q 连线的的点场强最大,3.在两点电荷电量一定时.两点电荷的距离越近(L 越小),场强最大的点离它们连线的中点越近,场强的最大值却越大。
两个正点电荷中垂线的场强最大值位置

两个正点电荷中垂线的场强最大值位置1. 引言在电学领域中,电场是一个重要的概念,它描述了空间中发生的电荷之间相互作用的力场。
在电场中,对于点电荷或者离散电荷分布,我们可以通过电场强度来描述电场的性质。
在研究电场时,我们经常会遇到两个电荷之间的相互作用问题。
本文将围绕着两个正点电荷中垂线的场强最大值位置展开讨论。
2. 问题描述假设空间中存在两个电荷 q1 和 q2,它们分别位于坐标(0, a)和(0, -a)处,我们希望找到位于中垂线上的某一点 P,使得在点 P 处的电场强度达到最大值。
我们需要找到这一最大值位置的具体坐标。
3. 解决思路为了解决这个问题,我们可以利用电场叠加原理和电场强度的计算公式,通过数学方法求解。
首先我们需要分别计算 q1 和 q2 对点 P 产生的电场强度,然后将两者叠加得到最终的电场强度。
我们需要通过微积分的方法,找到电场强度最大值对应的点P 的坐标。
在这个过程中,我们需要使用坐标系和向量等数学工具。
4. 计算过程我们需要利用库仑定律计算电场强度。
对于点电荷 q1 和 q2,它们分别产生的电场强度可以表示为:E1 = k * q1 / r1^2E2 = k * q2 / r2^2其中,k 为库仑常数,r1 和 r2 分别为点 P 到 q1 和 q2 的距离。
叠加得到点 P 处的总电场强度 E:E = E1 + E2 = k * q1 / r1^2 + k * q2 / r2^2我们需要求解 E 对坐标 P 的偏导数,并令其为零,从而得到最大值的位置。
假设点 P 的坐标为 (x, y),那么 r1 和 r2 分别为 (x, a-y) 和 (x, -a-y)。
将 E 对 x 和 y 求偏导,令偏导数为零,我们可以得到方程组:dE/dx = 0dE/dy = 0通过解这个方程组,我们可以求得最大值位置点 P 的具体坐标。
5. 结论经过以上的计算过程,我们可以得到最大值位置点 P 的坐标。
两个点电荷在其连线及中垂线上产生的场强 电势(有静心绘制的示意图)

电势电势能电势差场强之间的关系场强(矢量)——对应的是力;电势(标量)——对应的是能;两者通过力做功——造成能量变化,而联系在一起;-------------电场线与场强的关系:电场线越密的地方表示场强越大,电场线上每点的切线方向表示该点的场强方向。
电场线与电势的关系:沿着电场线方向,电势越来越低。
电场线与等势面的关系:电场线越密的地方等势面也越密,电场线与通过该处的等势面垂直。
场强数值与电势数值无直接关系:场强大(或小)的地方电势不一定大(或小),零电势可人为选取,而场强是否为零则由电场本身决定。
从电势和电势能的关系来看:ε=Uq由于通常规定无穷远处的电势为零,正的场电荷电场中的各点电势都为正值,负的场电荷的电场中的各点电势都为负值。
这一点与检验电荷的电性和电量无关。
这样,我们知道:ε=Uq1)正的场源电荷电场中:U>0,负检验电荷在场中,电量为负值,因此它的电势能为负值;正检验电荷在场中,电量为正值,因此它的电势能为正值;2)负的场源电荷电场中:U<0,负检验电荷在场中,电量为负值,因此它的电势能为正值;正检验电荷在场中,电量为正值,因此它的电势能为负值;从电势能的特点来看,正电荷在正电荷的电场中电势能为正值,负电荷在负电荷的电场中电势能也为正值,同种电荷之间为斥力的作用,其势能为斥力势能,斥力势能大于零,相当于若规定地球上的海平面为重力势能的零点,物体在海拔高于海平面处(高山)的重力势能则为正值一样;另一方面,正电荷在负电荷的电场中电势能为负值,负电荷在正电荷电场中电势能也为负值,异种电荷之间为引力的作用,其势能为引力势能,引力势能小于零,相当于若规定地球上的海平面为重力势能的零点,物体在海拔低于海平面处(盆地)的重力势能则为负值一样。
二、电势差。
电场中两点间的电势的差值叫做电势差,即:UAB =UA-UB,UBA=UB-UA,在电场中A、B两点间移动电荷时,电场力的功等于电量q和这两点间的电势差UAB 的乘积。
用初等数学方法求等量同种电荷中垂线上电场强度的极值

(
再 恒等 变换 成为
一
) 号
令 : ( 冬 ) ,
在 静 电场这 一 章 的练 习题 中常 常 能见 到 这 一 道题 目. 众所周 知, 等 量 同种 电荷 连 线 中垂 线 上 , 从 垂 足到 无 限远 , 电场 强 度 是先 增 大后 减 小 , 存 在 着一个 极 大值 . 要 正确 解 答 这道 习题 , 就 必须 解 出
上 的两 点 , O A < OB, 用
、 、 、
2 . 2 用 初 等数学 方法 求解 先 对 函数 E一
Q
・
求极值. 恒 等 变 换
分 别 表 示
P
O
图 1
成 为
E 一
A、 B 两 点 的 场 强 和 电
是 Q
势, 则 ( A)E A一定 大于 E , 咖 一 定大 于 B . ( B ) 不 一定 大于 E , 一 定大 于 . ( C )E 一 定 大于 Ee , 不 一定 大于 . ( D)E 不 一定 大于 E , 似 不 一定 大于 B .
极值 点 的位置 .
2 利 用 初 等 数 学 方 法 求 极 值
( 基+ 拳 ) 号 ,
。
根 据均值 不 等式n +6 +c ≥3、 3 / 口 D c J 尿埋 得
≥3
2 x7 2 x  ̄ % /
匹
3 d号
一
,
2 . 1 求 出 函数 式 设两 个 电荷 的 电荷量 均 为 Q, 连 线长 度 为 2 d,
动 代 替 质 点 系 的运 动 时 , 要 考 虑 质 点 系相 对 于质 心 的 动 能 . 关键 词 :质 心 等 效 法 ; 相对动 能
等量同种电荷中垂线上的场强最值位置探讨及迁移

等量同种电荷中垂线上的场强最值位置探讨及迁移作者:肖玲来源:《数码设计》2019年第14期摘要:本文主要介绍等量同种电荷中垂线场强的最大值的基础上,具体确定最值的位置。
介绍对场强表达式最值的三种求解方法,从定性到定量。
此模型,还可迁移到均匀带电圆环中轴线场强的分析上,帮助学生拓展思维。
关键词:等量同种电荷;场强;最值点;角度中图分类号:G634.7 文献标识码:A 文章编号:1672-9129(2019)14-0043-01Abstract:in this paper, we mainly introduce the maximum value of vertical field intensity in the same charge, and specify the position of the maximum value. This paper introduces threemethods of solving the maximum value of field strength expression, from qualitative to quantitative. This model can also be transferred to the analysis of the field strength of the central axis of the uniformly charged ring, to help students expand their thinking.Key words:the same amount of charge field intensity maximum point Angle电场历来是高中物理的难点,也是历年高考的必考点。
从点电荷形成的电场,到等量同种电荷形成的电场,等量异种电荷形成的电场。
这些基本电场,我们必须得弄清场强的大小和方向,电势的变化等等。
等量同种电荷中垂线上最大场强位置的推导

等量同种电荷中垂线上最大场强的位置及大小推导设两电荷间距为2L,中垂线上点P 离中点0的距离为x ,电荷到P 点连线与电荷连线夹角为θ。
一、推导:一个电荷在P 点产生的电场强度E,()222222222232222cos 2sin 222cos sin Q Q E k k r L x kQ LP E E Q kL x L x x kQ L x kQ Lθθθθ==⋅⋅⋅+=⋅⋅⋅'==++=⋅⋅⋅+=⋅⋅⋅⋅①②点的合场强为①②解法一:对①式,()()()()()()232232222222322322322222222-32026322439x y L x x x L x x L x xy L x y x L x x L x L x x x L KQ E L =++⋅+⋅'=⎡⎤+⎢⎥⎣⎦'=+=++=='=令对求导,令,有整理:解得:代入①式求得:解法二:对②式OPθ θEEL二、问题的结论及意义1.对相距为2L等量同种电荷Q连线的中垂线上,离连线中点距离为L的点2场强最大.且最大值为E=2.对相距为L的等量同种电荷Q连线的的点场强最大,3.在两点电荷电量一定时.两点电荷的距离越近(L越小),场强最大的点离它们连线的中点越近,场强的最大值却越大。
4场强最大的点与其中一个点电荷的连线与两点电荷的连线的夹角的正切值为tan。
等量同种电荷中垂线上最大场强位置的推导

等量同种电荷中垂线上最大场强的位置及大小推导设两电荷间距为2L,中垂线上点P 离中点0的距离为x ,电荷到P 点连线与电荷连线夹角为θ。
一、推导:一个电荷在P 点产生的电场强度E,()222222222232222cos 2sin 222 cos sin Q Q E k k r L x kQ LP E E Q x kL x L x x kQL x kQLθθθθ==⋅⋅⋅+=⋅⋅⋅'==++=⋅⋅⋅+=⋅⋅⋅⋅①②点的合场强为①②解法一:对①式,()()()()()()232232222222322322322222222-32026322439x y L x x x L x x L x xy L x y x L x x L x L x x x L KQ E L =++⋅+⋅'=⎡⎤+⎢⎥⎣⎦'=+=++=='=令对求导,令,有整理:解得:代入①式求得:解法二:对②式()()22322332cos sin -2cos sin cos cos -2sin cos cos 1-3sin 0cos 0,1-3sin 03sin 32cos 32tan 2439u u u u KQ E L θθθθθθθθθθθθθθθ='=+=+='=≠===='=令对一阶求导得令,因得或代入求得OPθEEL解法三:对②式, ()()()222222222223222233223cos sin 0.cos cos sin 1cos cos 2sin 2cos cos 2sin 22cos cos 2sin 3cos 2sin 3a b c abc a b c a b c a b u c ab u u c u θθθθθθθθθθθθθθθθθ=≥=⋅⋅=⋅⋅⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭++=⎛⎫⋅⋅≤ ⎪⎝⎭==++≥++≥++==由不等式性质即若一定,时令,,最为锐角,变式 因为定值当,大时31242327⎛⎫⋅= ⎪⎝⎭则场强最大值222 9kQ E uL L '===二、问题的结论及意义1.对相距为2L 等量同种电荷Q 连线的中垂线上,离连线中点距离为2L 的点场强最大.且最大值为E=2.对相距为L 的等量同种电荷Q 连线的的点场强最大,3.在两点电荷电量一定时.两点电荷的距离越近(L 越小),场强最大的点离它们连线的中点越近,场强的最大值却越大。
等量同种电荷中垂线场强最大值

等量同种电荷中垂线场强最大值等量同种电荷中垂线场强最大值1. 引言在物理学中,我们经常会遇到电荷与电场的相关问题。
其中,等量同种电荷中垂线场强的最大值是一个经典而又深刻的问题,是我们理解电场分布规律的重要例子之一。
在本文中,我们将从简单的电荷排列开始,逐步深入探讨垂线场强最大值的存在与计算,并结合实际情境加深理解。
2. 等量同种电荷排列让我们考虑最简单的情况:两个等量同种电荷在空间中的排列。
假设它们分别为正电荷 q,距离为 d。
我们希望找到一个位置,使得在这个位置上的垂线场强达到最大值。
3. 垂线场强的计算根据库仑定律,两个电荷之间的电场强度与它们之间的距离成反比,与电荷的量成正比。
如果我们沿着两个电荷之间的连线方向移动,垂线场强会随着距离的变化而变化。
我们可以通过对电场强度的数学表达式进行求导,找到使得场强达到最大值的位置。
4. 计算过程在这里,我们可以借助高等数学中的极值问题的知识,对电场强度进行求导,找到使得导数为 0 的位置。
在这个位置上,垂线场强将达到最大值。
5. 深入探讨接下来,我们将考虑更复杂的情况,比如三个或多个等量同种电荷的排列。
在这种情况下,我们需要利用更高级的数学工具,比如矢量分析和多元函数的极值求解。
6. 实际情境应用让我们考虑一个实际情境的应用问题:电荷在导体棒上的分布。
当我们知道导体棒上的电荷分布情况时,我们可以通过类似的方法,找到垂线场强的最大值位置。
这样的问题不仅涉及到理论知识,还可以对物理实验和工程应用产生重要意义。
7. 总结与展望通过本文的讨论,我们深入理解了等量同种电荷中垂线场强最大值问题的存在与求解方法。
我们也意识到这个问题背后的数学和物理知识的重要性。
在未来的学习和研究中,我们可以更加灵活地运用这些知识,解决更加复杂和实际的问题。
8. 个人观点对我而言,通过深入研究等量同种电荷排列的垂线场强最大值问题,我对电场分布规律有了更加深刻的理解。
我相信在今后的学习和工作中,这些知识会给我带来更多启发和帮助。
