等量同种电荷中垂线上最大场强位置的推导.doc
等量同种电荷中垂线上最大场强位置的推导
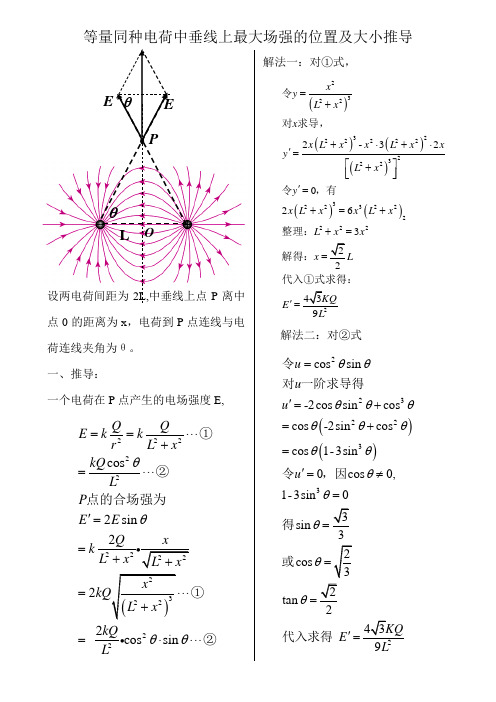
等量同种电荷中垂线上最大场强的位置及大小推导设两电荷间距为2L,中垂线上点P 离中点0的距离为x ,电荷到P 点连线与电荷连线夹角为θ。
一、推导:一个电荷在P 点产生的电场强度E,()222222222232222cos 2sin 222 cos sin Q Q E k k r L x kQ LP E E Q x kL x L x x kQL x kQLθθθθ==⋅⋅⋅+=⋅⋅⋅'==++=⋅⋅⋅+=⋅⋅⋅⋅①②点的合场强为①②解法一:对①式,()()()()()()232232222222322322322222222-32026322439x y L x x x L x x L x xy L x y x L x x L x L x x x L KQ E L =++⋅+⋅'=⎡⎤+⎢⎥⎣⎦'=+=++=='=令对求导,令,有整理:解得:代入①式求得:解法二:对②式()()22322332cos sin -2cos sin cos cos -2sin cos cos 1-3sin 0cos 0,1-3sin 03sin 32cos 32tan 2439u u u u KQ E L θθθθθθθθθθθθθθθ='=+=+='=≠===='=令对一阶求导得令,因得或代入求得OPθθEE L解法三:对②式, ()()()222222222223222233223cos sin 0.cos cos sin 1cos cos 2sin 2cos cos 2sin 22cos cos 2sin 3cos 2sin 3a b c abc a b c a b c a b u c ab u u c u θθθθθθθθθθθθθθθθθ=≥=⋅⋅=⋅⋅⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭++=⎛⎫⋅⋅≤ ⎪⎝⎭==++≥++≥++==由不等式性质即若一定,时令,,最为锐角,变式 因为定值当,大时31242327⎛⎫⋅= ⎪⎝⎭则场强最大值222 9kQ E uL L '===二、问题的结论及意义1.对相距为2L 等量同种电荷Q 连线的中垂线上,离连线中点距离为2L 的点场强最大.且最大值为E=2.对相距为L 的等量同种电荷Q 连线的的点场强最大,3.在两点电荷电量一定时.两点电荷的距离越近(L 越小),场强最大的点离它们连线的中点越近,场强的最大值却越大。
两等量点电荷的场强、电势、电势能的情况分析

两等量点电荷连线及中垂线上的场强、电势和电势能的情况分析1.等量同种电荷(1)两点电荷的连线上分析:在其连线上的中点,由于Q 相等,r相等,即E 大小相等,而两点电荷在的场强方向相反,故合场强为零,由||||212212r Q k r Q k E E E -=-=知,从中点往两边合场强增大,且关于中点对称。
(2)两点电荷的中垂线上分析:中垂线上的某点的场强由两点电荷分别在该点的场强叠加而成。
由于中垂线上的点到线两端的距离相等,由2rQ k E =知|E 1|=|E 2|,即大小相等,方向如图2所示:把E 1、E 2进行合成,故合场强E 如图所示。
所以从中垂线上中点往两边场强先是由零增大,但由2r Q k E =可知。
r 越大,E 减小,所以合场强又开始减小。
2.等量异种电荷(1)两点电荷的连线上分析:可根据电场线的疏密直接知中点最稀疏,故中点场强最小,往两边越密场强越大。
方向从正点荷指向负电荷。
(2)两点电荷的中垂线上分析:把正点荷、负点荷在中垂线上某点场强进行合成,合场强方向在连线上且由正电荷指向负电荷。
当A 点离中垂线中点越远,E 1、E 2大小越小,且夹角越大,所以合场强越小,又因为两边对称,可以中垂线上从中点经两边场强减小,方向与两点电荷的连线平行且由正电荷指向负电荷。
1.正电核电场线向外发散,负电荷电场线向内收缩,等势线总是和电场线垂直,在同一等势线上移动电荷,电场力不做功;2.电场力做正功,电势能减少,动能增加;电场力做负功,电势能增加,动能减少(不分正负电荷,通用)3.沿电场线方向,电势降落;沿电场线方向,电势降落最快。
等量同种电荷中垂线上的场强最值位置探讨及迁移

等量同种电荷中垂线上的场强最值位置探讨及迁移作者:肖玲来源:《数码设计》2019年第14期摘要:本文主要介绍等量同种电荷中垂线场强的最大值的基础上,具体确定最值的位置。
介绍对场强表达式最值的三种求解方法,从定性到定量。
此模型,还可迁移到均匀带电圆环中轴线场强的分析上,帮助学生拓展思维。
关键词:等量同种电荷;场强;最值点;角度中图分类号:G634.7 文献标识码:A 文章编号:1672-9129(2019)14-0043-01Abstract:in this paper, we mainly introduce the maximum value of vertical field intensity in the same charge, and specify the position of the maximum value. This paper introduces threemethods of solving the maximum value of field strength expression, from qualitative to quantitative. This model can also be transferred to the analysis of the field strength of the central axis of the uniformly charged ring, to help students expand their thinking.Key words:the same amount of charge field intensity maximum point Angle电场历来是高中物理的难点,也是历年高考的必考点。
从点电荷形成的电场,到等量同种电荷形成的电场,等量异种电荷形成的电场。
这些基本电场,我们必须得弄清场强的大小和方向,电势的变化等等。
等量同种电荷中垂线上最大场强位置的推导

等量同种电荷中垂线上最大场强的位置及大小推导设两电荷间距为2L,中垂线上点P 离中点0的距离为x ,电荷到P 点连线与电荷连线夹角为θ。
一、推导:一个电荷在P 点产生的电场强度E,()222222222232222cos 2sin 222cos sin Q Q E k k r L x kQ LP E E Q kL x L x x kQ L x kQ Lθθθθ==⋅⋅⋅+=⋅⋅⋅'==++=⋅⋅⋅+=⋅⋅⋅⋅①②点的合场强为①②解法一:对①式,()()()()()()232232222222322322322222222-32026322439x y L x x x L x x L x xy L x y x L x x L x L x x x L KQ E L =++⋅+⋅'=⎡⎤+⎢⎥⎣⎦'=+=++=='=令对求导,令,有整理:解得:代入①式求得:解法二:对②式OPθ θEEL二、问题的结论及意义1.对相距为2L等量同种电荷Q连线的中垂线上,离连线中点距离为L的点2场强最大.且最大值为E=2.对相距为L的等量同种电荷Q连线的的点场强最大,3.在两点电荷电量一定时.两点电荷的距离越近(L越小),场强最大的点离它们连线的中点越近,场强的最大值却越大。
4场强最大的点与其中一个点电荷的连线与两点电荷的连线的夹角的正切值为tan。
等量同种电荷中垂线上最大场强位置的推导

等量同种电荷中垂线上最大场强的位置及大小推导设两电荷间距为2L,中垂线上点P 离中点0的距离为x ,电荷到P 点连线与电荷连线夹角为θ。
一、推导:一个电荷在P 点产生的电场强度E,()222222222232222cos 2sin 222 cos sin Q Q E k k r L x kQ LP E E Q x kL x L x x kQL x kQLθθθθ==⋅⋅⋅+=⋅⋅⋅'==++=⋅⋅⋅+=⋅⋅⋅⋅①②点的合场强为①②解法一:对①式,()()()()()()232232222222322322322222222-32026322439x y L x x x L x x L x xy L x y x L x x L x L x x x L KQ E L =++⋅+⋅'=⎡⎤+⎢⎥⎣⎦'=+=++=='=令对求导,令,有整理:解得:代入①式求得:解法二:对②式()()22322332cos sin -2cos sin cos cos -2sin cos cos 1-3sin 0cos 0,1-3sin 03sin 32cos 32tan 2439u u u u KQ E L θθθθθθθθθθθθθθθ='=+=+='=≠===='=令对一阶求导得令,因得或代入求得OPθEEL解法三:对②式, ()()()222222222223222233223cos sin 0.cos cos sin 1cos cos 2sin 2cos cos 2sin 22cos cos 2sin 3cos 2sin 3a b c abc a b c a b c a b u c ab u u c u θθθθθθθθθθθθθθθθθ=≥=⋅⋅=⋅⋅⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭++=⎛⎫⋅⋅≤ ⎪⎝⎭==++≥++≥++==由不等式性质即若一定,时令,,最为锐角,变式 因为定值当,大时31242327⎛⎫⋅= ⎪⎝⎭则场强最大值222 9kQ E uL L '===二、问题的结论及意义1.对相距为2L 等量同种电荷Q 连线的中垂线上,离连线中点距离为2L 的点场强最大.且最大值为E=2.对相距为L 的等量同种电荷Q 连线的的点场强最大,3.在两点电荷电量一定时.两点电荷的距离越近(L 越小),场强最大的点离它们连线的中点越近,场强的最大值却越大。
等量同种电荷中垂线场强变化

等量同种电荷中垂线场强变化电荷分布在空间中构成了电场,是许多重要的物理现象的基础。
电荷的分布方式决定了电场的形式,其中最常见的是等量同种电荷的电场。
等量同种电荷的电场的特征是垂线的,即随着电荷间距的增加,电场强度也随之减小。
如果想了解电荷分布在空间中构成的电场强度如何变化,可以从等量同种电荷中垂线场强变化这一概念入手。
等量同种电荷垂线场强变化指的是,当两个等量同种电荷之间的距离变化时,电场强度也会相应地发生变化。
电场强度变化主要依赖于两个因素:一是电荷之间的距离;另一个是正负电荷之间的属性差异。
一般来说,当电荷间的距离变化时,电场的变化会存在指数衰减趋势。
另外,当正负电荷属性差异越大时,则电场强度也会变化得更明显。
在等量同种电荷中,电荷分布几何形状有很大的影响。
比如,当电荷排成线时,它们之间的距离是固定的,这样在垂线场强变化的规律是最为简单的,只有一个系数的影响;如果电荷形成平面,则它们之间的距离是不同的,这样则需要考虑距离的变化,此时的场强变化规律也比较复杂。
同样,如果电荷的分布是空间的,电场强度的变化还会受到距离的倒数的影响,而且要考虑向量的叠加,电场强度变化规律会非常复杂。
等量同种电荷垂线场强变化不仅受到电荷本身特性的影响,而且还受到其他力的影响,比如电子旋转等。
在实际应用中,电子可以在不同的力场中旋转,这样会使得电子受到另一个力的影响,同步导致电场强度的变化。
等量同种电荷垂线场强变化的概念,由来已久,可以说是电动力学的基础理论之一。
这一理论在实际工程应用中占有很重要的地位,特别是在电磁学方面,它可以被用来计算电荷之间的电场强度,帮助我们理解和掌握空间电场的分布状况,从而更有效地利用电荷在空间中的变化。
总之,等量同种电荷中垂线场强变化是一个重要的理论概念,由它可以帮助我们更好地了解电荷在空间中分布的变化,进而更好地利用电荷的变化,为我们的实际应用打下坚实的基础。
等量同种电荷中垂线上的场强最值位置探讨及迁移
DOI:10.19551/j.cnki.issn1672-9129.2019.14.039等量同种电荷中垂线上的场强最值位置探讨及迁移肖 玲(武汉市东西湖区吴家山中学 湖北 武汉 430040)摘要:本文主要介绍等量同种电荷中垂线场强的最大值的基础上,具体确定最值的位置。
介绍对场强表达式最值的三种求解方法,从定性到定量。
此模型,还可迁移到均匀带电圆环中轴线场强的分析上,帮助学生拓展思维。
关键词:等量同种电荷;场强;最值点;角度中图分类号:G634.7 文献标识码:A 文章编号:1672-9129(2019)14-0043-01Abstract:inthispaper,wemainlyintroducethemaximumvalueofverticalfieldintensityinthesamecharge,andspecifythepositionofthemaximumvalue.Thispaperintroducesthreemethodsofsolvingthemaximumvalueoffieldstrengthexpression,fromqualitativetoquantitative.Thismodelcanalsobetransferredtotheanalysisofthefieldstrengthofthecentralaxisoftheuniformlychargedring,tohelpstudentsexpandtheirthinking.Keywords:thesameamountofchargefieldintensitymaximumpointAngle 电场历来是高中物理的难点,也是历年高考的必考点。
从点电荷形成的电场,到等量同种电荷形成的电场,等量异种电荷形成的电场。
这些基本电场,我们必须得弄清场强的大小和方向,电势的变化等等。
纵观电场的高考试题,对等量同种电荷的连线和中垂线上的考点最多。
等量同种点电荷连线的中垂线上的哪一点的场强最大
龙源期刊网
等量同种点电荷连线的中垂线上的哪一点的场强最大
作者:牛刚张守中
来源:《新课程·教师》2010年第07期
一、问题的提出
高中物理教学中,在进行点电荷产生的电场教学时都要分析两个等量同种电荷产生从电场,既要分析讲解其电场线分布情况,又要分析讲解等势面分布情况,一般都是利用叠加原理进行分析讲解的。
其中的一些结论是:(1)在两点电荷连线上越靠近点电荷场强越大,两点电荷连线的中点处场强为零;(2)离两点电荷无穷远处场强也趋于零;(3)在两点电荷连线的中垂线上,从两者连线的中点向外,场强先由零逐渐增大,然后又会逐渐减小,到无穷远处趋于零。
在进行上述结论(3)时,学生可能会问:在两点电荷连线的中垂线上哪一点的场强最大?作为执教者自己可能也会产生这个问题。
二、问题的规整
根据上述问题,我们提设如下的问题:
如图,带电量均为+Q的A、B两个点电荷之间的距离为2L,它们连线的中点为O,并以O点作为坐标原点建立坐标轴y,试求:在它们连线的中垂线上,y取何值时场强E最大。
三、问题的解决
我们在y轴上取一点P,可以根据点电荷的场强公式,应用叠加原理及正交分解法,可得到P 点的场强的表达式。
等量同种电荷的中垂线上的电场强度分布——吴军
2015 年 第 6 期
物理通报
竞赛与物理专题研修
EM 方向如图3所示.
1.1 定性分析其场强大小的变化
当 M 位于A,B 连线中点O 时,θ=0,则EM =0; 当 M 位于A,B 连线的中垂线上且距O 点无穷远处
时,θ→90°,则EM →0;当 M 位于中垂线上其他任意 位置时,则 EM ≠0. 1.2 利用均值不等式定量分析
2kRQ2 cos2θsinθ
(6)
由 此 可 知 ,均 匀 带 电 圆 环 的 圆 心 处 场 强 为 零 ,轴
线上其他地方的电场 方 向 沿 轴 线 向 外,由 环 心 向 外
延伸场强先变大后变小.
【例4】(2014年高考江苏 卷)如 图 8 所 示,一 圆
环上均匀分布 着 正 电 荷,x 轴 垂 直 于 环 面 且 过 圆 心
— 62 —
2015 10
解析:带正电的 圆 环 轴 线 上 电 场 方 向 从 圆 心 O 沿 轴 线 向 外 ,电 子 在 圆 环 的 左 侧 所 受 电 场 力 向 右 ,电 子 做 加 速 运 动 ;电 子 在 圆 环 的 右 侧 所 受 电 场 力 向 左 , 电子做减速运动.从圆心O 向外场强先变大后变小, 若最大值在A 点右侧则电子从A 向O 运动的加速度 先增大后减小,故选项 A 正确.若最大值在 A 点的
3 程守洙,江之永.普通物理学·第二册(第五版).北京:高 等 教 育 出 版 社 ,1998.29
4 梁灿彬,秦光戎,梁竹健.普通物理学教程·电磁学(第二 版 ).北 京 :高 等 教 育 出 版 社 ,2004.26
两根无限长均匀带电直导线的电场线方程的两种推导方法
姜付锦
(武汉市黄陂区第一中学 湖北 武汉 430300) (收稿日期:2014 12 15)
等量同种(异种)电荷电场强度及电势规律
在连线上:中点电势最低,由中点向两边电势升 高,关于中点对称。
在中垂线上:从连线中点到无穷远电势逐渐减小, 无穷远处电势为0,电势关于连线中点对称。
等量同种(异种)点电荷在空间的场强分布比较复 杂,但在两条线(点电荷连线及其中垂线)上仍有其 规律性。
一、等量异种电荷
x
A
G
O
B
1、 两电荷连线上
图1
在两电荷连线中点O处场强最小,从O点向两侧逐
渐增大,数值关于O点对称。
证明:
EG= EA+ EB=
∵x+(L-x)等于定值L, ∴当x=(L-x),即x=
时,x与 (L-x)乘积最大, EG有最小值
2、 中垂线上 距O点越远EH越小,两侧电 场强度数值关于O点对称。
A
EA Hθ x EB
O
EH B
L 图2
EH=
2k Q c L2x2
os 2kQ
L2x2Βιβλιοθήκη 222 kQL
L2x2 2
3
L2x22 2
在连线上:由正电荷到负电荷电势逐渐降低。
在中垂线上:若规定无穷远处电势为0,则中垂 线上各点电势相等且为0。
二、等量同种电荷 1、在电荷连线上
从O点向两侧逐渐增大,数值关于O点对称,方 向相反。
N点电场强度大小:EN = ∴当x= 时,EN =0,即在两电荷连线中点O处
场强最小
2、中垂线上
合电场强度的大小随着距O点 的距离增大,先从零增大到 最大,然后逐渐减小。
由极限分析法易得:在O点处,E =0;在距O点 无限远处,E =0。说明中间某位置有极大值
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
等量同种电荷中垂线上最大场强的位置及大小推导
设两电荷间距为2L,中垂线上点P 离中点0的距离为x ,电荷到P 点连线与电荷连线夹角为θ。
一、推导:
一个电荷在P 点产生的电场强度E,
()
222
22
22
222
3
2
222cos 2sin 222 cos sin Q Q E k k r L x kQ L
P E E Q x k
L x L x x kQ
L x kQ
L
θθθθ==⋅⋅⋅+=⋅⋅⋅'==++=⋅⋅⋅+=⋅⋅⋅⋅①②点的合场强为①
②
解法一:对①式,
()
()()()()()2
3
223
2
222222
3223
223222
2
2
2
2
2-32026322
439x y L x x x L x x L x x
y L x y x L x x L x L x x x L KQ E L =
++⋅+⋅'=
⎡⎤+⎢⎥⎣⎦
'=+=++=='=
令对求导,令,有
整理:解得:代入①式求得:
解法二:对②式
()()22322332
cos sin -2cos sin cos cos -2sin cos cos 1-3sin 0cos 0,1-3sin 03
sin 32
cos 32
tan 2439u u u u KQ E L θθθθθθθθθθθθθθθ='=+=+='=≠==
=
=
'=
令对一阶求导得令,因得或代入求得
O
P
θ
θ
E
E L
解法三:对②式, (
)()()222222222223
222233223cos sin 0.cos cos sin 1
cos cos 2sin 2
cos cos 2sin 22cos cos 2sin 3cos 2sin 3a b c abc a b c a b c a b u c ab u u c u θθθθθθθθθθθθθθθθθ=≥=⋅⋅=⋅⋅⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭++=⎛⎫⋅⋅≤ ⎪
⎝⎭
==
++≥++≥++==由不等式性质即若一定,时令,,最为锐角,变式 因为定值当,大时3
1242327
⎛⎫⋅= ⎪⎝⎭则场强最大值
22
2 9kQ E u
L L '===
二、问题的结论及意义
1.对相距为2L 等量同种电荷Q 连线的
中垂线上,离连线中点距离为2
L 的点场强最大.且最大值为E=
2.对相距为L 的等量同种电荷Q 连线的
的点场强最大,
3.在两点电荷电量一定时.两点电荷的距离越近(L 越小),场强最大的点离它们连线的中点越近,场强的最大值却越大。
4场强最大的点与其中一个点电荷的连线与两点电荷的连线的夹角的正切值
为tan =
θ。
