中南大学硕士研究生入学结构力学考试试题
结构力学试题与答案汇总(完整版)
院(系) 学号 姓名 .密封线内不要答题 密封……………………………………………………………………………………………………………………………………………………结构力学试题答案汇总结构力学课程试题 ( B )卷考 试 成 绩题号 一二三四成绩得分一、选择题(每小题3分,共18分)1. 图 示 体 系 的 几 何 组 成 为 : ( ) A. 几 何 不 变 , 无 多 余 联 系 ; B. 几 何 不 变 , 有 多 余 联 系 ; C. 瞬变 ; D. 常 变 。
2. 静 定 结 构 在 支 座 移 动 时 , 会 产 生 : ( )A. 内 力 ;B. 应 力 ;C. 刚 体 位 移 ;D. 变 形 。
3. 在 径 向 均 布 荷 载 作 用 下 , 三 铰 拱 的 合 理 轴 线 为: ( )A .圆 弧 线 ;B .抛 物 线 ;C .悬 链 线 ;D .正 弦 曲 线 。
4. 图 示 桁 架 的 零 杆 数 目 为 : ( )A. 6;B. 7;C. 8;D. 9。
5. 图 a 结构的最后弯矩图为:()A.图 b; B.图 c ; C.图 d ; D.都不对。
6. 力法方程是沿基本未知量方向的:()A.力的平衡方程;B.位移为零方程;C.位移协调方程; D.力的平衡及位移为零方程。
二、填空题(每题3分,共9分)1.从几何组成上讲,静定和超静定结构都是_________体系,前者_________多余约束而后者_____________多余约束。
2. 图 b 是图 a 结构 ________ 截面的 _______ 影响线。
3. 图示结构 AB 杆 B 端的转动刚度为 ________, 分配系数为________, 传递系数为 _____。
三、简答题(每题5分,共10分)1.静定结构内力分析情况与杆件截面的几何性质、材料物理性质是否相关?为什么?2.影响线横坐标和纵坐标的物理意义是什么?四、计算分析题,写出主要解题步骤(4小题,共63分)1.作图示体系的几何组成分析(说明理由),并求指定杆1和2的轴力。
结构力学试题及答案大题汇总
(b)
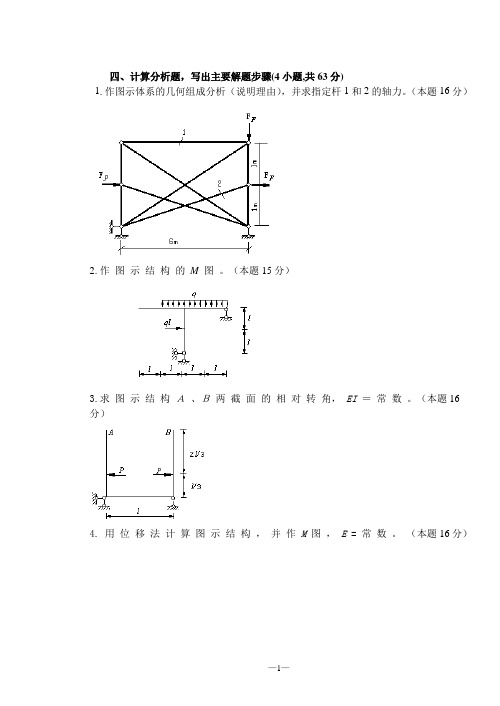
3、MEmax=∑qω=5×1/2×2/3×3=5kN·m 三、解:1、在 A 支座加单位水平力 P=1
2、作 M1 图,如图(a);作 MP 图,如图(b)
—41—
(a) 6
6
M1(m)
(b) 36 9
MP(m)
3、计算△:△=∑ω·y0/EI=(ω1y1+ω2y2)/EI
=(36×1/3×6×6×3/4+1/2×6×27×4)/EI=648/EI(
所示。 (a)
(b)
2kN·m
8kN
q
A
2EI
B
EI
C
EI
D
A
B
l
P
4m
8m
3m 3m
MFAB=-1/12·ql 2
MFBA =1/12·ql 2
A
P
B
l/2
l/2
MFAB=-3/16Pl
二、解:1、ME 的影响线(m) 2/3
2/3
2/3
2、MEmax 的最不利布置如图(a);MEmin 最不利布置如图(b); (a)
分析图示体系的几何组成。
(3 分)
五、(本大题 4 分)
根据位移法基本原理,草绘图示结构最后弯矩图形状为:
六、(本大题 6 分)
图示状态一与状态二,试证明功的互等定理对于该情况不成立。
(a)第一状态
(b)第二状态
七、(本大题 6 分)
—34—
试确定图示结构位移法基本未知量数目和基本结构。两根链杆 a 和 b 需考虑轴向变形。
(6)令
作 图,求
—20—
位移法方程是:
求得: (7)用
控制截面弯矩,作弯矩图 (左侧受拉) (右侧受拉)
中南大学《结构力学》课程作业二及参考答案

(一) 单选题1. 图(a)所示结构,杆件刚度EI常数。
用力法求解时,取图(b)所示基本系,要使力法方程中的副系数全部为零,刚x、y应满足下列哪个条件()。
(A) x a/3,y b/3;(B) x a/2,y b/2;(C) x a/3,y b/2;(D) x a/2,y b/3;参考答案:(A)2.图示(a)、(b)两结构,当A支座顺时钟发生单位角位移时,(a)、(b)两图中,与的关系为()。
(A)(B)(C)(D)参考答案:(C)3. 图示结构,在给定荷载作用下,支座反力(向右为正)和(向上为正),轴力(以拉为正)分别为()。
(A)(B)(C)参考答案: (C)4.图示对称结构受荷载作用,则D支座反力为()。
(A),方向向上;(B) ,方向向下;(C) ,方向向上;(D) ,方向向下;参考答案:(A)5.图(a)所示组合结构,取图(b)为其力法计算基本系,则,分别为()。
(A)(B)(C)(D)参考答案:(D)6. 图A图D所示结构均可作为图(a)所示结构的力法基本结构,使得力法计算最为简便的基本结构是()。
(A) A (B) B (C) C (D) D参考答案:(C)7. 图示超静定结构及其M图,要校核其正确性可采用下述哪种做法()。
点位移(A)计算E(B)计算D点水平位移及E 点竖向位移点位移(C)计算E参考答案:(BB)8. 图示超静定梁,截面的高度为h,线膨胀系数为,,。
图(a)中梁的上、下面的温度均长高,图(b)中梁上面的温度为,而梁下面的温度为,下面结论正确的是()。
(A) 图(a)、图(b)中梁的内力是一样的,只有轴力(B) 图(a)所示梁中只有轴力,图(b)所示梁中只有弯矩(C) 图(a)所示梁中有轴力和弯矩,图(b)所示梁中只有弯矩(D) 图(a)所示梁中只有轴力,图(b)所示梁中有轴力和弯矩参考答案:(A)9. 图示为结构及其力法基本系,则力法典型方程的自由项为()。
(A)参考答案:(B)10. 图示对称结构,力法求解时,未知量最少为()。
研究生入学专业课结构力学-1

研究生入学专业课结构力学-1(总分:100.00,做题时间:90分钟)一、选择题(总题数:7,分数:7.00)1.在工程中,瞬变体系不能作为结构的原因是______。
(分数:1.00)A.会发生微小位移B.约束的数量不足C.正常荷载作用下,可能产生很大内力√D.会产生较大的位移解析:2.以下关于瞬变体系的论述,正确的是______。
(分数:1.00)A.瞬变体系的总体约束数目不足,从而导致体系瞬时可变B.瞬变体系经微小位移后即成为几何不变,故可作为结构使用C.瞬变体系中必然存在多余约束√D.瞬变体系必定存在瞬铰解析:3.如图所示体系虽有3个多余约束,但为保证其几何不变,哪两根链杆是不能同时去掉的。
______(分数:1.00)A.a和eB.a和b √C.a和cD.c和e解析:[解析] 去掉a、b杆后,c、d杆组成几何瞬变部分。
4.连接三个刚片的铰结点,相当的约束个数为______。
(分数:1.00)A.2个B.3个C.4个√D.5个解析:[解析] 相当于2个单铰。
5.如图所示体系的几何组成为______。
(分数:1.00)A.几何瞬变,无多余约束B.几何不变C.几何常变D.几何瞬变,有多余约束√解析:6.欲使如图所示体系成为无多余约束的几何不变体系,则需在A端加入______。
(分数:1.00)A.固定铰支座B.固定支座√C.滑动铰支座D.定向支座解析:7.如图所示体系的几何构造性质是______。
(分数:1.00)A.常变体系B.瞬变体系C.无多余联系的几何不变体系√D.有多余联系的几何不变体系解析:[解析] 用两刚片规律分析,将中间Y形刚架看作一刚片,基础为另一刚片。
二、判断题(总题数:5,分数:5.00)8.仅用静力平衡方程即可确定全部反力和内力的体系是几何不变体系,且没有多余约束。
(分数:1.00)A.正确√B.错误解析:9.瞬变体系的计算自由度可能小于零。
(分数:1.00)A.正确√B.错误解析:10.下图中链杆1和2的交点O可视为虚铰。
结构力学练习题及答案
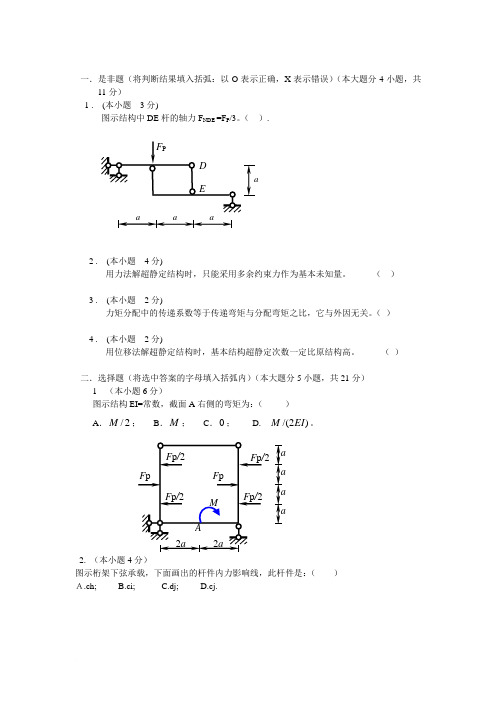
一.是非题(将判断结果填入括弧:以O 表示正确,X 表示错误)(本大题分4小题,共11分)1 . (本小题 3分)图示结构中DE 杆的轴力F NDE =F P /3。
( ).2 . (本小题 4分)用力法解超静定结构时,只能采用多余约束力作为基本未知量。
( )3 . (本小题 2分)力矩分配中的传递系数等于传递弯矩与分配弯矩之比,它与外因无关。
( )4 . (本小题 2分)用位移法解超静定结构时,基本结构超静定次数一定比原结构高。
( )二.选择题(将选中答案的字母填入括弧内)(本大题分5小题,共21分) 1 (本小题6分)图示结构EI=常数,截面A 右侧的弯矩为:( )A .2/M ;B .M ;C .0; D. )2/(EI M 。
2. (本小题4分)图示桁架下弦承载,下面画出的杆件内力影响线,此杆件是:( ) A.ch; B.ci; C.dj;D.cj.23. (本小题 4分)图a 结构的最后弯矩图为:A. 图b;B. 图c;C. 图d;D.都不对。
( )( a) (b) (c) (d)4. (本小题 4分)用图乘法求位移的必要条件之一是: A.单位荷载下的弯矩图为一直线; B.结构可分为等截面直杆段; C.所有杆件EI 为常数且相同; D.结构必须是静定的。
( ) 5. (本小题3分)图示梁A 点的竖向位移为(向下为正):( ) A.F P l 3/(24EI); B. F P l 3/(!6EI); C. 5F P l 3/(96EI); D. 5F P l 3/(48EI).三(本大题 5分)对图示体系进行几何组成分析。
F P=1四(本大题 9分)图示结构B 支座下沉4 mm ,各杆EI=2.0×105 kN ·m 2,用力法计算并作M 图。
五(本大题 11分) 用力矩分配法计算图示结构,并作M 图。
EI=常数。
六(本大题14分)已知图示结构,422.110 kN m ,10 kN/m EI q =⨯⋅=求B 点的水平位移。
中南大学研究生高等机构学考试作业题目

2012年《高等机构学》研究生考试试卷
姓名: 学号: 总分100分 成绩
图1所示为桥隧箱型梁内膜脱模机构的连杆(与侧模联接的构件)位置图,连杆上的标志线pq 在脱模前为p 1q 1,夹角α1,在脱模后为p 2q 2,夹角α2,脱模前p 1和q 1点的速度方向分别为β 和 γ;已知机架铰链A 0B 0长度为l A 0B 0,水平布置,连杆(侧模)质心为S 1,质量为M ,由液压缸驱动,其中支点C 1在连杆(侧模)上,另一支点C 0在机架上。
设坐标原点在机架铰链A 0上,各已知参数值见表1(每人一组数据)。
试计算:
1.用刚体导引机构的综合方法求A 0A 1长度、B 0B 1长度和A 1B 1长度 2.用向量环方程建立该内膜脱模机构的运动学模型并用Matlab 软件计算作出该内膜脱模机构由位置2移动至位置1时,液压缸的伸长量和两连架杆的的摆角大小。
3、用向量环方程建立该内膜脱模机构不考虑摩擦时的静力学模型,并用Matlab 软件计算作出该内膜脱模机构由位置2移动至位置1时,液压缸的驱动力和两连架杆受力的变化曲线。
(只考虑侧模重力,忽略各构件的惯性力)
图1 脱模机构的连杆位置图
A 0
B 0
1
p
2q
p 2
C 0
α2
表1 已知参数值 长度单位:mm 质量单位:kg。
中南大学土木工程学院《949结构力学》历年考研真题汇编

目 录2014年中南大学949结构力学考研真题2013年中南大学949结构力学考研真题2012年中南大学949结构力学考研真题2011年中南大学949结构力学考研真题2010年中南大学949结构力学考研真题2009年中南大学949结构力学考研真题2008年中南大学949结构力学考研真题2007年中南大学449结构力学考研真题2006年中南大学449结构力学考研真题2005年中南大学449结构力学考研真题2004年中南大学449结构力学考研真题2003年中南大学449结构力学考研真题2002年中南大学612结构力学考研真题2001年中南大学551结构力学考研真题2000年中南工业大学573结构力学考研真题2014年中南大学949结构力学考研真题料虬初页二(邮小84分,共20分)----1、用蹶炒瓣的必躁件之-是()A、B,岫做响C、所有种£7凯如相同D、博构必须珈定的2、麻'的麒、糠、质点也1!不变,下列靳辙自癞率费小:(}A、质1小,鞭J'B、醐大,剧度小C、质;f小,月艘大D、质,大林*3、下献示平面牌鞋为()'5A、几何秋且无多糊系B、几何不吸有多余取C、贱麻D、敝体系4危b是剧a中麋蚀面的勤8拂?A、B敏面B、D载面。
、B威面D、B诚面5、留秘构胸赣计算时基本未如1的敏诚少为()A、2B、3Cn.5D、6醐麟4小姗=.细(岫分,共20分)1、多自由席枸雌-翱解进行毓谶动翩—,而其相应的麒损动般林为_____2、君三段醐跨度、拱上勘碱不虹则妙肩平顶就平推加(大或小).,醐藏为_,一鹏949帏大学那婢时瞰生入精眦械姗共W,期页_-_____________________4、酬剜的期眦瓣的耿带劾.”静示娜(不计桢劾(jffm蛾为_个,坎殳麟4小鼬鼠林1S供95分)k渊示带购件a、b的内加(时)2,棚禾桀的M b、Fg F sb&的聊演并利用彩物求师荷■作肝M,的值,(2。
中南大学2020年《结构力学(下)》期末考试试卷

一、选择、填空题(共20分,每小题4分)1. 图1所示单元变形情况下所产生的六个杆端力组成了单元刚度矩阵中的第元素。
A.3列 B. 6行 C. 1列 D. 6列2. 在矩阵位移法中将单元集合成整体时应引入结构的和变形连续条件。
A.物理关系 B. 平衡条件 C. 几何关系 D. 单元的刚度性质3. 图2所示结构,不计杆件质量和轴向变形,其振动自由度是。
图1 图24.图3所示结构,只计集中质量m,弹簧刚度系数为k,则其自振动频率ω=。
图35.单自由度体系自由振动的振幅取决于。
A.初位移 B. 初速度 C. 初位移、初速度和质量D.初位移、初速度和结构自振动频率二、分析计算题(本题共50分)1. 按图4所示结构的节点、单元编号方式,作如下分析:(9分)1)以单刚子块的形式写出原始总刚子块K44,K36,K27。
2)总刚最大带宽是多少?3)缩减后总刚阶数是多少?图42.图5所示平面结构用矩阵位移法计算,求点2结点5的综合结点荷载列阵。
(13分)图53. 求图6所示梁的自振频率和主振型,已知m1=2m,m2=m,EI=常数,梁的自重不计。
(14分)两自由度结构自由振动振幅方程{(δ11m1−1ω2⁄)A1+δ12m2A2=0δ21m1A1+(δ22m2−1ω2⁄)A2=0图64.图7所示结构各杆EI=常数,P (t )=Psinθt ,θ=√3EI ml 3⁄,不计各杆质量,求其中质点1的无阻尼稳态强迫振动的振幅,并绘出结构最大动力弯矩图。
(14分)图7三、根据PF 程序的计算结果绘制图8所示结构的弯矩图(各单元的节点编号均有(i<j ,E =3×107kN/m 2 ,I =0.0128m 4, A =0.24m 2)。
(本题10分)The Terminal ForcesMember N(st) Q(st) M(st) N(en) Q(en) M(en) 1 329.76 -80.39 -65.56 -329.76 -159.61 223.992 419.55 9.80 176.33 -539.55 -169.80 272.70四、矩阵位移法上机题(20分,此题不用再作)1.作图示刚架的N F 、S F 、M 图,已知各杆截面均为矩形,柱截面宽0.5m,高0.5m, 梁截面宽0.4m,高0.5m ,各杆E=3.65×104 MPa 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中南大学硕士研究生入学结构力学考试试题
一、静定结构内力计算
1、(12分)作图示静定刚架的弯矩图。
(2006年)
1、(12分)作图示静定刚架的弯矩图。
(2005年)
1、(12分)作图示三铰刚架的弯矩图。
(2004年)
1、(13分)作图示结构的弯矩图。
(2003年)
1、(9分)作图示结构的弯矩图。
(2002年)
1、(12分)作图示结构的弯矩图。
(2001年)
1、(10分)试作图示静定结构的M图。
(2000年)
1、(10分)试作图示结构的弯矩图。
(1999年)
1、(7分)试作图示结构的弯矩M图。
(1998年)
1、(10分)作图示刚架的弯矩图。
(1997年)
二、影响线分析
2、(12分)作图示结构MEA、MCD、QF的影响线(P=1在DB段移动)。
(弯矩以下侧受拉为正)。
(2006年)
3、(12分)作图示结构M E、Q F的影响线(P=1在CD段移动)。
(M E 弯矩以左侧受拉为正)。
(2005年)
3、(12分)作图示结构M E、Q F的影响线(P=1在CD段移动)。
(弯矩以下侧受拉为正)。
(2004年)
3、(13分)作图示结构M KA、Q K左、Q K右的影响线(P=1在CD段移动)。
(2003年)
3、(10分)作图示结构中量值M K、Q F的影响线(P=1在CD段移动)。
(M E弯矩以右侧受拉为正)。
(2002年)
2、(12分)作图示多跨静定梁M B、Q B右的影响线(P=1在AG段移动)。
(2001年)
2、(12分)作图示多跨静定梁M B、Q B右的影响线(P=1在ABCDEF上移动)。
(2000年)
3、(10分)作图示多跨静定梁R A、M E、Q F的影响线(P=1在CD上移动)。
(1999年)
3、(分)作图示多跨静定梁R D、M E的影响线(P=1在ACF上移动)。
(1998年)
3、(10分)作图示结构M F、Q F的影响线(P=1在AFCDE部分移动)。
(1997年)
三、位移计算
3、(12分)求图示结构最大挠度。
EI为常数。
(2006年)
2、(10分)求图示结构C点竖向位移。
各杆EI为常数。
(2005年)
2、(12分)试求图示结构C点水平线位移。
(2004年)
2、(13分)试求图示结构C点水平线位移。
各杆EI为常数。
(2003年)
2、(9分)试求图示结构C截面的角位移。
(2002年)
2、(13分)试求图示结构A点竖向位移。
(1999年)
2、(8分)试求图示结构A点的水平位移。
(1998年)
2、(10分)求图示刚架C点的竖向线位移ΔCy。
EI为常数。
(1997年)
四、力法
4、(14分)用力法求图示结构的弯矩图,EI为常数,P=qL。
(2006年)
4、(14分)用力法求图示结构的弯矩图。
(2005年)
4、(14分)用力法求图示结构的弯矩图。
(2004年)
4、(14分)用力法求图示结构的弯矩图。
各杆EI为常数。
4、(11分)用力法求图示结构的弯矩图。
各杆EI为常数。
(2002年)
3、(12分)用力法求图示超静定结构的弯矩图。
各杆EI为常数。
(2001年)
3、(12分)用力法作图示刚架的M图。
各杆EI为常数。
(2000年)
4、(10分)用力法作图示结构的弯矩图。
各杆EI为常数。
(1999年)
4、(分)用力法求作图示结构的弯矩M图。
(1998年)
4、(10分)用力法求作图示结构的弯矩M图。
EI为常数。
(1997年)
五、位移法
5、(14分)用位移法求图示结构的弯矩图,各杆EI为常数。
(2006年)
5、(14分)用位移法求图示结构的弯矩图。
(2005年)
5、(14分)用位移法求图示结构的弯矩图。
各杆EI为常数。
(2004年)
5、(14分)用位移法求图示结构的弯矩图。
各杆EI为常数。
(2003年)
5、(11分)用位移法求图示结构的弯矩图。
各杆EI为常数。
(2002年)
4、(12分)用位移法作图示超静定刚架的弯矩图。
各杆EI为常数。
(2001年)
4、(12分)用位移法作图示刚架的M图。
各杆EI为常数。
(2000年)
5、(10分)用位移法求图示刚架的弯矩图。
各杆EI为常数。
(1999年)
5、(10分)用位移法求作图示结构的弯矩M图。
(1998年)
5、(10分)用位移法求作图示结构的弯矩M图。
(1997年)
六、矩阵位移法
6、(14分)图示平面结构用矩阵位移法计算,引入支承条件后的总体刚度矩阵为多少阶?并求结点2和8的综合结点荷载列阵。
(2006年)
6、(14分)试求图示平面结构中结点2的综合结点荷载列阵。
(2005年)
6、(12分)图示两跨两层平面刚架,用矩阵位移法求解时分为10个单元,试求:
(1)原始刚度矩阵中的子块[K44]、[K78]和[K59](用单刚子块表示);
(2)结点1的综合结点荷载列阵。
(2004年)
6、(13分)试求结点3的综合结点荷载列阵。
(2003年)
6、(10分)试求结构中结点2的综合结点荷载列阵。
(2002年)
5、(10分)试求图示结构(q=36kN/m,P=16kN,P作用于各横梁中点)用矩阵位移法求解时,
(a)结构原始刚度矩阵的阶数为多少?
(b)结点3的综合结点荷载{P3}=?(2001年)
5、(8分)求图示结构结点5的综合结点荷载列阵(P=qL,m=qL2)。
(2000年)
6、(10分)求图示结构结点5的综合结点荷载列阵(P=qL,m=qL2)。
(1999年)
6、(8分)试求图示结构中与结点3的角位移相对应的等效结点荷载(各杆长均为L,集中力作用于杆中点)。
(1998年)
6、(7分)设整体坐标下单元分块表示的单元刚度矩阵如下:
[K e]= [K ii e] [K ij e]
[K ji e] [K jj e]
(上标e为单元号)。
试写出以整体坐标系下单刚子块表示的原始刚度矩阵。
(1997年)
七、动力分析
7、(12分)图示结构,不计阻尼影响,不计杆质量。
试列出图示结构的振动微分方程(需求出方程中的系数,但不必求解方程),并求其自振频率。
(2006年)
7、(12分)图示悬臂梁有一重量G=10kN的集中质量,其上受振动荷载Psinθt作用,其中P=2kN,每分钟振动120次。
试求该梁最大竖向位移和最大负弯矩。
已知:L=4m,E=200Gpa,I=4*10-5m4。
(梁自重略去不计)。
(2005年)
7、(14分)图示结构,不计阻尼影响,不计杆质量,已知干扰力的频率θ=(EI/7ma3)1/2,试求质点的最大动位移。
各杆EI为常数。
(2004年)
7、(13分)试求图示结构的最大动弯矩图,(只计刚性杆质量,m’为刚性杆单位长度的质量),(不考虑阻尼影响)。
θ=(6EI/m’L4)1/2。
(2003年)
7、(9分)试求图示结构的自振频率,(只计刚性杆质量,m’为刚性杆单位长度的质量),(不考虑阻尼影响)。
(2002年)
6、(11分)试列出图示结构(不计杆质量)的振动微分方程(不必求解),并求其自振频率(EI为常数)。
(2001年)
6、(8分)图示结构,干扰力的频率θ=(3EI/4mL3)1/2,试求质点m 振动时的最大动挠度(EI为常数)。
(2000年)
6、(10分)试求图示结构中结点2的等效结点荷载列阵{P E2}。
(1999年)
7、(8分)求图示结构的自振频率(只计刚性杆质量,m’为刚性杆单位长度的质量)。
(1998年)
7、(10分)试求图示结构的自振频率(只计BC杆质量,m’为BC杆单位长度的质量,为一常数)。
(1997年)。
