对Tarjan算法复习总结.doc
c++中tarjan算法求割点

c++中tarjan算法求割点
摘要:
一、C++中Tarjan算法求割点简介
1.Tarjan算法的原理
2.C++中实现Tarjan算法求割点的步骤
二、C++中Tarjan算法求割点的具体实现
1.定义相关数据结构
2.初始化并处理未访问过的顶点
3.寻找割点
三、C++中Tarjan算法求割点的代码实例
1.代码展示
2.运行结果及解析
正文:
一、C++中Tarjan算法求割点简介
Tarjan算法是一种用于求解强连通分量(Strongly Connected Component,简称SCC)的算法。
它通过递归的方式,寻找一个有向图中的割点(Cut Point),即在一个强连通分量中,删除这个顶点后,原图不再保持强连通。
在C++中实现Tarjan算法求割点的过程中,需要先对给定的图进行预处理,然后遍历图中的顶点,最终找到所有的割点。
二、C++中Tarjan算法求割点的具体实现
1.定义相关数据结构
在C++中实现Tarjan算法求割点,首先需要定义一些相关的数据结构。
这里我们定义一个邻接表表示图,用一个数组vis表示顶点访问情况,用一个数组dfn表示顶点的发现时间,用一个数组low表示顶点的低度。
2.初始化并处理未访问过的顶点
遍历图中的顶点,对于未访问过的顶点,我们将其作为当前割点,并将其加入集合S中。
然后遍历与当前顶点相连的所有顶点,将它们加入集合S中,并更新它们的低度。
3.寻找割点
在遍历完所有顶点后,我们再次遍历图中的顶点,对于每个顶点,如果它的低度为1,那么它就是一个割点。
(转)全网最!详!细!tarjan算法讲解

(转)全⽹最!详!细!tarjan算法讲解全⽹最详细tarjan算法讲解,我不敢说别的。
反正其他tarjan算法讲解,我看了半天才看懂。
我写的这个,读完⼀遍,发现原来tarjan这么简单!tarjan算法,⼀个关于图的联通性的神奇算法。
基于DFS(迪法师)算法,深度优先搜索⼀张有向图。
!注意!是有向图。
根据树,堆栈,打标记等种种神(che)奇(dan)⽅法来完成剖析⼀个图的⼯作。
⽽图的联通性,就是任督⼆脉通不通。
的问题。
了解tarjan算法之前你需要知道:强连通,强连通图,强连通分量,解答树(解答树只是⼀种形式。
了解即可)不知道怎么办神奇海螺~:嘟噜噜~!强连通(strongly connected):在⼀个有向图G⾥,设两个点 a b 发现,由a有⼀条路可以⾛到b,由b⼜有⼀条路可以⾛到a,我们就叫这两个顶点(a,b)强连通。
强连通图:如果在⼀个有向图G中,每两个点都强连通,我们就叫这个图,强连通图。
强连通分量strongly connected components):在⼀个有向图G中,有⼀个⼦图,这个⼦图每2个点都满⾜强连通,我们就叫这个⼦图叫做强连通分量[分量::把⼀个向量分解成⼏个⽅向的向量的和,那些⽅向上的向量就叫做该向量(未分解前的向量)的分量]举个简单的栗⼦:⽐如说这个图,在这个图中呢,点1与点2互相都有路径到达对⽅,所以它们强连通.⽽在这个有向图中,点1 2 3组成的这个⼦图,是整个有向图中的强连通分量。
解答树:就是⼀个可以来表达出递归枚举的⽅式的树(图),其实也可以说是递归图。
反正都是⼀个作⽤,⼀个展⽰从“什么都没有做”开始到“所有结求出来”逐步完成的过程。
“过程!”神奇海螺结束tarjan算法,之所以⽤DFS就是因为它将每⼀个强连通分量作为搜索树上的⼀个⼦树。
⽽这个图,就是⼀个完整的搜索树。
为了使这颗搜索树在遇到强连通分量的节点的时候能顺利进⾏。
每个点都有两个参数。
1,DFN[]作为这个点搜索的次序编号(时间戳),简单来说就是第⼏个被搜索到的。
Tarjan算法

Tarjan算法Tarjan算法Tarjan求强连通分量概念:如果两个顶点互相可达,则它们是强连通的。
如果⼀幅有向图中任意两个顶点都是强连通的,则这幅有向图也是强连通的。
强连通分量就是图中具有连通性的⼀个最⼤⼦集,⼀般可以⽤来缩点,即相互到达的⼀堆点可以将他们有⽤的信息统⼀到⼀个点上去。
求解强连通分量的⽅法⼀般会使⽤Tarjan算法。
⾸先我们需要学会dfs树,定义⼏种边:树边,连接dfs树中的⽗节点和⼦节点的边。
横叉边,连接dfs树中的不在⼀个⼦树中的两个节点的边。
前向边,连接dfs树中的⼀个节点连向他的⼦树中深度差⼤于等于2,也就是不直接相连的两点的边。
后向边,连接dfs树中的⼀个节点连向他的祖先的边,⼜叫返祖边。
求解:dfn[i]表⽰i节点的时间戳,low[i]表⽰i节点的所属的强连通分量i的时间戳的最⼩值,也可以说是i或i的⼦树能够追溯到的最早的栈中节点的时间戳。
发现如果在dfs树中出现了后向边说明后向边连接的两点之间的环⼀定是强连通的,但不⼀定是最⼤⼦集。
我们有个性质:如果low[i]⽐dfn[i]⼩,说明他有⼀条连向祖宗的后向边,所以要保留在栈中。
如果当前low[i]等于dfn[i]说明他搜索的栈中没有可以连向他祖宗的边,当前栈中的点⼀定就是low[栈中的点]等于dfn[i]的点,也可以有能连向i的反向边。
有如果树边没有被找到过,则有low[u]=min(low[u],low[v]);也就是⽤v的所能连向的点的最⼩时间戳来更新u。
如果此点已经⼊栈,说明此时这是⼀条回边,因此不能⽤low[v]更新,⽽应该:low[u]=min(low[u],dfn[v]);因为,low[v]可能属于另⼀个编号更⼩的强连通分量⾥,⽽u可以连接到v但v不⼀定与u相连,所以可能u、v并不属于同⼀个强连通分量。
但是第⼀种情况如果low[v]⽐low[u]⼩的话,v⼀定有包括u的强连通分量,Tarjan求割点和桥概念:在⽆向连通图中,双连通分量分为点双和边双,点双为⼀个连通分量删去任意⼀个点都保持连通,边双为删去任意⼀条边都保持连通。
Tarjan详解

Tarjan详解⾸先,tarjan是⼲什么⽤的?在学之前,我就知道⼀个名为“缩点”的模板题要⽤tarjan算法来解决,所以我对这个算法是这样理解的。
把⼀堆点在不影响题⽬的情况下缩成⼀个点,以转化为DAG(有向⽆环图)快速求解。
其实我觉得模板题正⼤⼤体现了tarjan的优势,就拿模板题来讲⼀讲这个算法吧。
思路这题⾮常好的体现了tarjan的优势和⽤武之处。
如果⼀条边和⼀个点能⽆数次重复经过,那么也就是说只要两个点能相互到达,我们就可以把它看做⼀个点。
由于每个点的点权都是正的,那么缩成⼀个点绝对不会影响结果。
正确性很显然,如果你能两个点⼀起拿再回来,那为什么不拿呢?所以说只要把所有的强联通分量缩成⼀个点,然后进⾏拓扑排序dp即可。
代码说起来简单,但是代码如何实现呢?以下参考了《算法竞赛进阶指南》:⾸先从任意⼀个点开始深搜,搜到出度为0的节点停⽌,不重复经过同⼀个点,这样搜完之后将形成的树称为“搜索树”。
还有⼀个“强联通分量”的定义,按我⾃⼰的理解,就是⼀堆点都能通过它们之间的路径相互到达,那么这些点就构成⼀个强联通分量,也就是我们要执⾏缩点的⽬标。
开⼀个栈,来记录节点之间的⽗⼦关系。
dfn表⽰时间戳,第i个被访问的点时间戳就是i,low表⽰以这个点为⼦树的根结点,能访问到的最⼩编号的节点的编号。
由于我们是按搜索树编号的,所以很显然,搜索树上⼀条边的终点时间戳肯定⽐起点⼤。
所以说,如果两点能相互到达,那么肯定会更新这个点的low,所以说就是⼀个强联通分量,⽽且两点中间中间的所有具有⽗⼦关系的点都可以相互到达。
所以说如果⼀个点的low和dfn相等的话,那么它就已经不能和后⾯的点构成强联通分量了,就只能往前找,去靠拢前⾯的点。
void tarjan(int x){low[x]=dfn[x]=++num;sta[++top]=x;ins[x]=1;for(int i=head[x];i;i=Nxt[i]){int y=ver[i];if(!dfn[y]){//没有访问过就继续搜tarjan(y);low[x]=min(low[x],low[y]);//更新low}else{if(ins[y]){//如果有夫⼦关系,那么也更新low[x]=min(low[x],dfn[y]);}}}if(low[x]==dfn[x]){//这个点已经到头了,那么往回找while(1){int y=sta[top];ins[y]=0;//⼀定要出栈,因为它已经跟后⾯的点构不成强联通分量了c[y]=x;top--;if(x!=y){p[x]+=p[y];}else{break;}}}}这样tarjan就差不多了(主要是写给⾃⼰看的)然后再拓扑排序⼀下,简单dp就搞定了完整代码:#include<iostream>#include<cstdio>#include<algorithm>#include<cmath>#include<cstring>#include<vector>#include<queue>#define ll long longusing namespace std;const int N=200005,M=400005;int n,m,tot,top,tc,num,cnt;ll c[N],head[N],edge[M],Nxt[M],ver[M],low[N],dfn[N],sta[N],p[N],w[N],Nc[M],vc[M],hc[N],f[N],in[N],ans;bool ins[N];queue<int> q;void add(int x,int y){ver[++tot]=y;Nxt[tot]=head[x];head[x]=tot;}void add_c(int x,int y){vc[++tc]=y;Nc[tc]=hc[x];hc[x]=tc;}void tarjan(int x){low[x]=dfn[x]=++num;sta[++top]=x;ins[x]=1;for(int i=head[x];i;i=Nxt[i]){ int y=ver[i];if(!dfn[y]){tarjan(y);low[x]=min(low[x],low[y]); }else{if(ins[y]){low[x]=min(low[x],dfn[y]); }}}if(low[x]==dfn[x]){while(1){int y=sta[top];ins[y]=0;c[y]=x;top--;if(x!=y){p[x]+=p[y];}else{break;}}}}void topo(){for(int i=1;i<=n;i++){if(!in[i]&&c[i]==i){q.push(i);f[i]=p[i];// printf("%d\n",f[i]);}}while(!q.empty()){int x=q.front();q.pop();for(int i=hc[x];i;i=Nc[i]){int y=vc[i];in[y]--;f[y]=max(f[y],f[x]+p[y]); if(in[y]==0){q.push(y);}}}for(int i=1;i<=n;i++){ans=max(ans,f[i]);}}int main(){scanf("%d%d",&n,&m);for(int i=1;i<=n;i++){scanf("%lld",&p[i]);}for(int i=1;i<=m;i++){int x,y;scanf("%d%d",&x,&y);add(x,y);}for(int i=1;i<=n;i++){if(!dfn[i]) tarjan(i);}for(int x=1;x<=n;x++){for(int i=head[x];i;i=Nxt[i]){ int y=ver[i];if(c[x]==c[y]) continue;add_c(c[x],c[y]);in[c[y]]++;}}topo();printf("%lld\n",ans);return 0;}例题:思路发现这个题貌似⽐板⼦题还简单,都不⽤缩完点之后拓扑排序,缩完点直接看有⼏个点⼊度为0即可,因为⼊度为0的点不可能通过别的节点到达。
强连通算法--Tarjan个人理解+详解

强连通算法--Tarjan个⼈理解+详解⾸先我们引⼊定义:1、有向图G中,以顶点v为起点的弧的数⽬称为v的出度,记做deg+(v);以顶点v为终点的弧的数⽬称为v的⼊度,记做deg-(v)。
2、如果在有向图G中,有⼀条<u,v>有向道路,则v称为u可达的,或者说,从u可达v。
3、如果有向图G的任意两个顶点都互相可达,则称图 G是强连通图,如果有向图G存在两顶点u和v使得u不能到v,或者v不能到u,则称图G 是强⾮连通图。
4、如果有向图G不是强连通图,他的⼦图G2是强连通图,点v属于G2,任意包含v的强连通⼦图也是G2的⼦图,则乘G2是有向图G的极⼤强连通⼦图,也称强连通分量。
5、什么是强连通?强连通其实就是指图中有两点u,v。
使得能够找到有向路径从u到v并且也能够找到有向路径从v到u,则称u,v是强连通的。
然后我们理解定义:既然我们现在已经了解了什么是强连通,和什么是强连通分量,可能⼤家对于定义还是理解的不透彻,我们不妨引⼊⼀个图加强⼤家对强连通分量和强连通的理解:标注棕⾊线条框框的三个部分就分别是⼀个强连通分量,也就是说,这个图中的强连通分量有3个。
其中我们分析最左边三个点的这部分:其中1能够到达0,0也能够通过经过2的路径到达1.1和0就是强连通的。
其中1能够通过0到达2,2也能够到达1,那么1和2就是强连通的。
.........同理,我们能够看得出来这⼀部分确实是强连通分量,也就是说,强连通分量⾥边的任意两个点,都是互相可达的。
那么如何求强连通分量的个数呢?另外强连通算法能够实现什么⼀些基本操作呢?我们继续详解、接着我们开始接触算法,讨论如何⽤Tarjan算法求强连通分量个数:Tarjan算法,是⼀个基于Dfs的算法(如果⼤家还不知道什么是Dfs,⾃⾏百度学习),假设我们要先从0号节点开始Dfs,我们发现⼀次Dfs 我萌就能遍历整个图(树),⽽且我们发现,在Dfs的过程中,我们深搜到了其他强连通分量中,那么俺们Dfs之后如何判断他喵的哪个和那些节点属于⼀个强连通分量呢?我们⾸先引⼊两个数组:①dfn【】②low【】第⼀个数组dfn我们⽤来标记当前节点在深搜过程中是第⼏个遍历到的点。
Tarjan无向图的割点和桥(割边)全网详解算法笔记通俗易懂

Tarjan⽆向图的割点和桥(割边)全⽹详解算法笔记通俗易懂感谢@ ⼤佬,指出本⽂不够严谨的地⽅,万分感谢!Tarjan⽆向图的割点和桥(割边)导⾔在掌握这个算法前,咱们有⼏个先决条件.DFS搜索DFS序⼀张纸⼀⽀笔认真的⼤脑(滑稽) 认真的⼤脑~~(滑稽)~~如果您都具备了,那么您就是巨佬了,您就可以轻松解决Tarjan算法了.初学算法概念掌握割点概念定义什么的,看上去好烦好烦好烦的,怎么办呢?Acwing⼩剧场开播了,门票⼀枚AC币.现在Acwing推出了⼀款战略游戏,名为Tarjan⽆向图的割点和桥.贪玩Tarjan,介个是泥从未丸过的船新版本.整个游戏,由N个岛屿构成,⽽且有M条航线联络着这些岛屿.我们发现熊熊助教和y总这两个点⾮常重要,是整张地图的核⼼战略要塞.假如说缺少了任意⼀个点,我们发现总会有两个岛屿,不能联系了.因此我们得出了,核⼼战略要塞,就是交通联络点.所以这些点要重要中药保护,避免被破坏,因此我们把这些要重要保护的点,也就是交通联络点,称之为割点.概念定义割点删掉这个点和这个点有关的边,图就不是连通图,分裂成为了多个不相连的⼦图割边同样的有核⼼战略要塞,也就会有黄⾦⽔道.什么是黄⾦⽔道呢?难道是航运量⼤的航道?不不不不,这个概念不⼀样.如果说黄⾦⽔道被破坏了,那么将会有两个和两个以上的岛屿,不能够通航连接了.⽐如说,熊熊助教和y总连接的⼀条航道.还有熊熊助教和song666连接的航道.这就是我们的黄⾦⽔道,也就是战略航道.因此我们给这些战略航道定义为桥(割边).概念定义桥删除这条边后,图就不是连通图,分裂成为多个不相连的⼦图.时间戳其实啊,我们完全可以给这些岛屿们编号.这样便于管理,有利于愉悦⾝⼼健康.因此我们得出了下⾯这张图⽚.我们发现删除了⼀些多余的边,然后每个点多了⼀个学号.其实我们的学号,就是每⼀个节点的时间戳.什么是时间戳,就是每⼀个点的学号.但是这个学号是怎么来的呢?总不能是⼀顿瞎排的吧.其实这个学号,就是我们的DFS序,刚开始我们任意选择⼀个点开始,然后⼀次深度优先搜索,每新搜索到⼀个点后,就给这个点标记⼀个学号.然后来⼀个gif动画看⼀看.因此时间戳的定义我们就知道了.概念定义时间戳dfn[x]表⽰节点x第⼀次被访问的编号.这就是时间戳的概念,其实就是学号编辑的过程.追溯值追溯,追溯,就是寻找⼀个节点,以他为根,可以抵达的最⼩学号.我们设置⼀个⼩概念subtree(x)表⽰搜索树中以x节点为根的⼦树节点集合.⽐如说我们举⼀个例⼦.这些红⾊标记节点,其实也就是熊熊助教的搜索树.因此我们得出.subtree(熊熊助教)=(熊熊助教,song666,秦淮岸,Chicago)那么我们设置⼀下追溯值数组.low[x]定义为以下节点的时间戳的最⼩值.1. subtree(x)中的节点2. 通过1条不在搜索树上的边,能够抵达subtree(x)中的节点.这个第⼀条我们上⾯解释过了,那么第⼆条怎么解释呢,还是⼀样,我们再来⼀个解释gif.判定法则割边判断法则⽆向边(x,y)是桥,当且仅当搜索树上存在x的⼀个⼦节点y,满⾜dfn[x]<low[y]⾸先⼀个公式,很难让⼈理解,我们得有⼀点⼈性化理解.桥是⼲什么的?它是⽤来连接两个个连通块的,没有了桥,就没有连通性,就会出现世外桃源.什么是世外桃源,就是⾃成⼀派,与外⼈⽆往来.我们需要知道追溯值,是什么.就是⼀个节点可以在⾃⼰⼦树和⼦树可以拓展的节点中找到⼀个最⼩的编号.删掉了桥,那么在世外桃源,请问对于任何⼀个节点⽽⾔,他们存在,⼀个可以往外⾯拓展的节点吗?没有,因为他们是世外桃源,不与外⼈有任何连接.于是世外桃源内所有的节点,他们的最⼩追溯值⼀定不会⼩于宗主的编号.咱们要知道,⾃给⾃⾜是很难成功的,总得有⼀个⼈出去买加碘海盐,那么这个⼈就是吃货宗的宗主我们认为宗主就是所有节点中编号最⼩的节点,也就是有可能与外⼈有所连接的节点.换句话说,也就是(x,y)这个桥两端中,在世外桃源内的节点就是宗主y.正经语⾔说⼀说就是.因此当dfn[x]<low[y]的时候1. 我们发现从y节点出发,在不经过(x,y)的前提下,不管⾛哪⼀条边,我们都⽆法抵达x节点,或者⽐x节点更早出现的节点2. 此时我们发现y所在的⼦树似乎形成了⼀个封闭圈,那么(x,y)⾃然也就是桥了.割点判断法则其实和上⾯的判断,只有⼀点修改.若x不是搜索树的根节点,若x节点是割点,那么当且仅当搜索树上存在x的⼀个⼉⼦节点y,满⾜dfn[x]≤low[y]宗主节点,是所有⼈中实⼒最强⼤的,所以肯定是最先学习的.既然如此,那么显然他的dfn,就是代表学习的开始时间,必然就是最⼩的.⽽且割点是⼀个世外桃源和外界的唯⼀通道,所有的⼉⼦节点的dfn都必须⼤于等于它,不可以⼩于它,因此证毕.其实证明和上⾯的正经证明是⼀模⼀样的,只不过多了⼀个等于号罢了.特殊定义:请记住根是不是割点,必须保证有⾄少两个⼉⼦节点,否则不叫作割点.代码解析割边模板#include <bits/stdc++.h>using namespace std;const int N=1e5+20;int head[N],edge[N<<1],Next[N<<1],tot;int dfn[N],low[N],n,m,num;bool bridge[N<<1];void add_edge(int a,int b){edge[++tot]=b;Next[tot]=head[a];head[a]=tot;}void Tarjan(int x,int Edge){dfn[x]=low[x]=++num;//DFS序标记for(int i=head[x]; i; i=Next[i])//访问所有出边{int y=edge[i];//出边if (!dfn[y])//不曾访问过,也就是没有标记,可以认为是⼉⼦节点了{Tarjan(y,i);//访问⼉⼦节点y,并且设置边为当前边low[x]=min(low[x],low[y]);//看看能不能更新,也就是定义中的,subtree(x)中的节点最⼩值为low[x]if (low[y]>dfn[x]) //这就是桥的判定bridge[i]=bridge[i^1]=true;//重边也是桥} else if (i!=(Edge^1))low[x]=min(low[x],dfn[y]);//第⼆类定义,也就是通过1条不在搜索树上的边,能够抵达subtree(x)的节点}}{scanf("%d%d",&n,&m);tot=1;//边集从编号1开始for(int i=1; i<=m; i++){int a,b;scanf("%d%d",&a,&b);add_edge(a,b);add_edge(b,a);}for(int i=1;i<=n;i++)if (!dfn[i])//⼀个⽆向图,可能由多个搜索树构成Tarjan(i,0);for(int i=2;i<=tot;i+=2)//⽆向边不要管,直接跳2格if (bridge[i])printf("%d %d\n",edge[i^1],edge[i]);//桥的左右两端return 0;}割点模板#include <bits/stdc++.h>using namespace std;const int N=1e6+20;int head[N],edge[N<<1],Next[N<<1],tot;int dfn[N],low[N],n,m,num,root,ans;bool cut[N];void add_edge(int a,int b){edge[++tot]=b;Next[tot]=head[a];head[a]=tot;}void Tarjan(int x){dfn[x]=low[x]=++num;//DFS序标记int flag=0;for(int i=head[x]; i; i=Next[i])//访问所有出边{int y=edge[i];//出边if (!dfn[y])//不曾访问过,也就是没有标记,可以认为是⼉⼦节点了{Tarjan(y);//访问⼉⼦节点y,并且设置边为当前边low[x]=min(low[x],low[y]);//看看能不能更新,也就是定义中的,subtree(x)中的节点最⼩值为low[x]if (low[y]>=dfn[x]) //这就是割点的判定{flag++;//割点数量++if (x!=root || flag>1)//不能是根节点,或者说是根节点,但是有⾄少两个⼦树节点是割点cut[x]=true;}}else low[x]=min(low[x],dfn[y]);//第⼆类定义,也就是通过1跳不在搜索树上的边,能够抵达subtree(x)的节点 }}int main(){scanf("%d%d",&n,&m);memset(cut,false,sizeof(cut));for(int i=1; i<=m; i++){int a,b;scanf("%d%d",&a,&b);add_edge(a,b);add_edge(b,a);}for(int i=1; i<=n; i++)if (!dfn[i])//⼀个⽆向图,可能由多个搜索树构成root=i,Tarjan(i);for(int i=1; i<=n; i++) //统计割点个数if (cut[i])ans++;printf("%d\n",ans);for(int i=1; i<=n; i++) //顺序遍历,康康哪些点是割点if (cut[i])printf("%d ",i);return 0;}经典题⽬第⼀题 B城B城有n个城镇,m条双向道路。
图论之 Tarjan及其应用
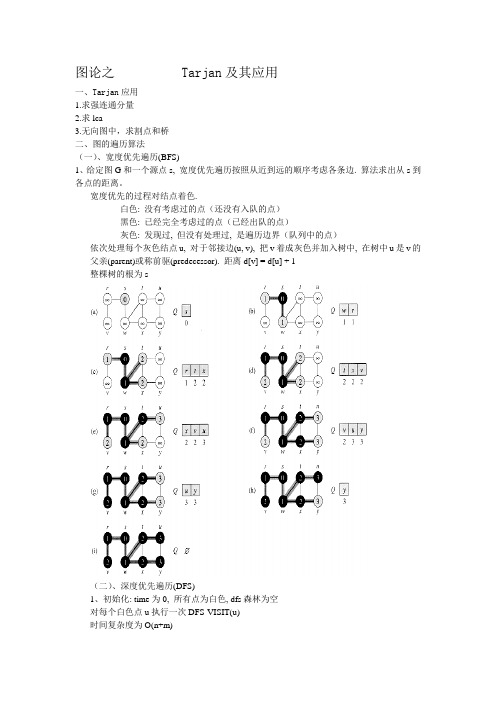
图论之 Tarjan及其应用一、Tarjan应用1.求强连通分量2.求lca3.无向图中,求割点和桥二、图的遍历算法(一)、宽度优先遍历(BFS)1、给定图G和一个源点s, 宽度优先遍历按照从近到远的顺序考虑各条边. 算法求出从s到各点的距离。
宽度优先的过程对结点着色.白色: 没有考虑过的点(还没有入队的点)黑色: 已经完全考虑过的点(已经出队的点)灰色: 发现过, 但没有处理过, 是遍历边界(队列中的点)依次处理每个灰色结点u, 对于邻接边(u, v), 把v着成灰色并加入树中, 在树中u是v的父亲(parent)或称前驱(predecessor). 距离d[v] = d[u] + 1整棵树的根为s(二)、深度优先遍历(DFS)1、初始化: time为0, 所有点为白色, dfs森林为空对每个白色点u执行一次DFS-VISIT(u)时间复杂度为O(n+m)2、伪代码三、DFS树的性质1、括号结构性质对于任意结点对(u, v), 考虑区间[d[u], f[u]]和[d[v], f[v]], 以下三个性质恰有一个成立: 完全分离u的区间完全包含在v的区间内, 则在dfs树上u是v的后代v的区间完全包含在u的区间内, 则在dfs树上v是u的后代2、定理(嵌套区间定理):在DFS森林中v是u的后代当且仅当d[u]<d[v]<f[v]<f[u], 即区间包含关系. 由区间性质立即得到。
四、边的分类1、一条边(u, v)可以按如下规则分类树边(Tree Edges, T): v通过边(u, v)发现后向边(Back Edges, B): u是v的后代前向边(Forward Edges, F): v是u的后代交叉边(Cross Edges, C): 其他边,可以连接同一个DFS树中没有后代关系的两个结点, 也可以连接不同DFS树中的结点。
判断后代关系可以借助定理12、算法当(u, v)第一次被遍历, 考虑v的颜色白色, (u,v)为T边灰色, (u,v)为B边(只有它的祖先是灰色)黑色: (u,v)为F边或C边. 此时需要进一步判断d[u]<d[v]: F边(v是u的后代, 因此为F边)d[u]>d[v]: C边(v早就被发现了, 为另一DFS树中)时间复杂度: O(n+m)定理: 无向图只有T边和B边(易证)3、实现细节if (d[v] == -1) dfs(v); //树边, 递归遍历else if (f[v] == -1) show(“B”); //后向边else if (d[v] > d[u]) show(“F”); // 前向边else show(“C”); // 交叉边注:d(入栈时间戳)和f 数组(出栈时间戳)的初值均为-1, 方便了判断四、强连通图1、在有向图G 中,如果两点互相可达,则称这两个点强连通,如果G 中任意两点互相可达,则称G 是强连通图。
Tarjan算法

Tarjan算法Taijan算法是求有向图强连通分量的算法。
Tarjan 算法主要是在 DFS 的过程中维护了⼀些信息:dfn、low 和⼀个栈。
1. 栈⾥存放当前已经访问过但是没有被归类到任⼀强连通分量的结点。
2. dfn[u] 表⽰ DFS 第⼀次搜索到 u 的次序。
3. Low(u) 记录该点所在的强连通⼦图所在⼦树的根节点的 Dfn 值。
基本思路: 在深度搜索中会搜索到已访问的节点,产⽣环,即连通分量的⼀部分,环与环的并集仍是连通分量。
由于深度搜索总是会回溯,所以将强连通图中最早搜索到的节点认为是根节点,它的dfn 和 low都是最⼩的。
之后会深度搜索⼦树的所有节点,确定所有与回边相关的环,在出现环时,环上的节点的值就会统⼀为环上最⼩的值。
直到回溯到根节点 dfn = low 的标志,输出连通分量,其他节点low相同,但dfn要⽐根节点⼤。
⾄于( u, v )访问到新的节点,在初始化下 v 的 low 值是递增的,但是 v 在进⼊深度搜索后,它返回的值会变化。
当 v 出现在环中被处理了, v 的 low 值会变⼩。
此时 u 也⼀定在环中, v 的low 值变⼩,是由于有⼀条回边连接到的 u 的⽗辈的节点,⽗辈的节点 - 顶点 - u - v - ⽗辈的节点构成了⼀个环。
伪码解析:Tarjan(u){DFN[u]=Low[u]=++Index // 为节点u递增地设定次序编号和Low初值Stack.push(u) // 存放已经访问过但没有被归类到任⼀强连通分量的结点for each (u, v) in E //深度搜索if ( v is not visted ) { Tarjan( v ) Low [ u ] = min( Low[ u ] , Low[ v ] ); // 初始化下 low[ v ] ⽐较⼤,若 low [ v ]变⼩, v 在环中,u 也在环中,且两个环相连通。
}else if (v in S) // 如果节点v还在栈内,出现回边,出现环Low [ u ] = min( Low[ u ], DFN[ v ] )if (DFN[u] == Low[u]) // 如果节点u是强连通分量的根v = S.pop // 将v退栈,print vuntil (u== v)}。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
M Tarjan 算法的总结
tarjan 专题 这是我在博客里整
理的有关tarjan 的内容。
最主要的分为两个板块,有向图和无向图
一、有向图
1 •缩点、强连通分量代码和注释
如果在一个有向图中,任意两个节点可以互相到达,那么这些点和它们之间的边构成的 图叫强连通分量,如果这些边没有边权,等价于一个点,如洛谷P2812校园网络。
如果这 些点有点权,那么它们所缩成的点最大点权等于强连通分量中点权之和,见洛谷P3387缩 点。
对于求强连通分量,我们由tarjan 算法来实现。
首先对每个没有遍历过的点为起点,进 行dfs ,每找到一个新点入栈一次,如果遍历到了已经遍历过的点,说明这个被二次遍历的 点可以通过一个有xy4hs wjyyy O 、tarjan 算法的大纲
厂 有向图 1 •缩点 tarja n< 〔2.强连通分量二> 3.环 树二> 4./ca 无向图2桥/害ij 边二> 5 •边双连通分量 割点二> 6 •点双连通
分量 I -------------------
7缩点
向环回溯到自己。
如果回溯所找到的时间戳小于自己所能回溯找到的最小时间戳(默认为自己的时间戳),那么将自己的回溯时间戳更新到更小。
当dfs的递归回溯到自己时,将自己的回溯时间戳更新到子节点和自己中最小的一个,如果无法更新到比自己更小,说明自己是一个强连通分量的根结点,把栈中所有自己以上的点全部出栈,认为在同一个强连通分量中,根据题目需要进行处理。
如果可以更新到更小,就把自己留在栈里,继续递归。
2 •环
在有向图中,我们一般找的是最小环,用一遍dfs就可以完成。
不需要栈,只需要一个dfn数组。
利用记忆化搜索的技巧,如果遍历到一个被搜过的点,它一定不能更新最小环为更小值,因为它的子树已经被遍历完了。
在遍历过程中,用bfs序给各节点打上时间戳,就可以求出最小环的长度了。
二、无向图
1. 树的最近公共祖先(lea )和树上点的距离
最近公共祖先详解树上距离例题
最近公共祖先(和树上距离)是可以通过倍增在0(NlogN)时间内跳出来的,不过是离线算法。
tarjan相比较更优,不仅是在线算法,而且一遍dfs复杂度只需要0(N)。
用到的技巧有并查集、前缀和等。
在dfs过程中,对于一个子树的根结点,它的所有孩子与它自己的最近公共祖先都是它自己,所以先不把当前祖先更新到子树的根结点的父亲。
等dfs结束后,子树内的询问处理完毕,
其他点与这个点的最近公共祖先就一定不在这个子树里,将当前祖先向上更新一级,放到上面一级去回溯。
这一找祖先的过程当节点关系不是直接父亲时需要用并查集来压缩路径。
树上前缀和就是在dfs过程中存储各个节点到根结点的距离,如果在同一条链上就可以直接相减。
而lea是一定与两个询问点分别和根结点“三点共链”的,因此可以快速求出两点之间的距离。
2. 双连通分・
①点双连通分量、割点:代码解析
在无向图中,对于一个分图,去掉其中任意一个点(及其有关边),其他各点仍然可以两两互达的分图叫做点双连通分量(包括一个点或两个相邻的点),往往处理一些割点问题。
割点就是去掉后可以把一个连通图分为两个互不干扰的连通图。
一张连通图上的所有割点,可以分这张图为多个双连通分量。
割点的求法:特殊情况:对于一个有多孩子的根结点,它是一个割点。
那么去掉这个点可分这棵树为一个森林,而如果只有一个孩子就不是森林了。
其他情况:如果一个点的孩子遍历完后,能回溯到的点不浅于这个点的时间戳(不能是回溯值,因为这个点可能属于另一端的双联通分量,可回溯过去),也就是low[son]>=dfn[x],说明这个点是一个割点,我们可以理解为这个点将它下面的点封锁了。
注意事项:在遍历过程中,双向边是可以访问到父亲的,但是要跳过,不然会乱了顺序。
②边双连通分量、割边/桥
在无向图中,对于一个分图,去掉其中任意一条边,其他各点仍可以两两互达的分图叫边双连通分量。
割边其实和割点是异曲同工的。
因为删去割点,它附近的边也随之失效,就促成了割边。
去掉割边,两侧互不干扰,但不一定为边双连通分量,而是连通图。
割边的求法:没有特殊情况,所有情况和割点一般情况相同,在判断时需要稍作改动。
因为割边两侧的点分属两个不同的区块,所以割边的一端(设为U )不能被另一端(设为V )的孩子遍历到,也就是回溯值不能小于V。
因为我们是在递归过程中判断的,所以对于U , 如果它的一棵子树的根结点的回溯值大于自己的时间戳(同样不能是回溯值),即low[v]>dfn[u]0那么这条连接u,v的边就是一条割边了。
因为割点影响了边,而割边没有影响点,所以割边的两端一定都是割点,而割点所连的边不一定是割边。
3. 缩点例题解析
无向图缩点可以同有向图一致,无向图只要不回溯到直接父亲,dfs序仍然是正确的,和有向图一样进栈找环就可以了。
不过因为无向图单独一个点就是一个双连通分量,所以无向图中的环一般找最大环。
4. 叶子连通块
这是我在做一些ta「jan题时想出来的一个概念,在一个连通图中,当所有割点/割边都删去
(打上标记)时,对于每一个剩下的连通块,将其视作一个点,与割边或割点及其所连 的边构成一个新图,此时可以保证新图是一棵树(环已经全部被缩掉了)0当这个点是叶子 节点时,(叶子节点即入度为1的点),推导到这里来,叶子连通块也就是指只连接一个割 点或一个割边的连通块。
叶子连通块的性质:图中任意一个点或任意一条边被删掉,图中剩下的所有点都可以通 过某种方式跑到叶子连通块处。
这样就为我们求“维修、坍塌”类问题建模提供了方便。
只要 解决所有叶子连通块的需求,其他所有点的需求就迎刃而解了。
所有的原因是,一旦某个叶 子连通块被单独分开,它也要解决自己的需求。
例题1解析例题2解析
各种算法都是同类算法中很优秀的算法,其中有一些异同的区分。
• 有向图、无向图都可以求环 • 有向图、无向图都可以缩点 • 缩点和求强/双连通分量时需要一个栈来存储;割点,割边则不用 • 割点去掉的是点和有关边,而割边只去掉了边。
总结。
